Novel Hybrid Processing Techniques for Wideband HF Signals Impaired by Ionospheric Propagation

Abstract

In this paper, hybrid space–time–polarization schemes for processing high-frequency (HF) radio signals transmitted through the ionospheric layers are proposed. Ionospheric radio wave propagation is characterized by several impairments, including attenuation, scintillation, dispersion, and Faraday rotation. The use of hybrid schemes combining spatial digital processing and a single-input multiple-output (SIMO) scheme based on the spatial and polarization principles is proposed. The simulation is based on a preliminary estimate of signal attenuation and spatial coordinates based on ray tracing at a distance of 1000 km between the transmitter and the receiving digital antenna array. Additionally, the bit error rates and data capacity are obtained for various configurations of hybrid spatial and polarizing types of the proposed architectures. In addition, an algorithm for modeling a broadband HF signal in the ionosphere based on the inverse discrete Fourier transform (IDFT) and the Watterson narrowband model is proposed. Schemes for processing the wideband orthogonal frequency division multiplexing (OFDM) signals after passing through the ionosphere layers are represented as well. Results indicate that the optimal configuration employs hybrid processing utilizing ordinary (O) and extraordinary (X) wave polarization, combined with spatial digital processing in a SIMO architecture.

1. Introduction

High-frequency electromagnetic wireless communication systems have undergone extensive recent development due to the fact that this type of transmission is cheaper than satellite communications [1,2]. However, the shortwave range has a number of features that make it difficult to achieve enhanced throughput and link robustness for consumer telecommunications devices. Such negative factors include high attenuation; the presence of many radio waves, the sources of which are both civilian and special services; and signal fading due to fluctuations in the state of the ionosphere [3].

A hybrid digital antenna array architecture can be considered a promising and currently relevant device due to its ability to improve signal integrity under harsh operational conditions, which are ionospheric channels. Conventionally, hybrid beamforming splits processing between analog (RF) and digital (baseband) domains to efficiently manage large antenna arrays, especially at millimeter-wave (mmWave) frequencies [4]; that is, currently, the connection of analog preliminary beamforming and subsequent digital processing with multiple antennas (MIMO) is used [5]. It has been shown that HF skywave communication systems with the MIMO configuration allow a capacity improvement to be obtained [6].

In addition, there is a class of antenna arrays combining polarization for processing with multiple antennas. The polarization diversity increases channel capacity, improves diversity, and optimizes wireless communication performance by using orthogonally polarized antennas (e.g., vertical and horizontal or left-hand (LHCP) and right-hand (RHCP) circular polarization) [7]. It has also been shown that an MIMO system using complementary circular polarizations reduces correlation and increases capacity [8].

In addition, it is known that directional antennas can enhance MIMO performance by focusing radiation in specific directions, improving signal strength, reducing interference, and increasing spatial multiplexing gains [9]. Further development of this technique can be the use of digital beam control [10]. The main fundamental difference between a proposed scheme that combines digital beamforming and SIMO and a hybrid one is that classical hybrid schemes combine analog beamforming and MIMO to reduce the computational load in the millimeter range. The suggested processing scheme is based entirely on digital processing to gain the desired signal, suppress powerful jammers, and mitigate signal fading after transmission through the ionospheric layers.

However, their joint applicability and a comprehensive analysis of their combined utility in the shortwave band have not been extensively investigated. Therefore, this paper proposes a hybrid scheme for processing HF signals based on digital preliminary beamforming to suppress interference and amplify desired signals with subsequent processing based on diversity by spatial or polarization feature. The use of the hybrid architectures will allow preliminary improvement of the signal/interference + noise ratio (SINR) with subsequent decoding to combat fading occurring in the HF channel. The results of the paper are presented based on modeling utilizing the narrowband Watterson model.

In addition, the possibility of modeling wideband HF signals after passing through the ionosphere over long distances has not been sufficiently studied. Several variations have been proposed [11,12], which possess limited spectral expansion. In this paper, an algorithm for modeling a wideband OFDM signal is proposed, which is based on the narrowband Watterson model. The simulation algorithm is used to process each subcarrier with subsequent combining in the time domain by means of the inverse discrete Fourier transform. This algorithm is supposed to be used for the hybrid processing of radio signals.

The key characteristic of contemporary techniques is that the ionospheric channel is viewed only from one perspective, i.e., either a channel model (such as MIMO) or solely using beamforming [13]. Thus, there is no solution for the transmission of telecommunication information through the ionosphere over long distances. The presented work offers the configuration of an antenna array for amplification of the desired signal, suppression of powerful interference, and fading mitigation, which will provide broadband transmission in the 3–30 MHz range.

The paper is organized as follows. Section 2 describes a narrowband model based on generally accepted relationships suitable for signal processing using antenna arrays. Section 3 and Section 4 are devoted to the description of the proposed design for processing HF signals after passing through the ionosphere and the modeling results, respectively. Section 5 describes the proposed easy-to-implement and understand algorithm for modeling a wideband HF OFDM signal after passing through the ionosphere. Furthermore, extended hybrid signal processing architectures are described, and bit error rate performance is evaluated.

2. HF Channel Model

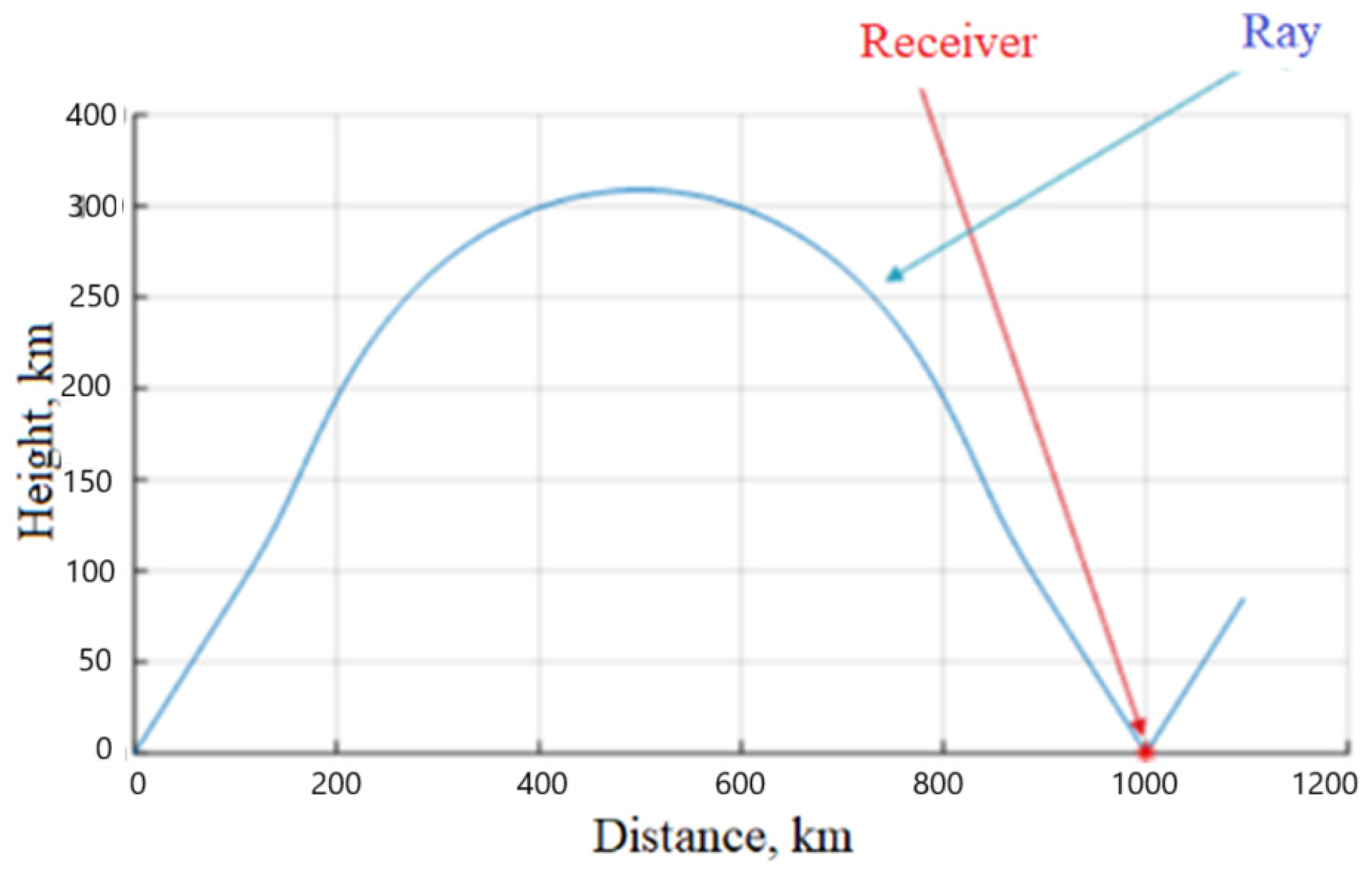
2.1. Raytracing

An analysis of high-frequency (HF) signal propagation through the ionosphere is presented. A two-dimensional isotropic model depending only on the altitude of the ionosphere is considered as follows [14,15]:

$$n=1-{\displaystyle \frac{f_p^2}{2f^2}}\pm {\displaystyle \frac{f_p^2{f}_g\cos \theta }{2f^3}}-{\displaystyle \frac{f_p^2}{4f^4}}\left[{\displaystyle \frac{f_p^2}{2}}+f_g^2\left(1+{\cos }^2\theta \right)\right],$$

(1)

$$f_p^2={\displaystyle \frac{N_e{e}^2}{4{\pi }^2{\epsilon }_0{m}_e}};f_g={\displaystyle \frac{eB}{2\pi m_e}},$$

(2)

where e is the electron charge, m_e is the electron mass, ε₀ is the permittivity of free space, and N_e is the electron concentration profile. The wave with the upper (+) sign in Equation (1) corresponds to the “O-wave” and is left-hand circularly polarized, whereas the wave related to the lower (−) sign corresponds to the “X-wave” and is right-hand circularly polarized [15,16].

Next, it is necessary to estimate quantities such as the signal’s attenuation due to ionospheric propagation and its direction of arrival, defined by the elevation angle, using the model, which is shown in Figure 1. A ray tracing algorithm based on the Hamilton expression is utilized in this paper in order to simulate the propagation of HF radio rays in the ionosphere [17]:

$$H\left(x,y,h,t,k_x,k_y,k_h,\omega \right)=\Re \left\{{\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{c^2}{{\omega }^2}}\left(k_x^2+k_y^2+k_h^2\right)-n^2\right]\right\},$$

(3)

where x and y are the ray coordinates; h is the height; k_x, k_y, and k_h are components of the wave number along the coordinates x, y, and h; c is the speed of light; and ω is the cyclic frequency.

2.2. Transmission Losses

In this section, the magnitude of signal attenuation resulting from ionospheric propagation is evaluated. First, the magnitude of the free space losses is determined as follows:

$$L_{pl}=20\lg \left({\displaystyle \frac{4\pi r}{\lambda }}\right),$$

(4)

where r is the ray path length, and λ is the wavelength.

The beam divergence is defined as follows [18]:

$$L_{div}={\displaystyle \frac{1}{\sqrt{r}}},$$

(5)

An important factor in the attenuation of radio waves is the absorption of the signal by the ionosphere itself, according to the following expression [19]:

$$L_a=-8.68{\displaystyle \int \kappa ds},$$

(6)

where κ is the imaginary part of a complex refractive index and depends on N_e.

Thus, the overall losses when passing through the layers of the ionosphere are determined as follows:

$$L(\mathsf{\partial }Б)=L_{pl}+L_{div}+L_a,$$

(7)

Therefore, knowing the transmitter power (P_t), the gain of the transmitting antenna (G_t), and the electron concentration of the ionosphere, it is possible to determine the magnitude of the field strength or power (P_r) at the receiving point located at a given distance.

$$P_r\left(dBm\right)=P_t+G_t-\left(L_{pl}+L_{div}+L_a\right),$$

(8)

The obtained values (4)–(8) based on ray tracing (1) are used to estimate the signal level at the receiving antenna array. Next, the following algorithm models signal amplitude fluctuations over time.

2.3. Watterson Model for Antenna Array

The Watterson model has found wide application for modeling a narrowband HF signal no wider than 12 kHz over a time interval of no more than 10 min [20]. This model assumes that the signal experiences fading with the Rayleigh distribution. In addition, it takes into account the fact that the electromagnetic wave experiences magneto-ion splitting into ordinary and extraordinary. Thus, the expression for the signal is as follows:

$$G_i\left(t\right)=G_{io}\left(t\right)e^{j2\pi f_{io}t}+G_{ix}\left(t\right)e^{j2\pi f_{ix}t},$$

(9)

where the indices “o” and “x” denote the ordinary and extraordinary waves, Gi is a complex Gaussian ergodic random process, and f is the magnitude of the frequency shift.

This model is improved to apply it to digital hybrid signal processing and is shown in Figure 1.

From Figure 1, it can be seen that the difference in path between the ordinary and extraordinary modes appears after magneto-ion splitting so that angles-of-arrival at the antenna array in azimuth and elevation, as well as the total attenuation, are taken into account for each wave separately. These additional parameters are determined at the ray tracing simulation according to the expression (3) at the receiving point. In addition, noise is taken into account, as is interference.

Thus, the HF signal at the output of an arbitrary antenna array after passing through the ionosphere will be determined by the following parameters:

$$x\left(t\right)\sim {\displaystyle \frac{1}{L}},G_i\left(t\right),\tau ,a\left(\varphi ,\theta \right),n(t),$$

(10)

i.e., attenuation L; fading Gi; the antenna array steering vector a(φ, θ), derived from the signal coordinates in azimuth θ and elevation angle φ; and other parameters, including the delay time of the beams O and X as well as noise.

The ray tracing and channel modeling in this work are based on a two-dimensional (2D) isotropic ionospheric model, which assumes horizontal homogeneity. This simplification was chosen to establish a clear baseline and manage computational complexity for a wide parameter study. It has limitations in determining azimuth coordinates, as well as additional transmission paths that would impact the DOA estimation and the performance of the spatial diversity schemes. However, as a starting point, this slight simplification can be compensated for by a wide parameter study.

3. Hybrid SIMO/Beamforming

3.1. Hybrid MIMO/Beamforming Polarization Scheme

Thus, it can be summarized that the propagation of radio signals in the ionosphere experiences the following problems: high attenuation; Rayleigh fading; magneto-ion splitting; spatially oriented interference, the power of which can greatly exceed the power of the desired signal; multipath propagation due to inhomogeneities in the layers of the ionosphere; and various electron concentrations at different altitudes. A hybrid scheme is proposed for the reception of long-distance telecommunication tasks using HF signals.

The hybrid scheme shown in Figure 2 is proposed based on the following relationship, which determines the capacity for an arbitrary channel over a given bandwidth (BW) and at a particular signal-to-interference + noise ratio [21]:

$$C=\log \left[\det \left(I_{N_R}+{\displaystyle \frac{SINR}{N_T}}H{H}^H\right)\right],$$

(11)

where N_T is the number of transmit antennas, N_R is the number of receive antennas, I_NR is the N_R × N_R identity matrix, and H is the N_R × N_T channel matrix. SINR is averaged over N_R receiving antennas and expressed in a linear scale.

From expression (11), it is clear that the capacity is determined by the channel matrix H, as well as the SINR value for a given number of receiving and transmitting antennas. In the case of ionospheric propagation, the number of antennas is limited by the occupied area and their physical dimensions. In addition, since the propagation of signals in the HF range is not regulated, the total interference power can be many times greater than the desired signal power due to the significant attenuation value.

Therefore, at the first stage of the architecture in Figure 2, digital beamforming is performed to increase the SINR before SIMO demodulation. In this case, there is an antenna array of an arbitrary number of elements, each of which has an element tuned to RHCP and an antenna with LHCP polarization. An example is “crossed dipole”. The number of such antenna elements for DOA estimation + digital beamforming is designated as $N_R^{BF}$, the distance between which is 0.5 λ. Thus, polarization diversity is realized here. In this case, N_R = 2 for subsequent SIMO demodulation. Therefore, the proposed scheme utilizes two antenna arrays with controlled maximums and zeros for subsequent combating of fading channels G_iO(t) and G_iX(t) using polarization SIMO.

The complex vectors of signals at the output of antenna elements corresponding to RHCP and LHCP polarizations are described by the following expressions for an arbitrary number of signals and interferences:

$$\begin{array}{r}{x}_O\left(t\right)={\displaystyle \sum _{i=0}^{S-1}\left[\left(a({\phi }_{iO},{\theta }_{iO})h_{iO}+a({\phi }_{iX},{\theta }_{iX}){\rho }_{1X}{h}_{iX}\right)\sqrt{0.5P_{it}}{s}_i\left(t\right)G_{it}\right]}\dots \\ +n_O(t)\end{array},$$

(12)

$$\begin{array}{r}{x}_X\left(t\right)={\displaystyle \sum _{i=0}^{S-1}\left[\left(a({\phi }_{iO},{\theta }_{iO}){\rho }_{iO}{h}_{iO}+a({\phi }_{iX},{\theta }_{iX})h_{iX}\right)\sqrt{0.5P_{it}}{s}_i\left(t\right)G_{it}\right]}\dots \\ +n_X(t)\end{array},$$

(13)

where S is the number of signal sources; $x\left(t\right)$ is the vector of dimension 1 × N, which describes the signals at the output of the antenna array; s is a signal; $\overrightarrow{n}\left(t\right)={\left[n_1(t),\dots ,n_N(t)\right]}^T$ is the noise vector; a(φ, θ) is the steering vector; ρ_O and ρ_X are represented by the ratio of cross-polarization components for ordinary and extraordinary waves, respectively; and $h=0.5{\displaystyle \frac{G\left(t\right)e^{j2\pi ft}{e}^{j2\pi f\tau }}{L}}$. The coefficient “0” corresponds to the desired signal, and the rest are spatial interferences. The amplitude and phase distribution vector for the circular receiving antenna array, which is used further during the simulation, is defined as follows:

$$a\left(\phi ,\theta ,\omega \right)=\left[\begin{array}{c}g\left(\phi ,\theta ,\omega \right)e^{j\left[-kR\cos \left(\theta -{\gamma }_0\right)\sin \left(\phi \right)\right]}\\ g\left(\phi ,\theta ,\omega \right)e^{j\left[-kR\cos \left(\theta -{\gamma }_1\right)\sin \left(\phi \right)\right]}\\ \dots \\ g\left(\phi ,\theta ,\omega \right)e^{j\left[-kR\cos \left(\theta -{\gamma }_{N-1}\right)\sin \left(\phi \right)\right]}\end{array}\right],$$

(14)

where g is the gain of an antenna element, R is the radius, k is the wavenumber, and γ is the coordinate of an antenna element.

The values of the coordinates θ_O, φ_O, θ_X, φ_X, delays τ_O and τ_X, and attenuations L_O and L_X are determined after ray tracing (3) for the specified ionosphere parameters (1). On the transmitter side, the power P_i and antenna gain G_i are specified based on the requirements of the researcher or developer. The same can be said about the receiving side, i.e., the geometry of the antenna array, as well as the shape of the directional pattern of the elements. The value of the cross-polarization level for antennas receiving O- and X-waves can be found for each specific antenna based on a known expression, such as a crossed dipole, or through the method of moments [22,23].

At the first stage, the MUSIC algorithm is used to estimate the spatial coordinates [24]:

$$P_{O|X MUSIC}(\phi ,\theta )={\displaystyle \frac{1}{{\overrightarrow{a}}_{O|X}^H(\phi ,\theta )E_{O|X N}{E}_{O|X}{}_N{}^H\overrightarrow{a}_{O|X}(\phi ,\theta )}},$$

(15)

From here and further, the index $O|X$ denotes the corresponding polarization, and E_N is the noise subspace matrix. Then, the minimum variance distortionless response (MVDR) algorithm is used as a beamformer [25]:

$${\overrightarrow{w}}_{O|X}={\displaystyle \frac{{\widehat{R}}_{O|X}^{-1}{\overrightarrow{a}}_{O|X}({\theta }_0,{\varphi }_0)}{{\overrightarrow{a}}_{O|X}{({\theta }_0,{\varphi }_0)}^H{\widehat{R}}_{O|X}^{-1}{\overrightarrow{a}}_{O|X}({\theta }_0,{\varphi }_0)}},$$

(16)

$${\widehat{R}}_{O|X}={\displaystyle \sum _{i=1}^N{x}_{O|X}\left(n\right)}{x}_{O|X}^H\left(n\right),$$

(17)

The desired source location is estimated by finding the peaks of the MUSIC spatial spectrum given by (15). Then, the signal after spatial processing of O- and X-waves is as follows:

$$y_{O|X}\left(n\right)={\overrightarrow{w}}_{O|X}^H{\overrightarrow{x}}_{O|X}\left(n\right),$$

(18)

After suppressing noise and interference, as well as steering the beam toward the desired signal, it is necessary to estimate the spatial coefficients:

$${\widehat{h}}_{O|X}={\overrightarrow{y}}_{O|X}\cdot code,$$

(19)

where code designates the training sequence.

At the final stage, the SIMO demodulation procedure named maximum ratio combining (MRC) is performed [26]:

$$\widehat{s}={\displaystyle \frac{\overrightarrow{\widehat{h}}{}^H\overrightarrow{y}}{{\overrightarrow{\widehat{h}}}^H\overrightarrow{\widehat{h}}}},$$

(20)

where $\overrightarrow{\widehat{h}}=\left[\begin{array}{c}{\widehat{h}}_O\\ {\widehat{h}}_X\end{array}\right]$.

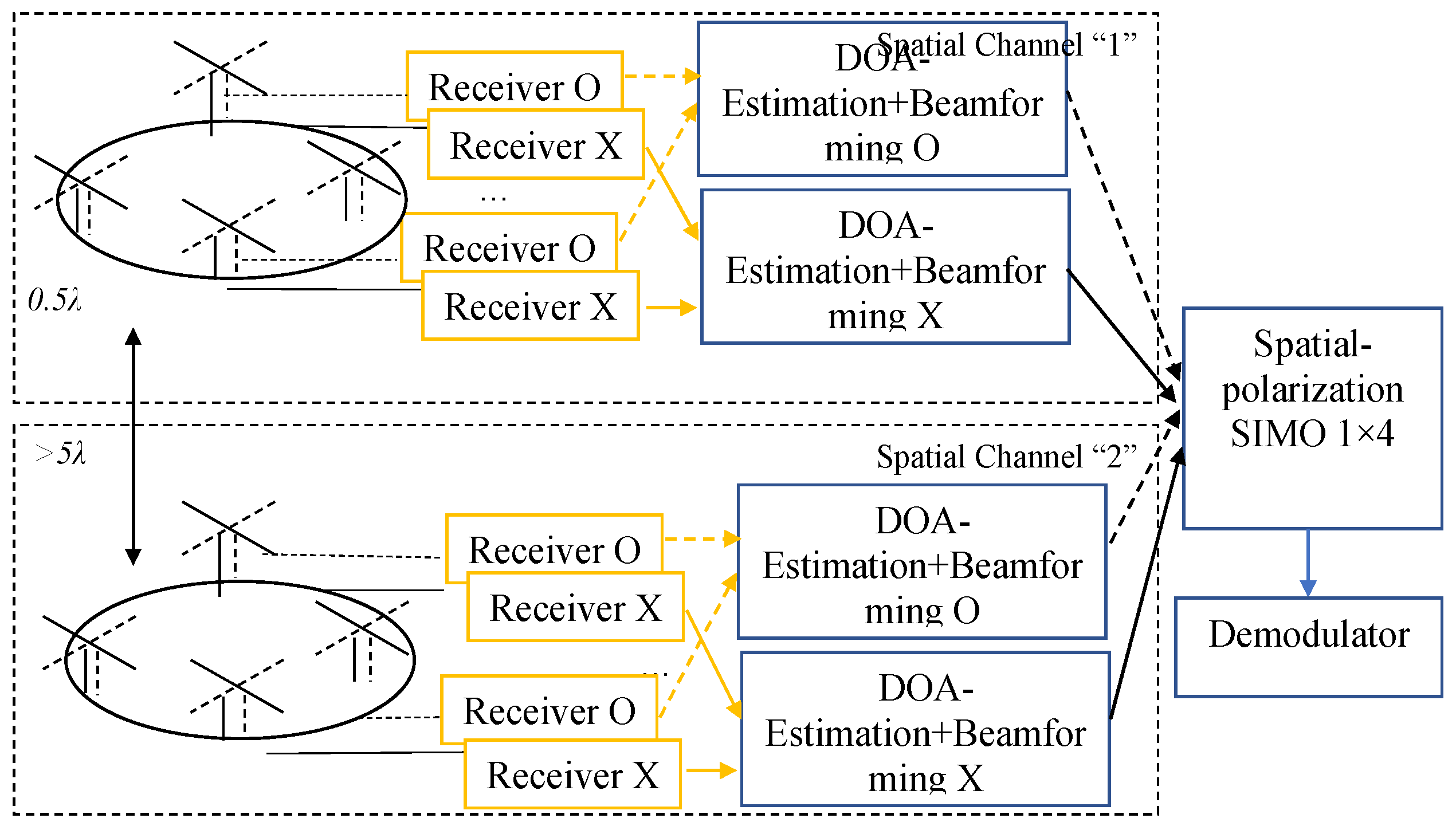
3.2. Hybrid SIMO/Beamforming Spatial Scheme

Consider a hybrid scheme that combines both digital beamforming and spatial multiplexing technology. This scheme is shown in Figure 3.

The proposed scheme consists of two spaced channels. Each channel uses preliminary beamforming and then a 1 × 2 SIMO scheme based on spatial diversity. The antennas receive a sum of the ordinary and extraordinary waves. The complex vector of signals at the output of antenna elements is described by the following expression [19]:

$$\begin{array}{r}{x}_m\left(t\right)={\displaystyle \sum _{i=0}^{S-1}\left[\left(a({\phi }_{m\_iO},{\theta }_{m\_iO})h_{m\_iO}+a({\phi }_{m\_iX},{\theta }_{m\_iX})h_{m\_iX}\right)\sqrt{0.5P_{it}}{s}_i\left(t\right)G_{it}\right]}\dots \\ +n_m(t),m=1\dots M\end{array},$$

(21)

where m is the spatial channel number, and $h_{m\_i|\left(O,X\right)}={\displaystyle \frac{G_{m\_i|\left(O,X\right)}\left(t\right)e^{j2\pi f_{m\_i|\left(O,X\right)}t}{e}^{j2\pi f_{m\_i|\left(O,X\right)}\tau }}{2L_{m\_i|\left(O,X\right)}}}$ for the corresponding waves and spatial processing channels.

The main difference is that in this modification, the receiving antennas combine signals with RHCP and LHCP polarization. In other words, receiving spatial diversity is implemented. In addition, preliminary digital beamforming is performed in each of the channels. It is worth saying that this scheme supports the combination of more than two spatial processors, although Figure 3 shows two channels (the upper and lower are separated physically).

In vector–matrix form, the expression (21) can be rewritten as follows:

$$x_m\left(t\right)=A_{m\_O}{A}_{m\_X}{H}_m\overrightarrow{s}+n_m(t),m=1\dots M,$$

(22)

where A_{m_O} and A_{m_X} are the matrices of the m-th antenna array of dimension $N_R^{BF}$ × S, and $H_m=\left[\begin{array}{ccc}\begin{array}{c}{h}_{m\_0O}\\ h_{m\_0X}\end{array}& \dots & \begin{array}{c}{h}_{m\_\left(S-1\right)O}\\ h_{m\_\left(S-1\right)X}\end{array}\end{array}\right]$ is the channel matrix.

Next, the digital beamforming is performed for each spatial channel. At the final stage, the streams are combined in the SIMO block for multiplexing and fading mitigation. Thus, this architecture uses two or more physically separated antenna arrays, each receiving a combined O+X wave. The digital beamforming is performed independently on each array. The beamformed outputs from the separate spatial locations are then combined using MRC. It can be concluded that this scheme exploits spatial diversity to obtain independent fading paths.

3.3. Hybrid MIMO/BEAMFORMING Spatial–Polarization Scheme

This chapter proposes a hybrid scheme integrating digital beamforming with spatial–polarization multiplexing, which is depicted in Figure 4.

The hybrid scheme in Figure 4 combines the two previous approaches. There is diversity both in space and polarization. Digital beamforming is performed at each stage. Thus, there are four spatial correlation channels that form a 1 × 4 SIMO. Let us rewrite the vector for an arbitrary number of signals at the output of the antenna arrays for the spatial–polarization scheme:

$$\begin{array}{r}{x}_{m\_\left(O|X\right)}\left(t\right)={\displaystyle \sum _{i=0}^{S-1}\left[\left(\begin{array}{l}a({\phi }_{m\_iO},{\theta }_{m\_ia}){\rho }_O{h}_{m\_iO}+\\ a({\phi }_{m\_iX},{\theta }_{m\_ib}){\rho }_X{h}_{m\_iX}\end{array}\right)\sqrt{0.5P_{it}}{s}_i\left(t\right)G_{it}\right]}\dots \\ +n_m(t),m=1\dots M\end{array},$$

(23)

where $h_{m\_i|\left(O,X\right)}={\displaystyle \frac{G_{m\_i|\left(O,X\right)}\left(t\right)e^{j2\pi f_{l\_i|\left(O,X\right)}t}{e}^{j2\pi f_{l\_i|\left(O,X\right)}\tau }}{L_{m\_i|\left(O,X\right)}}}$ for the corresponding waves and spatial processing channels, ρ_(O|X) are the cross-polarization coefficients for RHCP and LHCP antennas, respectively. In vector–matrix form, Equation (23) can be rewritten as follows:

$$x_m\left(t\right)=A_{m\_O}{A}_{l\_X}\left({\Gamma }_m\odot H_m\right)\overrightarrow{s}+n_m(t),m=1\dots M,$$

(24)

where A_{m_O} and A_{m_X}, the channel matrices in this case, are determined as $H={\Gamma }_m\odot H_m$, and ${\Gamma }_m=\left[\begin{array}{cc}{\rho }_O& {\rho }_X\\ {\rho }_X& {\rho }_O\end{array}\right]$ is the matrix of the cross-polarization coefficients for the m-th array.

This is the most comprehensive architecture, combining both previous approaches. It uses multiple, physically separated antenna arrays, each equipped with dual-polarized elements. The digital beamforming is performed on each sub-array, and the resulting four (or more) independent streams—representing both spatial and polarization diversity—are combined using a higher-order MRC. This scheme maximizes diversity gain by exploiting both spatial and polarization domains.

Moreover, the proposed hybrid schemes can be used not only for the HF band but also for others if appropriate antenna elements are used (for example, [27,28]). It is only necessary to know their radiation patterns exactly.

4. Simulations

In this chapter, electromagnetic rays in the layers of the ionosphere are modeled, the mathematical description of which is given in (1) and (2). An analysis of ionospheric propagation based on the ray tracing is initially conducted. The central frequency of the wave is 12 MHz. The distance between the transmitter and the receiving hybrid antenna array is 1000 km. The ionosphere model is depicted in Figure 5 [29].

Further, in Figure 6, the ordinary and extraordinary rays that passed through the ionosphere model in Figure 5 are shown using (1) and (2) and the “+” and “−” signs, respectively.

It can be seen from Figure 6 that the “O” and “X” waves traverse distinct paths, resulting in a differential path delay. First, it is necessary to find the rays that fall into the antenna array aperture. To solve this problem, this work uses an enumeration algorithm, i.e., selecting that (or those) ray(s) from all possible ones that satisfy a certain criterion, i.e., less than λ in our case. The location of the ray within the wavelength of the vertical coordinate of the digital antenna array is the acceptance criterion. An example of such a situation is depicted in Figure 7.

After the beam(s) have been found, it is necessary to assess their mutual phases and amplitudes at the antenna elements in accordance with the geometry of the antenna array, the difference in the total propagation distance, and the path loss. During the simulation, it was found that the delay between the rays “O” and “X” is less than 1 μs. The time delay was calculated in this case based on the obtained value of the path difference in the rays as follows:

$$\tau ={\displaystyle \frac{\Delta d}{c}}$$

(25)

where Δd is the path difference between the rays “O” and “X”.

The delay τ is used in the expressions in Section 2 and Section 3. The value corresponds to the quiet condition [30]. The attenuation value under the given conditions is 120 dB, according to (4)–(8). In addition, from the simulation results in Figure 6 and Figure 7, it was found that the waves arrive at the antenna array aperture at an elevation angle of about 85° on average [31]. The signal vector at the output of the circular antenna array, taking into account the channel matrix, is described in the previous section. A circular configuration is used as a receiving antenna array. Hybrid signal processing is performed as described in the previous section.

For subsequent SIMO demodulation, it is necessary to estimate the channel state vector h. The following frame structure is used in this work, as shown in Figure 8.

As can be seen from Figure 8, the frame consists of a 32-bit pilot sequence, followed by the data. The payload is 192 bits. The pilot sequence duration was chosen based on preliminary empirical research. A shorter sequence does not allow the channel to be estimated under high attenuation conditions, and a longer sequence will be distorted by a bigger change in the ionosphere state.

Thus, the final modeling algorithm looks as follows (Figure 9).

At the preliminary stage, the ionospheric parameters, the distance between the transmitter and the receiving antenna array, the attenuation, and the time delay between the ordinary and extraordinary waves are estimated. The main part consists of setting the vectors h, a, and x described in the previous section. At the final stage, the spatial coordinates are estimated, followed by the channel state estimation and SIMO demodulation. The implementation of the proposed hybrid processing is based on the following three approaches: polarization, spatial, and spatial–polarization.

The following parameters are selected for simulation. The signal power at the transmitter is 10 kW, and the average delay between the “O” and “X” waves is set as 1 μs. In addition, the level of the cross-polarization coefficient between the RHCP and LHCP antennas ρ is set to −20 dB. The attenuation varies from 168 dB to −102 dB on average. In addition, the elevation angle φ is changed uniformly within the range from 80° to 90°, and the azimuth coordinate θ is randomized by the Monte Carlo method. The signal modulation is phase-shift keying (QPSK).

Further, in the figures, the graphs of the estimated values of the bit error rates based on the simulations are represented. The following designations are adopted: “DAA”—digital beamforming, “DAA+SIMO”—sequential processing of beamforming and SIMO with the corresponding scheme, “PAA”—phased beamforming, and “PAA+SIMO”—phasing and SIMO. In addition, this work compares single pure schemes, such as only DAA, only PAA, and only SIMO.

Figure 10 indicates that under ionospheric conditions, a single desired signal propagation results in several key conclusions. The best results in terms of BER are obtained by hybrid schemes with digital or phased beamforming schemes, followed by SIMO at high signal attenuations, i.e., at extreme distances between stations. If the signal-to-noise ratio reaches high values, or in the case under consideration, attenuation is less than 134 dB, SIMO schemes using all available antennas, i.e., 1 × 16 for polarization and spatial schemes or 1 × 32 spatial–polarization, give the lowest bit error value. This is due to the fact that when using beamforming or phasing, the SNR is first increased, after which SIMO decoding is performed.

In the case of polarization and spatial–polarization schemes (Figure 10a,c), only beamforming or phasing does not allow a maximum to be formed in the direction of the desired signal. This is due to the fact that an erroneous coordinate estimation occurs, as the polarization signals are highly correlated. Therefore, subsequent SIMO decoding is necessary.

In general, the spatial–polarization hybrid processing scheme allows the lowest value of the bit error rate to be obtained in the case of a single desired signal. For example, the spatial–polarization hybrid scheme is 0.027, spatial is 0.044, and polarization is 0.053, with an attenuation of 134 dB.

Next, the analysis incorporates a strong interferer at 10 dB above the desired signal power. The interference signal is also simulated using the model in Figure 1.

Figure 11 demonstrates that the hybrid schemes incorporating digital beamforming with subsequent SIMO equalization achieve the lowest bit error rate. Only digital beamforming allows the interference to be suppressed in the case of the spatial diversity scheme (Figure 11b), but it does not allow getting rid of HF signal fading. In addition, highly correlated polarization components (Figure 11a,c) do not allow interference suppression and signal amplification due to the fact that the rank of the correlation matrix is reduced. The SIMO configuration mitigates fading through diversity schemes but provides no inherent interference suppression capability. In this case, due to the low SINR, the bit error rate does not fall below a certain limit of about 0.3. The hybrid phased scheme and SIMO also do not allow the BER to be reduced. The reason for this is that the phased antenna array is tuned to a more powerful interference, as shown below in Figure 12.

In general, it can be said that the spatial–polarization hybrid scheme allows the lowest error values to be obtained. However, the results are comparable with the spatial scheme (Figure 11b). For example, the spatial–polarization hybrid scheme is 0.052, spatial is 0.056, and polarization is 0.075, with attenuation of 134 dB in the case of a signal and interference. The small differences between spatial and spatial–polarization schemes can be explained by the fact that the spatial diversity has a more significant effect than the correlation coefficient between the RHCP and LHCP antennas, which is set to −20 dB.

Next, the capacity Equation (11), depending on the configuration of hybrid schemes, is considered.

It is evident from Figure 13 that in order to increase the capacity in the ionospheric channel, it is necessary to use a hybrid beamforming scheme with subsequent SIMO decoding. The polarization scheme has the highest capacity, which shows the lowest error values. At the same time, the spatial–polarization hybrid scheme yields superior performance compared to the spatial-only scheme due to the higher-order 1 × 4 versus 1 × 2, respectively. These results are consistent with the conclusion presented in [29], which states that more spatial diversity (e.g., using multiple antennas for redundancy) improves BER but reduces capacity. Conversely, more spatial multiplexing (e.g., transmitting independent streams) increases capacity but may worsen BER.

5. Wideband Model of Propagation in the Ionosphere

In this section, a model of propagation and spatiotemporal architecture of processing of wideband HF signals after passing through the ionosphere is proposed. The block diagram in Figure 14 illustrates an HF communication system model employing OFDM modulation. The main idea of the proposed simulation algorithm is that each subcarrier experiences amplitude and phase fluctuations over time.

The input data stream is split into multiple parallel streams containing both the payload and the training sequence for each subcarrier. The multiple parallel streams are then passed through the modified Watterson channels (Figure 1) that model both the ordinary and extraordinary waves on each subcarrier. The physical meaning is that it simulates the changes in the state of the electron concentration at different frequencies. The IDFT is then calculated for each time sample, after which the summation is fulfilled. The pseudocode is as follows (Algorithm 1).

Algorithm 1. Algorithm for modeling the OFDM signal HF band.

1. Initialization:

L_train (the length of the training sequence within each frame OFDM),

L_data (the length of the data sequence within each frame OFDM),

L = L_train + L_data,

N_ofdm (the number of subcarriers)

N (Number of antennas at the receiving side)

2 Generating the training sequence matrix of the dimension L_train × N_ofdm

3 Generating the data matrix L_data × N_ofdm

4 Formation of the matrix of overall sequences tx_sig of the dimension L × N_ofdm

5 Formation of a matrix of the steering vectors for each frequency for O- and X-waves A_O and A_X

6 Setting of attenuation and time shifts for each frequency

for f = 1:N_ofdm

reset the channel settings O

reset the channel settings X

tx_chan_O = function_channel_O(tx_sig(:,f))

tx_chan_X = function_channel_X(tx_sig(:,f))

rx_chann_O(:,:,f) = A_O(:,f)* tx_chan_O

rx_chann_X(:,:,f) = A_X(:,f)* tx_chan_X

end

for n = 1:N

for l = 1:L

frames_O(:,l) = ifft(rx_chann_O (n,l,:))

frames_X(:,l) = ifft(rx_chann_X (n,l,:))

end

rx_ifft_O(n,:) = frames_O(:)

rx_ifft_X(n,:) = frames_X(:)

end

Output:

channel O signal on the receiving antenna array rx_ifft_O

channel X signal on the receiving antenna array rx_ifft_X

Further, Figure 15 shows the proposed OFDM frame structure for the HF ionospheric communication channel.

The proposed OFDM signal structure consists of a training sequence and a block of transmitted information. The cyclic prefix is intentionally omitted. This decision assumes evaluating the resilience of the proposed hybrid processing schemes to the ionospheric transmission. The proposed model thus tests the ability of the spatial–polarization processing to mitigate intersymbol interference inherently, without this common guard interval. However, it can be added by minor algorithm changes, if necessary.

The training sequence at the beginning of each subcarrier is necessary for both estimating the channel state information at a given frequency using (19) and for estimating the time delays between the subcarriers. These mutual time shifts inevitably arise after the broadband signal passes through the ionospheric layers. Further, Figure 16 shows the formed OFDM signal in the time domain on different subcarriers after simulation of propagation through the ionospheric channel.

As can be seen from Figure 16, the X-wave signals have a delay relative to the O-wave. In addition, the graphs demonstrate non-coinciding power levels in time across different subcarriers. Then the data are combined into a single stream. In this paper, the cyclic prefix is not used, since the most common and simple signal construction scheme is chosen. The main part of the processing is devoted to the space–time and polarization hybrid array signal processing.

This work also proposes frequency–time–spatial processing techniques for the reception of wideband OFDM signals after ionospheric propagation. Let us consider the processing schemes using the example of polarization, spatial, and spatial–polarization beamforming + SIMO schemes, which are depicted in Figure 17, Figure 18 and Figure 19.

The circuits in Figure 17, Figure 18 and Figure 19 largely reproduce those proposed for narrowband signals. The primary contribution is a fast Fourier transform block for demodulating the OFDM signal. The FFT in OFDM demodulation converts the time-domain signal back into frequency-domain symbols, allowing the transmitted data to be extracted from each subcarrier. The final step is to estimate the channel using (19) and then demodulate using the MRC algorithm, combining signals received by multiple antennas (20). The pseudocode for signal processing on the receiving side is given below (Algorithm 2).

Algorithm 2. Algorithm for processing OFDM HF-band signal.

W_O—the vector of weight coefficients of channel O

W_X—the vector of weight coefficients of channel X

y_O—the signal vector of the antenna array O

y_X—the signal vector of the antenna array X

tx_Out—the vector of the training sequence

y_beam_O = W_O*y_O

y_beam_X = W_X*y_X

y_beam_fft_O = fft(y_beam_O)

y_beam_fft_X = fft((y_beam_X)

for f = 1:N_ofdm

y_ aligned_O = align(y_beam_fft_O, tx_Out)

y_ aligned_X = align(y_beam_fft_X, tx_Out)

h_ch _O = y_ aligned_O* tx_Out/L_train

h_ch _X = y_ aligned_X* tx_Out/L_train

h = [h_ch _O h_ch _X]

y = [y_ aligned_O y_ aligned_X]

y_mrc(f,:) = h’*y/(h*h’)

End

The simulation, according to the presented algorithm of OFDM signal propagation (Algorithm 1) in the shortwave range, taking into account the Watterson model, is carried out. The schemes of processing the received signals shown in Figure 17, Figure 18 and Figure 19 are also described in Algorithm 2. The bit error rates are estimated depending on the attenuation values. The number of subcarriers is equal to 32, the number of time samples is 64, the duration of the training sequence and the payload are equal to 32.

The results of the simulation are shown in Figure 20a when only the desired signal is present in the ionospheric channel. The results in Figure 20b include interference with power equal to that of the useful signal. As can be seen from the graphs in Figure 20, the hybrid scheme utilizing beamforming as well as SIMO based on polarization diversity from Figure 17 has the lowest error values. The spatial diversity scheme has the worst values because of the demodulation of OFDM using the fast Fourier transform. While the FFT is computationally efficient and fundamentally correct for ideal conditions, its performance degrades significantly in harsh links. In particular, it is sensitive to synchronization errors and impairments between spatial channels. Therefore, it is recommended to use advanced demodulation methods for broadband HF signals after spatial diversity.

6. Conclusions

This paper introduces hybrid processing schemes for HF signals subsequent to their traversal of the ionospheric channel. In particular, double hybridization is employed. First, beamforming together with SIMO equalization is combined. SIMO is based on polarization of O- and X-waves and/or spatial processing. The results are derived from the improved narrowband Watterson model, which accounts for wave polarization. In addition, an algorithm is proposed for modeling the propagation of a broadband OFDM signal through the ionosphere. It has been found that the best configuration for processing HF signals after the ionosphere is the hybrid scheme with beamforming followed by SIMO equalization based on polarization diversity.

For general-purpose fixed stations where spectral efficiency is a priority, and the interference environment is moderate, the polarization scheme is highly advantageous. It achieves high capacity using a single antenna array with dual-polarized elements, minimizing site footprint. For high reliability, the spatial–polarization scheme is recommended. Despite its highest complexity and cost, it delivers the lowest BER under jammers and the highest potential capacity by leveraging both spatial and polarization diversity.