Fault Process Modeling and Transient Stability Analysis of Grid-Following Photovoltaic Converter Grid-Connected System

Abstract

With the growing integration of renewable energy into power systems, transient stability throughout the whole fault process has become a critical issue. This process comprises three distinct stages: pre-fault, fault-on, and post-fault recovery. However, existing studies have largely overlooked the influence of active power recovery on transient stability, which leads to conservative estimates of critical fault clearing time (CCT) and potential misjudgment of stability analysis. Accordingly, this paper addresses this gap by examining a grid-following (GFL) photovoltaic (PV) converter grid-connected system. Therefore, this paper investigates the transient stability of a GFL PV converter grid-connected system during the whole fault process. Firstly, a transient stability analysis model is developed using the piecewise linearization method to represent the system behavior across the whole fault process. Secondly, based on the proposed model, the impact mechanism of the control strategy in the fault recovery stage on the transient stability of the system is revealed by using the equal area criterion (EAC). Finally, the accuracy of the theoretical analysis proposed in this paper is verified by the PSCAD/EMTDC simulation platform. The results show that a slower active power recovery rate enhances the system’s transient stability, as it creates a larger equivalent deceleration area. The critical fault clearing time calculated by the proposed model is less conservative.

1. Introduction

Photovoltaic (PV), wind power, and other renewable energy sources are environmentally friendly and renewable, leading to their widespread adoption in power systems. While the installed capacity of PV generation is expanding rapidly worldwide, its inherent intermittency and uncertainty pose significant challenges to power grid stability [1,2]. Furthermore, reduced system inertia caused by the decreasing share of synchronous generators (SG) has brought the stability of grid-following (GFL) PV grid-connected systems to the research focus [3,4,5].

The stability problem of a GFL-PV converter grid-connected system is mainly divided into small-disturbance stability and transient stability. Among these, small-signal stability has been extensively studied using linearization methods [6,7]. In [7], the impedance model of a PV power generation system is established, and the influence of maximum power point tracking (MPPT) control on the small-disturbance stability is evaluated. Due to the nonlinear and high-order characteristics of grid-following PV systems, the small-disturbance stability analysis methods mentioned above cannot be directly applied to transient stability studies [8]. Therefore, a series of studies have been carried out on the transient stability of GFL grid-connected systems in [9,10,11]. Reference [9] compares the mathematical similarities between a synchronous generator and a grid-following converter and employs the damping torque method to explain the multi-swing instability phenomenon from a damping perspective. In [10], a control strategy based on improved phase-locked loop (PLL) and energy dissipation is presented, aiming to enhance the transient stability of GFL converter grid-connected systems. In [11], the phase portrait method was employed to examine transient stability in the GFL converter during asymmetric faults, uncovering the coupling effects between positive- and negative-sequence PLLs.

A prevailing view in the existing literature identifies the PLL as the main cause of transient instability. However, studies [12,13,14,15,16] indicate that an analysis focusing exclusively on the PLL can yield inaccurate conclusions. Reference [12] investigates the impact of the interaction between the PLL and the current loop on the transient stability of GFL converters. The conclusion demonstrates that this interaction can degrade system stability. Reference [13] employs the perturbation-averaging method to investigate the effects of both hard limiter and circular limiter nonlinearities on the transient stability of GFL converters, thereby deriving the large-disturbance synchronization stability boundary of the system. An investigation into the effect of PLL filter delay in Reference [14] reveals its detrimental impact on the transient stability of GFL converters, showing that increased delay leads to performance deterioration. In [15], the transient stability of a GFL-PV converter grid-connected system is evaluated, considering control switching delays, based on the existence of the equilibrium point and the transient energy balance. Reference [16] qualitatively identifies the key control loops responsible for transient instability across different time scales. However, it does not establish the multi-time-scale dynamic equations, thus failing to quantitatively characterize the system’s transient stability margin. The aforementioned studies have explored the transient stability of GFL converter grid-connected systems from perspectives such as multi-loop interactions, control saturations, and time delays. However, existing research has rarely accounted for the impact of active power recovery dynamics after fault clearing on the transient stability of GFL-PV converter grid-connected systems.

To the end, in the research on the transient stability of GFL-PV converter grid-connected systems during the whole fault process, two main research gaps are currently encountered:

(1)

The lack of transient stability analysis models in previous research for the whole fault process makes it difficult to characterize the transient characteristics of the system during the fault recovery period.

(2)

The impact mechanism of active power recovery control on system transient stability remains unclear, which may lead to misjudgment of stability analysis results and an overly conservative design of system fault clearance.

To address the aforementioned research gaps, this paper focuses on fault process modeling and transient stability analysis of GFL-PV converter grid-connected systems. The main contributions of this paper are as follows:

(1)

A piecewise linear description method is utilized to approximate the dynamic characteristics of the phase difference between the PCC voltage and the grid voltage during the fault recovery process, thereby establishing a mapping relationship between the phase difference and time. A mathematical model capable of characterizing the system transient stability throughout the whole fault process is proposed.

(2)

The influence mechanism of active power recovery control on the transient stability of the GFL-PV converter system is revealed. The influence of the active power recovery rate on the transient stability of the system is analyzed.

(3)

Based on the proposed model, the critical fault clearing time (CCT) of the system is calculated, which reduces the conservatism in previous methods.

The paper is organized as follows: In Section 2, the control strategy of the GFL-PV converter grid-connected system in the whole process of fault is analyzed. In Section 3, the transient model of the whole fault process is established. In Section 4, the transient stability of the whole fault process is analyzed by using the EAC. In Section 5, the CCT calculation model is established to quantify the stability margin. Section 6 simulates the theory proposed in this paper. Section 7 is our conclusion.

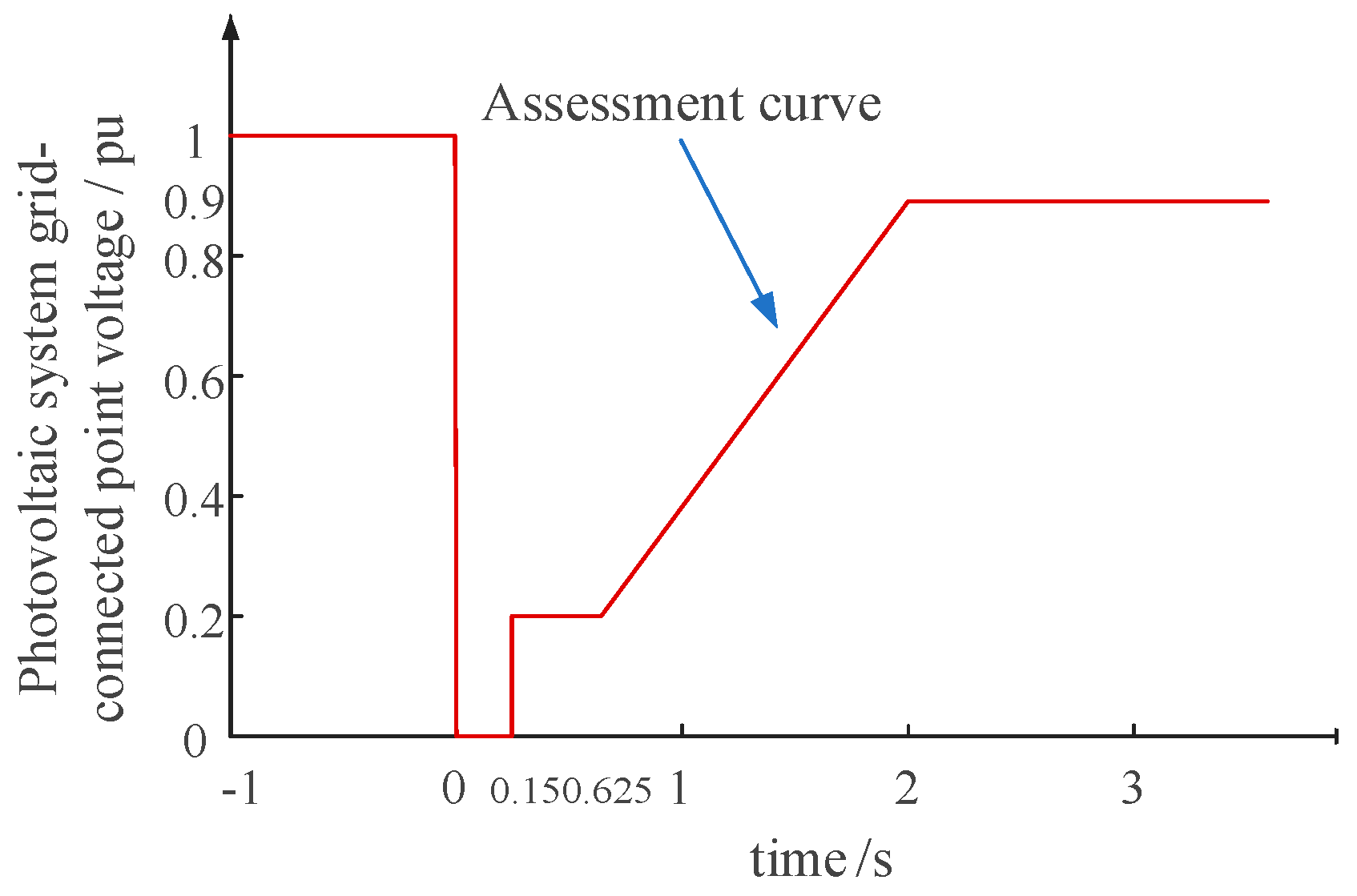
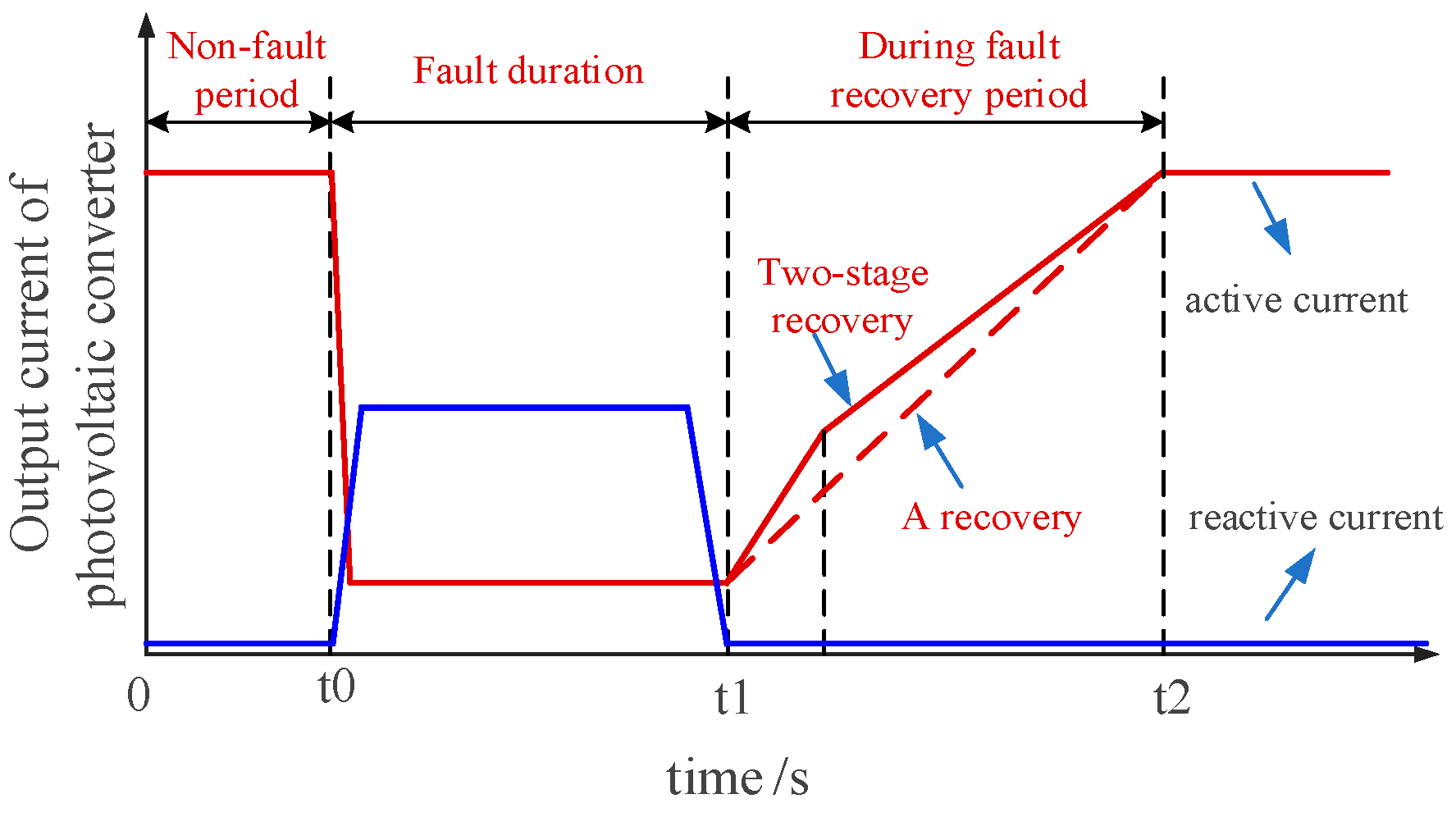
2. Control Strategy of GFL-PV Converter Grid-Connected System in the Whole Process of Fault

2.1. The Main Circuit Structure and Control Strategy of GFL-PV Converter

It can be seen from Figure 1 that the photovoltaic array is connected to the grid through the converter, filter, and grid impedance. Among them, i_dc is the DC side current, u_dc is the DC side voltage, u_gabc is the grid voltage, u_abc is the grid-connected point voltage, i_abc is the grid-connected current, C₁ is the DC capacitor, L₁ is the filter inductance, L_g is the grid inductance, and R_g is the grid resistance. u_dcref and i_dq0ref denote the DC-side voltage reference and the dq-axis current references, respectively. i_dq0 are the dq axis current components of i_abc. u^*_dq are the dq axis components of the converter terminal voltage. θ_PLL is the output phase angle of PLL. u_t denotes the per-unit value of the point of common coupling (PCC) voltage. I_n and P_n denote the rated current and power of the system.

The GFL-PV converter should have a certain low voltage ride through (LVRT) capability, which injects dynamic reactive current into the system to support the grid operation after the fault occurs [17]. The LVRT capability requirements of the photovoltaic converter are shown in Figure 2.

The specific meaning of the assessment curve in Figure 2 is as follows: (1) When the PCC voltage drops to 0 p.u., the photovoltaic converter needs to ensure grid-connected operation for 0.15 s. (2) When the PCC voltage is restored to 0.2 p.u. after 0.15 s, the GFL-PV converter needs to continue to ensure grid-connected operation to 0.65 s. (3) In the range of 0.65 s to 2 s, the PCC voltage needs to be restored from 0.2 p.u. to 0.9 p.u. After the fault, if the PCC voltage is in the area above the assessment curve, the GFL-PV converter must be continuously connected to the grid; if the PCC voltage is in the area under the assessment curve, the converter is allowed to be off-grid.

In addition, according to the LVRT standard of the State Grid Corporation of China, after the fault is cleared, the active power needs to be restored to the steady state with a power change rate of at least 30% of the rated power per second [17], as shown in Figure 3. In general, the PCC voltage can be restored to the amplitude before the fault immediately after the fault is cleared. Therefore, the active power recovery requirement is essentially a requirement on the recovery rate of the active current reference i_dref.

At present, there is no uniform standard for the recovery rate of the active current reference i_dref by different GFL-PV converter manufacturers. In addition, the characteristics of active current recovery are also different, mainly including one-stage recovery and two-stage recovery. The recovery characteristics of active current and reactive current during the fault recovery period are shown in Figure 3. In order to simplify the subsequent modeling and stability analysis, this paper uses a one-stage model of active current recovery. Therefore, the control strategy and current reference value of the whole fault process can be obtained, as follows.

(1)

Control strategy during non-fault period

When the system is operating in the non-fault period, the GFL-PV converter must operate at its maximum available active power. Therefore, the reactive current reference value i_qref during the non-fault period is 0, and the active current reference value i_dref is given by the DC voltage outer loop control. The active current and reactive current reference values during the non-fault period are expressed as

$$\left\{\begin{array}{l}{i}_{\mathrm{dref}}=k_{\mathrm{pdc}}(u_{\mathrm{dcref}}-u_{\mathrm{dc}})+k_{\mathrm{idc}}{\displaystyle \int (u_{\mathrm{dcref}}-u_{\mathrm{dc}})\mathrm{d}t}\hfill \\ i_{\mathrm{qref}}=0\hfill \end{array}\right.$$

(1)

where k_pdc and k_idc are the proportional coefficient and integral coefficient of the DC voltage outer loop PI controller, respectively. u_dc and u_dcref are the measured and reference values of the DC side voltage of the GFL-PV converter, respectively.

(2)

Control strategy during fault duration period

Upon detection of a grid voltage dip below 0.9 p.u. at the PCC, the GFL-PV converter activates its LVRT control strategy. Meanwhile, i_qref is determined by the PCC voltage, and its expression varies with the depth of the voltage dip. The expression of the i_qref fault duration period is shown in Equation (2).

$$i_{\mathrm{qref}}=\left\{\begin{array}{ll}0\hfill & u>0.9\hfill \\ 1.5I_{\mathrm{n}}(0.9-u)\hfill & 0.2\le u\le 0.9\hfill \\ 1.05I_{\mathrm{n}}\hfill & u<0.2\hfill \end{array}\right.$$

(2)

where I_n is the rated current of the GFL-PV grid-connected system. u is the PCC voltage per unit value.

During fault duration period, there is a risk that increasing only i_qref without reducing i_dref will cause a system overcurrent and trigger the protection. Therefore, to ensure stable grid-connected operation of the GFL-PV converter, the active current reference i_dref must be determined by i_qref. Therefore, the expression of i_dref during the fault duration is

$$i_{\mathrm{dref}}=\sqrt{{\left(1.1I_{\mathrm{n}}\right)}^2-{(i_{\mathrm{qref}})}^2}$$

(3)

(3)

Control strategy during fault recovery period

In this paper, the one-stage model of active current recovery is adopted. Therefore, the expression of i_dref during the fault recovery period is

$$i_{\mathrm{dref}}=\left\{\begin{array}{ll}k(t-t_1)I_{\mathrm{n}}+i_{\mathrm{dref}\_\mathrm{fau}},\hfill & P<P_n\hfill \\ i_{\mathrm{d}\_\mathrm{nor}},\hfill & P\ge P_n\hfill \end{array}\right.$$

(4)

where k is the active current recovery rate. t₁ is the fault clearing time. i_{dref_fau} is the active current value at the fault clearing time. i_{dref_nor} is the active current value during the non-fault period. P is the power measurement value of the fault recovery period. P_n is the rated power of the GFL-PV grid-connected system.

In summary, to ensure LVRT capability of the GFL-PV converter, appropriate control strategies must be deployed in accordance with the specific fault phase, as outlined in Figure 1.

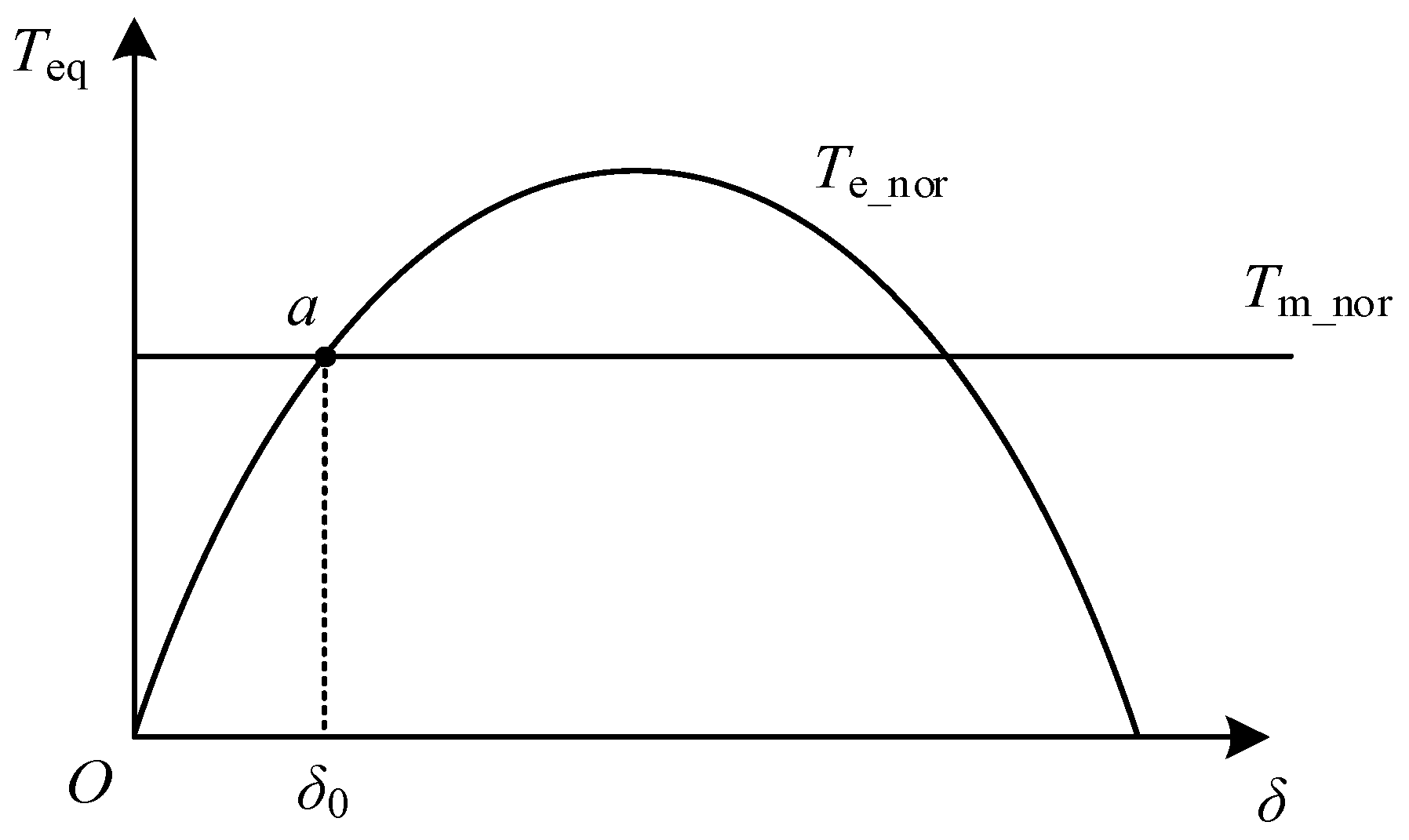
2.2. Impact of Active Power Recovery Control on Transient Stability of the System

Research on the transient stability of GFL-PV converter grid-connected systems has rarely accounted for the influence of active power recovery control. To evaluate the impact of active power recovery control on transient stability, comparative simulation models of a GFL-PV grid-connected system, with and without this control, were developed. The simulation was configured with the parameters in

Table 1. Photovoltaic grid-connected system parameters.

Parameter Name	Sign	Value
Nominal power	S	0.1 MW
Rated AC side voltage	U	0.4 kV
Rated angular frequency	ωg	100π rad/s
Filter inductance	Lf	2.5 mH
Grid inductance	Lg	2 mH
Grid resistance	Rg	0.2 Ω
Active current recovery slope	k	3
Phase-locked loop proportional gain	KpPLL	0.2221
Phase-locked loop integral gain	KiPLL	9.9

, introducing a voltage drop to 0.9 p.u. at t = 1.2 s for a duration of 95 ms. The simulation results are shown in Figure 4.

A comparison of the results in Figure 4 reveals that, for the same fault clearing time, the system without active power recovery control becomes transiently unstable, whereas the system with the control maintains stability. Since most GFL-PV converters in practical engineering incorporate active power recovery control, it is imperative to study its impact on transient stability. Such research is crucial for guiding stability analysis and determining critical fault clearing times in the GFL-PV converter grid-connected system, ultimately reducing the conservatism and enhancing the accuracy of stability assessments.

Furthermore, the above observations indicate that the traditional transient stability modeling and analysis neglecting active power recovery control are no longer applicable, thereby motivating the establishment of a comprehensive modeling and analysis study covering the whole fault process.

3. Transient Modeling of a GFL-PV Converter Grid-Connected System in the Whole Fault Process

According to Section 2, the control block diagram of the GFL-PV converter grid-connected system in the whole fault process can be obtained, as shown in Figure 1. The GFL-PV converter control strategy includes PLL, voltage outer loop, current loop, and LVRT. The PLL takes the PCC voltage u_abc as the input signal and outputs the phase θ_PLL, which provides the angle for the coordinate transformation of currents and voltages. The grid-connected current i_abc is transformed to the dq-axis current components i_dq through the Park transformation. Using i_dq and i_dqref as inputs, the current loop employs a PI controller to generate the dq-axis reference voltage u_dqref for the converter terminals. Finally, the switching signals for the power devices are generated through the inverse Park transformation and Pulse Width Modulation (PWM).

Compared with the PLL, the current loop has a larger bandwidth. Thus, in studies of transient stability for photovoltaic grid-connected systems, the influence of the current loop’s dynamic characteristics is often neglected [16,18]. This simplification is achieved by assuming that i_dq = i_dqref. The dq-axis current reference value i_dqref has different values in different fault periods, such as the non-fault period, fault duration, and fault recovery period. In particular, during the recovery period, the d-axis reference i_dref is defined as a function of time, a dependency that notably complicates the transient stability analysis of the PV grid-connected system throughout the whole fault sequence.

In this section, the transient model of the GFL-PV converter grid-connected system in the whole fault process will be established. This model provides the foundation for the subsequent transient stability analysis. Prior to establishing the model, two assumptions were adopted [15,16].

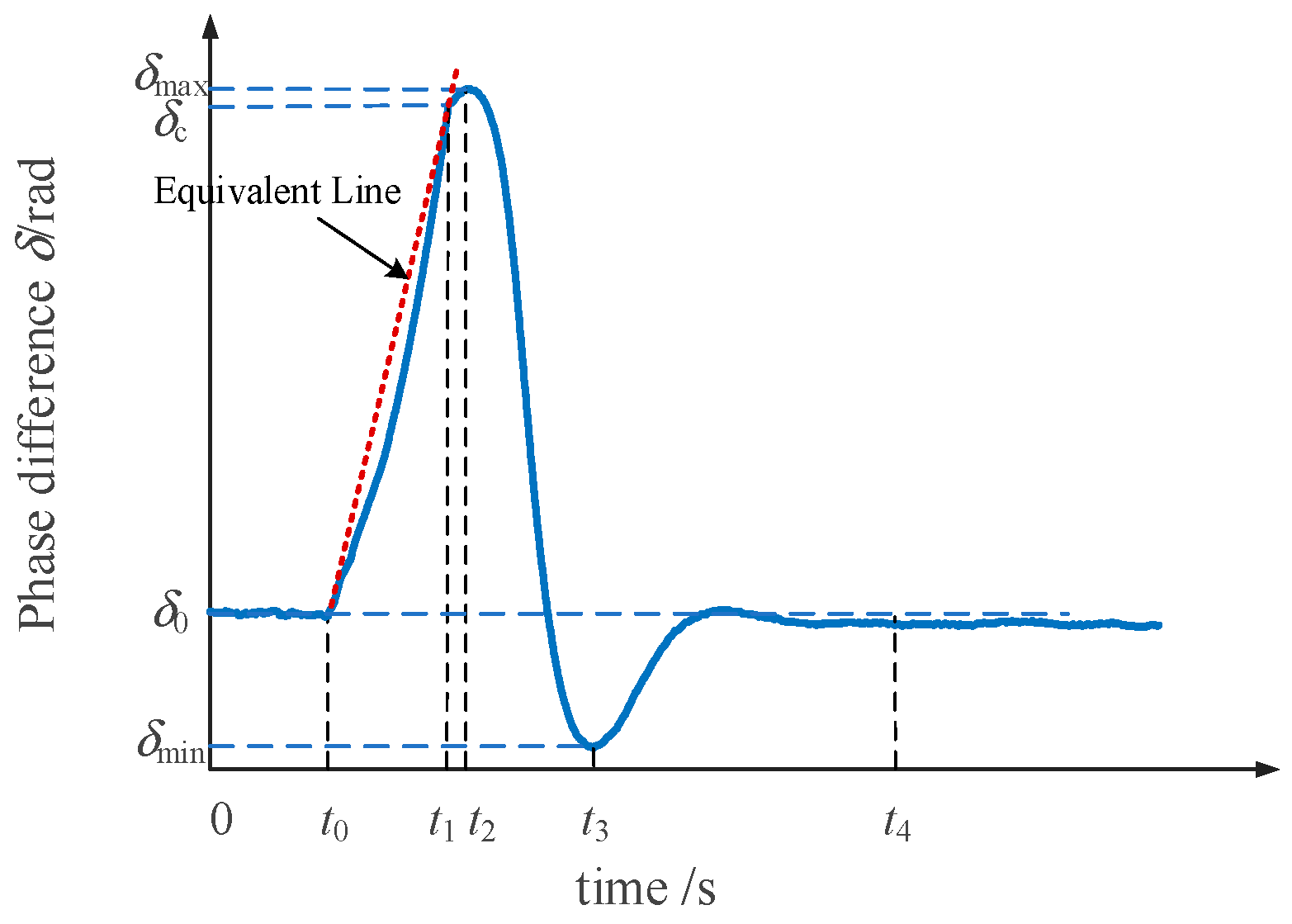
(1)

The time difference between the fault clearing instant t1 and instant t2 when the phase difference reaches its maximum is sufficiently small, allowing higher-order residual terms in the Taylor expansion to be neglected.

(2)

The current loop exhibits high bandwidth, thereby enabling the neglect of its dynamic characteristics.

3.1. Transient Modeling During Non-Fault Period

According to the main circuit structure of the GFL-PV converter grid-connected system in Figure 1, the expression of the PCC voltage can be obtained as

$$u_{\mathrm{abc}}=u_{\mathrm{gabc}}+L_{\mathrm{g}}{\displaystyle \frac{\mathrm{d}{i}_{\mathrm{abc}}}{\mathrm{d}t}}+R_{\mathrm{g}}{i}_{\mathrm{abc}}$$

(5)

where u_abc = U_tcosθ_PLL and U_t is the PCC voltage amplitude. u_gabc = U_gncosθ_g, U_gn is the grid voltage amplitude during the non-fault period, and θ_PLL and θ_g are the PCC voltage phase and the grid voltage phase, respectively. i_abc = I_tcosθ_PLL, and I_t is the amplitude of grid-connected current.

By applying the Park transformation to Equation (5), the dq-axis component of the PCC voltage is obtained as

$$\left\{\begin{array}{c}{u}_{\mathrm{d}}=U_{\mathrm{gn}}\cos \delta -{\omega }_{\mathrm{PLL}}{L}_{\mathrm{g}}{i}_{\mathrm{q}}+R_{\mathrm{g}}{i}_{\mathrm{d}}\\ u_{\mathrm{q}}=-U_{\mathrm{gn}}\sin \delta +{\omega }_{\mathrm{PLL}}{L}_{\mathrm{g}}{i}_{\mathrm{d}}+R_{\mathrm{g}}{i}_{\mathrm{q}}\end{array}\right.$$

(6)

where δ = θ_PLL − θ_g is the phase difference between the PCC voltage and the grid voltage. ω_PLL is the angular frequency of the PCC voltage.

During the non-fault period, the q-axis current component is i_qref = 0. Therefore, Equation (6) can be simplified as

$$u_{\mathrm{q}}=-U_{\mathrm{gn}}\sin \delta +{\omega }_{\mathrm{PLL}}{L}_{\mathrm{g}}{i}_{\mathrm{d}}$$

(7)

According to the control structure of PLL in the yellow frame of Figure 1, the dynamic equation of PLL can be obtained as

$${\theta }_{\mathrm{PLL}}={\displaystyle \int ({\omega }_{\mathrm{g}}+k_{\mathrm{pPLL}}{u}_{\mathrm{q}}+k_{\mathrm{iPLL}}{\displaystyle \int u_{\mathrm{q}}}\mathrm{d}t)\mathrm{d}t}$$

(8)

where ω_g is the angular frequency of the grid voltage. k_pPLL and k_iPLL are the proportional coefficient and integral coefficient of the PLL’s PI controller, respectively.

Combining Equations (7) and (8), the transient model of the GFL-PV grid-connected system during the non-fault period can be obtained

$$\left\{\begin{array}{l}\dot{\delta }=\mathrm{\Delta }{\omega }_{\mathrm{PLL}}={\omega }_{\mathrm{PLL}}-{\omega }_{\mathrm{g}}\hfill \\ J_{\mathrm{nor}}\ddot{\delta }=T_{\text{m\_nor}}-T_{\text{e\_nor}}-D_{\mathrm{nor}}\dot{\delta }\hfill \end{array}\right.$$

(9)

$$\left\{\begin{array}{l}{J}_{\mathrm{nor}}=1-k_{\mathrm{pPLL}}{L}_{\mathrm{g}}{i}_{\mathrm{dref}}\hfill \\ T_{\text{m\_nor}} = k_{\mathrm{iPLL}}{\omega }_{\mathrm{g}}{L}_{\mathrm{g}}{i}_{\mathrm{dref}}\hfill \\ T_{\text{e\_nor}} = k_{\mathrm{iPLL}}{U}_{\mathrm{gn}}\sin \delta \hfill \\ D_{\mathrm{nor}}=k_{\mathrm{pPLL}}{U}_{\mathrm{gn}}\cos \delta -k_{\mathrm{iPLL}}{L}_{\mathrm{g}}{i}_{\mathrm{dref}}\hfill \end{array}\right.$$

(10)

where Δω_PLL is the angular frequency deviation of the PLL output, J_nor is the equivalent inertial time constant during the non-fault period, T_{m_nor} is the equivalent mechanical torque during the non-fault period, T_{e_nor} is the equivalent electromagnetic torque during the non-fault period, and D_nor is the equivalent damping during the non-fault period [13]. In addition, i_dref is determined by Equation (1).

3.2. Transient Modeling During Fault Duration

It can be seen from Section 2.1 that the q-axis current reference value i_qref is determined by the LVRT control during the fault duration period. At this time, i_qref depends on the amplitude of the PCC voltage.

Compared with the non-fault period, the i_qref during the fault duration period becomes non-zero. At this time, the q-axis component of the PCC voltage is consistent with Equation (6). Therefore, combined with Equations (6) and (8), the transient model of the system during the fault duration period can be obtained as

$$\left\{\begin{array}{l}\dot{\delta }={\omega }_{\mathrm{PLL}}-{\omega }_{\mathrm{g}}\hfill \\ J_{\mathrm{dur}}\ddot{\delta }=T_{\text{m\_dur}} - T_{\text{e\_dur}} - D_{\mathrm{dur}}\dot{\delta }\hfill \end{array}\right.$$

(11)

$$\left\{\begin{array}{l}{J}_{\mathrm{dur}}=1-k_{\mathrm{pPLL}}{L}_{\mathrm{g}}{i}_{\mathrm{dref}}\hfill \\ T_{\text{m\_dur}} = k_{\mathrm{iPLL}}({\omega }_{\mathrm{g}}{L}_{\mathrm{g}}{i}_{\mathrm{dref}}+R_{\mathrm{g}}{i}_{\mathrm{qref}})\hfill \\ T_{\text{e\_dur}} = k_{\mathrm{iPLL}}{U}_{\mathrm{gf}}\sin \delta \hfill \\ D_{\mathrm{dur}}=-k_{\mathrm{pPLL}}{U}_{\mathrm{gf}}\cos \delta +k_{\mathrm{iPLL}}{L}_{\mathrm{g}}{i}_{\mathrm{dref}}\hfill \end{array}\right.$$

(12)

where U_gf is the grid voltage amplitude during the fault duration period, J_dur is the equivalent inertia time constant during the fault duration period, T_{m_dur} is the equivalent mechanical torque during the fault duration period, T_{e_dur} is the equivalent electromagnetic torque during the fault duration period, and D_dur is the equivalent damping during the fault duration period. In addition, the dq axis current reference values i_dref and i_qref are determined by Equations (2) and (3). The value of δ is [δ₀, δ_c].

3.3. Transient Modeling During Fault Recovery Period

It can be seen from Section 2.1 that the d-axis current reference value i_dref is determined by Equation (4) during fault recovery period, and the q-axis current reference value i_qref is 0. During the fault recovery period, the time required for the system to reach transient stability is shorter than that for the d-axis current to reach its rated value. Therefore, when establishing the transient model during the fault recovery period, it is sufficient to consider the i_dref expression only under the condition P < P_n.

By combining Equations (4) and (7), the q-axis component of the PCC voltage during the fault recovery period is obtained as follows:

$$u_{\mathrm{q}}=-U_{\mathrm{gn}}\sin \delta +{\omega }_{\mathrm{PLL}}{L}_{\mathrm{g}}(k(t-t_1)+i_{\mathrm{dref}\_\mathrm{fau}})$$

(13)

Furthermore, combined with Equations (8) and (13), the transient model of the system during the fault recovery period can be obtained as

$$\left\{\begin{array}{l}\dot{\delta }={\omega }_{\mathrm{PLL}}-{\omega }_{\mathrm{g}}\hfill \\ J_{\mathrm{cut}}\ddot{\delta }=T_{\text{m\_cut}} - T_{\text{e\_cut}}- D_{\mathrm{cut}}\dot{\delta }\hfill \end{array}\right.$$

(14)

$$\left\{\begin{array}{l}{J}_{\mathrm{cut}}=1-k_{\mathrm{pPLL}}{L}_{\mathrm{g}}(k(t-t_1)+i_{\mathrm{dref}\_\mathrm{fau}})\hfill \\ T_{\text{m\_cut}} = k_{\mathrm{iPLL}}{\omega }_{\mathrm{g}}{L}_{\mathrm{g}}(k(t-t_1)+i_{\mathrm{dref}\_\mathrm{fau}})+k_{\mathrm{pPLL}}k{\omega }_{\mathrm{g}}{L}_{\mathrm{g}}\hfill \\ T_{\text{e\_cut}} = k_{\mathrm{iPLL}}{U}_{\mathrm{gn}}\sin \delta \hfill \\ D_{\mathrm{cut}}=k_{\mathrm{pPLL}}{U}_{\mathrm{gn}}\cos \delta -k_{\mathrm{iPLL}}{L}_{\mathrm{g}}(k(t-t_1)+i_{\mathrm{dref}\_\mathrm{fau}})\hfill \end{array}\right.$$

(15)

where J_cut is the equivalent inertial time constant during fault recovery period, T_{m_cut} is the equivalent mechanical torque during fault recovery period, T_{e_cut} is the equivalent electromagnetic torque during fault recovery period, and D_cut is the equivalent damping during fault recovery period. i_{dref_fau} is the d-axis current reference at fault clearance.

Equations (14) and (15) show that the transient model of the GFL-PV grid-connected system during the fault recovery period contains a time variable t. Existing stability analysis methods cannot be directly applied to this model due to its time-dependent nature. The phase difference δ between the PCC voltage and the grid voltage evolves as a function of time, i.e., δ = f(t), as shown in Figure 5. Therefore, by providing the analytical expression for f(t) and employing a variable substitution for time t, Equation (17) can be transformed into a second-order system. This allows for the application of methods like the EAC to analyze the system’s transient stability.

As shown in Figure 5, the system operates during the non-fault period in [0, t₀], and the initial phase difference is δ₀. The voltage drop fault occurs in the system at t₀. In [t₀, t₁], the system operates during the fault duration period, and the phase δ increases under the LVRT control strategy of the GFL-PV converter. The system clears the fault at t₁, and the t₁ corresponds to the fault clearing angle δ_c. In [t₁, t₄], the system operates during the fault recovery period. The system reaches the maximum phase difference δ_max at t₂. Meanwhile, the system reaches the minimum phase difference δ_min at t₃. The system’s phase difference converges to δ₀ at t₄, when the d-axis current reference reaches its rated value, marking the end of the fault recovery period, as shown in Figure 5.

As observed in Figure 5, constructing a detailed mapping between phase δ and time t is challenging. Furthermore, since the system’s transient stability is primarily governed by the maximum phase difference δ_max, a direct focus on this critical value is more pertinent. The system is transiently stable if δ_max remains below the unstable equilibrium point (UEP), and becomes unstable if δ_max exceeds it. It is established that the dynamic characteristics within [t₂, t₄] are associated with the system’s equivalent damping and exert minimal influence on the transient stability. Consequently, the mapping relationship between δ and t over this interval is excluded from the scope of this study.

Establishing the mapping relationship between δ and t is a crucial step in developing the transient model for the fault recovery process. Common approaches include data-driven methods and piecewise linear approximation [19,20]. The former relies on experimental and measured datasets to build a data-driven model using intelligent algorithms, offering a novel solution for systems where analytical models are difficult to establish. Nevertheless, this method imposes high requirements on technical schemes and hardware specifications. The latter employs model reduction strategies through simplified linear models to approximate complex nonlinear dynamics, enabling high local accuracy within specific operational ranges. To capture the dynamics of δ in [t₁, t₂], this paper approximates its dynamics using a linear function, adopting a piecewise linearization approach [20].

A key issue in this paper is determining the appropriate linear function. By combining Equations (8) and (13), the expression for the phase difference δ as a function of time t during the fault recovery period can be derived as

$$\begin{array}{cc}\delta & =k_{\mathrm{pPLL}}\left[{\omega }_{\mathrm{g}}{L}_{\mathrm{g}}(i_{\mathrm{dref}\_\mathrm{fau}}-k{t}_1{I}_{\mathrm{n}})t+{\displaystyle \frac{{\omega }_{\mathrm{g}}{L}_{\mathrm{g}}k{I}_{\mathrm{n}}}{2}}{t}^2+{\displaystyle \int -U_{\mathrm{gn}}\sin \delta \mathrm{d}t}\right]\hfill \\ & +k_{\mathrm{iPLL}}\left[{\displaystyle \frac{{\omega }_{\mathrm{g}}{L}_{\mathrm{g}}(i_{\mathrm{dref}\_\mathrm{fau}}-k{t}_1{I}_{\mathrm{n}})}{2}}{t}^2+{\displaystyle \frac{{\omega }_{\mathrm{g}}{L}_{\mathrm{g}}k{I}_{\mathrm{n}}}{6}}{t}^3+{\displaystyle \int ({\displaystyle \int -U_{\mathrm{gn}}\sin \delta \mathrm{d}t})\mathrm{d}t}\right]\end{array}$$

(16)

By applying a Taylor series expansion to Equation (16) at the fault clearing point (t₁, δ_c), the expression can be obtained as

$$\begin{array}{l}\delta =f(\delta ,t)=f({\delta }_{\mathrm{c}},t_1)+\dot{f}({\delta }_{\mathrm{c}},t_1)(t-t_1)+{\displaystyle \frac{1}{2!}}\ddot{f}({\delta }_{\mathrm{c}},t_1){(t-t_1)}^2+R_n(t)\\ \dot{f}({\delta }_{\mathrm{c}},t_1)=k_{\mathrm{pPLL}}[{\omega }_{\mathrm{g}}{L}_{\mathrm{g}}{i}_{\mathrm{dref}\_\mathrm{fau}}-U_{\mathrm{gn}}\sin {\delta }_{\mathrm{c}}]+k_{\mathrm{iPLL}}\left[{\omega }_{\mathrm{g}}{L}_{\mathrm{g}}(i_{\mathrm{dref}\_\mathrm{fau}}-{\displaystyle \frac{1}{2}}k{I}_{\mathrm{n}}{t}_1)t_1\right]\\ \ddot{f}({\delta }_{\mathrm{c}},t_1)=k_{\mathrm{pPLL}}{\omega }_{\mathrm{g}}{L}_{\mathrm{g}}k{I}_{\mathrm{n}}+k_{\mathrm{iPLL}}\left[{\omega }_{\mathrm{g}}{L}_{\mathrm{g}}{i}_{\mathrm{dref}\_\mathrm{fau}}-U_{\mathrm{gn}}\sin {\delta }_{\mathrm{c}}\right]\end{array}$$

(17)

Given that the PLL operates on an electromagnetic transient timescale with exceptionally fast dynamics, the time difference between fault clearance and the maximum phase difference (t = t₂ − t₁) is very short. This brevity justifies neglecting second-order and higher-order terms. Consequently, the phase difference δ can be linearized as a function of time t in [t₁, t₂] as follows:

$$\delta =f(t)={\delta }_{\mathrm{c}}+k_1(t-t_1)={\delta }_{\mathrm{c}}+\dot{f}({\delta }_{\mathrm{c}},t_1)(t-t_1)$$

(18)

By integrating Equations (8), (13), and (18), the transient model for the GFL-PV grid-connected system during fault recovery is derived as

$$\left\{\begin{array}{l}\dot{\delta }={\omega }_{\mathrm{PLL}}-{\omega }_{\mathrm{g}}\hfill \\ J_{\mathrm{cut}}\ddot{\delta }=T_{\text{m\_cut}} - T_{\text{e\_cut}}- D_{\mathrm{cut}}\dot{\delta }\hfill \end{array}\right.$$

(19)

$$\left\{\begin{array}{l}{J}_{\mathrm{cut}}=1-k_{\mathrm{pPLL}}{L}_{\mathrm{g}}({\displaystyle \frac{k}{k_1}}(\delta -{\delta }_{\mathrm{c}})+i_{\mathrm{dref}\_\mathrm{fau}})\hfill \\ T_{\text{m\_cut}} = k_{\mathrm{iPLL}}{\omega }_{\mathrm{g}}{L}_{\mathrm{g}}{i}_{\mathrm{dref}\_\mathrm{fau}}+k_{\mathrm{iPLL}}{\omega }_{\mathrm{g}}{L}_{\mathrm{g}}{\displaystyle \frac{k}{k_1}}(\delta -{\delta }_{\mathrm{c}})\hfill \\ T_{\text{e\_cut}} = k_{\mathrm{iPLL}}{U}_{\mathrm{gn}}\sin \delta \hfill \\ \begin{array}{c}{D}_{\mathrm{cut}}=-k_{\mathrm{pPLL}}{U}_{\mathrm{gn}}\cos \delta +k_{\mathrm{iPLL}}{L}_{\mathrm{g}}({\displaystyle \frac{k}{k_1}}(\delta -{\delta }_{\mathrm{c}})+i_{\mathrm{dref}\_\mathrm{fau}})\\ \hspace{1em}\hspace{1em}+k_{\mathrm{pPLL}}{\omega }_{\mathrm{g}}{L}_{\mathrm{g}}{\displaystyle \frac{k}{k_1}}\hfill \end{array}\hfill \end{array}\right.$$

(20)

where δ the value is [δ_c, π].

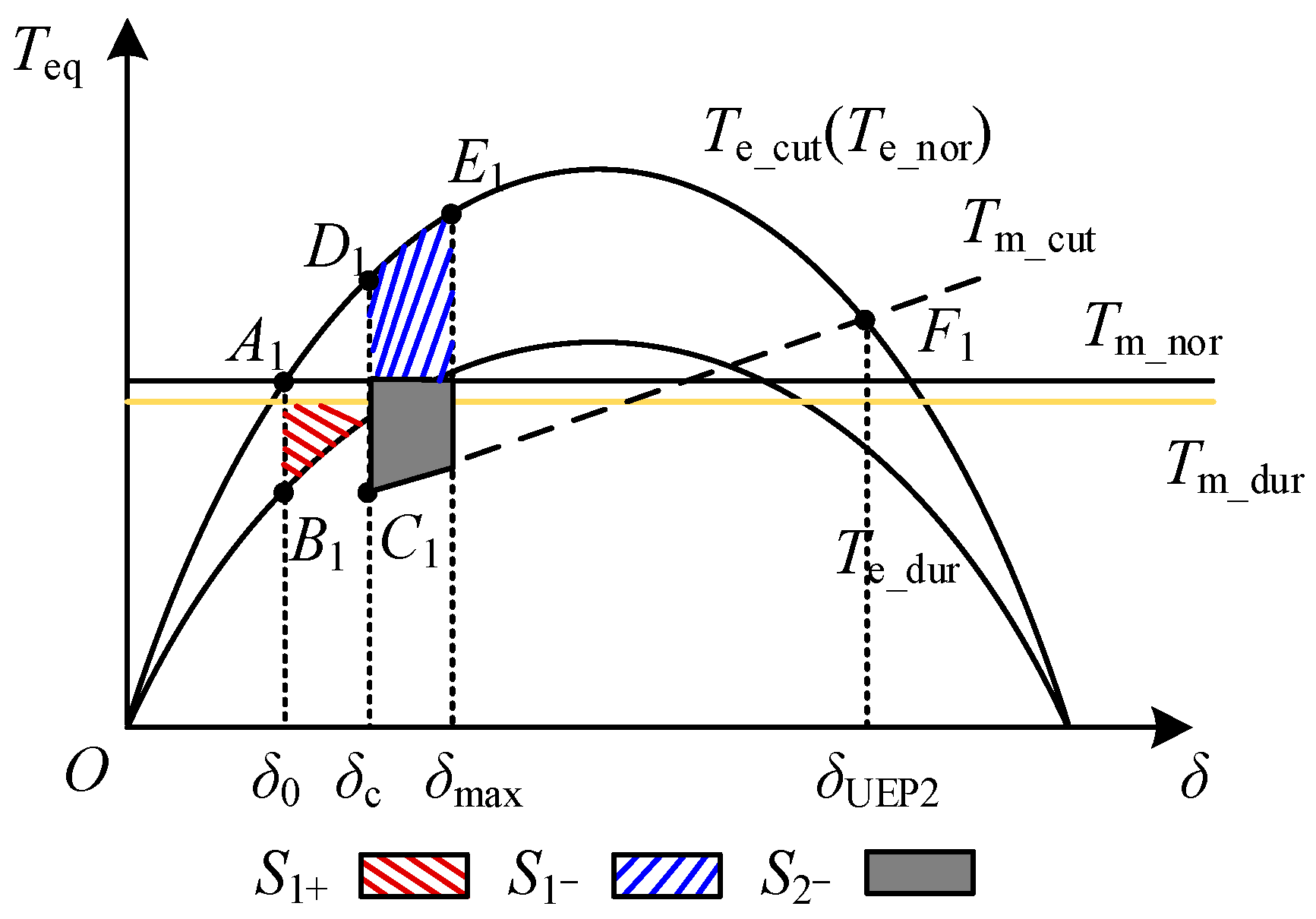
4. Transient Stability Analysis of GFL-PV Converter Grid-Connected System

The transient model of the GFL-PV converter grid-connected system during the whole fault process, established in Section 3, is a second-order differential equation, which has certain similarity with the synchronous generator swing equation.

Therefore, the transient stability of the system can be analyzed by the EAC [13,14,15,16]. Based on the proposed model, this section applies the EAC to evaluate the system’s transient stability during the whole fault process.

4.1. Transient Stability Analysis During Non-Fault Period

According to Equations (9) and (10), a schematic diagram of transient stability analysis during non-fault period can be drawn, as shown in Figure 6.

From Figure 6, it can be seen that the equivalent mechanical torque T_{m_nor} is equal to the equivalent electromagnetic torque T_{e_nor} during the non-fault period, and the phase δ is δ₀. Since the q-axis component of the PCC voltage u_q = 0 during the non-fault period, the initial phase δ₀ can be derived from Equation (7) as

$${\delta }_0=\arcsin {\displaystyle \frac{{\omega }_{\mathrm{PLL}}{L}_{\mathrm{g}}{i}_{\mathrm{dref}}}{U_{\mathrm{gn}}}}$$

(21)

where i_dref is determined by Equation (1).

4.2. Transient Stability Analysis During Fault Duration Period

After the fault occurs, the dynamic balance of the GFL-PV converter grid-connected system is disrupted, causing the phase δ to increase [21]. According to Equations (11) and (12), a schematic diagram of transient stability analysis during the fault duration period can be drawn, as shown in Figure 7.

According to Figure 7, after the voltage drop fault occurs, the equivalent mechanical torque of the system changes from T_{m_nor} to T_{m_dur}, and the equivalent electromagnetic torque changes from T_{e_nor} to T_{e_dur}. When the voltage drop fault is more serious, the GFL-PV grid-connected system will lose the static equilibrium point (SEP). At this time, Since T_{m_dur} consistently exceeds T_{e_dur}, the resulting torque difference causes an angular frequency deviation of PLL. The angular frequency deviation Δω_PLL continues to increase, which eventually leads to the transient instability of the system, as shown in Figure 7a.

When there is an SEP in the system after the fault occurs, the operating point of the system moves from point A to point B. At this time, T_{m_dur} > T_{e_dur}, and the torque difference will drive the PLL output. The Δω_PLL increases until T_{m_dur} = T_{e_dur}, and the phase of the system increases from δ₀ to δ_SEP1. At this time, the area of the operating point trajectory A → B → C is the acceleration area S₊. The acceleration area S₊ can be given as follows:

$$S_{+}={\displaystyle {\int }_{{\delta }_0}^{{\delta }_{\mathrm{c}}}(T_{\mathrm{m}\_\mathrm{dur}}-T_{\mathrm{e}\_\mathrm{dur}})\mathrm{d}\delta }$$

(22)

When the system operating point reaches C, the Δω_PLL > 0 causes the phase angle difference δ to continue increasing. When the operating point moves from C to D, T_{m_dur} < T_{e_dur} creates a decelerating torque difference Δω_PLL. At this time, the area formed by the operating point trajectory C → D is the deceleration area S₋. The deceleration area S₋ can be given as follows:

$$S_{-}={\displaystyle {\int }_{{\delta }_{\mathrm{c}}}^{{\delta }_{\max }}(T_{\mathrm{e}\_\mathrm{nor}}-T_{\mathrm{m}\_\mathrm{nor}})\mathrm{d}\delta }$$

(23)

Therefore, the transient stability criterion during the fault duration period is as follows: when S₊ < S₋, the system is transiently stable. When S₊ > S₋, the system is transiently unstable [13].

After the fault occurs, if the GFL-PV converter grid-connected system operates in the S₊ > S₋ condition of Figure 7b or Figure 7a; it is imperative to ensure timely fault clearance to maintain normal system operation.

4.3. Transient Stability Analysis During Fault Recovery Period

This paper investigates the transient stability of the GFL-PV converter grid-connected system during the fault recovery period, using the static equilibrium point as a representative case. According to Equations (19) and (20), a schematic diagram of transient stability analysis during fault recovery period can be drawn, as shown in Figure 8.

From the analysis of Section 4.2, it can be seen that phase δ increases after the fault occurs. When the phase increases from δ₀ to δ_c, the system clears the fault. At this time, the equivalent mechanical torque changes from T_{m_dur} to T_{m_cut}, and the equivalent electromagnetic torque changes from T_{e_dur} to T_{e_cut}. As shown in Figure 8, the system operating point first traverses rightward from B₁ along the T_{e_dur} curve, then undergoes a jump to C₁ at δ_c, and finally follows the path C₁ → D₁ → F₁. It can be seen from Figure 8 that the acceleration area is S₁₊, and the deceleration area is S_cut− = S₁₋ + S₂₋. The deceleration area S₋ can be given as follows:

$$\begin{array}{cc}{S}_{\mathrm{cut}-}& ={\displaystyle {\int }_{{\delta }_{\mathrm{c}}}^{{\delta }_{\max }}(T_{\mathrm{e}\_\mathrm{cut}}-T_{\mathrm{m}\_\mathrm{cut}})\mathrm{d}\delta }\hfill \\ & =\underset{S_{1-}}{{\displaystyle {\int }_{{\delta }_{\mathrm{c}}}^{{\delta }_{\max }}(T_{\mathrm{e}\_\mathrm{cut}}-T_{\mathrm{m}\_\mathrm{nor}})\mathrm{d}\delta }}+\underset{S_{2-}}{{\displaystyle {\int }_{{\delta }_{\mathrm{c}}}^{{\delta }_{\max }}(T_{\mathrm{m}\_\mathrm{nor}}-T_{\mathrm{m}\_\mathrm{cut}})\mathrm{d}\delta }}\end{array}$$

(24)

Therefore, the criterion during the fault recovery period is as follows: when S₁₊ < S₁₋ + S₂₋, the system transiently stable; when S₁₊ > S₁₋ + S₂₋, the system is transiently unstable.

The condition for critical stability is equality between the acceleration and deceleration areas, i.e., S₊ = S₋. The corresponding fault clearing time and power angle are known as CCT and the Critical Clearing Angle (CCA) δ_cr.

By comparing Equation (23) with Equation (24), it can be observed that the active power recovery control leads to an increase in the system’s deceleration area. Consequently, active power recovery control enables the system to accommodate a larger acceleration area, thereby permitting higher values for both the CCT and CCA. This observation reveals the underlying reason for the conservatism inherent in traditional transient stability analysis models.

4.4. Impact of Active Power Recovery Rate k on System Transient Stability

Following Equations (19) and (20), Figure 9 shows the transient stability analysis diagram under different active power recovery rates k. In Figure 9, T_{m_cut1} corresponds to the largest value of k, while curve T_{m_cut3} corresponds to the smallest. It can be seen from Figure 9 that when the equivalent electromagnetic torque is T_{m_cut1}, the system deceleration area is S₁₋ + S₂₁₋; when the equivalent electromagnetic torque is T_{m_cut2}, the system deceleration area is S₁₋ + S₂₁₋ + S₂₂₋; and when the equivalent electromagnetic torque is T_{m_cut3}, the system deceleration area is S₁₋ + S₂₁₋ + S₂₂₋ + S₂₃₋. Comparing the deceleration areas under different k, it can be concluded that a smaller k corresponds to a larger deceleration area, which improves the system’s transient stability.

5. Quantitative Calculation of CCT

The above research established a transient model for the whole fault process and employed EAC to analyze the impact of active power recovery control on transient stability. This section focuses on the quantitative calculation of CCT.

By combining Equations (9)–(12), (22), and (23), the previous CCT calculation model can be derived, as shown in Equation (24).

$$\begin{array}{l}{\delta }_{\mathrm{cr}1}=\arccos ({\displaystyle \frac{A+B+C_1}{U_{\mathrm{gn}}-U_{\mathrm{gf}}}})\\ \left\{\begin{array}{l}A=U_{\mathrm{gn}}\cos {\delta }_{\max }-U_{\mathrm{gf}}\cos {\delta }_0\hfill \\ B=({\omega }_{\mathrm{g}}{L}_{\mathrm{g}}{i}_{\mathrm{dref}\_\mathrm{fau}}+R_{\mathrm{g}}{i}_{\mathrm{qref}\_\mathrm{fau}})({\delta }_{\mathrm{c}}-{\delta }_0)\hfill \\ C_1={\omega }_{\mathrm{g}}{L}_{\mathrm{g}}{i}_{\mathrm{dref}}({\delta }_{\max }-{\delta }_{\mathrm{c}})\hfill \end{array}\right.\end{array}$$

(25)

By integrating Equations (9), (10), (19), (20), (22), and (24), the CCT calculation model that accounts for active power recovery control can be derived, as shown in Equation (25).

$$\begin{array}{l}{\delta }_{\mathrm{cr}2}=\arccos ({\displaystyle \frac{A+B+C_2}{U_{\mathrm{gn}}-U_{\mathrm{gf}}}})\\ \left\{\begin{array}{l}A=U_{\mathrm{gn}}\cos {\delta }_{\max }-U_{\mathrm{gf}}\cos {\delta }_0\hfill \\ B=({\omega }_{\mathrm{g}}{L}_{\mathrm{g}}{i}_{\mathrm{dref}\_\mathrm{fau}}+R_{\mathrm{g}}{i}_{\mathrm{qref}\_\mathrm{fau}})({\delta }_{\mathrm{c}}-{\delta }_0)\hfill \\ \begin{array}{l}{C}_2=n{\omega }_{\mathrm{g}}{L}_{\mathrm{g}}{i}_{\mathrm{dref}}({\delta }_{\max }-{\delta }_{\mathrm{c}})\\ n=\left[{\displaystyle \frac{k}{k_1}}{\displaystyle \frac{({\delta }_{\max }-{\delta }_{\mathrm{c}})}{2}}+{\displaystyle \frac{i_{\mathrm{dref}\_\mathrm{fau}}}{i_{\mathrm{dref}}}}\right]\end{array}\hfill \end{array}\right.\end{array}$$

(26)

where n the value is [0, 1].

The CCT calculation model is given as follows [13]:

$$\mathrm{CCT}= t_1-t_0={\displaystyle \frac{{\delta }_{\mathrm{c}}-{\delta }_0}{0.5\sqrt{\frac{S_{+}}{J_{\mathrm{dur}}}}}}$$

(27)

By applying the Newton–Raphson method to solve Equation (26), the CCA can be obtained. This result is then substituted into Equation (27) to determine the CCT that accounts for active power recovery control.

A comparison of Equations (25) and (26) shows that the proposed CCT model, which considers active power recovery control, features an additional coefficient n in the C₂ term. Furthermore, since the CCA calculation model is a decreasing function, C₂ ≤ C₁ always holds, which necessarily implies δ_cr2 ≥ δ_cr1. According to Equation (27), this condition results in a larger CCT when active power recovery control is considered. Therefore, the proposed model in this paper offers the dual advantage of higher accuracy and lower conservatism.

When the recovery rate k is sufficiently high, n approaches 1. Under this condition, the CCT models with and without active power recovery control become identical. This demonstrates that the previous CCT calculation model, which neglects recovery dynamics, constitutes a special case of the proposed CCT calculation model.

6. Simulation Verification

In order to verify the accuracy of the proposed transient model and theory, according to the circuit structure and control strategy of the photovoltaic converter grid-connected system in Figure 1, the simulation model is built in PSCAD/EMTDC. Table 1 gives the parameters of the system. The grid voltage amplitude drop fault is set at 1.2 s, and the drop amplitude is 0.9 p.u.

6.1. Validity Assessment of Transient Model

This paper establishes two case scenarios to assess the validity of the proposed transient model. In Case 1, the fault clearing time is set at 88 ms. In Case 2, the fault clearing time is set at 110 ms. The output results from the proposed model, the previous model, and the simulation model are presented in Figure 10.

As shown in Figure 10a, after fault clearance, both the proposed model and the simulation model indicate that the system remains transiently stable, whereas the previous model predicts transient instability. From Figure 10b, it can be observed that the proposed model, the previous model, and the simulation model all demonstrate transient instability. Therefore, the proposed model in this paper can be effectively applied to assess the transient stability of the system and to calculate a less conservative CCT.

6.2. Transient Stability Analysis Considering Active Power Recovery Control Strategy

Based on the proposed transient model, the critical fault clearing time of 99.9 ms is obtained by using the CCT calculation model in Section 5. In this paper, the fault clearing time of the photovoltaic converter grid-connected system is 99 ms (within CCT) and 103 ms (outside CCT), respectively. The simulation results are shown in Figure 11.

Table 2. Calculation results of acceleration and deceleration area of system with different fault clearing times.

CCT	Fault Clearing Time	Acceleration/Deceleration Area	Stability Analysis Results
within CCT	99 ms	S+ = S−	transient stability
without CCT	103 ms	S+ > S−	transient instability

shows the calculation results of the acceleration and deceleration area of the system with different fault clearing times.

From Figure 11, it can be seen that the fault clearing within CCT can maintain the transient stability of the system, which proves the accuracy of the proposed model. By using the previous model without considering the active power recovery, the CCT is shown in

Table 3. CCT calculation results using different models.

Calculation Model	CCT	CCT in Simulation	Error
Proposed model	99.9 ms	102.9 ms	2.92%
Previous model	90.4 ms	102.9 ms	12.14%

.

As shown in Table 3, the error between the CCT calculated by the proposed model and the simulated CCT is 2.92%, compared to 12.14% for the previous model. This result demonstrates a significant reduction in the conservativeness of the proposed model.

6.3. Impact of Active Power Recovery Rate k on System Transient Stability

In order to verify the impact of the active power recovery rate k on the transient stability of the system, this section uses the fault condition parameters in Table 1, and the fault clearing time is set to 99 ms. The active power recovery rate k is selected as 3 p.u./s, 30 p.u./s and 300 p.u./s, respectively. Based on the simulation model of the photovoltaic converter grid-connected system considering active power recovery control, the transient stability analysis is performed. The simulation results are shown in Figure 12.

It can be seen from Figure 12 that the higher active power recovery rate k after fault clearing adversely affects the transient stability of the system. When the rate k is high enough, it can be regarded as the system not having active power recovery control. Therefore, for the same fault clearing time, the system is more susceptible to transient instability.

Furthermore, CCTs under different active power recovery rates were quantitatively calculated using the proposed model, as presented in

Table 4. CCT calculation results with different k.

Active Power Recovery Rate	CCT Using Proposed Model	CCT in Simulation	Error
3	99.9 ms	102.9 ms	2.92%
30	96.5 ms	100.5 ms	3.98%
300	90.4 ms	98.4 ms	8.13%

. These values were then compared against those from the simulation model to analyze the impact of the active power recovery rate on the system’s transient stability. As observed in Table 4, a higher active power recovery rate leads to a shorter CCT, a trend that is consistently validated by both the proposed and simulation models. However, as the recovery rate increases, the error in CCT between the proposed model and the simulation results also becomes more pronounced.

7. Conclusions

This paper investigates the transient stability of grid-following photovoltaic converter grid-connected systems during the whole fault process. It reveals the influence mechanism of active power recovery control on system transient stability and characterizes the system stability boundary. The specific conclusions are as follows:

(1)

A transient stability analysis model considering the whole fault process is proposed based on the piecewise linear description method. This model addresses the existing gap in characterizing transient behavior throughout the whole fault duration.

(2)

The active power recovery control reduces the equivalent mechanical power during the fault recovery period, thereby increasing the decelerating area and enhancing the system’s transient stability.

(3)

The faster the active power recovery rate, the worse the system’s transient stability; conversely, the slower the recovery rate, the better the transient stability.

(4)

Based on the proposed model, the CCT exhibits lower conservatism, which enhances the accuracy of system transient stability assessment.

The model proposed in this paper can provide a theoretical foundation for transient stability analysis of grid-following photovoltaic converter grid-connected systems and guide fault-clearing operations. For photovoltaic power stations, the electrical distances from individual units to the collection bus vary significantly. Therefore, transient stability modeling, analysis, and control of PV power stations considering active power recovery control will be a key focus of future research.