- Article
Eigenstructure-Oriented Optimization Design of Active Suspension Controllers
- Yulong Du and
- Huping Mao
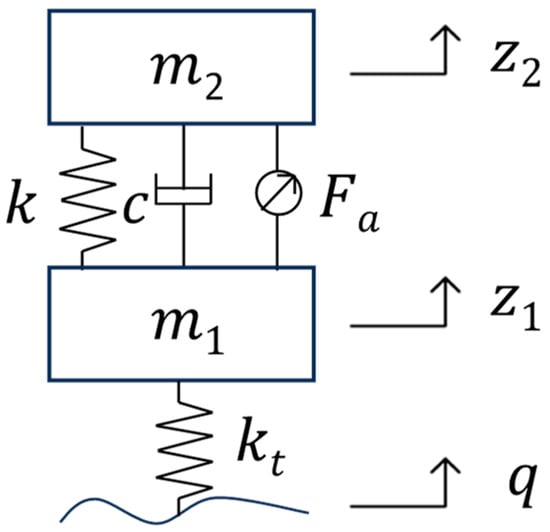
Active suspension systems can significantly enhance vehicle ride comfort and attitude stability, but often at the cost of increased energy consumption. To achieve both high dynamic performance and reduced energy usage, this study proposes an eigenstructure-oriented optimization method for active suspensions. Controller design is reformulated as a synergistic process of modal regulation and dynamic response optimization, in which partial eigenstructure assignment redistributes the dominant modes and system responses are computed using fourth-order Runge–Kutta integration. An energy-minimization optimization problem with performance constraints is then solved via the sequential quadratic programming (SQP) algorithm. Simulation results show that the proposed method markedly improves vibration performance: peak body acceleration is reduced from 3.48 m/s2 to 1.70 m/s2 (a 51.1% reduction), and the root mean square (RMS) acceleration decreases from 0.74 to 0.40 (a 45.6% reduction), while body displacement is also significantly suppressed. Compared with passive suspension and proportional–integral–derivative (PID) active suspension, the proposed system achieves superior performance in key indices such as body acceleration and displacement, leading to noticeably improved ride comfort and attitude stability. Furthermore, robustness analysis indicates that the method remains effective under variations in the receptance matrix, with only minor influence on system performance, demonstrating the practical applicability of the proposed control strategy.
1 January 2026