Physics-Informed Neural Network for Nonlinear Bending Analysis of Nano-Beams: A Systematic Hyperparameter Optimization
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Formulation
2.1.1. Nonlocal Strain Gradient Theory
2.1.2. Governing Equations
2.2. Solution Methodology
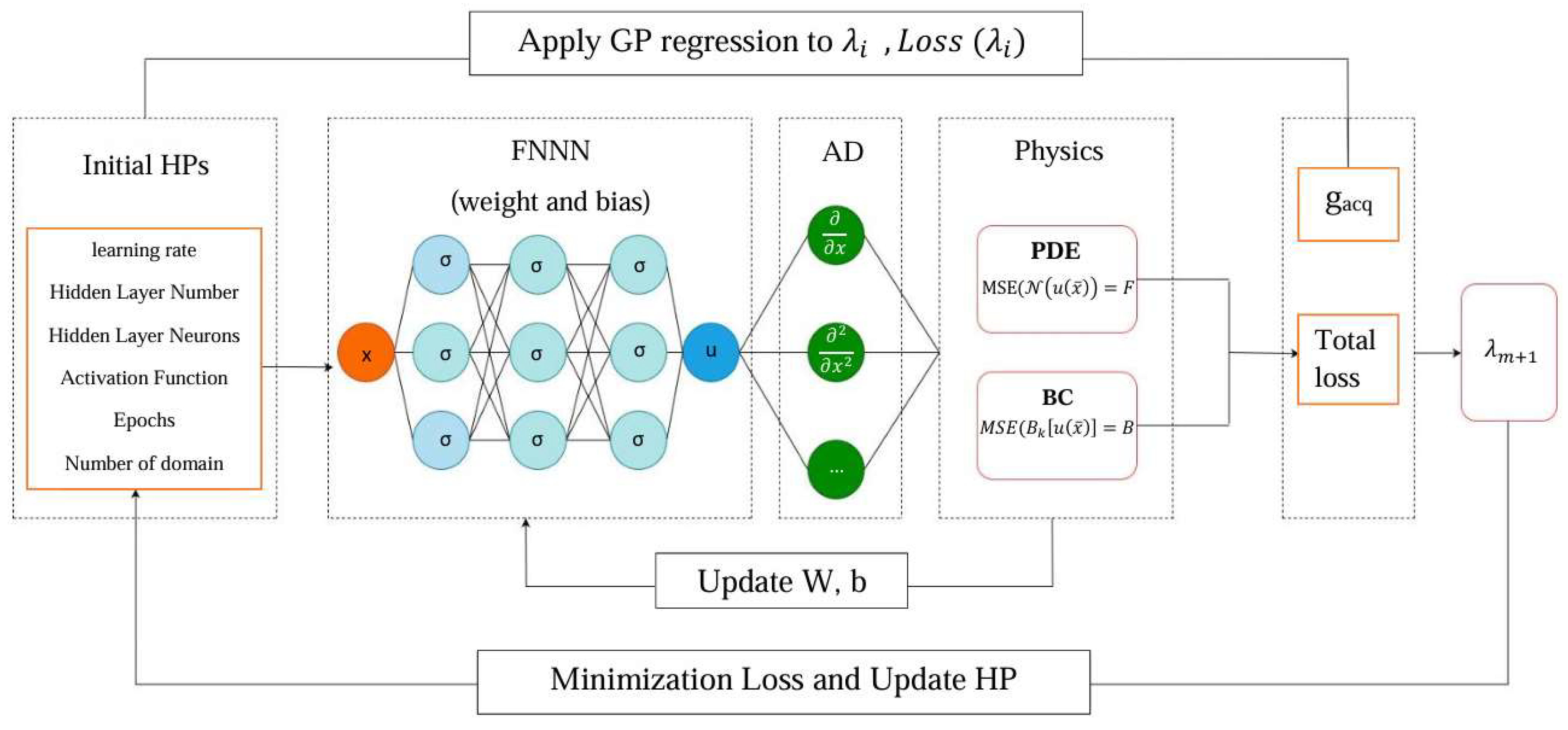
2.2.1. Physics-Informed Neural Network
2.2.2. Training Procedure
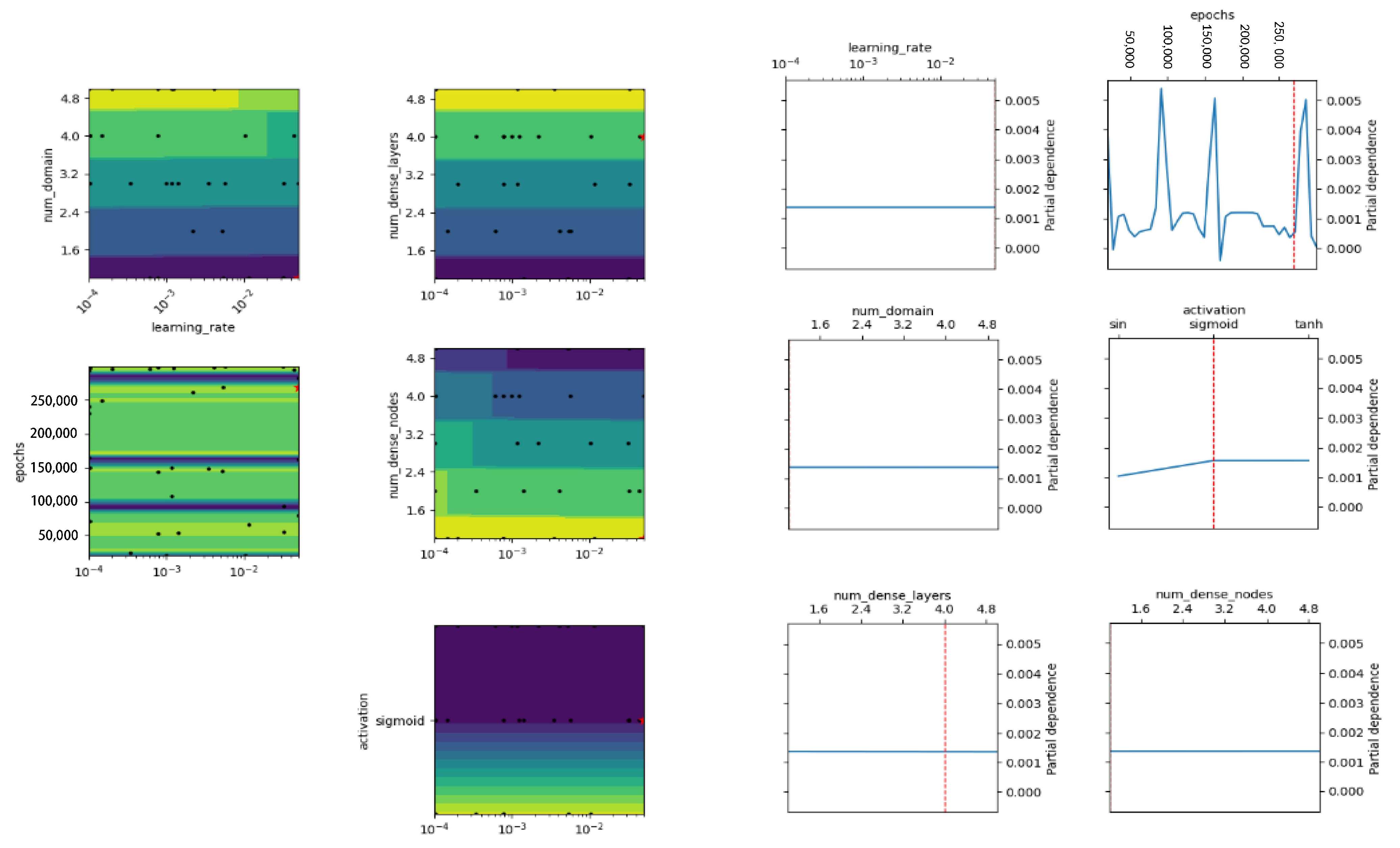
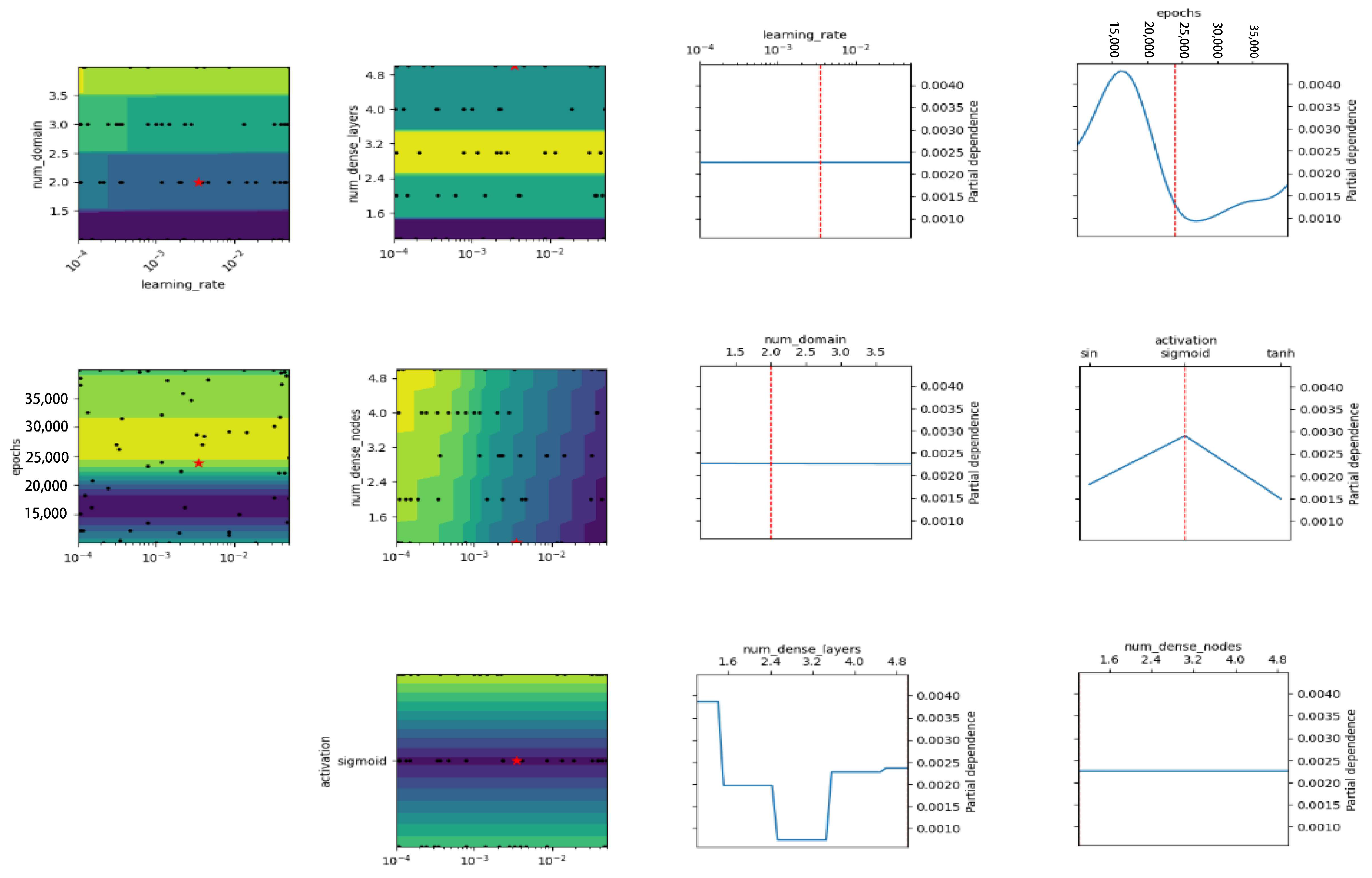
2.2.3. HPO via Gaussian Process-Based Bayesian Optimization
3. Results and Discussion
3.1. HPO via GP for Linear Bending
3.2. HPO via GP for S-S for Nonlinear Bending
3.3. HPO via GP for C-C for Nonlinear Bending
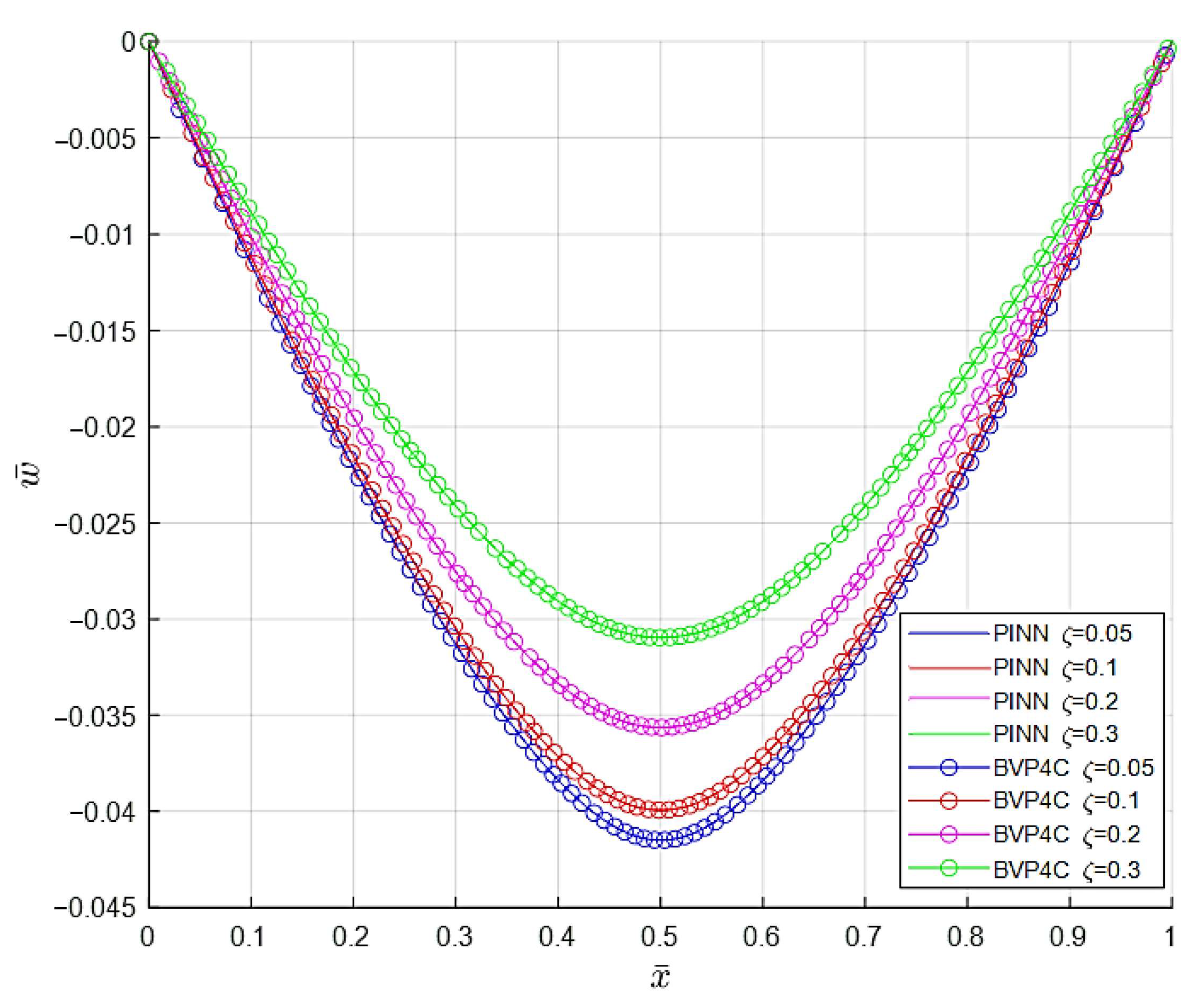
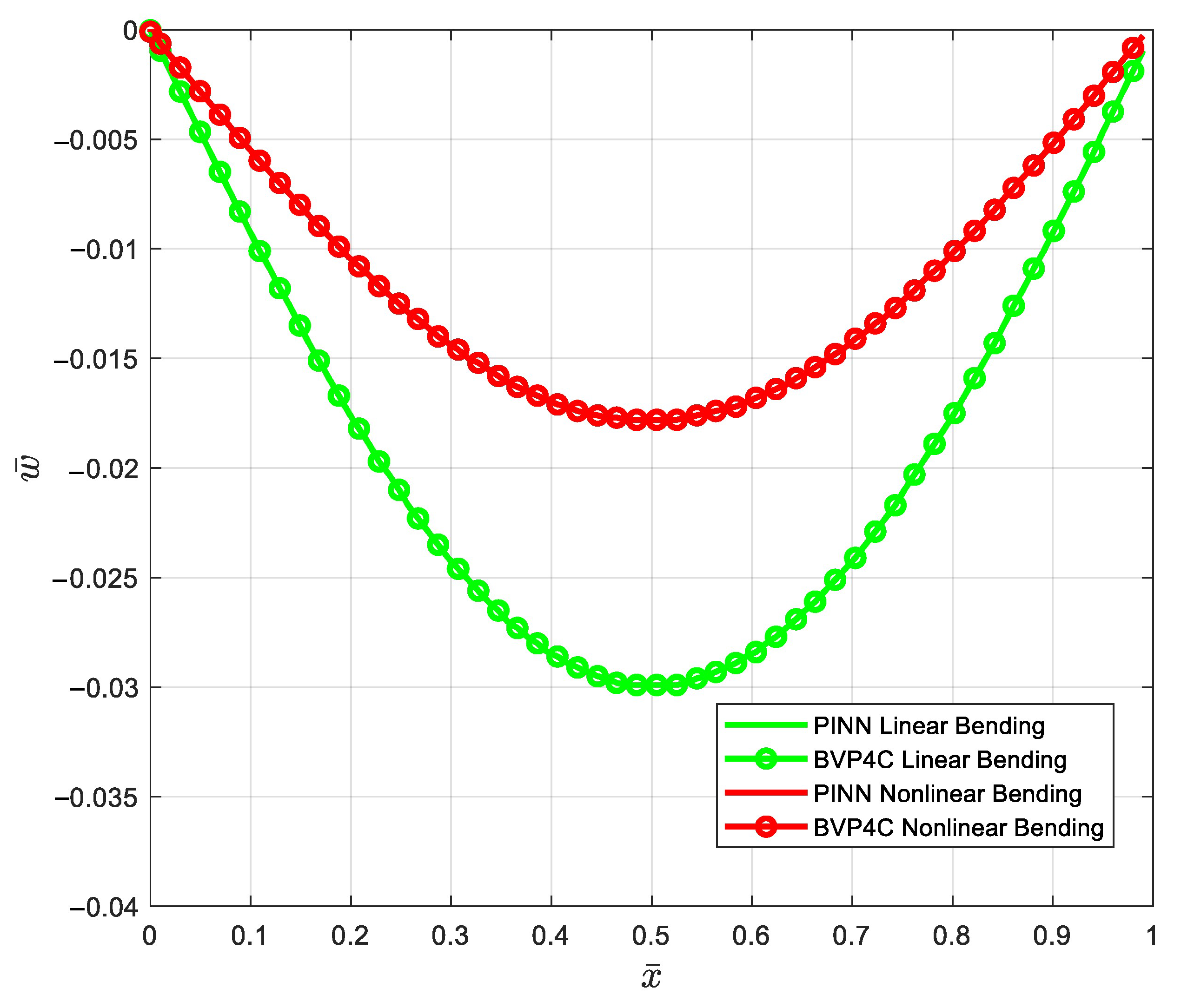
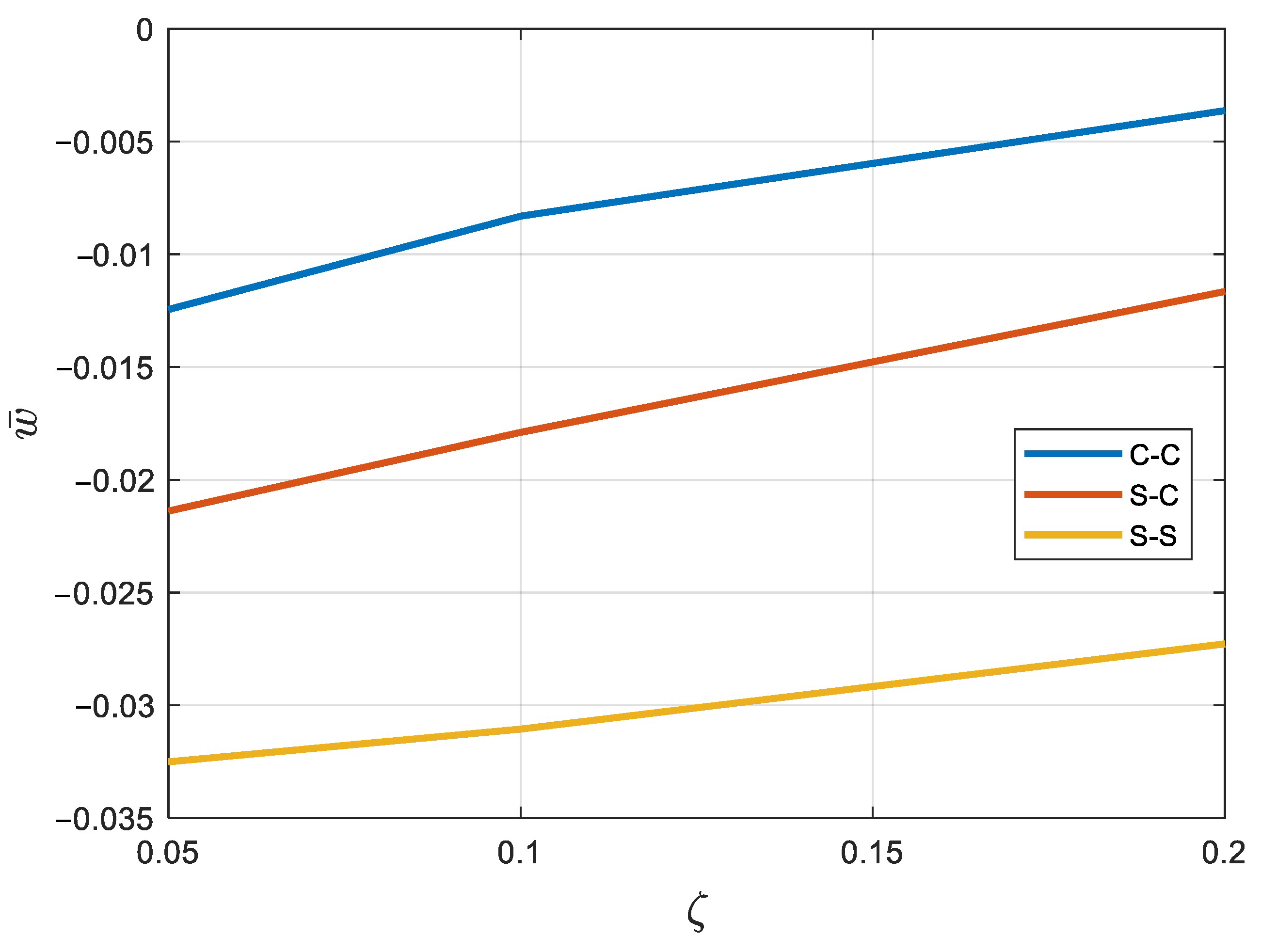
3.4. PINN Results for HPO Hyperparameters
4. Conclusions
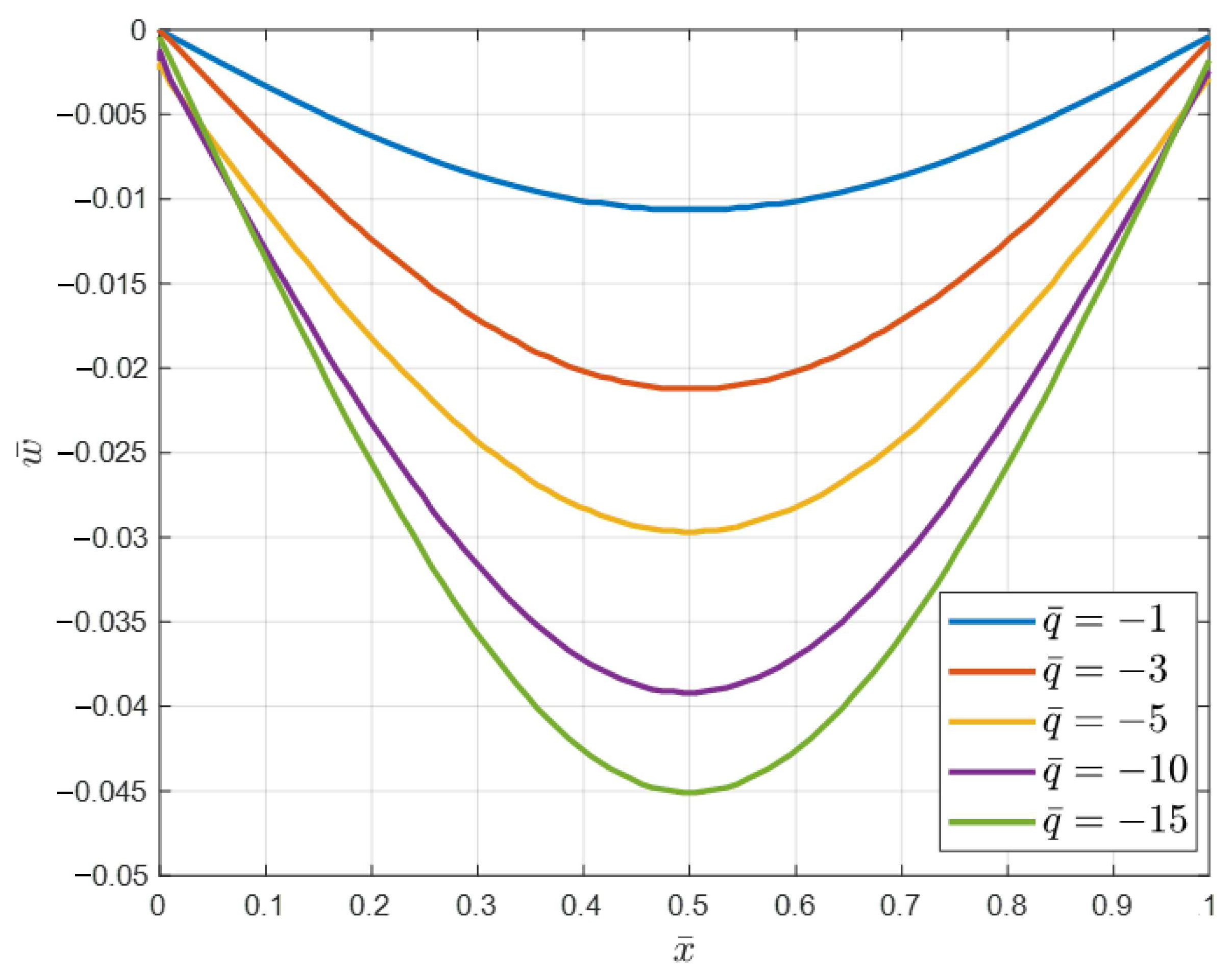
- The results indicate that when the dimensionless strain gradient parameter is elevated, the beam displays decreased deflection. Physically, a higher nonlocal parameter implies that each material point is influenced by a larger neighborhood, effectively increasing the material’s resistance to deformation. As a result, the beam exhibits higher stiffness and consequently lower deflection under the same loading conditions.
- Due to the geometric nonlinearity which causes a stiffening effect, the nonlinear dimensionless bending deflection is smaller than the linear deflection.
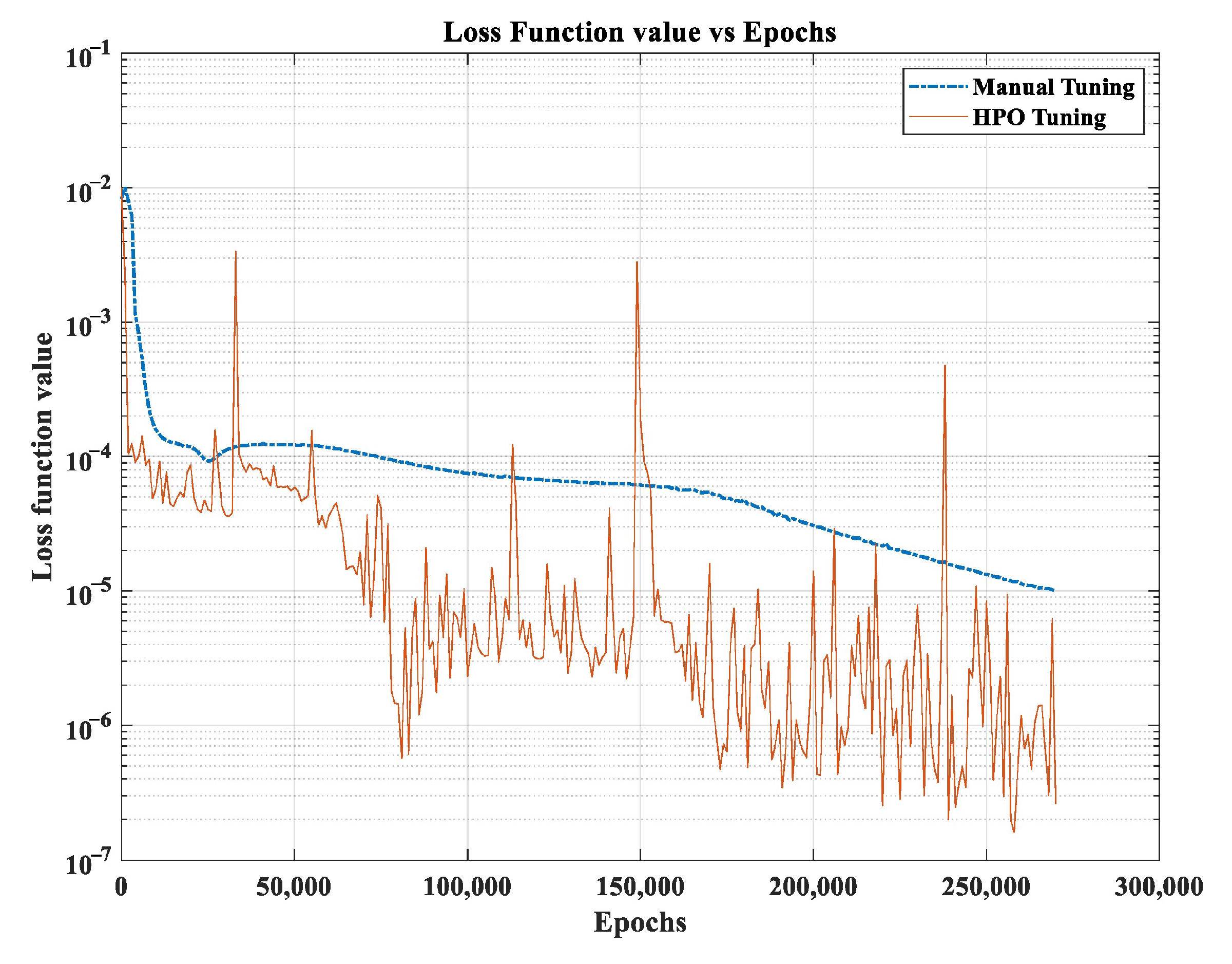
- HPO via GP can decrease the loss function in order to tune the hyperparameters, and the results are more reliable than manually tuning mostly for complicated problems.
- Although the HPO–GP method demonstrates great performance in finding the optimal HPs, decreasing the loss function, and improving accuracy, it comes with a high computational cost limitation, especially when applied to a large number of HPs or complex models.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PINN | Physics-Informed Neural Network |
| NN | Neural Network |
| HP | Hyperparameter |
| HPO | Hyperparameter Optimization |
| GP | Gaussian processes |
| BO | Bayesian Optimization |
References
- Chuang, T.-J.; Anderson, P.; Wu, M.-K.; Hsieh, S. Nanomechanics of Materials and Structures; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Reddy, J. Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 2007, 45, 288–307. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Tang, F.; He, S.; Shi, S.; Xue, S.; Dong, F.; Liu, S. Analysis of size-dependent linear static bending, buckling, and free vibration based on a modified couple stress theory. Materials 2022, 15, 7583. [Google Scholar] [CrossRef] [PubMed]
- Fleck, N.; Hutchinson, J. A reformulation of strain gradient plasticity. J. Mech. Phys. Solids 2001, 49, 2245–2271. [Google Scholar] [CrossRef]
- Gao, H.; Huang, Y.; Nix, W.D.; Hutchinson, J. Mechanism-based strain gradient plasticity—I. Theory. J. Mech. Phys. Solids 1999, 47, 1239–1263. [Google Scholar] [CrossRef]
- Bessaim, A.; Houari, M.S.A.; Bezzina, S.; Merdji, A.; Daikh, A.A.; Belarbi, M.-O.; Tounsi, A. Nonlocal strain gradient theory for bending analysis of 2D functionally graded nanobeams. Struct. Eng. Mech. Int’l J. 2023, 86, 731–738. [Google Scholar]
- Nejad, M.Z.; Hadi, A. Non-local analysis of free vibration of bi-directional functionally graded Euler–Bernoulli nano-beams. Int. J. Eng. Sci. 2016, 105, 1–11. [Google Scholar] [CrossRef]
- Reddy, J. Nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates. Int. J. Eng. Sci. 2010, 48, 1507–1518. [Google Scholar] [CrossRef]
- Mirsadeghi Esfahani, S.S.; Fallah, A.; Mohammadi Aghdam, M. Physics-informed neural network for bending analysis of two-dimensional functionally graded nano-beams based on nonlocal strain gradient theory. J. Comput. Appl. Mech. 2025, 56, 222–248. [Google Scholar]
- Li, X.; Li, L.; Hu, Y.; Ding, Z.; Deng, W. Bending, buckling and vibration of axially functionally graded beams based on nonlocal strain gradient theory. Compos. Struct. 2017, 165, 250–265. [Google Scholar] [CrossRef]
- Hadji, L.; Fallah, A.; Aghdam, M.M. Influence of the distribution pattern of porosity on the free vibration of functionally graded plates. Struct. Eng. Mech. Int’l J. 2022, 82, 151–161. [Google Scholar]
- Thomas, J.W. Numerical Solution of Partial Differential Equations: Finite Difference Methods; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Marzani, A.; Tornabene, F.; Viola, E. Nonconservative stability problems via generalized differential quadrature method. J. Sound Vib. 2008, 315, 176–196. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y. Nonlinear bending and free vibration analyses of nonlocal strain gradient beams made of functionally graded material. Int. J. Eng. Sci. 2016, 107, 77–97. [Google Scholar] [CrossRef]
- Yang, T.; Tang, Y.; Li, Q.; Yang, X.-D. Nonlinear bending, buckling and vibration of bi-directional functionally graded nanobeams. Compos. Struct. 2018, 204, 313–319. [Google Scholar] [CrossRef]
- Shan, W.; Li, B.; Qin, S.; Mo, H. Nonlinear bending and vibration analyses of FG nanobeams considering thermal effects. Mater. Res. Express 2020, 7, 125007. [Google Scholar] [CrossRef]
- Zhang, B.; Shen, H.; Liu, J.; Wang, Y.; Zhang, Y. Deep postbuckling and nonlinear bending behaviors of nanobeams with nonlocal and strain gradient effects. Appl. Math. Mech. 2019, 40, 515–548. [Google Scholar] [CrossRef]
- Abbaspour-Gilandeh, Y.; Molaee, A.; Sabzi, S.; Nabipur, N.; Shamshirband, S.; Mosavi, A. A combined method of image processing and artificial neural network for the identification of 13 Iranian rice cultivars. Agronomy 2020, 10, 117. [Google Scholar] [CrossRef]
- Azarmdel, H.; Jahanbakhshi, A.; Mohtasebi, S.S.; Muñoz, A.R. Evaluation of image processing technique as an expert system in mulberry fruit grading based on ripeness level using artificial neural networks (ANNs) and support vector machine (SVM). Postharvest Biol. Technol. 2020, 166, 111201. [Google Scholar] [CrossRef]
- Brown, B.P.; Mendenhall, J.; Geanes, A.R.; Meiler, J. General Purpose Structure-Based drug discovery neural network score functions with human-interpretable pharmacophore maps. J. Chem. Inf. Model. 2021, 61, 603–620. [Google Scholar] [CrossRef]
- Mignan, A.; Broccardo, M. Neural network applications in earthquake prediction (1994–2019): Meta-analytic and statistical insights on their limitations. Seismol. Res. Lett. 2020, 91, 2330–2342. [Google Scholar] [CrossRef]
- Le Glaz, A.; Haralambous, Y.; Kim-Dufor, D.-H.; Lenca, P.; Billot, R.; Ryan, T.C.; Marsh, J.; Devylder, J.; Walter, M.; Berrouiguet, S. Machine learning and natural language processing in mental health: Systematic review. J. Med. Internet Res. 2021, 23, e15708. [Google Scholar] [CrossRef] [PubMed]
- Brunton, S.L.; Kutz, J.N. Methods for data-driven multiscale model discovery for materials. J. Phys. Mater. 2019, 2, 044002. [Google Scholar] [CrossRef]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef]
- Yaghoubi, V.; Cheng, L.; Van Paepegem, W.; Kersemans, M. CNN-DST: Ensemble deep learning based on Dempster-Shafer theory for vibration-based fault recognition. arXiv 2021, arXiv:2110.07191. [Google Scholar] [CrossRef]
- Yaghoubi, V.; Cheng, L.; Van Paepegem, W.; Kersemans, M. An ensemble classifier for vibration-based quality monitoring. Mech. Syst. Signal Process. 2022, 165, 108341. [Google Scholar] [CrossRef]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A deep learning library for solving differential equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Zhu, Y.; Zabaras, N.; Koutsourelakis, P.-S.; Perdikaris, P. Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. J. Comput. Phys. 2019, 394, 56–81. [Google Scholar] [CrossRef]
- Zhao, H.; Storey, B.D.; Braatz, R.D.; Bazant, M.Z. Learning the physics of pattern formation from images. Phys. Rev. Lett. 2020, 124, 060201. [Google Scholar] [CrossRef]
- Khalid, S.; Yazdani, M.H.; Azad, M.M.; Elahi, M.U.; Raouf, I.; Kim, H.S. Advancements in Physics-Informed Neural Networks for Laminated Composites: A Comprehensive Review. Mathematics 2024, 13, 17. [Google Scholar] [CrossRef]
- Fallah, A.; Aghdam, M.M. Physics-Informed Neural Network for Solution of Nonlinear Differential Equations. In Nonlinear Approaches in Engineering Application: Automotive Engineering Problems; Jazar, R.N., Dai, L., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 163–178. [Google Scholar]
- Haghighat, E.; Raissi, M.; Moure, A.; Gomez, H.; Juanes, R. A physics-informed deep learning framework for inversion and surrogate modeling in solid mechanics. Comput. Methods Appl. Mech. Eng. 2021, 379, 113741. [Google Scholar] [CrossRef]
- Wu, L.; Kilingar, N.G.; Noels, L. A recurrent neural network-accelerated multi-scale model for elasto-plastic heterogeneous materials subjected to random cyclic and non-proportional loading paths. Comput. Methods Appl. Mech. Eng. 2020, 369, 113234. [Google Scholar] [CrossRef]
- Fallah, A.; Aghdam, M.M. Physics-informed neural network for bending and free vibration analysis of three-dimensional functionally graded porous beam resting on elastic foundation. Eng. Comput. 2023, 40, 437–454. [Google Scholar] [CrossRef]
- Bazmara, M.; Silani, M.; Mianroodi, M. Physics-informed neural networks for nonlinear bending of 3D functionally graded beam. Structures 2023, 49, 152–162. [Google Scholar] [CrossRef]
- Kianian, O.; Sarrami, S.; Movahedian, B.; Azhari, M. PINN-based forward and inverse bending analysis of nanobeams on a three-parameter nonlinear elastic foundation including hardening and softening effect using nonlocal elasticity theory. Eng. Comput. 2024, 41, 71–97. [Google Scholar] [CrossRef]
- Eshaghi, M.S.; Bamdad, M.; Anitescu, C.; Wang, Y.; Zhuang, X.; Rabczuk, T. Applications of scientific machine learning for the analysis of functionally graded porous beams. Neurocomputing 2025, 619, 129119. [Google Scholar] [CrossRef]
- Nopour, R.; Fallah, A.; Aghdam, M.M. Large deflection analysis of functionally graded reinforced sandwich beams with auxetic core using physics-informed neural network. Mech. Based Des. Struct. Mach. 2025, 53, 5264–5288. [Google Scholar] [CrossRef]
- Hu, H.; Qi, L.; Chao, X. Physics-informed Neural Networks (PINN) for computational solid mechanics: Numerical frameworks and applications. Thin-Walled Struct. 2024, 205, 112495. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. In Proceedings of the Advances in Neural Information Processing Systems 25 (NIPS 2012), Lake Tahoe, CA, USA, 3–8 December 2012. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. In Proceedings of the Advances in Neural Information Processing Systems 24 (NIPS 2011), Granada, Spain, 12–17 December 2011. [Google Scholar]
- Yu, T.; Zhu, H. Hyper-parameter optimization: A review of algorithms and applications. arXiv 2020, arXiv:2003.05689. [Google Scholar]
- Escapil-Inchauspé, P.; Ruz, G.A. Hyper-parameter tuning of physics-informed neural networks: Application to Helmholtz problems. Neurocomputing 2023, 561, 126826. [Google Scholar] [CrossRef]
- Lim, C.; Zhang, G.; Reddy, J. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Polyzos, D.; Fotiadis, D. Derivation of Mindlin’s first and second strain gradient elastic theory via simple lattice and continuum models. Int. J. Solids Struct. 2012, 49, 470–480. [Google Scholar] [CrossRef]
- Jang, T. A general method for analyzing moderately large deflections of a non-uniform beam: An infinite Bernoulli–Euler–von Kármán beam on a nonlinear elastic foundation. Acta Mech. 2014, 225, 1967–1984. [Google Scholar] [CrossRef]
- Fallah, A.; Aghdam, M.M. Nonlinear free vibration and post-buckling analysis of functionally graded beams on nonlinear elastic foundation. Eur. J. Mech.—A/Solids 2011, 30, 571–583. [Google Scholar] [CrossRef]
- Fallah, A.; Aghdam, M.M. Thermo-mechanical buckling and nonlinear free vibration analysis of functionally graded beams on nonlinear elastic foundation. Compos. Part B Eng. 2012, 43, 1523–1530. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific machine learning through physics–informed neural networks: Where we are and what’s next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- Bazmara, M.; Mianroodi, M.; Silani, M. Application of physics-informed neural networks for nonlinear buckling analysis of beams. Acta Mech. Sin. 2023, 39, 422438. [Google Scholar] [CrossRef]
- Li, W.; Bazant, M.Z.; Zhu, J. A physics-guided neural network framework for elastic plates: Comparison of governing equations-based and energy-based approaches. Comput. Methods Appl. Mech. Eng. 2021, 383, 113933. [Google Scholar] [CrossRef]
- Funahashi, K.-I. On the approximate realization of continuous mappings by neural networks. Neural Netw. 1989, 2, 183–192. [Google Scholar] [CrossRef]
- Zhuang, X.; Guo, H.; Alajlan, N.; Zhu, H.; Rabczuk, T. Deep autoencoder based energy method for the bending, vibration, and buckling analysis of Kirchhoff plates with transfer learning. Eur. J. Mech.—A/Solids 2021, 87, 104225. [Google Scholar] [CrossRef]
- Mhaskar, H.N.; Poggio, T. Deep vs. shallow networks: An approximation theory perspective. Anal. Appl. 2016, 14, 829–848. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 16), Savannah, GA, USA, 2–4 November 2016. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in pytorch. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Bergstra, J.; Breuleux, O.; Bastien, F.; Lamblin, P.; Pascanu, R.; Desjardins, G.; Turian, J.; Warde-Farley, D.; Bengio, Y. Theano: A CPU and GPU math expression compiler. In Proceedings of the Python for Scientific Computing Conference (SciPy), Austin, TX, USA, 28 June–3 July 2010; pp. 1–7. [Google Scholar]
- Chen, T.; Li, M.; Li, Y.; Lin, M.; Wang, N.; Wang, M.; Xiao, T.; Xu, B.; Zhang, C.; Zhang, Z. Mxnet: A flexible and efficient machine learning library for heterogeneous distributed systems. arXiv 2015, arXiv:1512.01274. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]







| Type of Boundary Condition | Constrained Items |
|---|---|
| Free edge | |
| Clamped edge | |
| Simply supported edge |
| HP | LR | NH | σ | Epochs | ND | ||
|---|---|---|---|---|---|---|---|
| Case of Study | |||||||
| C-C | [0.0001, 0.05] | [1, 5] | 5 | ] | [20,000, 300,000] | 50 | |
| S-S | |||||||
| Case | Optimum Loss Value | ) |
|---|---|---|
| C-C | 10−7 | |
| S-S | 10−9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirsadeghi Esfahani, S.S.; Fallah, A.; Mohammadi Aghdam, M. Physics-Informed Neural Network for Nonlinear Bending Analysis of Nano-Beams: A Systematic Hyperparameter Optimization. Math. Comput. Appl. 2025, 30, 72. https://doi.org/10.3390/mca30040072
Mirsadeghi Esfahani SS, Fallah A, Mohammadi Aghdam M. Physics-Informed Neural Network for Nonlinear Bending Analysis of Nano-Beams: A Systematic Hyperparameter Optimization. Mathematical and Computational Applications. 2025; 30(4):72. https://doi.org/10.3390/mca30040072
Chicago/Turabian StyleMirsadeghi Esfahani, Saba Sadat, Ali Fallah, and Mohammad Mohammadi Aghdam. 2025. "Physics-Informed Neural Network for Nonlinear Bending Analysis of Nano-Beams: A Systematic Hyperparameter Optimization" Mathematical and Computational Applications 30, no. 4: 72. https://doi.org/10.3390/mca30040072
APA StyleMirsadeghi Esfahani, S. S., Fallah, A., & Mohammadi Aghdam, M. (2025). Physics-Informed Neural Network for Nonlinear Bending Analysis of Nano-Beams: A Systematic Hyperparameter Optimization. Mathematical and Computational Applications, 30(4), 72. https://doi.org/10.3390/mca30040072







