Mathematical Modelling of Upper Room UVGI in UFAD Systems for Enhanced Energy Efficiency and Airborne Disease Control: Applications for COVID-19 and Tuberculosis
Abstract
1. Introduction
2. Materials and Methods
2.1. Analytical Modeling
2.2. CFD Modeling
2.2.1. Simulated Geometry
2.2.2. Mesh and Grid Independence Analysis
2.2.3. Thermal and Airflow Modeling
2.2.4. Airborne Pathogen Transport and UV Inactivation Modeling
2.2.5. Boundary Conditions
2.2.6. Numerical Solution
3. Energy Analysis
4. Results
4.1. Validation of the CFD-UV Model
- (a)
- In our previous work [46], the current CFD methodology was extensively validated against published experimental UFAD data on air temperature and velocity. It is widely accepted that the ability of the CFD model to accurately predict airflow patterns forms the foundation for reliably predicting the distribution of the pathogenic droplet nuclei concentration, treated as a passive scalar fully governed by the airflow.
- (b)
- The CFD-UV model was experimentally validated in our work [13], where it was proven to reasonably predict the efficacy of UVGI in disinfecting air in a stratified indoor environment at different pathogen-carrying particle sizes with a maximum error of 15%.
4.2. CFD Results
4.3. Substantiation of the Analytical Model
5. Case Study
5.1. System Description
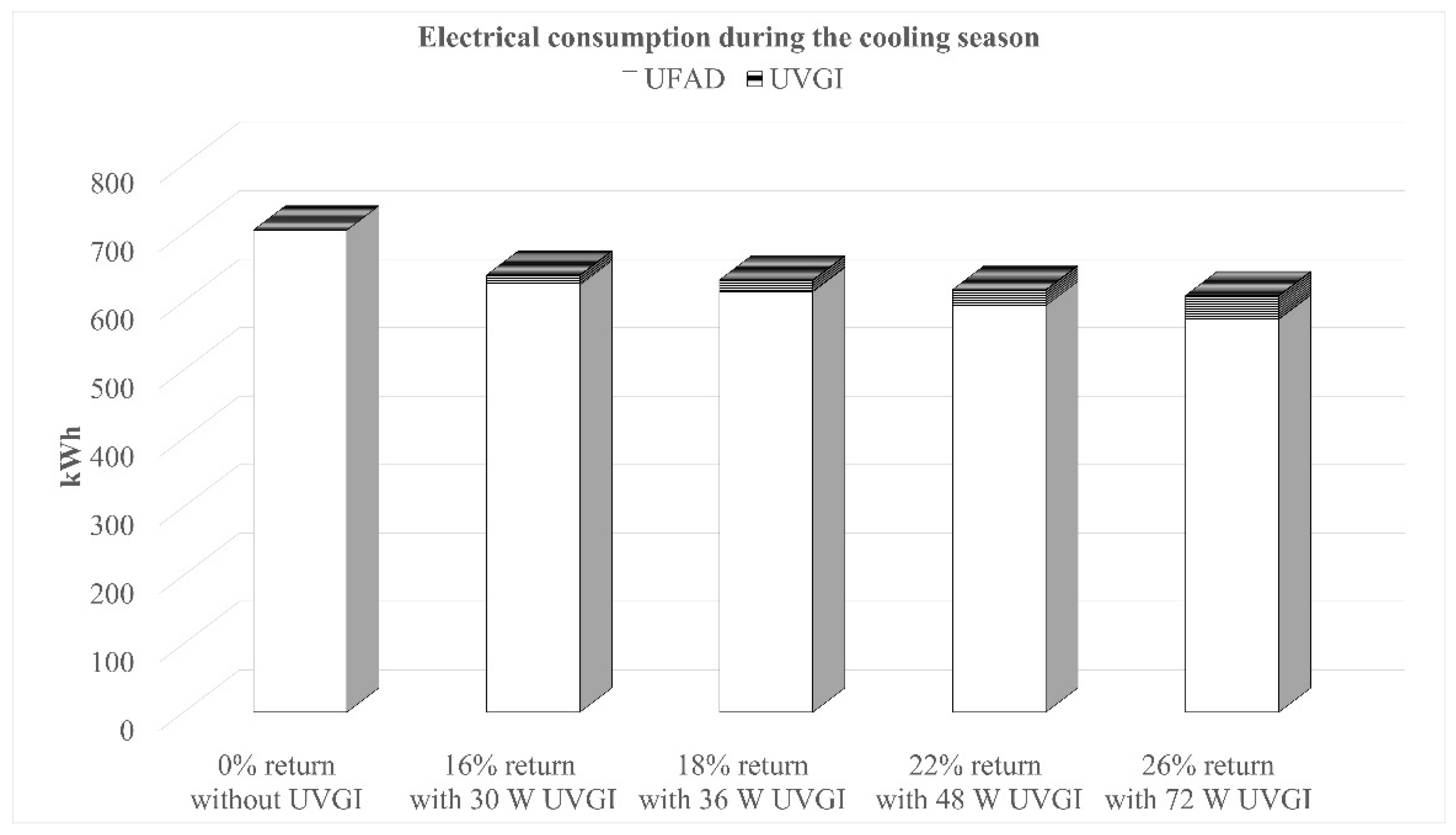
5.2. Results of Energy Simulations
6. Conclusions and Limitations
- The model is unsuitable for extremely high supply velocities, where the jet throw exceeds the terminal plume height. In such cases, the proposed space model becomes invalid, as the flow dynamics require an alternative layering approach.
- The model assumes equal heat sources; however, when heat sources have different strengths, more attention must be given to the terminal height of the plume. In their proposed space model, Habchi et al. [56] recognized the height of the most dominant plume as a crucial determinant in structuring the stratified indoor airflow.
- The model does not account for coalescing plumes, assuming that heat sources are spaced far enough apart to prevent thermal plume interference. However, if plume coalescence occurs below the upper mixing zone, it alters the height of the density interface [57].
- Only adiabatic walls are considered, and wall plumes are therefore excluded from the modeling. However, when warm walls are present, upward wall plumes must be considered, as they entrain air while expanding, facilitate contaminant transport, and affect the air density interface level. Additionally, the effects of thermal radiation and heat gain from the return plenum are disregarded.
- The model is applicable only to low-momentum expiratory activities performed by a seated individual, where the exhaled airflow remains confined within the thermal plume and all droplet nuclei are carried upward by it.
- Gravitational settling of expiratory droplets is neglected in the current modeling approach, as previously discussed. As a result, the model predictions may slightly overestimate the pathogenic concentration in indoor air. However, this provides the advantage of a more cautious and conservative approach for IAQ assessment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Reed, N.G. The History of Ultraviolet Germicidal Irradiation for Air Disinfection. Public Health Rep. 2010, 125, 15–27. [Google Scholar] [CrossRef]
- Nardell, E.A.; Bucher, S.J.; Brickner, P.W.; Wang, C.; Vincent, R.L.; Becan-McBride, K.; James, M.A.; Michael, M.; Wright, J.D. Safety of Upper-Room Ultraviolet Germicidal Air Disinfection for Room Occupants: Results from the Tuberculosis Ultraviolet Shelter Study. Public Health Rep. 2008, 123, 52–60. [Google Scholar] [CrossRef] [PubMed]
- Noakes, C.J.; Sleigh, P.A.; Fletcher, L.A.; Beggs, C.B. Use of CFD Modelling to Optimise the Design of Upper-Room UVGI Disinfection Systems for Ventilated Rooms. Indoor Built Environ. 2006, 15, 347–356. [Google Scholar] [CrossRef]
- Ko, G.; First, M.W.; Burge, H.A. The Characterization of Upper-Room Ultraviolet Germicidal Irradiation in Inactivating Airborne Microorganisms. Environ. Health Perspect. 2002, 110, 95–101. [Google Scholar] [CrossRef] [PubMed]
- Yao, G.; Liu, Z.; Liu, H.; Jiang, C.; Li, Y.; Liu, J.; He, J. Air Disinfection Performance of Upper-Room Ultraviolet Germicidal Irradiation (UR-UVGI) System in a Multi-Compartment Dental Clinic. J. Hazard. Mater. 2024, 477, 135383. [Google Scholar] [CrossRef]
- McDonagh, A.; Noakes, C.; Fletcher, L. Experimentally Evaluating the Effectiveness of an Upper-Room UVGI System. In Proceedings of the 11th REHVA World Congress Clima—Energy Efficient, Smart and Healthy Buildings, Prague, Czech Republic, 16–19 June 2013. [Google Scholar]
- Karam, J.; Ghali, K.; Ghaddar, N. Pulsating Jet Ventilation Add-Ons Performance for Reducing the Contaminant Spread in Classrooms: Portable Air Cleaners vs. Upper Room UVGI. Build. Environ. 2023, 229, 109946. [Google Scholar] [CrossRef]
- Kanaan, M.; Moughlbay, A.A. Comparative CFD Investigation of Upper Room UVGI Efficacy with Three Different Ventilation Systems. Int. J. Appl. Eng. Res. 2018, 13, 14897–14902. [Google Scholar]
- Park, S.; Mistrick, R.; Sitzabee, W.; Rim, D. Effect of Ventilation Strategy on Performance of Upper-Room Ultraviolet Germicidal Irradiation (UVGI) System in a Learning Environment. Sci. Total Environ. 2023, 899, 165454. [Google Scholar] [CrossRef]
- Pichurov, G.; Srebric, J.; Zhu, S.; Vincent, R.L.; Brickner, P.W.; Rudnick, S.N. A Validated Numerical Investigation of the Ceiling Fan’s Role in the Upper-Room UVGI Efficacy. Build. Environ. 2015, 86, 109–119. [Google Scholar] [CrossRef]
- Zhu, S.; Srebric, J.; Rudnick, S.N.; Vincent, R.L.; Nardell, E.A. Numerical Investigation of Upper-Room UVGI Disinfection Efficacy in an Environmental Chamber with a Ceiling Fan. Photochem. Photobiol. 2013, 89, 782–791. [Google Scholar] [CrossRef]
- Won, Y.; Rim, D.; Mistrick, R.; Bahnfleth, W. CFD Modeling of Room Airflow Effects on Inactivation of Aerosol SARS-CoV-2 by an Upper-Room Ultraviolet Germicidal Irradiation (UVGI) System. Sci. Technol. Built Environ. 2023, 29, 719–729. [Google Scholar] [CrossRef]
- Kanaan, M.; Ghaddar, N.; Ghali, K.; Araj, G. Upper Room UVGI Effectiveness with Dispersed Pathogens at Different Droplet Sizes in Spaces Conditioned by Chilled Ceiling and Mixed Displacement Ventilation System. Build. Environ. 2015, 87, 117–128. [Google Scholar] [CrossRef]
- Heidarinejad, G.; Shokrollahi, S.; Pasdarshahri, H. An investigation of thermal comfort, IAQ, and energy saving in UFAD systems using a combination of Taguchi optimization algorithm and CFD. Adv. Build. Energy Res. 2021, 15, 799–817. [Google Scholar] [CrossRef]
- Wang, C.; Shan, J.; Shuhong, L.I. Effect on the Performance of Underfloor Air Distribution (UFAD) system under different supply air parameters. IOP Conf. Ser. Earth Environ. Sci. 2020, 480, 012009. [Google Scholar] [CrossRef]
- Kanaan, M.; Amine, S.; Hmadi, M. Optimized Solar-Powered Evaporative-Cooled UFAD System for Sustainable Thermal Comfort: A Case Study in Riyadh, KSA. Thermo 2025, 5, 26. [Google Scholar] [CrossRef]
- Cheong, C.H.; Park, B.; Ryu, S.R. Effect of under-floor air distribution system to prevent the spread of airborne pathogens in classrooms. Case Stud. Therm. Eng. 2021, 28, 101641. [Google Scholar] [CrossRef]
- Kanaan, M.; Ghaddar, N.; Ghali, K.; Araj, G. New Airborne Pathogen Transport Model for Upper-Room UVGI Spaces Conditioned by Chilled Ceiling and Mixed Displacement Ventilation: Enhancing Air Quality and Energy Performance. Energy Convers. Manag. 2014, 85, 50–61. [Google Scholar] [CrossRef]
- Liu, H.; Liu, Z.; He, J.; Hu, C.; Rong, R.; Han, H.; Wang, L.; Wang, D. Reducing Airborne Transmission of SARS-CoV-2 by an Upper-Room Ultraviolet Germicidal Irradiation System in a Hospital Isolation Environment. Environ. Res. 2023, 237, 116952. [Google Scholar] [CrossRef]
- Fabian, P.; McDevitt, J.J.; DeHaan, W.H.; Fung, R.O.P.; Cowling, B.J.; Chan, K.H.; Leung, G.; Milton, D.K. Influenza Virus in Human Exhaled Breath: An Observational Study. PLoS ONE 2008, 3, e2691. [Google Scholar] [CrossRef]
- Lin, Y.J.P.; Linden, P.F. A Model for an under Floor Air Distribution System. Energy Build. 2005, 37, 399–409. [Google Scholar] [CrossRef]
- LIU, Q.A.; LINDEN, P.F. The Fluid Dynamics of an Underfloor Air Distribution System. J. Fluid Mech. 2006, 554, 323. [Google Scholar] [CrossRef]
- Webster, T.; Bauman, F.; Buhl, F.; Daly, A. Modeling of Underfloor Air Distribution (UFAD) Systems. In Proceedings of the Third National Conference of IBPSA-US, Berkeley, CA, USA, 30 July–1 August 2008. [Google Scholar]
- Jiang, N.; Yao, S.; Feng, L.; Sun, H.; Liu, J. Experimental Study on Flow Behavior of Breathing Activity Produced by a Thermal Manikin. Build. Environ. 2017, 123, 200–210. [Google Scholar] [CrossRef]
- Mundt, E. The Performance of Displacement Ventilation Systems-Experimental and Theoretical Studies. Ph.D. Thesis, Royal Institute of Technology, Stockholm, Sweden, 1996. [Google Scholar]
- Goodfellow, H.D. Industrial Ventilation Design Guidebook; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Kanaan, M. Modelling of Contaminant Dispersion in Underfloor Air Distribution Systems: Comparison of Analytical and CFD Methods. J. Build. Perform. Simul. 2019, 12, 759–769. [Google Scholar] [CrossRef]
- Rodi, W. Turbulent Buoyant Jets and Plumes: HMT: The Science & Applications of Heat and Mass Transfer. Reports, Reviews & Computer Programs; Elsevier: Amsterdam, The Netherlands, 2014; Volume 6. [Google Scholar]
- Kanaan, M.; Ghaddar, N.; Ghali, K. Simplified Model of Contaminant Dispersion in Rooms Conditioned by Chilled-Ceiling Displacement Ventilation System. HVACR Res. 2010, 16, 765–783. [Google Scholar] [CrossRef]
- Miller, S.L.; MacHer, J.M. Evaluation of a Methodology for Quantifying the Effect of Room Air Ultraviolet Germicidal Irradiation on Airborne Bacteria. Aerosol Sci. Technol. 2000, 33, 274–295. [Google Scholar] [CrossRef]
- Heidarinejad, M.; Srebric, J. Computational Fluid Dynamics Modelling of UR-UVGI Lamp Effectiveness to Promote Disinfection of Airborne Microorganisms. World Rev. Sci. Technol. Sustain. Dev. 2013, 10, 78. [Google Scholar] [CrossRef]
- Beggs, C.B.; Avital, E.J. Upper-Room Ultraviolet Air Disinfection Might Help to Reduce COVID-19 Transmission in Buildings: A Feasibility Study. PeerJ 2020, 8, e10196. [Google Scholar] [CrossRef]
- Walker, C.M.; Ko, G. Effect of Ultraviolet Germicidal Irradiation on Viral Aerosols. Environ. Sci. Technol. 2007, 41, 5460–5465. [Google Scholar] [CrossRef]
- Hauke, G.; Lanzarote, J. Computing Buoyancy Flows with Stabilized Finite Volume Method. In Proceedings of the Sixteenth International Conference Zaragoza-Pau on Mathematics and its Applications, Jaca, Spain, 7–9 September 2024. [Google Scholar]
- Barletta, A. The Boussinesq Approximation for Buoyant Flows. Mech. Res. Commun. 2022, 124, 103939. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. CFD Simulations of Near-Field Pollutant Dispersion with Different Plume Buoyancies. Build. Environ. 2018, 131, 128–139. [Google Scholar] [CrossRef]
- Lee, Y.-T.; Wen, C.-Y.; Shih, Y.-C.; Li, Z.; Yang, A.-S. Numerical and Experimental Investigations on Thermal Management for Data Center with Cold Aisle Containment Configuration. Appl. Energy 2022, 307, 118213. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Q. Comparison of the Eulerian and Lagrangian Methods for Predicting Particle Transport in Enclosed Spaces. Atmos. Environ. 2007, 41, 5236–5248. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Z.; Li, X.; Zhao, M.; Liu, Y. A Modified Turbulence Model for Simulating Airflow Aircraft Cabin Environment with Mixed Convection. Build. Simul. 2020, 13, 665–675. [Google Scholar] [CrossRef] [PubMed]
- Hathway, E.A.; Noakes, C.J.; Sleigh, P.A.; Fletcher, L.A. CFD Simulation of Airborne Pathogen Transport Due to Human Activities. Build. Environ. 2011, 46, 2500–2511. [Google Scholar] [CrossRef]
- Wu, C.L.; Yang, Y.; Wong, S.L.; Lai, A.C.K. A New Mathematical Model for Irradiance Field Prediction of Upper-Room Ultraviolet Germicidal Systems. J. Hazard. Mater. 2011, 189, 173–185. [Google Scholar] [CrossRef]
- Cao, Q.; Liu, M.; Li, X.; Lin, C.-H.; Wei, D.; Ji, S.; Zhang, T.; Chen, Q. Influencing Factors in the Simulation of Airflow and Particle Transportation in Aircraft Cabins by CFD. Build. Environ. 2022, 207, 108413. [Google Scholar] [CrossRef] [PubMed]
- Alsaad, H.; Voelker, C. Performance Assessment of a Ductless Personalized Ventilation System Using a Validated CFD Model. J. Build. Perform. Simul. 2018, 11, 689–704. [Google Scholar] [CrossRef]
- Izadyar, N.; Miller, W.; Rismanchi, B.; Garcia-Hansen, V. Numerical Simulation of Single-Sided Natural Ventilation: Impacts of Balconies Opening and Depth Scale on Indoor Environment. IOP Conf. Ser. Earth Environ. Sci. 2020, 463, 012037. [Google Scholar] [CrossRef]
- TLVs and BEIs; American Conference of Governmental Industrial Hygienists: Cincinnati, OH, USA, 1999.
- Kanaan, M.; Amine, S.; Gazo-Hanna, E. Optimizing Supply Conditions and Use of Return Air in UFAD System: Assessment of IAQ, Thermal Comfort and Energy Performance. Results Eng. 2024, 24, 103426. [Google Scholar] [CrossRef]
- Heseltine, E.; Rosen, J. WHO Guidelines for Indoor Air Quality: Dampness and Mould; World Health Organization: Geneva, Switzerland, 2009. [Google Scholar]
- World Health Organization. Indoor Air Quality: Biological Contaminants: Report on a WHO Meeting; World Health Organization Regional Office for Europe: Copenhagen, Denmark, 1988. [Google Scholar]
- Environmental Control for Tuberculosis: Basic Upper-Room Ultraviolet Germicidal Irradiation Guidelines for Healthcare Settings. Available online: https://www.govinfo.gov/app/details/GOVPUB-HE20_7000-PURL-gpo148482 (accessed on 21 July 2025).
- Zhao, W.; Lestinen, S.; Guo, M.; Kilpeläinen, S.; Jokisalo, J.; Kosonen, R. An Experimental Study on Airborne Transmission in a Meeting Room with Different Air Distribution Methods. Build. Environ. 2024, 256, 111522. [Google Scholar] [CrossRef]
- Mahaki, M.; Mattsson, M.; Salmanzadeh, M.; Hayati, A. Comparing Objects for Human Movement Simulation Regarding Its Air Flow Disturbance at Local Exhaust Ventilation. Energy Build. 2021, 247, 111117. [Google Scholar] [CrossRef]
- Lo, L.J.; Novoselac, A. Localized Air-Conditioning with Occupancy Control in an Open Office. Energy Build. 2010, 42, 1120–1128. [Google Scholar] [CrossRef]
- Habchi, C.; Ghali, K.; Ghaddar, N.; Chakroun, W.; Alotaibi, S. Ceiling Personalized Ventilation Combined with Desk Fans for Reduced Direct and Indirect Cross-Contamination and Efficient Use of Office Space. Energy Convers. Manag. 2016, 111, 158–173. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, L.; Qian, H. The Penetration Phenomenon of the Expiratory Airflow from Thermal Plume of Human Body in the Microenvironment around People. Build. Environ. 2024, 259, 111656. [Google Scholar] [CrossRef]
- ASHRAE Handbook—Fundamentals; American Society of Heating Refrigerating and Air-Conditioning Engineers: New York, NY, USA, 2021.
- Habchi, C.; Ghali, K.; Ghaddar, N. A Simplified Mathematical Model for Predicting Cross Contamination in Displacement Ventilation Air-Conditioned Spaces. J. Aerosol Sci. 2014, 76, 72–86. [Google Scholar] [CrossRef]
- Sodec, F. The Underfloor Air Supply System–The European Experience. In Proceedings of the ASHRAE Transactions, San Diego, CA, USA, 24–28 June 1990; ASHRAE Transactions: New York, NY, USA, 1990. [Google Scholar]

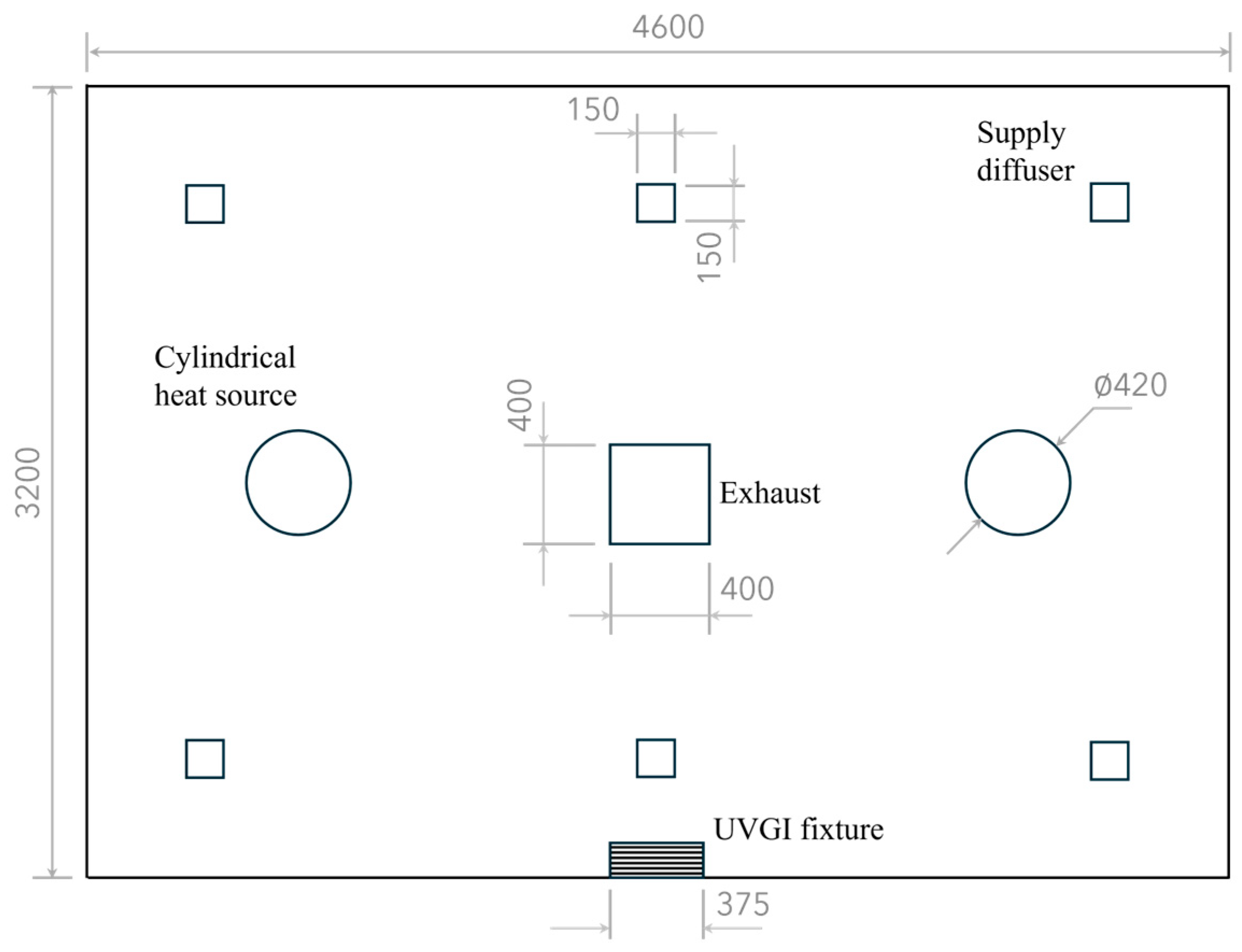

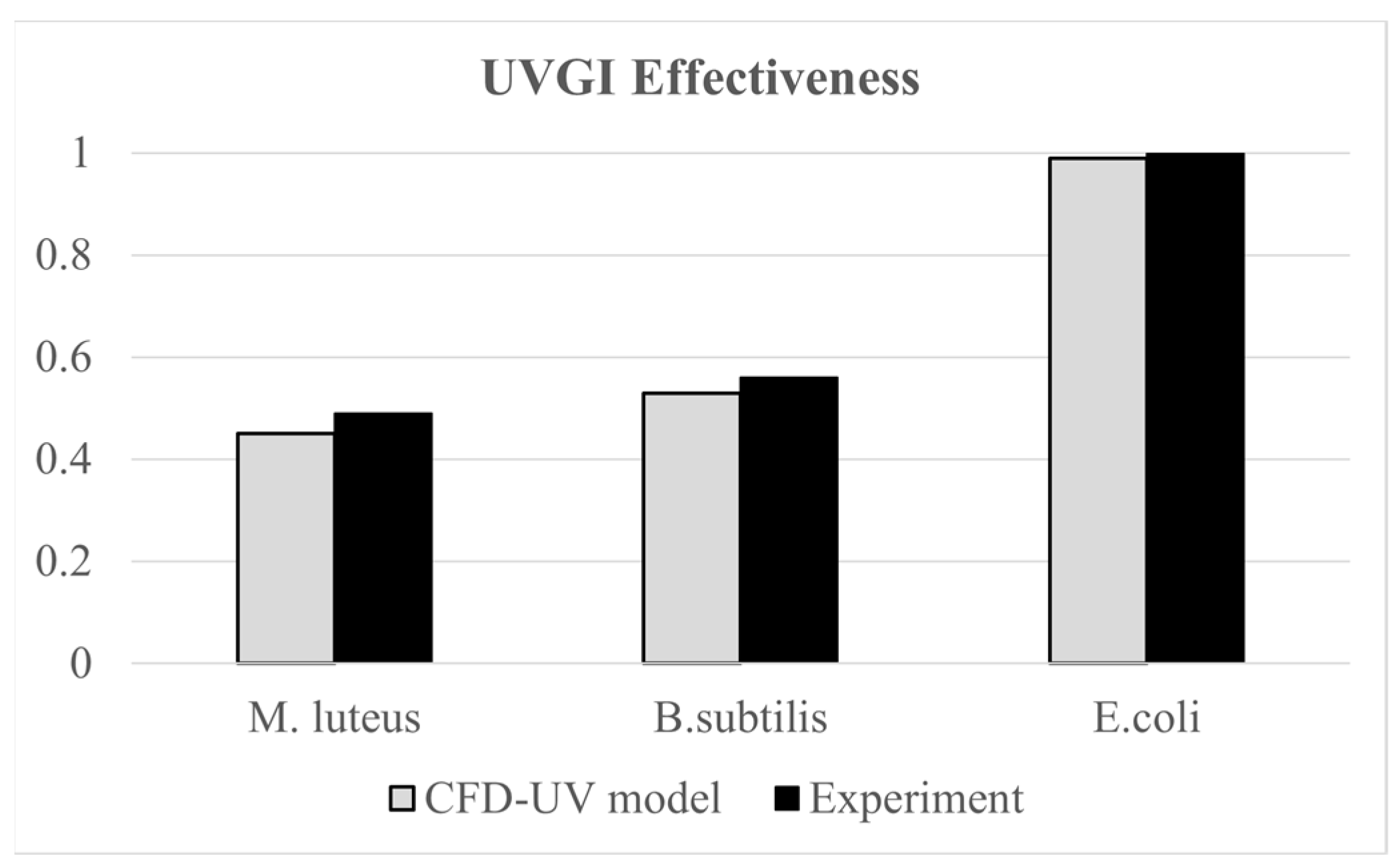

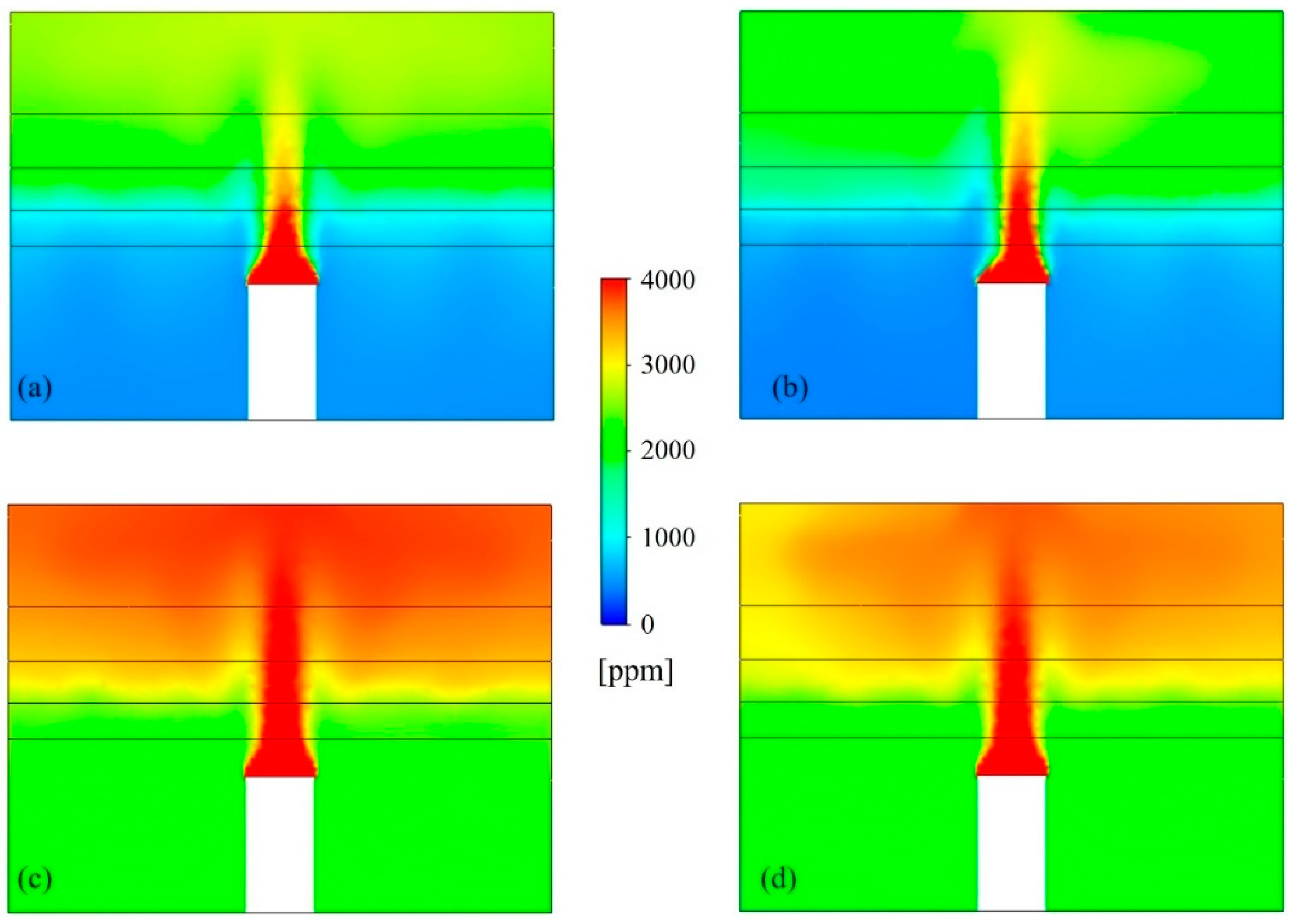

| Mesh Size | Average Temperature at the Exhaust, Kelvins | Average Velocity at the Exhaust, m/s | Average Virus Mole Fraction at the Exhaust |
|---|---|---|---|
| M1 (492,186 cells) | 297.015 | 0.380 | 0.00327 |
| M2 (934,792 cells) | 297.195 | 0.408 | 0.00248 |
| M3 (1,294,598 cells) | 297.198 | 0.411 | 0.00241 |
| Object | Boundary Type | Details |
|---|---|---|
| Supply diffuser | Velocity inlet | V = 0.4 m/s, T = 18 °C, species mole fraction: zero for the 100% fresh air case and the profile via UDF for return air recirculation, turbulent intensity: 5%, hydraulic diameter: 0.15 m |
| Pathogen source | Velocity inlet | Diameter: 1 cm, V = 0.42 m/s, T = 34 °C, species mole fraction: 1 |
| Exhaust/return vent | Outflow | Default values |
| Heated cylinder | No-slip | Heat flux: 51.18 W/m2 |
| Ceiling | No-slip | Heat flux (lighting): 12 W/m2 |
| UVGI fixture | No-slip | Heat flux: 84.3 W/m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanaan, M.; Gazo-Hanna, E.; Amine, S. Mathematical Modelling of Upper Room UVGI in UFAD Systems for Enhanced Energy Efficiency and Airborne Disease Control: Applications for COVID-19 and Tuberculosis. Math. Comput. Appl. 2025, 30, 85. https://doi.org/10.3390/mca30040085
Kanaan M, Gazo-Hanna E, Amine S. Mathematical Modelling of Upper Room UVGI in UFAD Systems for Enhanced Energy Efficiency and Airborne Disease Control: Applications for COVID-19 and Tuberculosis. Mathematical and Computational Applications. 2025; 30(4):85. https://doi.org/10.3390/mca30040085
Chicago/Turabian StyleKanaan, Mohamad, Eddie Gazo-Hanna, and Semaan Amine. 2025. "Mathematical Modelling of Upper Room UVGI in UFAD Systems for Enhanced Energy Efficiency and Airborne Disease Control: Applications for COVID-19 and Tuberculosis" Mathematical and Computational Applications 30, no. 4: 85. https://doi.org/10.3390/mca30040085
APA StyleKanaan, M., Gazo-Hanna, E., & Amine, S. (2025). Mathematical Modelling of Upper Room UVGI in UFAD Systems for Enhanced Energy Efficiency and Airborne Disease Control: Applications for COVID-19 and Tuberculosis. Mathematical and Computational Applications, 30(4), 85. https://doi.org/10.3390/mca30040085







