Spherical Shape Functions for a Six-Node Tri-Rectangular Prism and an Eight-Node Quadrangular Right Prism
Abstract
1. Introduction
2. Mathematical Formulation
2.1. Functions R(r)
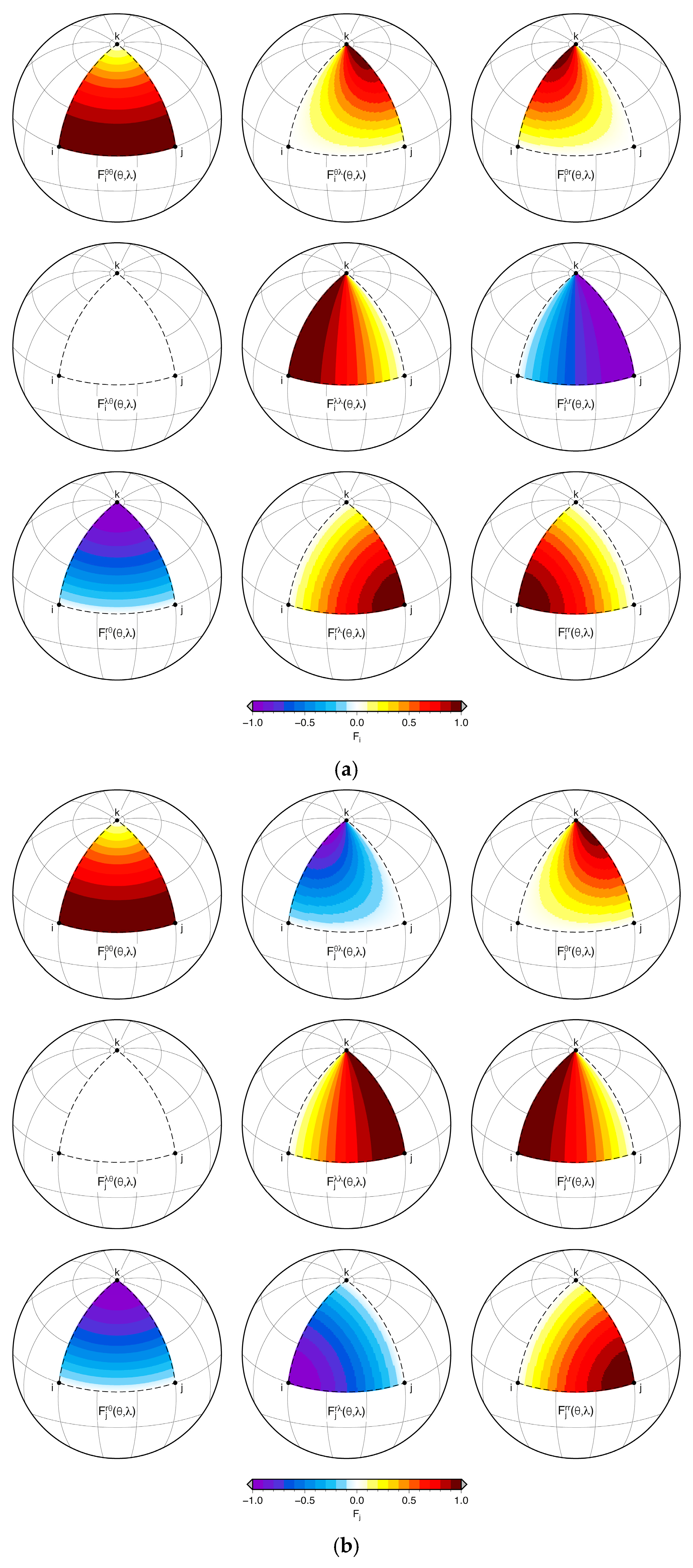
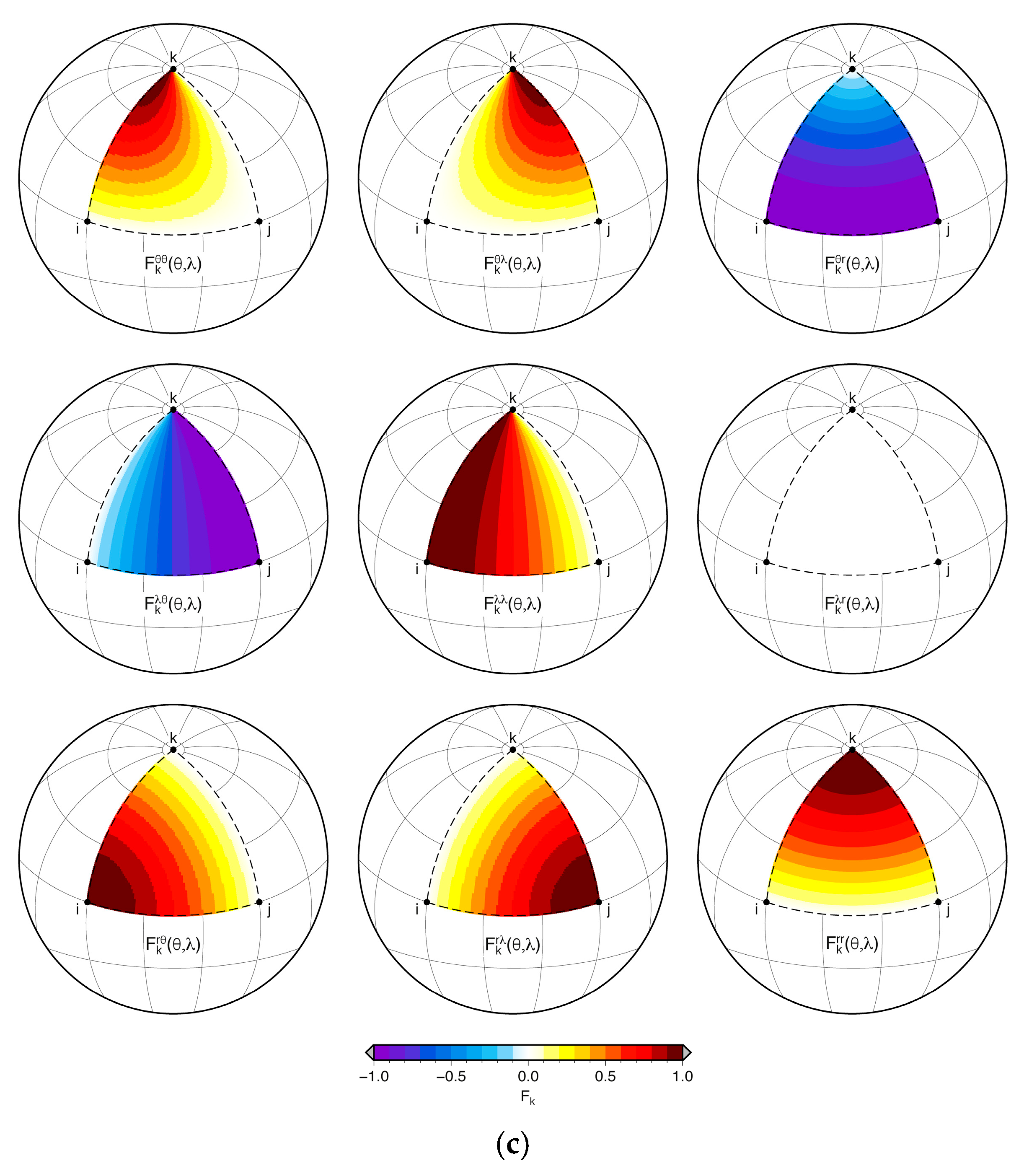
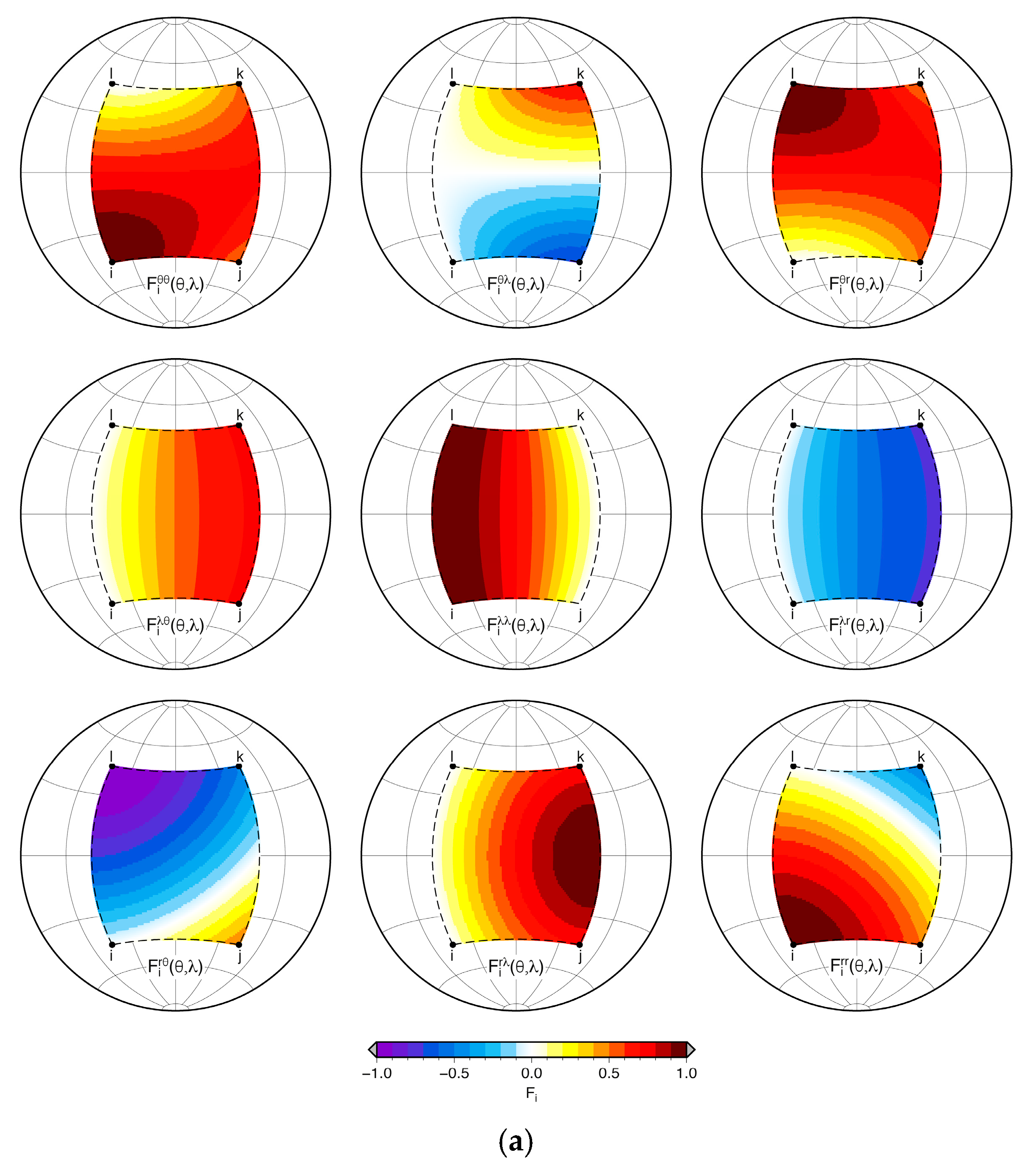
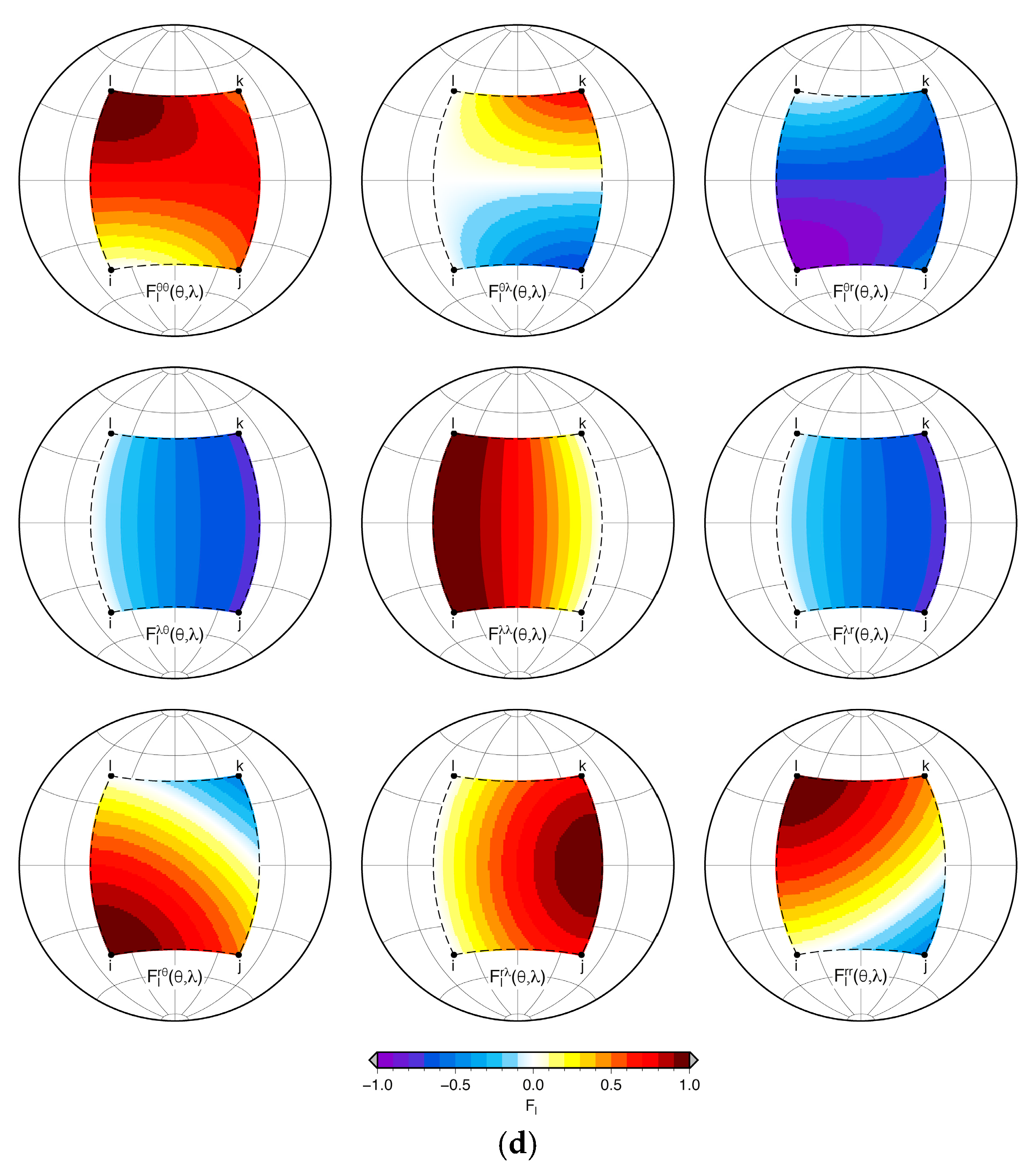
2.2. Functions F(θ,λ)
2.3. Functions A(θ,λ)
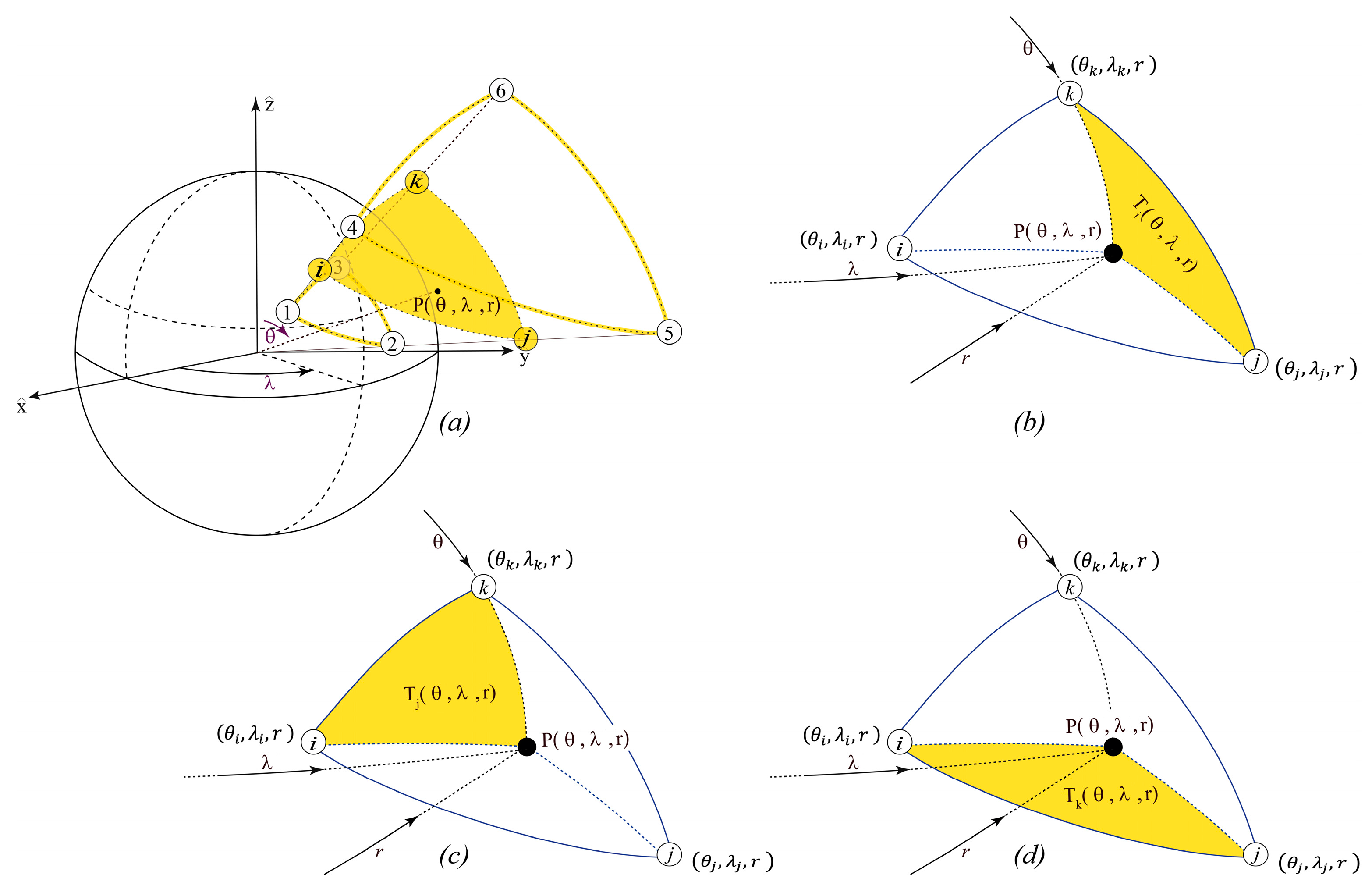
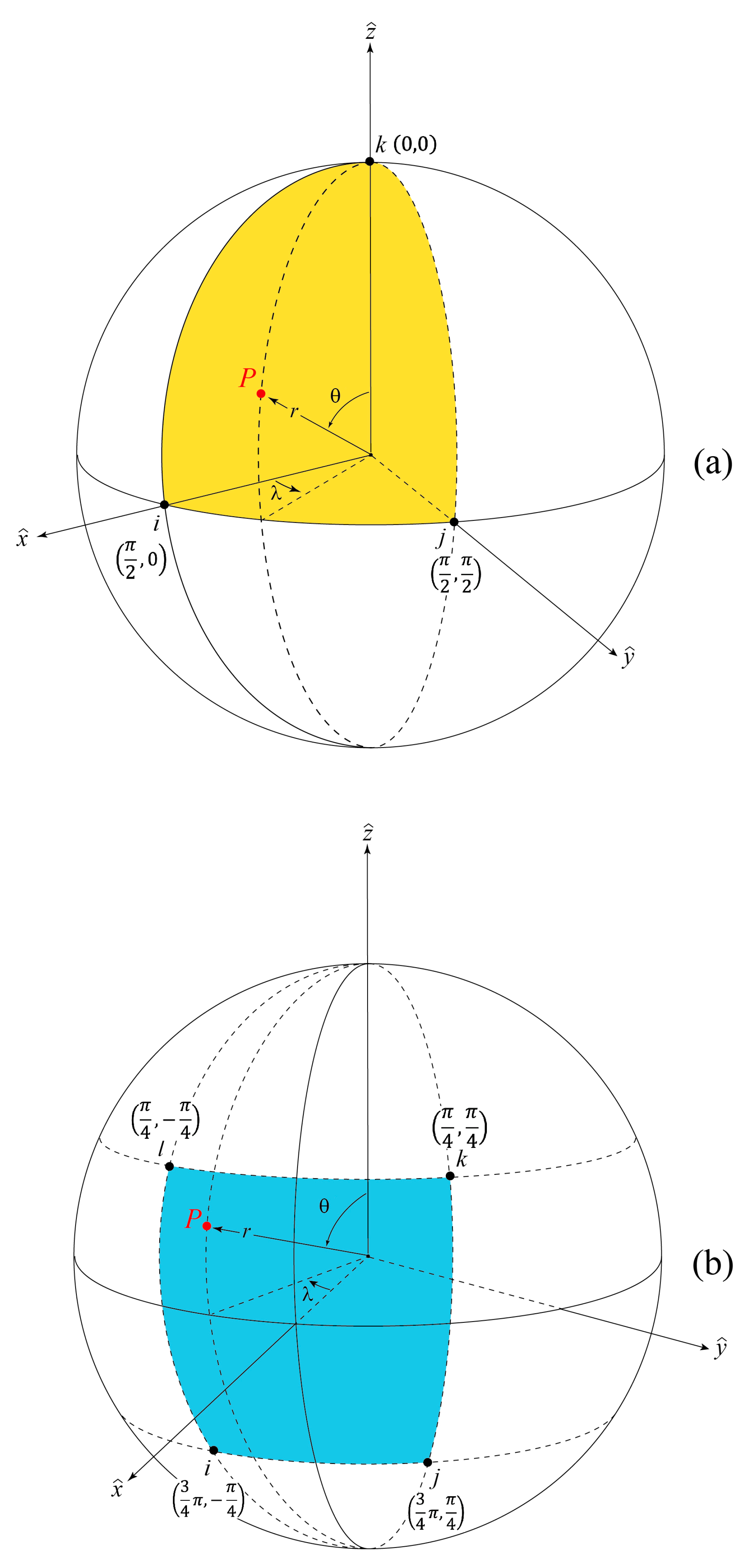
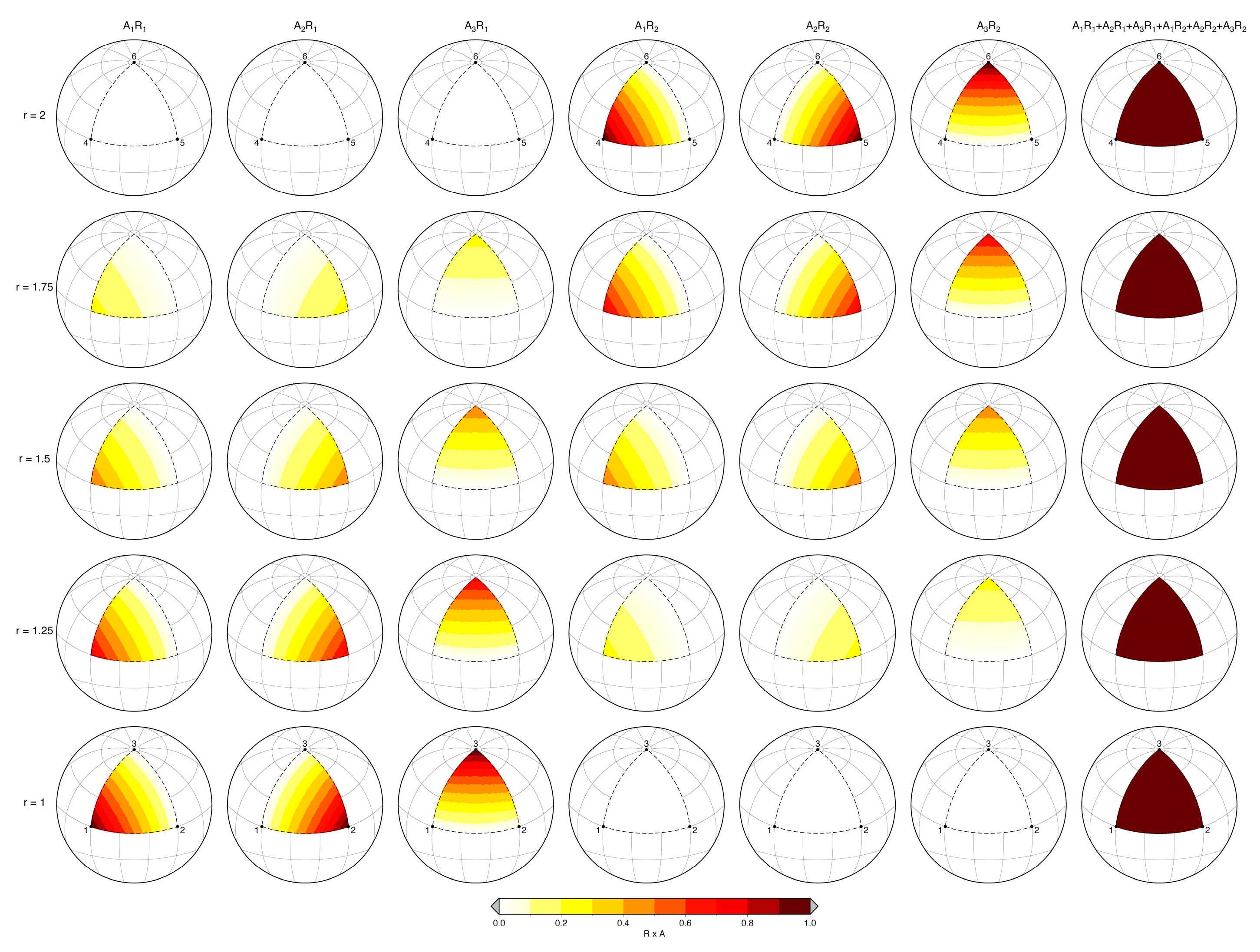
2.3.1. Spherical Six-Node Triangular Prism
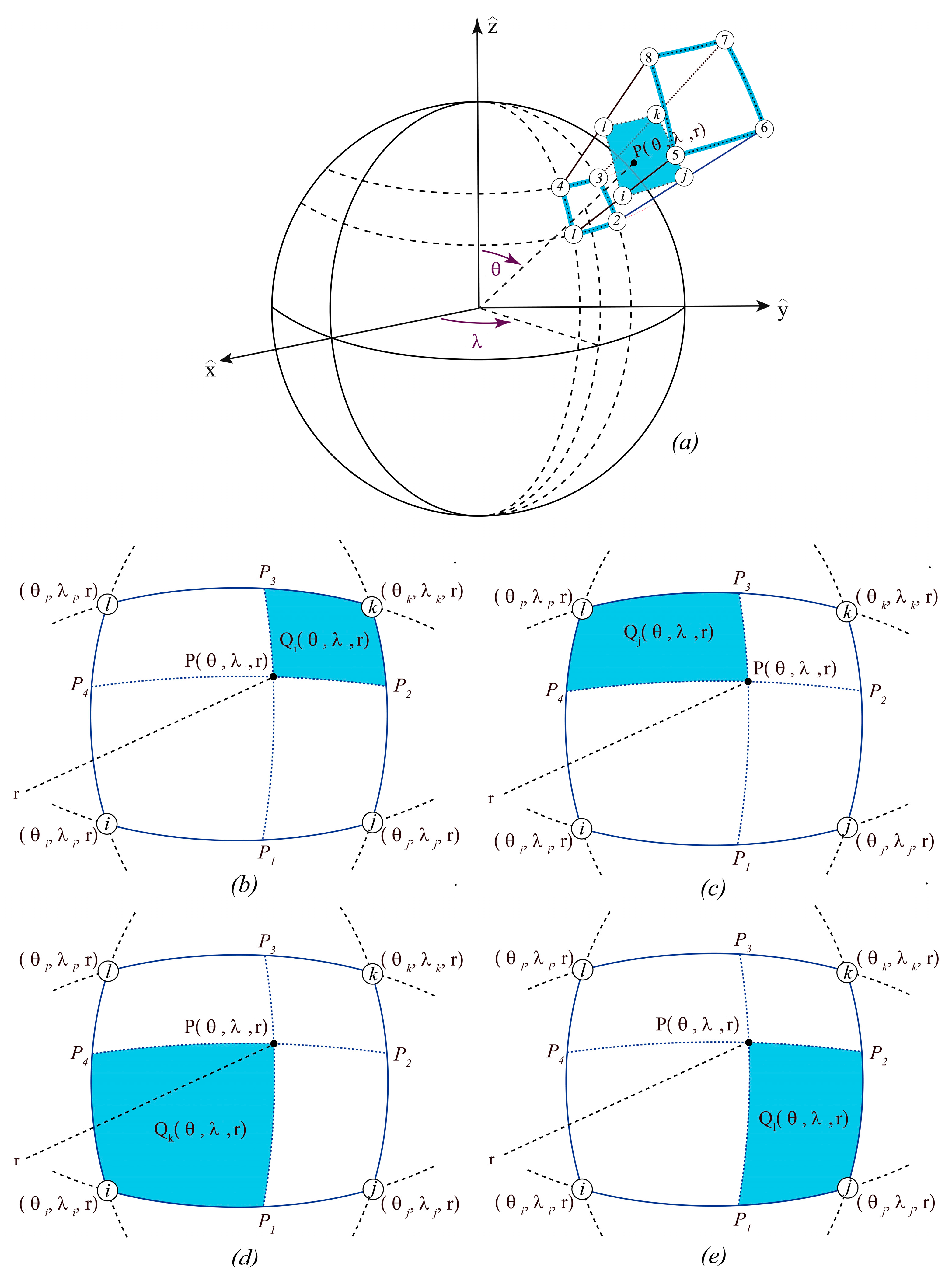
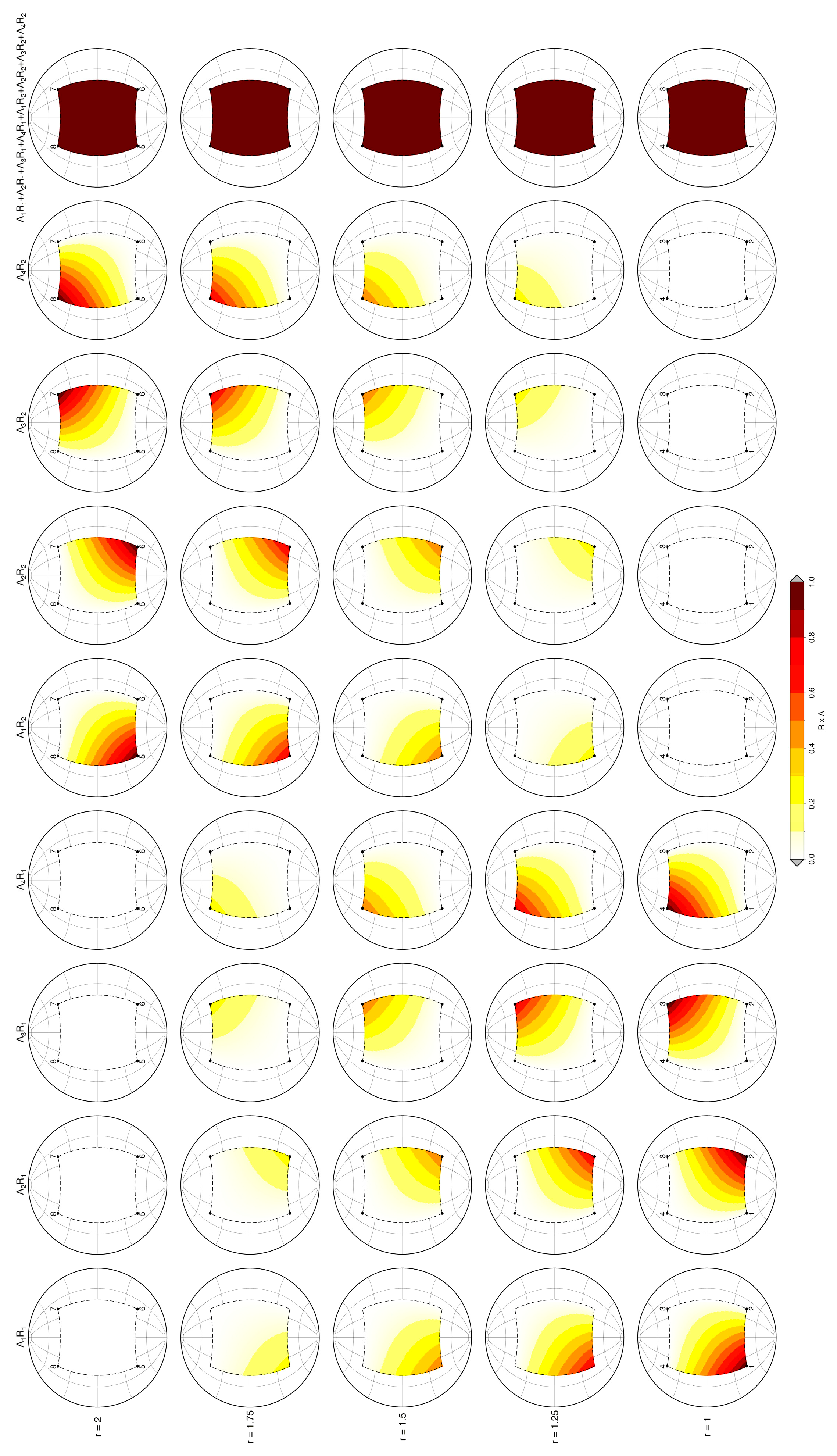
2.3.2. Spherical Eight-Node Quadrangular Right Prism
2.4. Shape Functions
2.4.1. Spherical Six-Node Tri-Rectangular Prism
2.4.2. Spherical Eight-Node Quadrangular Right Prism—Tesseroid
3. Rigid Displacement on a Sphere
4. Transformation from Global to Local Coordinates
4.1. Spherical Six-Node Tri-Rectangular Prism
4.2. Spherical Eight-Node Quadrangular Right Prism
5. Infinitesimal Volume—Global to Local
6. Validation Tests
6.1. Volume
6.1.1. Spherical Triangular Prism
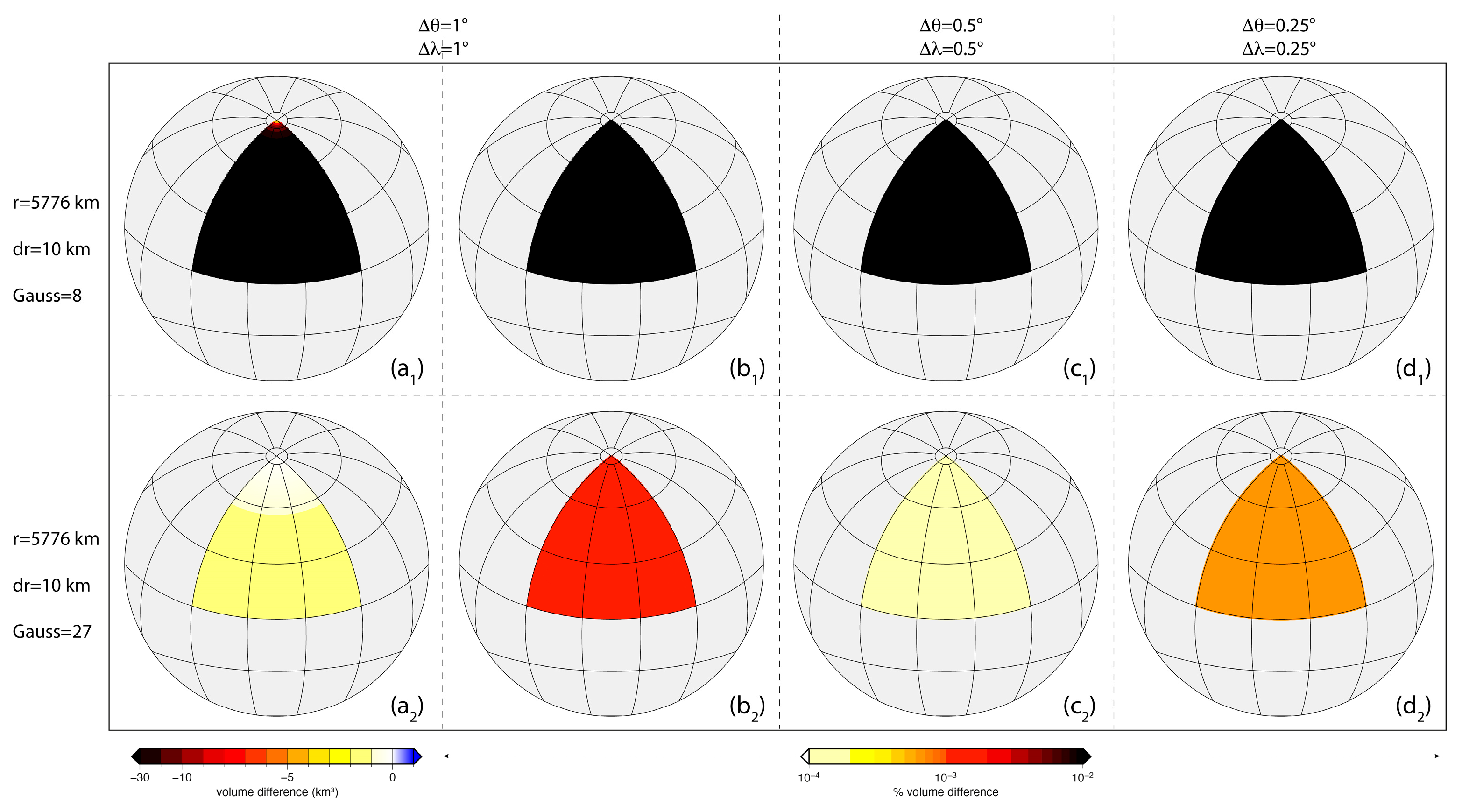
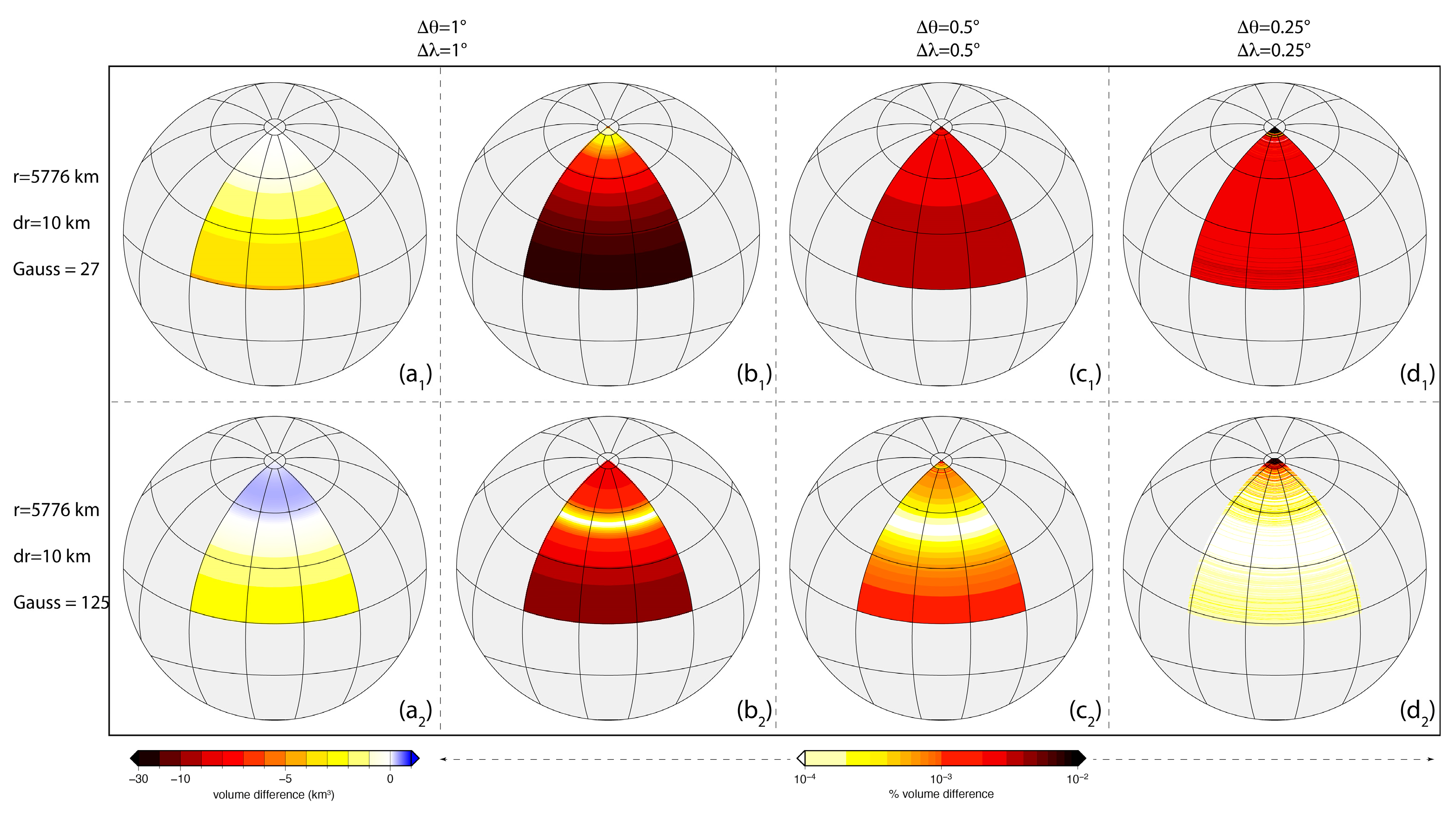
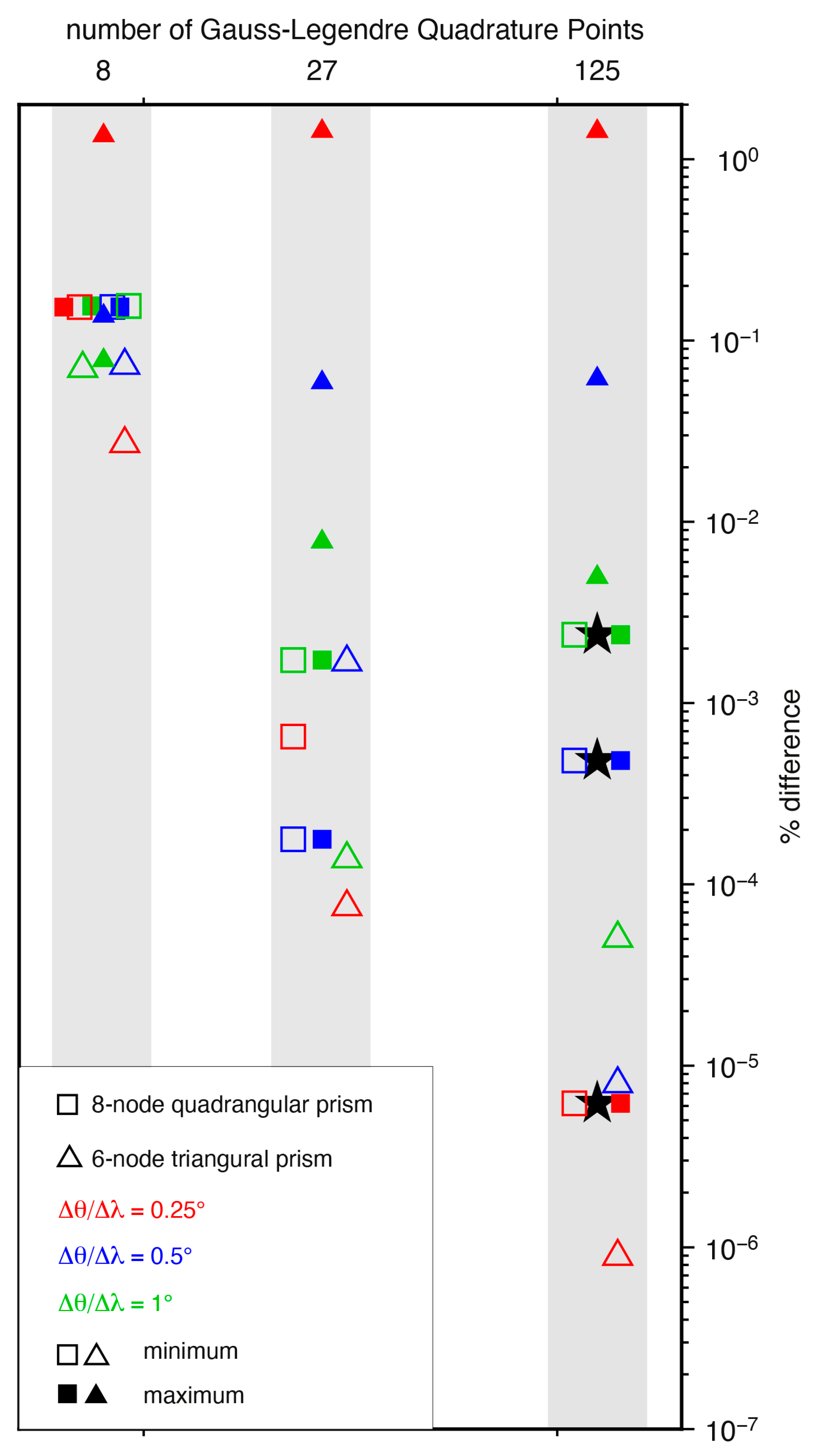
6.1.2. Spherical Quadrangular Prism–Tesseroid
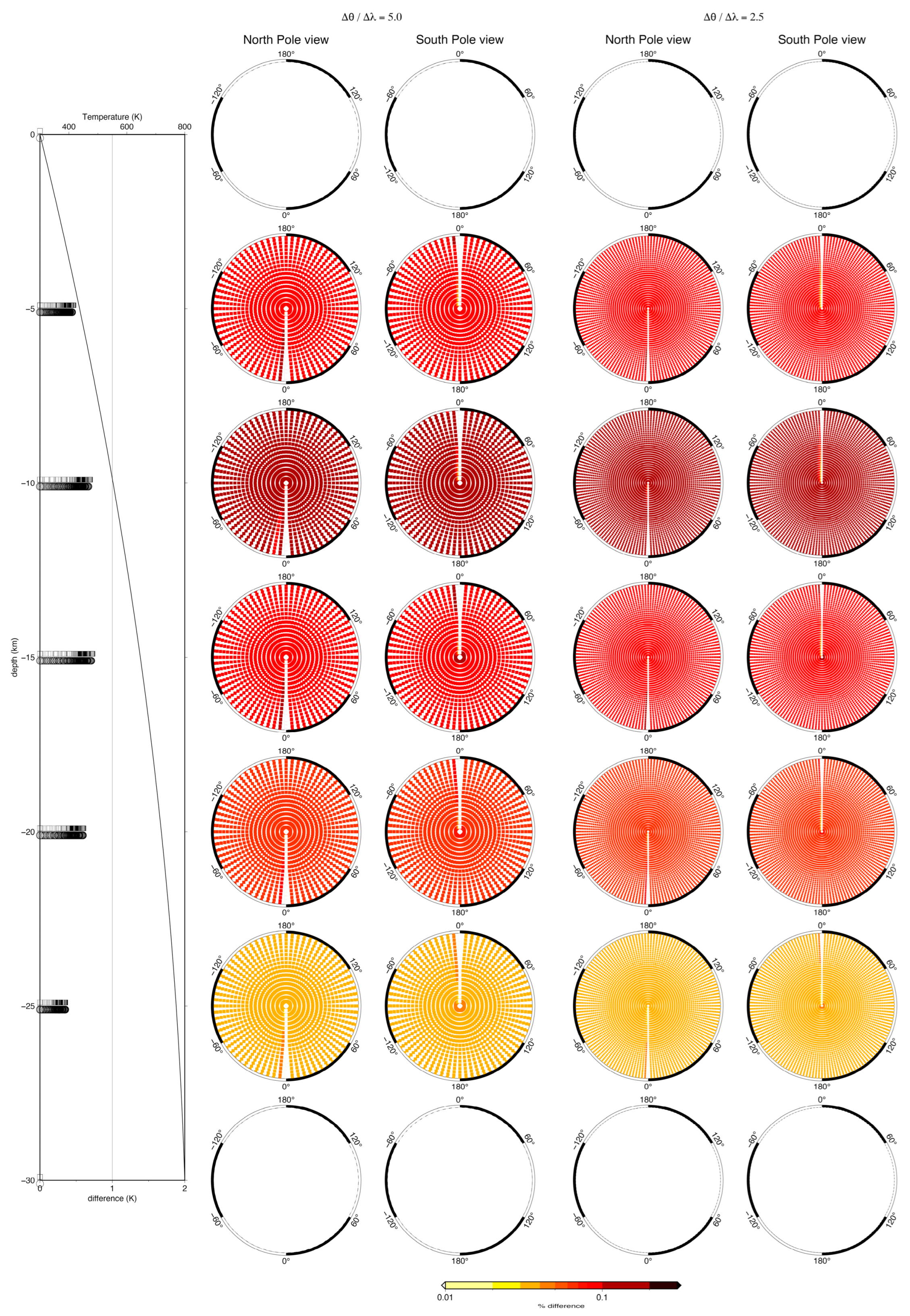
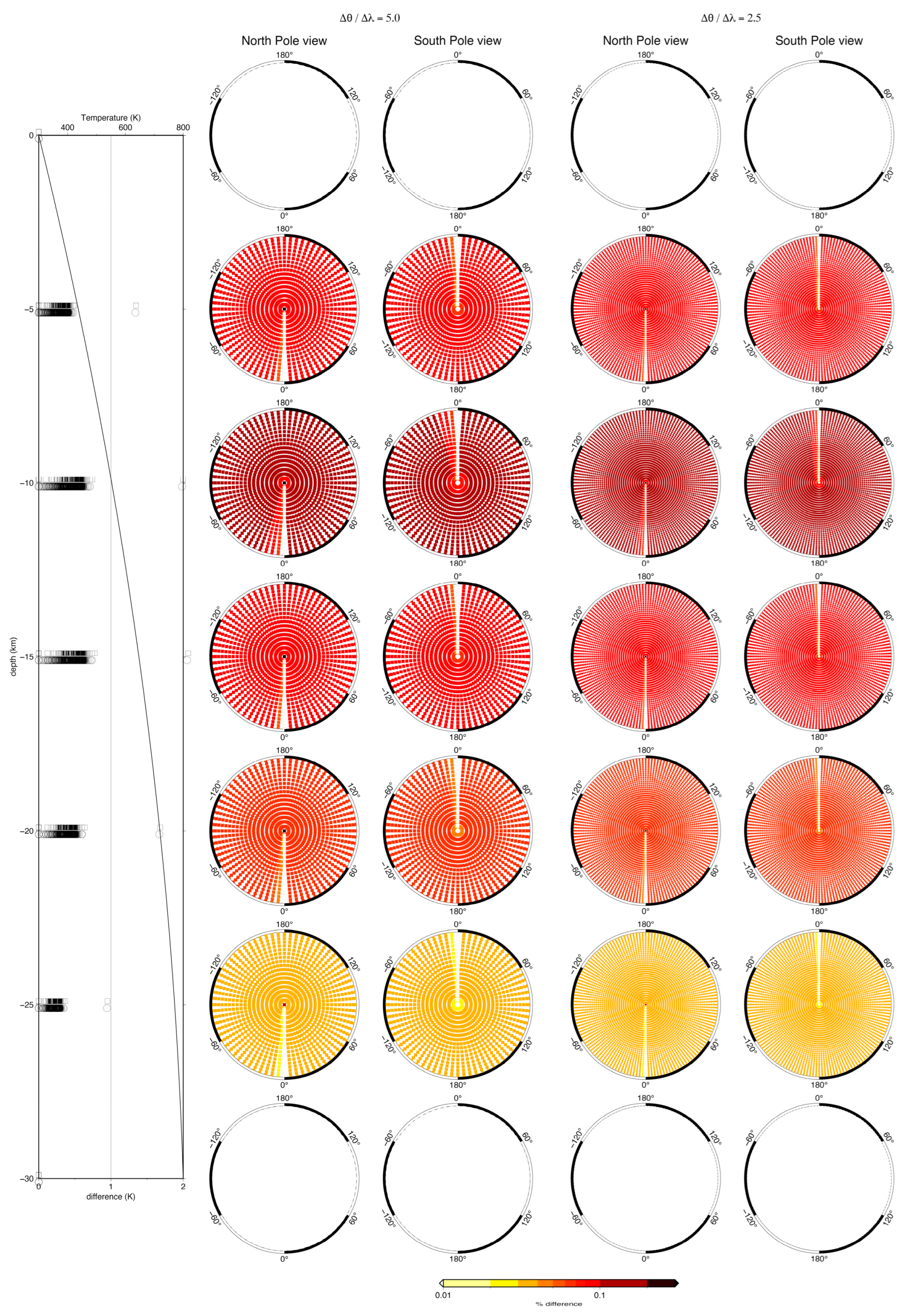
- The volume difference decreases from tens of kilometers to a few units as the radial dimension of the spherical quadrangular spherical decreases (compare, in the first column, the first two panels at the top, with radial dimension of 100 km, with the two panels at the bottom, with radial dimension of 10 km), and decreases from the equator to the poles.
- Despite these differences in the volume difference related to r, however, the percentage volume difference is totally independent of r and of colatitude and longitude. It depends only on the angular dimension of the prism along the colatitude () and the longitude () and decreases as both decrease, from to lower than when and vary from to . A decrease in the percentage volume difference occurs when 27 Gauss–Legendre points are used, up to two orders of magnitude, but still below . The accuracy of the numerical estimation of the volume degrades significantly, instead, if only eight Gauss–Legendre points are used (Figure 14). The invariance of the percentage volume difference from the distance from the center of the sphere, as well as from the radial dimensions of the prism, is also confirmed by the results obtained for a normalized sphere (Figure 15).

6.2. Steady-State Heat Conduction in a Sphere — Poisson and Laplace Problems
6.2.1. Numerical Integration of the Equation of Steady-State Heat Conduction in a Sphere with Internal Heat Production
6.2.2. Analytical Solution of the Equation of Steady-State Heat Conduction in a Sphere with Internal Heat Production
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Partial Derivatives of for a Spherical Six-Node Tri-Rectangular Prism
References
- Schmeling, H.; Babeyko, A.; Enns, A.; Faccenna, C.; Funiciello, F.; Gerya, T.; Golabek, G.; Grigull, S.; Kaus, B.; Morra, G.; et al. A benchmark comparison of spontaneous subduction models—Towards a free surface. Phys. Earth Planet. Inter. 2008, 171, 198–223. [Google Scholar] [CrossRef]
- Moresi, L.; Quenette, S.; Lemiale, V.; Meériaux, C.; Appelbe, B.; Mühlhaus, H.-B. Computational approaches to studying non-linear dynamics of the crust and mantle. Phys. Earth Planet. Inter. 2007, 163, 69–82. [Google Scholar] [CrossRef]
- Moresi, L.; Dufour, F.; Mühlhaus, H.B. A Lagrangian integration point finite element method for large deformation modeling of viscoelastic geomaterials. J. Comput. Phys. 2003, 184, 476–497. [Google Scholar] [CrossRef]
- O’Neill, C.; Moresi, L.; Müller, D.; Albert, R.; Dufour, F. Ellipsis 3D: A particle-in-cell finite-element hybrid code for modelling mantle convection and lithospheric deformation. Comp. Geosci. 2006, 32, 1769–1779. [Google Scholar] [CrossRef]
- Braun, J.; Thieulot, C.; Fullsack, P.; DeKool, M.; Beaumont, C.; Huismans, R. DOUAR: A new three-dimensional creeping flow numerical model for the solution of geological problems. Phys. Earth Planet. Inter. 2008, 171, 76–91. [Google Scholar] [CrossRef]
- Popov, A.; Sobolev, S. SLIM3D: A tool for three-dimensional thermomechanical modelling of lithospheric deformation with elasto-visco-plastic rheology. Phys. Earth Planet. Inter. 2008, 171, 55–75. [Google Scholar] [CrossRef]
- Zhu, G.; Gerya, T.; Yuen, D.; Honda, S.; Yoshida, T.; Connolly, T. Three-dimensional dynamics of hydrous thermal-chemical plumes in oceanic subduction zones. Geochem. Geophy. Geosy. 2009, 118, 4682–4698. [Google Scholar] [CrossRef]
- Thieulot, C. FANTOM: Two- and three-dimensional numerical modelling of creeping flows for the solution of geological problems. Phys. Earth Planet. Inter. 2011, 188, 47–68. [Google Scholar] [CrossRef]
- Pusok, A.E.; Kaus, B.J.P. Development of topography in 3-D continental-collision models. Geochem. Geophys. Geosystems 2015, 16, 1378–1400. [Google Scholar] [CrossRef]
- Zhong, S.; Zuber, M.T.; Moresi, L.; Gurnis, M. Role of temperature-dependent viscosity and surface plates in spherical shell models of mantle convection. J. Geophys. Res. Solid Earth 2000, 105, 11063–11082. [Google Scholar] [CrossRef]
- Moresi, L.; Zhong, S.; Han, L.; Conrad, C.; Tan, E.; Gurnis, M.; Choi, E.; Thoutireddy, P.; Manea, V.; McNamara, A.; et al. CitcomS v3.3.1. Available online: https://zenodo.org/records/7271920 (accessed on 19 May 2025).
- Thieulot, C. ELEFANT: A user-friendly multipurpose geodynamics code. Solid Earth Discuss. 2014, 6, 1949–2096. [Google Scholar] [CrossRef]
- Bangerth, W.; Dannberg, J.; Fraters, M.; Gassmoeller, R.; Glerum, A.; Heister, T.; Myhill, R.; Naliboff, J. ASPECT: Advanced Solver for Problems in Earth’s ConvecTion, User Manual. Available online: https://figshare.com/articles/journal_contribution/ASPECT_Advanced_Solver_for_Problems_in_Earth_s_ConvecTion_User_Manual/4865333?file=51103820 (accessed on 19 May 2025).
- Zienkiewich, O.C.; Taylor, R.L. The Finite Element Method, Volume 1: The Basis; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Cook, R.D.; David, S.M.; Michael, E.P. Concepts and Applications of Finite Element Analysis; Wiley: New York, NY, USA, 1989. [Google Scholar]
- Wessel, P.; Smith, W.H.F.; Scharroo, R.; Luis, J.F.; Wobbe, F. Generic Mapping Tools: Improved version released. Eos. Trans. AGU 2013, 94, 409–410. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marotta, A.M.; Barzaghi, R.; Sabadini, R. Spherical Shape Functions for a Six-Node Tri-Rectangular Prism and an Eight-Node Quadrangular Right Prism. Math. Comput. Appl. 2025, 30, 88. https://doi.org/10.3390/mca30040088
Marotta AM, Barzaghi R, Sabadini R. Spherical Shape Functions for a Six-Node Tri-Rectangular Prism and an Eight-Node Quadrangular Right Prism. Mathematical and Computational Applications. 2025; 30(4):88. https://doi.org/10.3390/mca30040088
Chicago/Turabian StyleMarotta, Anna Maria, Riccardo Barzaghi, and Roberto Sabadini. 2025. "Spherical Shape Functions for a Six-Node Tri-Rectangular Prism and an Eight-Node Quadrangular Right Prism" Mathematical and Computational Applications 30, no. 4: 88. https://doi.org/10.3390/mca30040088
APA StyleMarotta, A. M., Barzaghi, R., & Sabadini, R. (2025). Spherical Shape Functions for a Six-Node Tri-Rectangular Prism and an Eight-Node Quadrangular Right Prism. Mathematical and Computational Applications, 30(4), 88. https://doi.org/10.3390/mca30040088




