Adaptive Filtered-x Least Mean Square Algorithm to Improve the Performance of Multi-Channel Noise Control Systems
Abstract
1. Introduction
- Error reduction: The OCF achieves near-zero error values across all Mic channels with reduced crosstalk between Mics, and improved convergence behavior across nonstationary noise environments by inserting an adaptive weighting mechanism across secondary routes, even under challenging different noise types like White Gaussian, Brownian, and pink noise.
- Improved computational efficiency: Integrating the OCF and the algorithm reduces execution time from the standard McFxLMS’s 58.17 s to just 0.0436 s under White Gaussian noise, significantly improving real-time performance while maintaining high accuracy.
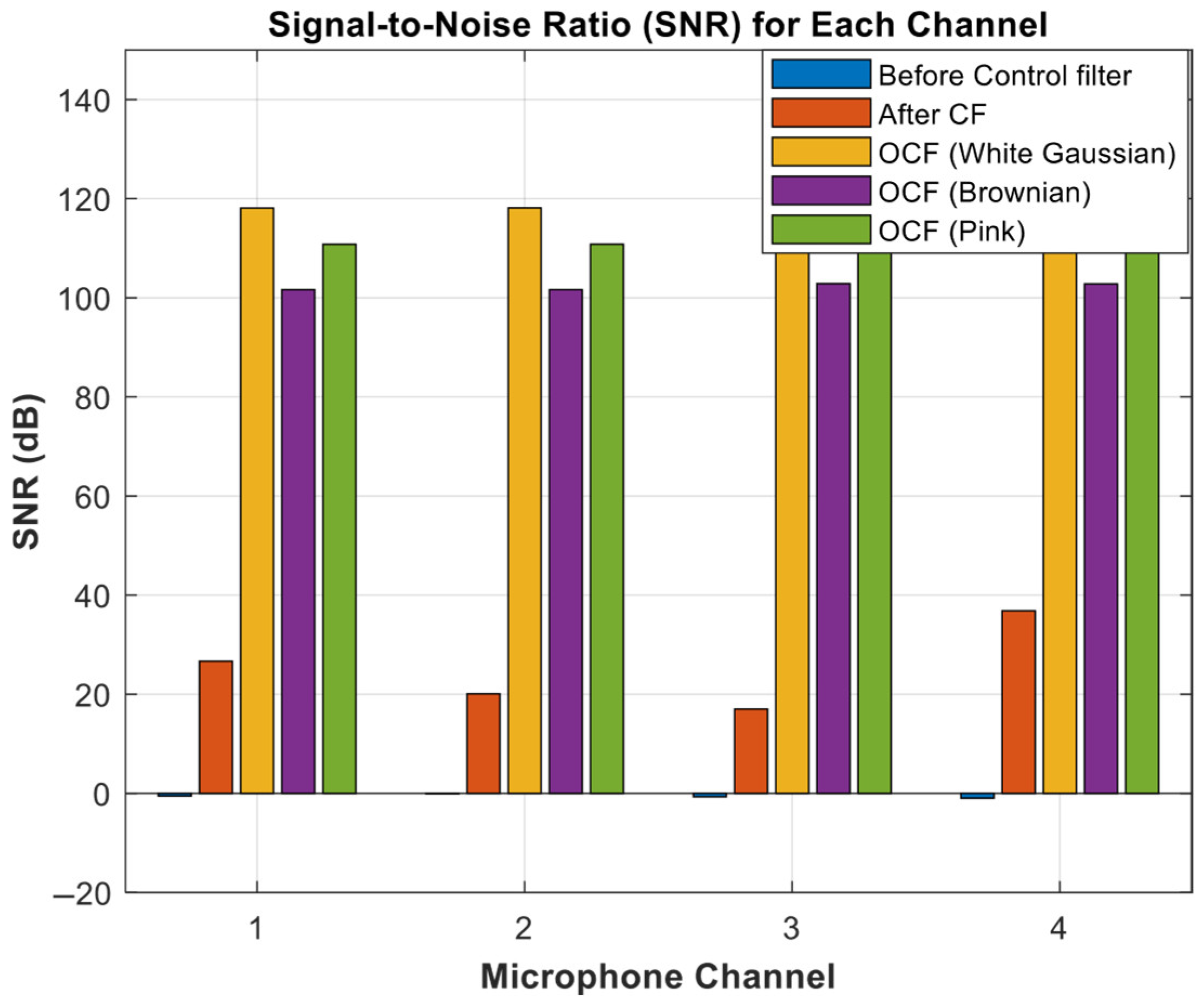
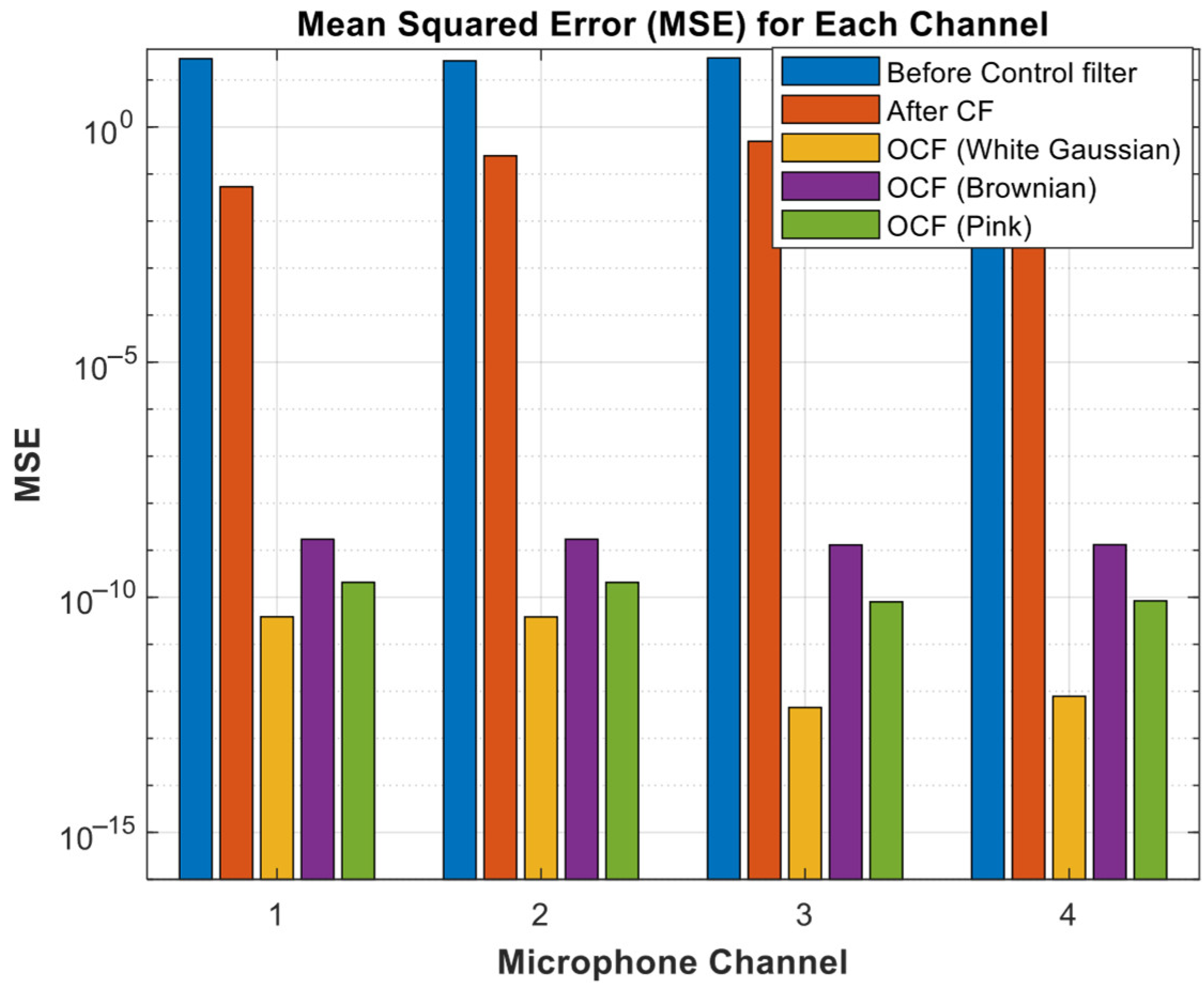
- Robust noise control: The OCF-McFxLMS achieves higher signal-to-noise ratio (SNR) values, up to 137.4 dB, and significantly lower MSE values across all Mics, ensuring robust performance across diverse noise types.
2. The Multi-Channel Active Noise Control Technique
- High computational complexity due to multiple adaptive filters running in parallel.
- Crosstalk effects between Mics can reduce the convergence and stability of the adaptive algorithm.
- Dependence between control channels, which limits the system’s ability to independently reduce errors across all Microphones.
- Inaccurate modeling of secondary routes leads to suboptimal adaptation and residual noise.
- Limited adaptability across varying noise types, particularly in nonstationary environments like pink, Brownian, or impulsive noise.
3. Methods
3.1. The Standard Multi-Channel Control Filtered Reference Least Mean Square Algorithm
3.2. The Proposed Optimized Control Filter with Multi-Channel Filtered Reference Least Mean Square Method
4. Simulation Results and Discussion
4.1. Simulation Results for the Standard Multi-Channel Control Filter Reference Least Mean Square Algorithm
4.2. Simulation Results of the Proposed Method with White Gaussian Noise
4.3. The Result Checking for the OCF-McFxLMS with Pink and Brownian Noises
4.4. Signal Noise Ratio and Mean Square Error
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hansen, C.N. Understanding Active Noise Cancellation; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Kajikawa, Y.; Gan, W.-S.; Kuo, S.M. Recent advances on active noise control: Open issues and innovative applications. APSIPA Trans. Signal Inf. Process. 2012, 1, e3. [Google Scholar] [CrossRef]
- Liebich, S.; Fabry, J.; Jax, P.; Vary, P. Signal processing challenges for active noise cancellation headphones. In Proceedings of the Speech Communication; 13th ITG-Symposium, Oldenburg, Germany, 10–12 October 2018; VDE: Offenbach am Main, Germany, 2018; pp. 1–5. [Google Scholar]
- Qiu, X. An Introduction to Virtual Sound Barriers; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Zhang, J. Active Noise Control over Spatial Regions. Ph.D. Thesis, The Australian National University (Australia), Acton, Australia, 2019. [Google Scholar]
- Ramesh, G.; Logeshwaran, J.; Gowri, J.; Mathew, A. The Management and Reduction of Digital Noise in Video Image Processing by Using Transmission Based Noise Elimination Scheme. ICTACT J. Image Video Process. 2022, 13, 2797. [Google Scholar]
- Chu, Y.; Wu, M.; Sun, H.; Yang, J.; Chen, M. Some practical acoustic design and typical control strategies for multichannel active noise control. Appl. Sci. 2022, 12, 2244. [Google Scholar] [CrossRef]
- Zhuang, Y.; Liu, Y. An adaptive constrained multi-channel active noise control filter design approach using convex cone optimization. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Grand Rapids, MI, USA, 15–18 May 2023; Institute of Noise Control Engineering: Wakefield, MA, USA, 2023; Volume 266, pp. 510–521. [Google Scholar]
- Cai, Y.; Dong, L.; Zhou, Y. A narrowband active noise control algorithm considering the harmonic noise of the loudspeaker. Int. J. Appl. Electromagn. Mech. 2020, 64, 229–235. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, W. A noise control method using adaptive adjustable parametric array loudspeakers to eliminate environmental noise in real time. Int. J. Environ. Res. Public Health 2021, 19, 269. [Google Scholar] [CrossRef]
- Yang, B.; Yin, J.; Ye, Z.; Yang, S.; Wang, L. Development and Testing of an Active Noise Control System for Urban Road Traffic Noise. Appl. Sci. 2024, 14, 175. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, H.; Zhang, Y. Stability guaranteed active noise control: Algorithms and applications. IEEE Trans. Control. Syst. Technol. 2023, 31, 1720–1732. [Google Scholar] [CrossRef]
- Antoñanzas, C.; Ferrer, M.; De Diego, M.; Gonzalez, A. Remote Microphone technique for active noise control over distributed networks. IEEE/ACM Trans. Audio Speech Lang. Process. 2023, 31, 1522–1535. [Google Scholar] [CrossRef]
- Yu, J.; Zheng, Z.; Li, Y.; Wang, H.; Hao, Y.; Liang, X.; Gao, J. An Investigation of Real-Time Active Noise Control for 10 kV Substation Noise Suppression. Sustainability 2023, 15, 13430. [Google Scholar] [CrossRef]
- Shi, D.; Shi, C.; Gan, W.S. A systolic FxLMS structure for implementation of feedforward active noise control on FPGA. In Proceedings of the 2016 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA), Jeju, Republic of Korea, 13–16 December 2016; pp. 1–6. [Google Scholar]
- Shi, D.; Gan, W.S.; Lam, B.; Shi, C. Two-gradient direction FXLMS: An adaptive active noise control algorithm with output constraint. Mech. Syst. Signal Process. 2019, 116, 651–667. [Google Scholar] [CrossRef]
- Wen, S.; Gan, W.S.; Shi, D. Convergence behavior analysis of FXLMS algorithm with different leaky term. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Seoul, Republic of Korea, 23–26 August 2020; Institute of Noise Control Engineering: Wakefield, MA, USA, 2020; Volume 261, pp. 728–739. [Google Scholar]
- Li, C.; Jin, G.; Liu, H.; Li, J. Active impulsive noise control algorithm based on adjustable hyperbolic tangent function. Circuits Syst. Signal Process. 2023, 42, 5559–5578. [Google Scholar] [CrossRef]
- Zhang, R.; Cheng, Y.; Chen, S. Maximum versoria criterion applied to hybrid active noise control algorithm for the impulsive noise. J. Low Freq. Noise Vib. Act. Control 2023, 42, 1743–1764. [Google Scholar] [CrossRef]
- Wang, J.; Lu, L.; Zheng, Z.; Yin, K.L.; Yu, Y.; Shi, L. Euclidean direction search algorithm with maximum correntropy criterion for active noise control system. Signal Process. 2025, 229, 109759. [Google Scholar] [CrossRef]
- Akhtar, M.T. A time-varying normalized step-size based generalized fractional moment adaptive algorithm and its application to ANC of impulsive sources. Appl. Acoust. 2019, 155, 240–249. [Google Scholar] [CrossRef]
- Long, G.; Lim, T.C. A new robust delayless subband adaptive filtering algorithm with variable step sizes for active control of broadband noise. Appl. Acoust. 2021, 176, 107858. [Google Scholar] [CrossRef]
- Ferrer, M.; Gonzalez, A.; de Diego, M.; Pinero, G. Convex combination filtered-x algorithms for active noise control systems. IEEE Trans. Audio Speech Lang. Process. 2012, 21, 156–167. [Google Scholar] [CrossRef]
- Zhuang, Y.; Mittal, M.; Fernando, R.; Corey, R.M.; Singer, A.C. Active noise control without tap length selection: A model order weighting method. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, New Orleans, LA, USA, 10–12 June 2024; Institute of Noise Control Engineering: Wakefield, MA, USA, 2024; Volume 269, pp. 902–913. [Google Scholar]
- Padhi, T.; Chandra, M.; Kar, A.; Swamy, M.N.S. A new hybrid active noise control system with convex combination of time and frequency domain filtered-x LMS algorithms. Circuits Syst. Signal Process. 2018, 37, 3275–3294. [Google Scholar] [CrossRef]
- Shi, D.; Gan, W.S.; Lam, B.; Shen, X. Comb-partitioned frequency-domain constraint adaptive algorithm for active noise control. Signal Process. 2021, 188, 108222. [Google Scholar] [CrossRef]
- Shi, D.; Gan, W.S.; Lam, B.; Luo, Z.; Shen, X. Transferable latent of cnn-based selective fixed-filter active noise control. IEEE/ACM Trans. Audio Speech Lang. Process. 2023, 31, 2910–2921. [Google Scholar] [CrossRef]
- Shi, D.; He, J.; Shi, C.; Murao, T.; Gan, W.S. Multiple parallel branch with folding architecture for multichannel filtered-x least mean square algorithm. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 1188–1192. [Google Scholar]
- Shi, D.; Lam, B.; Gan, W.S. Analysis of multichannel virtual sensing active noise control to overcome spatial correlation and causality constraints. In Proceedings of the ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 8499–8503. [Google Scholar]
- Shi, D.; Gan, W.S.; Lam, B.; Wen, S.; Shen, X. Active noise control based on the momentum multichannel normalized filtered-x least mean square algorithm. In Proceedings of the INTER-nOISE and NOISE-CON Congrzess and Conference Proceedings, Seoul, Republic of Korea, 23–26 August 2020; Institute of Noise Control Engineering: Wakefield, MA, USA, 2020; Volume 261, pp. 709–719. [Google Scholar]
- Shi, D.; Lam, B.; Wen, S.; Gan, W.S. Multichannel active noise control with spatial derivative constraints to enlarge the quiet zone. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 8419–8423. [Google Scholar]
- Shi, D.; Lam, B.; Gan, W.S.; Wen, S. Block coordinate descent based algorithm for computational complexity reduction in multichannel active noise control system. Mech. Syst. Signal Process. 2021, 151, 107346. [Google Scholar] [CrossRef]
- Luo, Z.; Shi, D.; Ji, J.; Gan, W.S. Implementation of multi-channel active noise control based on back-propagation mechanism. arXiv 2022, arXiv:2208.08086. [Google Scholar]
- Ji, J.; Shi, D.; Gan, W.S.; Shen, X.; Luo, Z. A computation-efficient online secondary path modeling technique for modified fxlms algorithm. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Chiba, Japan, 20–23 August 2023; Institute of Noise Control Engineering: Wakefield, MA, USA, 2023; Volume 268, pp. 5216–5226. [Google Scholar]
- Lai, C.K.; Shi, D.; Lam, B.; Gan, W.S. Mov-modified-fxlms algorithm with variable penalty factor in a practical power output constrained active control system. IEEE Signal Process. Lett. 2023, 30, 723–727. [Google Scholar] [CrossRef]
- Lai, C.K.; Lam, B.; Shi, D.; Gan, W.S. Real-time modelling of observation filter in the remote Microphone technique for an active noise control application. In Proceedings of the ICASSP 2023—2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar]
- Shen, X.; Shi, D.; Luo, Z.; Ji, J.; Gan, W.S. A momentum two-gradient direction algorithm with variable step size applied to solve practical output constraint issue for active noise control. In Proceedings of the ICASSP 2023—2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar]
- Shi, D.; Lam, B.; Shen, X.; Gan, W.S. Multichannel two-gradient direction filtered reference least mean square algorithm for output-constrained multichannel active noise control. Signal Process. 2023, 207, 108938. [Google Scholar] [CrossRef]
- Shi, D.; Lam, B.; Ji, J.; Shen, X.; Lai, C.K.; Gan, W.S. Computation-efficient solution for fully-connected active noise control window: Analysis and implementation of multichannel adjoint least mean square algorithm. Mech. Syst. Signal Process. 2023, 199, 110444. [Google Scholar] [CrossRef]
- Wang, B.; Shi, D.; Luo, Z.; Shen, X.; Ji, J.; Gan, W.S. Transferable Selective Virtual Sensing Active Noise Control Technique Based on Metric Learning. arXiv 2024, arXiv:2409.05470. [Google Scholar]
- Elliott, S.J.; Nelson, P.A. Active noise control. IEEE Signal Process. Mag. 1993, 10, 12–35. [Google Scholar] [CrossRef]
- Amjad, H.J.; Talaat, E.N.; Hameed, M.R.; Hameed, A.H. Design of adaptive observer-based backstepping control of cart-pole pendulum system. In Proceedings of the IEEE International Conference on Electrical, Computer and Communication Technologies (ICECCT 2019), Coimbatore, India, 20–22 February 2019; pp. 1–5. [Google Scholar]
- Al-Dujaili, A.Q.; Humaidi, A.J.; Allawi, Z.T.; Sadiq, M.E. Earthquake Hazard Mitigation for Uncertain Building Systems Based on Adaptive Synergetic Control. Appl. Syst. Innov. 2023, 6, 34. [Google Scholar] [CrossRef]
- Husain, S.S.; Al-Dujaili, A.Q.; Jaber, A.A.; Humaidi, A.J.; Al-Azzawi, R.S. Design of a Robust Controller Based on Barrier Function for Vehicle Steer-by-Wire Systems. World Electr. Veh. J. 2024, 15, 17. [Google Scholar] [CrossRef]
- Abbas, S.J.; Husain, S.S.; Al-Wais, S.; Humaidi, A.J. Adaptive Integral Sliding Mode Controller (SMC) Design for Vehicle Steer-by-Wire System. SAE Int. J. Veh. Dyn. Stab. NVH 2024, 8, 383–396. [Google Scholar] [CrossRef]
- Al-Dujaili, A.Q.; Hasan, A.F.; Humaidi, A.J.; Al-Jodah, A. Anti-disturbance control design of Exoskeleton Knee robotic system for rehabilitative care. Heliyon 2024, 10, e28911. [Google Scholar] [CrossRef]
- Hasan, M.Y.; Kadhim, D.J.; Humaidi, A.J. Prediction of electricity-consumption and residential bills based on artificial neural network. Int. Rev. Appl. Sci. Eng. 2025, 16, 142–152. [Google Scholar] [CrossRef]
- Ajel, A.R.; Humaidi, A.J.; Ibraheem, I.K.; Azar, A.T. Robust Model Reference Adaptive Control for Tail-Sitter VTOL Aircraft. Actuators 2021, 10, 162. [Google Scholar] [CrossRef]
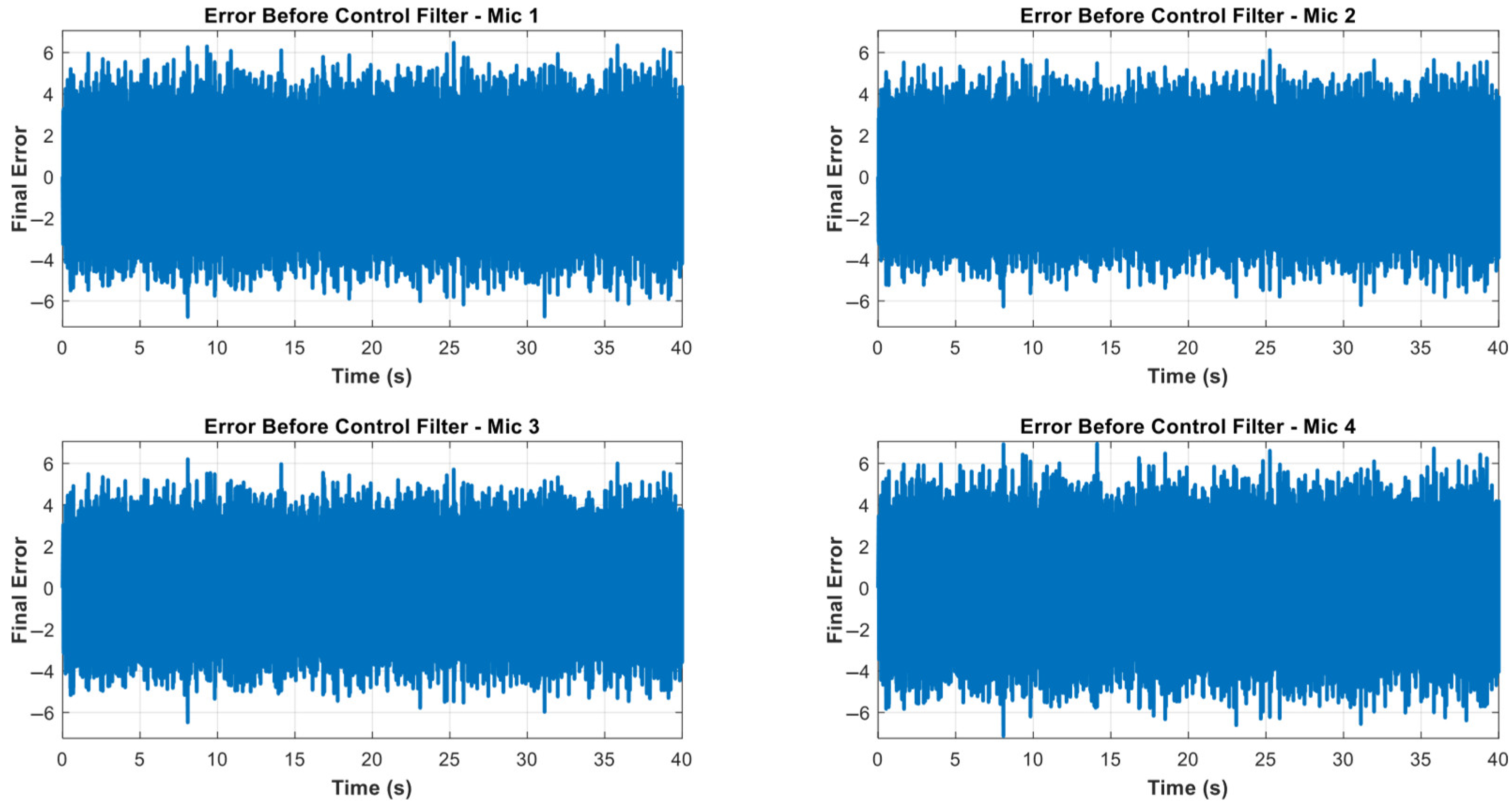
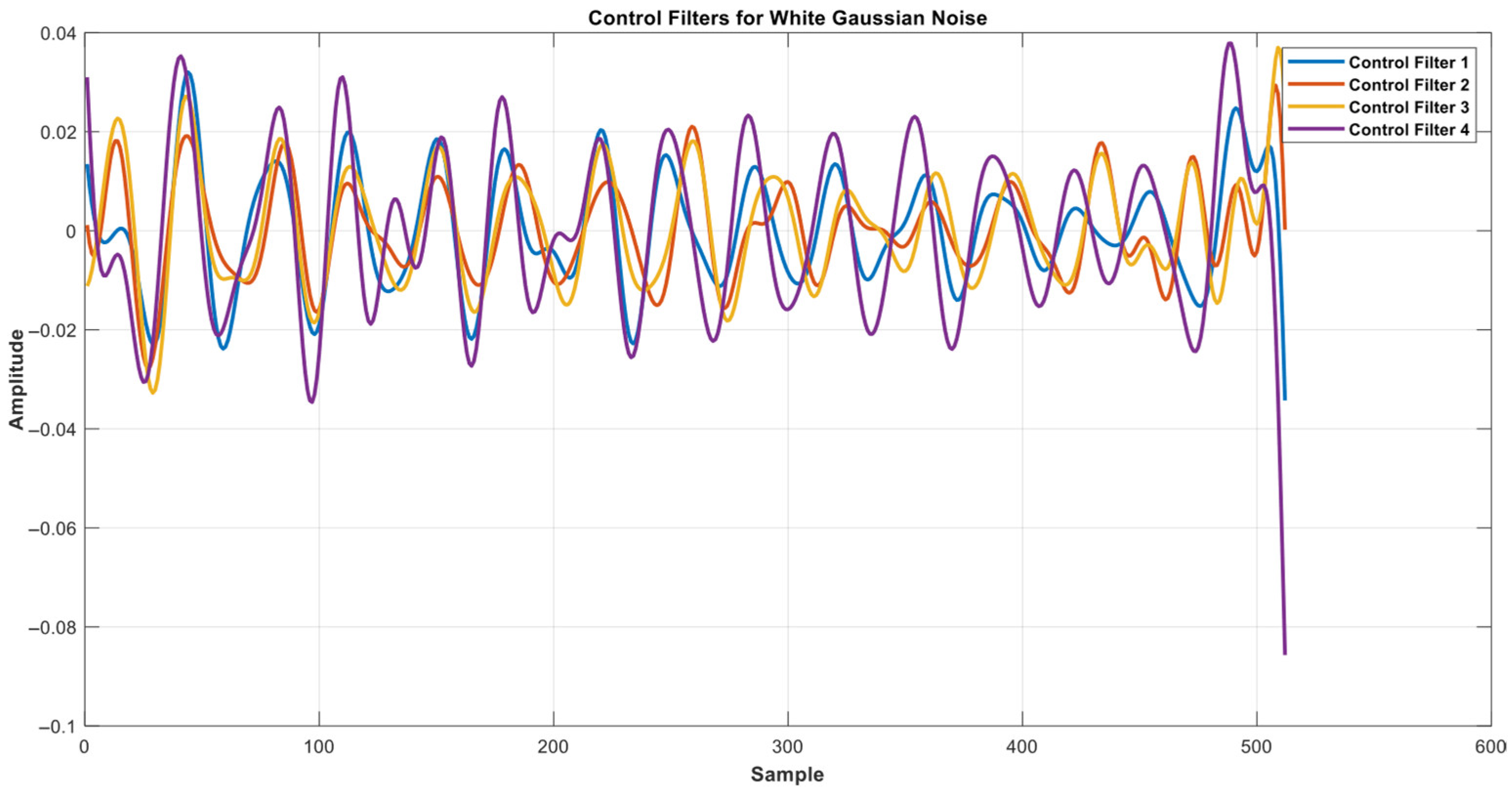

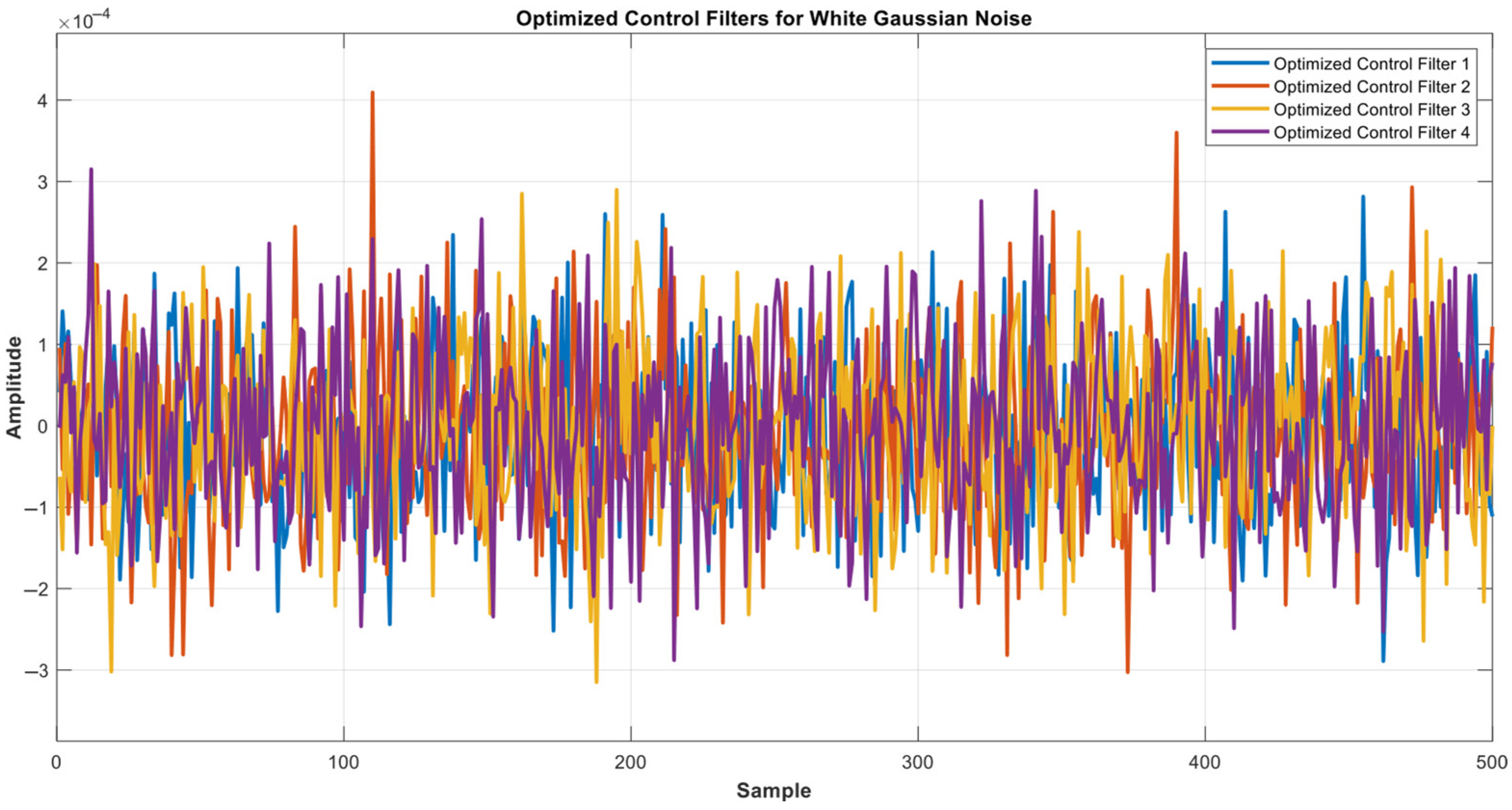

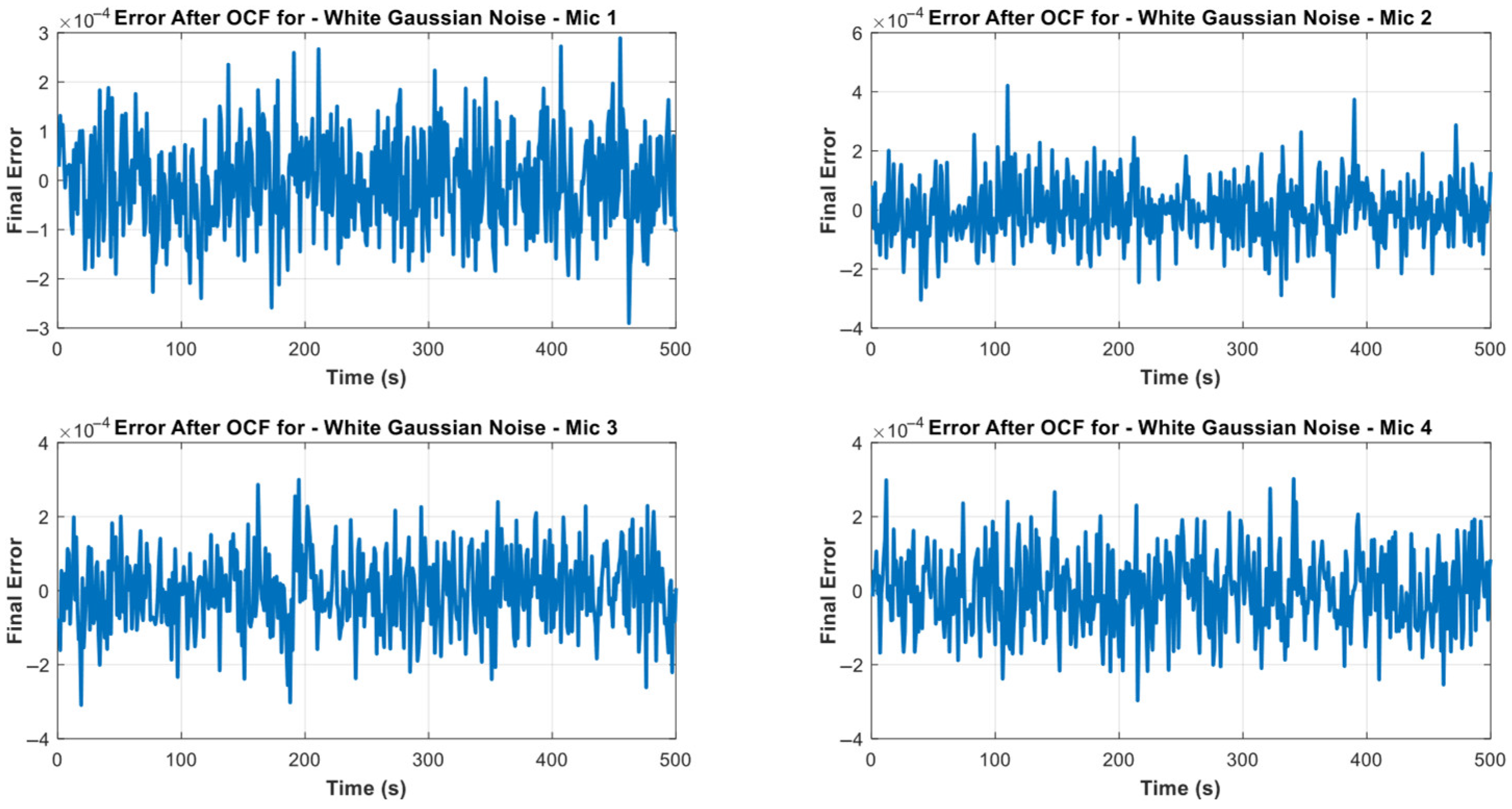
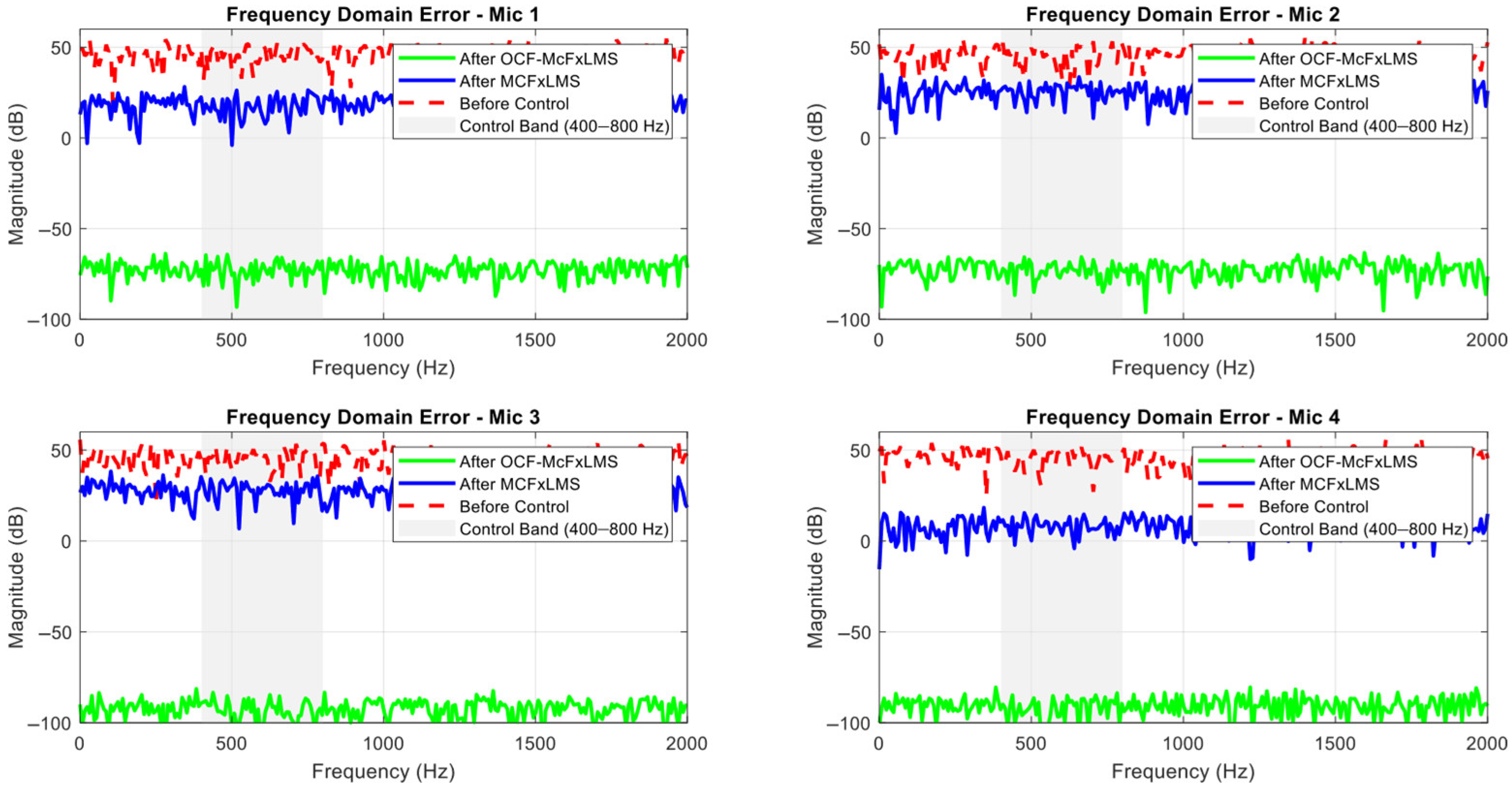

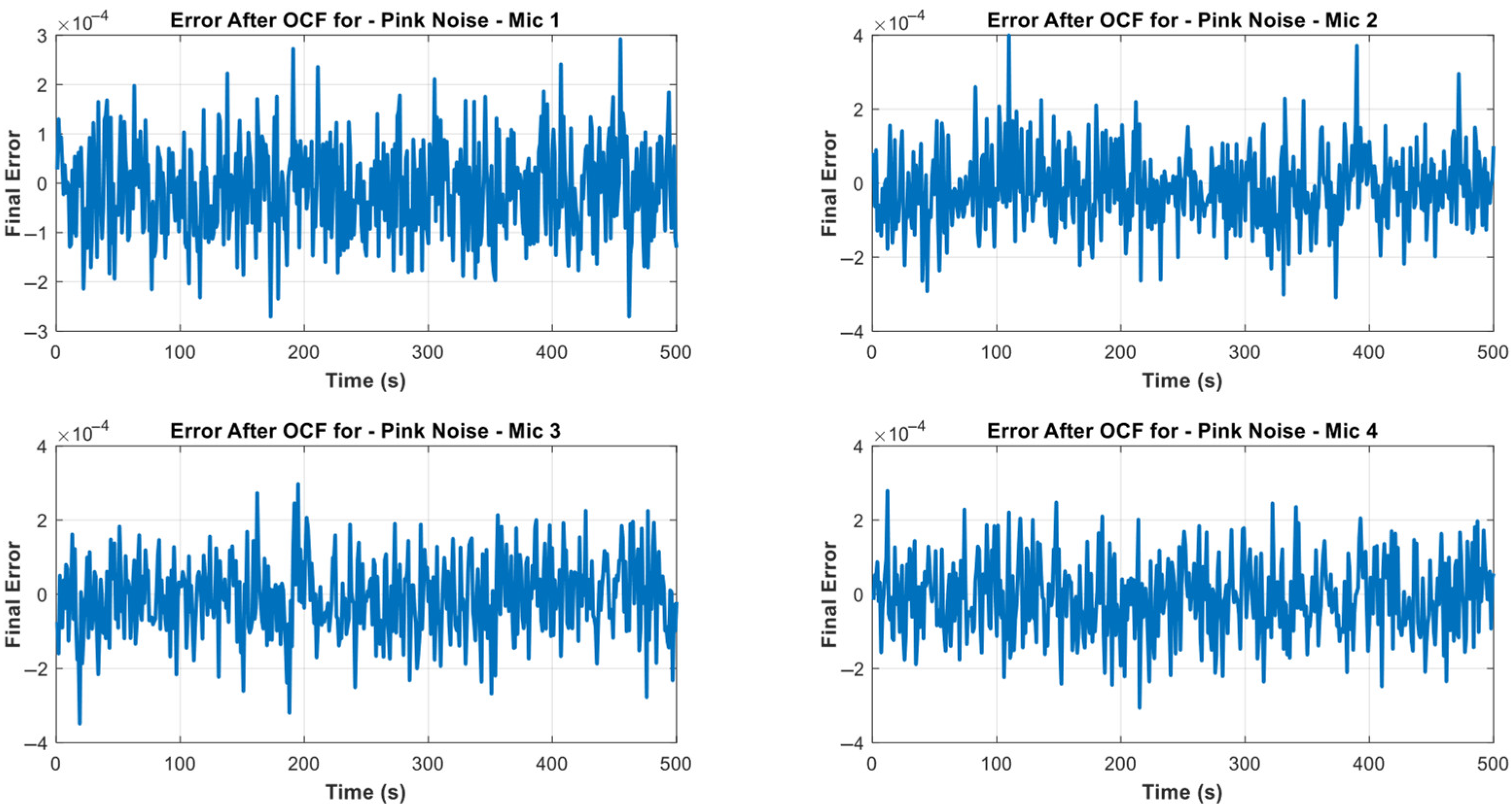
| Mic Channel Number | Final Error Value |
|---|---|
| Mic 1 | 5.3245 |
| Mic 2 | 5.0499 |
| Mic 3 | 5.4165 |
| Mic 4 | 5.5895 |
| Mic Channel Number | Final Error Value |
|---|---|
| Mic 1 | −0.2319 |
| Mic 2 | 0.4945 |
| Mic 3 | 0.7040 |
| Mic 4 | 0.0720 |
| Mic Channels Number | Final Error Value |
|---|---|
| Mic 1 | −6.2038 × 10−6 |
| Mic 2 | −6.18 × 10−6 |
| Mic 3 | −6.7335 × 10−7 |
| Mic 4 | −8.8564 × 10−7 |
| Noise Type | Execution Time (s) | Final Error | |||
|---|---|---|---|---|---|
| (Mic 1) | (Mic 2) | (Mic 3) | (Mic 4) | ||
| Brownian | 0.071637 | −4.1422 × 10−5 | −4.1398 × 10−5 | −3.6001 × 10−5 | −3.6209 × 10−5 |
| Pink | 0.054877 | −1.4418 × 10−5 | −1.4394 × 10−5 | −8.9426 × 10−5 | −9.1528 × 10−5 |
| Final SNR (dB) Values | Mic 1 | Mic 2 | Mic 3 | Mic 4 |
|---|---|---|---|---|
| Before any kind of Control filter | −0.5462 | −0.0863 | −0.6950 | −0.9681 |
| After CF with White Gaussian | 26.6734 | 20.0961 | 17.0279 | 36.8328 |
| OCF with White Gaussian | 118.1262 | 118.1596 | 137.4146 | 135.0343 |
| OCF with Brownian | 101.6348 | 101.6398 | 102.8531 | 102.8031 |
| OCF with Pink | 110.8013 | 110.8158 | 114.9501 | 114.7483 |
| Final MSE Values | Mic Channel 1 | Mic Channel 2 | Mic Channel 3 | Mic Channel 4 |
|---|---|---|---|---|
| Before any kind of Control filter | 28.3503 | 25.5015 | 29.3385 | 31.2425 |
| After CF White Gaussian Noise | 0.0538 | 0.2445 | 0.4956 | 0.0052 |
| OCF with White Gaussian Noise | 0.0038 × 10−8 | 0.0038 × 10−8 | 0.0000 × 10−8 | 0.0001 × 10−8 |
| OCF with Brownian Noise | 0.1716 × 10−8 | 0.1714 × 10−8 | 0.1296 × 10−8 | 0.1311 × 10−8 |
| OCF with Pink Noise | 0.0208 × 10−8 | 0.0207 × 10−8 | 0.0080 × 10−8 | 0.0084 × 10−8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasan, M.Y.; Alaraji, A.S.; Humaidi, A.J.; Al-Khazraji, H. Adaptive Filtered-x Least Mean Square Algorithm to Improve the Performance of Multi-Channel Noise Control Systems. Math. Comput. Appl. 2025, 30, 84. https://doi.org/10.3390/mca30040084
Hasan MY, Alaraji AS, Humaidi AJ, Al-Khazraji H. Adaptive Filtered-x Least Mean Square Algorithm to Improve the Performance of Multi-Channel Noise Control Systems. Mathematical and Computational Applications. 2025; 30(4):84. https://doi.org/10.3390/mca30040084
Chicago/Turabian StyleHasan, Maha Yousif, Ahmed Sabah Alaraji, Amjad J. Humaidi, and Huthaifa Al-Khazraji. 2025. "Adaptive Filtered-x Least Mean Square Algorithm to Improve the Performance of Multi-Channel Noise Control Systems" Mathematical and Computational Applications 30, no. 4: 84. https://doi.org/10.3390/mca30040084
APA StyleHasan, M. Y., Alaraji, A. S., Humaidi, A. J., & Al-Khazraji, H. (2025). Adaptive Filtered-x Least Mean Square Algorithm to Improve the Performance of Multi-Channel Noise Control Systems. Mathematical and Computational Applications, 30(4), 84. https://doi.org/10.3390/mca30040084









