Special Issue "Advances in Applied Statistical Mechanics"

Guest Editor
Dr. Antonio M. Scarfone
Istituto dei Sistemi Complessi, Consiglio Nazionale delle Ricerche (ISC-CNR), c/o DISAT, Politecnico di Torino, Corso Duca degli Abruzzi 24, I-10129 Torino, Italy
E-Mail: antonio.scarfone@polito.it
Interests: nonextensive statistical mechanics; nonlinear fokker-planck equations; geometry information; nonlinear schroedinger equation; quantum groups and quantum algebras; complex systems

Dear Colleagues,

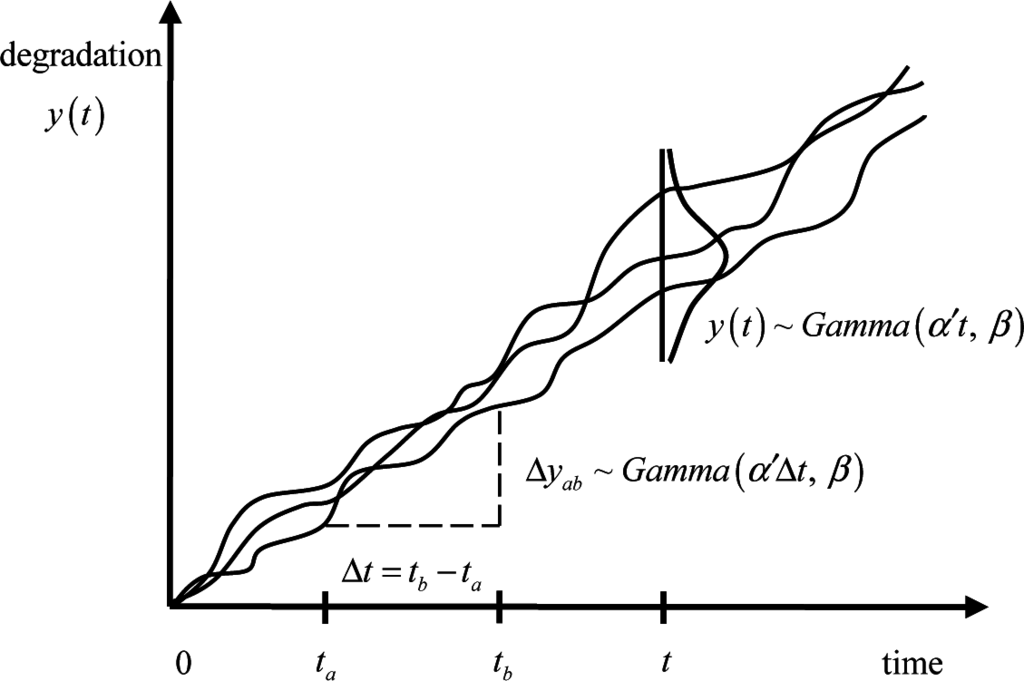
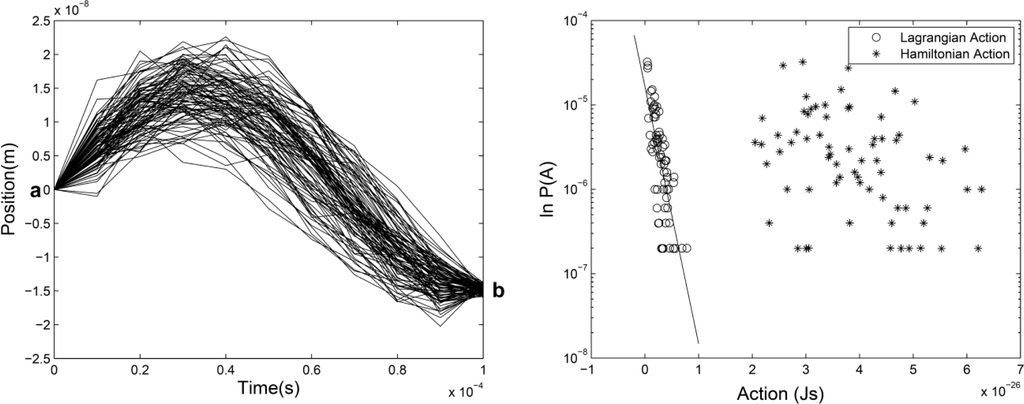
There is a diffuse belief that statistical properties of physical systems are well described by Boltzmann­Gibbs statistical mechanics. However, a constantly increasing amount of situations are known to violate the predictions of orthodox statistical mechanics. Systems where these emerging features are observed seem do not fulfill the standard ergodic and mixing properties on which the Boltzmann-Gibbs formalism are founded. In general, these systems are governed by nonlinear dynamics which establishes a deep relation among the parts. As a consequence, they reach a dynamical equilibrium in which the equilibrium probability distribution can differ deeply from the exponential shape typical of the Gibbs distribution.

In the last decades, we assisted to an intense research activity that has modified our understanding of statistical physics, extending and renewing its applicability considerably. Important developments, relating equilibrium and nonequilibrium statistical physics, kinetic theory, information theory and others, have produced a new understanding of the properties of complex systems that requires, in many
cases, the extension of the theory beyond the Boltzmann-Gibbs formalism.

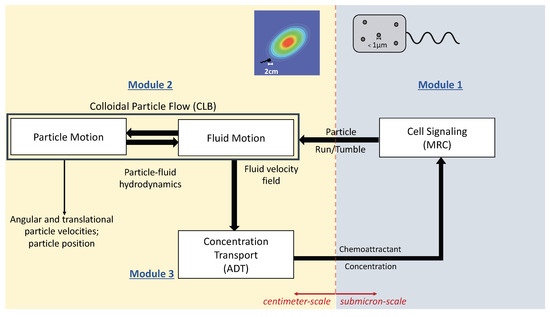
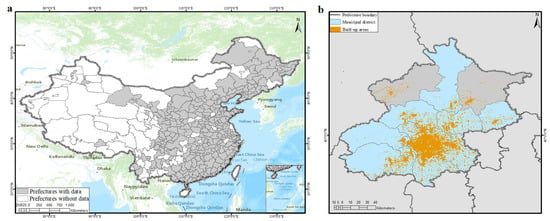
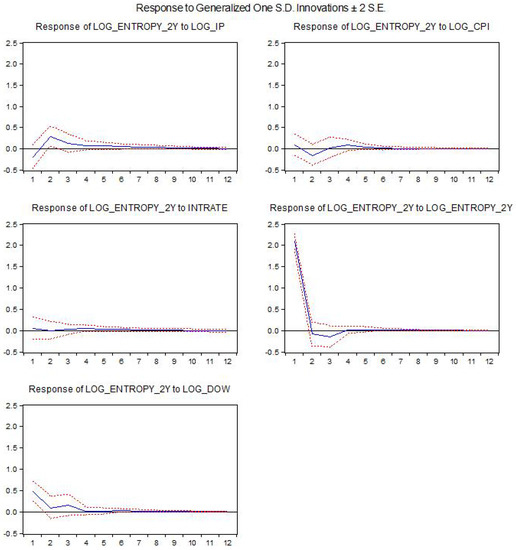
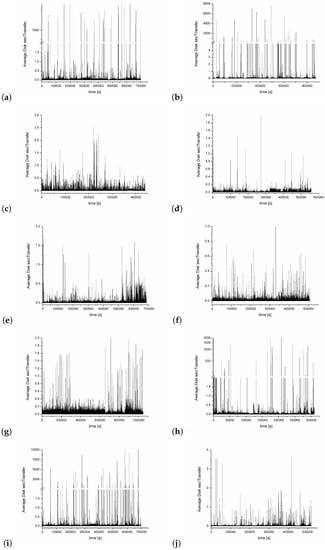
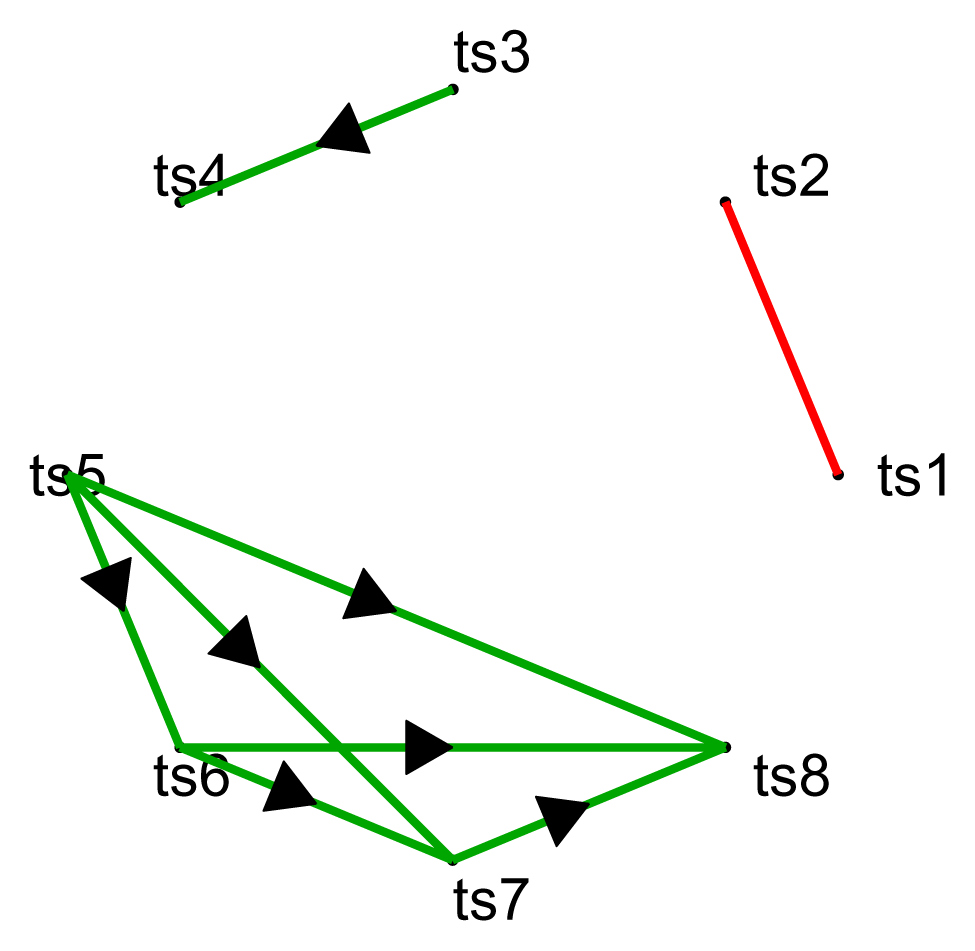
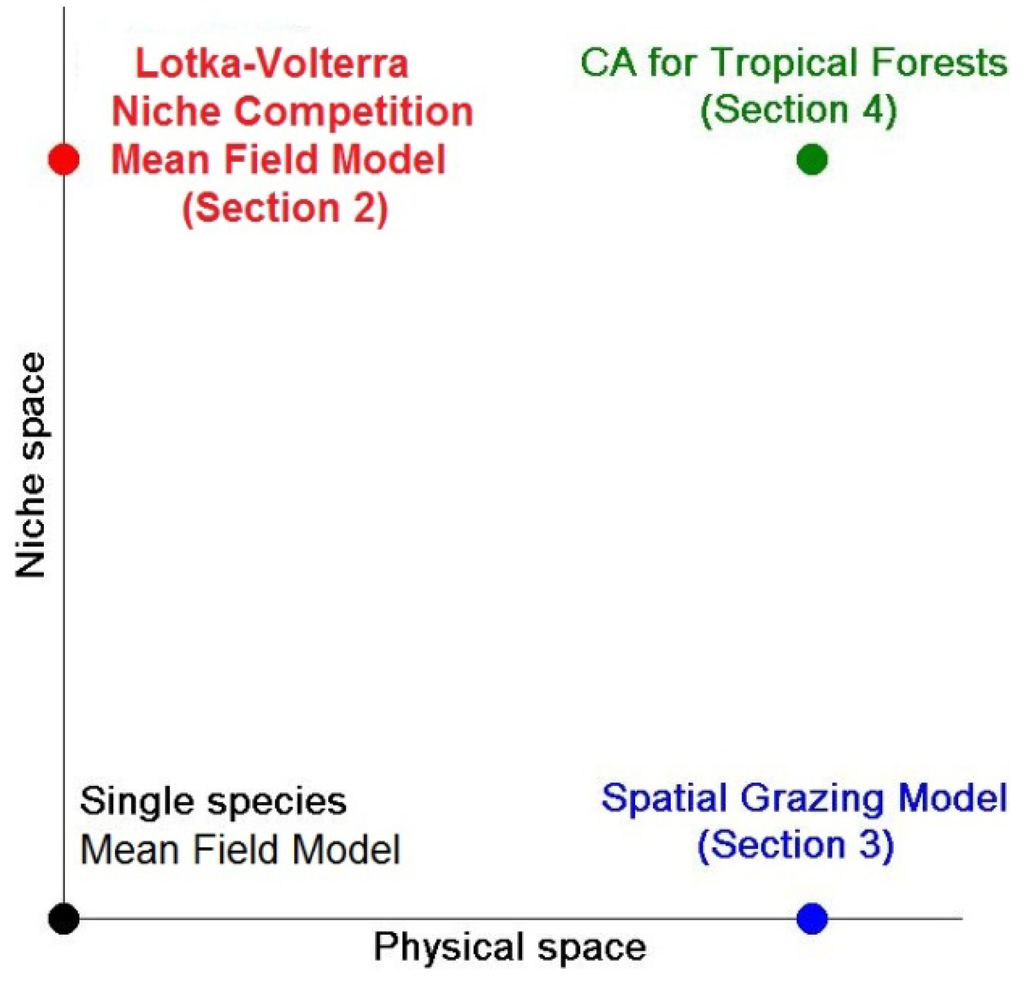
The aim of this special issue, is to collect papers in both the foundations and the applications of Statistical Mechanics going outside its traditional application. In particular, foundations regard classical and quantum aspects of statistical physics including generalized entropies, free-scale distributions, information theory, geometry information, nonextensive statistical mechanics, kinetic theory, long-range interactions and small systems. Applications are different and may include biophysics, seismology, econophysics, social systems, physics of networks, physics of risk, traffic flow, complex systems, fractal systems and others.

Specific topics of interest include (but are not limited to): * Generalized entropies * Boltzmann entropy * Renyi entropy * Non linear kinetic * Fokker-Planck equations * Quantum information * Geometry information * Fractal systems * Complex systems * Networks * Econophysics * Sociophysics * Biophysics

Dr. Antonio Maria Scarfone
Guest Editor

Submission

Manuscripts should be submitted online at www.mdpi.com by registering and logging in to this website. Once you are registered, click here to go to the submission form. Manuscripts can be submitted until the deadline. Papers will be published continuously (as soon as accepted) and will be listed together on the special issue website. Research articles, review articles as well as communications are invited. For planned papers, a title and short abstract (about 100 words) can be sent to the Editorial Office for announcement on this website.

Submitted manuscripts should not have been published previously, nor be under consideration for publication elsewhere (except conference proceedings papers). All manuscripts are refereed through a peer-review process. A guide for authors and other relevant information for submission of manuscripts is available on the Instructions for Authors page. Entropy is an international peer-reviewed Open Access monthly journal published by MDPI.

Please visit the Instructions for Authors page before submitting a manuscript. The Article Processing Charge (APC) for publication in this open access journal is 1200 CHF (Swiss Francs).

• non extensive systems
• generalized entropies
• boltzmann entropy
• renyi entropy
• non linear kinetic
• fokker-planck equations
• quantum information
• geometry information
• fractal systems
• complex systems
• networks
• econophysics
• sociophysics
• biophysics