Quadratic Mutual Information Feature Selection
Abstract
:1. Introduction
2. Related Work
2.1. Information-Theoretic Measures
2.2. Information-Theoretic Feature Selection Methods
3. The Proposed Method
| Algorithm 1: Quadratic mutual information feature selection—QMIFS |
| Data: Set of candidate features and output Y Result: Set of selected features indices Standardize and Y while ending condition not met do = 0 for do if then end end end |
4. Results and Discussion
4.1. Experimental Methodology
4.2. Classification Performance
4.3. Regression Performance
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Vergara, J.R.; Estévez, P.A. A review of feature selection methods based on mutual information. Neural Comput. Appl. 2014, 24, 175–186. [Google Scholar] [CrossRef]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Hall, M.A. Correlation-based feature selection of discrete and numeric class machine learning. In Proceedings of the Seventeenth International Conference on Machine Learning, Stanford, CA, USA, 29 June–2 July 2000; pp. 359–366. [Google Scholar]
- Fleuret, F. Fast binary feature selection with conditional mutual information. J. Mach. Learn. Res. 2004, 5, 1531–1555. [Google Scholar]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Principe, J.C. Information Theoretic Learning: Renyi’s Entropy and Kernel Perspectives; Springer Science & Business Media: New York, NY, USA, 2010. [Google Scholar]
- Brown, G. A new perspective for information theoretic feature selection. In Proceedings of the Twelfth International Conference on Artificial Intelligence and Statistics (AISTATS-09), Clearwater Beach, FL, USA, 16–18 April 2009; pp. 49–56. [Google Scholar]
- Gonçalves, L.B.; Macrini, J.L.R. Rényi entropy and Cauchy-Schwarz mutual information applied to mifs-u variable selection algorithm: A comparative study. Pesqui. Oper. 2011, 31, 499–519. [Google Scholar] [CrossRef]
- Sluga, D.; Lotric, U. Generalized information-theoretic measures for feature selection. In Proceedings of the International Conference on Adaptive and Natural Computing Algorithms, Lausanne, Switzerland, 4–6 April 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 189–197. [Google Scholar]
- Chow, T.W.; Huang, D. Estimating optimal feature subsets using efficient estimation of high-dimensional mutual information. IEEE Trans. Neural Netw. 2005, 16, 213–224. [Google Scholar] [CrossRef] [PubMed]
- Garcia, S.; Luengo, J.; Sáez, J.A.; Lopez, V.; Herrera, F. A survey of discretization techniques: Taxonomy and empirical analysis in supervised learning. IEEE Trans. Knowl. Data Eng. 2013, 25, 734–750. [Google Scholar] [CrossRef]
- Irani, K.B. Multi-interval discretization of continuous-valued attributes for classification learning. In Proceedings of the 13th International Joint Conference on Artificial Intelligence, Chambery, France, 28 August–3 September 1993; pp. 1022–1029. [Google Scholar]
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Katkovnik, V.; Shmulevich, I. Kernel density estimation with adaptive varying window size. Pattern Recognit. Lett. 2002, 23, 1641–1648. [Google Scholar] [CrossRef]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed]
- Walters-Williams, J.; Li, Y. Estimation of mutual information: A survey. In Proceedings of the International Conference on Rough Sets and Knowledge Technology, Gold Coast, QLD, Australia, 14–16 July 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 389–396. [Google Scholar]
- Sugiyama, M. Machine learning with squared-loss mutual information. Entropy 2012, 15, 80–112. [Google Scholar] [CrossRef]
- Beck, C. Generalised information and entropy measures in physics. Contemp. Phys. 2009, 50, 495–510. [Google Scholar] [CrossRef]
- Renyi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; pp. 547–561. [Google Scholar]
- Erdogmus, D.; Principe, J.C. Generalized information potential criterion for adaptive system training. IEEE Trans. Neural Netw. 2002, 13, 1035–1044. [Google Scholar] [CrossRef] [PubMed]
- Renyi, A. Some Fundamental Questions About Information Theory; Akademia Kiado: Budapest, Hungary, 1976; Volume 2. [Google Scholar]
- Battiti, R. Using mutual information for selecting features in supervised neural net learning. IEEE Trans. Neural Netw. 1994, 5, 537–550. [Google Scholar] [CrossRef] [PubMed]
- Kwak, N.; Choi, C.H. Input feature selection for classification problems. IEEE Trans. Neural Netw. 2002, 13, 143–159. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Moody, J. Feature selection based on joint mutual information. In Proceedings of the International ICSC Symposium on Advances in Intelligent Data Analysis, Rochester, NY, USA, 22–25 June 1999; pp. 22–25. [Google Scholar]
- Rajan, K.; Bialek, W. Maximally informative “stimulus energies” in the analysis of neural responses to natural signals. PLoS ONE 2013, 8, e71959. [Google Scholar] [CrossRef] [PubMed]
- Fitzgerald, J.D.; Rowekamp, R.J.; Sincich, L.C.; Sharpee, T.O. Second order dimensionality reduction using minimum and maximum mutual information models. PLoS Comput. Biol. 2011, 7, e1002249. [Google Scholar] [CrossRef] [PubMed]
- Rowekamp, R.J.; Sharpee, T.O. Analyzing multicomponent receptive fields from neural responses to natural stimuli. Netw. Comput. Neural Syst. 2011, 22, 45–73. [Google Scholar]
- Sánchez-Maroño, N.; Alonso-Betanzos, A.; Tombilla-Sanromán, M. Filter methods for feature selection—A comparative study. In Proceedings of the International Conference on Intelligent Data Engineering and Automated Learning, Birmingham, UK, 16–19 December 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 178–187. [Google Scholar]
- Frénay, B.; Doquire, G.; Verleysen, M. Is mutual information adequate for feature selection in regression? Neural Netw. 2013, 48, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; CRC Press: Boca Raton, FL, USA, 1986; Volume 26. [Google Scholar]
- Seth, S.; Príncipe, J.C. On speeding up computation in information theoretic learning. In Proceedings of the International Joint Conference on Neural Networks (IJCNN 2009), Atlanta, GA, USA, 14–19 June 2009; pp. 2883–2887. [Google Scholar]
- Lichman, M. UCI Machine Learning Repository. Available online: http://archive.ics.uci.edu/ml (accessed on 1 December 2016).
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
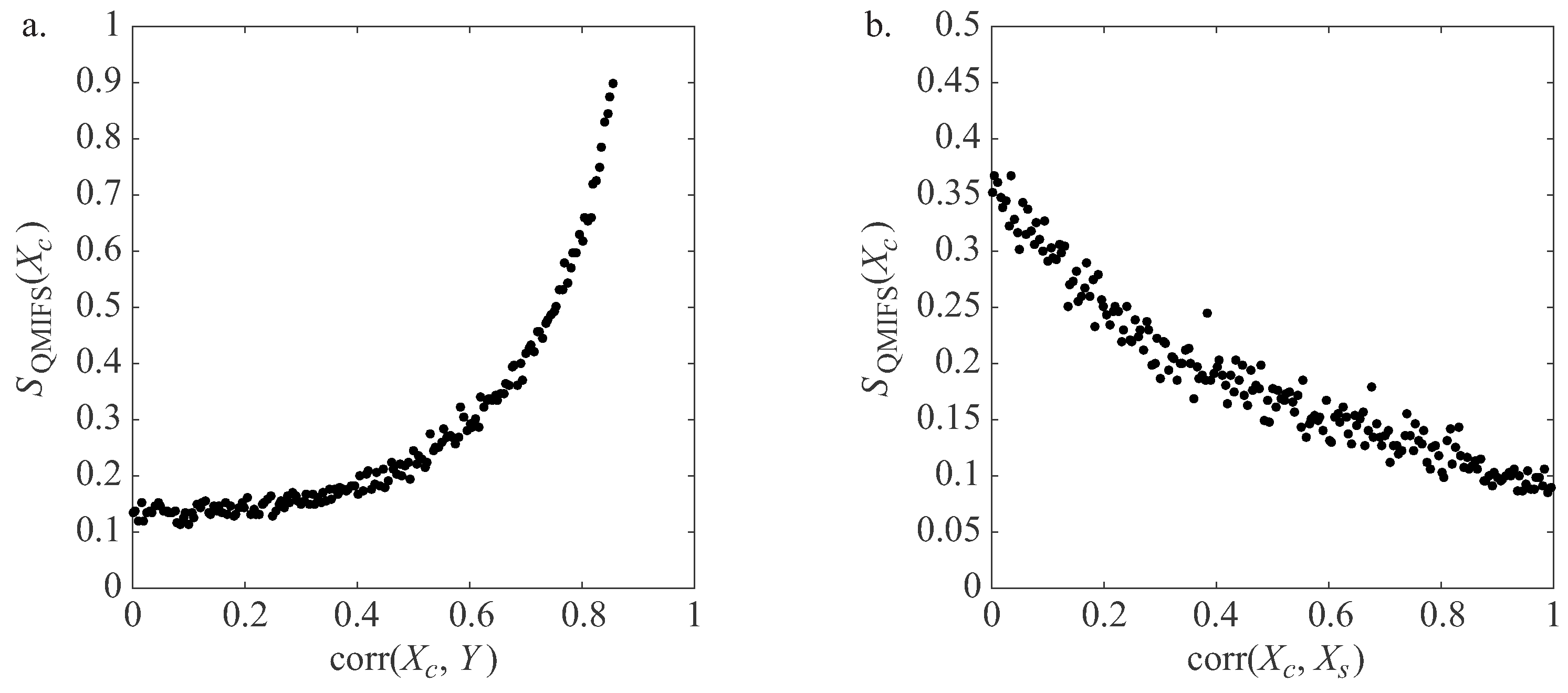
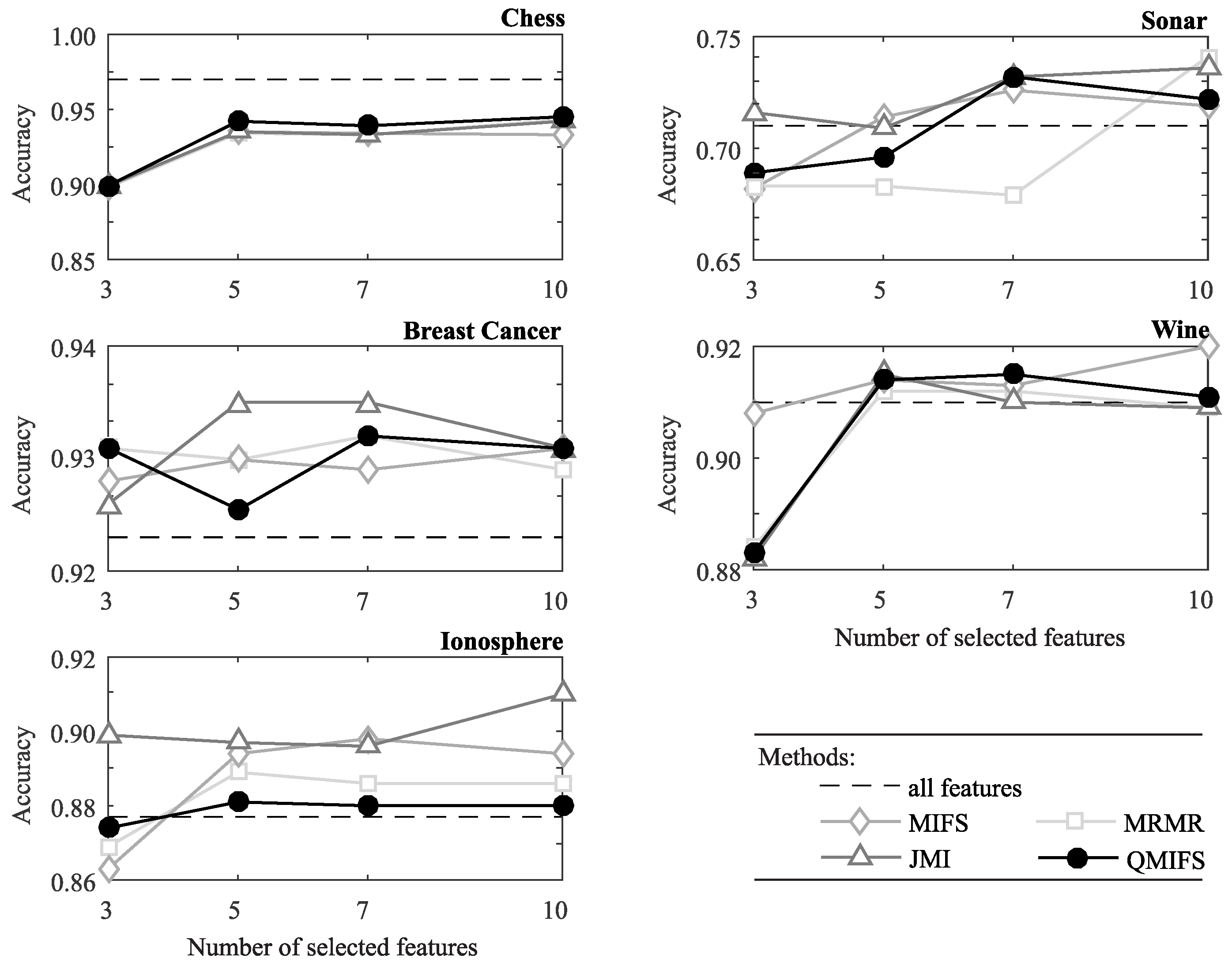
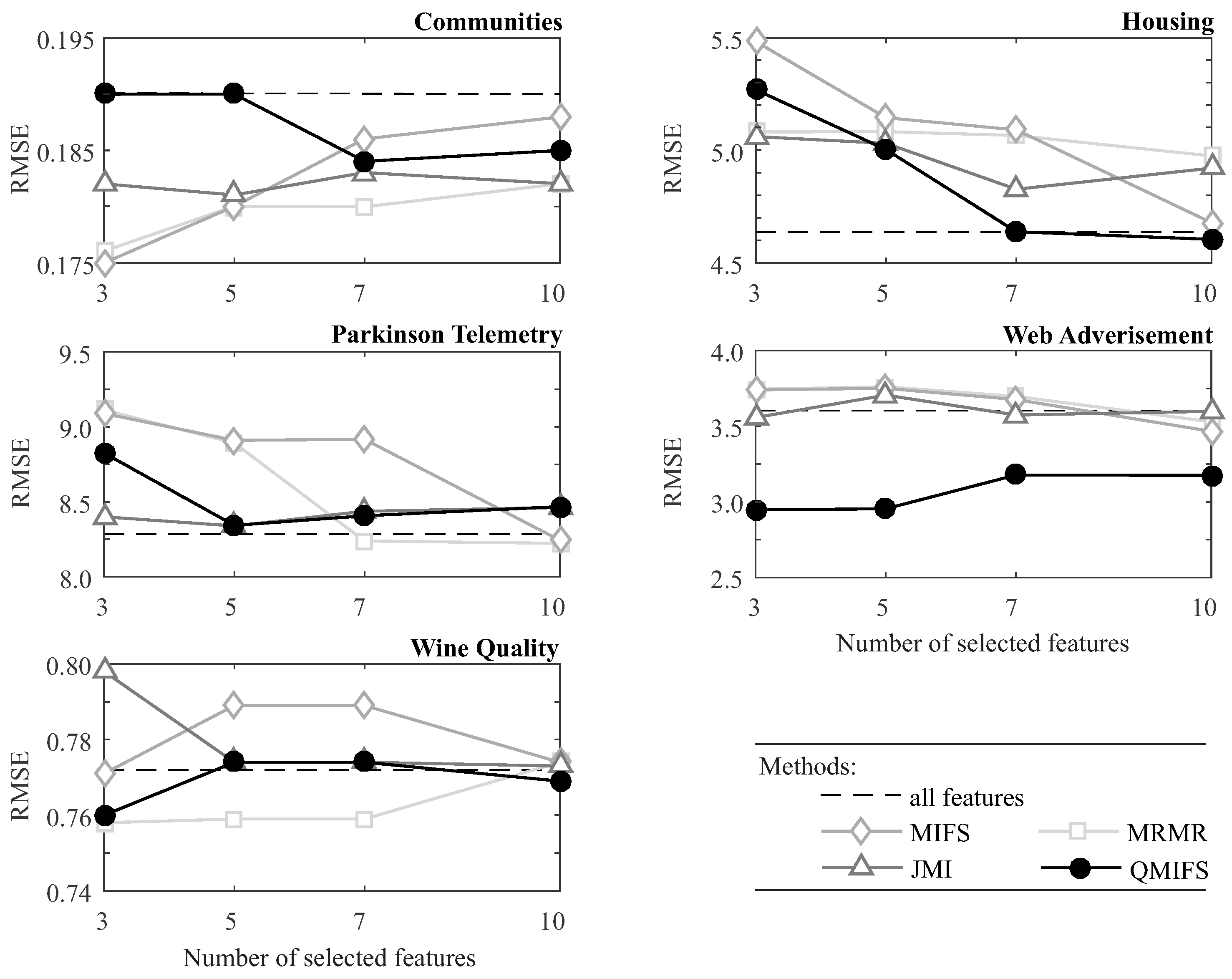
| Data Set | Instances | Features | Output | Problem Domain | |
|---|---|---|---|---|---|
| Discrete | Continuous | ||||
| Chess | 1000 | 36 | 0 | binary | Classification |
| Breast Cancer | 569 | 0 | 30 | binary | |
| Ionosphere | 351 | 0 | 34 | binary | |
| Sonar | 208 | 0 | 60 | binary | |
| Wine | 178 | 0 | 13 | ternary | |
| Communities | 1993 | 0 | 100 | continuous | Regression |
| Parkinson Telemonitoring | 1000 | 0 | 16 | continuous | |
| Wine Quality | 1599 | 0 | 11 | continuous | |
| Housing | 506 | 12 | 1 | continuous | |
| Web Advertisement | 950 | 38 | 8 | continuous | |
| Data Set | Method | Selected Features | |||
|---|---|---|---|---|---|
| 3 | 5 | 7 | 10 | ||
| Chess | MIFS | 21, 10, 33 | 32, 9 | 1, 2 | 3, 4, 5 |
| MRMR | 21, 10, 33 | 32, 15 | 8, 16 | 18, 6, 27 | |
| JMI | 21, 10, 33 | 32, 15 | 8, 16 | 18, 6, 7 | |
| QMIFS | 33, 10, 21 | 35, 6 | 8, 18 | 7, 15, 13 | |
| Breast cancer | MIFS | 23, 22, 5 | 19, 10 | 12, 15 | 30, 18, 29 |
| MRMR | 23, 22, 28 | 14, 27 | 21, 8 | 29, 25, 24 | |
| JMI | 23, 28, 24 | 8, 22 | 21, 4 | 7, 27, 14 | |
| QMIFS | 28, 2, 23 | 8, 27 | 21, 22 | 3, 7, 1 | |
| Ionosphere | MIFS | 5, 16, 2 | 18, 1 | 10, 30 | 32, 7, 24 |
| MRMR | 5, 16, 18 | 27, 3 | 6, 7 | 4, 34, 31 | |
| JMI | 5, 6, 3 | 33, 8 | 17, 21 | 4, 13, 29 | |
| QMIFS | 5, 6, 33 | 15, 8 | 7, 21 | 28, 31, 24 | |
| Sonar | MIFS | 11, 51, 36 | 44, 4 | 1, 2 | 3, 6, 7 |
| MRMR | 11, 51, 36 | 48, 12 | 9, 54 | 45, 4, 21 | |
| JMI | 11, 4, 12 | 48, 9 | 21, 45 | 10, 36, 49 | |
| QMIFS | 12, 27, 11 | 48, 10 | 16, 9 | 13, 49, 28 | |
| Wine | MIFS | 7, 1, 11 | 5, 3 | 4, 9 | 8, 10, 2 |
| MRMR | 7, 1, 13 | 11, 10 | 12, 6 | 5, 2, 4 | |
| JMI | 7, 1, 13 | 11, 10 | 12, 6 | 2, 5, 4 | |
| QMIFS | 7, 1, 13 | 12, 10 | 11, 6 | 5, 9, 4 | |
| Data Set | Method | Selected Features | Average | |||||
|---|---|---|---|---|---|---|---|---|
| 3 | 5 | 7 | 10 | |||||
| Chess | MIFS | 2.5/2.5/2.5 | 3/3/3 | 2/4/3 | 4/4/4 | 2.9/3.4/3.1 |  | |
| MRMR | 2.5/2.5/2.5 | 3/3/3 | 4/2.5/3 | 2.5/1.5/2.5 | 3.0/2.4/2.8 | |||
| JMI | 2.5/2.5/2.5 | 3/3/3 | 3/2.5/3 | 2.5/3/2.5 | 2.8/2.8/2.8 | |||
| QMIFS | 2.5/2.5/2.5 | 1/1/1 | 1/1/1 | 1/1.5/1 | 1.4/1.5/1.4 | |||
| Breast Cancer | MIFS | 3.5/4/3.5 | 2.5/3/3 | 4/2.5/4 | 2/4/2.5 | 3.0/3.4/3.3 | ||
| MRMR | 1.5/2/1.5 | 2.5/3/2 | 2/2.5/1.5 | 4/2/2.5 | 2.5/2.4/1.9 | |||
| JMI | 3.5/2/3.5 | 1/1/1 | 2/2.5/1.5 | 2/2/2.5 | 2.1/1.9/2.1 | |||
| QMIFS | 1.5/2/1.5 | 4/3/4 | 2/2.5/3 | 2/2/2.5 | 2.4/2.4/2.8 | |||
| Iono-sphere | MIFS | 3.5/3.5/3.5 | 1.5/3.5/2.5 | 1.5/2.5/1.5 | 2/2/2 | 2.1/2.9/2.4 | 2.5/2.9/2.7 | |
| MRMR | 3.5/3.5/3.5 | 3.5/2/2.5 | 3.5/2.5/3 | 3/3.5/3 | 3.4/2.9/3.0 | 3.0/2.8/2.8 | ||
| JMI | 1/1/1 | 1.5/1/1 | 1.5/1/1.5 | 1/1/1 | 1.3/1.0/1.1 | 2.1/2.1/2.1 | ||
| QMIFS | 2/2/2 | 3.5/3.5/4 | 3.5/4/4 | 4/3.5/4 | 3.3/3.3/3.5 | 2.4/2.3/2.4 | ||
| Sonar | MIFS | 3/3/3 | 1/1/1 | 2/2/2 | 3.5/3.5/3.5 | 2.4/2.4/2.4 | ||
| MRMR | 4/4/3 | 3.5/4/4 | 4/4/4 | 1.5/1.5/1.5 | 3.3/3.4/3.1 | |||
| JMI | 1/1.5/1 | 2/2.5/2 | 2/2/2 | 1.5/1.5/1.5 | 1.6/1.9/1.6 | |||
| QMIFS | 2/1.5/3 | 3.5/2.5/3 | 2/2/2 | 3.5/3.5/3.5 | 2.8/2.4/2.9 | |||
| Wine | MIFS | 1/2.5/1 | 2.5/3/3 | 2.5/2.5/3 | 1.5/1.5/2.5 | 1.9/2.4/2.4 | ||
| MRMR | 3/2.5/3 | 2.5/3/3 | 2.5/2.5/3 | 3.5/3/4 | 2.9/2.8/3.3 | |||
| JMI | 3/2.5/3 | 2.5/3/3 | 2.5/2.5/3 | 3.5/3/2.5 | 2.9/2.8/2.9 | |||
| QMIFS | 3/2.5/3 | 2.5/1/1 | 2.5/2.5/1 | 1.5/1.5/1 | 2.4/1.9/1.5 | |||
| Data Set | Method | Measure | ||||
|---|---|---|---|---|---|---|
| CA | AUC | Y-Index | FPR, TPR | Time (s) | ||
| Chess | MIFS | 0.934 | 0.956 | 0.865 | 0.106, 0.970 | 2.48 |
| MRMR | 0.932 | 0.964 | 0.866 | 0.099, 0.965 | 2.51 | |
| JMI | 0.933 | 0.965 | 0.866 | 0.098, 0.965 | 2.68 | |
| QMIFS | 0.938 | 0.976 | 0.886 | 0.032, 0.918 | 0.32 | |
| All features | 0.969 (±4) | 0.985 () | 0.943 () | 0.032, 0.975 | (±0.04) | |
| Breast cancer | MIFS | 0.929 | 0.939 | 0.858 | 0.095, 0.953 | 1.53 |
| MRMR | 0.932 | 0.942 | 0.868 | 0.080, 0.948 | 1.52 | |
| JMI | 0.935 | 0.944 | 0.873 | 0.074, 0.947 | 1.56 | |
| QMIFS | 0.932 | 0.941 | 0.866 | 0.080, 0.947 | 0.42 | |
| All features | 0.923 () | 0.927 () | 0.849 () | 0.093, 0.941 | (±0.02) | |
| Ionosphere | MIFS | 0.897 | 0.904 | 0.794 | 0.150, 0.944 | 1.15 |
| MRMR | 0.888 | 0.903 | 0.780 | 0.152, 0.931 | 1.17 | |
| JMI | 0.897 | 0.915 | 0.796 | 0.138, 0.933 | 1.21 | |
| QMIFS | 0.881 | 0.897 | 0.764 | 0.160, 0.924 | 0.39 | |
| All features | 0.877 () | 0.878 () | 0.755 () | 0.164, 0.919 | (±0.02) | |
| Sonar | MIFS | 0.728 | 0.755 | 0.504 | 0.267, 0.770 | 1.18 |
| MRMR | 0.681 | 0.711 | 0.424 | 0.301, 0.725 | 1.20 | |
| JMI | 0.731 | 0.759 | 0.510 | 0.280, 0.790 | 1.23 | |
| QMIFS | 0.734 | 0.759 | 0.506 | 0.270, 0.777 | 0.38 | |
| All features | 0.708 () | 0.724 () | 0.452 () | 0.302, 0.754 | (±0.02) | |
| Wine | MIFS | 0.911 | 0.919 | 0.826 | 0.050, 0.876 | 0.51 |
| MRMR | 0.910 | 0.917 | 0.828 | 0.070, 0.898 | 0.49 | |
| JMI | 0.911 | 0.916 | 0.829 | 0.069, 0.898 | 0.54 | |
| QMIFS | 0.915 | 0.923 | 0.839 | 0.068, 0.907 | 0.29 | |
| All features | 0.906 () | 0.912 () | 0.813 () | 0.066, 0.878 | (±0.02) | |
| Data Set | Method | Selected Features | |||
|---|---|---|---|---|---|
| 3 | 5 | 7 | 10 | ||
| Communities | MIFS | 45, 52, 67 | 95, 97 | 48, 36 | 24, 15, 89 |
| MRMR | 45, 52, 4 | 41, 51 | 72, 69 | 18, 3, 50 | |
| JMI | 45, 4, 44 | 50, 69 | 51, 46 | 41, 3, 16 | |
| QMIFS | 45, 41, 78 | 42, 44 | 4, 68 | 29, 39, 16 | |
| Parkinson Telemonitoring | MIFS | 15, 12, 14 | 16, 8 | 5, 10 | 2, 13, 4 |
| MRMR | 15, 12, 14 | 8, 16 | 2, 10 | 5, 13, 7 | |
| JMI | 15, 14, 2 | 6, 13 | 9, 4 | 10, 7, 11 | |
| QMIFS | 15, 14, 13 | 2, 10 | 8, 4 | 11, 9, 6 | |
| Wine Quality | MIFS | 11, 10, 6 | 4, 9 | 2, 5 | 8, 7, 3 |
| MRMR | 11, 10, 2 | 5, 7 | 8, 4 | 9, 3, 6 | |
| JMI | 11, 10, 8 | 3, 2 | 5, 7 | 1, 4, 6 | |
| QMIFS | 11, 10, 2 | 8, 3 | 7, 1 | 9, 6, 5 | |
| Housing | MIFS | 13, 11, 4 | 6, 12 | 7, 9 | 8, 2, 10 |
| MRMR | 13, 11, 6 | 12, 7 | 10, 4 | 3, 1, 5 | |
| JMI | 13, 6, 11 | 3, 1 | 10, 5 | 2, 7, 9 | |
| QMIFS | 13, 8, 3 | 6, 7 | 11, 5 | 10, 9, 4 | |
| Web Advertisement | MIFS | 29, 9, 21 | 44, 35 | 15, 13 | 12, 22, 6 |
| MRMR | 29, 9, 21 | 44, 35 | 39, 13 | 12, 15, 22 | |
| JMI | 29, 4, 41 | 30, 28 | 10, 39 | 31, 3, 37 | |
| QMIFS | 3, 8, 40 | 2, 4 | 46, 16 | 36, 10, 45 | |
| Data Set | Method | Selected Features | Average | |||||
|---|---|---|---|---|---|---|---|---|
| 3 | 5 | 7 | 10 | |||||
| Communities | MIFS | 1.5 | 2 | 4 | 4 | 2.9 |  | |
| MRMR | 1.5 | 2 | 1 | 2 | 1.6 | |||
| JMI | 3 | 2 | 2.5 | 1 | 2.1 | |||
| QMIFS | 4 | 4 | 2.5 | 3 | 3.4 | |||
| Parkinson Telemonitoring | MIFS | 3.5 | 3.5 | 4 | 1.5 | 3.1 | ||
| MRMR | 3.5 | 3.5 | 1 | 1.5 | 2.4 | |||
| JMI | 1 | 1.5 | 2.5 | 3.5 | 2.1 | |||
| QMIFS | 2 | 1.5 | 2.5 | 3.5 | 2.4 | |||
| Wine Quality | MIFS | 3 | 4 | 2.5 | 2.5 | 3.0 | 3.1 | |
| MRMR | 1.5 | 1 | 2.5 | 2.5 | 1.9 | 2.5 | ||
| JMI | 4 | 2.5 | 2.5 | 2.5 | 2.9 | 2.4 | ||
| QMIFS | 1.5 | 2.5 | 2.5 | 2.5 | 2.3 | 2.1 | ||
| Housing | MIFS | 4 | 3.5 | 3.5 | 2 | 3.3 | ||
| MRMR | 1.5 | 3.5 | 3.5 | 4 | 3.1 | |||
| JMI | 1.5 | 2 | 2 | 3 | 2.1 | |||
| QMIFS | 3 | 1 | 1 | 1 | 1.5 | |||
| Web Advertisement | MIFS | 3.5 | 3.5 | 3 | 2 | 3.0 | ||
| MRMR | 3.5 | 3.5 | 4 | 3 | 3.5 | |||
| JMI | 2 | 2 | 2 | 4 | 2.5 | |||
| QMIFS | 1 | 1 | 1 | 1 | 1.0 | |||
| Data Set | Method | RMSE | Time (s) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 5 | 7 | 10 | All Features | 3 | 5 | 7 | 10 | ||
| Communities | MIFS | 0.176 | 0.180 | 0.186 | 0.188 | 0.190 | 0.97 | 1.43 | 1.87 | 2.49 |
| MRMR | 0.176 | 0.180 | 0.180 | 0.181 | 0.97 | 1.42 | 1.86 | 2.50 | ||
| JMI | 0.182 | 0.181 | 0.183 | 0.183 | 1.53 | 2.34 | 3.22 | 4.49 | ||
| QMIFS | 0.190 | 0.190 | 0.183 | 0.185 | () | 2.74 | 4.06 | 5.46 | 7.51 (±0.02) | |
| Parkinson Telemonitoring | MIFS | 9.12 | 8.89 | 8.93 | 8.21 | 8.30 | 0.32 | 0.35 | 0.37 | 0.40 |
| MRMR | 9.11 | 8.92 | 8.23 | 8.23 | 0.32 | 0.35 | 0.37 | 0.40 | ||
| JMI | 8.40 | 8.32 | 8.43 | 8.48 | 0.38 | 0.43 | 0.48 | 0.54 | ||
| QMIFS | 8.83 | 8.34 | 8.42 | 8.45 | () | 0.49 | 0.59 | 0.66 | 0.77 (±0.01) | |
| Wine Quality | MIFS | 0.772 | 0.789 | 0.772 | 0.773 | 0.771 | 0.32 | 0.35 | 0.37 | 0.39 |
| MRMR | 0.760 | 0.758 | 0.773 | 0.773 | 0.32 | 0.35 | 0.37 | 0.39 | ||
| JMI | 0.798 | 0.775 | 0.770 | 0.772 | 0.36 | 0.42 | 0.45 | 0.48 | ||
| QMIFS | 0.760 | 0.774 | 0.771 | 0.770 | () | 0.42 | 0.43 | 0.46 | 0.48 (±0.01) | |
| Housing | MIFS | 5.49 | 5.12 | 5.12 | 4.74 | 4.63 | 0.29 | 0.30 | 0.30 | 0.32 |
| MRMR | 5.08 | 5.10 | 5.06 | 4.93 | 0.29 | 0.30 | 0.31 | 0.32 | ||
| JMI | 5.08 | 5.03 | 4.85 | 4.90 | 0.31 | 0.33 | 0.35 | 0.37 | ||
| QMIFS | 5.25 | 4.99 | 4.61 | 4.54 | () | 0.34 | 0.38 | 0.41 | 0.43 (±0.01) | |
| Web Advertisement | MIFS | 3.746 | 3.757 | 3.668 | 3.466 | 3.59 | 0.51 | 0.60 | 0.69 | 0.82 |
| MRMR | 3.746 | 3.755 | 3.703 | 3.526 | 0.51 | 0.60 | 0.72 | 0.84 | ||
| JMI | 3.562 | 3.699 | 3.567 | 3.582 | 0.63 | 0.88 | 1.12 | 1.43 | ||
| QMIFS | 2.953 | 2.956 | 3.174 | 3.175 | () | 3.19 | 3.49 | 3.76 | 4.17 (±0.02) | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sluga, D.; Lotrič, U. Quadratic Mutual Information Feature Selection. Entropy 2017, 19, 157. https://doi.org/10.3390/e19040157
Sluga D, Lotrič U. Quadratic Mutual Information Feature Selection. Entropy. 2017; 19(4):157. https://doi.org/10.3390/e19040157
Chicago/Turabian StyleSluga, Davor, and Uroš Lotrič. 2017. "Quadratic Mutual Information Feature Selection" Entropy 19, no. 4: 157. https://doi.org/10.3390/e19040157
APA StyleSluga, D., & Lotrič, U. (2017). Quadratic Mutual Information Feature Selection. Entropy, 19(4), 157. https://doi.org/10.3390/e19040157





