Asymptotic Behavior of Memristive Circuits
Abstract
1. Introduction
2. Memristive Circuits
Functional Complexity for Random Circuits
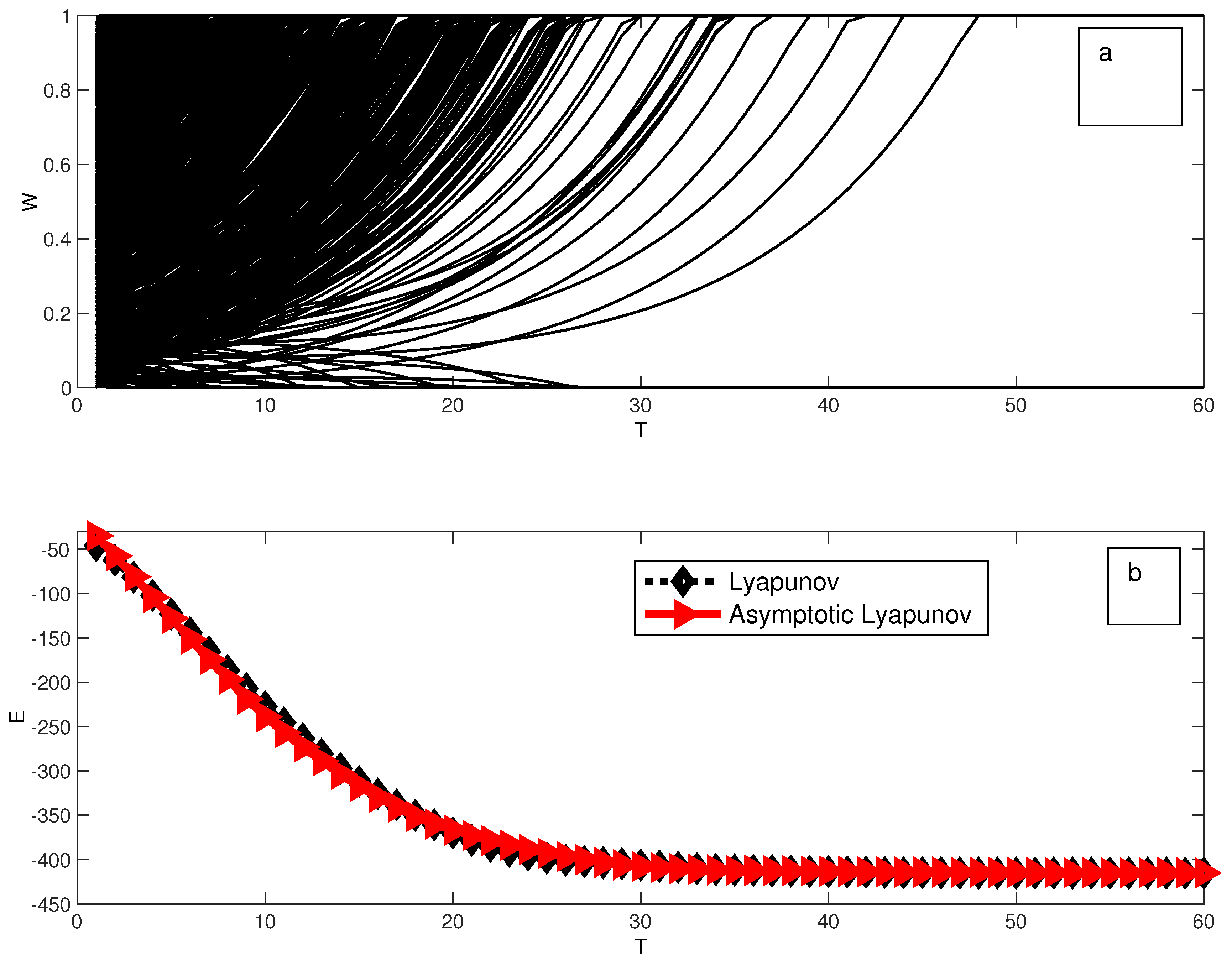
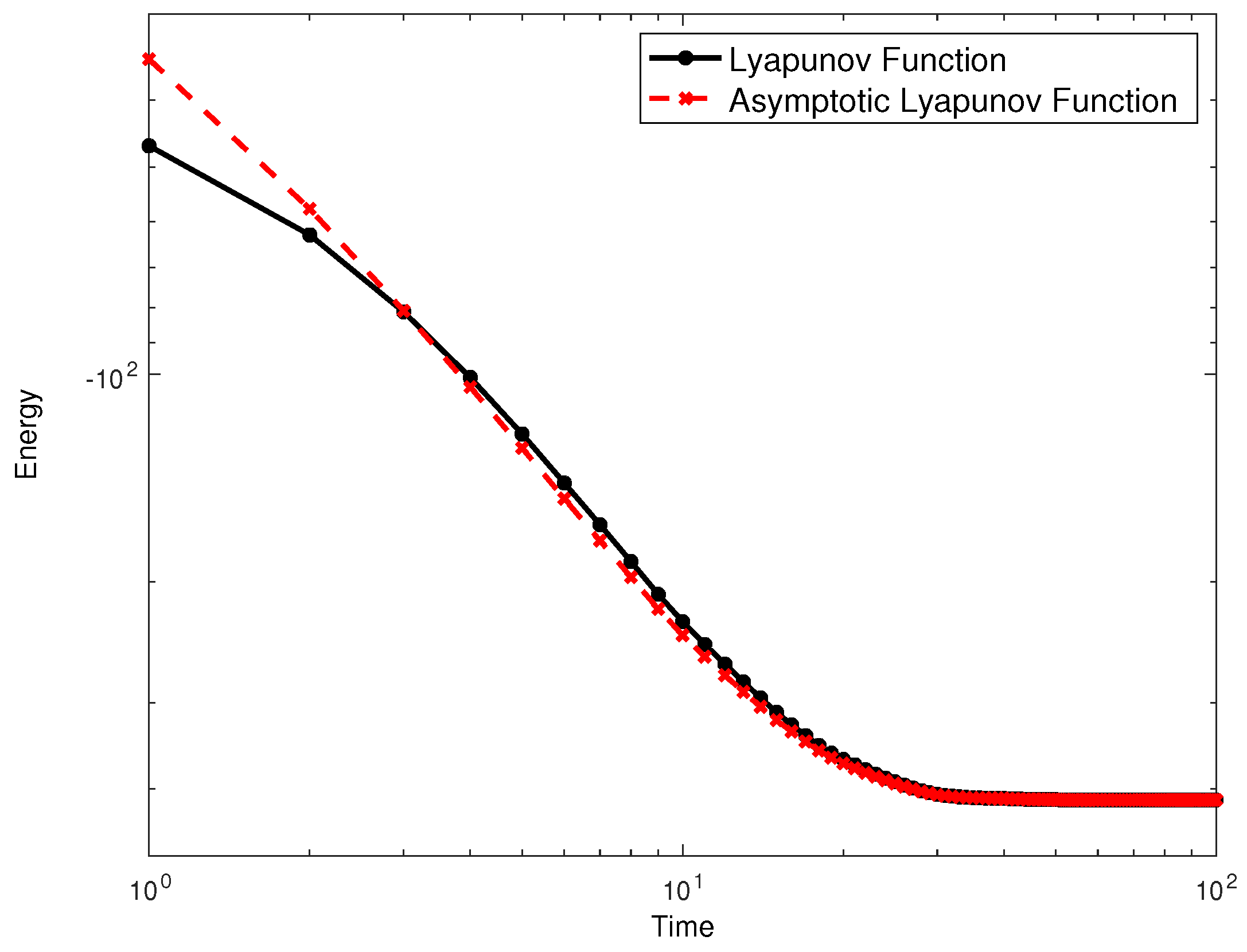
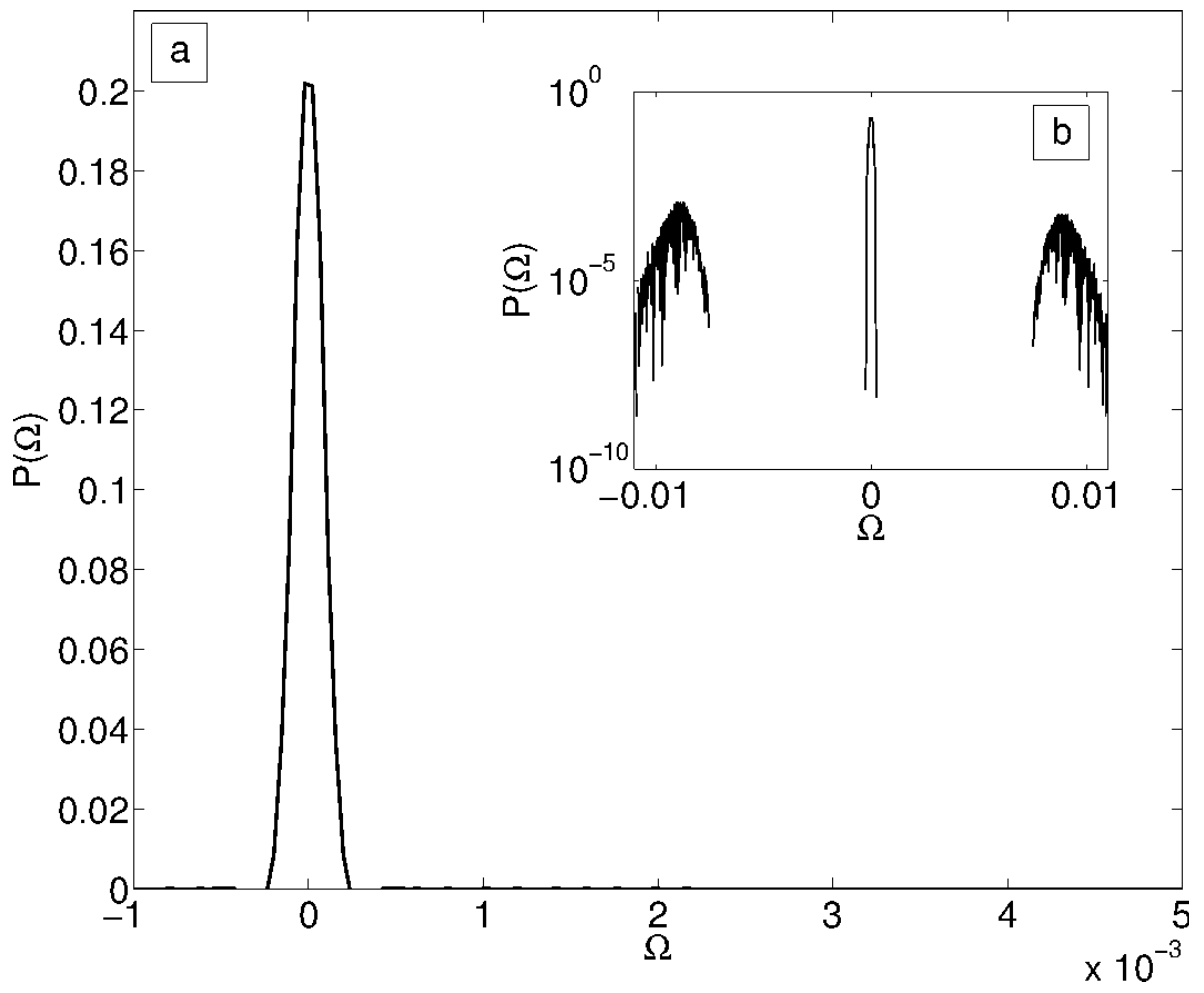
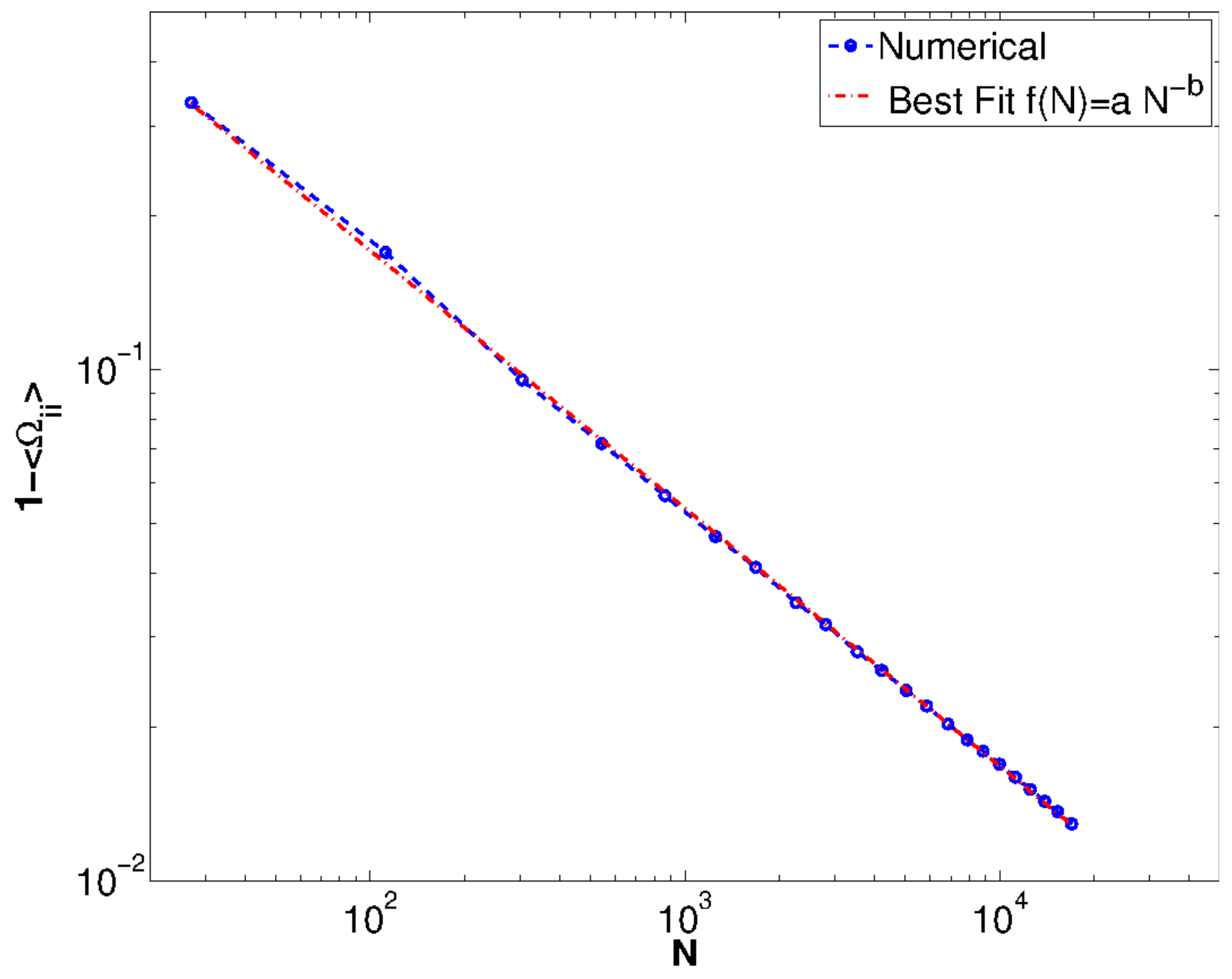
3. Asymptotic State Recollection and Combinatorial Optimization
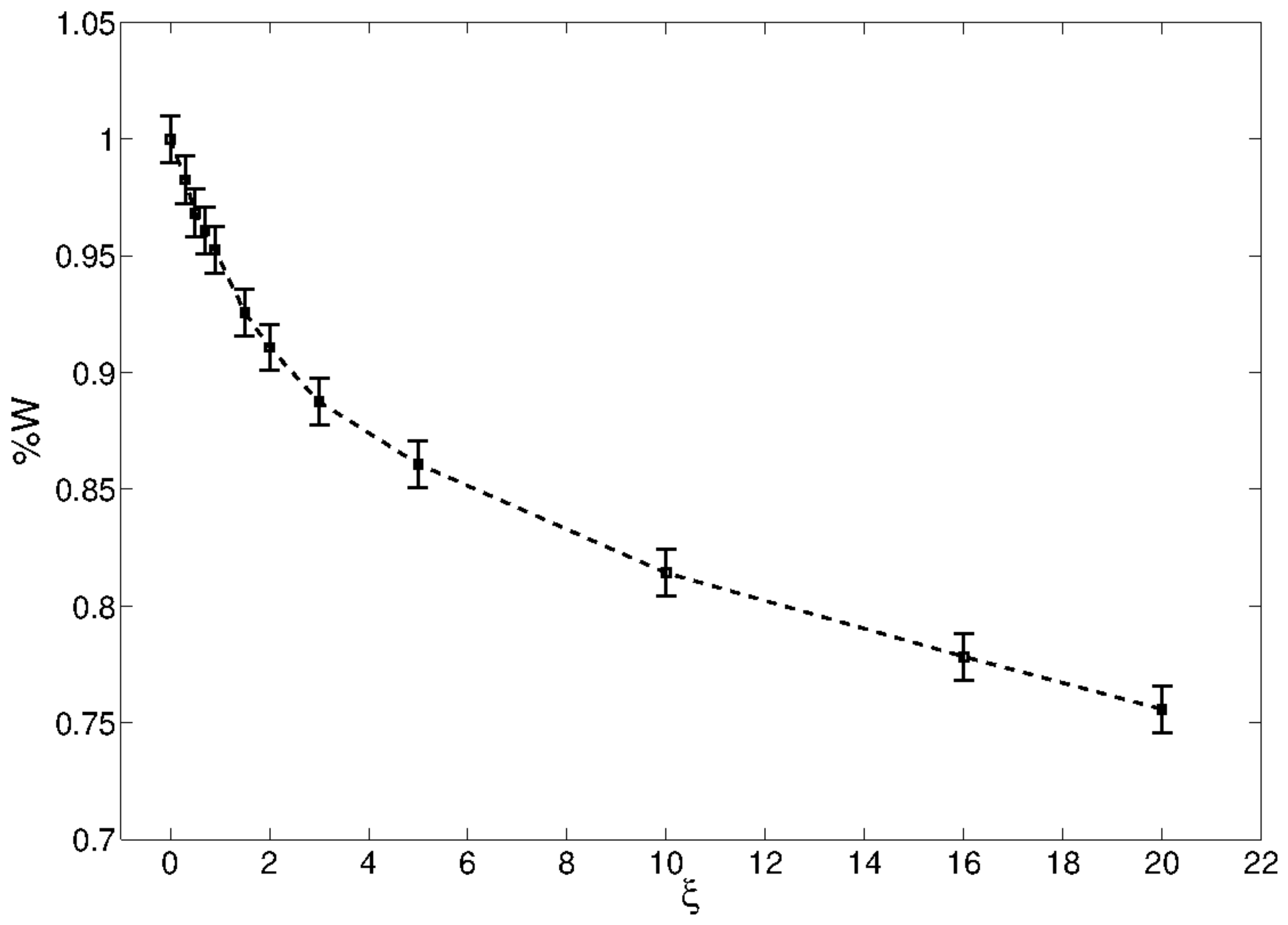
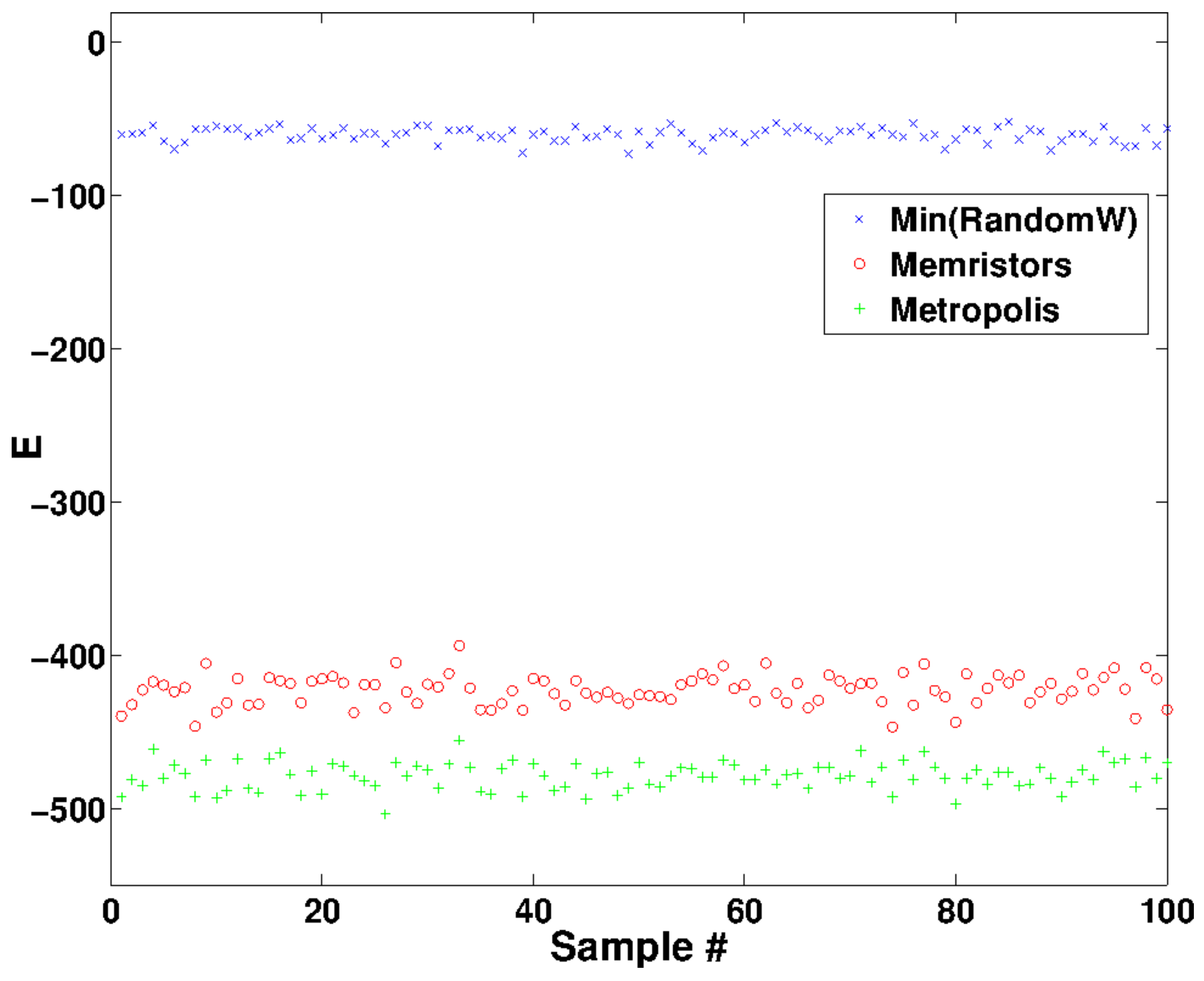
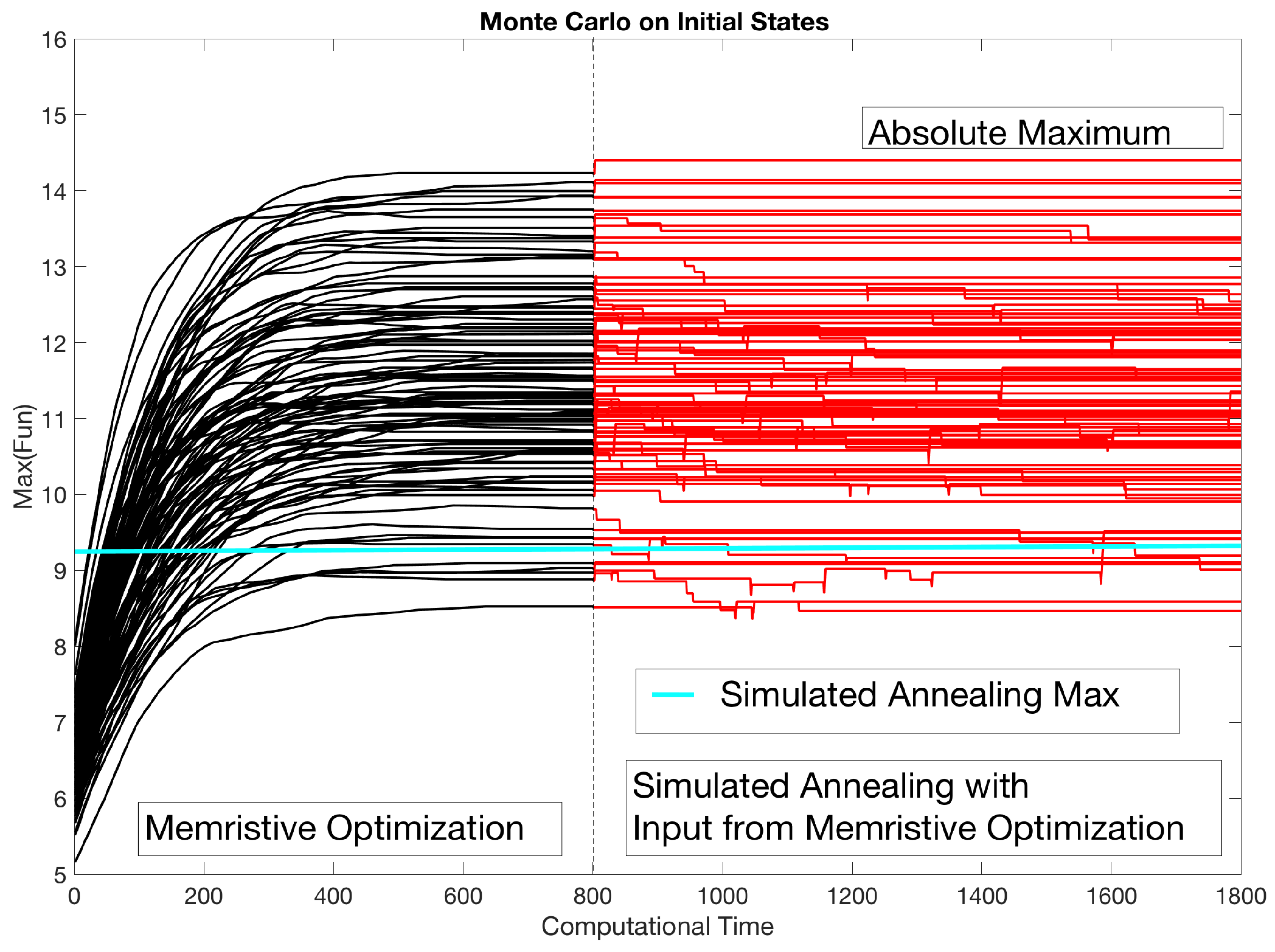
4. An Application: Minimization of a Quadratic Function
5. Concluding Remarks
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Properties of L(W)
Appendix A.1. Derivation of L(W)
Appendix A.2. Variation
Appendix B. Complexity of the Lyapunov Functional via Kac-Rice Formula
References
- Indiveri, G.; Liu, S.-C. Memory and information processing in neuromorphic systems. Proc. IEEE 2015, 103, 1379–1397. [Google Scholar] [CrossRef]
- Avizienis, A.V.; Sillin, H.O.; Martin-Olmos, C.; Shieh, H.H.; Aono, M.; Stieg, A.Z.; Gimzewski, J.K. Neuromorphic Atomic Switch Networks. PLoS ONE 2012, 7, e42772. [Google Scholar] [CrossRef] [PubMed]
- Stieg, A.Z.; Avizienis, A.V.; Sillin, H.O.; Martin-Olmos, C.; Aono, M.; Gimzewski, J.K. Emergent Criticality in Complex Turing B-Type Atomic Switch Networks. Adv. Mater. 2012, 24, 286–293. [Google Scholar] [CrossRef] [PubMed]
- Traversa, F.L.; di Ventra, M. Universal memcomputing machines. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2702–2715. [Google Scholar] [CrossRef] [PubMed]
- Caravelli, F.; Hamma, A.; di Ventra, M. Scale-free networks as an epiphenomenon of memory. Europhys. Lett. EPL 2015, 109, 28006. [Google Scholar] [CrossRef]
- Caravelli, F. Trajectories entropy in dynamical graphs with memory. Front. Robot. AI 2016, 3, 18. [Google Scholar] [CrossRef]
- Caravelli, F.; Carbajal, J.P. Memristors for the curious outsiders. Technologies 2018, 6, 118. [Google Scholar] [CrossRef]
- Zegarac, A.; Caravelli, F. Memristive networks: From graph theory to statistical physics. Europhys. Lett. EPL 2019, 125, 10001. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Chua, L.O.; Kang, S.M. Memristive devices and systems. Proc. IEEE 1976, 64, 209–223. [Google Scholar] [CrossRef]
- Yang, J.J.; Strukov, D.B.; Stewart, D.R. Memristive devices for computing. Nat. Nanotechnol. 2013, 8, 13–24. [Google Scholar] [CrossRef] [PubMed]
- Glover, F.; Kochenberger, G.; Du, Y. A Tutorial on Formulating and Using QUBO Models. arXiv 2019, arXiv:1811.11538. [Google Scholar]
- Ohno, T.; Hasegawa, T.; Nayak, A.; Tsuruoka, T.; Gimzewski, J.K.; Aono, M. Sensory and short-term memory formations observed in a Ag2S gap-type atomic switch. Appl. Phys. Lett. 2011, 99, 203108. [Google Scholar] [CrossRef]
- Wang, Z.; Joshi, S.; Savel’ev, S.E.; Jiang, H.; Midya, R.; Lin, P.; Hu, M.; Ge, N.; Strachan, J.P.; Li, Z.; et al. Memristors with diffusive dynamics as synaptic emulators for neuromorphic computing. Nat. Mater. 2017, 16, 101–108. [Google Scholar] [CrossRef] [PubMed]
- Caravelli, F.; Barucca, P. A mean-field model of memristive circuit interaction. Eur. Phys. Lett. 2018, 122. [Google Scholar] [CrossRef]
- Caravelli, F. Locality of interactions for planar memristive circuits. Phys. Rev. E 2017, 96, 052206. [Google Scholar] [CrossRef]
- Little, W.A. The existence of persistent states in the brain. Math. Biosci. 1974, 19, 101–120. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef]
- Hopfield, J.J.; Tank, D.W. Computing with neural circuits: A model. Science 1986, 233, 625–633. [Google Scholar] [CrossRef]
- Amit, D.J.; Gutfreund, H.; Sompolinsky, H. Spin-glass models of neural networks. Phys. Rev. A 1985, 32, 2. [Google Scholar] [CrossRef]
- Hu, S.G.; Liu, Y.; Liu, Z.; Chen, T.P.; Wang, J.J.; Yu, Q.; Deng, L.J.; Yin, Y.; Hosaka, S. Associative memory realized by a reconfigurable memristive Hopfield neural network. Nat. Commun. 2015, 6, 7522. [Google Scholar] [CrossRef]
- Kumar, S.; Strachan, J.P.; Williams, R.S. Chaotic dynamics in nanoscale NbO2 Mott memristors for analogue computing. Nature 2017, 548, 318–321. [Google Scholar] [CrossRef]
- Tarkov, M. Hopfield Network with Interneuronal Connections Based on Memristor Bridges. In Proceedings of the 13th International Symposium on Neural Networks, ISNN 2016, St. Petersburg, Russia, 6–8 July 2016; pp. 196–203. [Google Scholar]
- Adler, R.J.; Taylor, J.E. Random Fields and Geometry; Springer: New York, NY, USA, 2007. [Google Scholar]
- Fyodorov, Y.V. High-Dimensional Random Field and Random Matrix Theory. Markov Process. Relat. Fields 2015, 21, 483–518. [Google Scholar]
- Caravelli, F. The mise en scene of memristive networks: effective memory, dynamics and learning. Int. J. Par. Dist. Syst. 2018, 33, 350–366. [Google Scholar] [CrossRef]
- Parisi, G. A sequence of approximate solutions to the S-K model for spin glasses. J. Phys. A 1980, 13, L-115. [Google Scholar] [CrossRef]
- Poloni, F. Algorithms for Quadratic Matrix and Vector Equations; Theses (Scuola Normale Superiore); Edizioni della Normale: Pisa, Italy, 2011. [Google Scholar]
- Kavitha, T.; Liebchen, C.; Mehlhorn, K.; Michail, D.; Rizzi, R.; Ueckerdt, T.; Zweig, K.A. Cycle bases in graphs characterization, algorithms, complexity, and applications. Comput. Sci. Rev. 2009, 3, 199–243. [Google Scholar] [CrossRef]
- Chang, T.J.; Meade, N.; Beasley, J.E.; Sharaiha, Y.M. Heuristics for cardinality constrained portfolio optimisation. Comput. Oper. Res. 2000, 27, 1271–1302. [Google Scholar] [CrossRef]
- 225 Nikkei Asset Dataset, OR-Library. Available online: http://people.brunel.ac.uk/~mastjjb/jeb/orlib/files/port5.txt (accessed on 12 August 2019).
- Markowitz, H. Portfolio Selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Caravelli, F.; Traversa, F.L.; di Ventra, M. The complex dynamics of memristive circuits: Analytical results and universal slow relaxation. Phys. Rev. E 2017, 95, 2. [Google Scholar] [CrossRef]
- Traversa, F.L.; Ramella, C.; Bonani, F.; di Ventra, M. Memcomputing NP-complete problems in polynomial time using polynomial resources and collective states. Sci. Adv. 2015, 1, e1500031. [Google Scholar] [CrossRef]
- Pershin, Y.V.; di Ventra, M. Solving mazes with memristors: A massively-parallel approach. Phys. Rev. E 2011, 84, 046703. [Google Scholar] [CrossRef]
- Pershin, Y.V.; di Ventra, M. Self-organization and solution of shortest-path optimization problems with memristive networks. Phys. Rev. E 2013, 88, 013305. [Google Scholar] [CrossRef]
- Dorigo, M.; Gambardella, L.M. Ant colonies for the traveling salesman problem. Biosystems 1997, 43, 73–81. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caravelli, F. Asymptotic Behavior of Memristive Circuits. Entropy 2019, 21, 789. https://doi.org/10.3390/e21080789
Caravelli F. Asymptotic Behavior of Memristive Circuits. Entropy. 2019; 21(8):789. https://doi.org/10.3390/e21080789
Chicago/Turabian StyleCaravelli, Francesco. 2019. "Asymptotic Behavior of Memristive Circuits" Entropy 21, no. 8: 789. https://doi.org/10.3390/e21080789
APA StyleCaravelli, F. (2019). Asymptotic Behavior of Memristive Circuits. Entropy, 21(8), 789. https://doi.org/10.3390/e21080789



