Intra-Day Trading System Design Based on the Integrated Model of Wavelet De-Noise and Genetic Programming
Abstract
:1. Introduction
2. Literature Review
2.1. Technical Analysis
2.2. Genetic Programming
2.3. Applications of Wavelet in Financial Analysis
2.4. Intra-Day Trading System
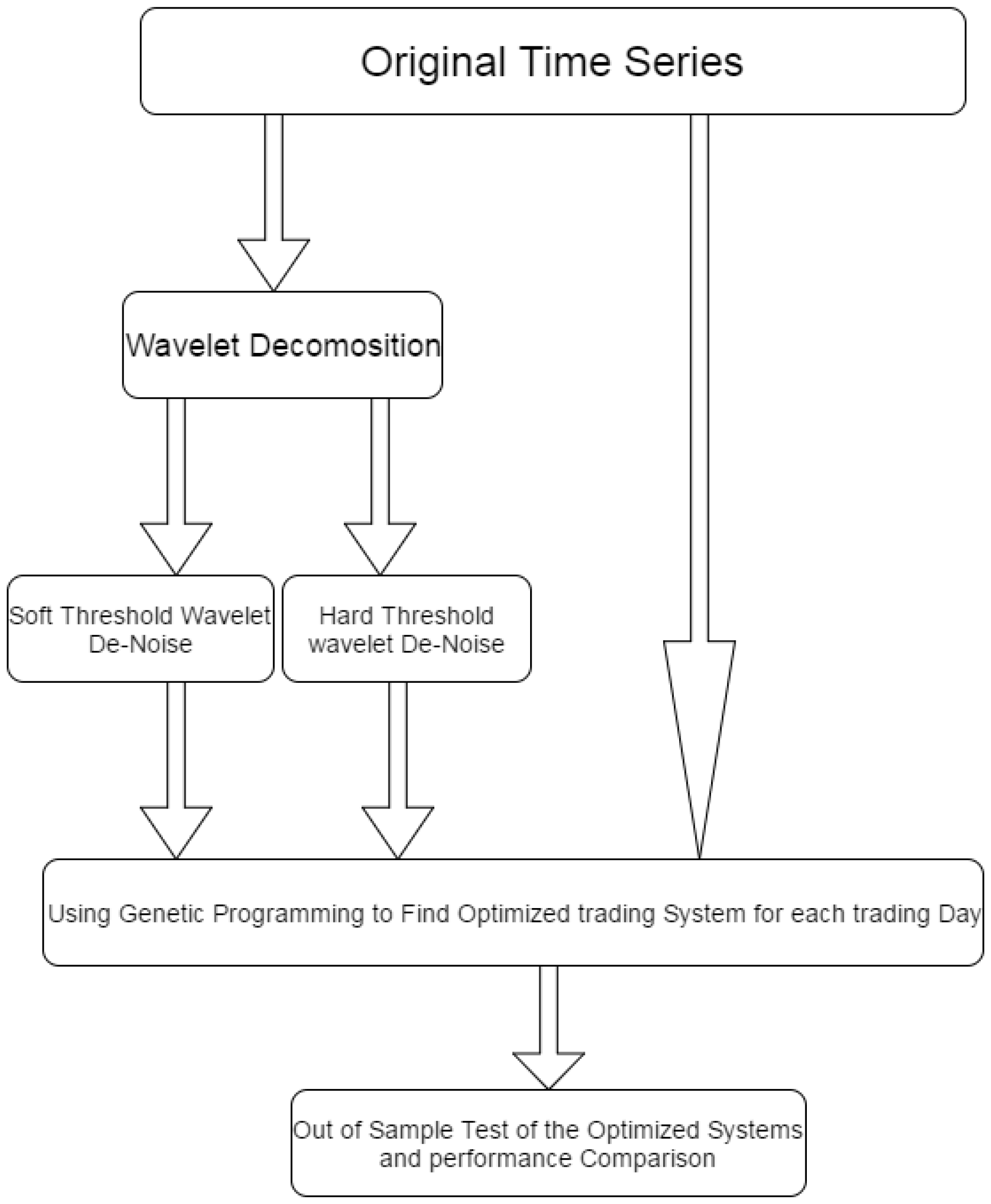
3. Methodology
3.1. Wavelet and Wavelet De-Noise
3.1.1. The Discrete Wavelet Transform
3.1.2. Wavelet De-Noise
- Decomposition of the financial time series;
- Selection of the decomposed part based on wavelet coefficients;
- Reconstruction of the time series using the selected decomposed part of the original series. The dropped part of the original series is treated as noise that should be removed from this process.
3.2. Generating Trading Rules with Genetic Programming
3.2.1. Encoding of the Technical Indicators
- Functions:
- Arithmetic operators: +, −, *, /;
- Boolean operators: , , ;
- Relations operators: <, >;
- Boolean functions: if-then-else.
- Real functions (user defined functions, here are the technical indicators)
- Technical Indicators, Variable s Represents Constant Price:
- : absolute value of the difference between real number;
- : average of price over the past n periods;
- : exponential moving average of the past n periods;
- : maximum value of price over the past n periods;
- : minimum value of price over the past n periods;
- : price value lagged by n periods;
- : variance in returns over the past n periods;
- : relative strength index;
- : rate of change.: , is the set of minutes with rising prices, is the set of minutes with falling prices and is the return of minute i, which is positive when the price is rising and negative otherwise.
- Terminals:
- Constants: chosen in the interval , where 270 is the approximate number of minutes in a single trading day;
- Boolean: True, False;
- Others: Price
- Real variable: P price of the current minute;
- Order Types: Entry order and Exit order
- Entry order: Market Entry order: enter into the market at market price;
- Stop Entry order: these orders are placed above the market for a long entry and below the market for a short entry;
- Limit Entry order: these orders are placed below the market for a long entry and above the market for a short entry;
- Exit order: Exit at target profit, Exit at target percentage profit, Exit at Target price, Protective Stop, Trailing Stop, Exit after N Bars, Exit after N Bars profit, Exit after N Bars loss, Exit after certain time, Exit at Market, Exit End-of-Day.
3.2.2. Fitness Evaluation Criteria
3.2.3. Initialization of the Base Population
3.2.4. Crossover, Mutation, Reproduction and Selection
3.3. Design of the Experiment in This Paper
4. Empirical Experiment
4.1. Parameter Settings
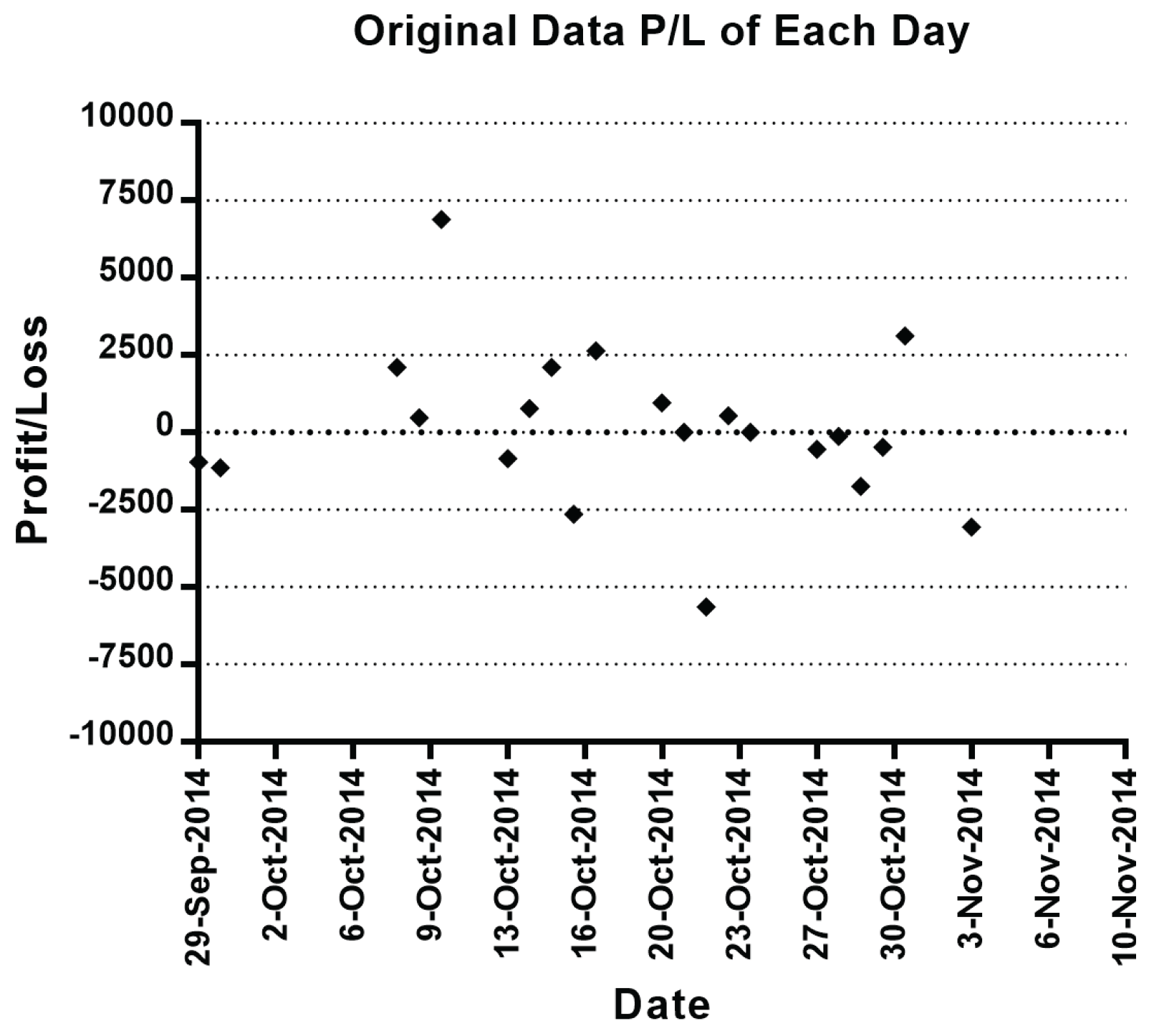
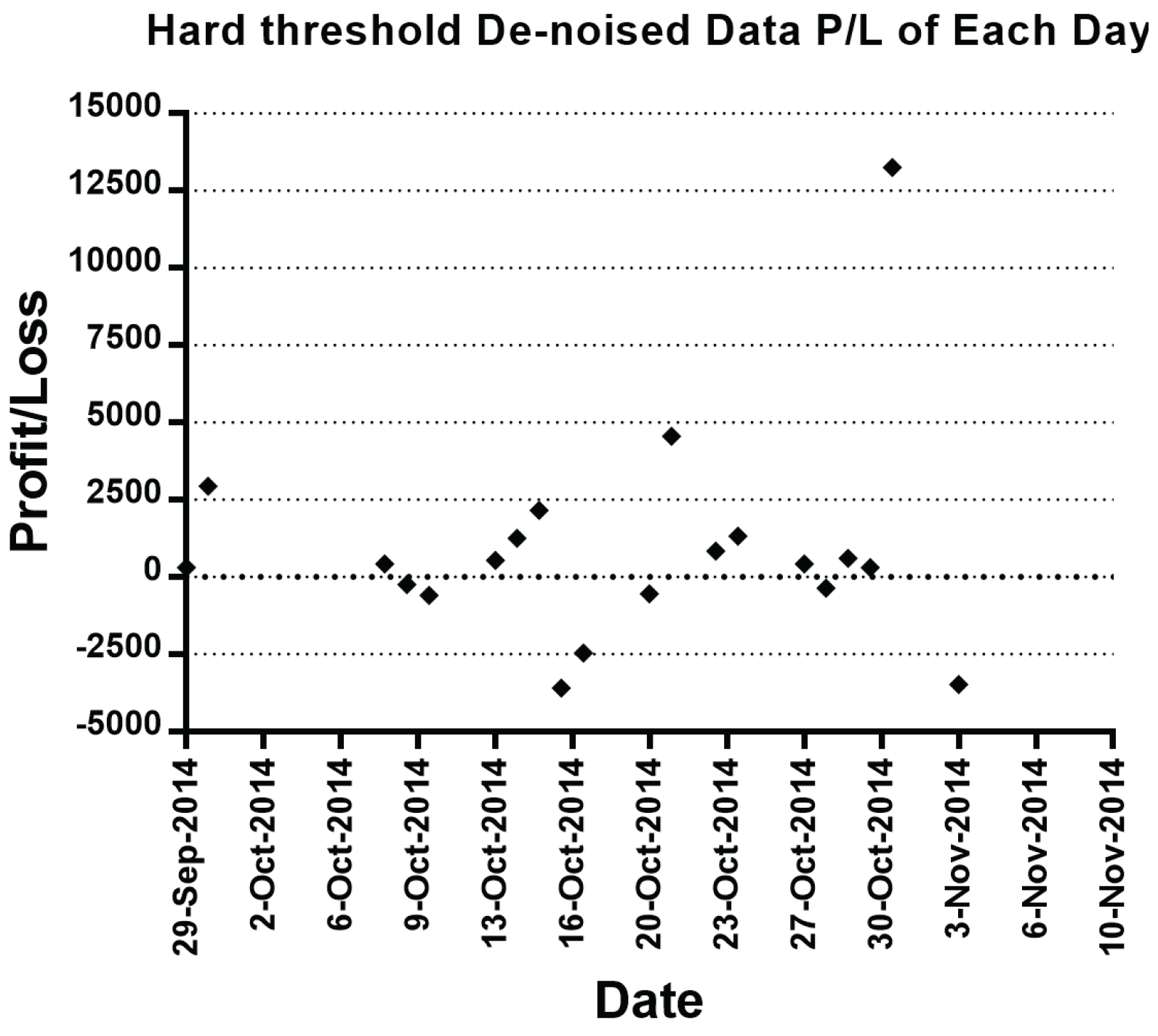
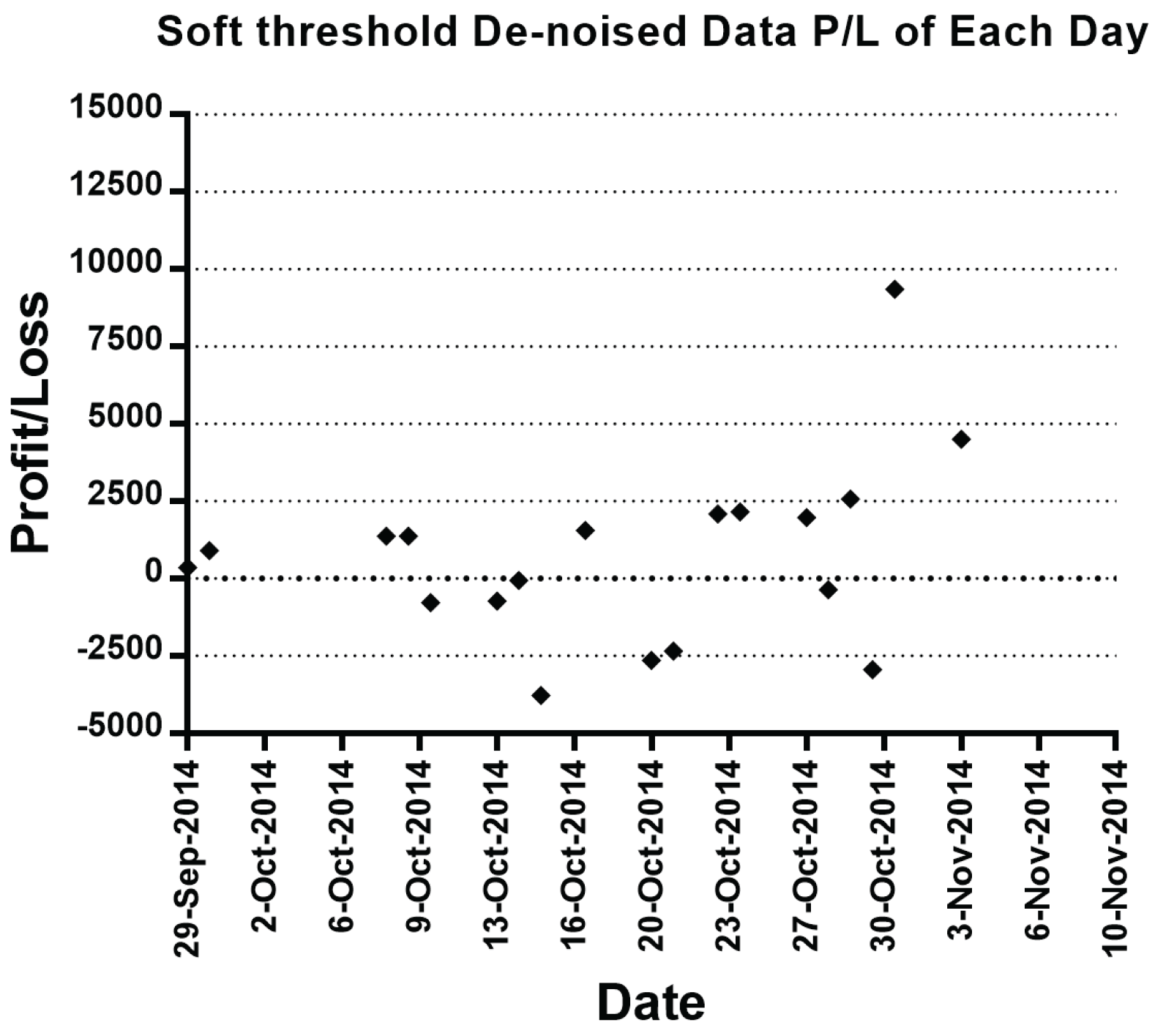
4.2. Experiment Results
5. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Alexander, S.S. Price movements in speculative markets: Trends or random walks. Ind. Manag. Rev. 1961, 2, 7. [Google Scholar]
- Malkiel, B.G.; Fama, E.F. Efficient capital markets: A review of theory and empirical work. J. Financ. 1970, 25, 383–417. [Google Scholar] [CrossRef]
- Pruitt, S.W.; White, R.E. The CRISMA trading system: Who says technical analysis can’t beat the market? J. Portf. Manag. 1988, 14, 55–58. [Google Scholar] [CrossRef]
- Brock, W.; Lakonishok, J.; LeBaron, B. Simple technical trading rules and the stochastic properties of stock returns. J. Financ. 1992, 47, 1731–1764. [Google Scholar] [CrossRef]
- Bessembinder, H.; Chan, K. The profitability of technical trading rules in the Asian stock markets. Pac. Basin Financ. J. 1995, 3, 257–284. [Google Scholar] [CrossRef]
- Sweeney, R.J. Beating the foreign exchange market. J. Financ. 1986, 41, 163–182. [Google Scholar] [CrossRef]
- Gencay, R. The predictability of security returns with simple technical trading rules. J. Emp. Financ. 1998, 5, 347–359. [Google Scholar] [CrossRef]
- Fernandez-Rodrıguez, F.; Gonzalez-Martel, C.; Sosvilla-Rivero, S. On the profitability of technical trading rules based on artificial neural networks: Evidence from the Madrid stock market. Econ. Lett. 2000, 69, 89–94. [Google Scholar] [CrossRef]
- Chavarnakul, T.; Enke, D. A hybrid stock trading system for intelligent technical analysis-based equivolume charting. Neurocomputing 2009, 72, 3517–3528. [Google Scholar] [CrossRef]
- Taylor, M.P.; Allen, H. The use of technical analysis in the foreign exchange market. J. Int. Money Financ. 1992, 11, 304–314. [Google Scholar] [CrossRef]
- Holland, J.H. Outline for a logical theory of adaptive systems. J. ACM 1962, 9, 297–314. [Google Scholar] [CrossRef]
- Bauer, R.J. Genetic Algorithms and Investment Strategies; Wiley: Hoboken, NJ, USA, 1994. [Google Scholar]
- Potvin, J.Y.; Bengio, S. The vehicle routing problem with time windows part II: Genetic search. INFORMS J. Comput. 1996, 8, 165–172. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT press: Cambridge, MA, USA, 1992. [Google Scholar]
- Chen, S.H.; Yeh, C.H. Toward a computable approach to the efficient market hypothesis: An application of genetic programming. J. Econ. Dyn. Control 1997, 21, 1043–1063. [Google Scholar] [CrossRef]
- Allen, F.; Karjalainen, R. Using genetic algorithms to find technical trading rules. J. Financ. Econ. 1999, 51, 245–271. [Google Scholar] [CrossRef]
- Neely, C.; Weller, P.; Dittmar, R. Is technical analysis in the foreign exchange market profitable? A genetic programming approach. J. Financ. Quant. Anal. 1997, 32, 405–426. [Google Scholar] [CrossRef]
- Neely, C.J.; Weller, P.A. Technical trading rules in the European monetary system. J. Int. Money Financ. 1999, 18, 429–458. [Google Scholar] [CrossRef]
- Marney, J.P.; Tarbert, H.; Fyfe, C. Technical Trading Versus Market Efficiency—A Genetic Programming Approach. Available online: http://econpapers.repec.org/paper/scescecf0/169.htm (accessed on 1 Decemder 2016).
- Potvin, J.Y.; Soriano, P.; Vallée, M. Generating trading rules on the stock markets with genetic programming. Comput. Oper. Res. 2004, 31, 1033–1047. [Google Scholar] [CrossRef]
- Mallick, D.; Lee, V.; Ong, Y.S. An empirical study of genetic programming generated trading rules in computerized stock trading service system. In Proceedings of the 2008 International Conference on Service Systems and Service Management, Melbourne, Australia, 30 June–2 July 2008; pp. 1–6.
- Esfahanipour, A.; Karimi, B.; Mousavi, S. The profitability of technical trading rules in tehran stock exchange: An application of genetic programming. In Proceedings of the International Symposium on INnovations in Intelligent SysTems and Applications, Trabzon, Turkey, 29 June–1 July 2009.
- Straßburg, J.; Gonzàlez-Martel, C.; Alexandrov, V. Parallel genetic algorithms for stock market trading rules. Procedia Comput. Sci. 2012, 9, 1306–1313. [Google Scholar] [CrossRef]
- Hongguang, L.; Ping, J. Generating Intraday Trading Rules on Index Future Markets Using Genetic Programming. Int. J. Trade Econ. Financ. 2015, 6, 112. [Google Scholar]
- Luengo, S.; Winkler, S.; Barrero, D.F.; Castaño, B. Optimization of trading rules for the spanish stock market by genetic programming. In Current Approaches in Applied Artificial Intelligence; Springer: Cham, Switzerland, 2015; pp. 623–634. [Google Scholar]
- Huang, C.F.; Chang, B.R.; Cheng, D.W.; Chang, C.H. Feature selection and parameter optimization of a fuzzy-based stock selection model using genetic algorithms. Int. J. Fuzzy Syst. 2012, 14, 65–75. [Google Scholar]
- Hu, Y.; Liu, K.; Zhang, X.; Su, L.; Ngai, E.; Liu, M. Application of evolutionary computation for rule discovery in stock algorithmic trading: A literature review. Appl. Soft Comput. 2015, 36, 534–551. [Google Scholar] [CrossRef]
- Ramsey, J.B. The contribution of wavelets to the analysis of economic and financial data. Philos. Trans. R. Soc. Lond. A 1999, 357, 2593–2606. [Google Scholar] [CrossRef]
- Addison, P.S. The Illustrated Wavelet Transform Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Walnut, D.F. An Introduction to Wavelet Analysis; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Walker, J.S. A Primer on Wavelets and Their Scientific Applications; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Daubechies, I. Ten Lectures on Wavelets; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Yu, I.-K.; Kim, C.; Song, Y.H. A novel short-term load forecasting technique using wavelet transform analysis. Electr. Mach. Power Syst. 2000, 28, 537–549. [Google Scholar]
- Sandoval, J.; Hernandez, G. High-frequency trading strategies using wavelet-transformed order book information and dynamic Bayesian networks. In Proceedings of the 2015 Science and Information Conference, London, UK, 28–30 July 2015; pp. 435–442.
- Zhang, B.L.; Coggins, R.; Jabri, M.A.; Dersch, D.; Flower, B. Multiresolution forecasting for futures trading using wavelet decompositions. IEEE Trans. Neural Netw. 2001, 12, 765–775. [Google Scholar] [CrossRef] [PubMed]
- Renaud, O.; Murtagh, F.; Starck, J.L. Wavelet-Based Forecasting of Short and Long Memory Time Series. Available online: http://www.unige.ch/ses/metri/cahiers/2002_04.pdf (accessed on 1 Decemder 2016).
- Schleicher, C. An Introduction to Wavelets for Economists. Available online: http://www.bankofcanada.ca/wp-content/uploads/2010/02/wp02-3.pdf (accessed on 1 Decemder 2016).
- Crowley, P.M. An Intuitive Guide to Wavelets for Economists. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=787564 (accessed on 1 Decemder 2016).
- Yousefi, S.; Weinreich, I.; Reinarz, D. Wavelet-based prediction of oil prices. Chaos Solitons Fractals 2005, 25, 265–275. [Google Scholar] [CrossRef]
- Li, J.; Shi, Z.; Li, X. Genetic programming with wavelet-based indicators for financial forecasting. Trans. Inst. Meas. Control 2006, 28, 285–297. [Google Scholar] [CrossRef]
- Stolojescu, C.; Railean, I.; Lenca, S.M.P.; Isar, A. A wavelet based prediction method for time series. In Proceedings of the 2010 International Conference Stochastic Modeling Techniques and Data Analysis, Chania, Greece, 8–11 June 2010.
- Kirilenko, A.A.; Kyle, A.S.; Samadi, M.; Tuzun, T. The flash crash: The Impact of High Frequency Trading on an Electronic Market. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1686004 (accessed on 1 Decemder 2016).
- Kablan, A.; Falzon, J. The Use of Dynamically Optimised High Frequency Moving Average Strategies for Intraday Trading. World Acad. Sci. Eng. Technol. 2012, 6, 301–307. [Google Scholar]
- Donoho, D.; Johnstone, I.; Johnstone, I.M. Ideal Spatial Adaptation by Wavelet Shrinkage. Biometrika 1993, 81, 425–455. [Google Scholar] [CrossRef]

| Underlying Index | CSI 300 Index |
|---|---|
| Contract Multiplier | CNY 300 |
| Unit | Index point |
| Tick Size | 0.2 point |
| Contract Months | Monthly: current month, next month, next two calendar quarters (four total) |
| Trading Hours | 09:30 a.m.–11:30 a.m., 01:00 p.m.–03:00 p.m. |
| Limit Up/Down | +/−10% of settlement price on the previous trading day |
| Margin Requirement | 8% of the contract value |
| Last Trading Day | Third Friday of the contract month, postponed to the next business day if it falls on a public holiday |
| Delivery Day | Third Friday, same as “Last Trading Day” |
| Settlement Method | Cash Settlement |
| Transaction Code | IF |
| Exchange | China Financial Futures Exchange |
| Parameters | Value |
|---|---|
| Population size | 300 |
| Number of generations | 30 |
| Crossover percentage | 60% |
| Mutation percentage | 50% |
| Tree depth | 5 |
| Tournament size | 5 |
| Limit of entries per day | 8 |
| Wait for exit before entering new trade | Yes |
| Max bars looking back for Indicators | 30 |
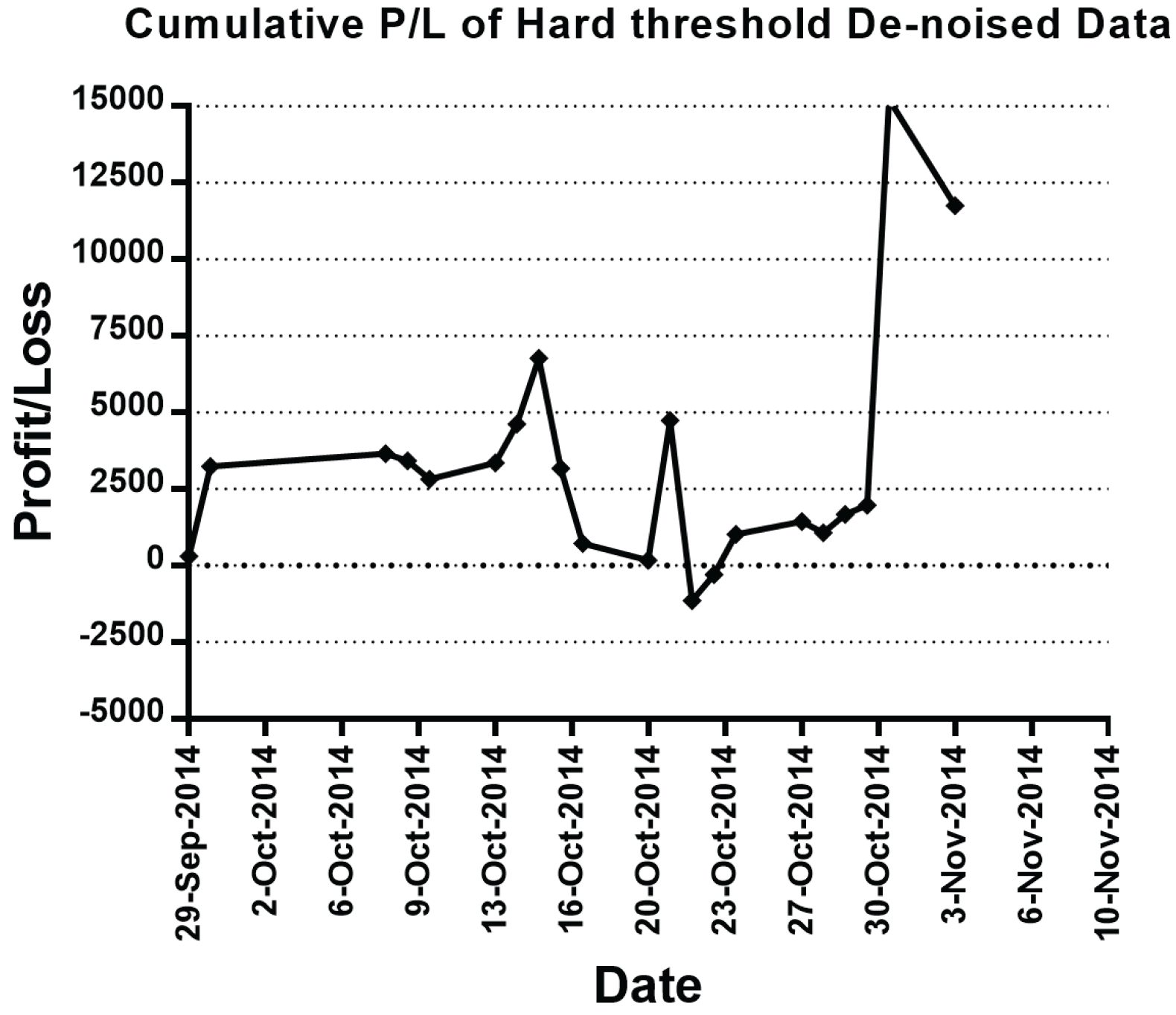
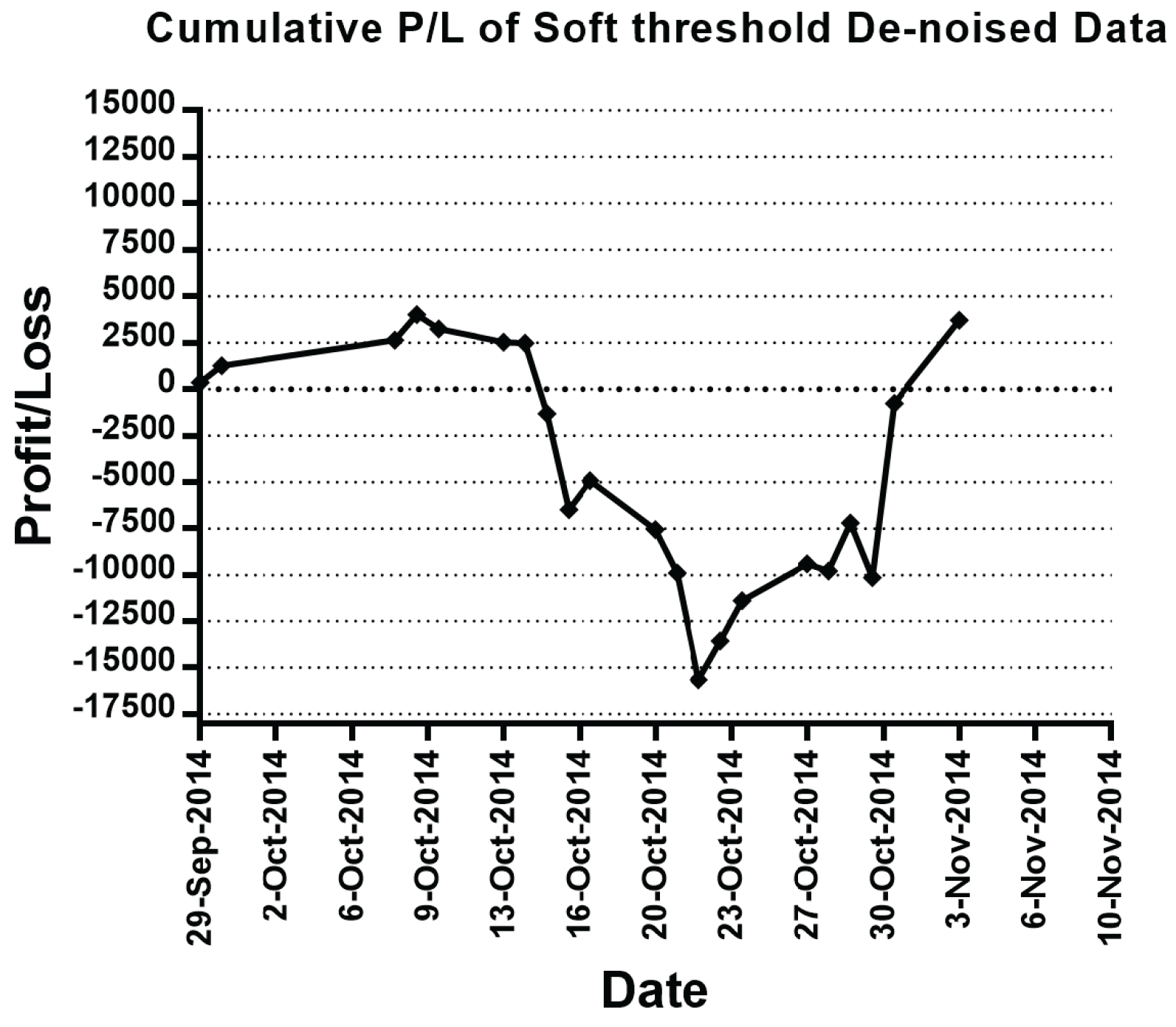
| Date | Out-of-Sample P/L | Out-of-Sample Cumulative P/L | Out-of-Sample P/L | Out-of-Sample Cumulative P/L | Out-of-Sample P/L | Out-of-Sample Cumulative P/L |
|---|---|---|---|---|---|---|
| 29 Sep. 2014 | −960.00 | −960.00 | 300.00 | 300.00 | 360.00 | 360.00 |
| 30 Sep. 2014 | −1140.00 | −2100.00 | 2940.00 | 3240.00 | 900.00 | 1260.00 |
| 8 Oct. 2014 | 2100.00 | 0.00 | 420.00 | 3660.00 | 1380.00 | 2640.00 |
| 9 Oct. 2014 | 480.00 | 480.00 | −240.00 | 3420.00 | 1380.00 | 4020.00 |
| 10 Oct. 2014 | 6900.00 | 7380.00 | −600.00 | 2820.00 | −780.00 | 3240.00 |
| 13 Oct. 2014 | −840.00 | 6540.00 | 540.00 | 3360.00 | −720.00 | 2520.00 |
| 14 Oct. 2014 | 780.00 | 7320.00 | 1260.00 | 4620.00 | −60.00 | 2460.00 |
| 15 Oct. 2014 | 2100.00 | 9420.00 | 2160.00 | 6780.00 | −3780.00 | −1320.00 |
| 16 Oct. 2014 | −2640.00 | 6780.00 | −3600.00 | 3180.00 | −5160.00 | −6480.00 |
| 17 Oct. 2014 | 2640.00 | 9420.00 | −2460.00 | 720.00 | 1560.00 | −4920.00 |
| 20 Oct. 2014 | 960.00 | 10,380.00 | −540.00 | 180.00 | −2640.00 | −7560.00 |
| 21 Oct. 2014 | 0.00 | 10,380.00 | 4560.00 | 4740.00 | −2340.00 | −9900.00 |
| 22 Oct. 2014 | −5640.00 | 4740.00 | −5880.00 | −1140.00 | −5760.00 | −15,660.00 |
| 23 Oct. 2014 | 540.00 | 5280.00 | 840.00 | −300.00 | 2100.00 | −13,560.00 |
| 24 Oct. 2014 | 0.00 | 5280.00 | 1320.00 | 1020.00 | 2160.00 | −11,400.00 |
| 27 Oct. 2014 | −540.00 | 4740.00 | 420.00 | 1440.00 | 1980.00 | −9420.00 |
| 28 Oct. 2014 | −120.00 | 4620.00 | -360.00 | 1080.00 | −360.00 | −9780.00 |
| 29 Oct. 2014 | −1740.00 | 2880.00 | 600.00 | 1680.00 | 2580.00 | −7200.00 |
| 30 Oct. 2014 | −480.00 | 2400.00 | 300.00 | 1980.00 | −2940.00 | −10,140.00 |
| 31 Oct. 2014 | 3120.00 | 5520.00 | 13,260.00 | 15,240.00 | 9360.00 | −780.00 |
| 3 Nov. 2014 | −3060.00 | 2460.00 | −3480.00 | 11,760.00 | 4500.00 | 3720.00 |
| Min | −5640 | −2100 | −5880 | −1140 | −5740 | −15,660 |
| Max | 6900 | 10,380 | 13,260 | 15,240 | 9360 | 4020 |
| Std | 2484 | NULL | 3619 | NULL | 3313 | NULL |
| Date | Out-of-Sample Profit/Loss of Model Trained with Original Data | Out-of-Sample Profit/Loss of Model Trained with Hard Threshold De-Noised Data | Out-of-Sample Profit/Loss of Model Trained with Soft Threshold De-Noised Data |
|---|---|---|---|
| 24 Oct.–3 Nov. 2014 | −37,320 | −34,140 | −22,260 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Ji, P.; Jin, J. Intra-Day Trading System Design Based on the Integrated Model of Wavelet De-Noise and Genetic Programming. Entropy 2016, 18, 435. https://doi.org/10.3390/e18120435
Liu H, Ji P, Jin J. Intra-Day Trading System Design Based on the Integrated Model of Wavelet De-Noise and Genetic Programming. Entropy. 2016; 18(12):435. https://doi.org/10.3390/e18120435
Chicago/Turabian StyleLiu, Hongguang, Ping Ji, and Jian Jin. 2016. "Intra-Day Trading System Design Based on the Integrated Model of Wavelet De-Noise and Genetic Programming" Entropy 18, no. 12: 435. https://doi.org/10.3390/e18120435
APA StyleLiu, H., Ji, P., & Jin, J. (2016). Intra-Day Trading System Design Based on the Integrated Model of Wavelet De-Noise and Genetic Programming. Entropy, 18(12), 435. https://doi.org/10.3390/e18120435






