Initial Results of Testing Some Statistical Properties of Hard Disks Workload in Personal Computers in Terms of Non-Extensive Entropy and Long-Range Dependencies
Abstract
:1. Introduction
2. Non-Extensive Statistical Mechanics and Long-Range Dependencies
2.1. Definitions of Non-Extensive Entropy
2.2. Probability Distributions in Entropy
- is out of equilibrium [29];
- some of its statistical properties (especially second moment) are difficult to be interpreted [30];
- is governed by long-term (time domain) and long-range (spatial domain) dependencies [31];
- is described by multifractals and scaling phenomena [32];
- has complex spatial structure and collective dynamics [33].
2.3. Long-Range Dependencies
3. Experiment Details
- Average Disk sec/Transfer (that consists of a sum of counters Average Disk sec/Read and Average Disk sec/Write). It represents the average time the disk transfers (reads/writes, I/O requests) took to complete, in seconds (the counter has a millisecond precision). It does not include the time that is necessary to be spent in the system queue but is the most important counter that reflects the physical disk properties; they are usually related to the disk speed, and, for many computer systems, one can find some recommendations about their suggested or critical values [52].
- Disk Transfers/s. It is a counter that shows the number of transfers (consisting of disc read/write) during a time unit (1 s for the purpose of this paper). It shows how many different application requests are necessary to be handled by the disk.
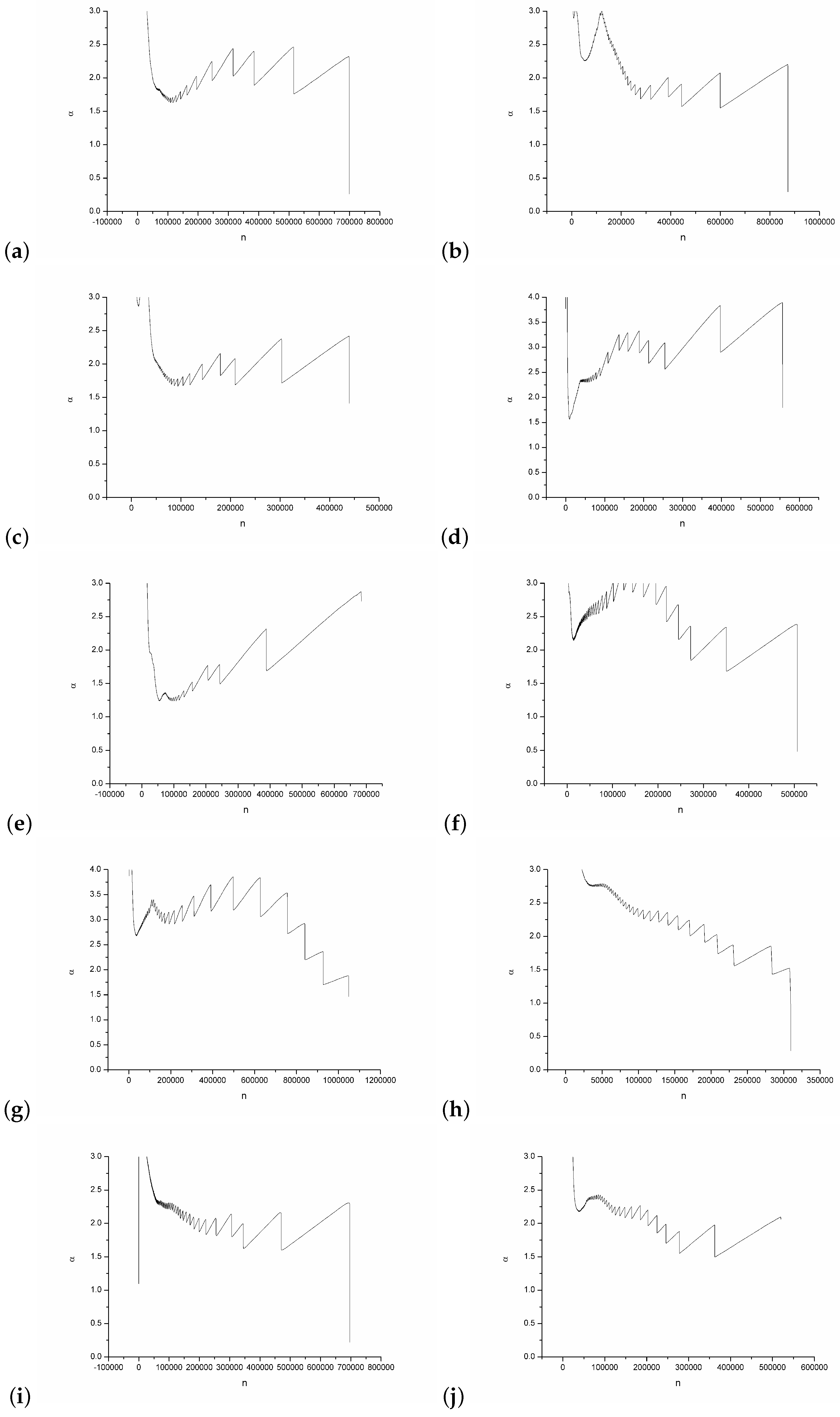
4. Experiment Results
5. Conclusions
Conflicts of Interest
References
- Wescott, B. Every Computer Performance Book; Create Space Independent Publishing Platform: Charleston, SC, USA, 2013. [Google Scholar]
- Silberschatz, A.; Galvin, P.B.; Gagne, G. Operating System Concepts; John Wiley & Sons, Inc.: Somerset, NJ, USA, 2012. [Google Scholar]
- Grabowski, F. Nonextensive model of self-organizing systems. Complexity 2013, 18, 28–36. [Google Scholar] [CrossRef]
- Wegner, P.; Goldin, D. Computation beyond Turing Machines. Commun. ACM 2003, 46, 100–102. [Google Scholar] [CrossRef]
- Wegner, P. Research paradigms in computer science. In Proceedings of the 2nd International Conference on Software Engineering, San Francisco, CA, USA, 13–15 October 1976; pp. 322–330. [Google Scholar]
- Waldrop, M.M. Complexity: The Emerging Science at the Edge of Order and Chaos; Simon and Schuster: New York, NY, USA, 1992. [Google Scholar]
- Dum, R. Science of Complex Systems for Tackling Challenges of the 21st Century: A Brief Overview. Eur. Manag. Rev. 2007, 4, 73–76. [Google Scholar] [CrossRef]
- Jacobson, M.J.; Wilensky, U. Complex Systems in Education: Scientific and Educational Importance and Implications for the Learning Sciences. J. Learn. Sci. 2006, 15, 11–34. [Google Scholar] [CrossRef]
- Benham-Hutchins, M.; Clancy, T.R. Social networks as embedded complex adaptive systems. J. Nurs. Adm. 2010, 40, 352–356. [Google Scholar] [CrossRef] [PubMed]
- Arthur, W.B.; Durlauf, S.N.; Lane, D.A. (Eds.) The Economy as an Evolving Complex System, II, Santa Fe Institute Studies in the Sciences of Complexity Proceedings; Addison-Wesley: Reading, UK, 1997; Volume XXVII. [Google Scholar]
- Arthur, W.B. Complexity Economics: A Different Framework for Economic Thought; SFI Working Paper; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Anand, M.; Gonzalez, A.; Guichard, F.; Kolasa, J.; Parrott, L. Ecological Systems as Complex Systems: Challenges for an Emerging Science. Diversity 2010, 2, 395–410. [Google Scholar] [CrossRef]
- Rosenthal, S.B.; Twomey, C.R.; Hartnett, A.T.; Wu, H.S.; Couzin, I.D. Revealing the hidden networks of interaction in mobile animal groups allows prediction of complex behavioral contagion. Proc. Natl. Acad. Sci. USA 2015. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.; Luo, Y.; Ahmad, A. Analysing complex behaviour of hydrological systems through a system dynamics approach. Environ. Model. Softw. 2009, 24, 1363–1372. [Google Scholar] [CrossRef]
- Lipsitz, L.A. Understanding Health Care as a Complex System. J. Am. Med. Assoc. 2012, 308, 243–244. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Ailamaki, A.; Faloutsos, C. Capturing the spatio-temporal behavior of real traffic data. In Proceedings of the Performance 2002, IFIP International Symposium on Computer Performance Modeling, Measurement and Evaluation, Rome, Italy, 23–27 September 2002; pp. 147–163. [Google Scholar]
- Gómez, M.E.; Santonja, V. Self-Similarity in I/O Workload: Analysis and Modelling. In Proceedings of the Workload Characterization: Methodology and Case Studies, Based on the First Workshop on Workload Characterization, Dallas, TX, USA, 29 November 1998; pp. 97–104. [Google Scholar]
- Riska, A.; Riedel, E. Long-Range Dependence at the Disk Drive Level. In Proceedings of the Third International Conference on the Quantitative Evaluation of Systems—(QEST’06), Riverside, CA, USA, 11–14 September 2006; pp. 41–50. [Google Scholar]
- Riska, A.; Riedel, E. Evaluation of disk-level workloads at different time-scales. In Proceedings of the 2009 IEEE International Symposium on Workload Characterization (IISWC), Austin, TX, USA, 4–6 October 2009; pp. 158–167. [Google Scholar]
- Kavalanekar, S.; Worthington, B.; Zhang, Q.; Sharda, V. Characterization of storage workload traces from production Windows Servers. In Proceedings of the 2008 IEEE International Symposium on Workload Characterization, Seattle, WA, USA, 14–16 September 2008; pp. 119–128. [Google Scholar]
- Hong, B.; Madhyastha, T.M. The relevance of long-range dependence in disk traffic and implications for trace synthesis. In Proceedings of the 22nd IEEE/13th NASA Goddard Conference on Mass Storage Systems and Technologies (MSST’05), Monterey, CA, USA, 11–14 April 2005; pp. 316–326. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Di Matteo, T. The Physics of Complex Systems (New Advances and Perspectives); Mallamace, F., Stanley, H.E., Eds.; IOS Press: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Mohazzabi, P.; Mansoori, G.A. Nonextensivity and Nonintensivity in Nanosystems: A molecular dynamics simulation. J. Comput. Theor. Nanosci. 2005, 2, 138–147. [Google Scholar]
- Tsallis, C.; Baldovin, F.; Cerbino, R.; Pierobon, P. Introduction to Nonextensive Statistical Mechanics and Thermodynamics. In The Physics of Complex Systems (New Advances and Perspectives); Mallamace, F., Stanley, H.E., Eds.; IOS Press: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Tsallis, C. Nonadditive entropy and nonextensive statistical mechanics—An overview after 20 years. Braz. J. Phys. 2009, 39, 337–355. [Google Scholar] [CrossRef]
- Tsallis, C. Nonextensive statistical mechanics, anomalous diffusion and central limit theorems. Milan J. Math. 2005, 73, 145–176. [Google Scholar] [CrossRef]
- Tsallis, C.; Levy, S.V.F.; Souza, A.M.C.; Maynard, R. Statistical-mechanical foundation of the ubiquity of Lévy distributions in nature. Phys. Rev. Lett. 1995, 75, 3589. [Google Scholar] [CrossRef] [PubMed]
- Gallet, F.; Arcizet, D.; Bohec, P.; Richert, A. Power Spectrum of Out-of-Equilibrium Forces in Living Cells: Amplitude and Frequency Dependence. Soft Matter 2009, 5, 2947–2953. [Google Scholar] [CrossRef]
- Buchanan, M. Laws, power laws and statistics. Nat. Phys. 2008, 4, 339. [Google Scholar] [CrossRef]
- Makowiec, D.; Gała̧ska, R.; Dudkowska, A.; Rynkiewicz, A.; Zwierz, M. Long-range dependencies in heart rate signals-revisited. Phys. A Stat. Mech. Appl. 2006, 369, 632–644. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Multifractal Power Law Distributions: Negative and Critical Dimensions and Other “Anomalies” Explained by a Simple Example. J. Stat. Phys. 2003, 110, 739–774. [Google Scholar] [CrossRef]
- Tsallis, C. The Nonadditive Entropy Sq and Its Applications in Physics and Elsewhere: Some Remarks. Entropy 2011, 13, 1765–1804. [Google Scholar] [CrossRef]
- Borland, L. Option Pricing Formulas Based on a Non-Gaussian Stock Price Model. Phys. Rev. Lett. 2002, 89, 098701. [Google Scholar] [CrossRef] [PubMed]
- Feder, J. Fractals; Plenum Press: New York, NY, USA, 1988. [Google Scholar]
- Cajueiro, D.O.; Tabak, B.M. Is the expression H = 1/(3 − q) valid for real financial data? Phys. A 2007, 373, 593–602. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770. [Google Scholar]
- Weron, A.; Burnecki, K.; Mercik, S.; Weron, K. Complete description of all self-similar models driven by Lévy stable noise. Phys. Rev. E Stat. Nonlinear Soft 2005, 71, 016113. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, F. Logistic equation of arbitrary order. Phys. A Stat. Mech. Appl. 2010, 389, 3081–3093. [Google Scholar] [CrossRef]
- Taqqu, M.S.; Teverovsky, V. On Estimating the Intensity of Long-Range Dependence in Finite and Infinite Variance Time Series. In A Practical Guide to Heavy Tails: Statistical Techniques and Applications Book Contents; Birkhauser Boston Inc.: Cambridge, MA, USA, 1998; pp. 177–217. [Google Scholar]
- Shahzad, F.; Mushtaq, M.F.; Ullah, S.; Siddique, M.A.; Khurram, S.; Saher, N. Improving Queuing System Throughput Using Distributed Mean Value Analysis to Control Network Congestion. Commun. Netw. 2015, 7, 21–29. [Google Scholar] [CrossRef]
- Lazowska, E.D.; Zahorjan, J.; Graham, G.S.; Sevcik, K.C. Quantitative System Performance: Computer System Analysis Using Queueing Network Models; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 1984. [Google Scholar]
- Simchi-Levi, D.; Trick, M.A. Introduction to “Little’s Law as Viewed on Its 50th Anniversary”. Oper. Res. 2013, 59, 535. [Google Scholar] [CrossRef]
- Strzałka, D.; Grabowski, F. Processes in systems with limited resources in the context of non-extensive thermodynamics. Fundam. Inform. 2008, 85, 455–464. [Google Scholar]
- Wilk, G.; Włodarczyk, Z. Nonextensive information entropy for stochastic networks. Acta Phys. Pol. B 2004, 35, 871. [Google Scholar]
- Overview of Windows Performance Monitor. Available online: https://technet.microsoft.com/en-us/library/cc749154.aspx (accessed on 26 June 2016).
- How to Measure IOPS for Windows. Available online: http://blog.synology.com/?p=2086 (accessed on 26 June 2017).
- How Often Should Perfmon Sample? Available online: https://blogs.technet.microsoft.com/yongrhee/2011/11/13/how-often-should-perfmon-sample/ (accessed on 26 June 2017).
- Windows Performance Monitor. Available online: https://technet.microsoft.com/en-us/library/cc749249.aspx (accessed on 26 June 2017).
- Boxma, O.J.; Cohen, J.W. Heavy-traffic analysis for the GI/G/1 queue with heavy-tailed distributions. Queuing Syst. 1999, 33, 177–204. [Google Scholar] [CrossRef]
- Roughan, M.; Veitch, D.; Rumsewicz, M. Computing queue-length distributions for power-law queues. In Proceedings of the IEEE of Seventeenth Annual Joint Conference of the IEEE Computer and Communications Societies, San Francisco, CA, USA, 29 March–2 April 1998; pp. 356–363. [Google Scholar]
- Troubleshooting Slow Disk I/O in SQL Server. Available online: https://blogs.msdn.microsoft.com/askjay/2011/07/08/troubleshooting-slow-disk-io-in-sql-server/ (accessed on 26 June 2017).
- Cady, F.; Zhuang, Y.; Harchol-Balter, M. A Stochastic Analysis of Hard Disk Drives. Int. J. Stoch. Anal. 2011, 2011, 390548. [Google Scholar] [CrossRef]
- Crovella, M.E.; Taqqu, M.S. A Tool for Estimating the Heavy Tail Index from Scaling Properties. Methodol. Comput. Appl. Probab. 1999, 1, 55. [Google Scholar] [CrossRef]
- Kim, J.H.T.; Kim, J. A parametric alternative to the Hill estimator for heavy-tailed distributions. J. Bank. Financ. 2015, 54, 60–71. [Google Scholar] [CrossRef]
- Nguyen, T.; Samorodnitsky, G. Tail inference: Where does the tail begin? Extremes 2012, 15, 437. [Google Scholar] [CrossRef]
- Strzalka, D. Non-Extensive Statistical Mechanics—A Possible Basis for Modelling Processes in Computer Memory System. Acta Phys. Pol. Ser. A Gen. Phys. 2010, 117, 652. [Google Scholar] [CrossRef]
- Janicki, A.; Weron, A. Simulation and Chaotic Behavior of Alpha-Stable Stochastic Processes; Marcel Dekker: New York, NY, USA, 2000. [Google Scholar]
- Cao, J.; Cleveland, W.S.; Lin, D.; Sun, D.X. Internet Traffic Tends Toward Poisson and Independent as the Load Increases. In Lecture Notes in Statistics, Nonlinear Estimation and Classification; Springer: New York, NY, USA, 2003; Volume 171, pp. 83–109. [Google Scholar]
- Rak, R.; Ziȩba, P. Multifractal Flexibly Detrended Fluctuation Analysis. Acta Phys. Pol. B 2015, 46, 1925. [Google Scholar] [CrossRef]
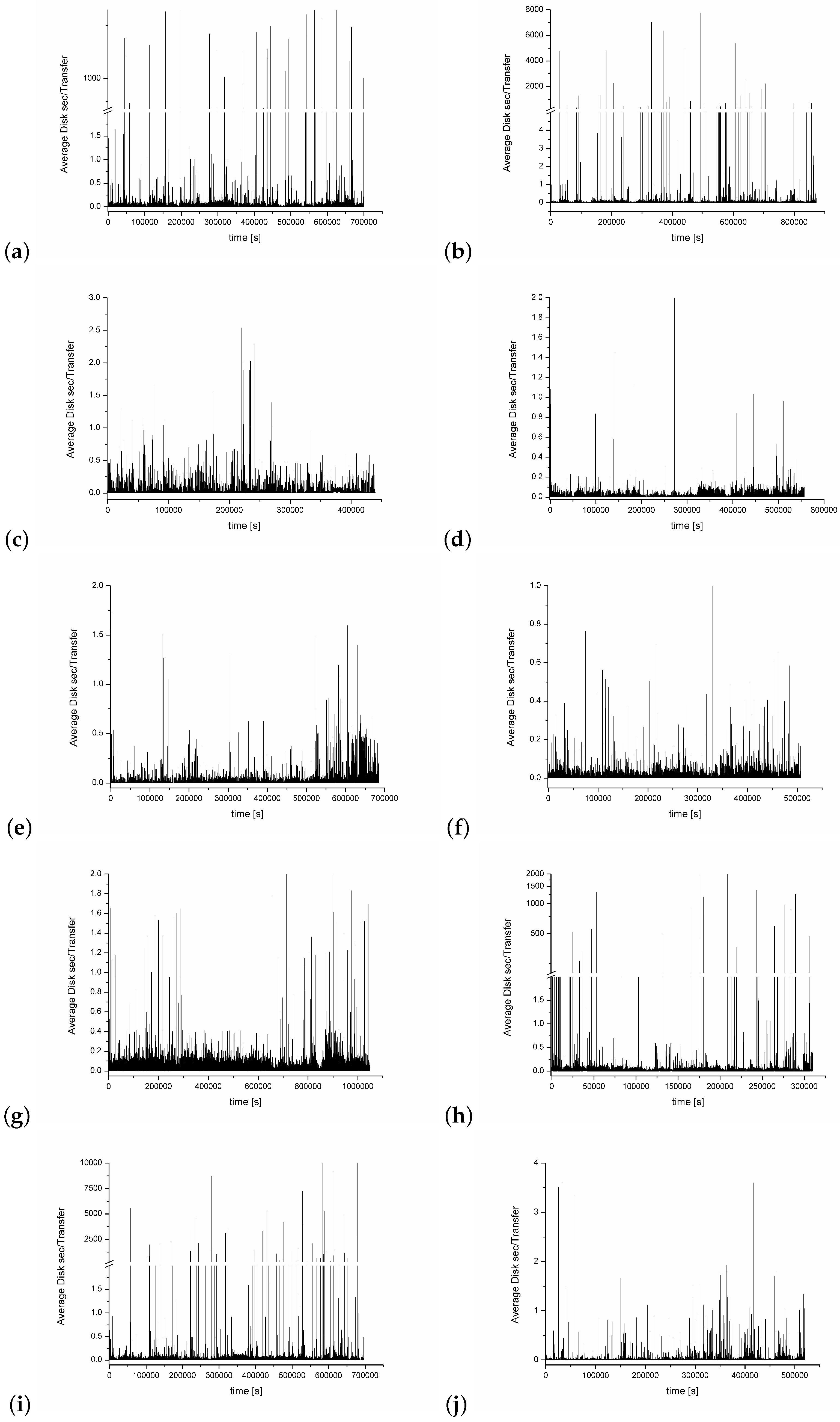
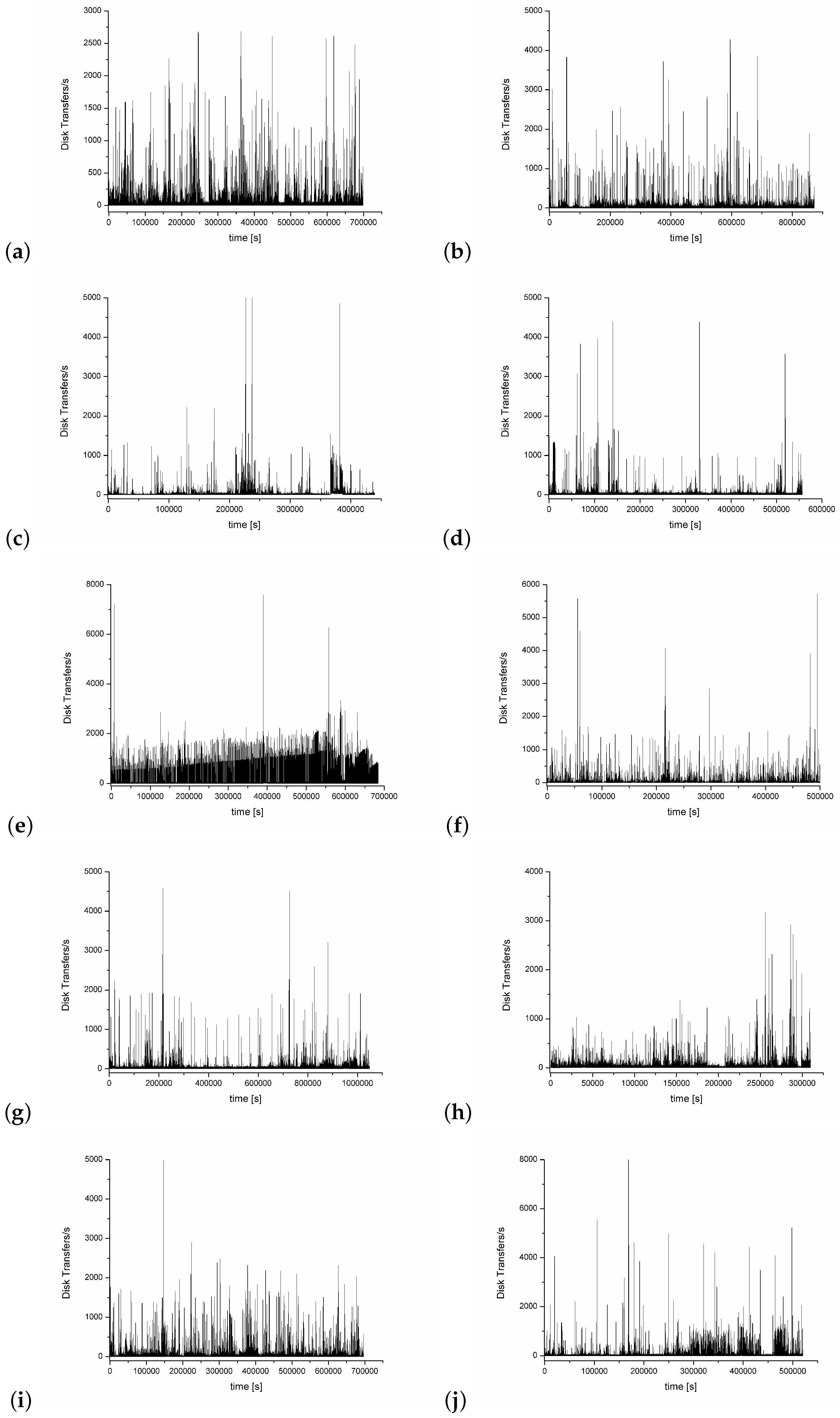
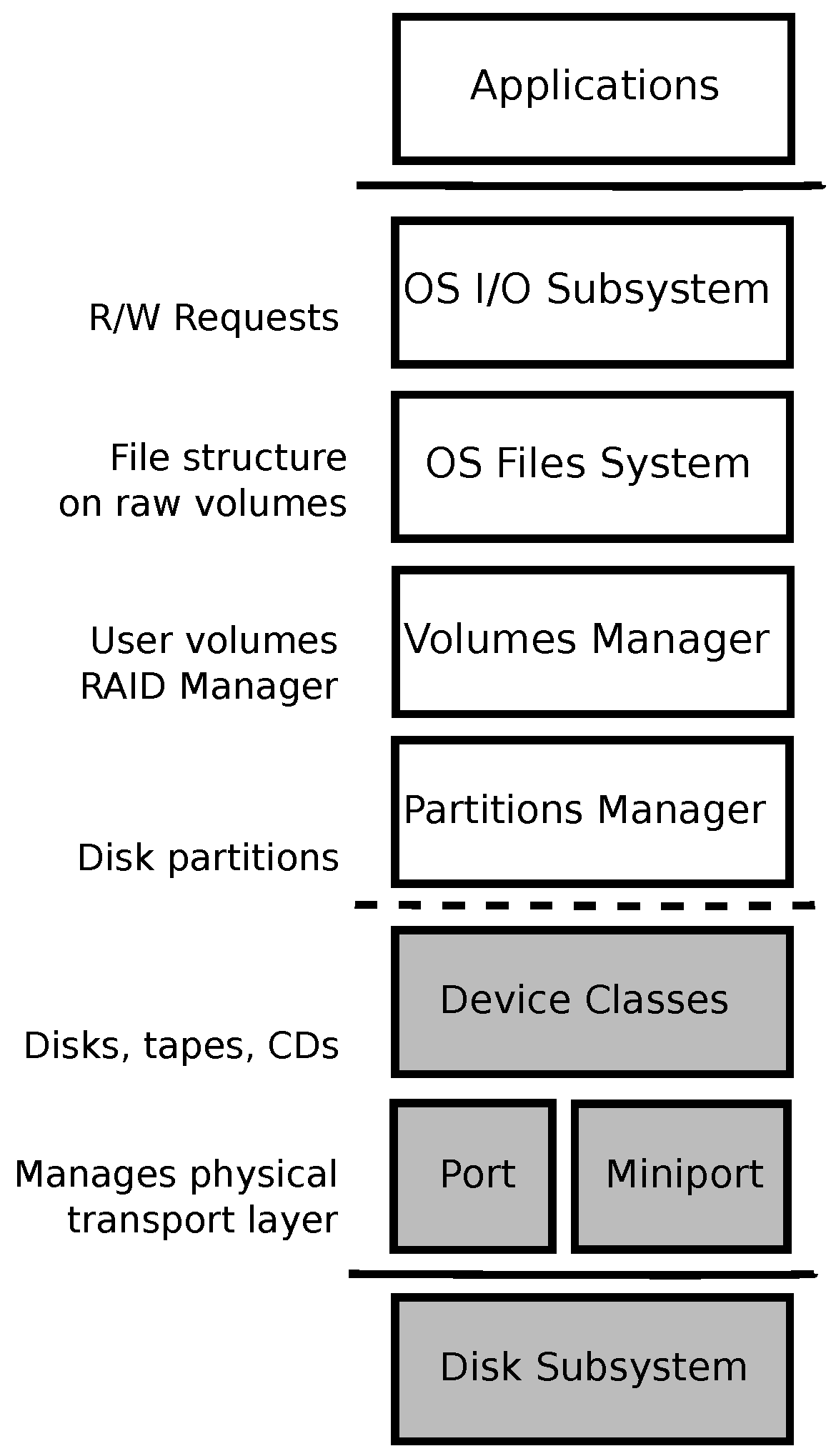
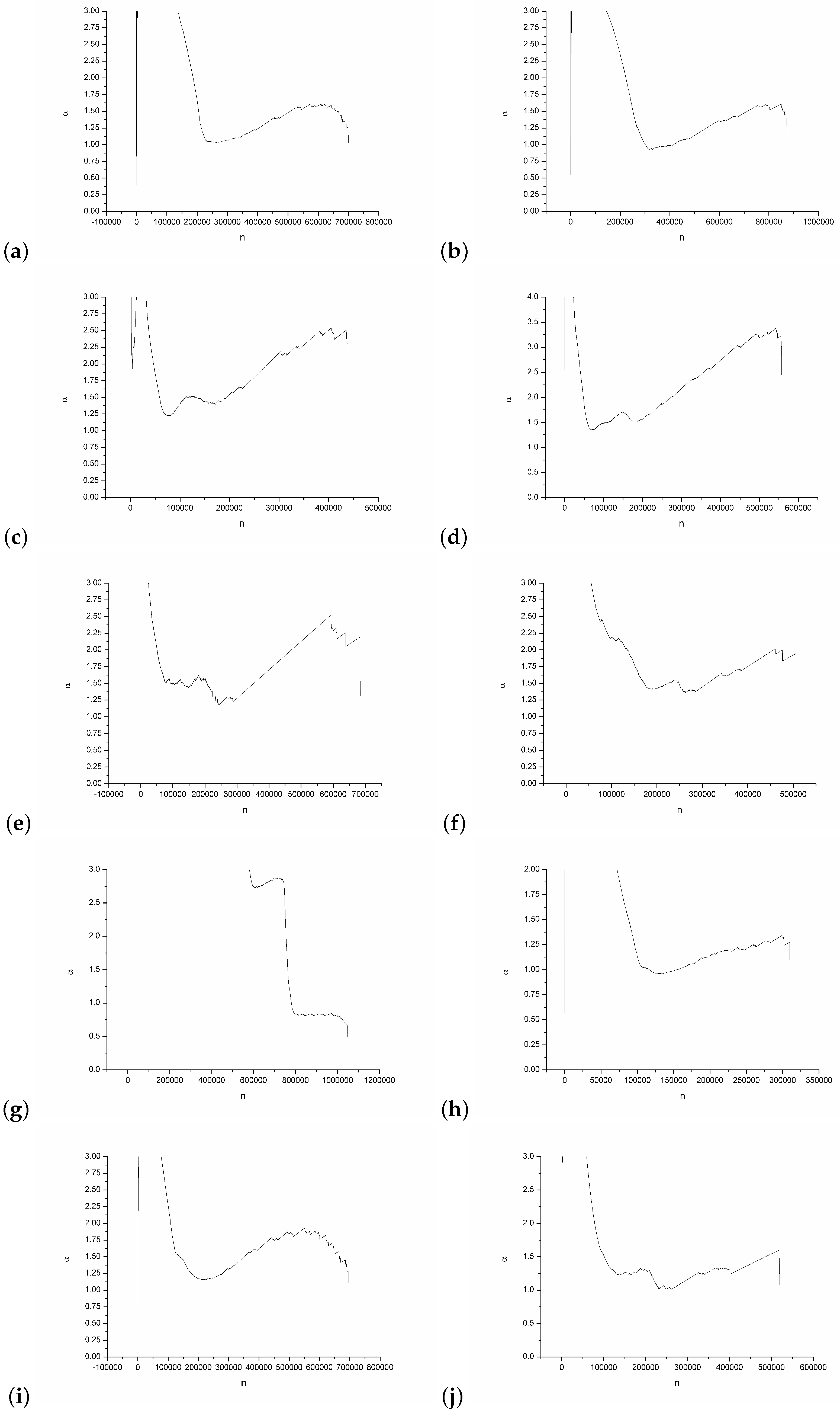
| Id | CPU | RAM | HDD | OS | Number of Records |
|---|---|---|---|---|---|
| 1 | AMD Athlon X2 Dual-Core QL-65 2.10 GHz | 2.0 GB DDR2 | Hitachi HTS5432225L9A300 ATA | Win 7 | 698848 |
| 2 | DualCore Intel Core i5 450 M, 2.666 GHz | 4.0 GB DDR3 | Western Digital WD5000BEVT-22A0RT0 | Win 7 | 872891 |
| 3 | Intel Core i5 CPU M 520 2.4 GHz | 8.0 GB DDR3 | Seagate ST9500420AS ATA | Win 7 | 439615 |
| 4 | DualCore AMD Athlon II X2 250, 2.952 GHz | 4.0 GB DDR2 | Seagate ST3500418AS ATA | Win 7 | 557020 |
| 5 | QuadCore AMD Phenom II X4 Black Edition 955, 3.2 GHz | 8.0 GB DDR2 | Seagate ST31000528AS ATA | Win 7 | 684518 |
| 6 | Intel Pentium Dual-Core E5200 2.5 GHz | 2.0 GB PC800 CL4 | Seagate ST3500320AS ATA | Win 7 | 506599 |
| 7 | Intel Core 2 Duo CPU, T5450, 1.66 GHz | 3.0 GB DDR2 | Seagate ST9250827AS ATA | Win 7 | 1048569 |
| 8 | Intel Core 2 duo P7350 2.00 GHz | 3.0 GB DDR2 | Fujitsu MHZ2320BH G2 ATA | Win 7 | 309766 |
| 9 | AMD Athlon 64 X2 Dual-Core TK-55 1.80 GHz | 3.0 GB DDR2 | Hitachi HTS542512K9SA00 ATA | Win 7 | 696955 |
| 10 | Intel Core i5 650 3.20 GHz | 4.0 GB DDR2 | Seagate ST3500320AS ATA | Win 7 | 519946 |
| Id | Min. | Max. | ||
|---|---|---|---|---|
| 1 | 0.15315 | 27.84289 | 1.99998 × 10 | 9293.79366 |
| 2 | 0.0905 | 18.10498 | 1.50105 × 10 | 7757.53781 |
| 3 | 0.00582 | 0.03968 | 2.50004 × 10 | 2.5388 |
| 4 | 0.00288 | 0.01095 | 3.17642 × 10 | 2.19522 |
| 5 | 0.00261 | 0.01501 | 7.37 × 10 | 1.71806 |
| 6 | 0.00315 | 0.03627 | 1.99997 × 10 | 25.07448 |
| 7 | 0.00879 | 0.01669 | 0 | 2.13655 |
| 8 | 0.08761 | 15.45299 | 1.49874 × 10 | 7599.39 |
| 9 | 0.24258 | 35.72358 | 1.49984 × 10 | 15,152.58086 |
| 10 | 0.00293 | 0.01852 | 0 | 3.6076 |
| Average Disk Sec/Transfer | Disk Transfers/s | |||
|---|---|---|---|---|
| Id | ||||
| 1 | 2.19 | 1.62 | 1.54 | 1.78 |
| 2 | 1.88 | 1.69 | 1.67 | 1.74 |
| 3 | 2.37 | 1.59 | 1.79 | 1.71 |
| 4 | 2.01 | 1.66 | 1.23 | 1.89 |
| 5 | 2.14 | 1.63 | 1.64 | 1.75 |
| 6 | 2.28 | 1.61 | 1.63 | 1.75 |
| 7 | 2.15 | 1.63 | 1.95 | 1.67 |
| 8 | 1.64 | 1.75 | 1.85 | 1.70 |
| 9 | 1.88 | 1.69 | 2.03 | 1.66 |
| 10 | 1.67 | 1.74 | 1.74 | 1.73 |
| Average Disk Sec/Transfer | Disk Transfers/s | |||
|---|---|---|---|---|
| Id | DFA | Spectrum | DFA | Spectrum |
| 1 | 0.501 | 0.53 | 0.92 | 0.91 |
| 2 | 0.494 | 0.5 | 1.04 | 0.98 |
| 3 | 0.988 | 0.99 | 0.96 | 0.95 |
| 4 | 0.858 | 0.78 | 0.98 | 0.99 |
| 5 | 0.791 | 0.77 | 0.86 | 0.79 |
| 6 | 0.654 | 0.55 | 0.94 | 0.89 |
| 7 | 0.878 | 0.83 | 0.84 | 0.88 |
| 8 | 0.488 | 0.5 | 0.90 | 0.93 |
| 9 | 0.509 | 0.51 | 0.77 | 0.8 |
| 10 | 0.773 | 0.74 | 0.70 | 0.91 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strzałka, D. Initial Results of Testing Some Statistical Properties of Hard Disks Workload in Personal Computers in Terms of Non-Extensive Entropy and Long-Range Dependencies. Entropy 2017, 19, 335. https://doi.org/10.3390/e19070335
Strzałka D. Initial Results of Testing Some Statistical Properties of Hard Disks Workload in Personal Computers in Terms of Non-Extensive Entropy and Long-Range Dependencies. Entropy. 2017; 19(7):335. https://doi.org/10.3390/e19070335
Chicago/Turabian StyleStrzałka, Dominik. 2017. "Initial Results of Testing Some Statistical Properties of Hard Disks Workload in Personal Computers in Terms of Non-Extensive Entropy and Long-Range Dependencies" Entropy 19, no. 7: 335. https://doi.org/10.3390/e19070335
APA StyleStrzałka, D. (2017). Initial Results of Testing Some Statistical Properties of Hard Disks Workload in Personal Computers in Terms of Non-Extensive Entropy and Long-Range Dependencies. Entropy, 19(7), 335. https://doi.org/10.3390/e19070335





