Evolution of Caprock Sealing Capacity Under CO₂–Mechanical Coupling in Geological Carbon Storage

Abstract

Caprock sealing capacity is paramount for the safety and efficacy of geological carbon storage. This study investigates the evolution of mudstone caprock sealing capacity under CO₂–mechanical coupling, integrating experimental rock mechanics with fluid–solid coupling numerical simulations. Laboratory experiments reveal that caprock permeability exhibits strong stress sensitivity, decreasing exponentially with increasing effective stress. The stress sensitivity coefficient is highly dependent on initial pore pressure and porosity, being greatest under low-pore-pressure and high-porosity conditions. Furthermore, permeability loss during loading is partially irreversible due to plastic deformation. Numerical simulations, conducted using an integrated Petrel + Visage + Eclipse workflow, quantify the influence of caprock physical and mechanical properties on sealing capacity during CO₂ injection. The results demonstrate that vertical total stress increases with increasing porosity, Young’s modulus, and permeability, with permeability exerting the most significant control. Conversely, vertical effective stress decreases with increases in these parameters, with porosity causing the largest variation. We conclude that lower caprock permeability and porosity are most critical for enhancing sealing integrity, while a higher Young’s modulus improves mechanical stability. These findings provide a theoretical basis and practical methodology for evaluating caprock sealing capacity and ensuring the secure storage of CO₂.

1. Introduction

Currently, Carbon Capture, Utilization, and Storage (CCUS) has emerged as a pivotal technology for achieving carbon neutrality, garnering significant attention across various sectors worldwide [1,2,3,4,5]. CO₂ geological utilization and storage, a core component of the CCUS framework, possesses substantial emission reduction potential [2,3,4,5,6], driving the rapid advancement of numerous large-scale CCUS demonstration projects globally. Crucially, any leakage of stored CO₂ could not only harm the local ecosystem but also pose direct risks to human health in surrounding areas. Consequently, the sealing integrity of the caprock is a primary and essential criterion in the selection of CO₂ storage sites.

The CO₂ injection phase represents a critical period for assessing caprock sealing integrity. The rapid pore pressure buildup during this short-term phase can significantly compromise the mechanical integrity of the caprock [5,6,7,8,9,10], underscoring the dominant influence of stress on early-stage sealing capacity. For the caprock, its permeability directly governs the extent of CO₂ intrusion. Therefore, under coupled CO₂–mechanical conditions, the evolution of caprock permeability constitutes the fundamental intrinsic mechanism determining whether the caprock can “seal effectively” and “seal reliably over the long term”. Investigating caprock permeability thus serves as a key starting point for studying the early-stage sealing integrity of CO₂ geological storage [9,10,11,12,13,14].

Currently, in the field of microscopic sealing mechanisms and dynamic evolution, research focus has shifted from single capillary effects to multi-field coupling interactions. Experimental studies have revealed that mudstone caprocks rich in clay minerals can undergo significant illitization in CO₂-water environments, leading to alterations in pore structure and reductions in permeability, thereby highlighting the positive contribution of chemical precipitation to fracture self-healing [1,5,14]. Meanwhile, the application of digital rock physics has enabled the reconstruction of three-dimensional pore structures in salt rock caprocks [1,2,4,5,8,12,13,14]. Through hydrodynamic simulations, this approach visually demonstrates the dynamic balance between the initiation and closure of micro-fractures under stress disturbances, emphasizing the critical role of thermal–hydro-mechanical–chemical (THMC) coupling effects [1,2,4,8,10,11,12,13,14].

Furthermore, field cases and inversion analyses provide crucial validation for theoretical research. Long-term monitoring data inversion from large-scale CCS projects such as Sleipner and Quest indicates that the caprock’s response to injection-induced pressure perturbations exhibits significant heterogeneity [1,3,4,11,12,13,14]. These field observations challenge the direct extrapolation of laboratory-derived parameters to the field scale and underscore that assessing caprock integrity under real geological conditions must account for macroscopic structures (e.g., faults, lateral sealing) and their synergistic response with the reservoir [1,2,4,5,11,12,13,14].

Accordingly, this study focuses on typical mudstone caprocks. We employ rock mechanics experiments to reveal the dynamic evolution of mudstone permeability under CO₂–mechanical coupling. Integrated with fluid–solid coupled numerical simulations, we aim to identify the main controlling factors governing mudstone caprock sealing integrity under this mechanism. This work seeks to provide a theoretical foundation and methodological support for the safe geological storage of CO₂.

2. Samples and Methods

2.1. Samples

Six core samples from the study area were analyzed for mineral composition using a Germany Bruker D8 Advance X-ray diffractometer. The results, detailed in

Table 1. Characteristics of mineral composition content of caprock.

Mineral	Maximum (%)	Minimum (%)	Average (%)
Chlorite	50.7	38.0	48.3
Illite	3.2	1.4	2.6
Calcite	15.6	8.2	12.6
Quartz	25.0	11.2	22.6
Other	15.1	7.7	13.9

, identify the caprock lithology as mudstone. Minerals are dominated by chlorite (38.0–50.7%), quartz (11.2–25.0%), and calcite (8.2–15.6%), with lesser amounts of illite (1.4–3.2%). The presence of quartz and calcite provides a rigid framework, while the abundance of chlorite, a key clay mineral, can significantly influence the caprock’s geomechanical properties and sealing capacity.

2.2. Experiment

Rock permeability directly influences fluid migration and accumulation. For caprocks, permeability is thus a key indicator for evaluating sealing capacity. In this study, the steady-state method was utilized to determine the permeability of caprock samples [15,16]. The principle of the steady-state permeability measurement is as follows: First, confining pressure is applied to the core sample. After the confining pressure stabilizes at the target value, CO₂ is injected into the sample at a constant rate. The readings from the differential pressure gauge are monitored and recorded. Once both the fluid flow rate and the differential pressure gauge readings stabilize, the data from the gauge is recorded. Assuming that the flow of gas or liquid phase in the rock follows Darcy’s law, the permeability ($K$) for incompressible fluids is

$$K={\displaystyle \frac{Q_w{\mu }_w}{A}}{\displaystyle \frac{L}{\left({P_1-P}_0\right)}}$$

(1)

For compressible fluids, the effective permeability ($K_{\mathrm{eg}}$) is

$$K_{\mathrm{eg}}={\displaystyle \frac{-Q_g{\mu }_{g}L}{A}}{\displaystyle \frac{2P_0}{({P_0}^2-{P_1}^2)}}$$

(2)

where $Q_{\mathrm{w}}$ and $Q_{\mathrm{g}}$ are the flow rates of water and gas at the outlet, respectively; ${\mu }_{\mathrm{w}}$ and ${\mu }_g$ are the dynamic viscosities of water and gas, respectively; $P_0$ and $P_1$ are the pressures at the outlet and inlet, respectively; $A$ is the cross-sectional area of the core sample; and $L$ is the length of the core sample.

The steady-state method yields stable and reliable relative permeability data over a wide range of saturations. However, the permeability of low-permeability rocks like mudstone is typically very low, requiring several hours or even days to reach equilibrium during testing. Furthermore, altering the gas–liquid flow rate ratio necessitates re-determining the water saturation of the mudstone, complicating the procedure. To mitigate hysteresis effects, the direction of saturation change should be controlled to be unidirectional, i.e., either consistently increasing or decreasing [15,16].

2.3. Numerical Simulation

This study employed the integrated software platform (2020) Petrel + Visage + Eclipse to construct a 3D geological model for simulating the coupled seepage and stress fields within the caprock during CO₂ injection. The coupled simulation workflow encompassed 3D grid generation, assignment of mechanical property models, pore pressure initialization, boundary condition definition, finite element computation, and result analysis. The geomechanical simulator VISAGE is designed for coupled calculations with the reservoir simulator ECLIPSE. After configuring the iteration step size and numerical scheme, Petrel’s two-way coupling procedure automatically executes ECLIPSE and VISAGE in sequence. This ensures seamless integration between the two sets of computational grids, maintaining high efficiency and precision throughout the reservoir-geomechanics coupling process. Within this two-way coupling mechanism, ECLIPSE first computes the temperature and pressure fields and transmits them to VISAGE. VISAGE then calculates the current stress field, updates the permeability and pore volume accordingly, and feeds these modified properties back to ECLIPSE for the subsequent time step’s temperature and pressure calculations. This two-way data exchange occurs at every step [17].

The model used in this study is idealized, featuring a 50 m thick caprock, a 100 m thick reservoir, a top depth of 2500 m, and lateral dimensions of 510 m by 510 m. The dimensions of the mechanical model are 1.5 times those of the property model in all directions. The injection well is located at the model center, with a CO₂ injection rate of 25,000 sm³/d and a bottom-hole pressure limit of 500 bar. The Poisson’s ratios for the caprock and reservoir are set to 0.4 and 0.2, respectively, with compressive strengths of 700 bar and 1000 bar, respectively. The simulation period spans 20 years.

This study established a benchmark numerical model to systematically investigate the impact of caprock physico-mechanical properties on sealing efficiency following CO₂ injection. The model’s caprock was parameterized with a porosity of 7%, anisotropic permeabilities (0.0001 mD in I- and J-directions, and 0.00001 mD in K-direction), and a Young’s modulus of 5 GPa. These values (denoted as P2, K2, E2) constitute the baseline configuration. The porosity and permeability values in this study were determined from a systematic experimental analysis of core samples from the target formation, with the average values adopted as representative parameters. The mechanical parameters were based on data from reference [18] and were slightly adjusted according to the specific geomechanical characteristics of the study area. This calibration ensures that the model better conforms to the actual geological conditions, thereby guaranteeing the reliability of the simulation results.

Holding reservoir properties constant, six additional numerical simulation scenarios were designed by varying one of the caprock’s key parameters (porosity, permeability, or Young’s modulus) at a time while keeping all others unchanged (

Table 2. Mechanical and physical parameters characteristics of numerical simulation models (The petrophysical and mechanical data were derived from experiments and literature review, respectively.).

Models	Porosity (%)	Permeability (mD)	Young’s Modulus (GPa)
P-2 K-2 E-2	7	I = 0.0001 J = 0.0001 K = 0.00001	5
P-1	4	I = 0.0001 J = 0.0001 K = 0.00001	5
P-3	10
K-1	7	I = 0.0001 J = 0.0001 K = 0.0001	5
K-3		I = 0.001 J = 0.001 K = 0.001
E-1	7	I = 0.0001 J = 0.0001 K = 0.00001	10
E-3			15

). This approach allows for the calculation of parameter variations at the reservoir-caprock interface (the bottom grid layer of the caprock).

It is important to note that this study is based on an idealized model, which treats the reservoir as a homogeneous medium and only accounts for the vertical and horizontal variations in permeability regarding caprock heterogeneity. Moreover, the model assumes a single central injection well and does not incorporate complex geological structures such as faults. Due to these simplifications of actual geological conditions, the conclusions drawn may have limitations in their general applicability.

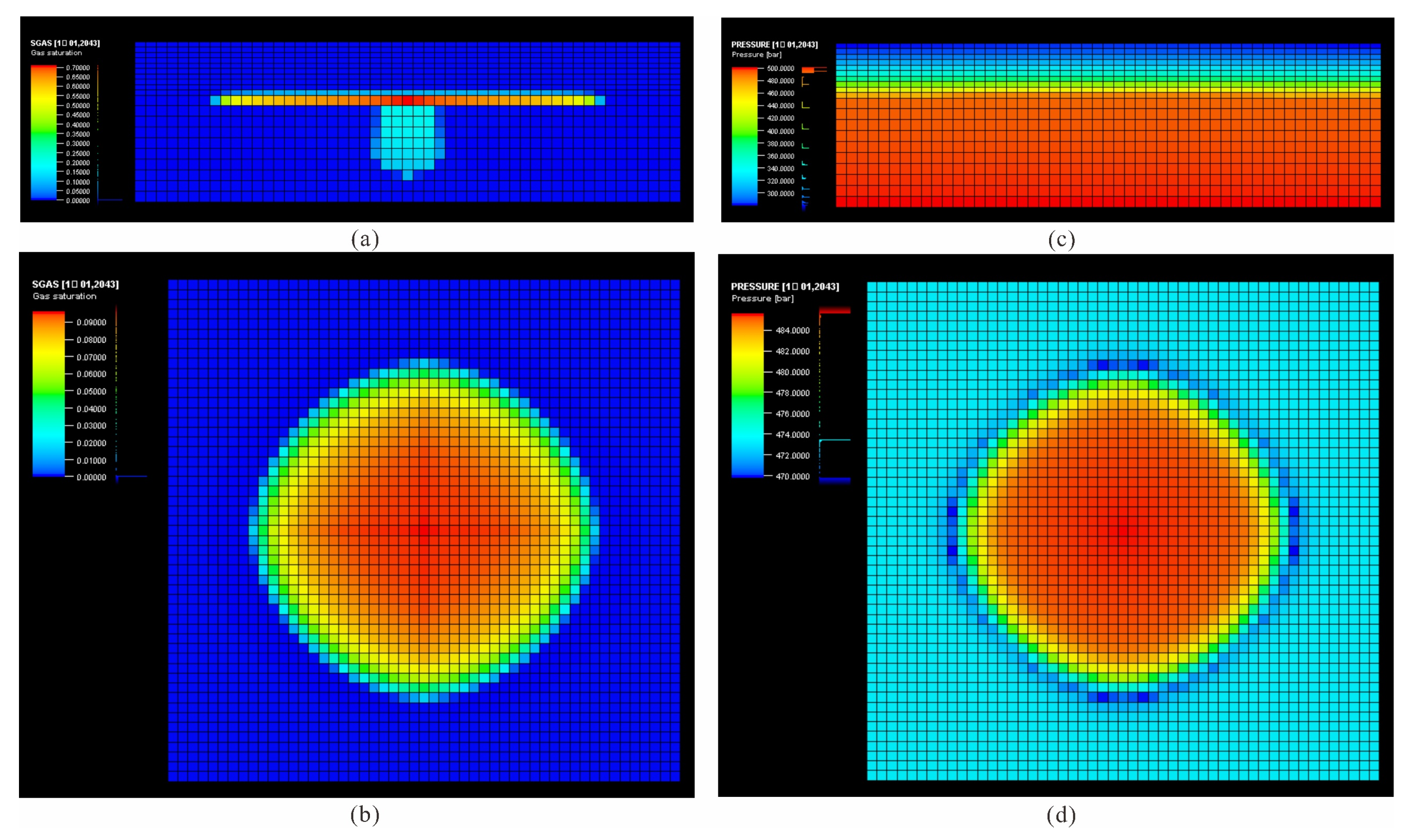
3. Results and Discussion

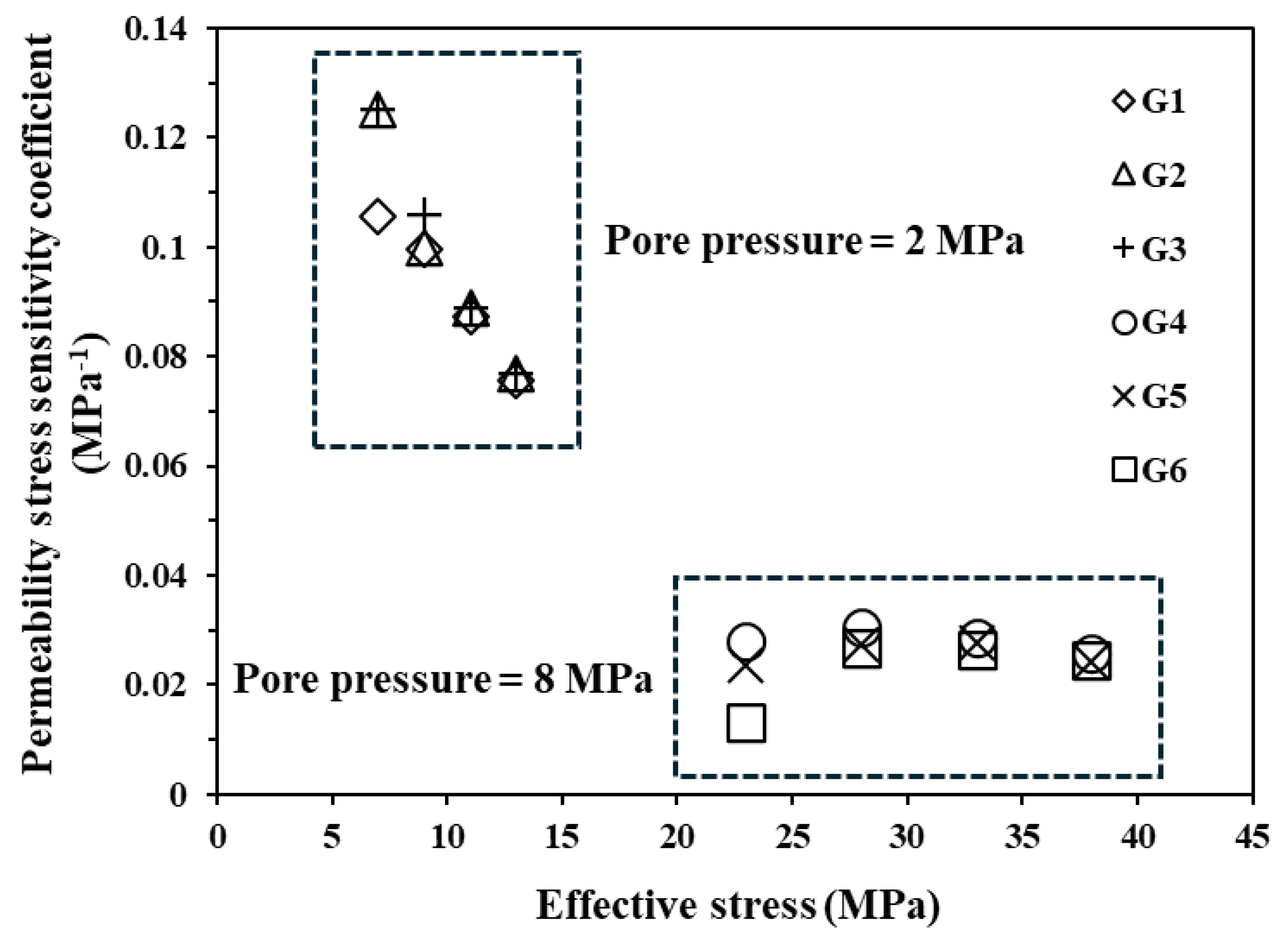
3.1. Stress Sensitivity Characteristics of Caprock Permeability

Caprock, a porous medium composed of various minerals, undergoes differential deformation under stress due to the varying compressibility of mineral particles, clay materials, and cements [18,19,20]. The stress sensitivity of caprock permeability was analyzed through high-pressure, high-temperature displacement experiments on six mudstone samples with differing physical properties. Generally, a larger permeability stress sensitivity coefficient indicates greater susceptibility of caprock permeability to pressure changes, whereas a smaller coefficient suggests weaker sensitivity and a gentler permeability decline with increasing pressure [19,20,21,22,23].

At a constant pore pressure of 2 MPa, the permeability stress sensitivity coefficient decreases markedly with increasing effective stress. In contrast, at a higher pore pressure of 8 MPa, the rate of decrease in the coefficient slows overall and exhibits a wavy pattern (Figure 1). The change in caprock permeability under effective stress fundamentally reflects the evolution of pore-throat geometry. Consequently, at low pore pressures, caprock pore-throat size demonstrates very strong stress sensitivity. At high pore pressures, this sensitivity weakens and displays fluctuating behavior.

The permeability stress sensitivity coefficient increases with decreasing pore pressure or increasing porosity (Figure 2). Under stress, numerous pores and micro-fractures may form within the caprock, while the rock skeleton compacts, reducing some pore spaces. If the initial porosity is higher or the pore pressure is lower, the pore-throat system is more susceptible to alteration under stress, leading to a higher stress sensitivity coefficient. Therefore, the inherent porosity and pore pressure of the caprock directly govern the intensity of pore-throat changes under stress, and a sufficient burial depth forms the basis for adequate caprock sealing capacity [21,22,23,24].

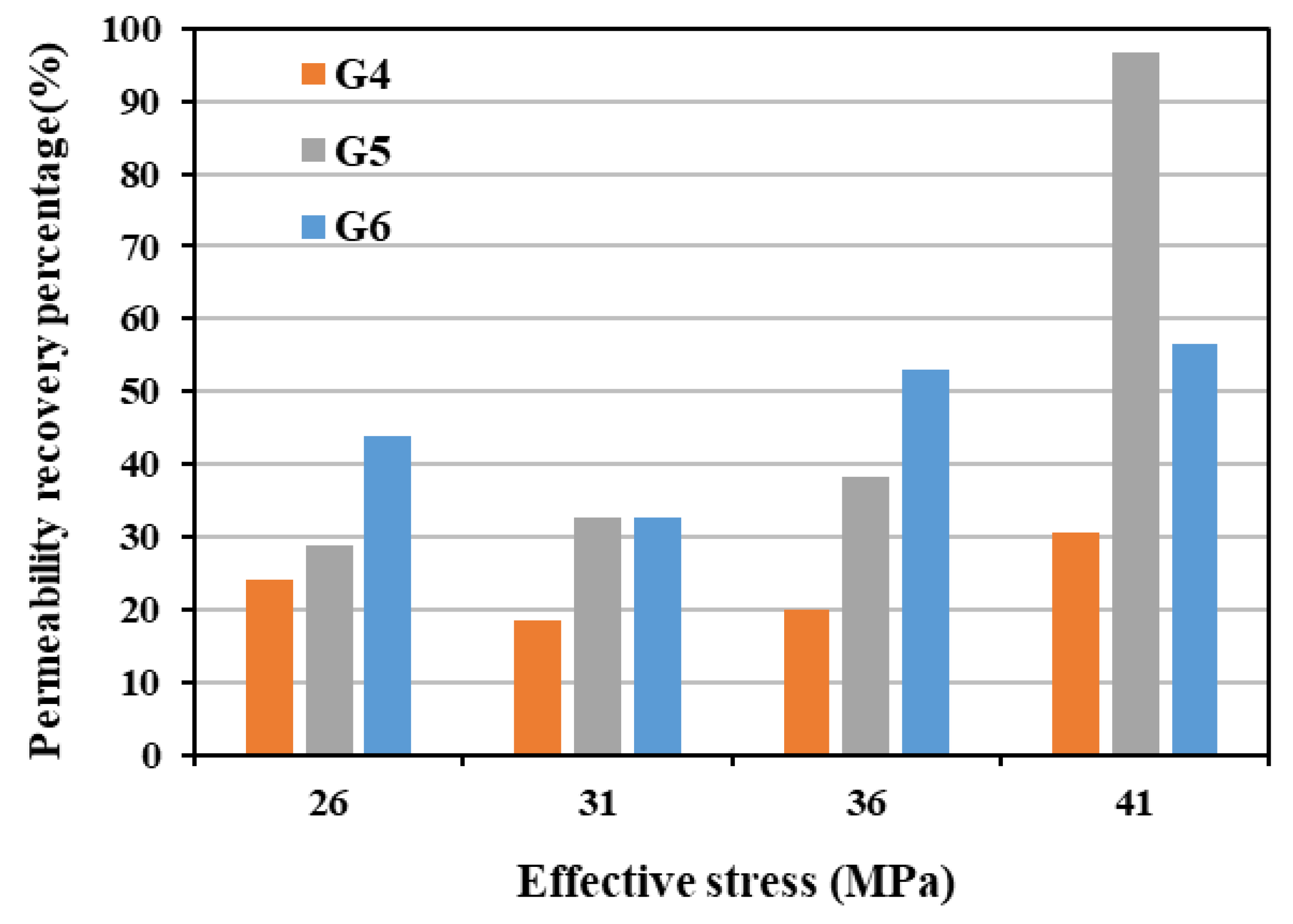
3.2. Evolution of Caprock Permeability Under Stress

As shown in Figure 3, caprock permeability decreases exponentially with increasing effective stress. This indicates that pore-throat connectivity varies relatively little beyond a certain effective stress threshold. Therefore, from an economic standpoint, deeper caprocks are not necessarily optimal for CO₂ storage. Higher caprock pore pressure corresponds to a smaller permeability stress sensitivity coefficient and a slower rate of permeability reduction, suggesting that a higher initial pore pressure is more favorable for CO₂ storage (Figure 3). This implies that the controlling effect of pore pressure on permeability is significantly stronger than that of confining pressure, and sufficient pore pressure can potentially compensate for shallower caprock depths.

The observed permeability reduction under effective stress loading and its incomplete recovery during unloading (Figure 4) are direct consequences of the caprock’s specific mineral assemblage. The mechanical response is governed by the pervasive, platy clay matrix, predominantly composed of chlorite with minor illite (Table 1). These clay minerals facilitate irreversible plastic deformation through pore compaction and the permanent closure of microcracks, which are initially induced by the stress relief during coring. The platy morphology of the clays is responsible for a pronounced stress hysteresis effect, which hinders elastic rebound. Furthermore, the presence of rigid quartz and calcite minerals creates significant stiffness contrasts within the rock fabric. This heterogeneity localizes strain during loading, intensifying irreversible damage within the more compliant clay matrix. Consequently, this unique mineralogy fundamentally dictates that a portion of the permeability loss is permanent [23,24,25].

The irreversible permeability loss revealed in Figure 4 should be unequivocally attributed to plastic deformation induced by compaction. Under high pressure, irreversible changes such as grain rearrangement, crushing, or pore collapse occur within the rock skeleton, permanently clogging the critical flow pathways, the throats, resulting in irreversible permeability reduction. This mechanism has a dual impact on the long-term sealing capacity of the caprock: From a short-term perspective, it creates a “self-healing” effect, whereby the caprock exhibits a lower baseline permeability after enduring the initial high-pressure test, thereby enhancing its ability to withstand subsequent pressure fluctuations. However, from a long-term perspective, plastic damage may accumulate over multiple injection-production cycles, ultimately triggering the propagation of microcrack networks, which instead degrades its integrity and potentially forms dominant flow pathways. Therefore, accurately evaluating this compaction effect is crucial for scientifically establishing safe injection pressure limits, predicting the long-term evolution of the caprock, and ensuring the lifelong safety of the storage project.

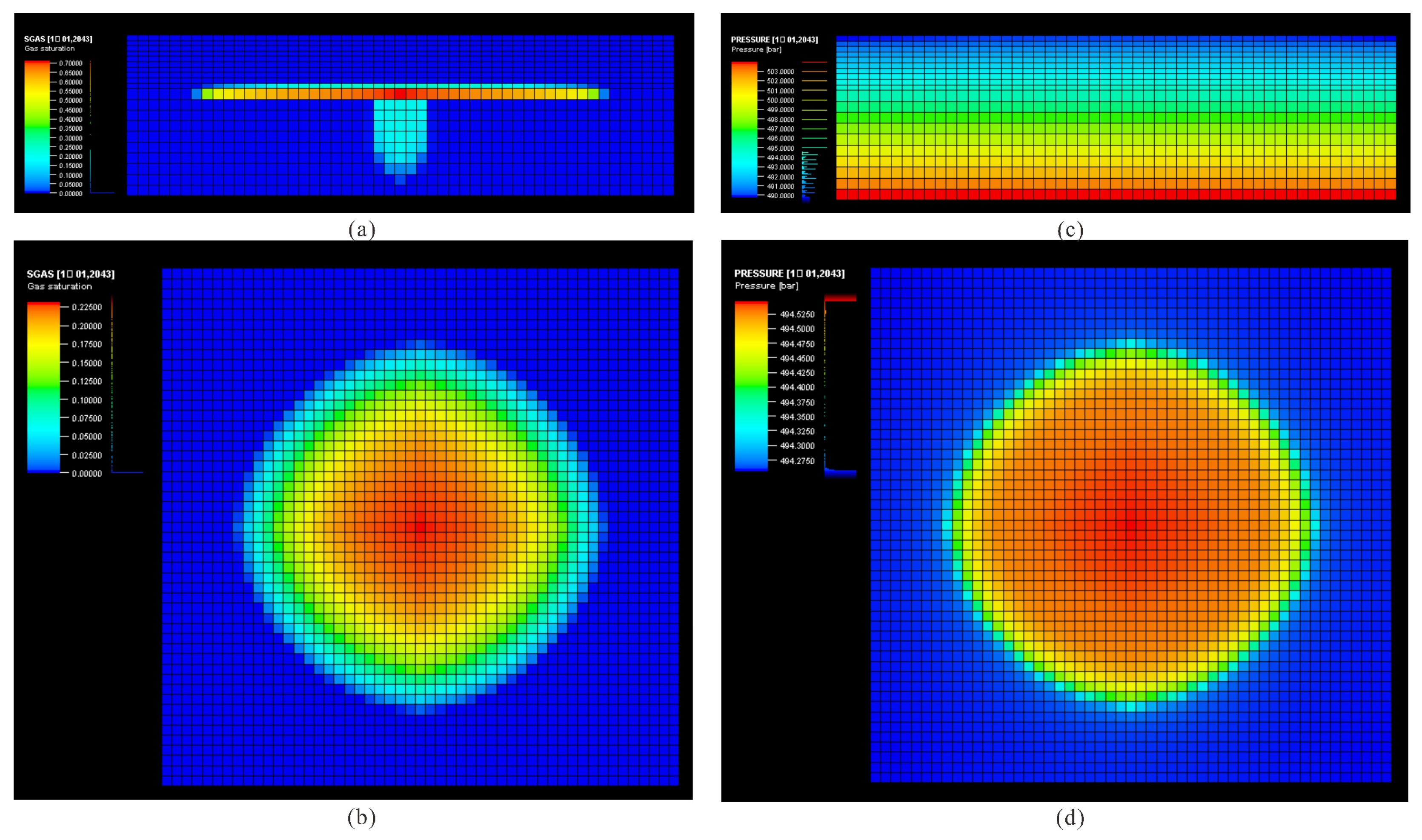
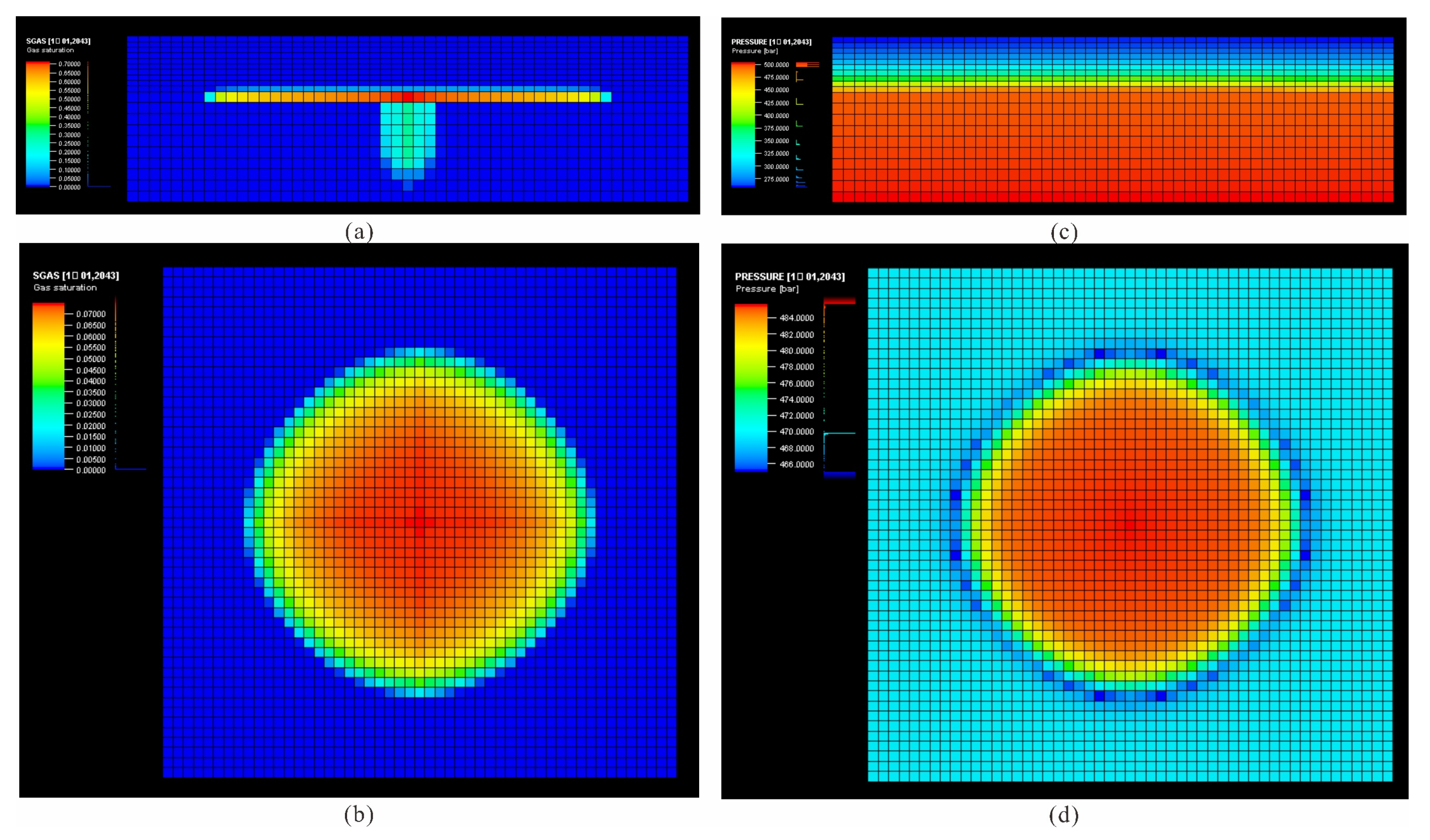
3.3. Influence of Physical Properties on Caprock Sealing Capacity

Within CO₂ storage sites, the injection of large volumes of CO₂ alters the in situ stress field of both the reservoir and caprock. These stress field changes cause variations in the regional Coulomb failure stress, potentially reducing caprock strength and inducing instability. Therefore, examining the impact of different physical properties on caprock sealing integrity is crucial. Figure 5a,b show the distribution of the CO₂ plume within the reservoir-caprock system of the benchmark model after 20 years of injection, while Figure 5c,d show the corresponding pore pressure distribution. Overall, in the benchmark model by year 2043, pore pressure ranges from 257.6 to 485.7 bar, with significantly higher pressures in the reservoir than in the caprock. The maximum gas saturation in the reservoir reaches 71.3%, whereas only the lower portion of the caprock is invaded by CO₂, with a maximum gas saturation of merely 7.49%.

As shown in Figure 5, upon reaching the caprock, the upward-migrating CO₂ plume is effectively confined vertically, leading to pronounced lateral spreading. This process results in a characteristic conical-shaped dispersal pattern beneath the seal, which is narrow at the base and widens upward, with its maximum lateral extent observed at the bottom of the caprock. This spatial configuration clearly illustrates the dominant migration pathways and accumulation behavior of CO₂ during and after injection.

Figure 6a shows the influence of different caprock porosities (4%, 7%, and 10%) on sealing capacity. Generally, the vertical total stress at the reservoir-caprock interface increases as porosity decreases. At any given time, the vertical total stress follows the relationship: P-0.04 < P-0.07 < P-0.10. The vertical total stress rises rapidly during early injection, with this effect diminishing over time, correlating with the reduced injection rate and the gradual dispersion of the CO₂ plume later on. Lower porosity has a more pronounced effect on increasing vertical total stress at the interface, indicating that reduced porosity significantly elevates pore pressure, thereby enhancing the vertical total stress within the caprock.

Figure 6b shows the effect of porosity on the vertical effective stress at the interface. During the 20-year injection period, the vertical effective stress gradually stabilizes, suggesting that porosity variations have minimal influence on the overall distribution of the CO₂ plume. Higher caprock porosity corresponds to lower pore pressure, resulting in greater vertical effective stress. The rapid decrease in vertical effective stress during early injection reflects the significant pore pressure buildup due to CO₂ accumulation at the interface, an effect that weakens as the plume disperses over time.

With CO₂ injection, the vertical total stress in caprocks with different permeabilities increases, following the relationship: K-0.00001 < K-0.0001 < K-0.001 (Figure 6c). This indicates that higher permeability facilitates greater CO₂ intrusion, leading to increased vertical total stress. Permeability exerts a more significant influence on vertical total stress than porosity, with distinct differences observed between caprocks of varying permeability, especially during early injection. As injection proceeds and the CO₂ plume disperses, pore pressure decreases, causing the vertical total stress for different permeability cases to converge and stabilize.

Regarding vertical effective stress, it decreases as pore pressure at the interface increases with CO₂ injection (Figure 6d), a trend similar to the porosity effect. The rapid initial drop in vertical effective stress again signifies substantial early pore pressure buildup, weakening over time. However, the influence of permeability on vertical effective stress exhibits distinct temporal characteristics: during early injection, higher permeability corresponds to higher vertical effective stress; during middle and late stages, higher permeability results in lower vertical effective stress. This is because, initially, higher permeability allows CO₂ to enter more readily, reducing stress concentration at the caprock base. Later, higher permeability promotes broader CO₂ migration and pressure dissipation within the caprock, lowering the internal pore pressure and thus the effective stress.

Taking model K-3 as an example (Figure 7), CO₂ saturation in the caprock ranges from 0 to 0.3, while the pressure field shows minimal variation (493–494 bar). This indicates that lower permeability heterogeneity leads to a more uniform pressure distribution. This can be explained as follows: in early stages, higher permeability facilitates CO₂ entry, reducing localized stress and increasing effective stress; in later stages, it promotes pressure dissipation, lowering the overall pore pressure and thus the effective stress.

3.4. Influence of Mechanical Properties on Caprock Sealing Capacity

The intrinsic mechanical properties of the caprock are also critical for its stability after CO₂ injection. To investigate this, numerical simulations were conducted by varying the caprock’s Young’s modulus while keeping other parameters constant. As shown in Figure 8a, with CO₂ injection, the vertical total stress increases for caprocks with different Young’s moduli, following the relationship: E-15 < E-10 < E-5. This suggests that a lower Young’s modulus leads to higher plastic deformation intensity upon pore pressure increase, resulting in the caprock bearing greater stress. Differences in vertical total stress between caprocks with different moduli are small initially but become more pronounced during middle and late injection stages as the CO₂ injection rate decreases and the plume disperses. Caprocks with lower moduli show a more continuous increase in vertical total stress, whereas those with higher moduli stabilize more readily.

Vertical effective stress decreases with increasing pore pressure at the interface, consistent with the trends observed for porosity and permeability. The rapid early decrease reflects significant pore pressure buildup from CO₂ accumulation. Unlike vertical total stress, the caprock’s Young’s modulus has a relatively minor impact on vertical effective stress (Figure 8b). In early stages, vertical effective stress is similar across different moduli; in later stages, caprocks with higher Young’s moduli exhibit slightly lower vertical effective stress.

In the E-1 model (lower Young’s modulus), the CO₂ saturation in the caprock ranges from 0 to 0.2, but the pressure field exhibits the strongest heterogeneity (485–490 bar, Figure 9). This indicates that a smaller Young’s modulus leads to stronger deformation heterogeneity and more uneven pore pressure distribution within the caprock. This is primarily because a lower modulus makes the caprock more susceptible to deformation. While deformation may locally relieve pore pressure, the resultant deformation and squeezing of other pore spaces can ultimately lead to an increase in vertical effective stress in those areas.

During CO₂ injection, vertical effective stress decreases with increasing porosity and permeability over time, with porosity variation causing the largest difference in this stress component. Concurrently, vertical total stress increases with increasing porosity and permeability, with permeability exerting a stronger influence than porosity. Therefore, caprock permeability significantly affects both the pore pressure and the Coulomb failure stress within the caprock, thereby controlling its mechanical stability.

4. Conclusions

(1)

Mudstone caprocks show strong stress-sensitive permeability at low pore pressures. Once effective stress exceeds about 20 MPa, the permeability stress sensitivity drops markedly. The degree of permeability change is controlled by the caprock’s inherent porosity and pore pressure: higher porosity or lower pore pressure increases stress sensitivity and alters pore-throat connectivity more significantly.

(2)

For mudstone caprocks, vertical total stress increases with porosity, permeability, and Young’s modulus, with permeability being the most influential factor. In contrast, vertical effective stress decreases as these parameters increase, but is most affected by porosity, then permeability, and lastly Young’s modulus.

(3)

Lower permeability and porosity generally enhance the sealing performance of the caprock. Simultaneously, during CO₂ injection, a higher Young’s modulus contributes to greater mechanical stability of the caprock.