Fault Location in Onshore Wind Farms Using Heuristic Methods and Current Estimation of Wind Generators

Abstract

This work proposes a method for fault location in onshore wind farms’ collector circuits based on metaheuristic optimization. The approach minimizes differences between voltage and current phasors measured and calculated at the Collector Bus (CB) using a Particle Swarm Optimization (PSO) algorithm. By optimizing this objective function, the method achieves accurate identification of fault locations. Additionally, to improve the method’s precision, the CB measurement data were employed to estimate the current injected by the wind generators during the fault. The proposed solution was evaluated through extensive simulations in PSCAD/EMTDC v5.0.2, covering short-circuit scenarios with variations in fault type, location, resistance, and affected segments, including both overhead and underground cables. The results demonstrated high fault location accuracy, even under diverse and challenging conditions. Additionally, the method successfully identified the fault resistance and the specific circuit segment where the fault occurred, thereby reducing the possibility of multiple fault locations. Sensitivity analysis further confirmed the robustness of the methodology, validating its applicability through errors in phasor measurements and line parameters. These findings highlight the proposed method’s potential as a practical and reliable tool for enhancing fault diagnosis and resilience in wind farm collector circuits.

1. Introduction

The global power sector has seen a rapid expansion in the use of renewable energy sources, driven by the pursuit of a more sustainable and resilient energy future. Renewable energy capacity has reached over 3870 GW globally. This growth, which represents 86% of capacity additions in the electricity sector, demonstrates the dominance of renewable sources [1]. However, it is essential to note that the distribution is not uniform globally, indicating that challenges remain to be addressed to achieve the global goal of increasing renewable energy capacity. This situation underscores the pressing need to develop and implement advanced technological solutions that optimize the integration of renewable energy sources into electricity grids, thereby ensuring the stability and reliability of the electricity supply. The need for innovation and the importance of research and development are further accentuated by the complex nature of renewable energy configurations, particularly wind farms, which pose challenges in grid operation [2].

Among the technical challenges posed by wind farms, fault location stands out due to the complexity of their configurations, which include aerial and buried cables, as well as the distributed nature of the generation units. As wind farms grow in size and connect to increasingly complex grid structures, traditional fault location methods may become less effective or computationally impractical. These limitations have motivated the exploration of advanced techniques capable of handling complex circuit configurations and adapting to the dynamic behavior of such systems. In this context, there is a lack of methods capable of adequately locating faults in the collecting circuits of wind farms. Thus, the following section presents a review of the main contributions found in the literature regarding fault location methods in electrical grids.

1.1. Literature Review

The scientific literature proposes various methodologies to overcome the challenges inherent in locating faults, such as grid complexity, the variability of energy sources, and the presence of components such as wind turbines and long-distance transmission lines. Existing approaches have been primarily classified into artificial intelligence (AI)-based methods and traditional methods [3,4].

AI-based methods, such as ref. [5], have proposed an optimized GWO-WELM (Grey Wolf Optimization—Weighted Extreme Learning Machine) model for fault diagnosis using simulated phasor measurement unit (PMU) data in a 9-bus IEEE system. The applied method has demonstrated high accuracy in fault classification (99.83%) and localization (95.48%). However, the specific application in wind power generation systems, which present specific dynamic and noise characteristics, has required additional adaptations and validations. By obtaining data from PMUs, the model has been analyzed with measurement data from real-life scenarios, improving the application of the proposal.

The method proposed in ref. [6] for fault detection and classification utilizes convolutional neural networks (CNNs). The authors have demonstrated significant potential in their application. The execution of this method achieved a classification accuracy of 100% and an ideal response time of 0.047 s for a 9-bus IEEE test system. However, in larger and more complex wind power systems, which present different types of deficiencies and operating conditions, a more thorough evaluation of the model’s robustness and generalizability has been required.

Following the line of neural network–based approaches, the method presented in ref. [7] employs artificial neural networks (ANNs) for short-circuit fault detection and classification. The technique achieved high accuracy in locating faults by analyzing phasor quantities measured at the transmission line’s terminals. Nevertheless, the implementation of ANNs required considerable computational resources, leading to relatively long processing times. This drawback becomes more pronounced in large-scale networks, where the volume of measurement data grows significantly [8].

In ref. [9], a method was proposed for applying AI algorithms, such as neural networks, ANN, and random forest, showing achieved good accuracy (90%) in classifying and locating faults in distribution networks with renewable generation. The authors applied the method to a 14-bus electrical distribution system adapted from the IEEE. This electrical model enabled the visualization of AI methods in wind energy systems.

The authors of ref. [10] developed a method based on AI, including deep learning, to assist control center operators in fault location. However, the method’s effectiveness has depended on the quantity of the available training data, as well as the model’s ability to handle the diversity of faults and network configurations in wind power generation systems.

In ref. [11], the authors introduced a fault detection and location scheme that leverages travelling-wave (TW) phenomena for multi-sectional cross-bonded export cables in offshore wind farms. The work developed detailed cable models and TW principles under realistic operating conditions, incorporating an impedance-aggregation technique that preserves the frequency characteristics of the offshore collecting circuit. Wavelet-based TW simulations were also performed to provide independent verification. The results confirmed that TW-based relays are suitable for offshore environments, supported by evidence from both simulation studies and hardware relay tests.

The authors of ref. [12] proposed a phasor-based multi-method fault location strategy tailored to onshore wind farm collector circuits. The method uses measurements at the (CB) and selects the most accurate fault location technique depending on the fault type. It was validated through PSCAD simulations, considering diverse fault scenarios. Despite having good precision, a key limitation of the method is its difficulty in identifying the specific faulted section in collecting circuits with lateral derivations, which may result in multiple possible fault locations along different branches.

In ref. [13], a two-stage fault-location scheme was introduced for offshore wind farm collector systems, where detection is difficult due to cables buried deep under the seabed. The first stage identifies the faulted zone using compressed sensing, enhanced through improved data measurement, $\lambda$-NIM dictionary design, and an optimized CoSaMP algorithm. The second stage applies an equation to find asymmetric faults within the identified segment. Despite its accuracy gains, the method requires measurements at multiple nodes of the collector grid, rather than only at the circuit breaker (CB), which limits its practicality for wind farms instrumented solely at the CB. Additionally, its applicability to branched collector circuits is unclear, often resulting in multiple possible fault locations.

In ref. [14], the authors developed a synthetic-image strategy for detecting defects in transmission lines. Using information collected by the Fault Patrol Transmission Line Inspection Robot (FPTLIR), they generated the Synthetic Defect Component Dataset (SDFC), which served as training data for an enhanced YOLOv5 model. This customized version, named CSH-YOLOv5, incorporates both the Convolutional Block Attention Module (CBAM) and the SimCSPSPPF module to enhance feature extraction and detection precision. The study demonstrates that this framework can significantly strengthen automated fault detection in transmission lines and provides useful insights for practical applications in the power transmission field.

In ref. [15], a fault-classification approach was proposed using a Fault Identification Matrix (FIM) constructed from changes in the component current samples and the sign of their rates of change ($\alpha$ and $\beta$) measured at both terminals of a transmission line. The technique also relied on the second-order harmonic component of the line currents—recomputed via the Clarke transform—to distinguish among fault types. The authors evaluated the method through extensive PSCAD/EMTDC v5.0.2 simulations covering all short-circuit categories and several atypical operating scenarios. Across the full set of tests, the approach consistently identified and classified faults within a single cycle, demonstrating rapid response, robustness, and minimal dependence on network parameters.

The work ref. [16] presents a fault location approach that relies on optimization techniques for application in series-compensated transmission lines. This algorithm estimates the position of the fault by minimizing the error between measured post-fault phasors and those computed from a grid model, utilizing a dynamic differential evolution strategy. One of the main strengths of this method is that its performance does not depend on the particular configuration, impedance values, or location of the series-compensation equipment. Its effectiveness was demonstrated using a 500-kV double-circuit transmission line modeled in ATP/EMTP [17], where the approach proved robust under various compensation arrangements. However, although several studies have explored optimization-based methods in power systems, recent findings suggest that optimal placement and sizing of distributed renewable resources also play a significant role in improving network performance. In ref. [18], for example, applied a Wild Horse Optimizer-based strategy and reported substantial reductions in active power losses and enhanced voltage regulation when photovoltaic and wind-based distributed generation were jointly optimized instead of being deployed independently. This further reinforces the relevance of optimization frameworks in modern power systems while also highlighting the shifting focus from traditional transmission protection toward challenges associated with renewable-dominated and inverter-based distribution architectures.

In ref. [19], the authors presented a fault-location technique grounded in electromagnetic time-reversal (EMTR) theory, introducing a criterion based on the minimum reflected energy of the fault current signal. This method evaluates how the fault current signal energy is distributed in the frequency domain by considering different ground-fault impedance values in the forward-time simulation. The corresponding time-domain response was then validated through power system computer-aided design tools, confirming the feasibility of the proposed approach.

Time-of-arrival analysis methods have been based on traveling-wave (TW) techniques, which offer high accuracy and precision. However, their effectiveness may be compromised in systems with distributed generation and scenarios with low DC filter impedance, as mentioned in ref. [20]. Application in networks with wind power injection may require consideration of more complex wave propagation phenomena due to the presence of different energy sources.

The method proposed in ref. [21] used TW time difference and PSO to locate faults in active distribution networks with distributed generators. Studies such as refs. [22,23] applied TW analysis to multiple opposite terminals, calculating the fault distance by averaging the results. Ref. [24] proposed a technique to identify the fault location using the correlation of the initial TW arrival times.

The work [25] proposes a travelling–wave–based protection scheme for multi-terminal HVDC transmission lines, incorporating undecimated morphological wavelet decomposition for signal processing. Detecting a fault within the protected zone, the primary relay issues a trip command to the corresponding hybrid DC circuit breakers. The scheme also provides a backup mechanism for enhanced reliability.

In ref. [26], the authors presented an improved fault-location scheme rooted in Electromagnetic Time Reversal (EMTR). The method exploits the characteristic frequency of the travelling wave reflected from the fault to determine its position. Its performance was assessed through PSCAD simulations and controlled laboratory experiments, enabling a direct comparison with traditional EMTR techniques. The results demonstrated that the proposed approach performs especially well in complex line configurations and exhibits strong robustness when dealing with high-impedance faults (HIFs).

In ref. [27], the authors developed a method in which a high-resolution data acquisition system captures disturbances and transient events in a designated section of a medium-voltage network. The recorded signals are subsequently analyzed using a post-processing routine based on time-reversal principles, forming the foundation of the FasTR technique for pinpointing event locations. The study demonstrated that a compact, rooftop-mounted unit can reliably identify transient faults in real-time, even in networks with complex configurations.

In ref. [28], the authors introduced a single-ended, phasor-based fault-location (SEPHFL) framework that combines multiple independent algorithms. Using actual digital fault recorder (DFR) measurements, the method aggregates the outputs of different SEPHFL techniques to derive both precise point estimates of the fault location and broader search regions. This hybrid strategy enhanced the accuracy of the estimated distances and, simultaneously, provided practical guidance for narrowing inspection areas along the transmission line.

High-impedance faults (HIFs) are challenging to detect and locate once they exhibit a nonlinear nature and unpredictable behavior. To address this issue, ref. [29] proposed a two-stage data-driven method that combines line-impedance estimation with fault-location comparison, achieving high identification accuracy in tests on the IEEE 33-bus system. In turn, ref. [30] developed an automated scheme for real-time detection, classification, and localization of HIFs in 13.8 kV delta-connected distribution networks, providing utilities with timely diagnostic information to support emergency maintenance.

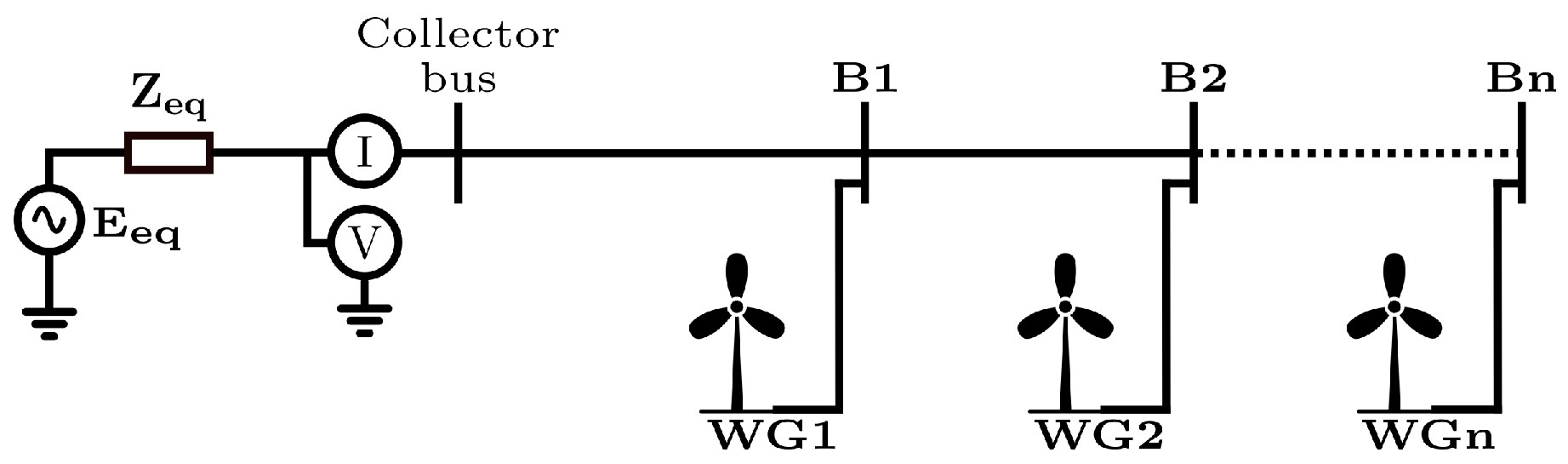
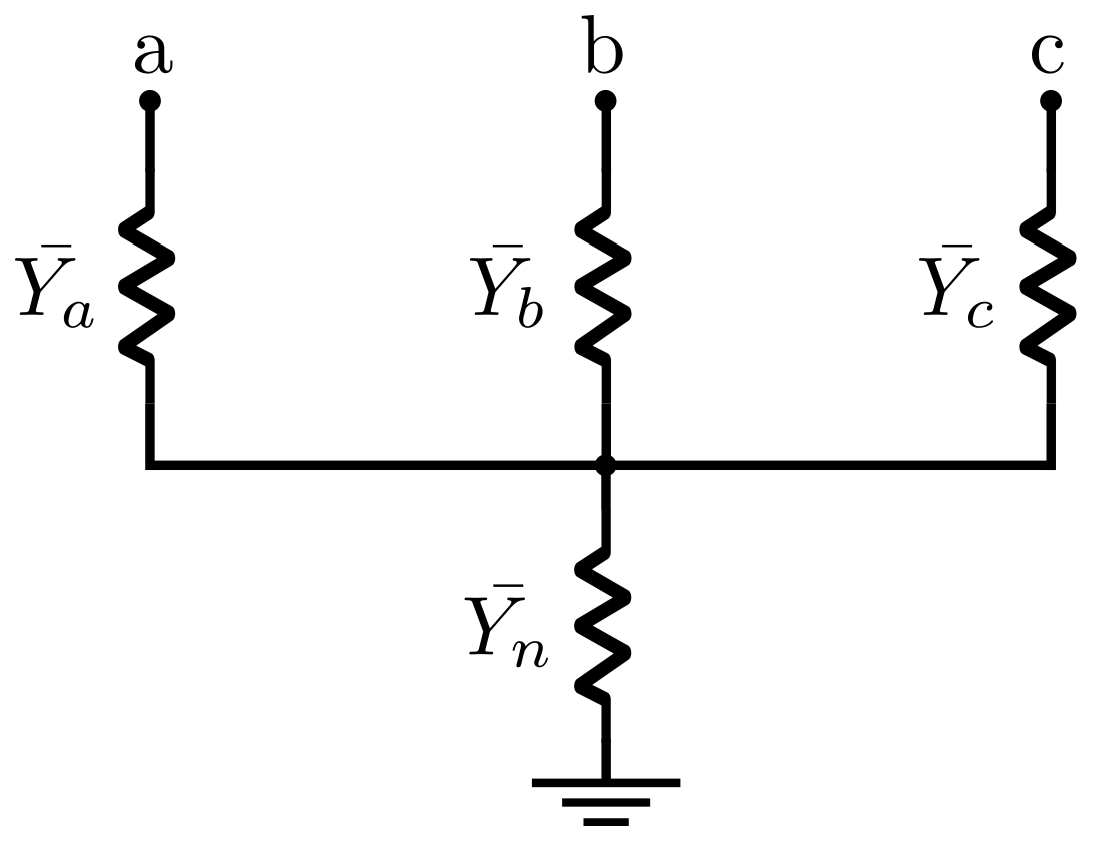
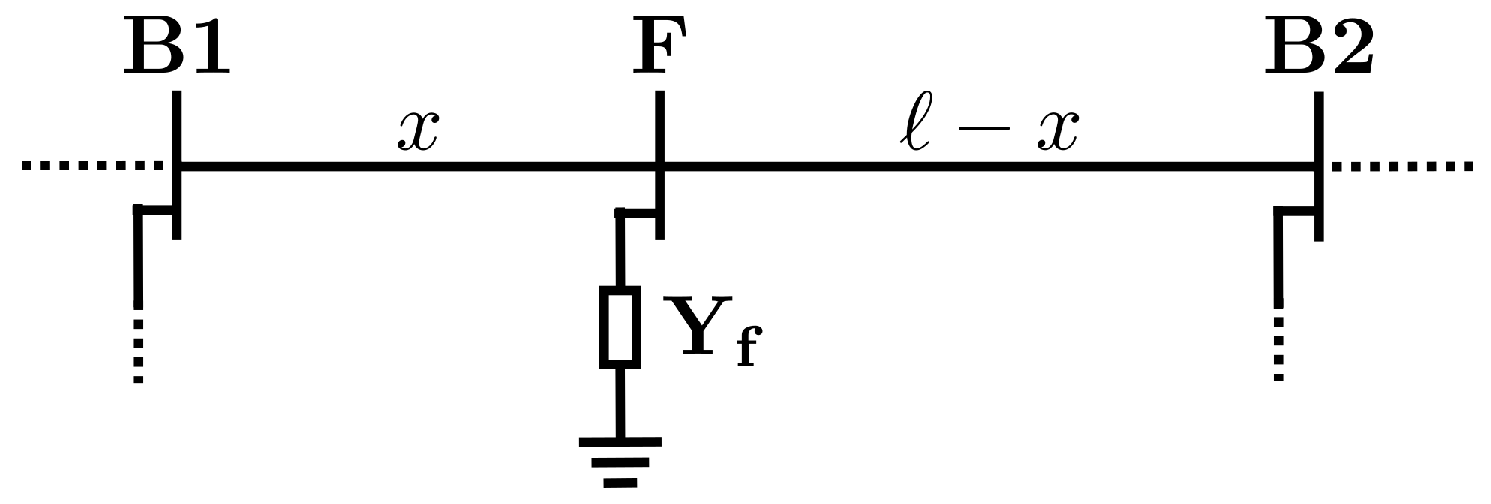
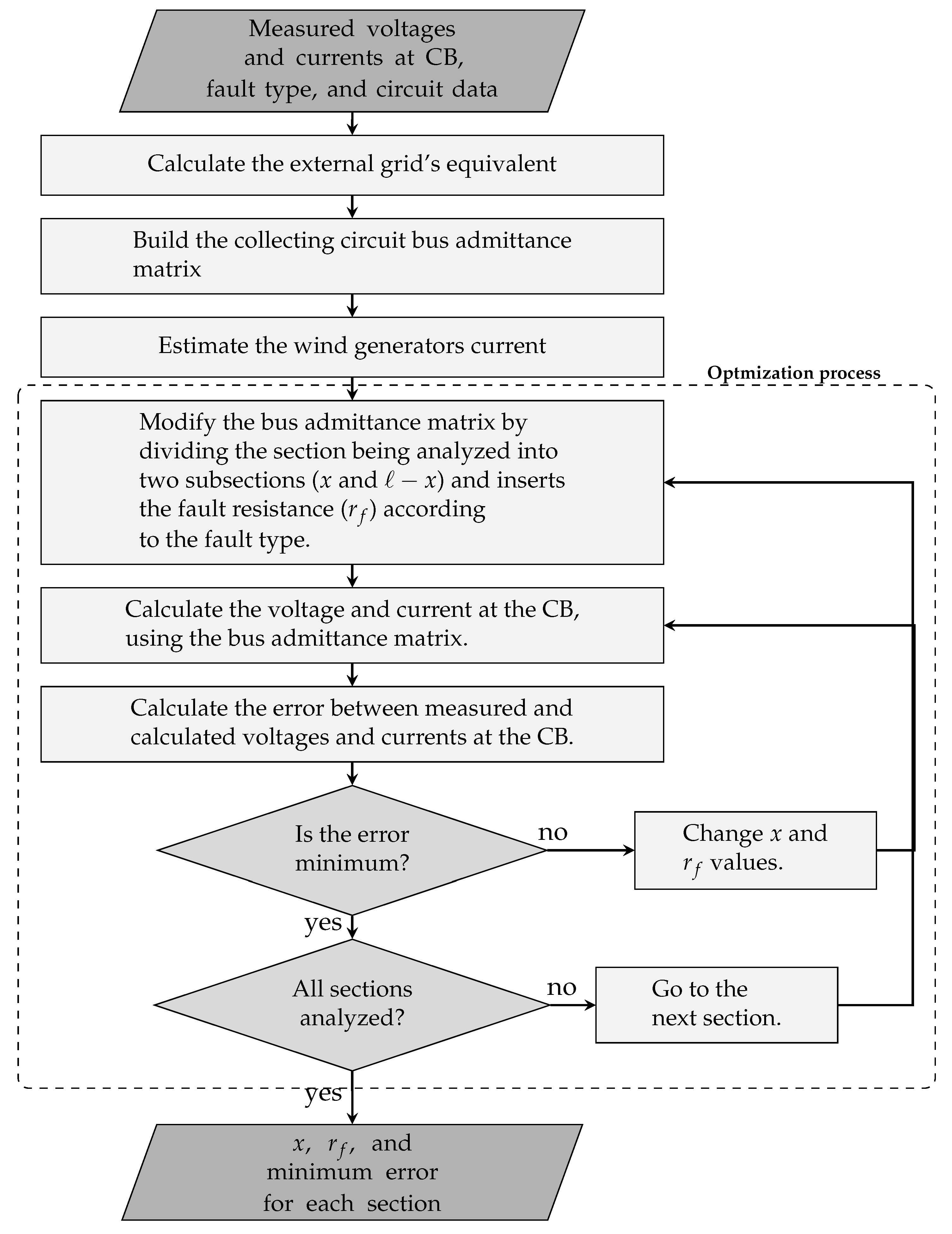
Therefore, this work proposed a fault location algorithm specifically designed for wind farms, addressing critical challenges that have not been thoroughly investigated in the existing literature. The proposed methodology uses current and voltage phasors measured only at the collecting bus (CB). These phasors were used as inputs to a PSO algorithm, which efficiently determined the faulted segment, avoiding multiple locations, and estimated the fault impedance. According to the literature surveyed, no previously published method has comprehensively addressed these fault location issues in such detail for onshore wind farms.

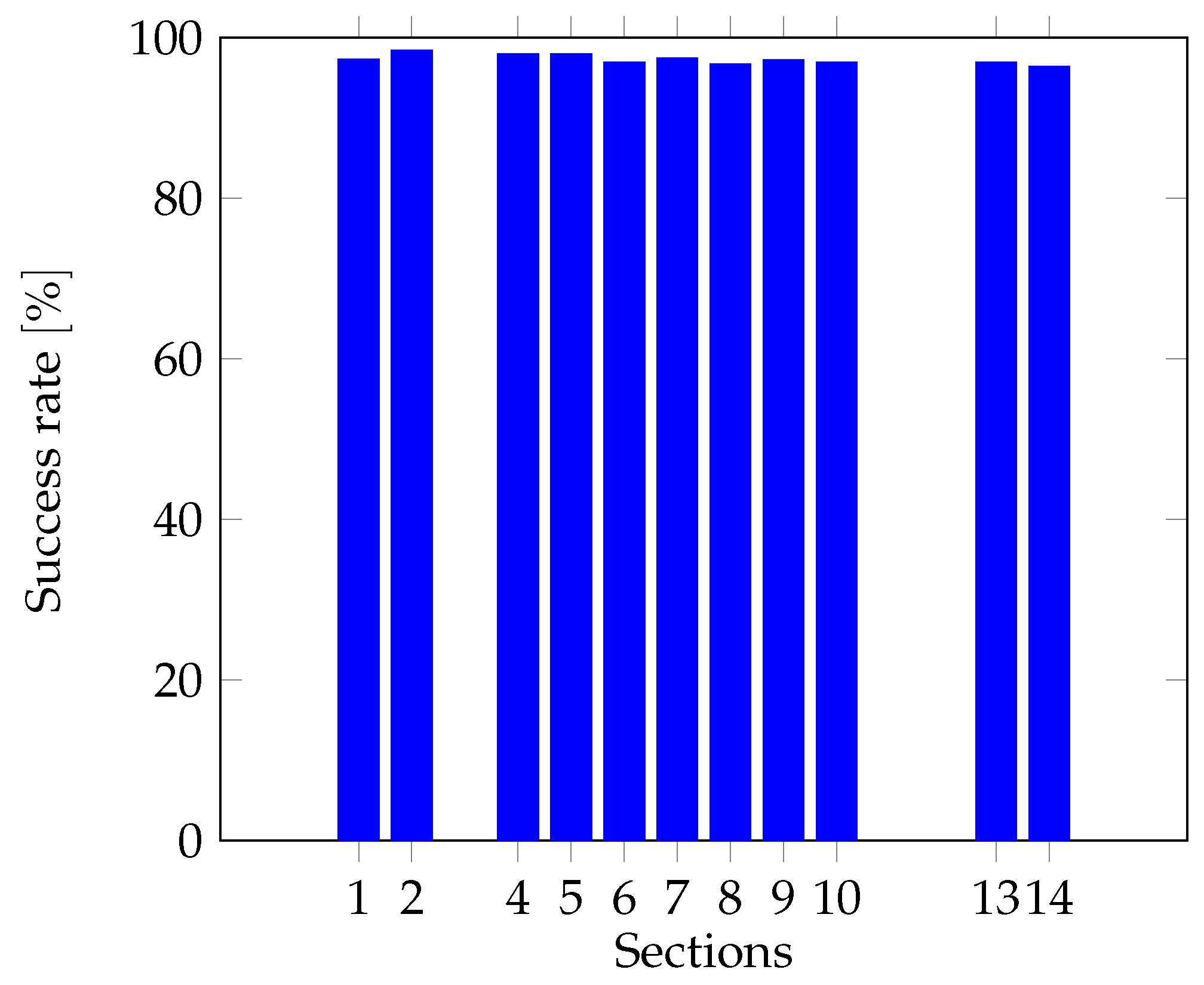
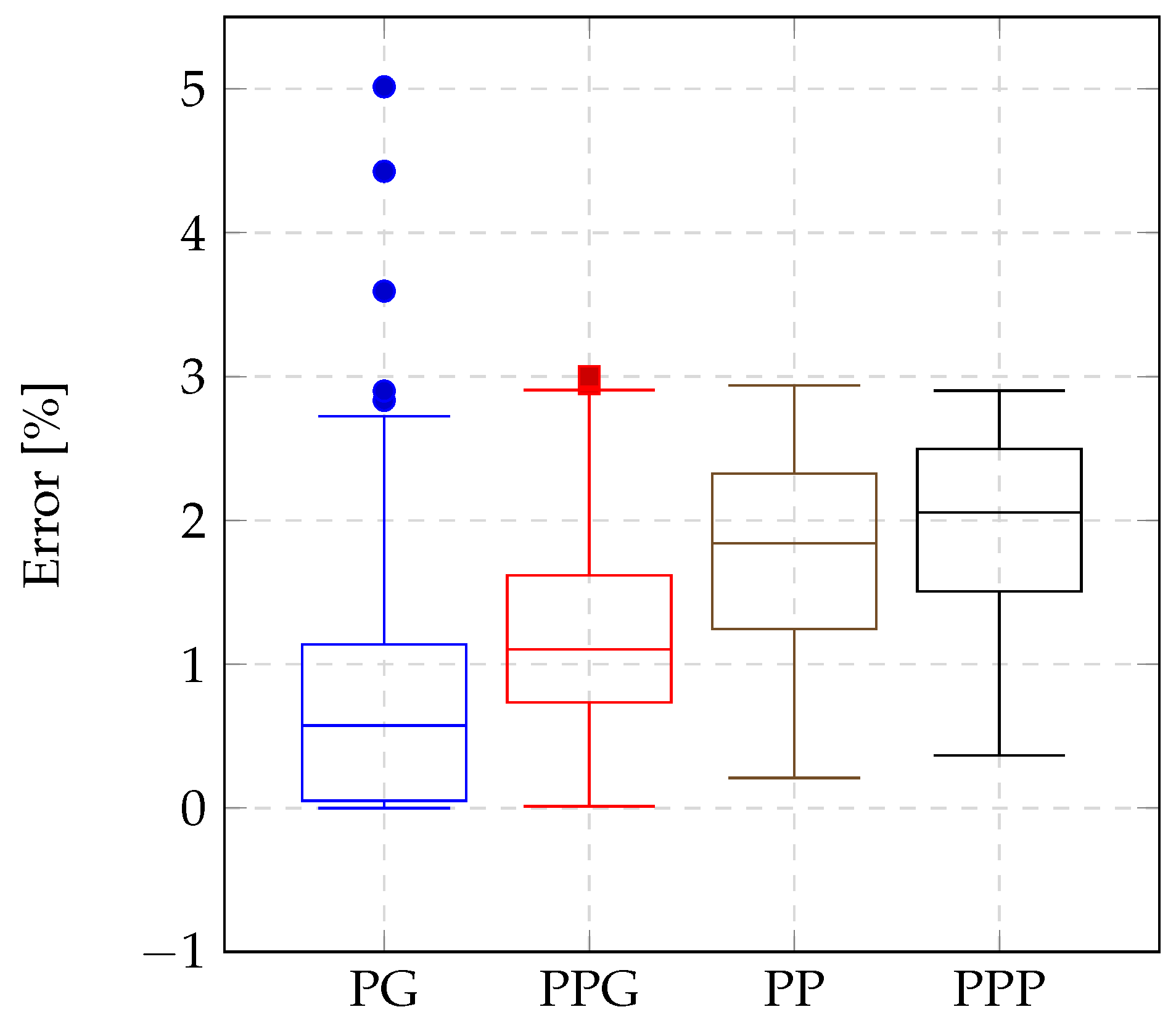
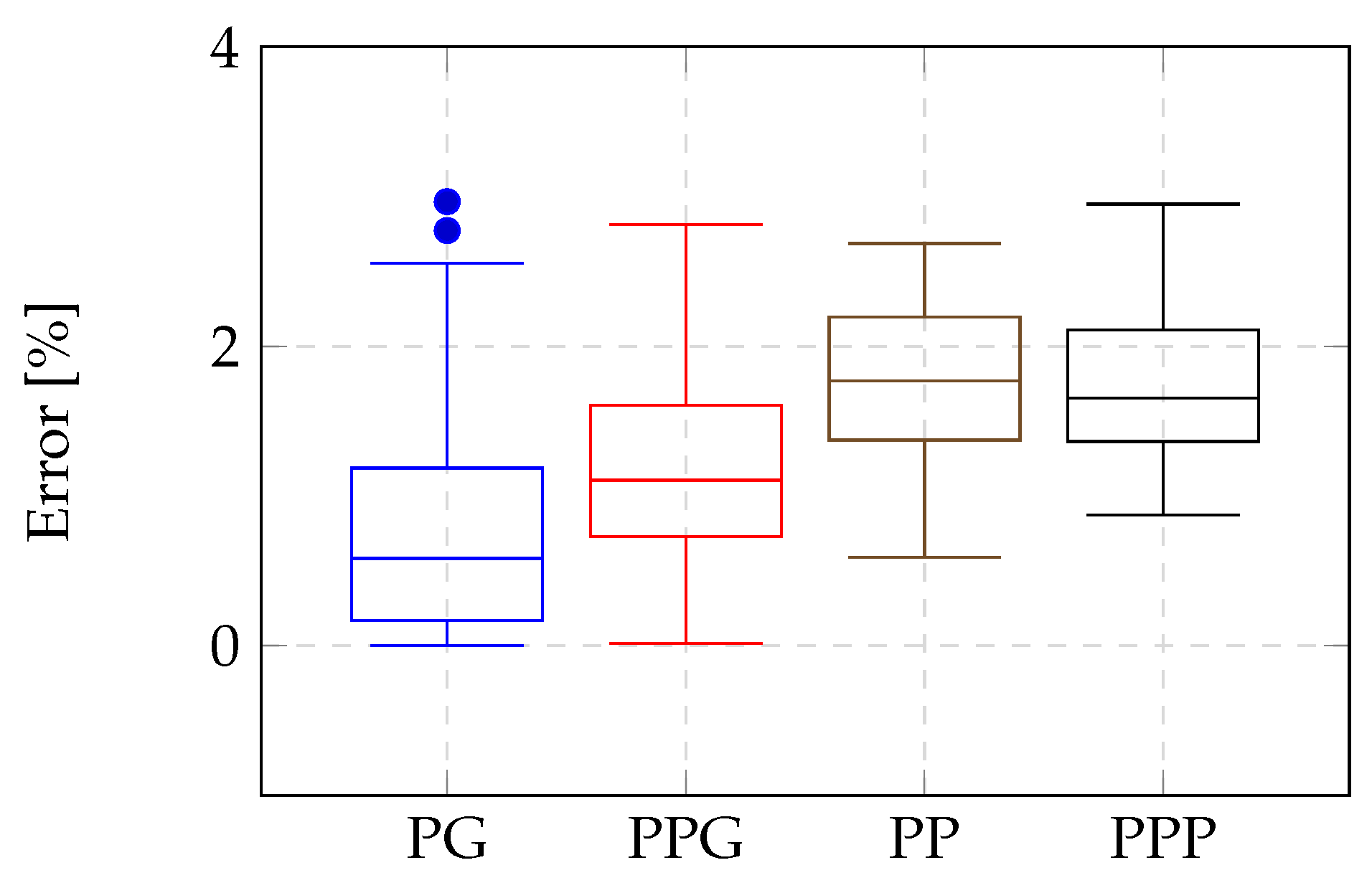
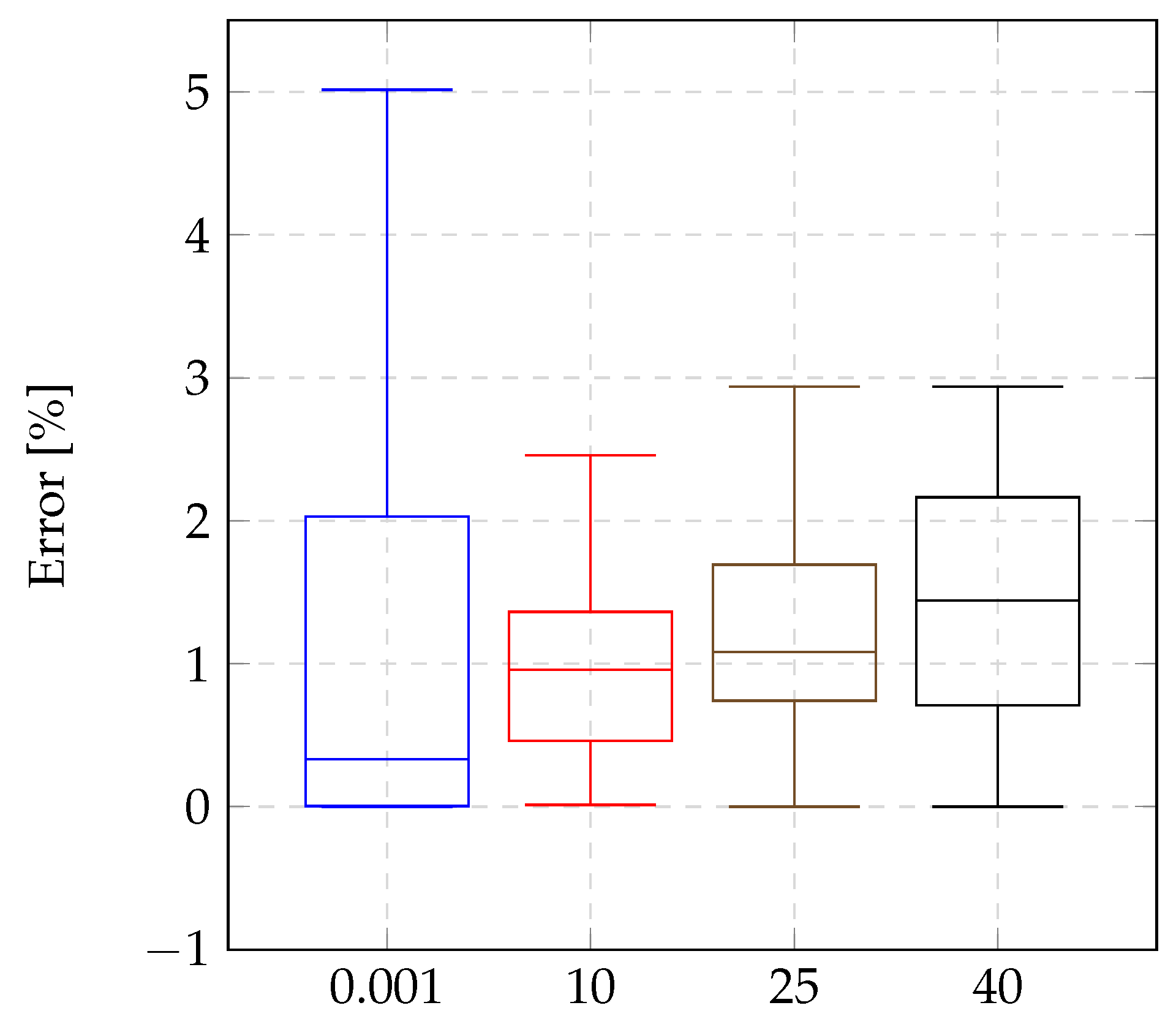
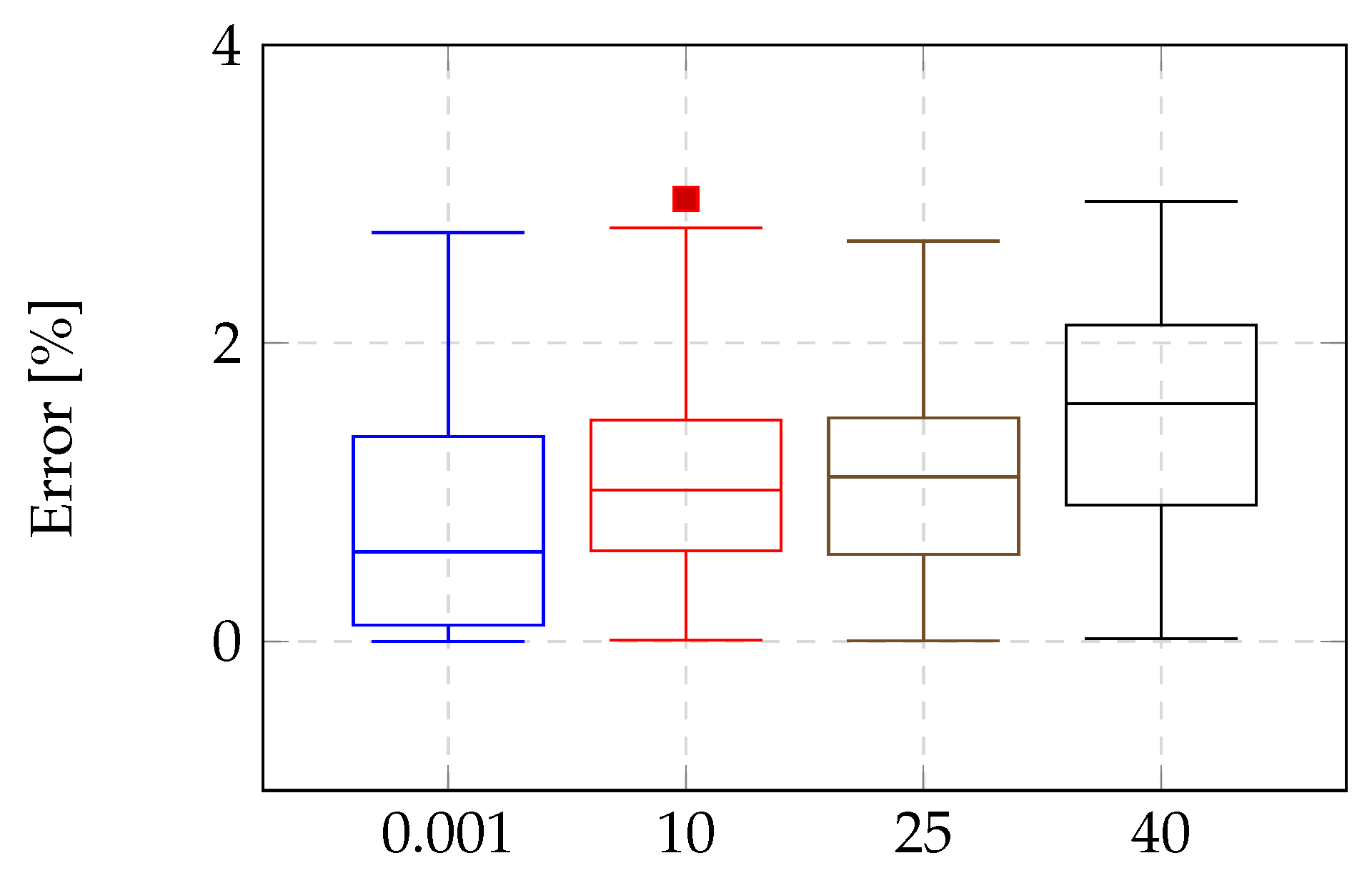
The authors validated the proposed method through 3456 fault simulations (1728 cases without errors in phasors and line section parameters and 1728 cases considering errors) conducted on a 34.5 kV wind farm circuit using the PSCAD/EMTDC v5.0.2 simulation software. The results showed that the algorithm consistently achieved high accuracy in pinpointing fault locations across all fault types, even under challenging conditions such as high-resistance faults, phasor estimation errors, and mismatches in overhead and underground line parameters.

Table 1. Comparison of fault location methods.

Reference	Method	Application	Main Characteristic	Limitation
[11,20,22,23,24,25,26]	Traveling Waves	Transmission Lines	High-speed location	Not robust for branched topologies of data collection networks
[5,6,7,8,9,10,14]	Machine learning	Transmission Lines, Simple Radial Networks	Good rating and location	Degraded performance in complex topologies with branching
[10,12,13,18]	Phasor, compressed sensing and ranging equation, multi-method, optimization	Onshore wind farm collector circuits, and photovoltaic generation	Enhanced localization in systems with Distributed Generation	It does not consider the topological complexity of branched circuits with multiple estimation
[19,27,28,29,30]	Time Reversal and HIF	Distribution Networks	Effective location	Focus on high-impedance faults or single lines
[16,17]	Phasor via Optimization	Transmission Lines and Lines with Series Compensation	It determines the location by minimizing phasor errors	Requires synchronized measurements from both ends
Proposed method	Optimization	Onshore wind farm collector circuits.	High precision and addresses multiple estimation	Depends on the estimation of wind generators injected current

presents a summary of the main characteristics of the approaches reported in the literature alongside the method developed in this work.

1.2. Manuscript Structure

The structure of this article is as follows. Section 1 reviews the main fault-location techniques reported in the literature. Section 2 describes the proposed method for locating faults in wind farms. Section 3 discusses the results obtained for different fault types, resistances, locations, and variations in cable parameters. Section 4 provides brief remarks on potential practical applications of the method. Finally, Section 5 presents the conclusions and recommendations derived from this study.

2. Methodology

The literature shows a wide range of fault-location techniques, including AI-based approaches, travelling-wave methods, and impedance-based solutions. Recently, machine learning (ML) has gained attention for processing the large volumes of data obtained from measurement and protection devices, allowing faults to be located across the network. Despite these advances, ML-based strategies often demand substantial computational effort, and the practical time required for field crews to locate the fault in the system can still be significant.

There is, therefore, a clear need for fault-location methods that reduce computational burden, rapidly pinpoint fault positions, and support faster service restoration. In this context, this work presents a novel algorithm designed explicitly for fault location in onshore wind farms. The method identifies the faulted point within the electrical network and provides an estimate of the corresponding fault resistance. The subsequent sections provide a detailed description of the proposed approach.

2.1. Data Processing

The input data are collected at the circuit breaker (CB), where current and voltage signals are measured for both pre-fault and post-fault conditions. These signals undergo a filtering stage designed to suppress noise and harmonic distortion. Once filtered, the algorithm estimates the voltage and current phasors through a data processing routine that combines Prony’s method and the Fast Fourier Transform (FFT). Prony’s approach is employed to eliminate aperiodic components that may impact the transient response of the measured signals. The post-fault phasors are obtained from the first three cycles following the fault occurrence [31], and they are subsequently used as inputs to the fault location algorithm.

The signals are sampled at 64 points per 60 Hz cycle. The filter parameters were defined with a passband cutoff frequency of 90 Hz and a maximum attenuation of 3 dB, while the stopband cutoff frequency was set to 1920 Hz with a minimum attenuation of 40 dB. The exact fault instant determines the time window to isolate the pre- and post-fault data segments.

2.2. Modeling of Systems Components

The proposed fault-location approach considers various electrical component models within the system to accurately determine the fault position. The following sections describe the modeling of each element, ensuring the method’s applicability under realistic operating conditions. Figure 1 is presented to assist in understanding the structure and operation of the proposed methodology.

2.2.1. Equivalent Network

The external portion of the electrical network, beyond the wind farm’s circuit breaker (CB), is modeled as an equivalent circuit composed of an ideal voltage source in series with positive- and zero-sequence impedances.

To compute the equivalent source voltage and impedance, the method uses the voltage and current phasors measured at the CB in both pre-fault and post-fault conditions. From these quantities, the positive-sequence source voltage $\dot{E}eq1$ and impedance $\overline{Z}eq1$ are obtained by solving the system of equations in (1).

$$\begin{array}{c}\hfill {\dot{V}}_{CB1-pre}^m={\dot{E}}_{eq1}-{\overline{Z}}_{eq1}{\dot{I}}_{CB1-pre}^m\\ \hfill {\dot{V}}_{CB1-post}^m={\dot{E}}_{eq1}-{\overline{Z}}_{eq1}{\dot{I}}_{CB1-post}^m\end{array}$$

(1)

The zero sequence voltage at the CB bus is calculated according to (2) as follows:

$$\begin{array}{c}\hfill {\dot{V}}_{CB0-post}^m=-{\overline{Z}}_{eq0}{\dot{I}}_{CB0-post}^m\end{array}$$

(2)

where ${\overline{Z}}_{eq0}$ is the equivalent zero sequence impedance, ${\dot{V}}_{CB1-pre}^m$ and ${\dot{V}}_{CB1-post}^m$ are, respectively, the pre- and post-fault positive sequence voltages measured at the CB. ${\dot{I}}_{CB1-pre}^m$ and ${\dot{I}}_{CB1-post}^m$ are, respectively, the pre- and post-fault positive sequence currents measured at the CB. ${\dot{V}}_{CB0-post}^m$ and ${\dot{I}}_{CB0-post}^m$ are, respectively, the post-fault zero sequence voltage and current measured at the CB.

2.2.2. Fault Model

In this study, the fault representation illustrated in Figure 2 is adopted. The model is capable of describing all fault types through appropriate adjustments of the fault admittance parameters. A primitive admittance matrix for a general fault condition was formulated, as shown in (3), in which each fault type is defined by setting certain admittance terms to zero. For example, in a phase-A-to-ground fault, $\overline{Y_b}$ and $\overline{Y_c}$ are set to zero, $\overline{Y_n}$ is assigned a large value of $1\times {10}^6$, and $\overline{Y_a}$ is taken as the inverse of the chosen fault resistance. The analysis covers single-line-to-ground, double-line-to-ground, line-to-line, and three-phase fault conditions.

$${\mathbf{Y}}_{\mathbf{f}}=\left[\begin{array}{ccc}\overline{Y_a}-{\displaystyle \frac{{\overline{Y_a}}^2}{\overline{Y_t}}}& -{\displaystyle \frac{\overline{Y_a}\overline{Y_b}}{\overline{Y_t}}}& -{\displaystyle \frac{\overline{Y_a}\overline{Y_c}}{\overline{Y_t}}}\\ -{\displaystyle \frac{\overline{Y_b}\overline{Y_a}}{\overline{Y_t}}}& \overline{Y_b}-{\displaystyle \frac{{\overline{Y_b}}^2}{\overline{Y_t}}}& -{\displaystyle \frac{\overline{Y_b}\overline{Y_c}}{\overline{Y_t}}}\\ -{\displaystyle \frac{\overline{Y_c}\overline{Y_a}}{\overline{Y_t}}}& -{\displaystyle \frac{\overline{Y_c}\overline{Y_b}}{\overline{Y_t}}}& \overline{Y_c}-{\displaystyle \frac{{\overline{Y_c}}^2}{\overline{Y_t}}}\end{array}\right]$$

(3)

where, $\overline{Y_t}=\overline{Y_a}+\overline{Y_b}+\overline{Y_c}+\overline{Y_n}$.

2.2.3. Wind Farm’s Collecting Circuit

The proposed method constructs the bus admittance matrix to represent the wind farm collecting circuit. This matrix integrates all grid components, such as line sections, equivalents, and transformers, by representing them as primitive admittance matrices.

In the case of line sections, the method uses the $\pi$-equivalent transmission line model to represent the line series impedance and shunt admittances. In this work, the line sections are balanced and are considered to have the same self and mutual impedance and admittance among phases. It is worth mentioning that the method solves the equations in the phase domain, allowing for unbalanced line sections.

The method constructs the bus admittance matrix by solving for ${\mathbf{Y}}_{\mathbf{bus}}$, where $\mathbf{A}$ is the incidence matrix of the nodes and ${\mathbf{Y}}_{\mathbf{pr}}$ is the primitive admittance matrix of all components.

$${\mathbf{Y}}_{\mathbf{bus}}={\mathbf{A}}^T{\mathbf{Y}}_{\mathbf{pr}}\mathbf{A}$$

(4)

The node incidence matrix is obtained by solving (5), where it is constructed by the following rule [32,33]:

• $a_{ij}=1$ when the current in branch i flows out of node j;
• $a_{ij}=-1$ when the current in branch i flows into node j;
• $a_{ij}=0$ when branch i is not connected to node j.

The primitive admittance matrices of the components are 3 × 3 matrices. Therefore, instead of using the values 1, −1, and 0 as outlined in the incidence matrix rule, this method represents the connections between branches and nodes using the identity matrix $\mathbf{I}$, the negative identity matrix $-\mathbf{I}$, and a 3 × 3 zero matrix.

$$\mathbf{A}=\begin{array}{c}\\ {\mathbf{Y}}_{\mathbf{eq}}\\ {\mathbf{Y}}_{\mathbf{CB}-\mathbf{B}\mathbf{1}}\\ ⋮\\ {\mathbf{Y}}_{\mathbf{B}(\mathbf{n}-\mathbf{1})-\mathbf{Bn}}\\ ⋮\\ {\mathbf{Y}}_{\mathbf{Bn}-\mathbf{WGn}}\end{array}\begin{array}{c}\begin{array}{cccccc}CB & B1 & \dots & Bn & \dots & WGn \end{array}\\ \begin{array}{c}\left[\begin{array}{cccccc}\mathbf{I} & 0 & \dots & 0 & \dots & 0 \\ \mathbf{I} & -\mathbf{I} & \dots & 0 & \dots & 0 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 0 & 0 & \dots & -\mathbf{I} & \dots & 0 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 0 & 0 & \dots & \mathbf{I}& \dots & -\mathbf{I} \end{array}\right]\end{array}\end{array}$$

(5)

The primitive admittance matrix of all components is constructed by putting the 3 × 3 admittance matrix of each component into the main diagonal of ${\mathbf{Y}}_{\mathbf{pr}}$, as shown in (6).

$${\mathbf{Y}}_{\mathbf{pr}}=\left[\begin{array}{cccc}{\mathbf{Y}}_{\mathbf{eq}}& 0& \dots & 0\\ 0& {\mathbf{Y}}_{\mathbf{CB}-\mathbf{B}\mathbf{1}}& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & {\mathbf{Y}}_{\mathbf{Bn}-\mathbf{WGn}}\end{array}\right]$$

(6)

Then, the method builds the bus admittance matrix by solving (7):

$${\mathbf{Y}}_{\mathbf{bus}}={\mathbf{A}}^T{\mathbf{Y}}_{\mathbf{pr}}\mathbf{A}$$

(7)

2.2.4. Wind Turbine Model

Figure 3 shows the wind turbines modeled as current sources, which inject a constant post-fault current. The post-fault current is unknown since no measurements are available at the wind generators’ (WG) buses.

Thus, a method to estimate the post-fault current provided by the wind generators using the positive sequence voltage measured at the CB was proposed. The method utilizes the positive sequence voltage when the wind generator is of a Full Converter type, which injects only positive sequence current, even in unbalanced fault scenarios. ${\mathbf{I}}_{\mathbf{WG}}$ is the three-phase current vector.

Section 2.3 gives a detailed explanation of the proposed estimation method.

2.3. Wind Turbine Current Estimation Algorithm

The magnitude and angle of each sequence current injected by the wind generators during a fault event are estimated by analyzing the corresponding sequence voltage magnitude, measured at the wind farm’s CB, against the magnitude and angle of the current injected by a simulated wind generator model provided by the manufacturer.

Several scenario conditions to evaluate the current magnitude and angle of the wind generator were analyzed. These scenarios include variations in generation levels and different types of faults with different resistances. As a result, a specific curve was generated for each fault type, showing the relationship between current magnitude and angle versus the magnitude of each sequence voltage at the CB. A single-phase fault in phase AG, for instance, produced one curve, while a fault in phase BG resulted in another, and so on until all ten curves were completed. Additionally, the angle of the sequence voltage at the CB was a reference for the current angles provided by the wind turbines.

According to ref. [34], the voltage measured at the wind turbine terminal is typically used as the reference for the current injected by the wind turbine during fault events. However, in practical scenarios, direct measurements of voltage and current at the turbine terminals may not be available. In such cases, it becomes necessary to estimate the injected current using the voltage measurements at the CB. Consequently, the current angle is referenced to the voltage angle at the CB, which may differ from the actual voltage angle at the wind turbine terminal. It is important to emphasize that referencing the injected current angle to the CB’s voltage angle does not contravene the grid code requirements established for the wind turbine. This is because the terminal voltage of the wind turbine is also ultimately referenced to the CB’s voltage.

Afterwards, all curves for each fault type were consolidated into a single curve to reduce computational effort during fault location. Thus, for instance, the single-phase faults (AG, BG, CG) are merged into a single representative curve, rather than the initial three individual curves. This same consolidation was applied to two-phase, two-phase-to-ground, and three-phase faults.

Analyzing the curves reveals an exponential relationship between the injected current magnitude and angle, and the magnitude of the positive sequence CB voltage during a fault. Thus, (8) presents the mathematical model representing the behavior of the curves.

$$\begin{array}{c}\hfill \left|{\dot{I}}_{WG}^{012}\right|=a+b{e}^{c\left|{\dot{V}}_{CB012-post}^m\right|}\\ \hfill \angle \left({\dot{I}}_{WG}^{012}\right)=f+g{e}^{h\left|{\dot{V}}_{CB012-post}^m\right|}\end{array}$$

(8)

where, $\left|{\dot{I}}_{WG}^{012}\right|$ and $\angle \left({\dot{I}}_{WG}^{012}\right)$ are, respectively, the magnitude and angle of the wind generator sequence current injected during the fault, and $a,b,c,f,g,h$ are constants of the exponential function. Each sequence is considered separately from the others.

Section 3.2 presents the curves obtained for each fault type.

2.4. Procedure to Locate the Fault

The proposed fault-location method is based on the technique originally presented in ref. [16]. That method, developed by one of the authors of the present work, was designed for locating faults in series-compensated transmission lines using voltage and current measurements from both line terminals. In contrast, the new approach requires only voltage and current phasors measured at the circuit breaker (CB), along with the estimated currents injected by the wind turbines during the fault, the topology of the wind farm collector system, and the corresponding cable parameters. Additionally, the algorithm requires the fault type and the instant of occurrence as inputs, which can be obtained from intelligent electronic devices (IEDs) or a dedicated detection algorithm.

Once the input data are acquired, the algorithm computes the equivalent representation of the external grid by solving (1) and (2). It then constructs the bus admittance matrix of the collector system based on the network topology and cable parameters, as described in Section 2.2.3.

Next, the algorithm determines the positive-sequence voltage phasor from the phase voltages measured at the CB. Using this information, it retrieves from known current curves the magnitude and phase angle of the currents injected by the wind generators, as detailed in Section 2.3. It is worth noting that all wind turbines are assumed to inject identical current magnitudes during a fault. As demonstrated in Section 3, this approximation does not significantly impact the precision of the results.

Afterward, the fault-location routine is initiated. In this stage, all collector system sections are analyzed to identify the faulted segment through an optimization process executed for each section.

The fault-location analysis for a given section is carried out by modifying the bus admittance matrix. The line section under analysis is divided into two subsections connected through an intermediate node, denoted as node F, where the fault is represented by the admittance matrix ${\mathbf{Y}}_{\mathbf{f}}$. The elements of ${\mathbf{Y}}_{\mathbf{f}}$ are defined according to the fault type and resistance. For illustration, Figure 4 presents the collector circuit section between nodes B1 and B2, of total length ℓ, containing a fault located at a distance x from node B1.

For example, for an AG fault, the matrix ${\mathbf{Y}}_{\mathbf{f}}$ is arranged as follows:

$${\mathbf{Y}}_{\mathbf{f}}=\left[\begin{array}{ccc}{\displaystyle \frac{1}{r_f}}& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]$$

(9)

Then, the fault location routine initiates the optimization process to minimize the errors between measured and calculated voltages and currents at the CB, having x and $r_f$ as variables to be optimized. Thus, in this context, the PSO algorithm, which minimizes errors due to its superior performance, was used. Alternative methods, including Pattern Search and Genetic Algorithm, were also evaluated; however, for the problem addressed in this study, the PSO approach consistently achieved higher accuracy and faster convergence than the other techniques.

PSO [35] is a population optimization algorithm inspired by the collective behavior observed in flocks of birds and schools of fish. Its basic principle consists of a set of particles that move through the search space in search of the best solution, updating their positions according to individual and collective experiences. Each particle adjusts its speed based on two components: the best point already found by itself and the best point identified by the group. This mechanism of cooperation and smooth competition allows PSO to balance exploration and exploitation of the solution space. Due to its simplicity of implementation, low computational cost, and good ability to find satisfactory solutions in complex and multimodal problems, PSO has become widely used in areas such as electrical engineering, artificial intelligence, power systems, and model parameter optimization. In the application of PSO to the problem of fault location in wind farms, the position of the particles is used to determine the fault resistance and the position of occurrence of the fault in the network under evaluation. And, in each iteration, each particle is evaluated through the simulation of a short circuit defined from the parameters assigned to it (resistance and fault position). The calculated values are compared with the measurements available at the collector bus, calculating the error from the difference modulus between the values for the residual phase voltages and the short-circuit currents.

When analyzing a section, the optimization process calculates the phase-sequence voltage ${\mathbf{V}}_{\mathbf{CB}-\mathbf{post}}^{\mathbf{c}}$ and current ${\mathbf{I}}_{\mathbf{CB}-\mathbf{post}}^{\mathbf{c}}$ at the CB by solving (10) and (11).

$$\left[\begin{array}{c}{\mathbf{V}}_{\mathbf{CB}-\mathbf{post}}^{\mathbf{c}}\\ {\mathbf{V}}_{\mathbf{B}\mathbf{1}}^{\mathbf{c}}\\ ⋮\\ {\mathbf{V}}_{\mathbf{Bn}}^{\mathbf{c}}\\ ⋮\\ {\mathbf{V}}_{\mathbf{WGn}}^{\mathbf{c}}\\ {\mathbf{V}}_{\mathbf{F}}\end{array}\right]={\mathbf{Y}}_{\mathbf{bus}}{(x,r_f)}^{-1}\left[\begin{array}{c}{\mathbf{I}}_{\mathbf{eq}}\\ 0\\ ⋮\\ 0\\ ⋮\\ {\mathbf{I}}_{\mathbf{WGn}}\\ 0\end{array}\right]$$

(10)

$${\mathbf{I}}_{\mathbf{CB}-\mathbf{post}}^{\mathbf{c}}={\mathbf{I}}_{\mathbf{eq}}-{\mathbf{Y}}_{\mathbf{eq}}{\mathbf{V}}_{\mathbf{CB}-\mathbf{post}}^{\mathbf{c}}$$

(11)

where ${\mathbf{Y}}_{\mathbf{bus}}(x,r_f)$ is the modified ${\mathbf{Y}}_{\mathbf{bus}}$ having the divided line section with variables x and $r_f$. ${\mathbf{I}}_{\mathbf{eq}}$ is the phase-sequence current injected by the external grid’s equivalent. ${\mathbf{I}}_{\mathbf{WGn}}$ is the estimated current provided by the $n^{th}$ wind generator. ${\mathbf{V}}_{\mathbf{CB}-\mathbf{post}}^{\mathbf{c}}$ is the calculated post-fault voltages in phase-sequence at the CB. ${\mathbf{I}}_{\mathbf{CB}-\mathbf{post}}^{\mathbf{c}}$ is the calculated post-fault currents in phase-sequence at the CB.

Then, the error between the phase-sequence voltages and currents is calculated by solving the following objective function (12) (the indexes c and m state for calculated and measured, respectively, and n is the index representing the phase-sequences r, s, and t):

$$\begin{array}{cc}\hfill f_{obj}& ={\displaystyle \frac{{\sum }_{n=r}^t\left(\left|{\dot{V}}_{CBn-post}^c-{\dot{V}}_{CBn-post}^m\right|\right)}{max\left|{\mathbf{V}}_{\mathbf{CB}-\mathbf{post}}^{\mathbf{m}}\right|}}\hfill \\ \hfill & +{\displaystyle \frac{{\sum }_{n=r}^t\left(\left|{\dot{I}}_{CBn-post}^c-{\dot{I}}_{CBn-post}^m\right|\right)}{max\left|{\mathbf{I}}_{\mathbf{CB}-\mathbf{post}}^{\mathbf{m}}\right|}}\hfill \end{array}$$

(12)

Subjected to the following constraints:

$$\begin{array}{c}{10}^{-6}\le x/\ell \le 1\hfill \\ {10}^{-6}\le r_f\le 1000 \Omega \hfill \end{array}$$

At the end of the section analysis, the optimization process provides the fault location routine with the objective-function value and the corresponding estimates of x and $r_f$ that yield its minimum. This procedure is repeated until all sections have been analyzed.

Upon completing the analysis across all sections, the fault location routine outputs the results to the operator. These results include the objective function value for each section, along with the corresponding x and $r_f$ estimates. Based on this information, the operator may dispatch the maintenance team to the section with the lowest objective value or select an alternative section if deemed appropriate.

Figure 5 presents the flowchart of the proposed methodology.

3. Results

In this section, the test results used to evaluate the fault-location approach developed in this study are discussed. This method was tested under various fault conditions by applying several fault cases to a wind farm’s circuit. The cases were constructed by altering the fault instant, type, resistance, section, and distance within the sections, considering the wind generators injecting 10% and 75% of their rated power. All the variations resulted in 1728 cases. Errors were also introduced in the measured voltage and current phasors, as well as the line parameters, to evaluate the method’s sensitivity, running all 1728 cases under these conditions.

3.1. Modeled System Description

The wind farm’s electrical grid, depicted in Figure 6, was used to validate the proposed method. This electrical grid, which was modeled in PSCAD/EMTDC v5.0.2 software, is a 34.5 kV collecting circuit of an existing wind farm installed in Rio Grande do Norte, Brazil. The collecting circuit consists of five 4.2 MW wind turbines, each connected to a 5.15 MVA 0.72/34.5 kV step-up transformer, that together with other 24 collecting circuits deliver power to a 500 kV transmission system through two 560 MVA 500/34.5/34.5/13.8 kV four-winding transformers. The method treats the electrical system beyond the CB, where the analyzed circuit connects, as an external grid. Therefore, it calculates the equivalent of this external grid, as detailed in Section 2.2.1.

The collecting circuit is formed by aerial and underground sections with positive and zero sequence parameters shown by

Table 2. Line sections’ parameters.

Section	Type	${\overline{\mathit{Z}}}_0$ [Ω/km] ${\overline{\mathit{Y}}}_0$ [μS/km]	${\overline{\mathit{Z}}}_1$ [Ω/km] ${\overline{\mathit{Y}}}_1$ [μS/km]
1	Aerial	0.284 + j1.859	0.110 + j0.375
		j1.638	j4.436
2, 3, 4, 5,	Aerial	0.501 + j1.901	0.327 + j0.418
7, 8, 9		j1.569	j3.963
6, 10, 11,	Underground	0.569 + j2.473	0.391 + j0.137
12, 13, 14		j66.512	j66.512

.

3.2. Estimated Wind Generators’ Injected Current Curve

As part of the fault-location procedure, the algorithm incorporates the current injected by the wind turbines during the fault as an input. The wind generator model considered was a Vestas V150-4.2 MW full-converter [36] which inject only positive sequence current during faults. These currents are incorporated into the grid system to compute the phase voltages and the currents at the CB, as explained in Section 2.4.

The modeling details regarding the wind generator is as follows: protection settings and control modes.

• LVRT: The system is designed to keep the turbine connected during voltage sag events. Its control function is activated when the terminal voltage drops to 0.85 pu. From that moment, the converter regulates the current injection, giving priority to reactive current to mitigate the voltage dip.
• DC-Link Chopper: This control regulates the DC-link voltage by dissipating the excess energy that is temporarily not being transferred to the grid.
• Islanding: This control issues a TRIP command to the turbine circuit breaker if the terminal voltage exceeds 1.25 pu within 5 ms, indicating an islanding condition.

The current magnitude is expressed per unit of the wind turbine generator’s loading and voltage. The analysis considers current values corresponding to minimum and maximum wind speed scenarios, representing active power injections of 10% and 75%. Similarly, the same per-unit approach is employed to analyze the current angle associated with the wind turbine generators. The reference for angular measurements is the positive-sequence voltage measured at the CB. All 1728 cases were considered to generate the curves.

Figure 7a presents the magnitude and angle curves for the wind generator’s injected current during phase-to-ground faults (PG), Figure 7b during phase-to-phase-to-ground faults (PPG), Figure 7c during phase-to-phase faults (PP), and Figure 7d during three-phase faults (PPP).

3.3. Optimization Process Setup

The proposed method was executed on a workstation equipped with an Intel^® Core i7-13700H processor (2.4 GHz, 14 cores) and 32 GB of RAM, utilizing MATLAB 2025a^® software.

Table 3. PSO parameters.

Acceleration coefficient	$C_1$	1
	$C_2$	1.5
Inertia factor (weight)	$W_{max}$	0.9
	$W_{min}$	0.4
Number of particles		80
Maximum number of iterations		200
Stopping criterion		<10−6
Random seed		42
Search space	$X_{max}$	[100% 50 Ω]
	$X_{min}$	[0 0]

presents the parameters used in the PSO to execute the method’s optimization routine.

The inertia weight was linearly reduced from 0.9 to 0.4, while the cognitive and social acceleration coefficients were set to 1.0 and 1.5, respectively. The algorithm was executed for a maximum of 200 iterations or terminated earlier (early stopping) when no significant improvement (<10⁻⁶) was observed in 20 consecutive iterations. A fixed random seed (42) was used to ensure reproducibility. With this configuration, the method takes an average execution time of 11.4 s per section.

To illustrate the convergence process, Figure 8 shows the spread performance for locating a 10 $\Omega$ single-phase fault at the middle of the longest section of the collecting circuit.

3.4. Method Evaluation Setup

The method was evaluated under various fault scenarios, considering fault resistances with 0.001 $\Omega$, 10 $\Omega$, 25 $\Omega$, and 40 $\Omega$ for fault types AG, BG, CG, ABG, BCG, and CAG and 0.001 $\Omega$ and 10 $\Omega$ for fault types AB, BC, CA, and ABC. These faults that do not involve the ground typically have low resistance. All the faults were applied in the sections and distances from the CB shown in

Table 4. Fault points.

Section	Bus	Fault Distance from CB [m]
1	$CB-B_1$	0
		1760.35
		3520.70
5	$B_4-B_5$	4000.55
6	$B_5-B_6$	4059.25
8	$B_4-B_8$	4309.78
9	$B_1-B_9$	3628.85
13	$B_8-B_{13}$	4619.01
14	$B_7-B_{14}$	4185.15

. All the faults were also introduced at three different instants: 0, 45, and 90 degrees of the phase A voltage measured at the CB. In all cases, the wind generators were considered to be injecting 10% and 75% of their rated power.

Section 3.5 presents the results produced by the test cases and discusses their implications.

The sensitivity of the method was evaluated by adding zero-mean errors with a standard deviation of 5.0% to the voltage and current phasors measured at the CB, as well as to the line parameters [16]. Thus, all cases were re-executed under this condition. Section 3.6 presents the results and discussion of this sensitivity analysis.

3.5. Method Evaluation

Table 5. Fault location for 10% of wind power injection.

Fault Type	Error [%]	R [Ω]
PG	0.70 ± 0.62	0.001 ± 0
PPG	1.08 ± 0.25	0.001 ± 0
PP	1.60 ± 0.68	0.001 ± 0
PPP	1.73 ± 0.46	0.001 ± 0
PG	0.95 ± 0.87	10 ± 0.10
PPG	1.16 ± 0.60	10 ± 0.03
PP	1.99 ± 0.61	10 ± 0.22
PPP	2.27 ± 0.58	10 ± 0.20
PG	0.26 ± 0.82	25 ± 0.45
PPG	1.78 ± 0.90	25 ± 0.69
PG	1.08 ± 0.48	40 ± 0.16
PPG	0.91 ± 0.72	40 ± 0.52

and

Table 6. Fault location for 75% of wind power injection.

Fault Type	Error [%]	R [Ω]
PG	0.66 ± 0.53	0.001 ± 0
PPG	1.01 ± 0.60	0.001 ± 0
PP	1.35 ± 0.35	0.001 ± 0
PPP	1.45 ± 0.26	0.001 ± 0
PG	1.08 ± 0.47	10 ± 0.16
PPG	1.12 ± 0.72	10 ± 0.14
PP	2.17 ± 0.28	10 ± 0.22
PPP	2.15 ± 0.54	10 ± 0.20
PG	0.18 ± 0.17	25 ± 0.48
PPG	1.44 ± 0.55	25 ± 0.23
PG	1.03 ± 0.75	40 ± 0.30
PPG	1.12 ± 0.56	40 ± 0.35

show the results obtained for the cases applied to the method. The results are organized by fault type, including the mean fault distance error with its standard deviation, and the mean fault resistance with its respective standard deviation. The percentage fault distance errors are relative to the distances depicted in Table 4.

The findings reveal that the level of power injected by the wind generators exerts minimal influence on the fault-location method. Also, the mean error tends to rise with fault resistance for all faults. Despite the rise in errors, the mean error was below 2.27 ± 0.58%, indicating the method’s effectiveness in determining the fault distance.

Thus, for PG faults, the minimum mean error was 0.66 ± 0.53% for fault resistance of 0.001 $\Omega$ and a maximum of 1.08 ± 0.48% for fault resistance of 40 $\Omega$. For PPG faults, the minimum error was 1.01 ± 0.60% for fault resistance of 0.001 $\Omega$ and a maximum of 1.78 ± 0.903% for fault resistance of 25 $\Omega$. For PP faults, the minimum error was 1.35 ± 0.35% for fault resistance of 0.001 $\Omega$ and a maximum of 2.17 ± 0.28% for fault resistance of 10 $\Omega$. For PPP faults, the minimum error was 1.45 ± 0.26% for fault resistance of 0.001 $\Omega$ and a maximum of 2.27 ± 0.58% for fault resistance of 10 $\Omega$.

Figure 9 illustrates how effectively the method located faults in each section within the test wind farm. The PSO-based algorithm computes an objective function for each section, selecting the one with the minimum error as the estimated fault location. In most cases, the algorithm correctly identifies the section where the fault occurred. However, in some cases, it selects a neighboring section. Even in these misclassifications, the estimated fault distance often lies near the actual location, resulting in low distance error despite incorrect section identification.

For instance, consider a fault near the end of Section 1, close to bus B1. If the algorithm identifies Section 2 as the faulted section but the estimated distance places the fault near the boundary with Section 1, the resulting distance error may be low, indicating that, although the section classification is incorrect, the algorithm still provides a precise fault location in terms of physical distance. The percentages in Figure 9 represent the frequency with which the algorithm correctly identified the faulted section, reaching an average value of 97.22%, highlighting the method’s precision and practical reliability for fault diagnosis and maintenance in wind farm systems.

Figure 10 presents the boxplot of fault distance errors for each fault type under 10% wind power generation, aggregating all fault resistances and line sections. Thus, for PG faults, the mean error was 0.75 ± 0.79% with the 25th at 0.05% and the 75th at 1.16%. The blue/red dots represent outliers.

Even the worst outlier was an acceptable 5.01% error. For only five cases the error exceeded the confidence interval. It is noteworthy that this occurred for the phase-to-ground fault, which is the fault type most influenced by the uncertainty arising from the fault resistance. For these cases, the configuration used for the algorithm converged to points where the error was greater than 2.83%. Note that a 5.01% error represents a deviation of 176 m, which is reasonable practice for guiding field teams in locating problems. However, these five cases represent only 1.5% of all simulated cases for the phase-to-ground short circuit. And, increasing the search space to try to make the algorithm converge to points that provide smaller errors would imply a loss of algorithm performance compared to the small gain to be achieved.

For PPG faults, the mean error was 1.23 ± 0.74% with the 25th at 0.74% and the 75th at 1.62%. For PP faults, the mean error was 1.79 ± 0.67% with the 25th at 1.27% and the 75th at 2.94%. For PPP faults, the mean error was 2.00 ± 0.60% with the 25th at 1.52% and the 75th at 2.53%.

Figure 11 presents the boxplot of fault distance errors for each fault type under 75% wind power generation, aggregating all fault resistances and line sections. Thus, for PG faults, the mean error was 0.74 ± 0.64% with the 25th at 0.17% and the 75th at 1.20%. The blue/red dots represent outliers.

Even the worst outlier was an acceptable 2.97% error. For PPG faults, the mean error was 1.18 ± 0.63% with the 25th at 0.73% and the 75th at 1.61%. For PP faults, the mean error was 1.76 ± 0.51% with the 25th at 1.38% and the 75th at 2.21%. For PPP faults, the mean error was 1.82 ± 0.54% with the 25th at 1.37% and the 75th at 2.12%.

As illustrated in Figure 12, the mean error increases with fault resistance, which is an expected behavior. However, the errors observed around 5% may occur due to two possible factors: the optimization algorithm may become trapped in a local minimum, or there may be inaccuracies in the phasor calculation caused by the exponentially decaying transient component, which has a longer decay time.

Therefore, to assess the algorithm’s sensitivity to phasor-calculation errors, a sensitivity analysis was performed as described in Section 3.6.

It can be observed in Figure 13 that, for a 75% power injection from the wind turbines, the errors were reduced due to the higher current injection.

3.6. Sensitivity Analysis

This section reports the results from the sensitivity analysis performed on the method.

3.6.1. Phasor Measurements and Line Parameters Uncertainties

The purpose of this sensitivity analysis is to verify the algorithm’s performance against possible variations in line parameters resulting from inaccuracies in line length registration and ambient temperature effects. A variation of 5% is considered more than sufficient to analyze this aspect in onshore wind farms [12]. It is important to mention that the proposed methodology focuses on wind farms that predominantly have medium-voltage overhead networks. For wind farms where the network is predominantly composed of underground cables, there is also a need to analyze the influence of cable aging on line parameters.

Table 7. Sensitivity analysis—fault location for 10% of wind power injection.

Fault Type	Error [%]	R [Ω]
PG	0.71 ± 0.46	0.001 ± 0
PPG	1.10 ± 0.81	0.001 ± 0
PP	1.61 ± 0.38	0.001 ± 0
PPP	1.76 ± 0.06	0.001 ± 0
PG	1.01 ± 0.72	10 ± 0.23
PPG	1.25 ± 0.66	10 ± 0.10
PP	2.02 ± 0.23	10 ± 0.11
PPP	2.33 ± 0.24	10 ± 0.18
PG	0.33 ± 0.19	25 ± 0.16
PPG	1.87 ± 0.42	25 ± 0.40
PG	1.15 ± 0.10	40 ± 0.18
PPG	0.89 ± 0.68	40 ± 0.40

and

Table 8. Sensitivity analysis—fault location for 75% of wind power injection.

Fault Type	Error [%]	R [Ω]
PG	0.68 ± 0.37	0.001 ± 0
PPG	1.05 ± 0.89	0.001 ± 0
PP	1.70 ± 0.33	0.001 ± 0
PPP	1.88 ± 0.33	0.001 ± 0
PG	1.16 ± 0.53	10 ± 0.28
PPG	1.27 ± 0.67	10 ± 0.20
PP	2.18 ± 0.14	10 ± 0.37
PPP	2.43 ± 0.14	10 ± 0.25
PG	0.21 ± 0.18	25 ± 0.16
PPG	1.86 ± 0.39	25 ± 0.32
PG	1.16 ± 0.81	40 ± 0.16
PPG	1.27 ± 0.57	40 ± 0.69

present the results obtained for the 1728 test cases evaluated using the proposed method. In these simulations, normally distributed errors with zero mean and a standard deviation of 5% were introduced into the measured voltage and current phasors, as well as into the line-section parameters.

The results are organized by fault type, including the mean fault distance error with its standard deviation, and the fault mean resistance with its respective standard deviation. The percentage fault distance errors are relative to the distances shown in Table 4.

The results demonstrate that introducing errors has a minimal impact on the method’s output, highlighting its robustness and precision even in non-ideal scenarios. Similar to cases without errors, the wind generators’ power injection level has a minimal impact on the location of the fault. Also, the mean error tends to rise with fault resistance for all faults. Despite the rise in errors, the mean error was below 2.43 ± 0.14%, evidencing the method’s effectiveness in determining the fault distance.

Thus, for PG faults, the minimum mean error was 0.68 ± 0.37% for fault resistance of 0.001 $\Omega$ and a maximum of 1.16 ± 0.81% for fault resistance of 40 $\Omega$. For PPG faults, the minimum error was 0.89 ± 0.68% for fault resistance of 40 $\Omega$ and a maximum of 1.87 ± 0.42% for fault resistance of 25 $\Omega$. For PP faults, the minimum error was 1.61 ± 0.38% for fault resistance of 0.001 $\Omega$ and a maximum of 2.18 ± 0.14% for fault resistance of 10 $\Omega$. For PPP faults, the minimum error was 1.76 ± 0.06% for fault resistance of 0.001 $\Omega$ and a maximum of 2.43 ± 0.14% for fault resistance of 10 $\Omega$.

According to the analysis described in Section 3.5, Figure 14 presents the percentage of correct fault localizations for each section where a fault occurred under the errors applied to the phasors and line parameters. Similarly to Figure 9, Figure 14 shows the precision of fault localization for each section, yielding an average success rate of 95.97% across all sections. Therefore, the errors applied to the phasors and line parameters caused a minimum impact on the method’s ability to find the fault occurrence section.

3.6.2. Uncertainties Due to Line Unbalance

To confirm that the algorithm remains effective in untransposed line configurations, we considered the sections of the test system shown in Figure 6 without transposition and, additionally, further unbalanced the impedance and admittance matrices of these sections. Thus, for example, the section between the CB and B1, which is the longest section of the network, with a length of 3520.7 m, resulted in the following impedance and admittance matrices:

$$\overline{z}=\left[\begin{array}{ccc}0.16623+j0.66958& 0.05811+j0.48501& 0.05811+j0.45613\\ 0.05811+j0.48501& 0.16623+j0.86958& 0.05811+j0.54247\\ 0.05811+j0.45613& 0.05811+j0.54247& 0.16623+j1.86958\end{array}\right]$$

(13)

$$\overline{y}=j\left[\begin{array}{ccc}0.003302& -0.000883& -0.000577\\ -0.000883& 0.003773& -0.001431\\ -0.000577& -0.001431& 0.003637\end{array}\right]$$

(14)

A solid single line-to-ground fault (AG) was simulated at bus B1, i.e., at 3520.7 m from the CB. This type of fault was chosen because it is located at the end of the longest section of the network, presents greater asymmetry, and has a zero fault resistance, resulting in a higher fault current.

Accordingly, the proposed method identified the fault at 3415.1 m with a fault resistance of 1E-6 $\Omega$, corresponding to an error of 105.6 m, which is a highly acceptable deviation considering the cable lengths of the analyzed wind farm.

3.6.3. Uncertainties Due to Wind Generator Current Injection

To demonstrate that the algorithm can accurately locate faults even when each wind generator injects a distinct current into the circuit during the fault, we considered a deviation of ±20% among the currents injected by each wind generator during PG, PPG, PP, and PPP faults, with fault resistances varying from 0.001 $\Omega$ to 40 $\Omega$, applied at the midpoint of the section between CB and B1.

Table 9. Fault location for 75 % of wind power injection.

Fault Type	Error [%]	R [Ω]
PG	0.17 ± 0.02	0.001
PPG	0.18 ± 0.02
PP	0.04 ± 0.04
PPP	0.01 ± 0.002
PG	1.79 ± 0.75	10
PPG	2.31 ± 0.43
PP	2.02 ± 0.42
PPP	3.92 ± 0.002
PG	4.06 ± 3.92	25
PPG	2.25 ± 0.97
PG	10.2 ± 3.73	40
PPG	17.13 ± 2.74

presents the results. It is worth noting that the mean error varied from 0.01% for a fault resistance of 0.001 $\Omega$ to 17.13% for 40 $\Omega$, with the largest errors occurring for higher fault resistances. Increasing the fault resistance reduces the fault current, and the influence of the current injected by the wind generators on the fault location becomes more significant.

It is also noteworthy that for fault resistances of 40 $\Omega$ and above, the location error tends to follow the deviation in the current injected by the wind generators. In this study, a deviation of ±20% resulted in a mean error of 17.13%. Nevertheless, such large deviations are unlikely in practice, since wind generators connected to a common collector circuit are typically separated by only a few hundred meters and therefore experience nearly the same terminal voltage.

4. Practical Applications of the Proposed Methodology

The proposed fault location method was developed using fault data obtained through simulations conducted in PSCAD/MTDC v5.0.2 software as a reference for testing.

One of the main challenges encountered in validating the methodology was access to real fault data from the wind farm. However, one of the key input parameters of this methodology is the short-circuit phasor values, which can be easily obtained from intelligent relays responsible for the system’s electrical protection—especially when these are integrated into the Supervisory Control and Data Acquisition (SCADA) system at the wind farm’s operations center.

Therefore, the proposed methodology could be readily applied and integrated into a generation management system (GMS), together with the wind farm’s supervisory system, automating the fault location process immediately after fault detection and ultimately reducing the downtime of the wind farm.

Artificial intelligence–based methodologies, as seen in the literature, rely on large amounts of historical data to train models and are also susceptible to network topology changes (for example, circuit expansion), which would require retraining. In contrast, the proposed methodology offers greater simplicity in terms of input data availability, type, and quantity, as well as enhanced flexibility in the event of modifications to the network topology.

5. Conclusions

This article presented a fault location method for wind farm collecting circuits. It addresses operational challenges that can compromise power continuity due to fault events. The proposed method uses only voltage and current phasors measured at the CB, eliminating the need for data acquisition from the wind generator buses. The method significantly reduces computational overhead by leveraging heuristic optimization techniques while maintaining high accuracy. The fault location routine compares measured phasors with those calculated for various fault scenarios, enabling the precise identification of the affected feeder section and estimation of the fault resistance across all fault types. Preprocessing steps, including signal denoising and harmonic filtering, ensure robust phasor extraction from field measurements. The simulation results demonstrate the method’s effectiveness, with average maximum location errors remaining below 2.33%, corresponding to less than 110 m. The performance is consistent regardless of the total line length, underscoring the method’s scalability and reliability. The proposed method’s efficiency and robustness make it suitable for integration into existing SCADA systems and real-time protection frameworks. Thus, it provides operators with rapid and accurate fault location, supporting prompt restoration of service.