Journal Description
Foundations
Foundations
is an international, peer-reviewed, open access journal on mathematics, physics and chemistry published quarterly online by MDPI.
- Open Access free for readers, with article processing charges (APC) paid by authors or their institutions.
- Rapid Publication: manuscripts are peer-reviewed and a first decision is provided to authors approximately 34.7 days after submission; acceptance to publication is undertaken in 4.4 days (median values for papers published in this journal in the second half of 2025).
- Recognition of Reviewers: APC discount vouchers, optional signed peer review, and reviewer names published annually in the journal.
- Foundations is a companion journal of Molecules, Entropy and Mathematics.
Latest Articles
Existence and Uniqueness Results for (k, ψ)-Caputo Fractional Boundary Value Problems Involving Multi-Point Closed Boundary Conditions
Foundations 2025, 5(4), 37; https://doi.org/10.3390/foundations5040037 - 8 Dec 2025
Abstract
In this paper, we investigate a new class of nonlinear fractional boundary value problems (BVPs) involving
In this paper, we investigate a new class of nonlinear fractional boundary value problems (BVPs) involving
(This article belongs to the Section Mathematical Sciences)
Open AccessArticle
Bias-Corrected Root Mean Square Deviation Estimators
by
Alexander Robitzsch
Foundations 2025, 5(4), 36; https://doi.org/10.3390/foundations5040036 - 28 Nov 2025
Abstract
The root mean square deviation (RMSD) is a widely used item fit statistic in item response models. However, the sample RMSD is known to exhibit positive bias in small samples. To address this, seven alternative bias-corrected RMSD estimators are proposed and evaluated in
[...] Read more.
The root mean square deviation (RMSD) is a widely used item fit statistic in item response models. However, the sample RMSD is known to exhibit positive bias in small samples. To address this, seven alternative bias-corrected RMSD estimators are proposed and evaluated in a simulation study involving items with uniform differential item functioning (DIF). The results demonstrate that the proposed estimators effectively reduce the bias of the original RMSD statistic. Their performance is compared, and the most favorable estimators are highlighted for empirical research. Finally, the application of the various RMSD statistics is illustrated using PISA 2006 reading data.
Full article
(This article belongs to the Section Mathematical Sciences)
►▼
Show Figures

Figure 1
Open AccessArticle
PCT vs. FEP: A Comparison Between Reorganization Theory and Bayesian Inference
by
Ty Roachford, Warren Mansell and Rodrigo Pena
Foundations 2025, 5(4), 35; https://doi.org/10.3390/foundations5040035 - 27 Oct 2025
Abstract
Perceptual Control Theory (PCT) and the Free Energy Principle (FEP) are two foundational, principle-based frameworks originally developed to explain brain function. However, since their initial proposals, both frameworks have been generalized to account for the behavior of living systems more broadly. Despite their
[...] Read more.
Perceptual Control Theory (PCT) and the Free Energy Principle (FEP) are two foundational, principle-based frameworks originally developed to explain brain function. However, since their initial proposals, both frameworks have been generalized to account for the behavior of living systems more broadly. Despite their conceptual overlap and practical successes, a mathematical comparison of the two frameworks has yet to be undertaken. In this article, we briefly introduce and compare the philosophical foundations underlying PCT and FEP. We then introduce and compare their experimental and mathematical foundations concretely in the context of bacterial chemotaxis. With these foundations in place, we can use tools from category theory to argue that PCT can be formally understood as a subset of the FEP framework; however, it is worth noting that the mathematical machinery unique to FEP is not required to successfully model bacterial chemotaxis. Finally, we conclude with a proposal for a mathematical synthesis where each framework plays an orthogonal yet complementary role.
Full article
(This article belongs to the Section Mathematical Sciences)
►▼
Show Figures

Figure 1
Open AccessArticle
Probabilistic Geometry Based on the Fuzzy Playfair Axiom
by
Edward Bormashenko
Foundations 2025, 5(4), 34; https://doi.org/10.3390/foundations5040034 - 1 Oct 2025
Abstract
A probabilistic version of geometry is introduced. The fifth postulate of Euclid (Playfair’s axiom) is adopted in the following probabilistic form: consider a line and a point not on the line—there is exactly one line through the point with probability P, where
[...] Read more.
A probabilistic version of geometry is introduced. The fifth postulate of Euclid (Playfair’s axiom) is adopted in the following probabilistic form: consider a line and a point not on the line—there is exactly one line through the point with probability P, where
(This article belongs to the Section Mathematical Sciences)
►▼
Show Figures

Figure 1
Open AccessArticle
On Relative Stability for Strongly Mixing Sequences
by
Adam Jakubowski and Zbigniew Stanisław Szewczak
Foundations 2025, 5(4), 33; https://doi.org/10.3390/foundations5040033 - 25 Sep 2025
Abstract
We consider a class of strongly mixing sequences with infinite second moment. This class contains important GARCH processes that are applied in econometrics. We show the relative stability for such processes and construct a counterexample. We apply these results and obtain a new
[...] Read more.
We consider a class of strongly mixing sequences with infinite second moment. This class contains important GARCH processes that are applied in econometrics. We show the relative stability for such processes and construct a counterexample. We apply these results and obtain a new CLT without the requirement of exponential decay of mixing coefficients, and provide a counterexample to this as well.
Full article
(This article belongs to the Section Mathematical Sciences)
Open AccessHypothesis
From Magnetic Field Seeds to Planetary and Galactic Magnetism
by
Angelo De Santis, Roberto Dini and Gianfranco Cianchini
Foundations 2025, 5(4), 32; https://doi.org/10.3390/foundations5040032 - 23 Sep 2025
Abstract
This study investigates the origin and amplification of magnetic fields in planets and galaxies, emphasizing the foundational role of a seed magnetic field (SMF) in enabling dynamo processes. We propose a universal mechanism whereby an SMF arises naturally in systems where an orbiting
[...] Read more.
This study investigates the origin and amplification of magnetic fields in planets and galaxies, emphasizing the foundational role of a seed magnetic field (SMF) in enabling dynamo processes. We propose a universal mechanism whereby an SMF arises naturally in systems where an orbiting body rotates non-synchronously with respect to its central mass. Based on this premise, we derive a general equation for the SMF applicable to both planetary and galactic scales. Incorporating parameters such as orbital distance, rotational velocity, and core radius, we then introduce a dimensionless factor to characterize the amplification of this seed field via dynamo processes. By comparing model predictions with magnetic field data from the solar system and the Milky Way, we find that the observed magnetic fields can be interpreted as the product of a universal gravitationally induced SMF and a body-specific amplification factor. Our results offer a novel perspective on the generation of magnetic fields in a wide range of astrophysical contexts and suggest new directions for theoretical investigation, including the environments surrounding black holes.
Full article
(This article belongs to the Section Physical Sciences)
►▼
Show Figures

Figure 1
Open AccessArticle
Emerging Near-Surface Solar MHD Dynamos
by
Alexander Bershadskii
Foundations 2025, 5(3), 31; https://doi.org/10.3390/foundations5030031 - 19 Sep 2025
Abstract
Using the results of numerical simulations and solar observations, this study shows that the transition from deterministic chaos to hard turbulence in the magnetic field generated by the emerging small-scale, near-surface (within the Sun’s outer 5–10% convection zone) solar MHD dynamos occurs through
[...] Read more.
Using the results of numerical simulations and solar observations, this study shows that the transition from deterministic chaos to hard turbulence in the magnetic field generated by the emerging small-scale, near-surface (within the Sun’s outer 5–10% convection zone) solar MHD dynamos occurs through a randomization process. This randomization process has been described using the concept of distributed chaos, and the main parameter of distributed chaos
(This article belongs to the Section Physical Sciences)
►▼
Show Figures

Figure 1
Open AccessArticle
The Extended Uncertainty Principle from a Projector-Valued Measurement Perspective
by
Thomas Schürmann
Foundations 2025, 5(3), 30; https://doi.org/10.3390/foundations5030030 - 1 Sep 2025
Abstract
We revisit the Extended Uncertainty Principle (EUP) from an operational viewpoint, replacing wavefunction-based widths with apparatus-defined position constraints such as a finite slit of width
We revisit the Extended Uncertainty Principle (EUP) from an operational viewpoint, replacing wavefunction-based widths with apparatus-defined position constraints such as a finite slit of width
(This article belongs to the Section Mathematical Sciences)
Open AccessArticle
Incorporating Finite Particle Number and Heat-Temperature Differences in the Maxwell–Boltzmann Speed Distribution
by
Everett M. Criss and Anne M. Hofmeister
Foundations 2025, 5(3), 29; https://doi.org/10.3390/foundations5030029 - 25 Aug 2025
Abstract
The often used analytical representation of the Maxwell–Boltzmann classical speed distribution function (F) for elastic, indivisible particles assumes an infinite limit for the speed. Consequently, volume and the number of particles (n) extend to infinity: Both infinities contradict assumptions
[...] Read more.
The often used analytical representation of the Maxwell–Boltzmann classical speed distribution function (F) for elastic, indivisible particles assumes an infinite limit for the speed. Consequently, volume and the number of particles (n) extend to infinity: Both infinities contradict assumptions underlying this non-relativistic formulation. Finite average kinetic energy and temperature (T) result from normalization of F removing n: However, total energy (i.e., heat of the collection) remains infinite because n is infinite. This problem persists in recent adaptations. To better address real (finite) systems, wherein T depends on heat, we generalize this one-parameter distribution (F, cast in energy) by proposing a two-parameter gamma distribution function (F*) in energy which reduces to F at large n. Its expectation value of kT (k = Boltzmann’s constant) replicates F, whereas the shape factor depends on n and affects the averages, as expected for finite systems. We validate F* via a first-principle, molecular dynamics numerical model of energy and momentum conserving collisions for 26, 182, and 728 particles in three-dimensional physical space. Dimensionless calculations provide generally applicable results; a total of 107 collisions suffice to represent an equilibrated collection. Our numerical results show that individual momentum conserving collisions in three-dimensions provide symmetrical speed distributions in all Cartesian directions. Thus, momentum and energy conserving collisions are the physical cause for equipartitioning of energy: Validity of this theorem for other systems depends on their specific motions. Our numerical results set upper limits on kinetic energy of individual particles; restrict the n particles to some finite volume; and lead to a formula in terms of n for conserving total energy when utilizing F* for convenience. Implications of our findings on matter under extreme conditions are briefly discussed.
Full article
(This article belongs to the Section Physical Sciences)
►▼
Show Figures

Figure 1
Open AccessArticle
Knots in Polymer Molecules Under Poiseuille Flow
by
Maurice P. Schmitt and Andrey Milchev
Foundations 2025, 5(3), 28; https://doi.org/10.3390/foundations5030028 - 13 Aug 2025
Abstract
Knots are ubiquitous in polymers and biological macromolecules such as DNA and proteins, yet their behavior and functionality are still not sufficiently explored. Here we investigate the impact of Poiseuille flow on simple knots in flexible polymers placed in a quasi-rectangular micro-channel by
[...] Read more.
Knots are ubiquitous in polymers and biological macromolecules such as DNA and proteins, yet their behavior and functionality are still not sufficiently explored. Here we investigate the impact of Poiseuille flow on simple knots in flexible polymers placed in a quasi-rectangular micro-channel by systematically varying the flow strength for different chain lengths. Hydrodynamic interactions are accounted for by means of Multi-Particle Collision Dynamics (MPCD). We find that initially loosely localized knots in polymer coils typically tighten under shear to several segments beyond a certain body force threshold. At higher shear rates, intermittent transition from chain stretching to tumbling is observed which correlates with strong fluctuations in the knot size. Somewhat unexpectedly, our results indicate that the influence of channel width on tightening steadily increases with growing width even at equal mean shear rate
(This article belongs to the Section Physical Sciences)
►▼
Show Figures

Graphical abstract
Open AccessArticle
Probabilistic Multiple-Integral Evaluation of Odd Dirichlet Beta and Even Zeta Functions and Proof of Digamma-Trigamma Reflections
by
Antonio E. Bargellini, Daniele Ritelli and Giulia Spaletta
Foundations 2025, 5(3), 27; https://doi.org/10.3390/foundations5030027 - 11 Aug 2025
Abstract
The aim of this work was to construct explicit expressions for the summation of Dirichlet Beta functions with odd arguments and Zeta functions with even arguments. In the established literature, this is typically done using Fourier series expansions or Bernoulli numbers and polynomials.
[...] Read more.
The aim of this work was to construct explicit expressions for the summation of Dirichlet Beta functions with odd arguments and Zeta functions with even arguments. In the established literature, this is typically done using Fourier series expansions or Bernoulli numbers and polynomials. Here, instead, we achieve our goal by employing tools from probability: specifically, we introduce a generalisation of a technique based on multiple integrals and the algebra of random variables. This also allows us to increase the number of nested integrals and Cauchy random variables involved. Another key contribution is that, by generalising the exponent of Cauchy random variables, we obtain an original proof of the reflection formulae for the Digamma and Trigamma functions. These probabilistic proofs crucially utilise the Mellin transform to compute the integrals needed to determine probability density functions. It is noteworthy that, while understanding the presented topic requires knowledge of the rules for calculating multiple integrals (Fubini’s Theorem) and the algebra of continuous random variables, these are concepts commonly acquired by second-year university students in STEM disciplines. Our study thus offers new perspectives on how the mathematical functions considered relate and shows the significant role of probabilistic methods in promoting comprehension of this research area, in a way accessible to a broad and non-specialist audience.
Full article
(This article belongs to the Collection Editorial Board Members’ Collection Series: Feature Papers in Mathematical Sciences)
Open AccessOpinion
Relation Between Diffusion Equations and Boundary Conditions in Bounded Systems
by
Fabio Sattin and Dominique Franck Escande
Foundations 2025, 5(3), 26; https://doi.org/10.3390/foundations5030026 - 31 Jul 2025
Abstract
Differential equations need boundary conditions (BCs) for their solution. It is widely acknowledged that differential equations and BCs are representative of independent physical processes, and no correlations between them are required. Two recent studies by Hilhorst, Chung et al. argue instead that, in
[...] Read more.
Differential equations need boundary conditions (BCs) for their solution. It is widely acknowledged that differential equations and BCs are representative of independent physical processes, and no correlations between them are required. Two recent studies by Hilhorst, Chung et al. argue instead that, in the specific case of diffusion equations (DEs) in bounded systems, BCs are uniquely constrained by the form of transport coefficients. In this paper, we revisit how DEs emerge as fluid limits out of a picture of stochastic transport. We point out their limits of validity and argue that, in most physical systems, BCs and DEs are actually uncorrelated by virtue of the failure of diffusive approximation near the system’s boundaries. When, instead, the diffusive approximation holds everywhere, we show that the correct chain of reasoning goes in the direction opposite to that conjectured by Hilhorst and Chung: it is the choice of the BCs that determines the form of the DE in the surroundings of the boundary.
Full article
(This article belongs to the Section Physical Sciences)
Open AccessHypothesis
Beyond Classical Multipoles: The Magnetic Metapole as an Extended Field Source
by
Angelo De Santis and Roberto Dini
Foundations 2025, 5(3), 25; https://doi.org/10.3390/foundations5030025 - 14 Jul 2025
Cited by 1
Abstract
We introduce the concept of the magnetic metapole—a theoretical extension of classical multipole theory involving a fractional j pole count (related to the harmonic degree n as j = 2n). Defined by a scalar potential with colatitudinal dependence and no radial
[...] Read more.
We introduce the concept of the magnetic metapole—a theoretical extension of classical multipole theory involving a fractional j pole count (related to the harmonic degree n as j = 2n). Defined by a scalar potential with colatitudinal dependence and no radial variation, the metapole yields a magnetic field that decays as 1/r and is oriented along spherical surfaces. Unlike classical multipoles, the metapole cannot be described as a point source; rather, it corresponds to an extended or filamentary magnetic distribution as derived from Maxwell’s equations. We demonstrate that pairs of oppositely oriented metapoles (up/down) can, at large distances, produce magnetic fields resembling those of classical monopoles. A regularized formulation of the potential resolves singularities for the potential and the field. When applied in a bounded region, it yields finite field energy, enabling practical modeling applications. We propose that the metapole can serve as a conceptual and computational framework for representing large-scale magnetic field structures particularly where standard dipole-based models fall short. This construct may have utility in both geophysical and astrophysical contexts, and it provides a new tool for equivalent source modeling and magnetic field decomposition.
Full article
(This article belongs to the Section Physical Sciences)
►▼
Show Figures

Figure 1
Open AccessArticle
Fisher Information in Helmholtz–Boltzmann Thermodynamics of Mechanical Systems
by
Marco Favretti
Foundations 2025, 5(3), 24; https://doi.org/10.3390/foundations5030024 - 4 Jul 2025
Abstract
In this paper, we review Helmholtz–Boltzmann thermodynamics for mechanical systems depending on parameters, and we compute the Fisher information matrix for the associated probability density. The divergence of Fisher information has been used as a signal for the existence of phase transitions in
[...] Read more.
In this paper, we review Helmholtz–Boltzmann thermodynamics for mechanical systems depending on parameters, and we compute the Fisher information matrix for the associated probability density. The divergence of Fisher information has been used as a signal for the existence of phase transitions in finite systems even in the absence of a thermodynamic limit. We investigate through examples if qualitative changes in the dynamic of mechanical systems described by Helmholtz–Boltzmann thermodynamic formalism can be detected using Fisher information.
Full article
(This article belongs to the Section Physical Sciences)
►▼
Show Figures

Figure 1
Open AccessArticle
Mathematical Formalism and Physical Models for Generative Artificial Intelligence
by
Zeqian Chen
Foundations 2025, 5(3), 23; https://doi.org/10.3390/foundations5030023 - 24 Jun 2025
Abstract
This paper presents a mathematical formalism for generative artificial intelligence (GAI). Our starting point is an observation that a “histories” approach to physical systems agrees with the compositional nature of deep neural networks. Mathematically, we define a GAI system as a family of
[...] Read more.
This paper presents a mathematical formalism for generative artificial intelligence (GAI). Our starting point is an observation that a “histories” approach to physical systems agrees with the compositional nature of deep neural networks. Mathematically, we define a GAI system as a family of sequential joint probabilities associated with input texts and temporal sequences of tokens (as physical event histories). From a physical perspective on modern chips, we then construct physical models realizing GAI systems as open quantum systems. Finally, as an illustration, we construct physical models realizing large language models based on a transformer architecture as open quantum systems in the Fock space over the Hilbert space of tokens. Our physical models underlie the transformer architecture for large language models.
Full article
(This article belongs to the Section Physical Sciences)
Open AccessArticle
Cross-Analysis of Magnetic and Current Density Field Topologies in a Quiescent High Confinement Mode Tokamak Discharge
by
Marie-Christine Firpo
Foundations 2025, 5(2), 22; https://doi.org/10.3390/foundations5020022 - 17 Jun 2025
Cited by 1
Abstract
In axisymmetric fusion devices like tokamaks, the winding of the magnetic field is characterized by its safety profile
In axisymmetric fusion devices like tokamaks, the winding of the magnetic field is characterized by its safety profile
(This article belongs to the Section Physical Sciences)
►▼
Show Figures
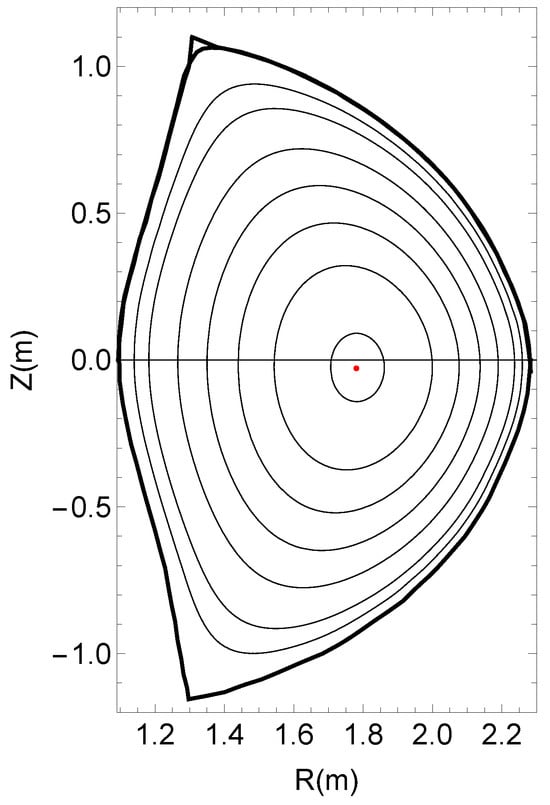
Figure 1
Open AccessArticle
Foreground Emission Randomization Due to Dynamics of Magnetized Interstellar Medium: WMAP and Planck Frequency Bands
by
Alexander Bershadskii
Foundations 2025, 5(2), 21; https://doi.org/10.3390/foundations5020021 - 10 Jun 2025
Cited by 2
Abstract
Using the results of numerical simulations and astrophysical observations (mainly in the WMAP and Planck frequency bands), it is shown that Galactic foreground emission becomes more sensitive to the mean magnetic field with the frequency, resulting in the appearance of two levels of
[...] Read more.
Using the results of numerical simulations and astrophysical observations (mainly in the WMAP and Planck frequency bands), it is shown that Galactic foreground emission becomes more sensitive to the mean magnetic field with the frequency, resulting in the appearance of two levels of its randomization due to the chaotic/turbulent dynamics of a magnetized interstellar medium dominated by magnetic helicity. The galactic foreground emission is more randomized at higher frequencies. The Galactic synchrotron and polarized dust emissions have been studied in detail. It is shown that the magnetic field imposes its level of randomization on the synchrotron and dust emission. The main method for the theoretical consideration used in this study is the Kolmogorov–Iroshnikov phenomenology in the frames of distributed chaos notion. Despite the vast differences in the values of physical parameters and spatio-temporal scales between the numerical simulations and the astrophysical observations, there is a quantitative agreement between the results of the astrophysical observations and the numerical simulations in the frames of the distributed chaos notion.
Full article
(This article belongs to the Section Physical Sciences)
►▼
Show Figures

Figure 1
Open AccessArticle
Comparing Different Specifications of Mean–Geometric Mean Linking
by
Alexander Robitzsch
Foundations 2025, 5(2), 20; https://doi.org/10.3390/foundations5020020 - 6 Jun 2025
Abstract
Mean–geometric mean (MGM) linking compares group differences on a latent variable
Mean–geometric mean (MGM) linking compares group differences on a latent variable
(This article belongs to the Section Mathematical Sciences)
►▼
Show Figures

Figure 1
Open AccessArticle
Numerical Evidence for a Bipartite Pure State Entanglement Witness from Approximate Analytical Diagonalization
by
Paul M. Alsing and Richard J. Birrittella
Foundations 2025, 5(2), 19; https://doi.org/10.3390/foundations5020019 - 4 Jun 2025
Abstract
We show numerical evidence for a bipartite
We show numerical evidence for a bipartite
(This article belongs to the Section Mathematical Sciences)
►▼
Show Figures
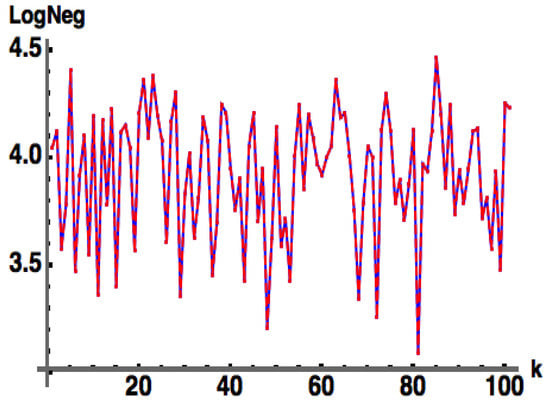
Figure 1
Open AccessReview
Advances in Fractional Lyapunov-Type Inequalities: A Comprehensive Review
by
Sotiris K. Ntouyas, Bashir Ahmad and Jessada Tariboon
Foundations 2025, 5(2), 18; https://doi.org/10.3390/foundations5020018 - 27 May 2025
Cited by 3
Abstract
In this survey, we have included the recent results on Lyapunov-type inequalities for differential equations of fractional order associated with Dirichlet, nonlocal, multi-point, anti-periodic, and discrete boundary conditions. Our results involve a variety of fractional derivatives such as Riemann–Liouville, Caputo, Hilfer–Hadamard,
In this survey, we have included the recent results on Lyapunov-type inequalities for differential equations of fractional order associated with Dirichlet, nonlocal, multi-point, anti-periodic, and discrete boundary conditions. Our results involve a variety of fractional derivatives such as Riemann–Liouville, Caputo, Hilfer–Hadamard,
(This article belongs to the Section Mathematical Sciences)
Highly Accessed Articles
Latest Books
E-Mail Alert
News
Topics

Conferences
Special Issues
Topical Collections
Topical Collection in
Foundations
Editorial Board Members’ Collection Series: Feature Papers in Mathematical Sciences
Collection Editors: Ravi P. Agarwal, Dimplekumar N. Chalishajar
Topical Collection in
Foundations
Editorial Board Members’ Collection Series: Theory and Its Applications in Problems of Mathematical Physics and of Mathematical Chemistry
Collection Editors: Ioannis K. Argyros, Lorentz Jäntschi







