Probabilistic Geometry Based on the Fuzzy Playfair Axiom

Abstract

A probabilistic version of geometry is introduced. The fifth postulate of Euclid (Playfair’s axiom) is adopted in the following probabilistic form: consider a line and a point not on the line—there is exactly one line through the point with probability P, where $0\le P\le 1$. Playfair’s axiom is logically independent of the rest of the Hilbert system of axioms of the Euclidian geometry. Thus, the probabilistic version of the Playfair axiom may be combined with other Hilbert axioms. $P=1$ corresponds to the standard Euclidean geometry; $P=0$ corresponds to the elliptic- and hyperbolic-like geometries. $0<P<1$ corresponds to the introduced probabilistic geometry. Parallel constructions in this case are Bernoulli trials. Theorems of the probabilistic geometry are discussed. Given a triangle and a line drawn from a vertex parallel to the opposite side, the event that this line is actually parallel occurs with probability P. Otherwise, the line may intersect the side or diverge. Parallelism is not transitive in the probabilistic geometry. Probabilistic geometry occurs on the surface with a stochastically variable Gaussian curvature. Alternative geometries adopting various versions of the probabilistic Playfair axiom are introduced. Probabilistic non-Archimedean geometry is addressed. Applications of the probabilistic geometry are discussed.

1. Introduction

For centuries, the Elements of Euclid represented the very model of scientific and deductive reasoning [1,2]. Elements were published, translated, edited, and commented upon thousands of times, and these publications shaped the scientific method and the mathematical style of thinking of many centuries [1,2]. Euclid’s approach was used to build further mathematical theories. Moreover, the deductive structure of the Euclid proofs was studied by mathematicians, physicists, logicians, and epistemologists as the perfect ideal of scientific reason itself [1,2]. The fifth postulate of Euclid, often called the parallel postulate, has a rich and complex history that spans more than two millennia. In Euclidean geometry, postulates (also called axioms) are the basic assumptions or starting points that are accepted without proof. From these, all theorems and propositions in geometry are logically deduced [1,2]. Among other postulates, the fifth postulate (abbreviated below FP) was not self-evident and less intuitive. In its original form, the FP states that if a secant cuts two straight lines forming side angles whose sum is less than two straight, two long enough lines are cut on this same side. Or, in other words, if a line segment intersects two straight lines forming two interior angles on the same side that are less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles. The philosopher Proclus (c. 412–485 AD), a late Neoplatonist commentator on Euclid, questioned why it should be accepted as a postulate rather than proven [3]. Many geometers (including Leibnitz) throughout history tried to prove it from the other four, believing it to be a theorem rather than an axiom [4]. Ibn al-Haytham (Alhazen, c. 965–1040), a key figure in the Islamic Golden Age, made a deep and innovative critique of the FP, and suggested that lines equidistant from one another never meet (a kind of converse to the parallel postulate) [5]. Omar Khayyam (c. 1048–1131), the Persian mathematician, poet, and astronomer, re-shaped the FP as follows: if two straight lines intersect a third line such that the sum of the interior angles on the same side is equal to two right angles, and if the lines are perpendicular to a common transversal, then the distance between them remains constant, and they do not intersect—that is, they are parallel [6].

The exact meaning and status of the FP of Euclidian geometry continue to attract the attention of scientists [7,8,9]. Hilbert’s Euclidean Axiom of Parallels is formulated as follows: for every line l and every point A not on l, there does not exist more than one line through A parallel to l [10]. This formulation is equivalent to Playfair’s axiom (1795), stating that through a given point not on a given line, there is exactly one line parallel to the given line [7,8,9].

The development and eventual replacement of Euclid’s FP by Lobachevski and others marked a turning point in the history of mathematics, leading to the birth of non-Euclidean geometry [11,12]. Lobachevski was first to explicitly reject the FP and systematically develop a consistent geometry without it. Lobachevski himself called his system “imaginary geometry”, now known as “hyperbolic geometry”. In Lobachevski’s geometry, given a line and a point not on it, infinitely many parallels can be drawn through the point [11,12,13]. The sum of angles in a triangle is less than $\pi$, and there is a maximum area for triangles with given angle sums. The first presentation of new geometry took place at the Department of Physical and Mathematical Sciences, at Kazan University, on 7 February 1826. Lobachevski published his results in 1829 paper “On the Principles of Geometry”, published in Russian. János Bolyai, a Hungarian mathematician, independently developed hyperbolic geometry around the same time [13]. His work was published in an appendix to his father Farkas Bolyai’s book in 1832 [13]. Carl Friedrich Gauss independently developed ideas of non-Euclidean geometry but never published them. These results promoted the development of Riemannian geometry, which plays a central role in general relativity [14,15,16].

The next intellectual step is suggested in the development of the Euclidian geometry. The probabilistic nature of the FP is assumed; namely, we adopt that for a given line l and point $A\notin l$, there is exactly one line through A with probability P, where $0\le P\le 1$. The suggested geometry is labeled in the presented paper as “probabilistic geometry”, in order to distinguish it from “fuzzy geometry”, which is a study of interaction of uncertain geometric objects [17,18,19]. Objects of the fuzzy geometry are associated with probability distributions or membership functions [17,18,19]. For example, a point is represented not by a single coordinate but by a probability density function or a fuzzy set over the plane [17,18,19].

We introduce the geometry, in which one of the axioms is probabilistic/fuzzy. In other words, this axiom is correct with the prescribed probability, thus resembling the famous fuzzy logic developed by Lotfi Aliasger Zadeh [20,21,22,23]. Fuzzy logic is a form of probabilistic logic that allows for reasoning with degrees of truth, rather than the binary true/false values used in classical (Boolean) logic [20,21,22,23].

The suggested framework may be useful for quantum gravity and cosmology. In quantum gravity and cosmology, space-time may be fundamentally non-deterministic or/and discrete. Loop quantum gravity and causal dynamic triangulation approaches to quantum gravity suggest that the structure of space-time fluctuates quantum-mechanically. An introduced probabilistic geometry could be used to simulate local violations of the parallel postulate, giving representative models of a fluctuating space-time structure. Instead of assuming that the parallel postulate (Playfair’s axiom) always holds, it is possible to assume that it holds with probability P in each local region (or event). Each realization gives a random local geometric structure. This naturally fits the suggested framework. The introduced approach is different from the stochastic geometry, probabilistic metric spaces, and uncertain geometry, as will be discussed below in detail.

The paper is organized as follows: Section 1 covers the history of the fifth postulate and introduces the conceptual motivation for developing a probabilistic version of Euclidean geometry, in which one of the axioms (Playfair’s axiom) is probabilistic, and the need to incorporate a probabilistic structure into foundational geometry. Section 2 introduces the proposed framework, in which Groups I–III and V of the Hilbert geometry remain unchanged, but the fifth postulate is probabilistic. The examples and theorems of the modified Hilbert probabilistic geometry are supplied and discussed. Section 3 explores possible applications in the physical sciences and engineering and addresses the novelty of the introduced approach. Finally, Section 4 summarizes the presented Hilbert probabilistic geometry.

2. Results

2.1. System of Axioms of Hilbert-P Geometry and Its Consequences

Let us start from summarizing Hilbert’s system of axioms. Hilbert’s axioms of Euclidean geometry include the following:

(i)

Group I: Axioms of Incidence. These axioms describe how points, lines, and planes relate.

• I.1: For every two distinct points, there exists a line that contains both of them.
  I.2: A line contains at least two points.
  I.3: There exist at least three non-collinear points (not all on the same line).
  I.4: For any three points not on a line, there is a plane that contains them.
  I.5: Every plane contains at least three non-collinear points.
  I.6: If two points of a line lie in a plane, the entire line lies in the plane.
  I.7: If two planes intersect, their intersection is a line.
  I.8: There exist at least four points not lying in the same plane.

(ii)

Group II: Axioms of Order (“betweenness”). These axioms define the concept of one point lying between two others.

• II.1: If point B lies between A and C, then all three points are distinct and lie on the same line.
  II.2: For any two points A and C, there exists a point B on the line AC such that C lies between A and B.
  II.3: Of any three points on a line, exactly one lies between the other two.
  II.4: Given three points on a line, we can name them A, B, C such that B is between A and C.
  II.5 (Pasch’s Axiom): If a line entering a triangle from one side intersects one side, then it must also intersect another side.

(iii)

Group III: Axioms of Congruence. These axioms deal with the equality of segments and angles.

• III.1: Given a segment AB and a ray CD, there is a unique point E on that ray such that segment AB = CE.
  III.2: Congruence is symmetric and transitive.
  III.3: If two segments are congruent to the same segment, they are congruent to each other.
  III.4: Given two angles, there is a congruent copy of one angle placed at a given ray.
  III.5: (Side–Angle–Side): If in two triangles, two sides and the included angle are congruent, then the triangles are congruent.

(iv)

Group IV: Axiom of Parallels

This is Hilbert’s version of Euclid’s fifth postulate.

• IV (Playfair’s Axiom): Given a line l and a point A not on l, there is at most one line through A parallel to l.

(v)

Group V: Axioms of Continuity. These axioms ensure the completeness of the geometric space (similar to real numbers being complete).

• V.1 (Axiom of Archimedes): There is no infinitely small or infinitely large length; segments can be added finitely to surpass any given segment.
  V.2 (Axiom of Line Completeness/Dedekind Cut Axiom): If a line is divided into two classes such that every point of the first lies to the left of every point of the second, then there exists a unique point separating the two classes.

We adopt the aforementioned Hilbert system of axioms, with one, however, essential exception. We replace Euclid’s fifth postulate (Playfair’s axiom) with its probabilistic version:

Probabilistic Parallel Axiom.

Given a line l and a point   $A\notin l$, there is exactly one line through A with probability P, where $0\le P\le 1$.

Or, as formally written,

for any point A and line l $A\notin l$, the event

$\exists !m\left(linem\right):A\in m\wedge m\parallel l$ occurs with probability $P\in \left[0,1\right]$.

Let us supply the exact meaning to the probability P. It is understood as a frequency of prescribed events (to be unique parallel to line l) in a statistical ensemble of lines passing through a fixed point A. Let $\mathsf{\Gamma }\left(A\right)$ be a set of lines passing A. We equip $\mathsf{\Gamma }\left(A\right)$ with a natural probability measure ${\eta }_A$, which is uniform if Γ(A) is finite, and it is an angular measure if $\mathsf{\Gamma }\left(A\right)$ continuous. Now, the probabilistic statement of the Playfair axiom is formulated as follows: The probability that, for a randomly chosen line $m\in \mathsf{\Gamma }\left(A\right)$, m is the unique line through A parallel to some external line l (implicitly defined by the slope/direction of m) equals P.

$$P\left(A\right)={\eta }_A\left(\left\{m\in \Gamma \left(A\right):m\text{ is unique line throughis }A\right\}\right),$$

(1)

where ${\eta }_A$ is a normalized, non-negative, additive measure on the ensemble of lines through A.

If we accept the probabilistic version of the Playfair axiom, the statement S of the geometry G$\left(S\right)$ also becomes probabilistic. This introduces a modal probabilistic operator $\widehat{P}\left(S\right)=P$, where S is a logical statement and P its probability. This yields Equation (2):

$$\widehat{P}\left(\exists !m\text{ such as that }A\in m\wedge m\parallel l\right)=P$$

(2)

The probability P in Hilbert–P–Geometry is defined as follows. Let S be the set of elementary geometrical statements constructed from the primitives (points, lines, planes) using the usual logical operations. A probability assignment is a function:

$$P:S\to \left[0,1\right],$$

(3)

such that for any statement S, P(S) expresses the likelihood that S holds in a given realization of the geometry G(S). The basic objects (primitives, using the Hilbert language) of geometry (points, lines, and planes) remain undefined, in the Hilbertian sense; axioms themselves define the primitives. Probability, in turn, is not a geometric object, but a valuation on statements, analogous to generalized truth values in probabilistic or fuzzy logic [20,21,22,23]. The introduced probability $P\left(S\right)$ fulfils the usual demands to probability, namely,

(i)

Normalization $P\left(T\right)=1$, where T is a tautological statement (always true).

(ii)

Non-negativity; namely, for every statement S, $0\le P\left(S\right)\le 1$.

(iii)

Additivity: if $S_1$ and $S_2$ are mutually exclusive statements,

$$P\left(S_1\vee S_2\right)=P\left(S_1\right)+P\left(S_2\right)$$

(4)

(iv)

Monotonicity, i.e., if  $S_1\to S_2$, then $P\left(S_1\right)\le P\left(S_2\right)$.

Probability P(S) within the suggested approach is not a primitive geometrical object (using the Hilbert wording for undefined terms), but a valuation on statements, extending the binary truth values of classical geometry into the unit interval $\left[0,1\right]$.

Now, let us rigorously re-formulate the Hilbert-P system of axioms. Let $H^0$ denote Hilbert’s axiom system without the fifth postulate (we keep Groups I–III and V untouched and omit Group IV). Thus, $H^0$ is the common scaffold of incidence, order, congruence, betweenness, and continuity axioms. A probabilistic geometric model is defined as follows:

(i)

Consider the class $Mod\left(H^0\right)$ of models of $H^0$. A model of $H^0$ denoted $Mod\left(H^0\right)$ means a mathematical structure (a set of points and lines, with relations like incidence, betweenness, congruence, etc.) that satisfies all those axioms.

(ii)

Assign a probability measure μ to the space of models $Mod\left(H^0\right)$. Although only Playfair’s axiom is taken as probabilistic, the statements of geometries labeled G(S) become probabilistic (with the exception of the axioms $H^0$, which remain deterministic). For any geometric statement S (in the language of Hilbert’s geometry), we define its probability of truth P(S) (see Equations (2) and (3)):

$$P\left(S\right)=\mu \left\{M\in Mod\left(H^0:M⊢S\right)\right\},$$

(5)

where M is one possible geometry (a mathematical structure) built on the primitives (points, lines, incidence, betweenness, congruence, etc.), i.e., $M_E\mathrm{i}\mathrm{s}$ the Euclidean plane (all Hilbert axioms belonging to $H^0$ hold), including the fifth Playfair postulate; $M_H$ is the hyperbolic geometry occurring on the hyperbolic plane, i.e., two-dimensional geometric surface with constant negative curvature (Groups I–III and V hold, but the fifth postulate does not); and $M_S$ is the sphere with great circles (elliptic geometry). It should be emphasized that Hilbert axioms from Groups I–III and V are left deterministic, and their probability P equals unity. Indeed, the probability of truth for each deterministic Hilbert axiom in $H^0$ equals unity, since every model in $Mod\left(H^0\right)$ satisfies them. The probabilistic geometry G(S) is defined over the entire class of models $Mod\left(H^0\right)$, equipped with a probability measure $\mu$. Now, Hilbert-P-Geometry is a pair $\left(Mod\left(H^0,\mu \right)\right),\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mu$ is the probability measure on $H^0$. Rigorously speaking, we suggest the probabilistic interpretation of the classical Hilbert system of axioms.

This approach creates a hybrid geometric model, blending elements of Euclidean and non-Euclidean geometry, governed by a random choice at each parallel construction event.

It can easily be seen that well-known geometries appear as the particular cases of the Hilbert–P probabilistic geometry, namely,

(i)

$P=1$ corresponds to the standard Euclidean geometry $\left(M_E\right)$: Playfair’s axiom holds always. All classical theorems of the Euclidian geometry remain valid (e.g., triangle angle sum $S=\alpha +\beta +\gamma =\pi$ remains valid).

(ii)

$P=0$ corresponds to the elliptic-like geometry $\left(M_S\right)$. No parallels through external points (like great circles on a sphere). $S=\alpha +\beta +\gamma >\pi$ holds.

(iii)

$P=0$ corresponds to hyperbolic-like geometry $\left(M_H\right)$, with the interpretation that multiple parallels are allowed. In hyperbolic geometry, through a point not on a line, there are infinitely many lines that do not intersect the given line—i.e., infinitely many parallels. In the suggested probabilistic axiom, only one parallel with probability P is possible, not multiple. So, to properly correspond to hyperbolic geometry, we interpret $P=0.$

(iv)

$0<P<1$ corresponds to the introduced probabilistic Hilbert geometry. Parallel constructions in this case are Bernoulli trials. Geometric consequences become probabilistic statements. Theorems take the following form: with probability $P^n$, there exist n successive parallels to a given line.

Let $l_1$ and $l_2$ be two lines constructed through a sequence of k probabilistic parallel choices. Then, the probability they are parallel is $P^k$. Now, the existence of unique parallels is not guaranteed. Consider a line l and a point $A\notin l$: there is a line through A with probability P, where $0\le P\le 1$; otherwise, either none or many exist. If the parallel fails (with probability $1-P$), we may enter a non-Euclidean branch.

Let us exemplify the suggested approach and address the angle sum S of a triangle, which becomes random within the introduced probabilistic geometry. With probability P, the triangle is Euclidean and $S=\pi ;$ with probability $1-P,$ the triangle may be non-Euclidean (say hyperbolic), and then $S<\pi$ (if hyperbolic-like behavior dominates). This gives rise to a probabilistic angle sum, with expected value $ℇ\left(S\right)$:

$$ℇ\left(S\right)=P\left(S\right)·\pi +\left(1-P\left(S\right)\right)\mathcal{E}\left(S_{non-euclidian}\right)$$

(6)

What is the exact meaning of $ℇ\left(S\right)?$ It supplies within the suggested approach the average value of the angle sum S of a triangle, over many repeated constructions, where each construction involves drawing parallels with probability $P\left(S\right)$. In the suggested Hilbert-P-probabilistic geometry, since parallelism is probabilistic, the outcome of a triangle’s angle sum is not deterministic. It depends on whether the “parallel step” succeeded. With probability $P:S=\pi$, and with probability $1-P:S_{non-euclidian}<\pi .$ Thus, $ℇ\left(S\right)$ given by Equation (6) is the weighted average of these two possible outcomes. Hence, the following theorem is demonstrated, based on the Hilbert-P system of axioms:

Theorem 1 (Expected angle sum of a triangle).

The expected angle sum of a triangle $ℇ\left(S\right)$ is given by $ℇ\left(S\right)=P\left(S\right)·\pi +\left(1-P\left(S\right)\right)ℇ(S_{non-euclidian)}$.

A number of theorems of the Hilbert-P geometry are of the probabilistic nature. Let us list some of these theorems.

Theorem 2 (Probability of parallel side in triangle).

Given a triangle and a line drawn from a vertex parallel to the opposite side, the event that this line is actually parallel occurs with probability P. Otherwise, the line may intersect the side or diverge.

Formal statement: BC is a triangle, formed by points A, B, C and line BC. Then,

$$\widehat{P}\left[\exists !m\left(linem\right)\wedge A\in m\wedge m\parallel BC\right]=P$$

(7)

Theorem 3.

Non-deterministic Midpoint Theorem.

In triangle ABC, let M and N be midpoints of sides AB and AC, respectively. Then, line MN is parallel to BC with probability P, and not parallel with probability $1-P.$

Corollary 1.

The segment MN has length ${\displaystyle \frac{1}{2}}BC$ with probability P.

$$\widehat{P}\left[MN\parallel BC\wedge (lengthMN={\displaystyle \frac{1}{2}}lengthBC)=P\right]$$

(8)

Theorem 4 (Stochastic behavior of parallelograms, parallelogram closure).

If a quadrilateral has opposite sides built using “parallel” constructions, it closes into a parallelogram with probability $P^2$, since both pairs must independently satisfy the parallel condition.

Theorem 5 (Parallelism is not transitive).

If $a\parallel b$ with probability $P_1$, and $b\parallel c$ with probability $P_2$, then $a\parallel c$ with a probability at most $P_1{P}_2$ assuming the independence of events.

Let us exemplify the suggested approach with the following examples.

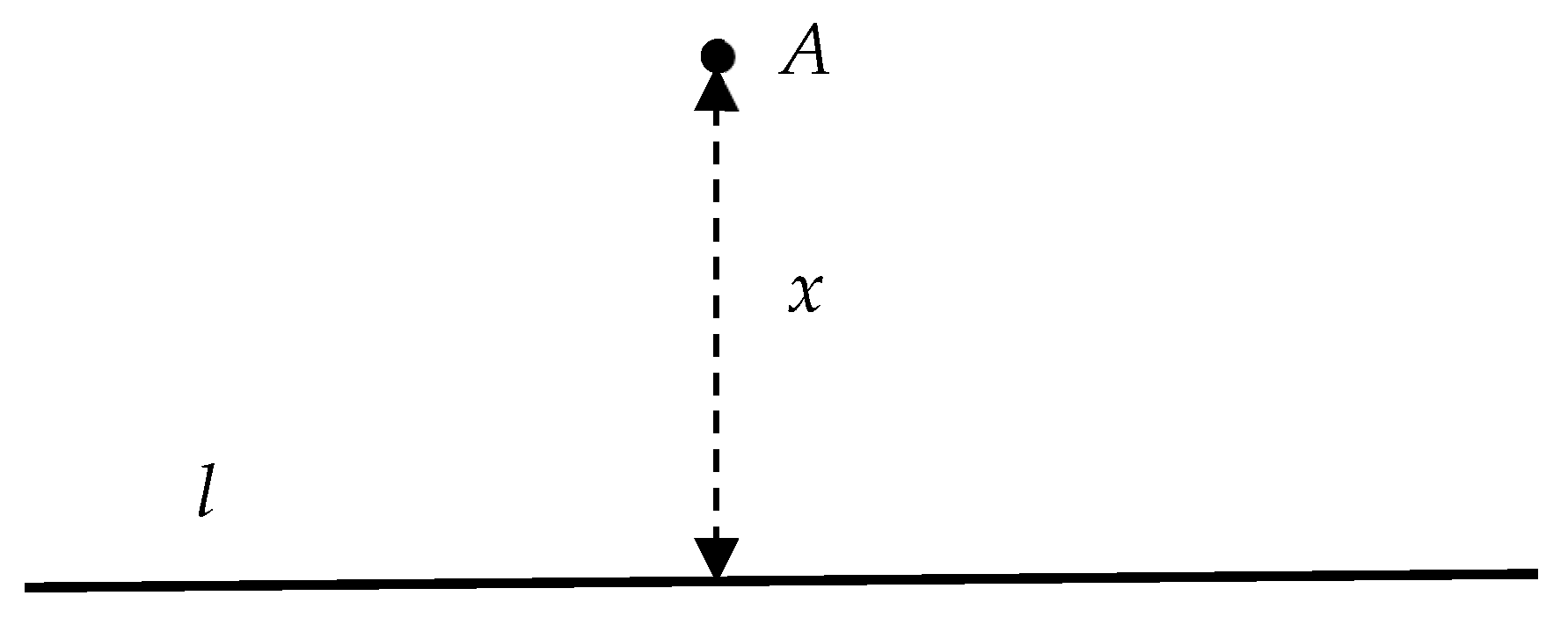
Example 1.

Consider line l and point A at the distance x from l, as depicted in Figure 1.

Assume that the probability a constructed line through a point at perpendicular distance x from a given line is the unique parallel is given by Equation (9):

$$P\left(x\right)=1-e^{-\alpha x},\alpha \ge 0,x\ge 0$$

(9)

It is easy to demonstrate that the parametrized density of the probability measure  $\tilde{\mu }\left(\tau \right)$ is given by  $\tilde{\mu }\left(\tau \right)=\alpha e^{-\alpha \tau },\tau \in \left[0,\infty \right]$;  $P\left(x\right)={\int }_0^x\tilde{\mu }\left(\tau \right)d\tau ={\int }_0^x\alpha e^{-\alpha \tau }d\tau =1-e^{-\alpha x}$. The properties of the probability distribution are listed as follows:  $\underset{x\to \infty }{\lim }P\left(x\right)=1$; i.e., far away, the probability of producing a parallel tends to 1. Far away from the line l, the Euclidean situation is almost recovered. The other limiting case is $P\left(0\right)=0$. If  $\alpha x\ll 1$  is assumed,  $P\left(x\right)\cong \alpha x$ is true. The probability density  $\tilde{P}\left(x\right)={\displaystyle \frac{dP}{dx}}=\alpha e^{-\alpha x}$ fulfills the normalization demands, namely,

$${\int }_0^{\infty }\tilde{P}\left(x\right)dx={\int }_0^{\infty }\alpha e^{-\alpha x}dx=1$$

(10)

Consider a 1D grid of the equally spaced points  $\left\{x_1,\dots x_N\right\}$, where the spacing  $s>0\text{ is constant; }{x}_k=ks$. The expected number of successful parallels is given by Equation (11):

$$ℇ\left(N\right)={\sum }_{k=1}^N\left(1-e^{-\alpha ks}\right)=N-e^{-\alpha s}{\displaystyle \frac{1-e^{-\alpha Ns}}{1-e^{-\alpha s}}}$$

(11)

using the geometric series for  $e^{\alpha Ns}$. Let us calculate the normalized continuous-density limit. If candidate points are dense over an interval  $\left[0,L\right]$, we replace sums by integrals:

$${\displaystyle \frac{1}{L}}ℇ\left(N\right)\cong {\displaystyle \frac{1}{L}}{\int }_0^L\left(1-e^{-\alpha x}\right)dx=1-{\displaystyle \frac{1-e^{-\alpha L}}{\alpha L}}$$

(12)

As  $L\to \infty$, the average success fraction tends to 1, which is intuitively clear. Indeed, far-away points almost surely give parallels.

Nearby points “see” the line as slightly “fuzzy” and fail to construct a clean parallel, but faraway points almost surely obtain the Euclidean parallel. This somewhat mimics optical parallax: if you are close to a mirror, reflected rays are distorted, while at infinity, the geometry stabilizes.

Example 2.

Consider the line l and point A at the fixed distance  $x_0$ from the line. Axis x is perpendicular to line l. Line and point A fix the plane $\zeta =〈l,A〉$. We introduce the Euclid fifth postulate of geometry re-formulated as follows: the density of the probability of building a single line via fixed point A parallel to the given line l is given by $\tilde{P}=\delta \left(x-x_0\right)$, where $\delta \left(x\right)$ is the delta-function of Dirack. Thus, it is possible to build the parallel line only via point A. The probability of building the straight line parallel to l via points belonging to $\zeta =〈l,A〉$ other than A is zero. Rigorously speaking, we replace the Playfair axiom with the following statement:

Fix a point A. Let x denote the perpendicular distance from A to the reference line l. The probability that a construction procedure produces exactly one line through A parallel to l is given by the generalized density  $\tilde{P}=\delta \left(x-x_0\right)$. The logical-symbolic formulation appears as follows:

$$\exists l\exists A\left(A\notin l\wedge d\left(A,l\right)=x_0\wedge \forall B\left(B\notin l\to P\left(\exists !m\left(m\parallel l\wedge B\in m\right)\right)=\tilde{P}(d\left(B,l\right)\right)\right),$$

(13)

where  $d\left(A,l\right)$ is the fixed perpendicular distance  $x_0$ from l. For every other point B not on l,  $\forall B\notin l$, we have

$$P\left(\exists !m\left(m\parallel l\wedge B\in m\right)\right)=\delta \left(d\left(B,l\right)-x_0\right),$$

(14)

so, if  $B=A$, then  $d\left(B,l\right)=x_0$ and  $\tilde{P}=1$; if  $B\ne A$,  $d\left(B,l\right)\ne x_0$, and hence,  $\tilde{P}=0$.

It is possible to parameterize lines through a fixed point A by their angle  $\theta \in \left[0,\pi \right]$. There is a unique  ${\theta }_0$ for which the line is parallel to l. Then, one may model the probability density on  $\widehat{p}\left(\theta \right)=\delta \left(\theta -{\delta }_0\right),$ i.e., the random construction always chooses the specific direction ${\theta }_0$. This is equivalent (for a fixed A) to deterministic uniqueness of the parallel. However, this is not the usual Euclidean/Playfair postulate for all points; it singles out a locus of points (distance  $x_0$) that behave classically, while all other points behave “non-Euclidean” (no parallels).

Now, consider the problem already addressed in Example 1. Take a lattice of horizontal rows at  $\left\{x_1,\dots x_N\right\}$, starting from the line l, spacing  $s>0,x_k=ks$. Let  $x_0=ma$ for some integer m. Under the strict delta axiom, only the row  $k=m$ produces parallels (each lattice point there yields one parallel with probability 1). So, the expected number of parallels per column equals unity (from the one special row) and 0 elsewhere.

Example 3.

Now, we replace the Playfair axiom with the following statement:

Consider the line l and a point A at the distance  $x_0$ from the line. Line and point A fix the plane  $\zeta =〈l,A〉$. Axis x is perpendicular to line l. Now, the density of the probability of building a single line via any point A parallel to the given line l is given by  $\tilde{P}=\delta \left(x-x_0\right)$, where  $\delta \left(x\right)$ is the delta-function of Dirack. Thus, it is possible to build the parallel line via any point A. We replace the Playfair axiom with the following statement:

The probability of building exactly one line m through any point A parallel to l is given by the generalized density  $\tilde{P}=\delta \left(x-x_0\right)$ for any point belonging to  $\zeta =〈l,A〉.$

This δ-formulation simply reproduces Euclidean geometry, because for each chosen point, the δ-function peaks at its own  $x_0$, ensuring one parallel, and may be summarized as follows:

$$\forall A\in \zeta \setminus l:P\left(\exists !m\wedge m\parallel l\right)=\tilde{P}\left(A\right)=\delta \left(x\left(A\right)-x_0\right)$$

(15)

Example 4.

Now, we replace the Dirack $\delta -$ function from the previous example with the probability density ${\tilde{P}}_{\epsilon }\left(x\right)$, which concentrates at $x_0$ when $\epsilon \to 0$:

$${\tilde{P}}_{\epsilon }\left(x\right)={\displaystyle \frac{1}{\sqrt{2\pi }}}exp\left(-{\displaystyle \frac{{\left(x-x_0\right)}^2}{2{\epsilon }^2}}\right)$$

(16)

Clearly,  ${\int }_{-\infty }^{+\infty }{\tilde{P}}_{\epsilon }\left(x\right)dx=1$, and as  $\epsilon \to 0$,  ${\tilde{P}}_{\epsilon }\left(x\right)\to \delta \left(x-x_0\right)$. Now, consider the example already addressed in Example 1. Take a lattice of horizontal rows at  $\left\{x_1,\dots x_N\right\}$, starting from the line l, spacing  $s>0,x_k=ks$. Let  $x_0=ma$ for some integer m; the expected number of parallels per column is

$${\sum }_{k\in Z}{\tilde{P}}_{\epsilon }\left(ka\right)={\displaystyle \frac{1}{a}}{\int }_{-\infty }^{+\infty }{\tilde{P}}_{\epsilon }\left(x\right)dx={\displaystyle \frac{1}{a}}$$

(17)

2.2. Physical Realization of the Hilbert-P Probabilistic Geometry

Consider the surface with a variable Gaussian curvature $K=k_1{k}_2$, where $k_1$ and $k_2$ are the principal curvatures at a point on the surface. Adopt that within time $\tau$ the Gaussian curvature of the surface is $K=0$ (this corresponds to a plane), and within the same time $\tau$, the Gaussian curvature of the surface is $K<0$ (hyperbolic surface with a saddle point). Consider a triangle on the surface. The angle sum S of a triangle is random within the probabilistic geometry. With probability $={\displaystyle \frac{1}{2}}$, the triangle is Euclidean and $S=\pi ;$ with probability $1-P={\displaystyle \frac{1}{2}},$ the triangle may be non-Euclidean (say, hyperbolic), and then $S=S_{non-eucliduan}<\pi$ (if hyperbolic-like behavior dominates). The expected value of the angles’ sum $ℇ\left(S\right)$ is calculated with Equation (1), as follows: $ℇ\left(S\right)={\displaystyle \frac{1}{2}}\pi +{\displaystyle \frac{1}{2}}\mathcal{E}{S}_{non-euclidian}$.

Now, consider the more general case, in which the Gaussian curvature of the surface is $K=0$ within time ${\tau }_1,$ and within ${\tau }_2$ the Gaussian curvature of the surface is $K<0$. Thus,

$$P\left(S=\pi \right)={\displaystyle \frac{{\tau }_1}{{\tau }_1+{\tau }_2}}=P_1$$

(18)

And correspondingly,

$$P\left(S<\pi \right)={\displaystyle \frac{{\tau }_2}{{\tau }_1+{\tau }_2}}=P_2$$

(19)

Clearly, the normality condition $P_1+P_2=1$ holds. Thus, the introduced probabilistic geometry works for random, stochastic surfaces with a variable curvature.

2.3. Alternative Probabilistic Geometries

The introduced probabilistic geometry is not unique. Alternative probabilistic geometries are possible.

Consider the probabilistic geometry while adopting the Hilbert system of axioms and FP formulated as follows (the Probabilistic Parallels Axiom 1 is supplied by Equaitons (1) and (2):

Probabilistic Parallels Axiom 2.

Given a line l and a point $A\notin l$, no line parallel to l through A with probability $P^{\prime }$ is possible, where $0\le P\le 1$.

Consider one more version of the probabilistic geometry adopting the Hilbert system of axioms and the FP formulated as follows:

Probabilistic Parallels Axiom 3.

Given a line l and a point $A\notin l$, more than one line parallel to l through A with probability $P^{″}$ is possible, where $0\le P\le 1$.

Let us summarize the suggested systems of axioms of the probabilistic geometry in

Table 1. Applicability of various types of probabilistic geometry for particular surfaces.

Geometry	${\mathit{P}}^{\prime }$	P	${\mathit{P}}^{″}$
Elliptic	1	0	0
Euclidean	0	1	0
Hyperbolic	0	0	1

.

2.4. Probabilistic Geometry Adopting the Fuzzy Version of the First Axiom of the Hilbert Geometry

Additional versions of the probabilistic geometry are possible. The first axiom of the Hilbert geometry states the following: for every two distinct points, there exists a line that contains both of them.

We modify the first axiom as follows: For every two distinct points, there exists with probability $0\le P\le 1$ a line that contains both of them. This creates a new version of stochastic/randomized/probabilistic geometry. Under this probabilistic axiom, for two points A and B, a line may or may not exist through them. The existence of such a line is not deterministic, but follows a pre-fixed probability distribution. The introduced axiom interferes with other axioms of the Hilbert geometry. Consider Axiom II.1: If point B lies between A and C, then all three points are distinct and lie on the same line. Betweenness requires a line between the points. If no line exists between A and C (or others), betweenness is undefined. Thus, the entire system of Hilbert axioms should be changed. Thus, we supply only a very preliminary sketch of this version of the probabilistic geometry. For example, the theorem establishing the probability of triangle existence appears now as follows:

Theorem 6.

Probability of Triangle Existence.

Given three non-collinear points A, B, C, the probability of all three pairwise connecting lines AB, BC, CA is $P^3.$ It should be emphasized that the probabilistic version of the first Hilbert axiom destroys the entire version of the Hilbert/Euclidian geometry, due to the fact that it interferes with other axioms. In classical Euclidian/Hilbert geometry, any two points determine a unique line. Now, for a pair A, B, the probability that there is a line through both is P. Thus, there may exist pairs of points not connected by a line, i.e., geometrically disconnected pairs. Hence, collinearity becomes probabilistic. Congruence axioms (Group III, Section 2.1) fail. If segment AB does not exist, then its congruence relations are undefined. The probabilistic modification of Axiom I.1 interacts with any version of the parallel postulate. Even if the parallel postulate holds, lines connecting points may not exist. The concept of parallelism now has a domain of definition: only among point–line pairs where both exist. Thus, this version of a probabilistic system of axioms touches the entire axiomatic system, it reflects a randomized or discrete space, where geometry may fail locally due to missing connections, and it resembles percolation models in statistical physics: some connections exist, and others do not. When $P=1,$ it recovers classical Euclidean geometry, and when, in turn, $P=0,$ all space is disconnected, namely, no lines exist. We conclude that the probabilistic version of the first axiom of the Euclid/Hilbert axiomatic system entails deep changes in the entire structure of geometry due to the fact that this version interferes with other axioms. The situation is quite different when we change the Axiom of Archimedes (Axiom V.1, see Section 2.1).

2.5. Geometry Emerging from the Probabilistic Version of the Axiom of Archimedes

The situation is quite different when the continuity axioms (Group V) are adopted in their probabilistic version. Hilbert introduced continuity axioms (implying Dedekind completeness or Archimedean properties, see Section 2.1, Group V). These axioms are independent of incidence, order, and congruence. Modifying or removing them leads to non-Archimedean or discrete geometries. Thus, they can be changed independently. Recall the Axiom of Archimedes as it appears in Book V of Euclid’s Elements as Definition 4:

Given any two segments AB and CD, there exists a positive integer n, such that when laying off the segment CD consecutively n times along a ray starting at A, the total length exceeds the length of AB.

The Axiom of Archimedes states that there is no infinitely long segment: even a tiny length can add up to pass any large segment with enough repetitions. There is also no infinitely small segment: if a segment were truly “infinitely small”, no matter how many times you stacked it, it would never pass a finite segment—which contradicts the axiom.

Now, we introduce the following probabilistic version of the Axiom of Archimedes:

Given any two segments AB and CD, there exists with a probability $0\le P\le 1$ a positive integer n such that when laying off the segment CD consecutively n times along a ray starting at A, the total length exceeds the length of AB. What do we have in extremal cases?

Let us start from $P=1.$ This is the standard Archimedean case, just expressed probabilistically; namely, with certainty, we can lay off CD repeatedly to surpass AB.

The geometry behaves like standard Euclidean geometry; namely,

(i)

No infinitesimal segments exist.

(ii)

Segment lengths can be compared meaningfully.

(iii)

Triangle inequality and other classical theorems still hold.

(iv)

The real number system underlies the segment-length arithmetic.

The second extremal case corresponds to $P=0$. This is the non-Archimedean case. There is zero probability that any finite number of consecutive CD segments laid from A will ever surpass AB. In this case,

(i)

CD is infinitesimal compared to AB.

(ii)

No finite sum n CD ever comes close to AB.

(iii)

Segment length comparison fails: the field of segment lengths is now non-Archimedean. The geometry becomes non-Euclidean in a fundamental way.

(iv)

Triangle inequality may break down or become trivial.

(v)

This setting resembles non-standard analysis or hyperreal geometries, where infinitesimals exist.

Of course, we supplied only a brief sketch of probabilistic, non-Archimedean geometry to be developed in the future investigations. However, it should be emphasized that modification of the Archimedean axiom does not touch other groups of the Euclid/Hilbert geometry.

3. Discussion

3.1. Novelty of the Introduced Approach

The proposed axiomatic framework preserves the logical structure of axiomatic Hilbert geometry while allowing uncertainty in the truths of axioms (Playfair axiom in our case). This is a new paradigm: instead of geometry being fully determined, we treat it as an ensemble of geometries, covering the Euclidean, hyperbolic, elliptic geometries and also the probabilistic geometry itself. The introduced approach opens the door to studying geometric properties statistically (expected theorems, variance of configurations, etc.). In classical David Hilbert geometry, axioms are deterministic: every axiom is either true or false. In the suggested system, each geometric statement S is assigned a probability $P\left(S\right)\in \left[0.1\right]$ that expresses how likely it is to hold in a given realization of the geometry (Hilbert’s axiom system without the fifth postulate, denoted $H^0,$ i.e., groups I–III and V of axioms remain untouched and deterministic).

This creates a new meta-layer over the traditional logical structure: it merges axiomatic geometry with probability theory, which has not been carried out in standard axiomatics. To the best of our knowledge, this is the first attempt to incorporate probabilistic reasoning directly into the axiomatic foundations of geometry.

The suggested Hilbert-P-Geometry is different from the stochastic geometry [24]. Stochastic geometry studies random geometric structures in a fixed deterministic geometric space (usually Euclidean space) [24]. The randomness of the stochastic geometry is in the objects, not in the axioms or logical structure. The introduced approach is fundamentally different because it changes the logical layer of geometry, not the geometric objects or their measurements. It introduces a probability measure on the space of logical statements, not on points, lines, or distances. It is also different from probabilistic metric spaces [25]. The reported approach does not assign distributions to distances; instead, it assigns probabilities to the truth of whole geometric statements. Hilbert-P-Geometry is different from uncertain geometry, which is used in computational geometry or computer graphics [26]. Uncertain geometry handles imprecise or noisy data—for example, points whose coordinates are not known exactly but within some confidence region. The introduced approach is axiomatic and ontological: it assumes that the geometry itself is a random structure, not just our knowledge about it.

3.2. Directions of Future Investigations

In the future investigations, the relation of the suggested probabilistic geometry to the stochastic Riemannian geometry in which distances and angles can have expected values, variances, and even distributions should be established [24]. It is possible to define a random metric space where the usual metric axioms hold probabilistically [24]. Thus, the suggested probabilistic geometry may model space-time with probabilistic local curvature in quantum gravity analogies [25,26,27,28]. The introduced probabilistic geometry is well-expected to be useful in robotics/computer vision, when robots/computers operate in environments with uncertain or partially known geometry [29]. The introduced framework may be useful for computer-aided design (CAD); mechanical parts always have manufacturing tolerances; ideal geometry is never achieved exactly. Thus, probabilistic geometry can model geometric dimensioning and tolerancing with estimated functional deviations rather than worst-case bounds.

4. Conclusions

Euclidean geometry has for centuries provided a perfect and inspiring model of scientific and deductive reasoning. David Hilbert, one of the most influential mathematicians of the late 19th and early 20th centuries, proposed the axiomatization of physics as a part of his broader program to bring mathematical rigor and formalism to all sciences. His vision was to build physics—especially theoretical physics—on a foundation as solid and precise as Euclidean geometry, reducible to axioms, known today as Hilbert axioms. The fifth postulate of Euclid, also known as the Parallels Postulate, has a long and fascinating history marked by attempts to either prove it from other axioms or to replace it altogether. The Hilbert system of axioms contains the fifth postulate of the Euclidean geometry, reshaped as the Playfair axiom: given a line l and a point A not on l, there is at most one line through A parallel to l. The rejection of the inviolability of the fifth postulate gave rise to non-Euclidean geometries, developed by Nikolay Lobachevski and János Bolyai. The next intellectual step is suggested in the presented paper, enabling probabilistic development of the Euclidean geometry. The probabilistic nature of the fifth postulate is assumed; namely, we adopt that for a given a line l and a point $A\notin l$, there is exactly one line through A with probability P, where $0\le P\le 1$. The introduced geometry is labeled the “probabilistic geometry”, thus resembling the famous fuzzy logic developed by Lotfi Aliasger Zadeh. The suggested geometry is different from the “fuzzy geometry”, which is a study of interaction of uncertain geometric objects. In our approach, the geometrical objects (points, lines, etc.) remain untouched; axioms themselves are taken as fuzzy. The probability is understood as a frequency of prescribed events (to be unique parallel to line l) in a statistical ensemble of lines passing through a fixed point A. The introduced approach embeds the classical Hilbert system of axioms of Euclidean geometry inside a probabilistic semantic framework [30].

In the limiting cases, we obtain the well-known geometries; namely, $P=1$ corresponds to the standard Euclidean geometry, whereas $P=0$ corresponds to the elliptic- and hyperbolic-like geometries. The situation when $0<P<1$ corresponds, in turn, to the kind of stochastic geometry, which is labeled in the paper as the “probabilistic geometry”. Introduced probabilistic geometry is also essentially different from the conventional stochastic geometry, in which traditional systems of axioms are adopted and remain untouched. In the introduced probabilistic geometry, one of the axioms (say the Playfair axiom) is probabilistic. Parallel constructions now are Bernoulli trials. Theorems of the probabilistic geometry are discussed. Given a triangle and a line drawn from a vertex parallel to the opposite side, the event that this line is actually parallel occurs with probability P. Otherwise, the line may intersect the side or diverge. Parallelism is not transitive in the probabilistic geometry. If a quadrilateral has opposite sides built using “parallel” constructions, it closes into a parallelogram with probability $P^2$, since both pairs must independently satisfy the parallel condition.

Different versions of probabilistic parallel axioms are considered. The Playfair axiom is logically disconnected from the other Hilbert axioms of Euclidean geometry. Thus, the probabilistic versions of the fifth postulate may be smoothly assembled with other Hilbert axioms. Probabilistic axioms of incidence may be introduced. However, adopting these axioms destroys the entire internal structure of the Euclidean geometry. Contrastingly, the probabilistic version of the Axiom of Archimedes may be consistently assembled with the Hilbert axioms. The suggested probabilistic geometry reveals the unexplored field of mathematical investigations, to be developed in future. The presented paper is no more than a brief introduction into the probabilistic geometry. The probabilistic geometry may model space-time with probabilistic local curvature in quantum gravity. The introduced probabilistic geometry is well-expected to be useful in robotics/computer vision, when robots/computers operate in environments with uncertain or partially known geometry. We conclude that the introduced probabilistic geometry represents a fascinating and unexplored probabilistic extension of the Euclidean geometry.