Research on a Degradation Identification Method for GIS UHF Partial Discharge Sensors Based on S-Parameters
Abstract
1. Introduction
2. Material and Methods
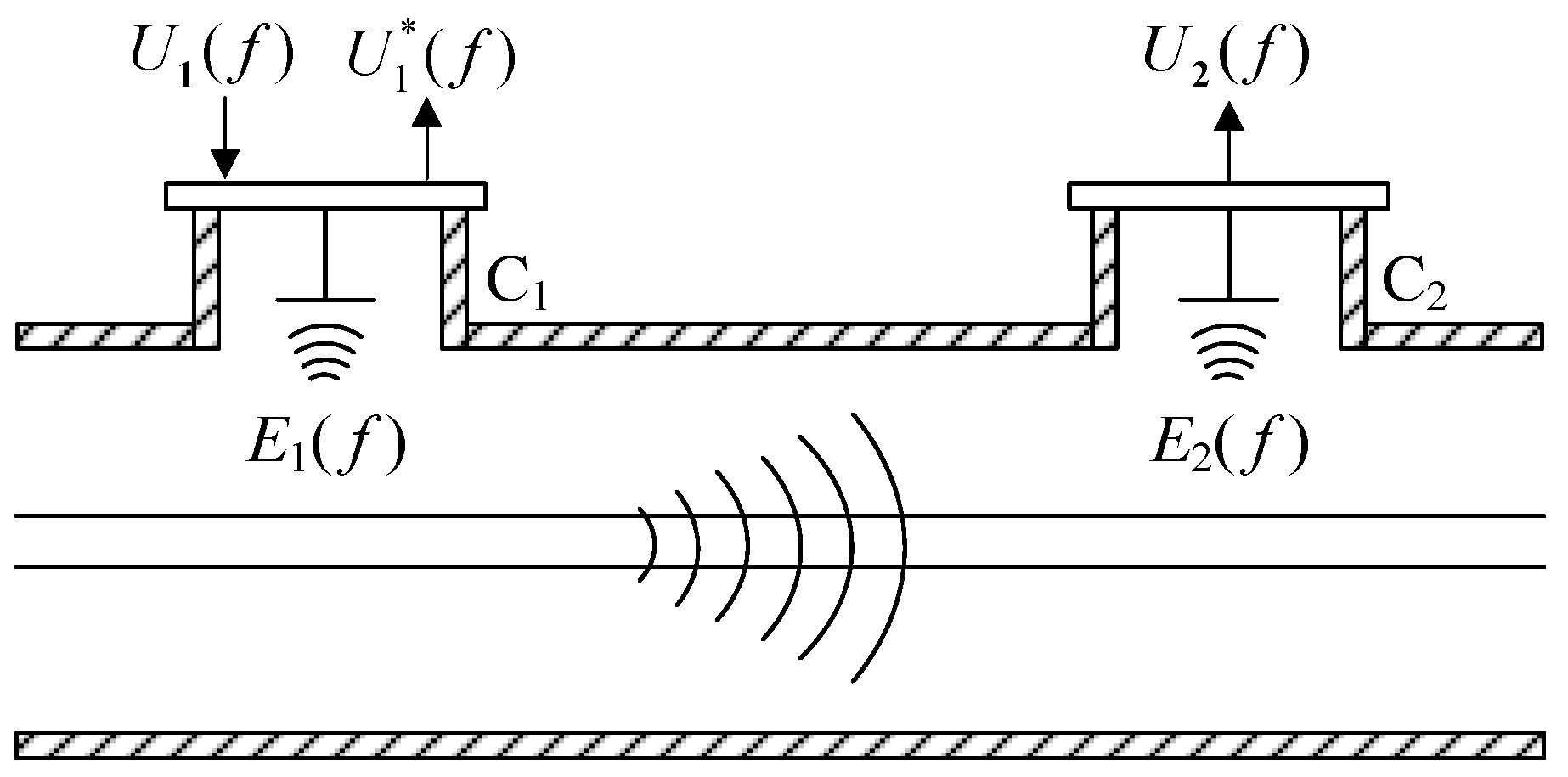
2.1. S-Parameter Network
2.2. S11 and S21 Change Mechanism
2.3. Verification Method Based on Cross-Comparison of S11 and S21
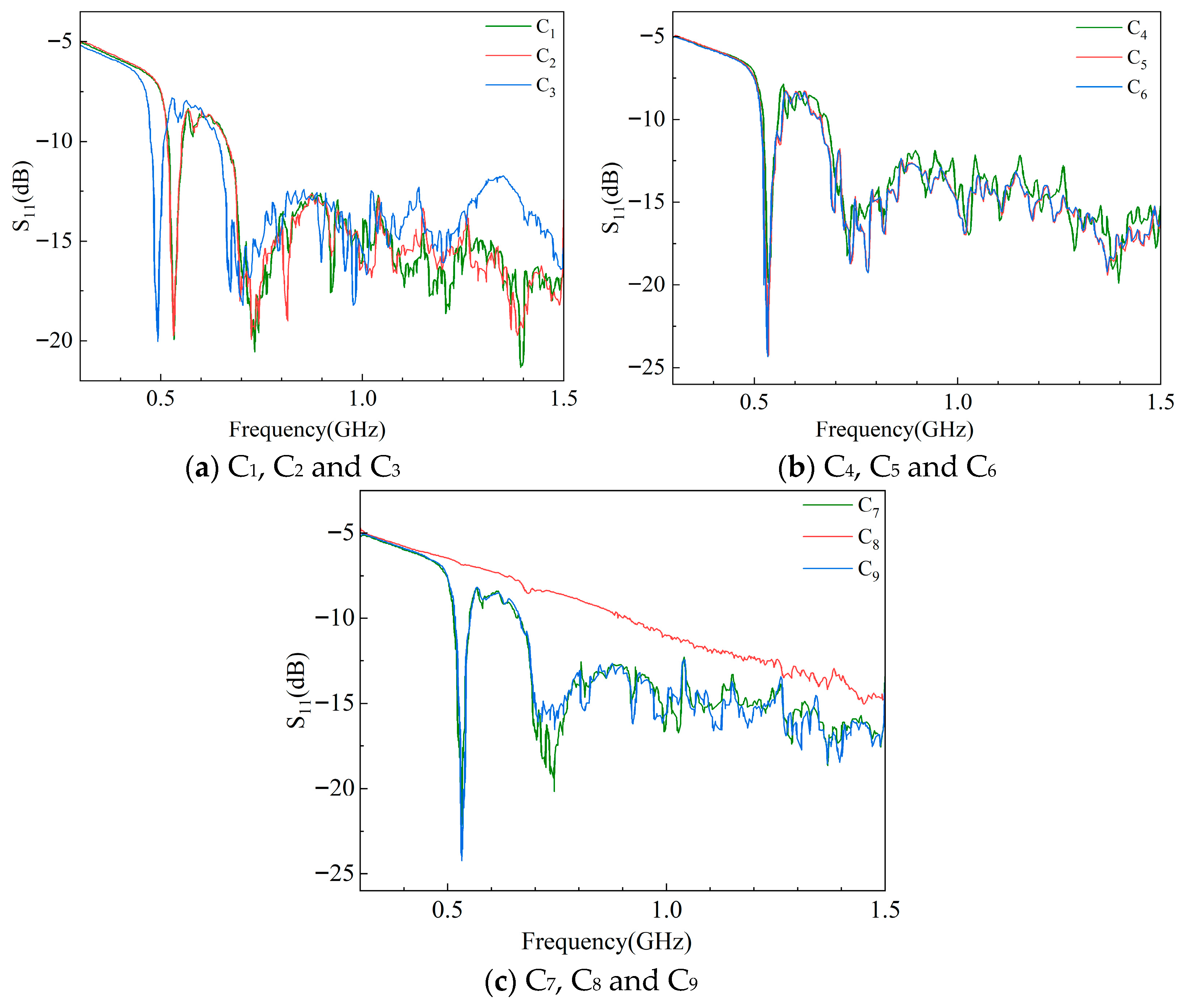
3. Simulations
3.1. Modeling of the UHF Sensor
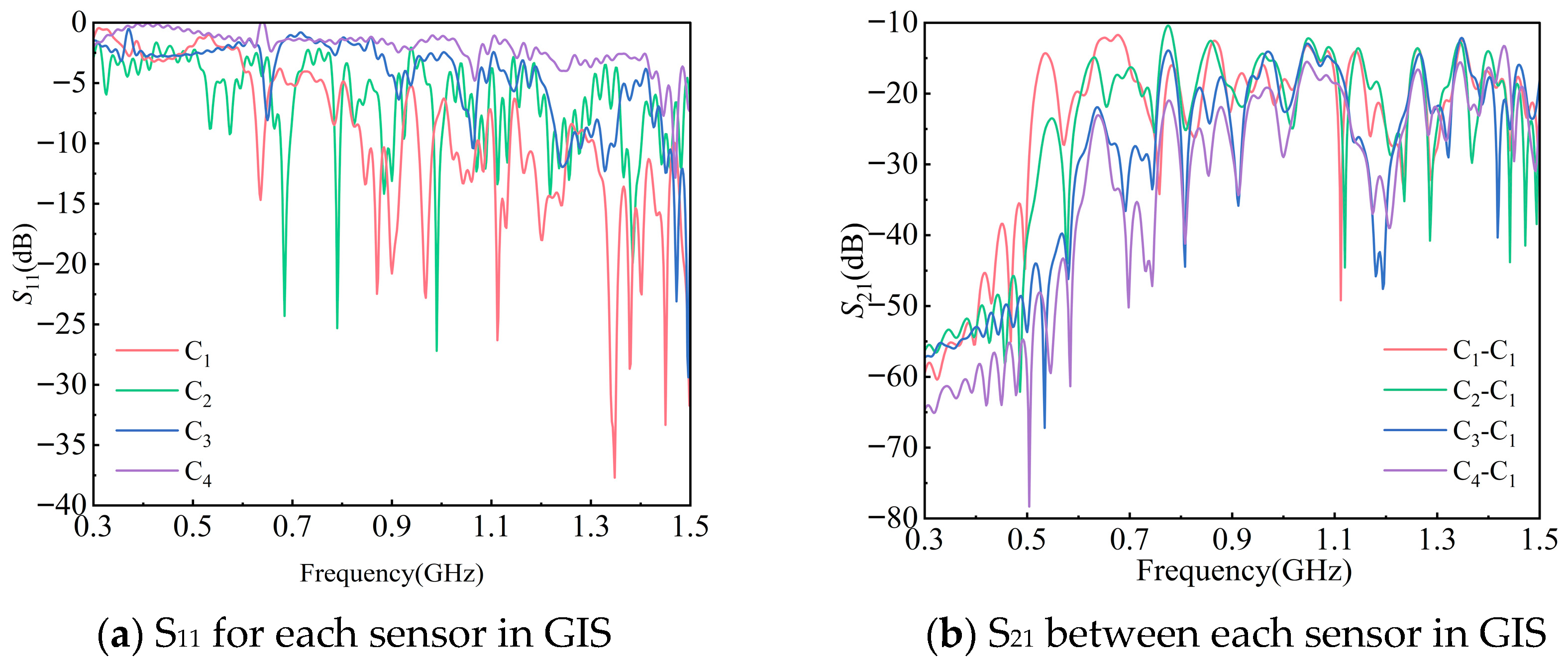
3.2. GIS UHF Sensor Verification Model
3.3. Analysis of Simulation Results
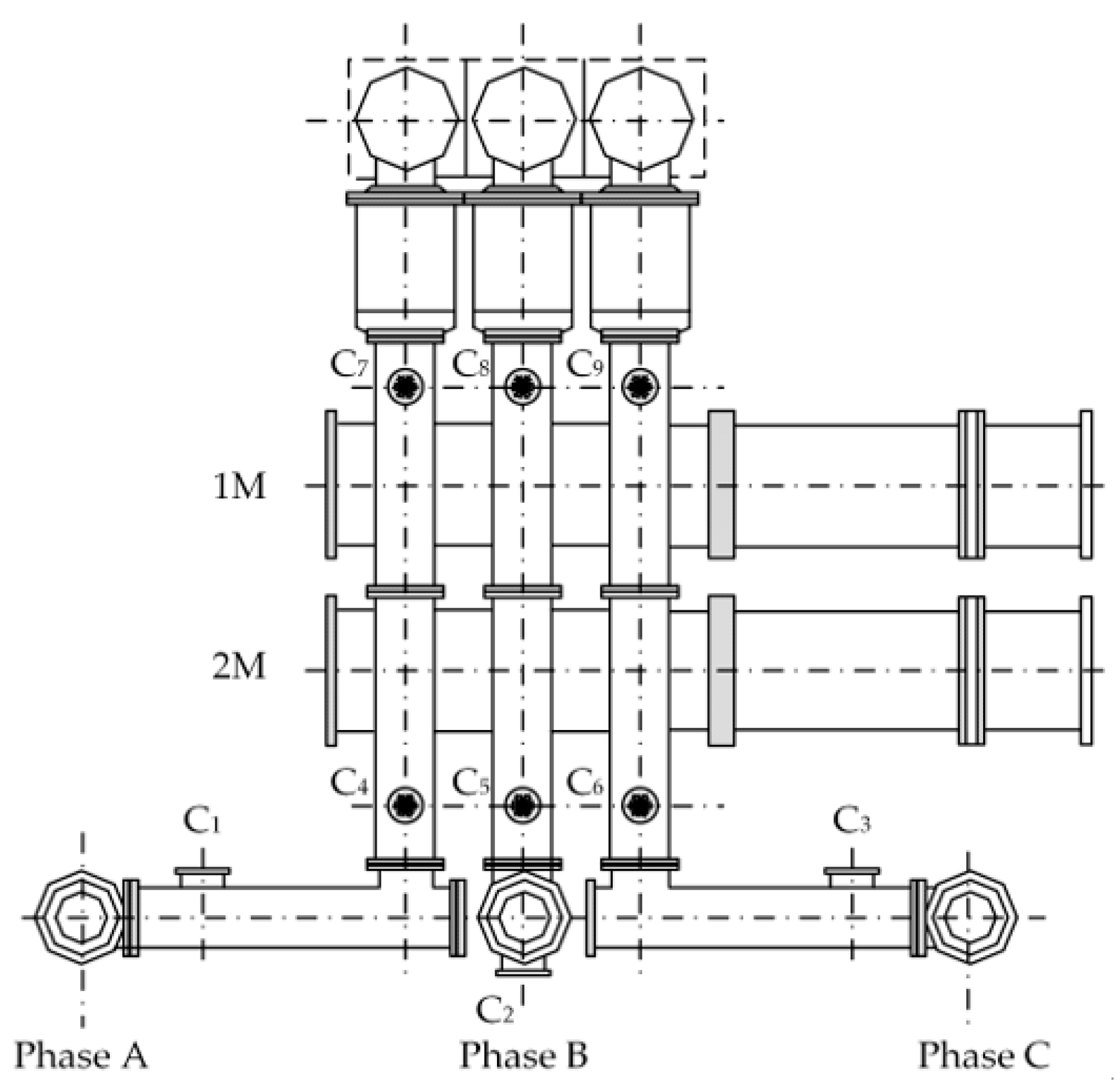
4. Experiments
4.1. Verification Process
4.2. Analysis of Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schichler, U.; Koltunowicz, W.; Gautschi, D.; Girodet, A.; Hama, H.; Juhre, K.; Lopez-Roldan, J.; Okabe, S.; Neuhold, S.; Neumann, C.; et al. UHF Partial Discharge Detection System for GIS: Application Guide for Sensitivity Verification. In VDE High Voltage Technology 2016; ETG-Symposium: Berlin, Germany, 2016; pp. 1–9. [Google Scholar]
- Metwally, I. Status review on partial discharge measurement techniques in gas-insulated switchgear/lines. Electr. Power Syst. Res. 2004, 69, 25–36. [Google Scholar] [CrossRef]
- Chai, H.; Phung, B.; Mitchell, S. Application of UHF Sensors in Power System Equipment for Partial Discharge Detection: A Review. Sensors 2019, 19, 1029. [Google Scholar] [CrossRef] [PubMed]
- Behrmann, G.J.; Gross, D.; Neuhold, S. Limitations of Attempting Calibration of Partial Discharge Measurements in VHF and UHF Ranges. In Proceedings of the 2020 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), East Rutherford, NJ, USA, 18–30 October 2020; pp. 155–159. [Google Scholar]
- Escurra, C.M. VHF Magnetic and Electric Sensors for Partial Discharge Measurements in GIS. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2024. [Google Scholar]
- Xavier, G.V.R.; Silva, H.S.; da Costa, E.G.; Serres, A.J.R.; Carvalho, N.B.; Oliveira, A.S.R. Detection, Classification and Location of Sources of Partial Discharges Using the Radiometric Method: Trends, Challenges and Open Issues. IEEE Access 2021, 9, 110787–110810. [Google Scholar] [CrossRef]
- Ishak, A.M.b. Calibration and Design of UHF Partial Discharge Sensors Using Finite-Difference Time-Domain Modelling. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2013. [Google Scholar]
- Pan, J.; Gao, Q.; Liu, Q.; Guo, Z.; Yuan, F.; Pan, F. Field Calibration Method of GIS Partial Discharge UHF Sensor Based on Network Analyzer. In Proceedings of the 2017 International Conference on Computer Technology, Electronics and Communication (ICCTEC), Dalian, China, 19–21 December 2017; pp. 834–838. [Google Scholar]
- Tang, J.; Xu, Z.; Zhang, X.; Sun, C. GIS partial discharge quantitative measurements using UHF microstrip antenna sensors. In Proceedings of the 2007 Annual Report—Conference on Electrical Insulation and Dielectric Phenomena, Vancouver, BC, Canada, 14–17 October 2007; pp. 116–119. [Google Scholar]
- Hussain, G.A.; Hassan, W.; Mahmood, F.; Shafiq, M.; Rehman, H.; Kay, J.A. Review on Partial Discharge Diagnostic Techniques for High Voltage Equipment in Power Systems. IEEE Access 2023, 11, 51382–51394. [Google Scholar] [CrossRef]
- Siegel, M.; Coenen, S.; Beltle, M.; Tenbohlen, S.; Weber, M.; Fehlmann, P.; Hoek, S.M.; Kempf, U.; Schwarz, R.; Linn, T.; et al. Calibration Proposal for UHF Partial Discharge Measurements at Power Transformers. Energies 2019, 12, 3058. [Google Scholar] [CrossRef]
- BHabib, B.; Al Zaabi, O.; Harid, N.; Al Hosani, K.; Alkhatib, M. Condition Monitoring Based on Partial Discharge Diagnostics Using UHF Sensors: A Comprehensive State-of-the-Art Review. IEEE Trans. Dielectr. Electr. Insul. 2024, 31, 2860–2873. [Google Scholar]
- Roslizan, N.D.; Rohani, M.N.K.H.; Wooi, C.L.; Isa, M.; Ismail, B.; Rosmi, A.S.; Mustafa, W.A. A Review: Partial Discharge Detection using UHF sensor on High Voltage Equipment. J. Phys. Conf. Ser. 2020, 1432, 012003. [Google Scholar] [CrossRef]
- Chen, H.; Wang, H.; Zhang, Z.; Guo, R.; Han, X.; Zhang, X.; Li, J. A Novel Composite Sensor for UHF Partial Discharge and Gas State Measurement in GIS. IEEE Trans. Instrum. Meas. 2024, 73, 1501410. [Google Scholar] [CrossRef]
- Mor, A.R.; Heredia, L.C.C.; Muñoz, F.A. A Novel Approach for Partial Discharge Measurements on GIS Using HFCT Sensors. Sensors 2018, 18, 4482. [Google Scholar] [CrossRef] [PubMed]
- Darwish, A.N.A. Design and Modeling of UHF Partial Discharge Sensors: FE-Based PD Signal Propagation in High Voltage Systems. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2021. [Google Scholar]
- Zhou, L.; Tan, X.; Yan, J.; Shaoquan, Z. GIS UHF Partial Discharge On-line Monitoring Device Evaluation. IOP Conf. Ser. Mater. Sci. Eng. 2018, 439, 052026. [Google Scholar] [CrossRef]
- Mahdi, A.S.; Abdul-Malek, Z.; Arshad, R.N. SF6 Decomposed Component Analysis for Partial Discharge Diagnosis in GIS: A Review. IEEE Access 2022, 10, 27270–27288. [Google Scholar] [CrossRef]
- Shu, S.; Chen, J.; Chen, B.; Huang, H.; Ye, Z.; Chen, M.; Liu, C. A field calibration method based on forward transport coefficient for UHF partial discharge detection sensors in GIS. In Proceedings of the 2016 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Chengdu, China, 19–22 September 2016; pp. 1–4. [Google Scholar]
- Birla, R.; Mohammad, S.; Hashmi, G.; Zahrani, M. Partial Discharge Monitoring to Predict Failures in 230 kV GIS Substation using UHF and Ultrasonic Sensors. In Proceedings of the 2024 IEEE Electrical Insulation Conference (EIC), Minneapolis, MN, USA, 2–5 June 2024; pp. 112–116. [Google Scholar]
- Liang, R.; Wu, S.; Chi, P.; Peng, N.; Li, Y. Optimal Placement of UHF Sensors for Accurate Localization of Partial Discharge Source in GIS. Energies 2019, 12, 1173. [Google Scholar] [CrossRef]
- Álvarez, F.; Garnacho, F.; Ortego, J.; Sánchez-Urán, M.Á. Application of HFCT and UHF Sensors in On-Line Partial Discharge Measurements for Insulation Diagnosis of High Voltage Equipment. Sensors 2015, 15, 7360–7387. [Google Scholar] [CrossRef] [PubMed]
- Yadam, Y.R.; Sarathi, R.; Arunachalam, K. Numerical and Experimental Investigations on Influence of Internal Defect Parameters on Partial Discharge Induced UHF Signals in Gas Insulated Switchgear. IEEE Access 2022, 10, 110785–110795. [Google Scholar] [CrossRef]
- Shao, X.; He, W.; Xu, J.; Zhu, M.; Zhang, G. Partial discharge detection by extracting UHF signal from inner grading electrode of insulating spacer in GIS. IET Sci. Meas. Technol. 2018, 12, 90–97. [Google Scholar] [CrossRef]
- Mier, C.; Mor, A.R.; Castro, L.; Vaessen, P. Magnetic and electric antennas calibration for partial discharge charge estimation in gas-insulated substations. Int. J. Electr. Power Energy Syst. 2022, 141, 108226. [Google Scholar] [CrossRef]
- Rao, M.M.; Kumar, M. Ultra-High Frequency (UHF) Based Partial Discharge Measurement in Gas Insulated Switchgear (GIS). In Proceedings of the 2019 International Conference on High Voltage Engineering and Technology (ICHVET), Hyderabad, India, 7–8 February 2019; pp. 1–5. [Google Scholar]
- Escurra, C.M.; Khamlichi, A.; Dalstein, M.; Vidal, J.R.; Garnacho, F.; Mor, A.R.; Vu-Cong, T. Methods for Partial Discharge Calibration in Gas-Insulated Substations for HVDC Power Grids and Charge Evaluation Uncertainty. IEEE Sens. J. 2023, 23, 23486–23493. [Google Scholar] [CrossRef]
- Ahmed, R.; Abd-Rahman, R.; Ullah, Z.; Ullah, R.; Yousof, M.F.M.; Ullah, K. Partial Discharge Characterization of HFO(E) Gas Using Ultra-High Frequency (UHF) Antenna for Medium Voltage Switchgear Application. IEEE Access 2024, 12, 81196–81205. [Google Scholar] [CrossRef]
- Zhang, K.; Reid, A.; Clark, D.; Michelarakis, M.; Haddad, A.M. Diagnostics of Partial Discharge Measurements Utilizing Multi-Sensor Temporal Pulse Sequence Analysis. IEEE Access 2024, 12, 88992–89001. [Google Scholar] [CrossRef]
- Wu, X.; Han, X.; Zhang, L.; Li, X.; Ma, Y.; Li, J. Study on PD detection method in GIS under oscillating impulse voltage based on UHF method. In Proceedings of the 2017 1st International Conference on Electrical Materials and Power Equipment (ICEMPE), Xi’an, China, 14–17 May 2017; pp. 305–308. [Google Scholar] [CrossRef]
- Xu, H.; Yuan, C.; Ding, X.; Xu, Z.; Zhu, L. Simulation study of partial discharge UHF signal propagation characteristics in GIS. J. Phys. Conf. Ser. 2023, 2661, 012021. [Google Scholar] [CrossRef]
- Wang, S.; Xu, P.; Ren, M.; Li, S.; Ji, Y. Propagation Characteristics of UHF Partial Discharge Signals in GIS. In Proceedings of the 2023 8th Asia Conference on Power and Electrical Engineering (ACPEE), Tianjin, China, 14–16 April 2023; pp. 1470–1474. [Google Scholar] [CrossRef]


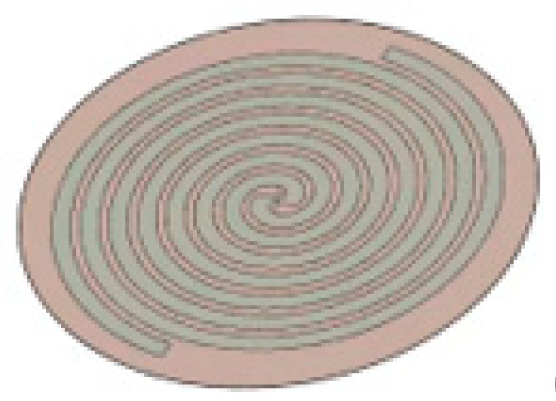



| Parameter | Assigned Value |
|---|---|
| Spiral inner diameter 2 r0/mm | 10 |
| Spiral outer diameter rm/mm | 166 |
| Spiral linewidth W/mm | 7.7 |
| Number of turns N | 3.7 |
| Spiral thickness D/mm | 0.035 |
| Substrate radius r/mm | 90 |
| Substrate thickness d/mm | 0.15 |
| Substrate relative permittivity εr | 4.6 |
| Sensor ID | Parameter Adjustment |
|---|---|
| C2 | Local relative permittivity εr increased to 6 |
| C3 | coil turns; N reduced to 1.7 |
| C4 | Antenna feed port disconnected |
| Calibration Index | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| −11.343 | −6.607 | −5.459 | −2.315 |
| Sensor Number | /dB | /dB |
|---|---|---|
| C1 | −9.264 | −24.513 |
| C2 | −6.382 | −25.681 |
| C3 | −4.610 | −29.520 |
| C4 | −2.052 | −33.441 |
| Serial | Name | Performance Parameters |
|---|---|---|
| 1 | multimeter | The maximum rated voltage should be no less than 800 V AC |
| 2 | N-type adapter | L-shaped 2 pieces (male connects to female), T-shaped 2 pieces (1 male connector and 2 female connectors) |
| 3 | RF cable | The attenuation characteristic should not exceed 3 dB |
| 4 | network analyzer | S11, S21 parametric test function frequency range: 1 MHz to 6.5 GHz test frequency interval not greater than 2 MHz |
| 5 | UHF sensor | frequency range: 500 MHz to 1500 MHz sensitivity: −70 dBm gain: 20 dBm |
| Sensor Number | /dB | /% | Qualified |
|---|---|---|---|
| C1 | −15.309 | 0 | yes |
| C2 | −14.471 | 5.47 | yes |
| C3 | −13.505 | 11.78 | no |
| C4 | −13.755 | 4.91 | yes |
| C5 | −14.335 | 0.90 | yes |
| C6 | −14.465 | 0 | yes |
| C7 | −14.077 | 1.08 | yes |
| C8 | −10.445 | 26.60 | no |
| C9 | −14.231 | 0 | yes |
| Sensor Number | /dB | /% | Qualified |
|---|---|---|---|
| C1-C4 | −72.129 | 7.72 | yes |
| C2-C5 | −66.959 | 0 | yes |
| C3-C6 | −84.915 | 26.81 | no |
| C4-C7 | −73.217 | 3.96 | yes |
| C5-C8 | −85.018 | 20.71 | no |
| C6-C9 | −70.430 | 0 | yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, T.; Cui, Y.; Tan, H.; Lu, W.; Zhang, F.; Liu, K.; Chen, X.; Wang, L. Research on a Degradation Identification Method for GIS UHF Partial Discharge Sensors Based on S-Parameters. Sensors 2025, 25, 6860. https://doi.org/10.3390/s25226860
Cao T, Cui Y, Tan H, Lu W, Zhang F, Liu K, Chen X, Wang L. Research on a Degradation Identification Method for GIS UHF Partial Discharge Sensors Based on S-Parameters. Sensors. 2025; 25(22):6860. https://doi.org/10.3390/s25226860
Chicago/Turabian StyleCao, Tienan, Yufei Cui, Haotian Tan, Wei Lu, Fuzeng Zhang, Kai Liu, Xiaoguo Chen, and Lujia Wang. 2025. "Research on a Degradation Identification Method for GIS UHF Partial Discharge Sensors Based on S-Parameters" Sensors 25, no. 22: 6860. https://doi.org/10.3390/s25226860
APA StyleCao, T., Cui, Y., Tan, H., Lu, W., Zhang, F., Liu, K., Chen, X., & Wang, L. (2025). Research on a Degradation Identification Method for GIS UHF Partial Discharge Sensors Based on S-Parameters. Sensors, 25(22), 6860. https://doi.org/10.3390/s25226860






