Leveraging Transformer Models for Seismic Fragility Assessment of Non-Engineered Masonry Structures in Malawi
Abstract
1. Introduction
2. Soft Computing Approaches for Seismic Vulnerability and Fragility Modeling
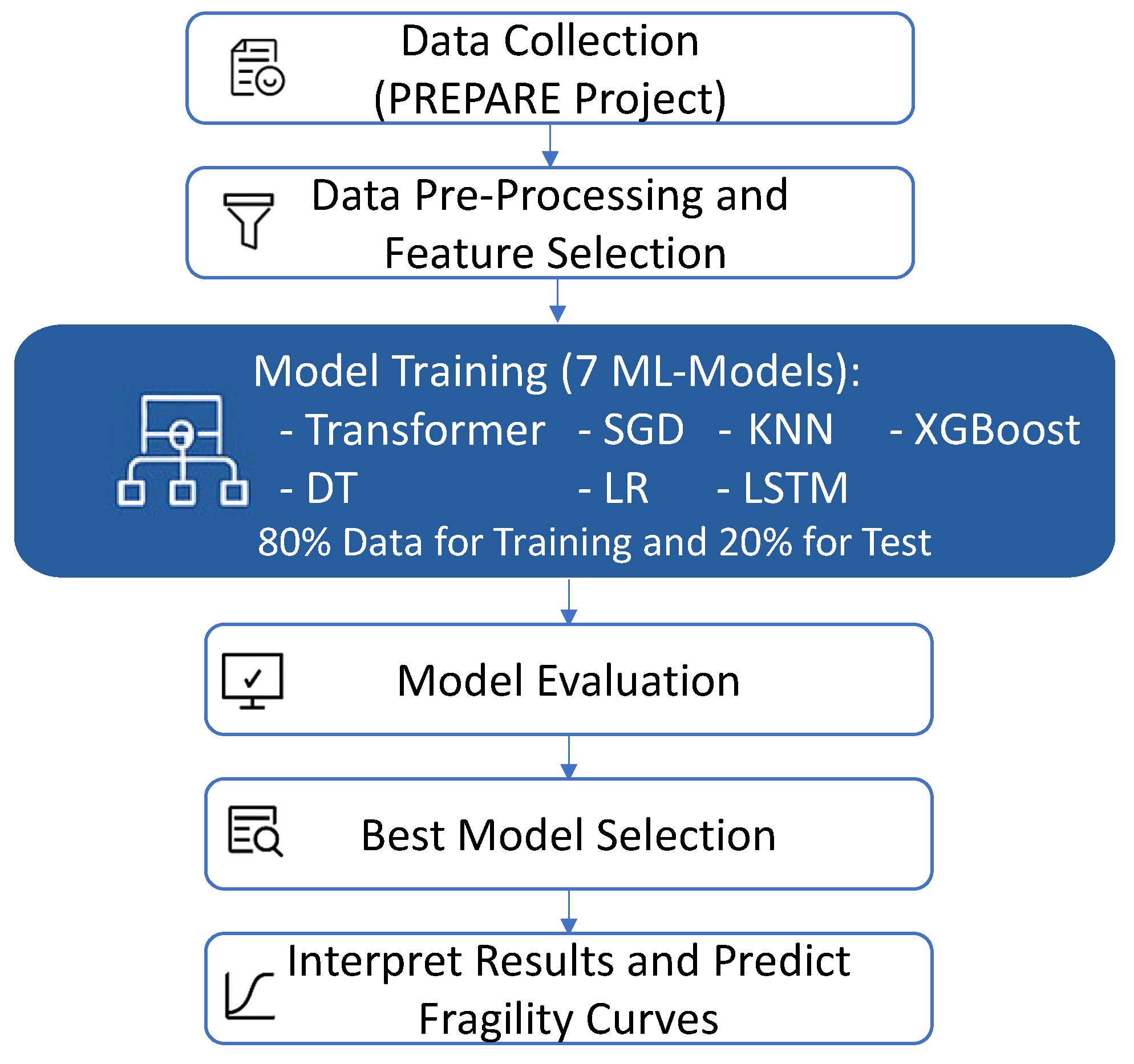
3. Methodology and Data
- Feature Selection: Structural parameters influencing seismic response were identified from field survey data, collected during the PREPARE project;
- Data Pre-processing: Categorical and ordinal structural parameters (variables) were encoded numerically for ML compatibility;
- Parameter Filtering: Among these features, those with high relevance to collapse probability under different PGA levels were retained;
- Dataset Splitting: The data was divided into training and test sets to build and evaluate predictive models;
- Model Training: Selected ML algorithms were trained on the prepared dataset;
- Performance Assessment: Model accuracy was evaluated using appropriate metrics;
- Application: Trained models were used to estimate collapse probabilities under unknown seismic scenarios.
3.1. Input Parameter
3.2. Output Parameter
- Structural and Material Data Collection:Detailed surveys were conducted on 323 buildings (646 façades) to record their geometric characteristics, construction typologies, and other relevant structural attributes. Simultaneously, laboratory tests were conducted to determine the mechanical properties of materials, including masonry units and mortar.
- Failure Mode Identification: The Failure Mechanism Identification and Vulnerability Evaluation method (FaMIVE) [50,53] was employed to identify the governing failure modes for each façade. These included out-of-plane, in-plane, gable, and strip failures, determined based on the physical configuration and material characteristics of the structures.
- Static Pushover (SPO) Modelling: Each façade was idealized as a single-degree-of-freedom (SDOF) system, and SPO curves were developed under three behavioral assumptions: (a) instability driven by geometry, (b) limited post-elastic deformation capacity, and (c) gradual strength degradation.
- Incremental Dynamic Analysis (IDA): The SPO curves were transformed into IDA curves using the SPO2IDA method, allowing the modeling of dynamic structural response under increasing levels of seismic excitation.
- PGA Derivation: Spectral acceleration values at various damage thresholds, obtained from IDA, were translated into corresponding PGA values using a suitable ground motion prediction equation.
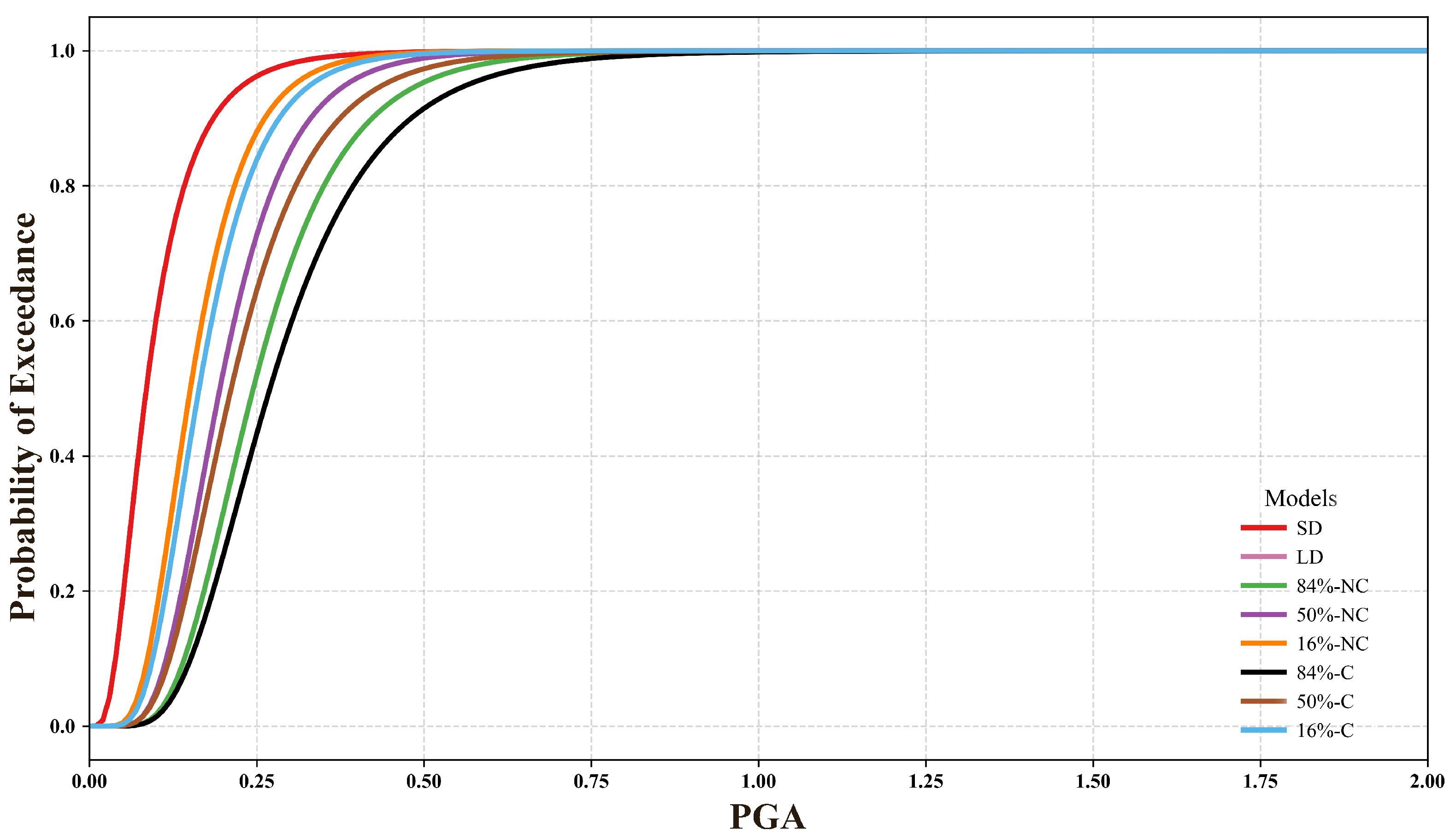
- Fragility Curve Construction: Finally, lognormal fragility functions were fitted to the PGA values associated with each damage state. For nonlinear behaviors (e.g., near collapse and collapse), variability due to different ground motion records was incorporated. In contrast, for more linear states (light and moderate damage), deterministic thresholds were applied across façades.
3.3. Data Preparation
4. Model Implementation and Validation
4.1. K-Nearest Neighbors (KNN)
4.2. Linear Regression (LR)
4.3. Stochastic Gradient Descent (SGD)
4.4. Decision Tree (DT)
4.5. Long Short-Term Memory (LSTM)
4.6. Extreme Gradient Boosting (XGBoost)
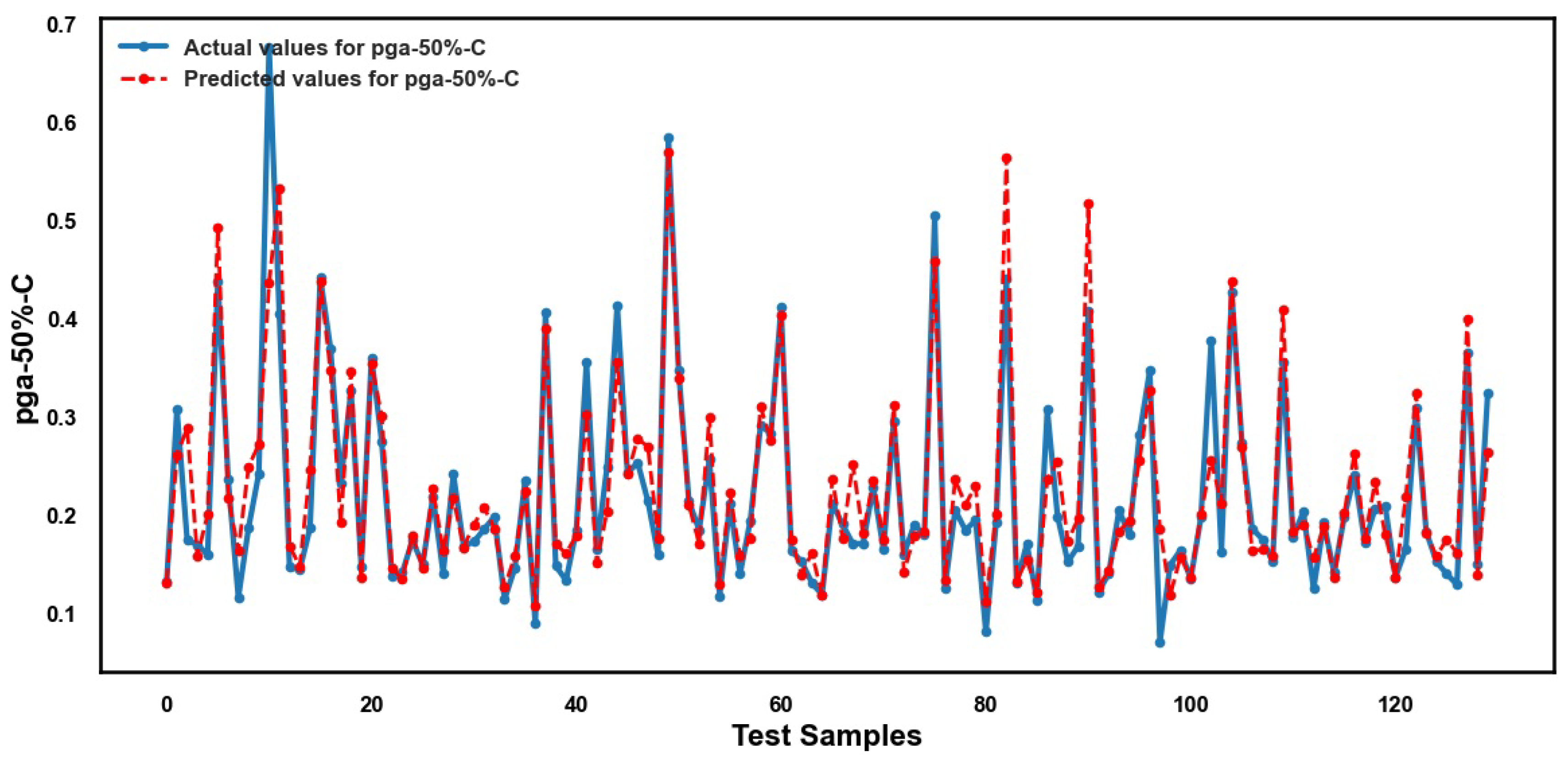
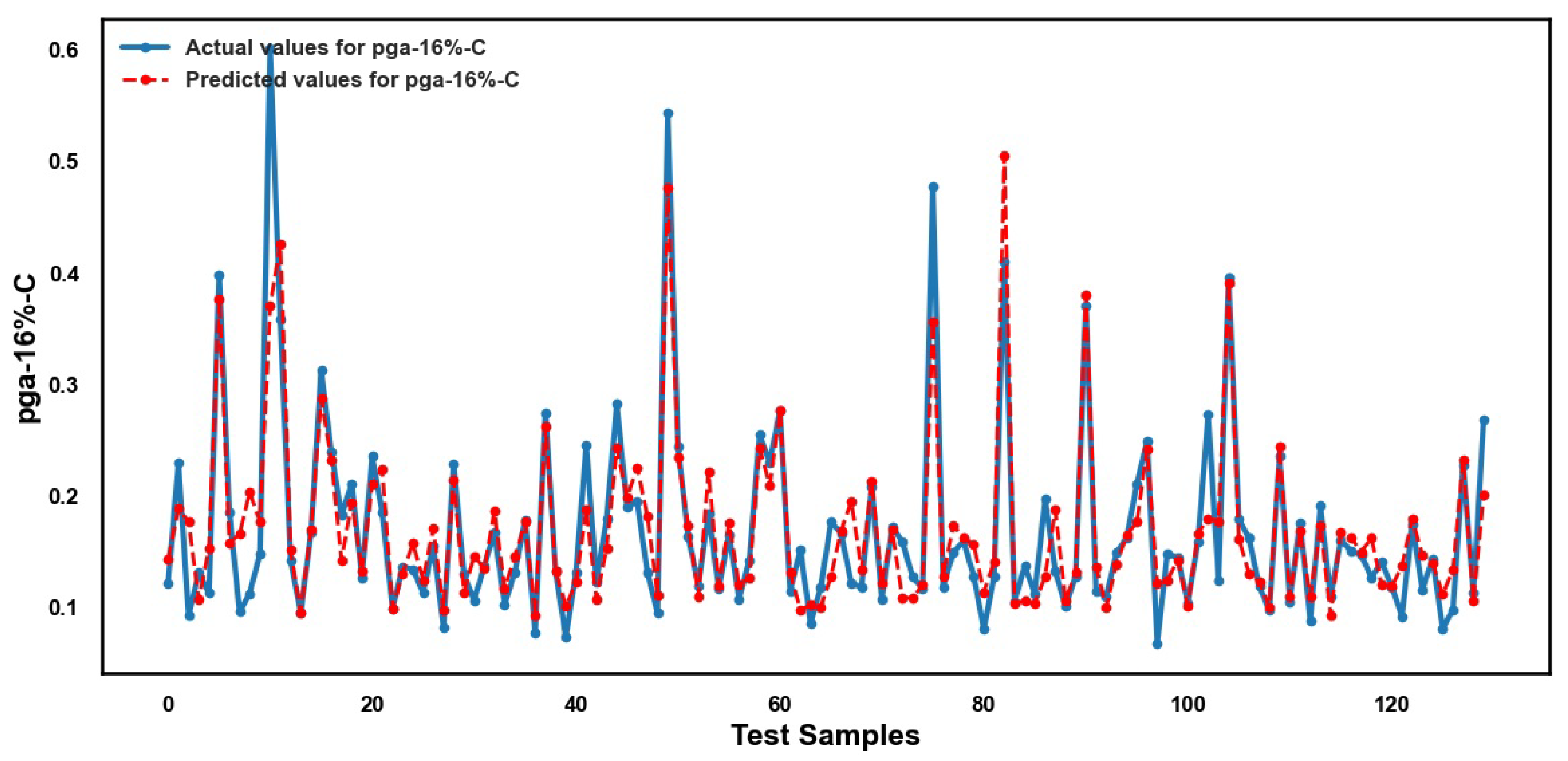
4.7. Transformer
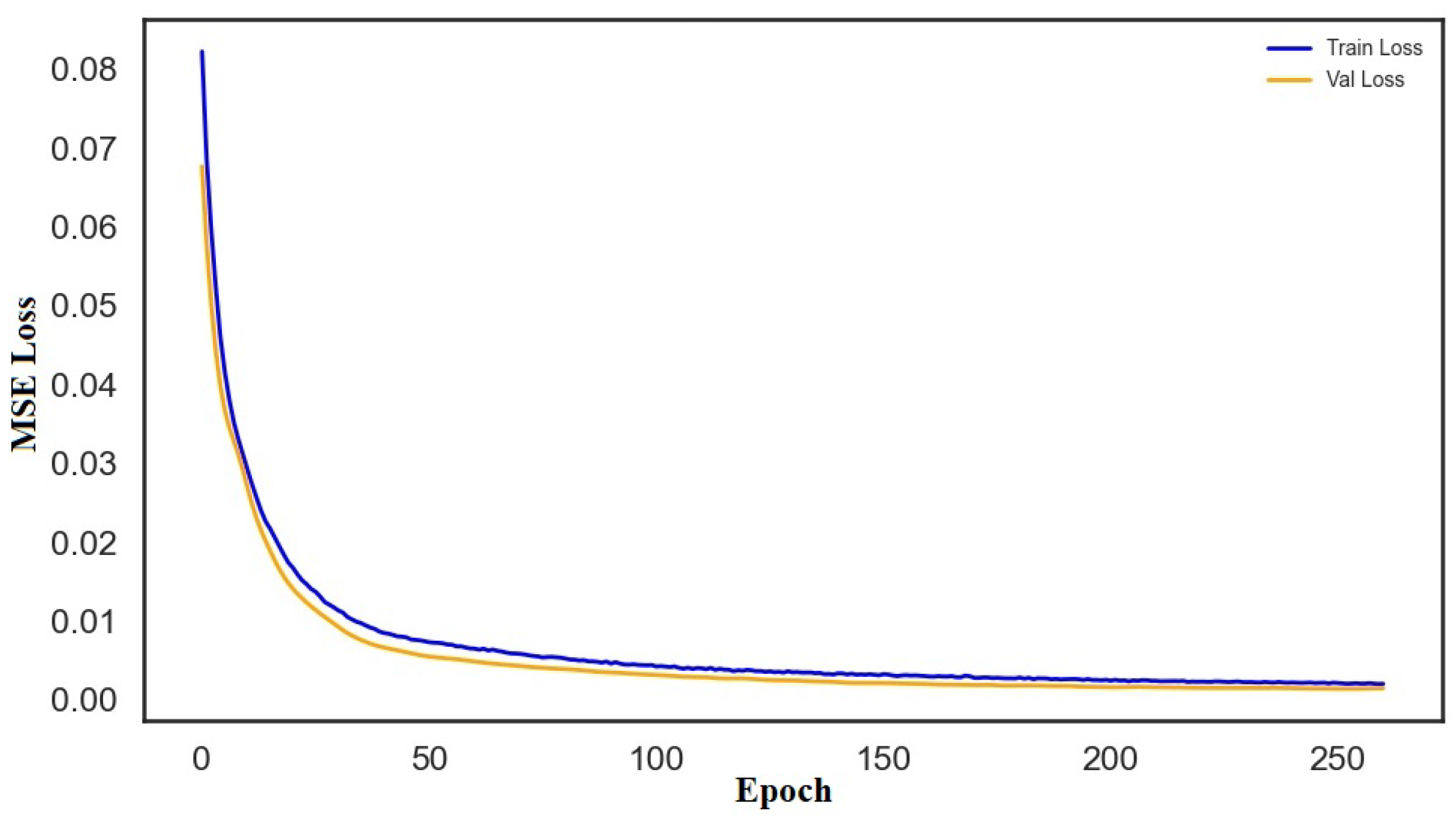
- Early Stopping: Training was monitored with patience of 10 epochs to prevent overtraining.
- Regularization: Weight decay () was incorporated into the Adam optimizer to penalize large weights.
- Learning Curve Analysis: Training and validation losses were tracked across epochs, showing that the validation loss remained stable and did not diverge notably from the training loss.
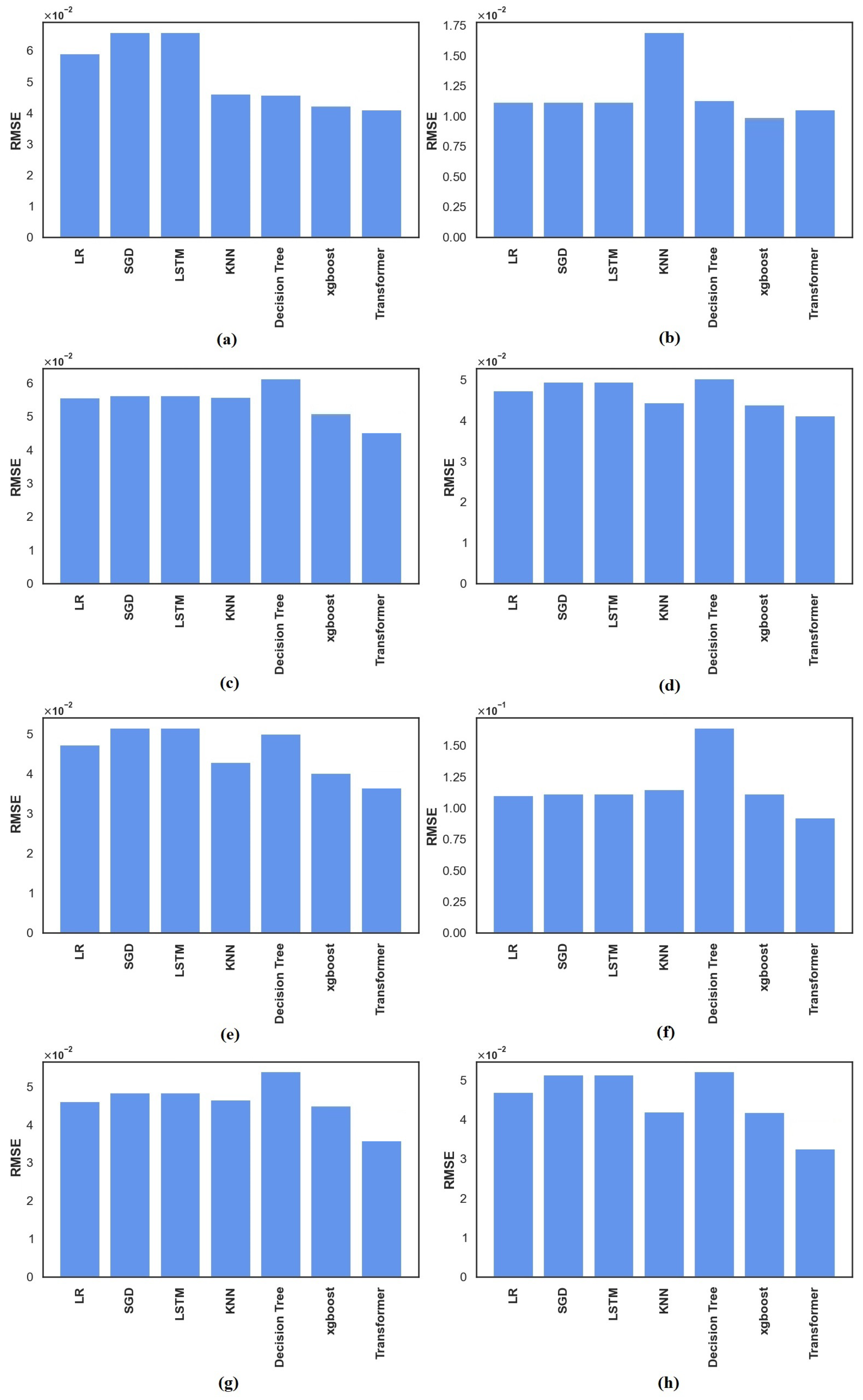
4.8. Model Evaluation Metrics
- MSE: Measures the average of the squared differences between predicted and actual values; fewer values are better.
- RMSE: As the root of MSE, it gives an interpretable error metric in the same unit as the target variable.
- MAPE: Shows the prediction error as a percentage, making it easier to understand the accuracy of the model relative to the actual values.
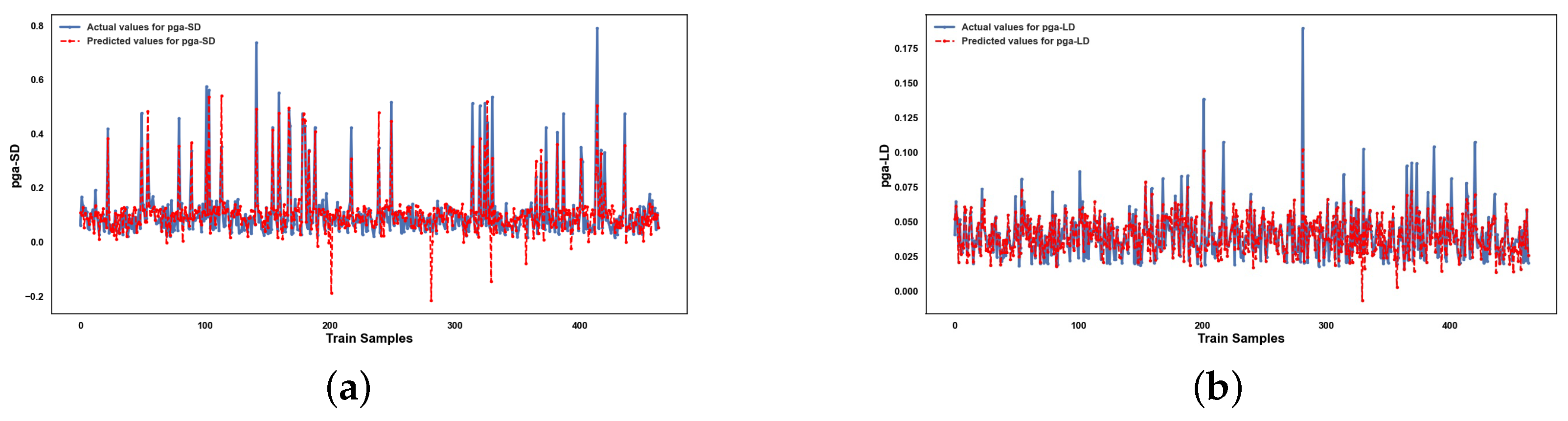
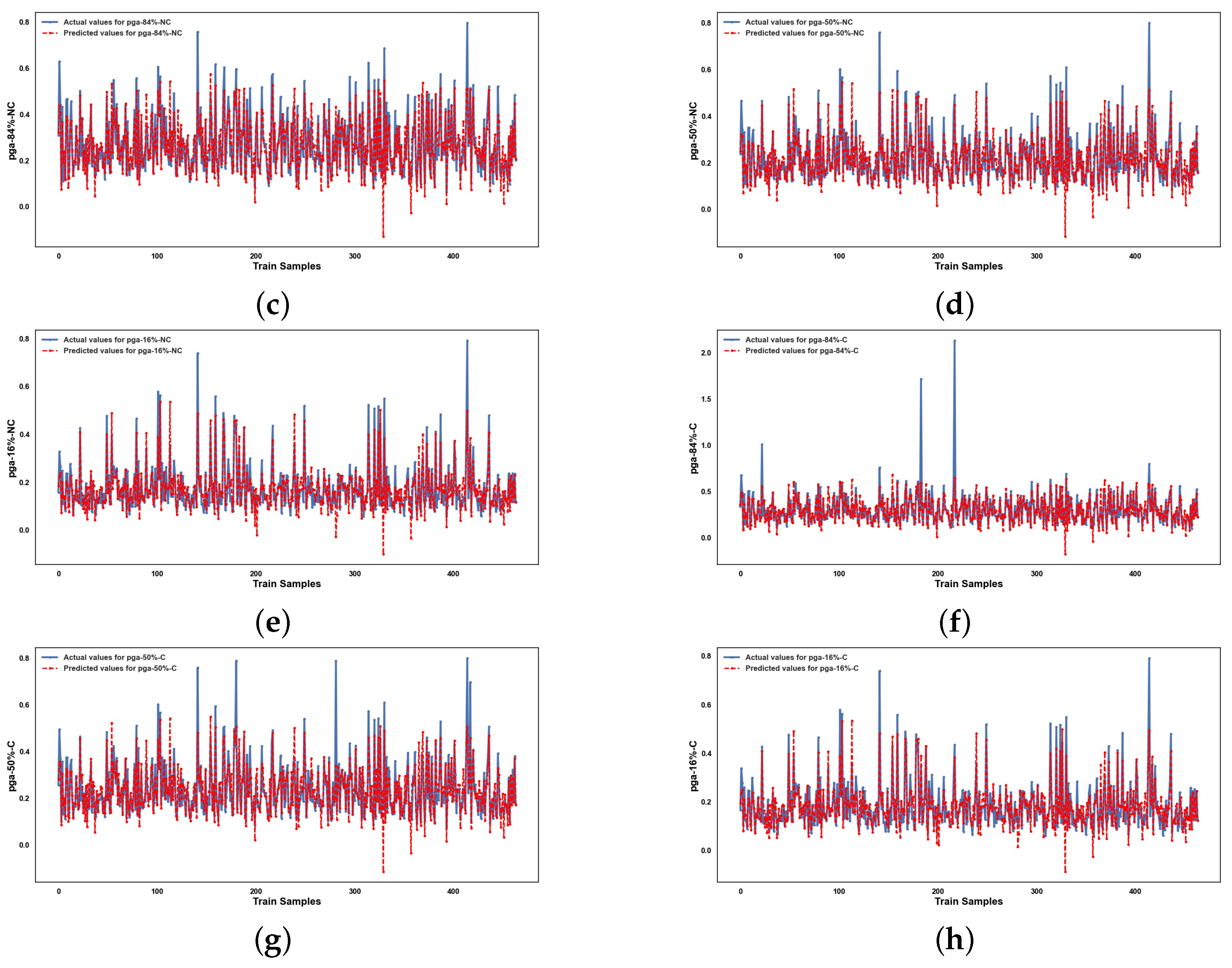
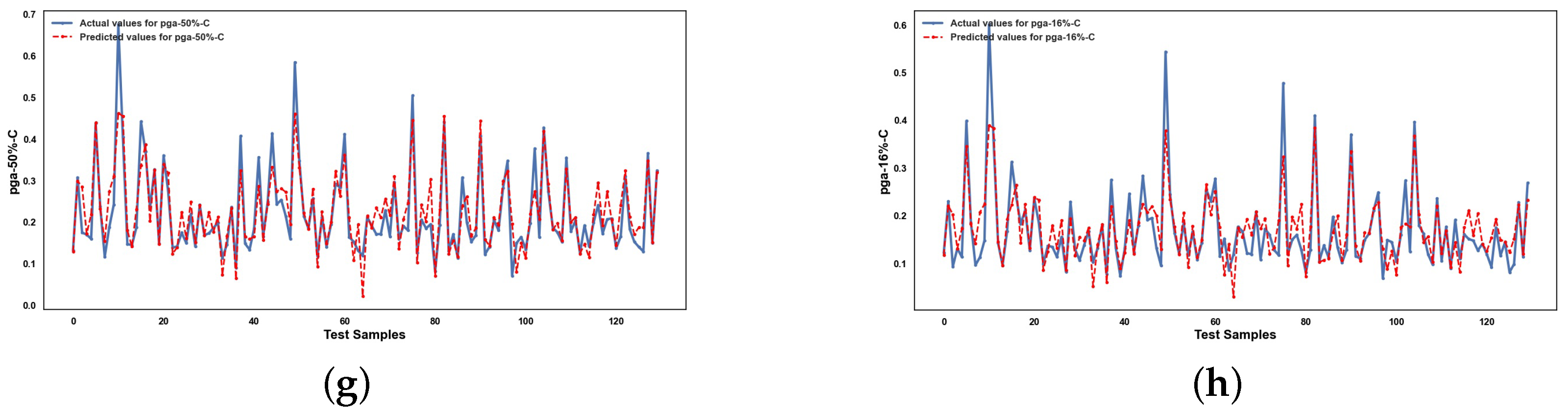
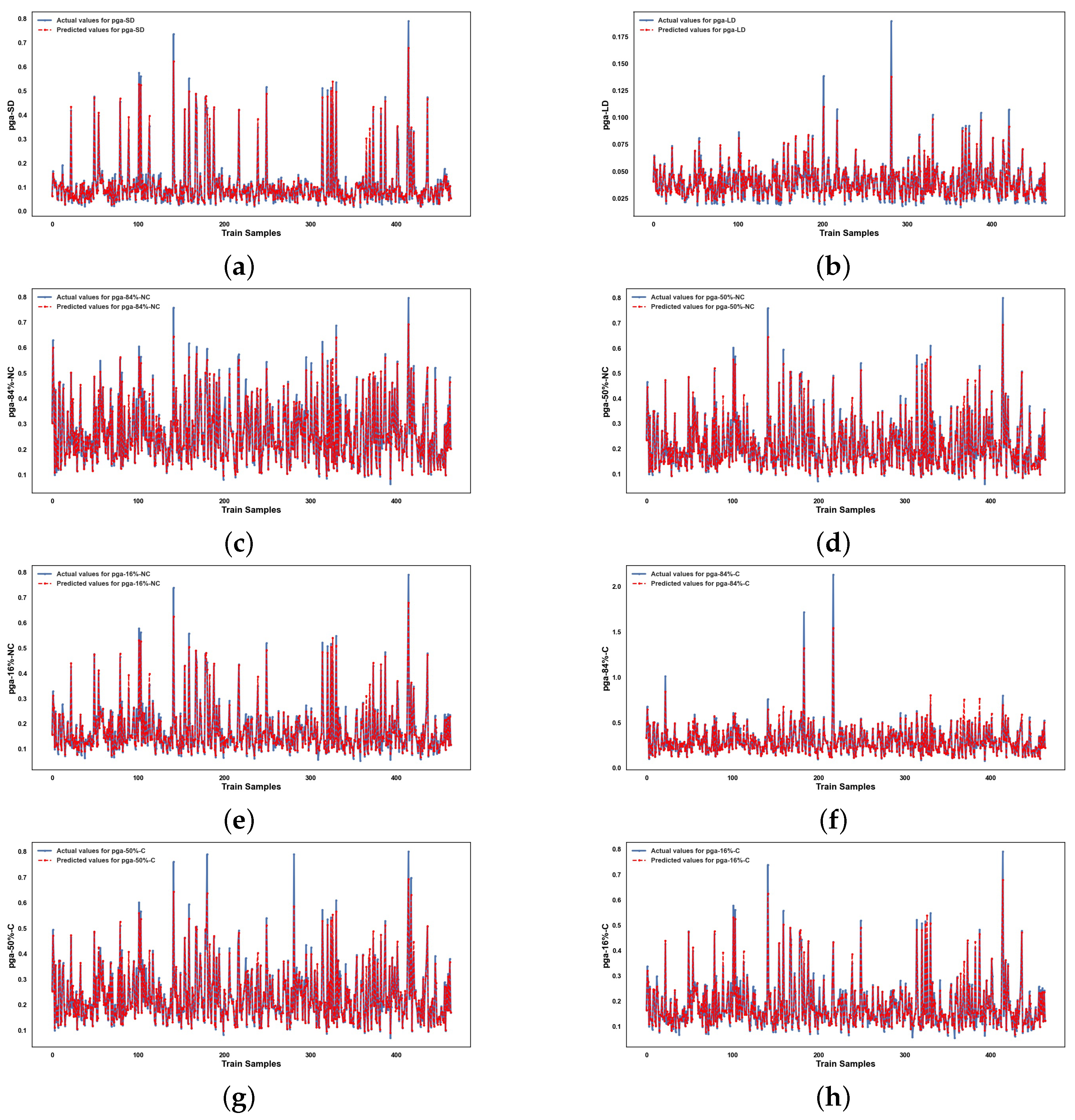
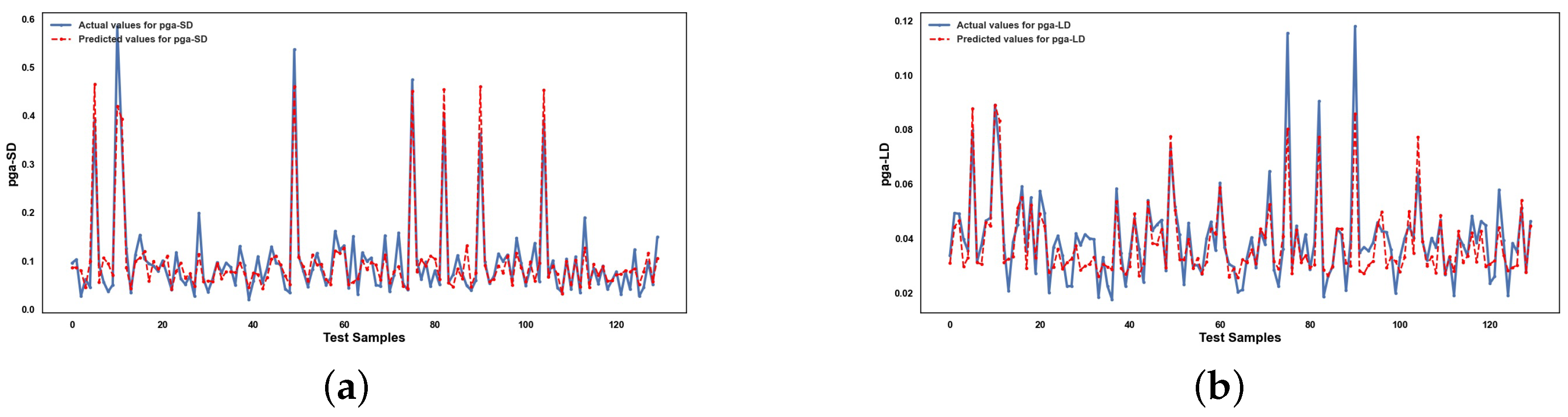
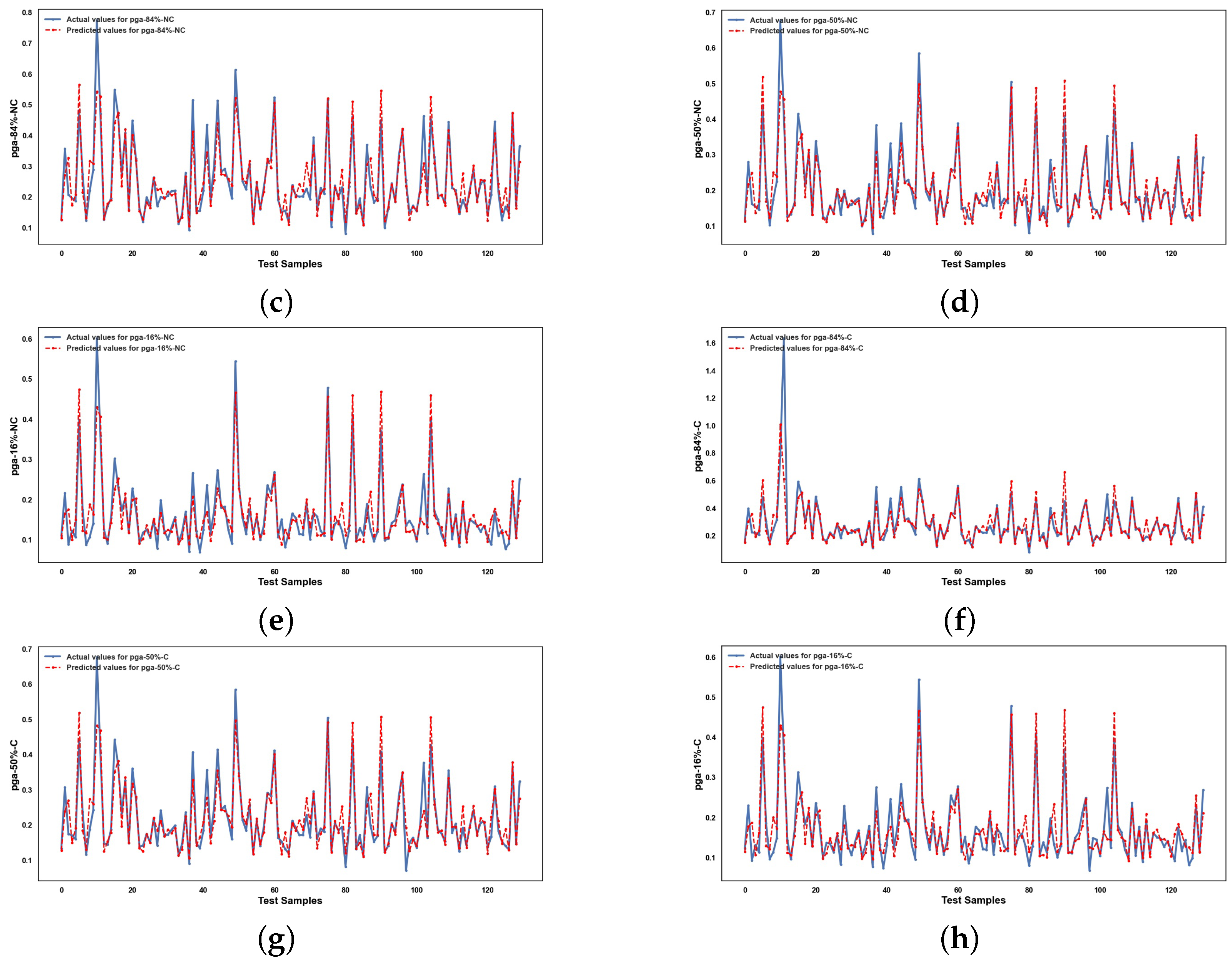
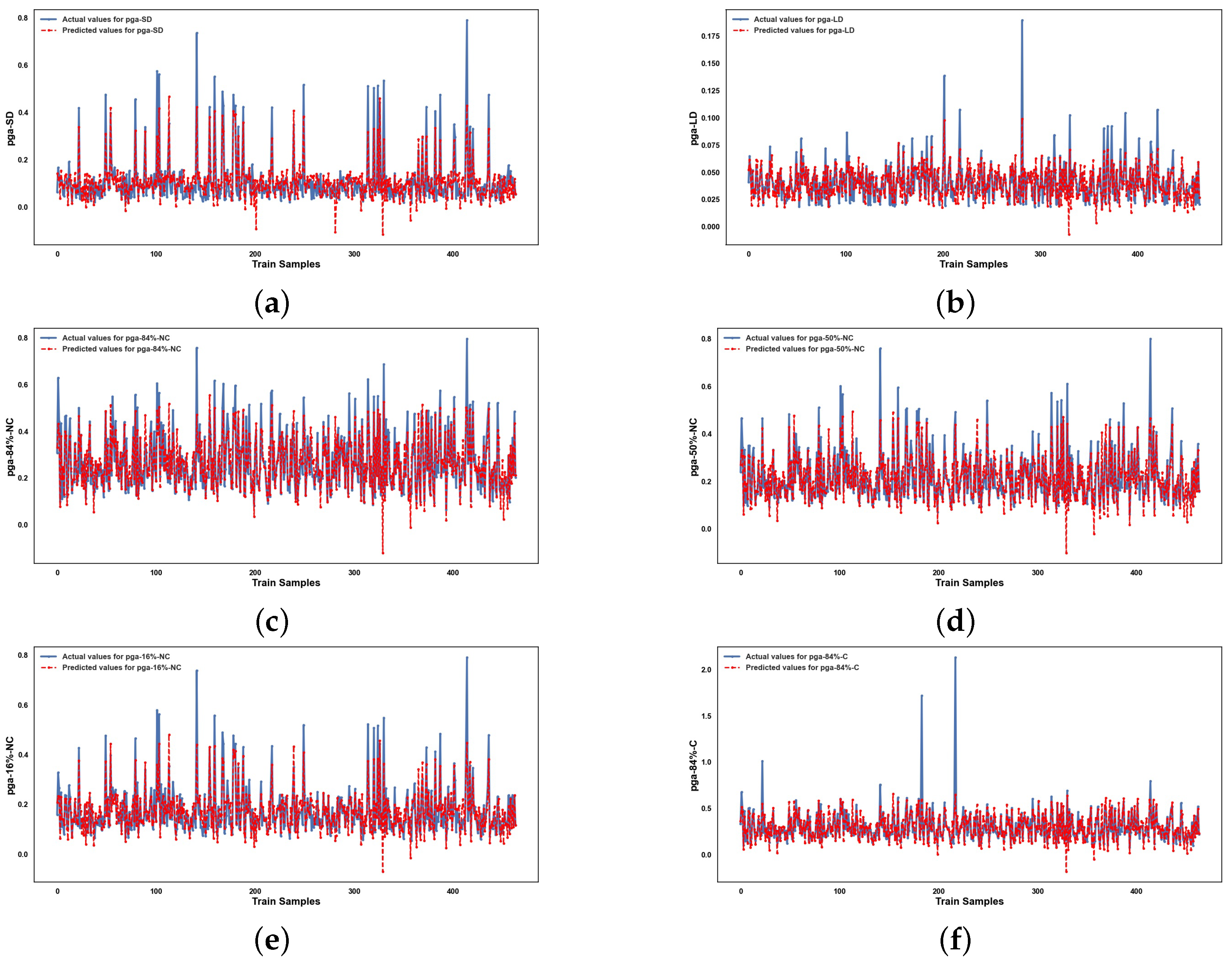
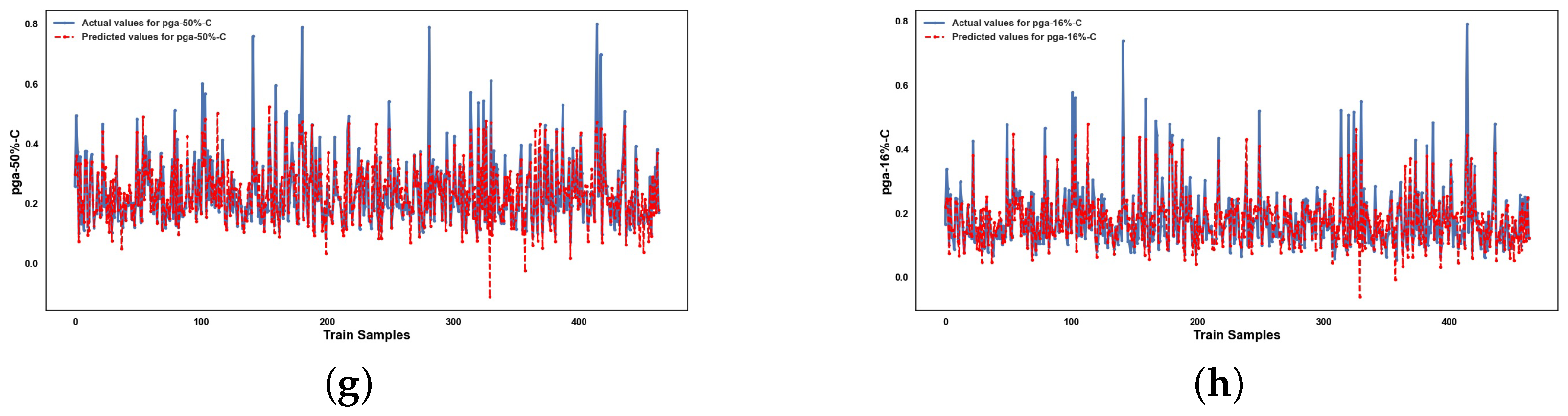
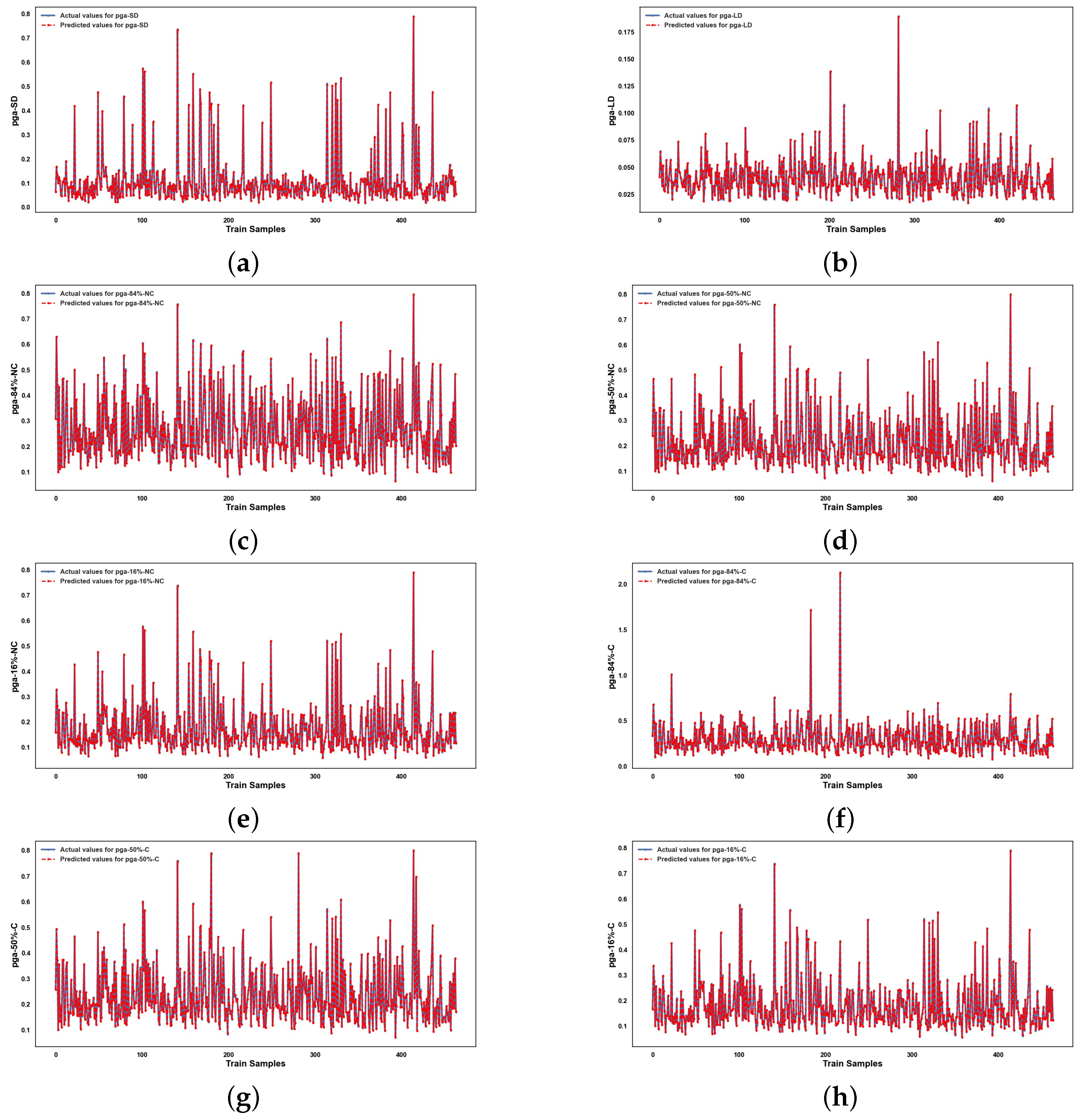
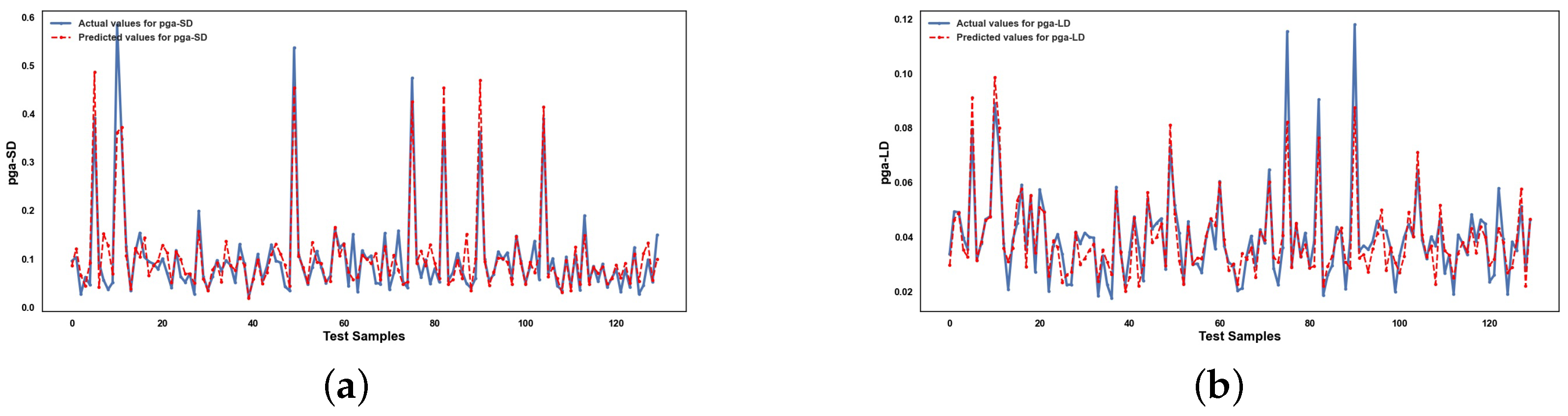
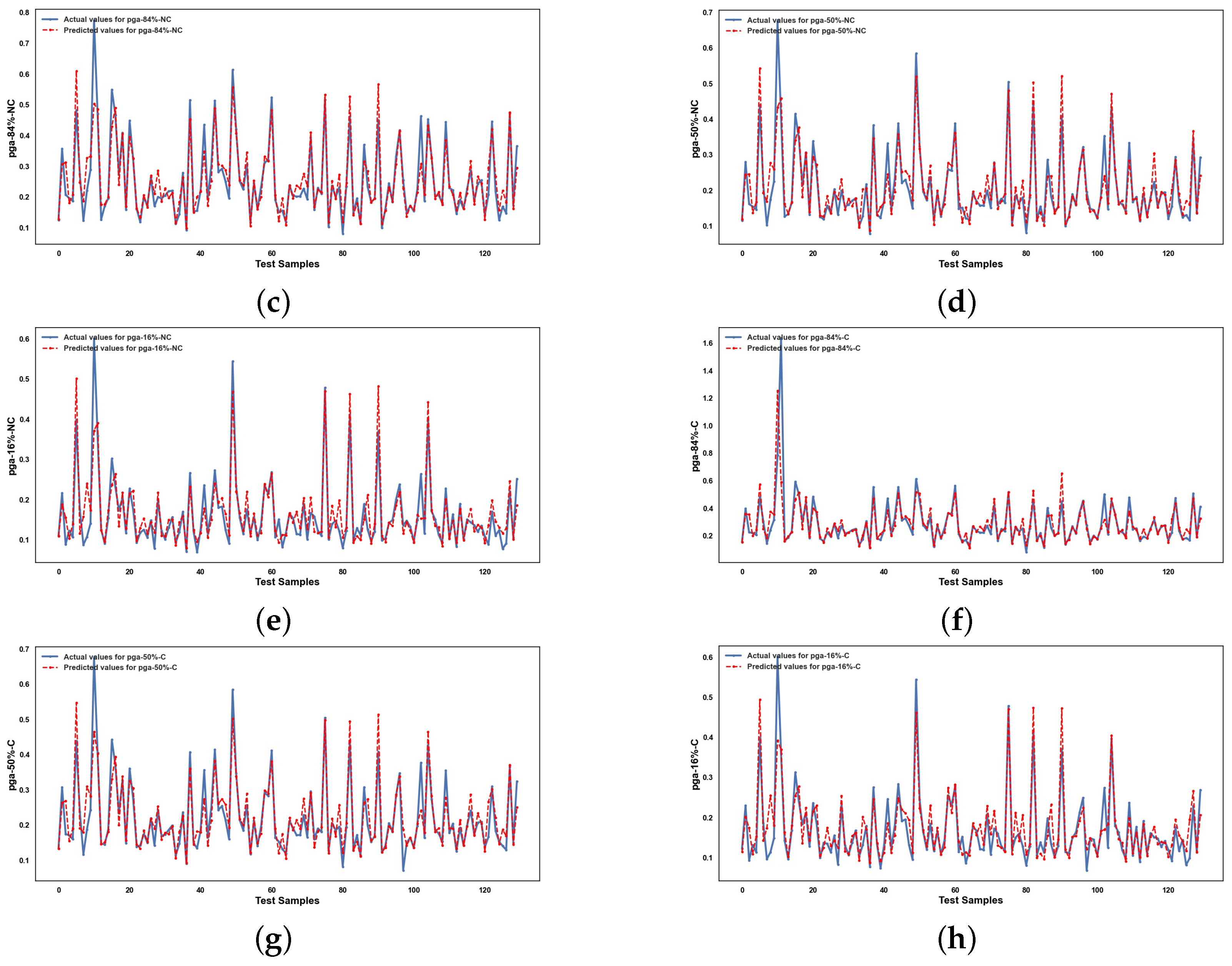
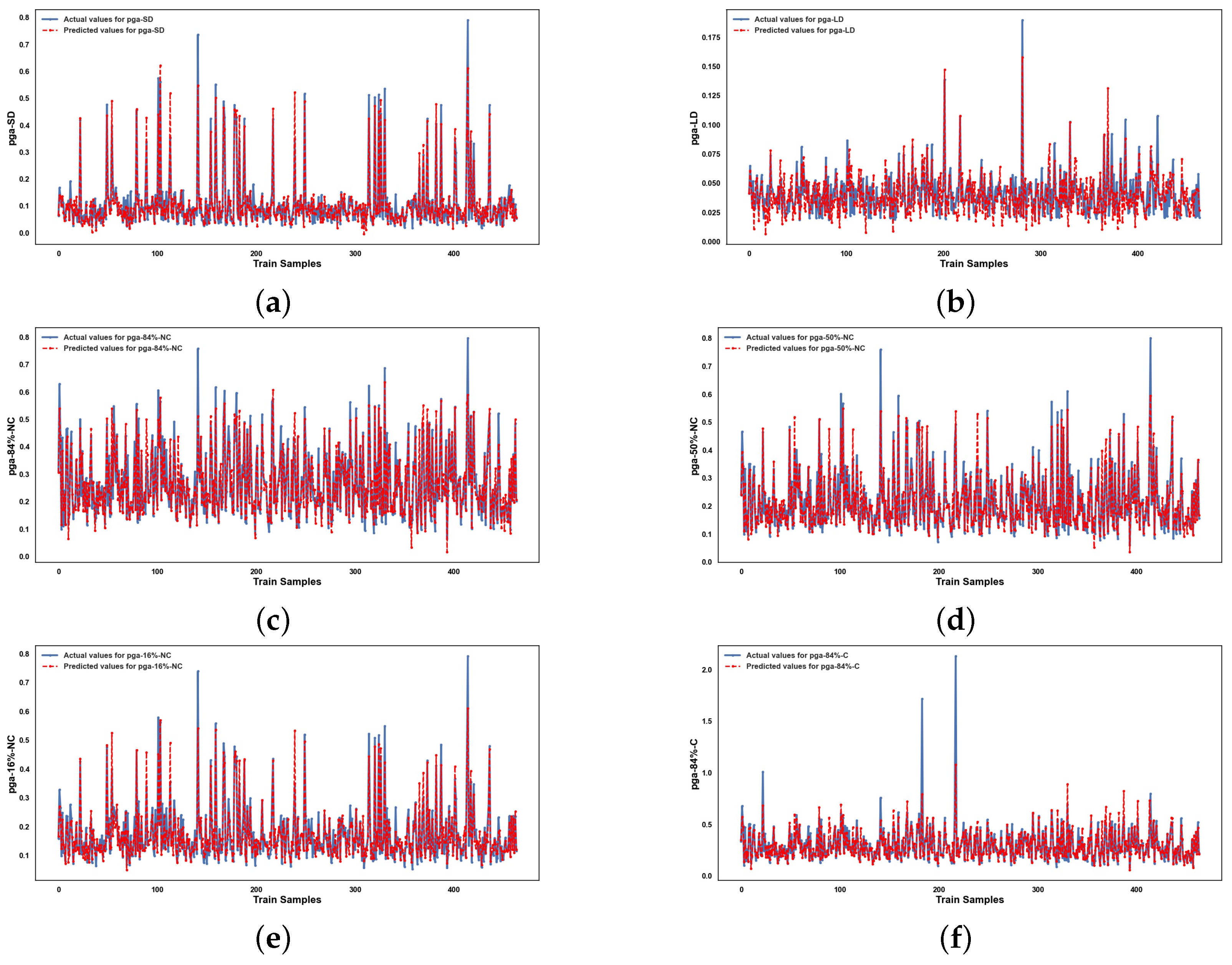
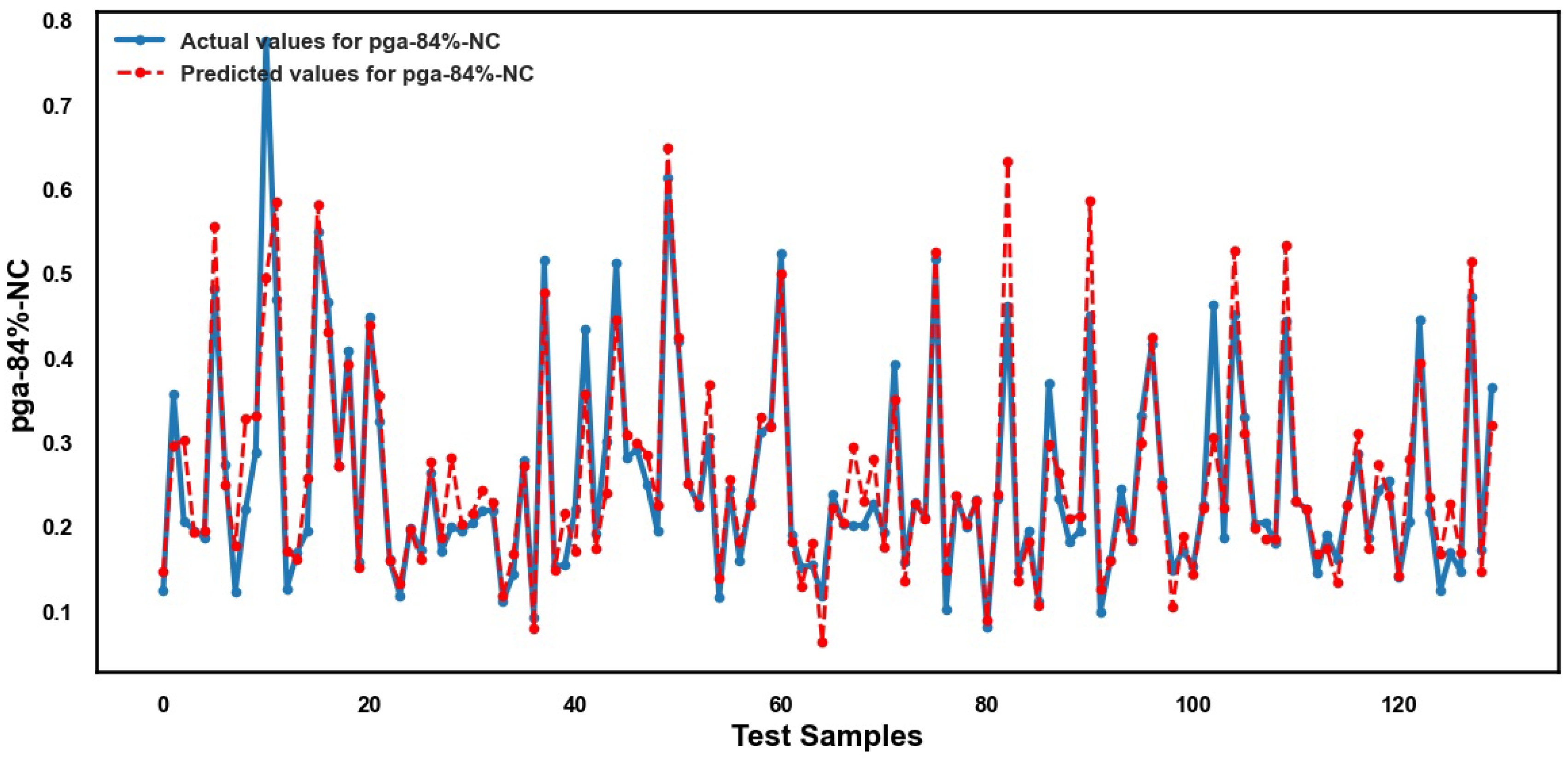
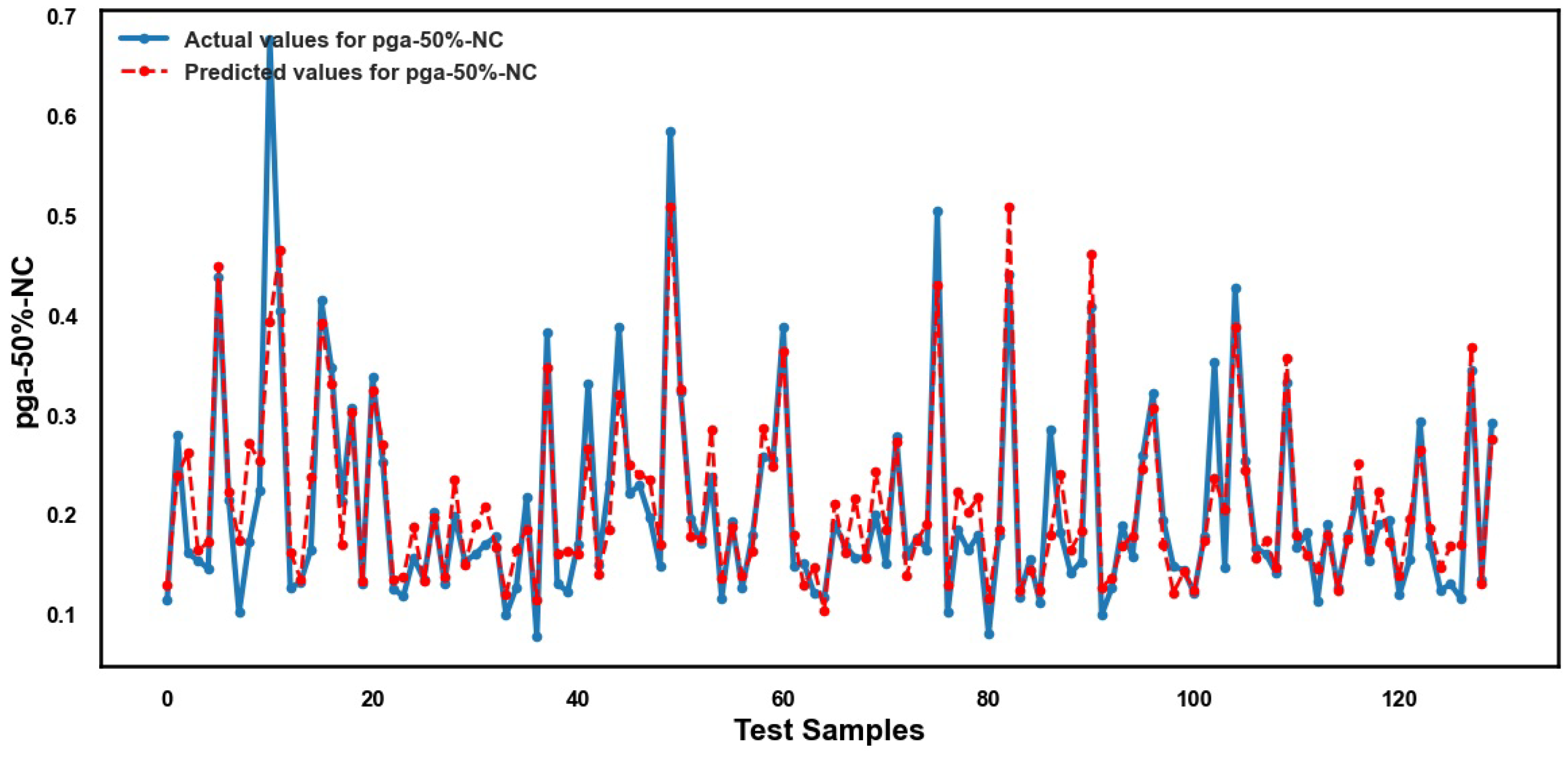
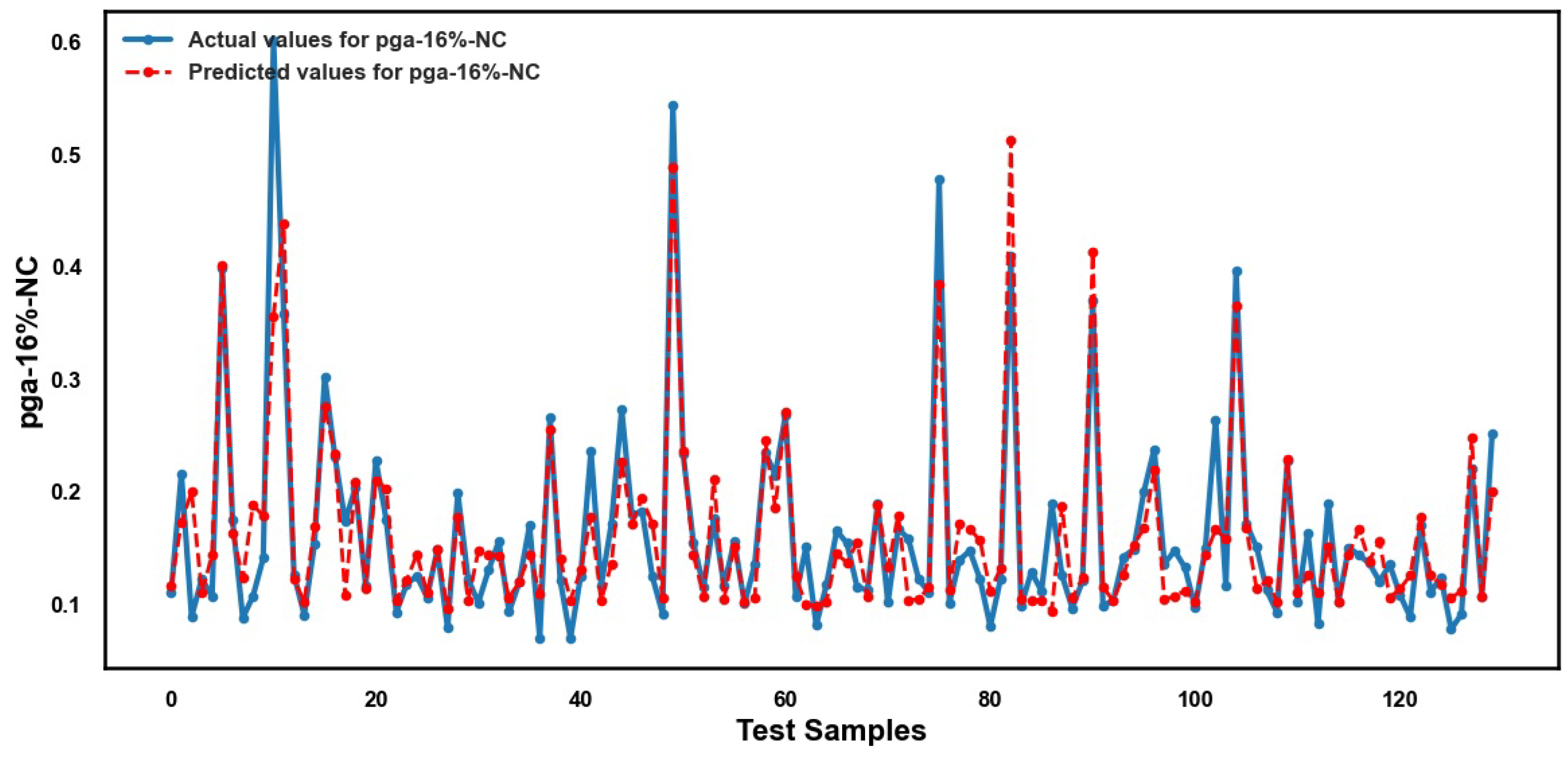
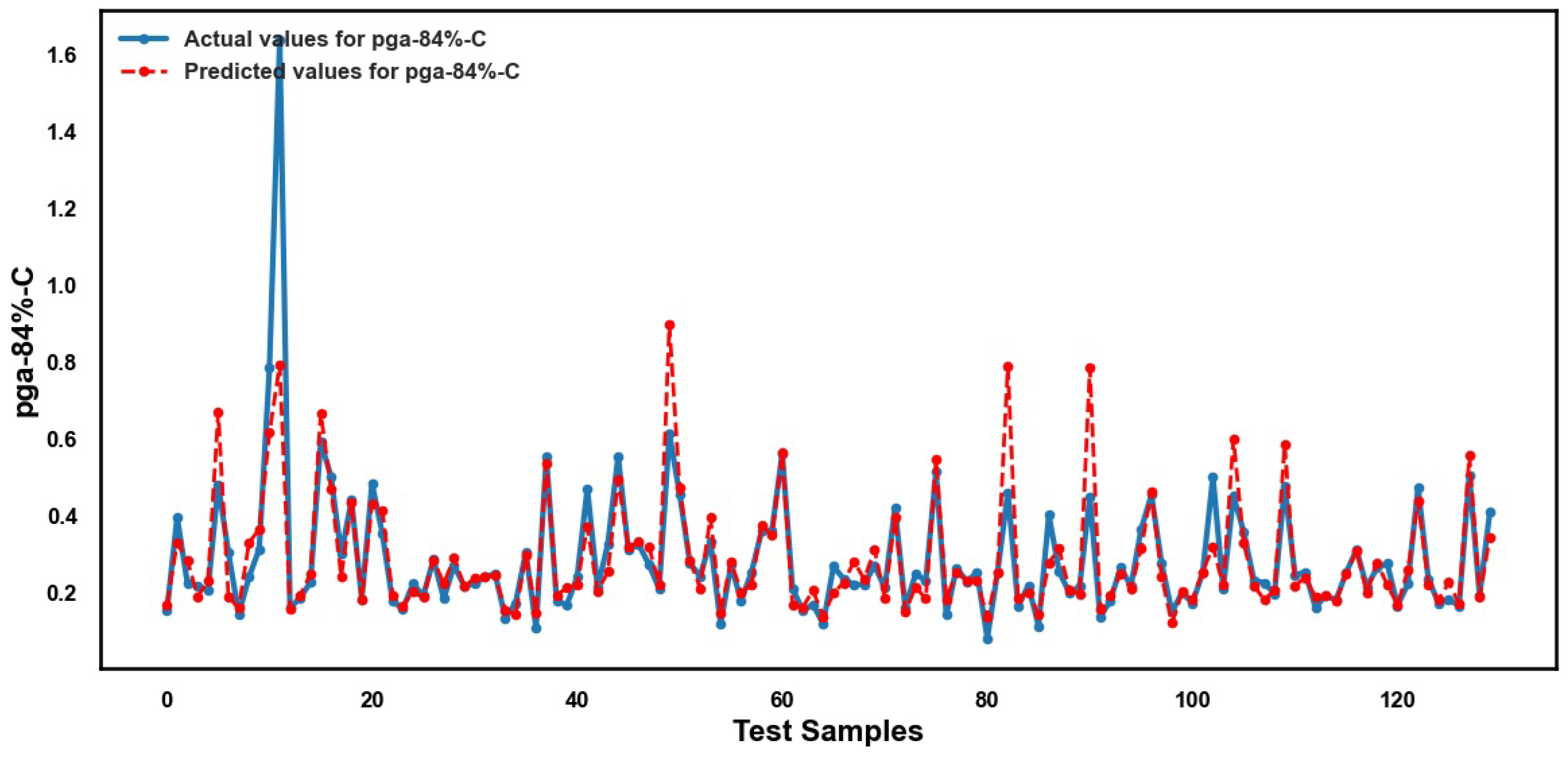
5. Results and Discussion
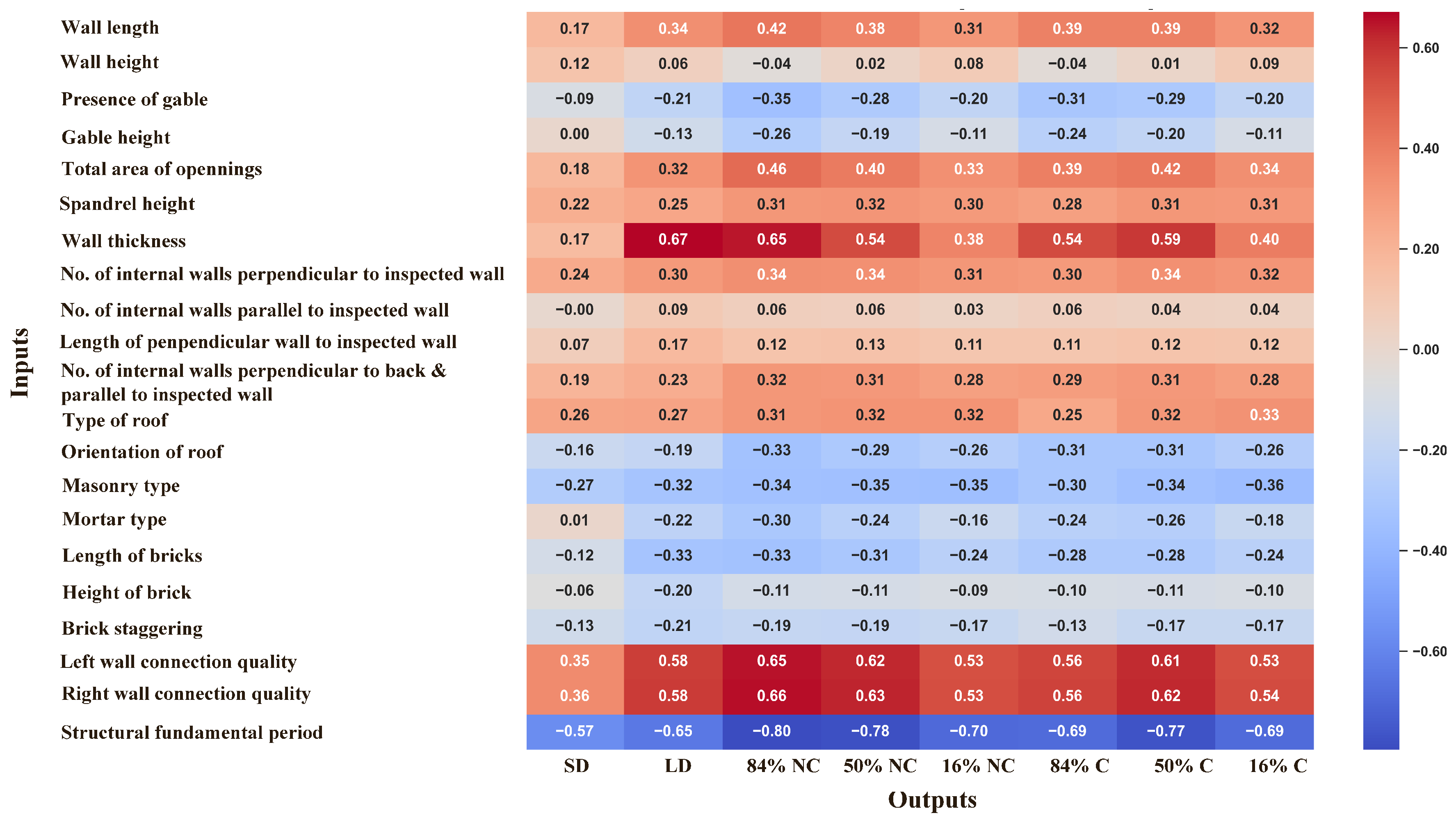
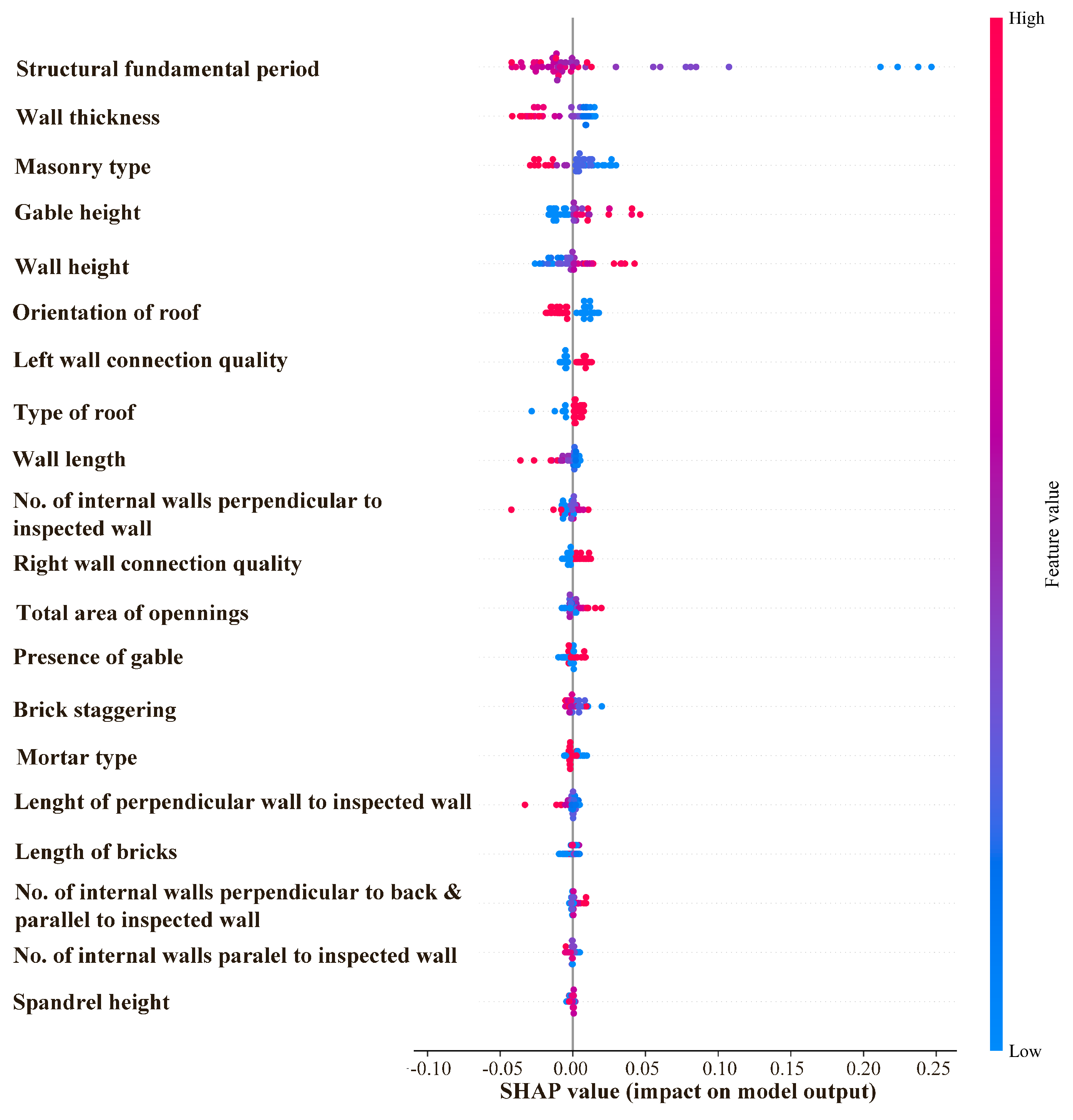
5.1. Correlation Between Input and Output Features
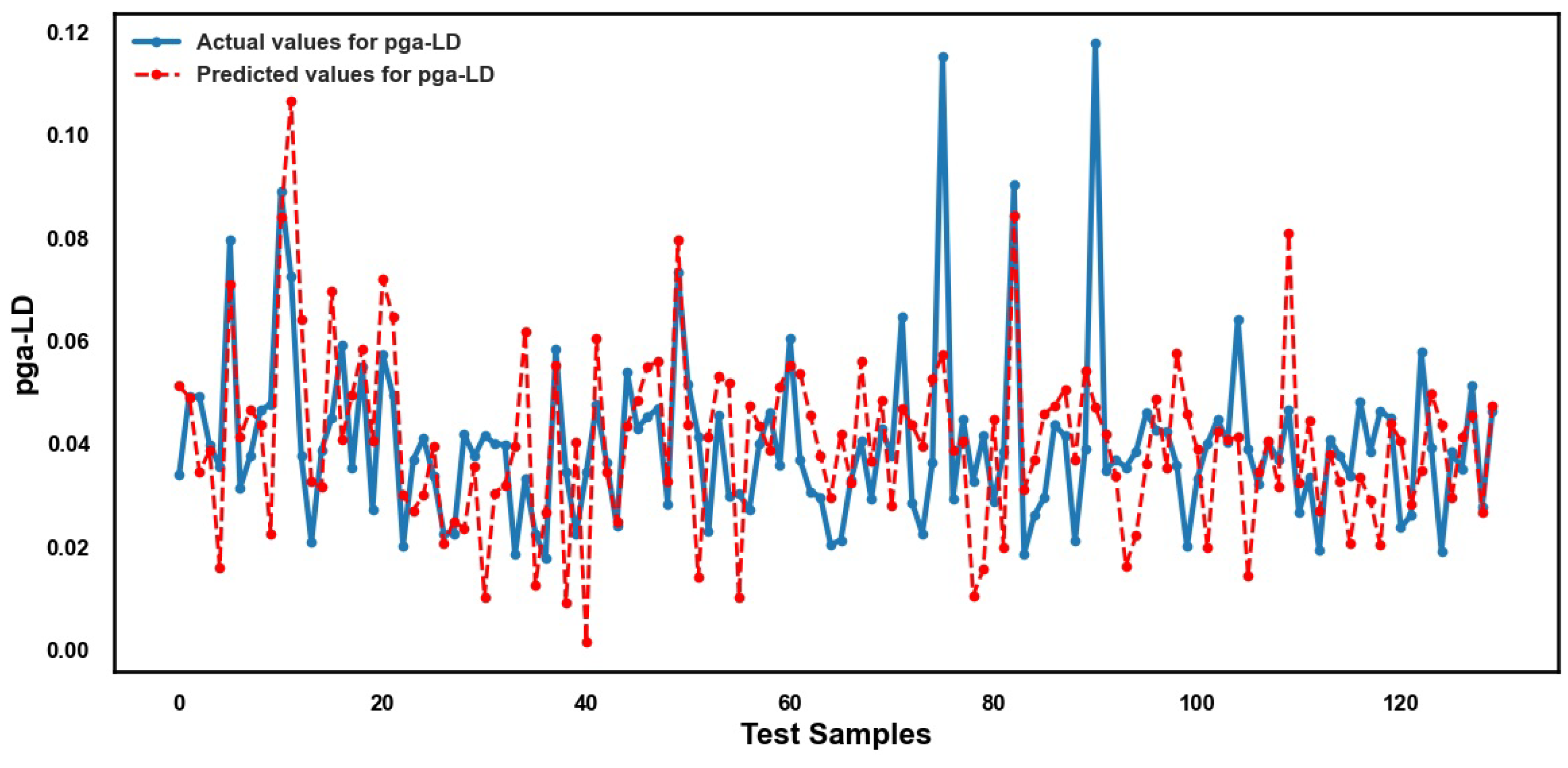
5.2. Performance of ML Methods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| C | Collapse |
| DT | Decision Tree |
| IDA | Incremental Dynamic Analysis |
| KNN | K-Nearest Neighbors |
| LD | Light Damage |
| LR | Linear Regression |
| LSTM | Long Short-Term Memory |
| MAPE | Mean Absolute Percentage Error |
| ML | Machine Learning |
| MSE | Mean Squared Error |
| NC | Near Collapse |
| PGA | Peak Ground Acceleration |
| RMSE | Root Mean Square Error |
| SD | Severe Damage |
| SGD | Stochastic Gradient Descent |
| SHAP | SHapley Additive exPlanations |
| SPO | Static Pushover |
| XGBoost | Extreme Gradient Boosting |
Appendix A

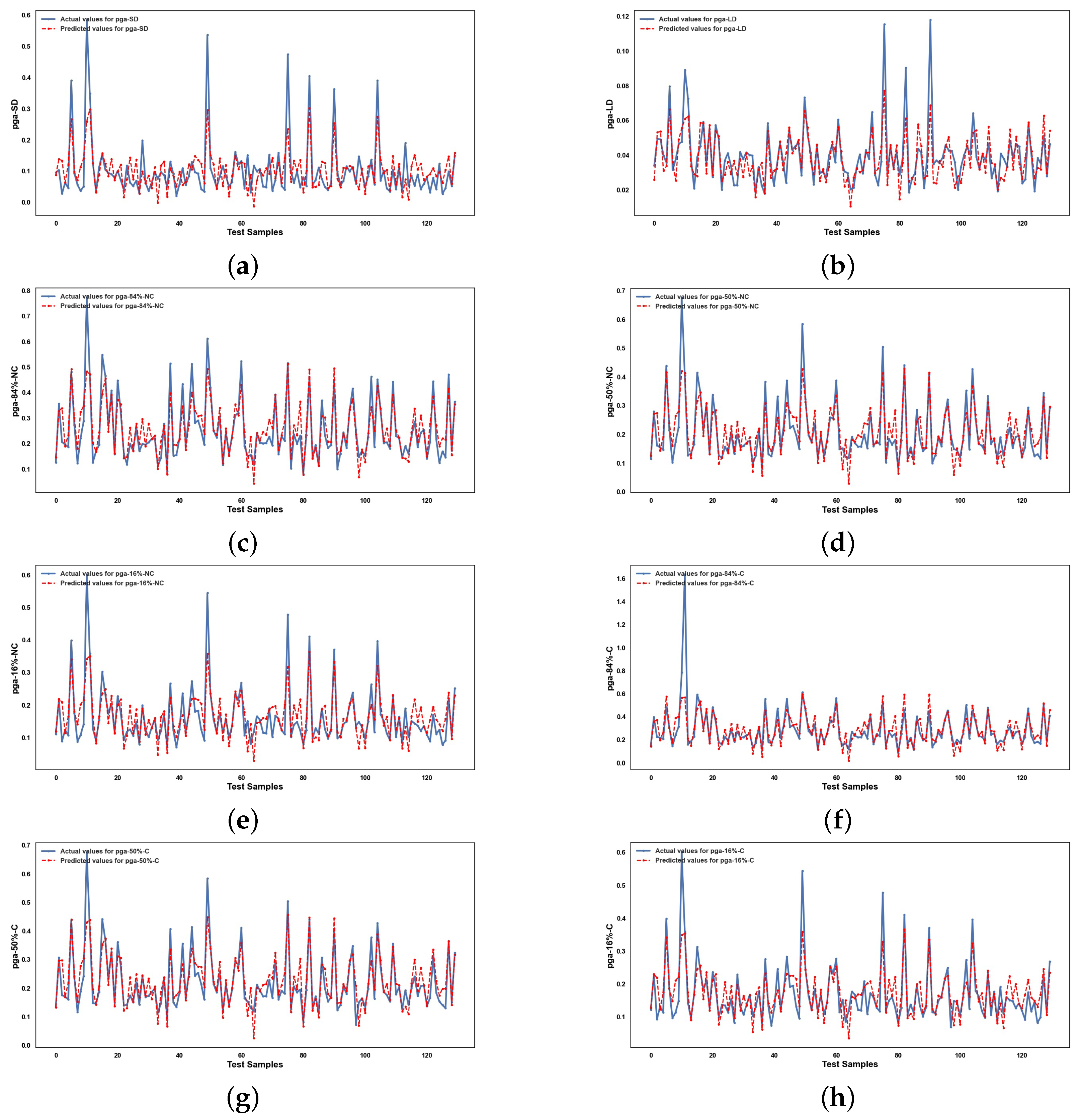
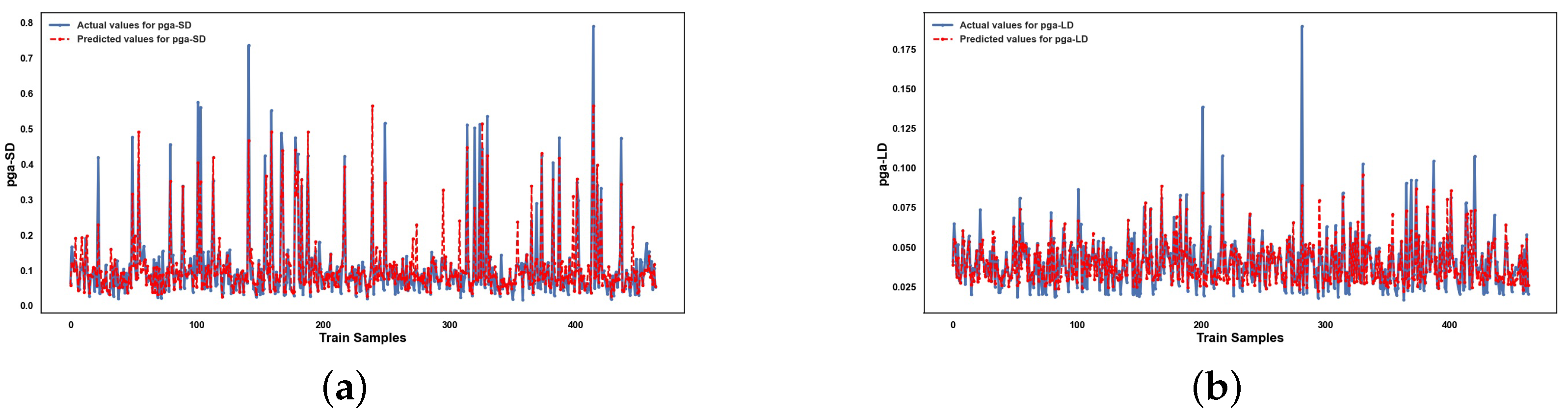
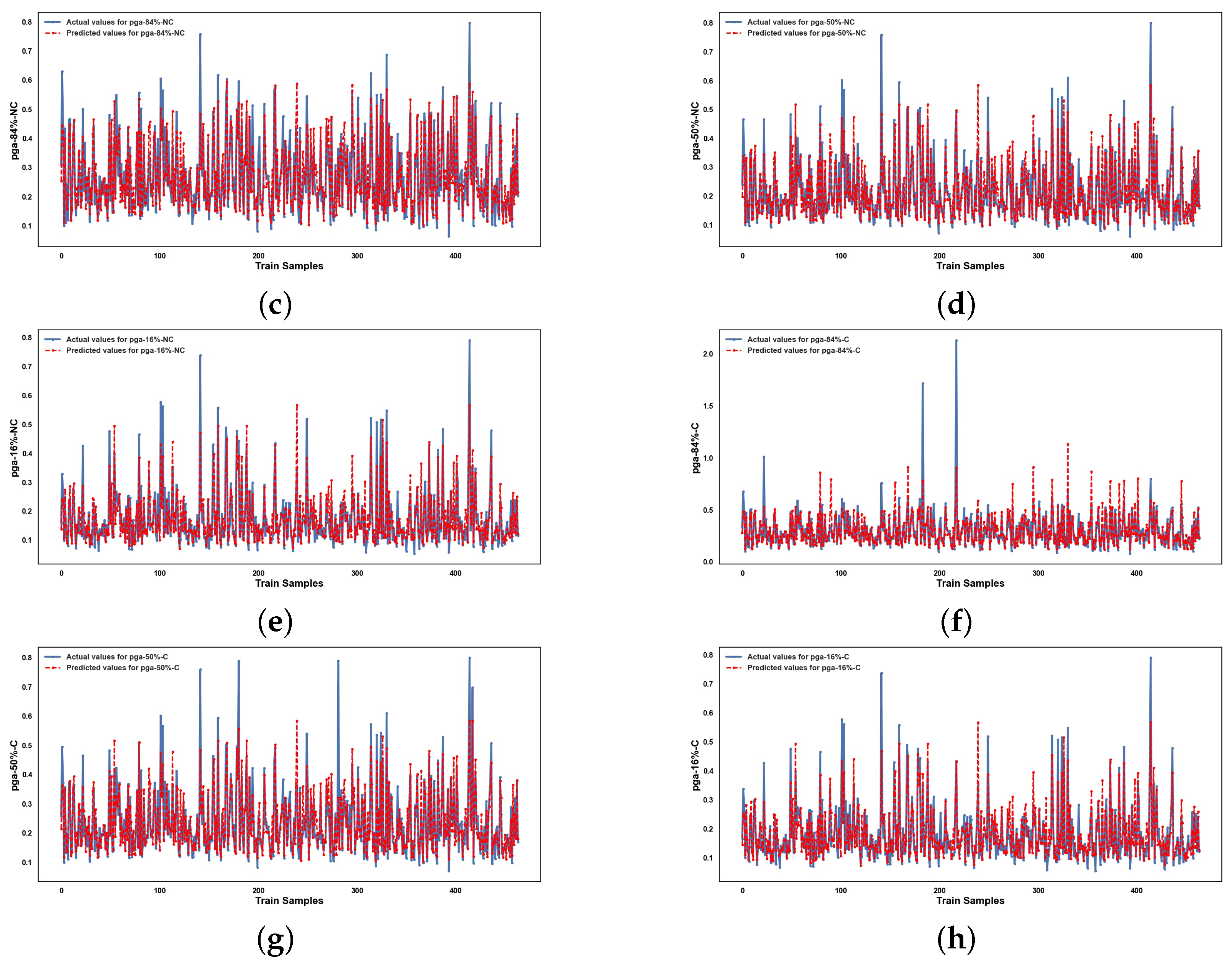

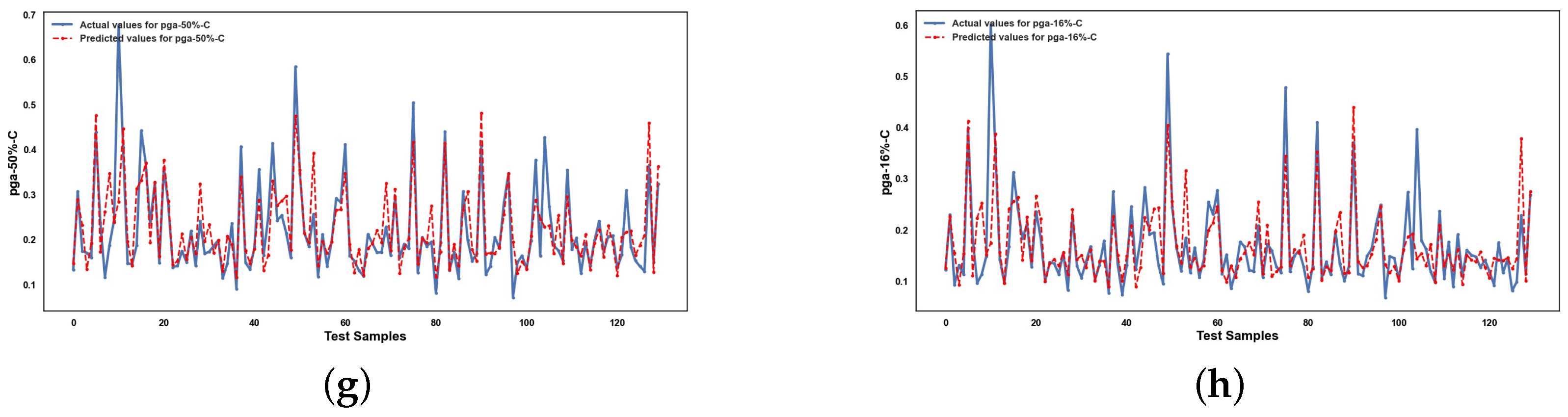
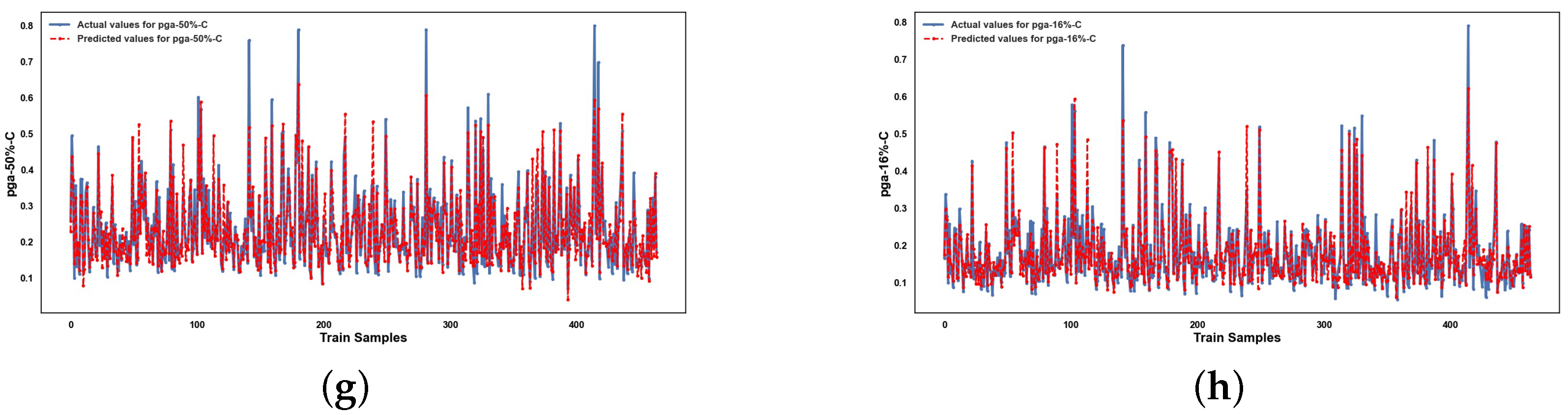
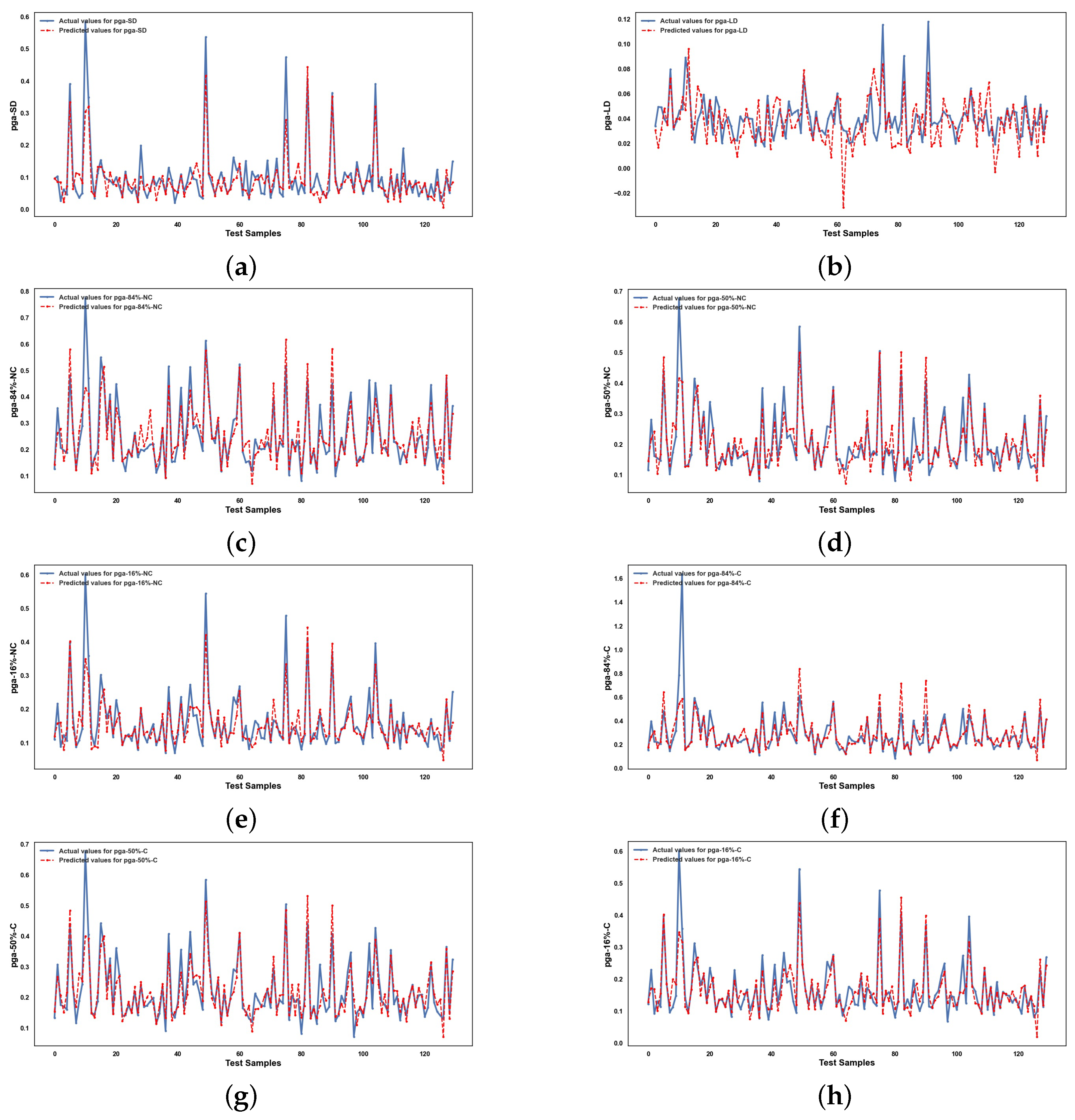
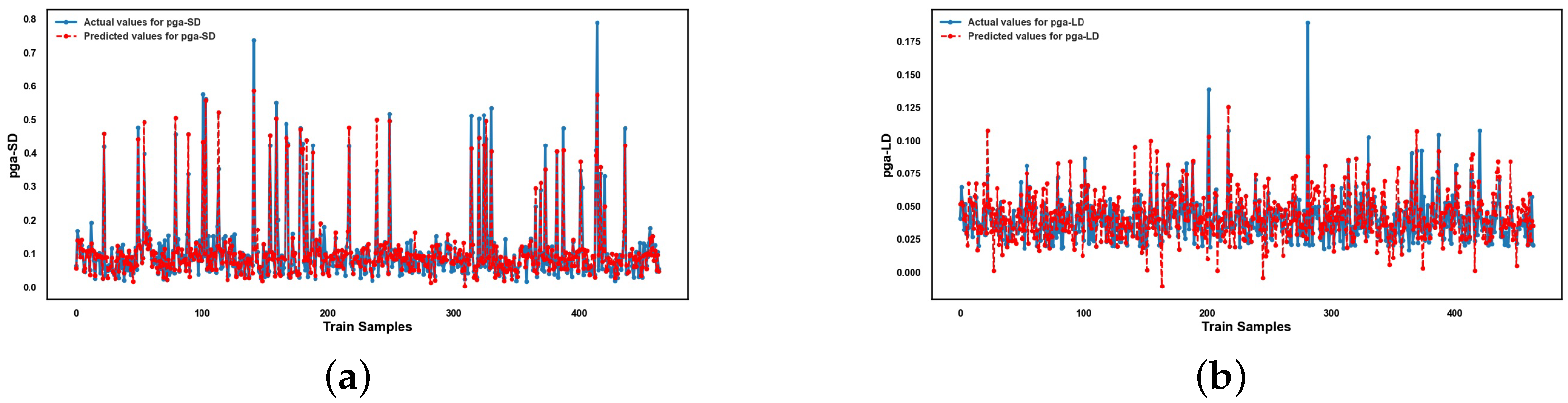
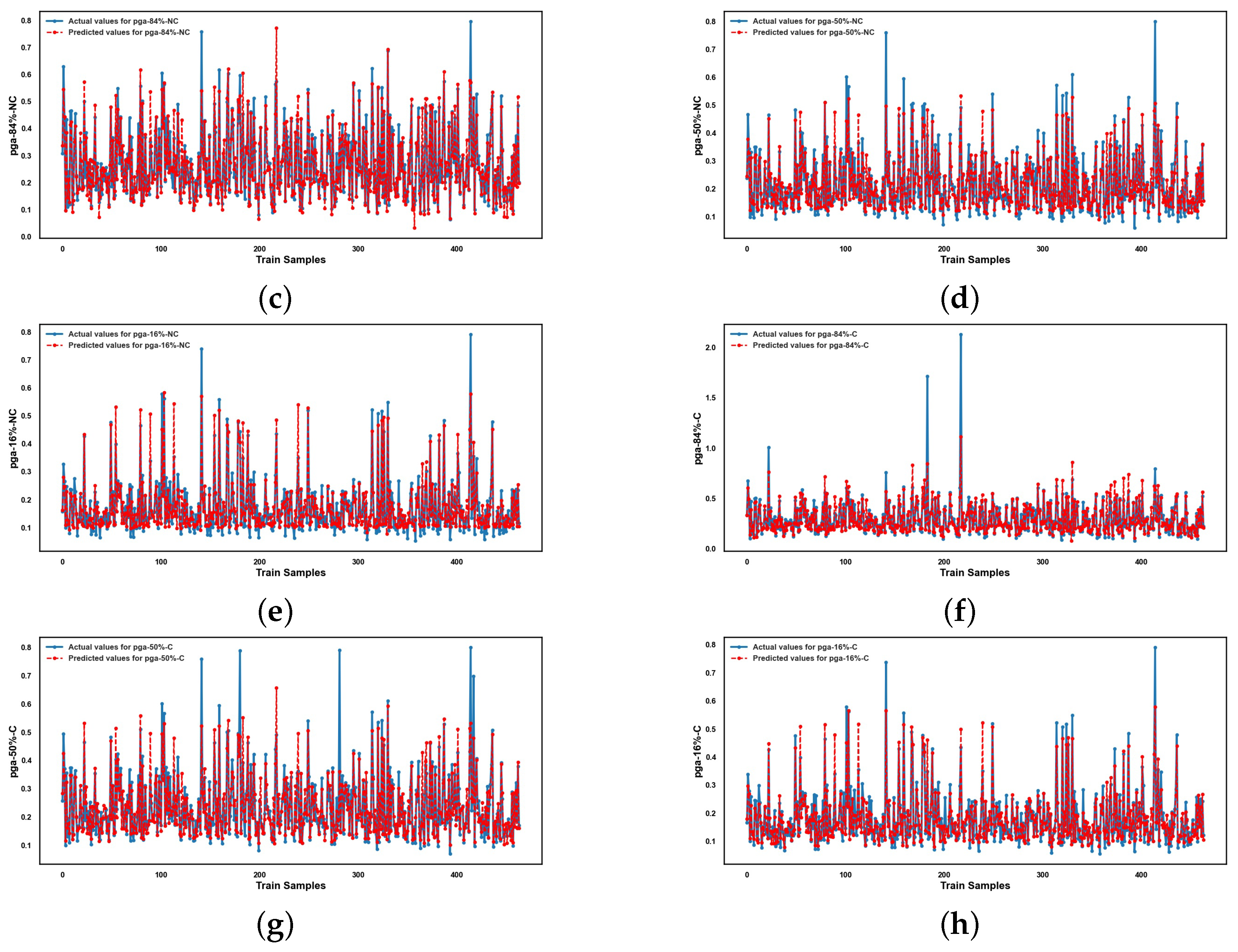
References
- Bazzurro, P.; Cornell, C.; Menun, C.; Motahari, M. Guidelines for seismic assessment of damaged buildings. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; Volume 1708. [Google Scholar]
- Nirandjan, S.; Koks, E.E.; Ye, M.; Pant, R.; Van Ginkel, K.C.; Aerts, J.C.; Ward, P.J. Physical vulnerability database for critical infrastructure multi-hazard risk assessments–A systematic review and data collection. Nat. Hazards Earth Syst. Sci. Discuss. 2024, 24, 4341–4368. [Google Scholar] [CrossRef]
- Rota, M.; Penna, A.; Strobbia, C. Processing Italian damage data to derive typological fragility curves. Soil Dyn. Earthq. Eng. 2008, 28, 933–947. [Google Scholar] [CrossRef]
- Yepes-Estrada, C.; Silva, V.; Crowley, H. Gem vulnerability database for the openquake-platform. In Proceedings of the Second European Conference on Earthquake Engineering and Seismology, Istanbul, Turkey, 25–29 August 2014. [Google Scholar]
- Di Ludovico, M.; De Martino, G.; Prota, A.; Manfredi, G.; Dolce, M. Relationships between empirical damage and direct/indirect costs for the assessment of seismic loss scenarios. Bull. Earthq. Eng. 2022, 20, 229–254. [Google Scholar] [CrossRef]
- Ahmad, S.; Kyriakides, N.; Pilakoutas, K.; Neocleous, K.; Zaman, Q.U. Seismic fragility assessment of existing sub-standard low strength reinforced concrete structures. Earthq. Eng. Eng. Vib. 2015, 14, 439–452. [Google Scholar] [CrossRef]
- Khalfan, M.; El-Dakhakhni, W.W.; Tait, M.J. Seismic risk assessment of nonengineered residential buildings in developing countries. J. Perform. Constr. Facil. 2016, 30, 4016013. [Google Scholar] [CrossRef]
- Novelli, V.; Risi, R.; Ngoma, I.; Kafodya, I.; Kloukinas, P.; Macdonald, J.; Goda, K. Fragility curves for non-engineered masonry buildings in developing countries derived from real data based on structural surveys and laboratory tests. Soft Comput. 2021, 25, 6113–6138. [Google Scholar] [CrossRef]
- Khalfan, M. Fragility Curves for Residential Buildings in Developing Countries: A Case Study on Non-Engineered Unreinforced Masonry Homes in Bantul, Indonesia. Master’s Thesis, McMaster University, Hamilton, ON, Canada, 2013. [Google Scholar]
- Dai, K.Y.; Yu, X.H.; Lu, D.G.; Qian, K. Fragility functions for corroded reinforced concrete columns. J. Build. Eng. 2024, 82, 108124. [Google Scholar] [CrossRef]
- Yu, X.; Li, Z.; Yang, A.; Li, Y.; Lu, D.; Dai, K. Time-Dependent Seismic Fragility of Coastal RC Frames Considering Effect of Distance from Coastline. Buildings 2025, 15, 737. [Google Scholar] [CrossRef]
- Sabetta, F.; Goretti, A.; Lucantoni, A. Empirical fragility curves from damage surveys and estimated strong ground motion. In Proceedings of the 11th European Conference on Earthquake Engineering, Paris, France, 6–11 September 1998; pp. 1–11. [Google Scholar]
- Du, A.; Wang, X.; Xie, Y.; Dong, Y. Regional seismic risk and resilience assessment: Methodological development, applicability, and future research needs–An earthquake engineering perspective. Reliab. Eng. Syst. Saf. 2023, 233, 109104. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, P.; Wang, J.; Li, S.; Guan, Z. A novel framework for seismic fragility analysis with the combination of Box-Cox transformation and Bayesian inference. Eng. Struct. 2023, 277, 115436. [Google Scholar] [CrossRef]
- Işık, E.; Bilgin, H.; Avcil, F.; İzol, R.; Arkan, E.; Büyüksaraç, A.; Harirchian, E.; Hysenlliu, M. Seismic performances of masonry educational buildings during the 2023 Türkiye (Kahramanmaraş) Earthquakes. GeoHazards 2024, 5, 700–731. [Google Scholar] [CrossRef]
- Giordano, N.; De Risi, R.; Voyagaki, E.; Kloukinas, P.; Novelli, V.; Kafodya, I.; Ngoma, I.; Goda, K.; Macdonald, J. Seismic fragility models for typical non-engineered URM residential buildings in Malawi. Structures 2021, 32, 2266–2278. [Google Scholar] [CrossRef]
- Harirchian, E.; Hosseini, S.E.A.; Jadhav, K.; Kumari, V.; Rasulzade, S.; Işık, E.; Wasif, M.; Lahmer, T. A review on application of soft computing techniques for the rapid visual safety evaluation and damage classification of existing buildings. J. Build. Eng. 2021, 43, 102536. [Google Scholar] [CrossRef]
- Dabiri, H.; Faramarzi, A.; Dall’Asta, A.; Tondi, E.; Micozzi, F. A machine learning-based analysis for predicting fragility curve parameters of buildings. J. Build. Eng. 2022, 62, 105367. [Google Scholar] [CrossRef]
- Thedy, J.; Liao, K.W. Machine Learning-Enhanced Fragility Curves: Advancing Reliability and Safety of Structures in Seismic Risk Assessment. Reliab. Eng. Syst. Saf. 2025, 264, 111361. [Google Scholar] [CrossRef]
- Rajapaksha, R.; Siriwardana, C. A systematic review on different approaches used in the development of fragility curves for buildings. In Proceedings of the 12th International Conference on Structural Engineering and Construction Management, Kandy, Sri Lanka, 17–19 December 2021; Springer: Singapore, 2023; pp. 407–426. [Google Scholar]
- Harirchian, E.; Lahmer, T.; Kumari, V.; Jadhav, K. Application of Support Vector Machine Modeling for the Rapid Seismic Hazard Safety Evaluation of Existing Buildings. Energies 2020, 13, 3340. [Google Scholar] [CrossRef]
- Michalski, R.S.; Carbonell, J.G.; Mitchell, T.M. Machine Learning: An Artificial Intelligence Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Sun, H.; Burton, H.V.; Huang, H. Machine learning applications for building structural design and performance assessment: State-of-the-art review. J. Build. Eng. 2021, 33, 101816. [Google Scholar] [CrossRef]
- Thai, H.T. Machine learning for structural engineering: A state-of-the-art review. Structures 2022, 38, 448–491. [Google Scholar] [CrossRef]
- Harirchian, E.; Jadhav, K.; Kumari, V.; Lahmer, T. ML-EHSAPP: A prototype for machine learning-based earthquake hazard safety assessment of structures by using a smartphone app. Eur. J. Environ. Civ. Eng. 2022, 26, 5279–5299. [Google Scholar] [CrossRef]
- Hwang, S.H.; Mangalathu, S.; Shin, J.; Jeon, J.S. Machine learning-based approaches for seismic demand and collapse of ductile reinforced concrete building frames. J. Build. Eng. 2021, 34, 101905. [Google Scholar] [CrossRef]
- Mangalathu, S.; Jeon, J.S. Classification of failure mode and prediction of shear strength for reinforced concrete beam-column joints using machine learning techniques. Eng. Struct. 2018, 160, 85–94. [Google Scholar] [CrossRef]
- Charalampakis, A.E.; Tsiatas, G.C.; Kotsiantis, S.B. Machine learning and nonlinear models for the estimation of fundamental period of vibration of masonry infilled RC frame structures. Eng. Struct. 2020, 216, 110765. [Google Scholar] [CrossRef]
- Wu, J.R.; Di Sarno, L. A machine-learning method for deriving state-dependent fragility curves of existing steel moment frames with masonry infills. Eng. Struct. 2023, 276, 115345. [Google Scholar] [CrossRef]
- Chomacki, L.; Rusek, J.; Słowik, L. Machine learning methods in damage prediction of masonry development exposed to the industrial environment of mines. Energies 2022, 15, 3958. [Google Scholar] [CrossRef]
- Rezaie, A.; Godio, M.; Achanta, R.; Beyer, K. Machine-learning for damage assessment of rubble stone masonry piers based on crack patterns. Autom. Constr. 2022, 140, 104313. [Google Scholar] [CrossRef]
- Siam, A.; Ezzeldin, M.; El-Dakhakhni, W. Machine learning algorithms for structural performance classifications and predictions: Application to reinforced masonry shear walls. Structures 2019, 22, 252–265. [Google Scholar] [CrossRef]
- Harirchian, E.; Hosseini, S.E.A.; Novelli, V.; Lahmer, T.; Rasulzade, S. Utilizing advanced machine learning approaches to assess the seismic fragility of non-engineered masonry structures. Results Eng. 2024, 21, 101750. [Google Scholar] [CrossRef]
- Kazemi, F.; Asgarkhani, N.; Jankowski, R. Machine learning-based seismic fragility and seismic vulnerability assessment of reinforced concrete structures. Soil Dyn. Earthq. Eng. 2023, 166, 107761. [Google Scholar] [CrossRef]
- Zain, M.; Dackermann, U.; Prasittisopin, L. Machine learning (ML) algorithms for seismic vulnerability assessment of school buildings in high-intensity seismic zones. Structures 2024, 70, 107639. [Google Scholar] [CrossRef]
- Chen, H.; Nemni, E.; Vallecorsa, S.; Li, X.; Wu, C.; Bromley, L. Dual-tasks siamese transformer framework for building damage assessment. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1600–1603. [Google Scholar]
- Chen, Y.; Sun, Z.; Zhang, R.; Yao, L.; Wu, G. Attention mechanism based neural networks for structural post-earthquake damage state prediction and rapid fragility analysis. Comput. Struct. 2023, 281, 107038. [Google Scholar] [CrossRef]
- Soleimani-Babakamali, M.H.; Esteghamati, M.Z. Estimating seismic demand models of a building inventory from nonlinear static analysis using deep learning methods. Eng. Struct. 2022, 266, 114576. [Google Scholar] [CrossRef]
- Harirchian, E.; Lahmer, T. Developing a hierarchical type-2 fuzzy logic model to improve rapid evaluation of earthquake hazard safety of existing buildings. Structures 2020, 28, 1384–1399. [Google Scholar] [CrossRef]
- Li, S.Q. A simplified prediction model of structural seismic vulnerability considering a multivariate fuzzy membership algorithm. J. Earthq. Eng. 2024, 28, 707–730. [Google Scholar] [CrossRef]
- Lallam, M.; Djebli, A.; Mammeri, A. Fuzzy analytical hierarchy process for assessing damage in old masonry buildings: A case study. Int. J. Archit. Herit. 2025, 19, 408–427. [Google Scholar] [CrossRef]
- Kiani, H.; Nasrollahzadeh, K. Fuzzy logic approach for seismic fragility analysis of RC frames with applications to earthquake-induced damage and construction quality. Structures 2023, 55, 1122–1143. [Google Scholar] [CrossRef]
- Alizadeh, M.; Hashim, M.; Alizadeh, E.; Shahabi, H.; Karami, M.R.; Beiranvand Pour, A.; Pradhan, B.; Zabihi, H. Multi-criteria decision making (MCDM) model for seismic vulnerability assessment (SVA) of urban residential buildings. ISPRS Int. J. Geo-Inf. 2018, 7, 444. [Google Scholar] [CrossRef]
- Alemdar, K.D. Seismic risk assessment of transportation networks for the impending Istanbul earthquake with GIS-based MCDM approach. Nat. Hazards 2025, 121, 10085–10123. [Google Scholar] [CrossRef]
- Cruz, A.; Chieffo, N.; Karimzadeh, S.; Ortiz, A.; Sandoval, E.; Lourenço, P.B. Earthquake vulnerability assessment of non-engineered URM residential buildings. Int. J. Disaster Risk Reduct. 2025, 122, 105476. [Google Scholar] [CrossRef]
- Kloukinas, P.; Novelli, V.; Kafodya, I.; Ngoma, I.; Macdonald, J.; Goda, K. A building classification scheme of housing stock in Malawi for earthquake risk assessment. J. Hous. Built Environ. 2020, 35, 507–537. [Google Scholar] [CrossRef]
- Ngoma, I.; Kafodya, I.; Kloukinas, P.; Novelli, V.; Macdonald, J.; Goda, K. Building classification and seismic vulnerability of current housing construction in Malawi. Malawi J. Sci. Technol. 2019, 11, 57–72. [Google Scholar]
- Voyagaki, E.; Kloukinas, P.; Novelli, V.; De Risi, R.; Kafodya, I.; Ngoma, I.; Goda, K.; Macdonald, J.H. Masonry panel testing in Malawi. In Proceedings of the 17th World Conference on Earthquake Engineering, Sendai, Japan, 27 September–2 October 2020. [Google Scholar]
- Kloukinas, P.; Kafodya, I.; Ngoma, I.; Novelli, V.; Macdonald, J.; Goda, K. Strength of materials and masonry structures in Malawi. In Advances in Engineering Materials, Structures and Systems: Innovations, Mechanics and Applications; CRC Press: London, UK, 2019; pp. 1697–1702. [Google Scholar]
- D’Ayala, D.F. Force and displacement based vulnerability assessment for traditional buildings. Bull. Earthq. Eng. 2005, 3, 235–265. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Allin Cornell, C. Direct estimation of the seismic demand and capacity of oscillators with multi-linear static pushovers through IDA. Earthq. Eng. Struct. Dyn. 2006, 35, 1097–1117. [Google Scholar] [CrossRef]
- Boore, D.M.; Stewart, J.P.; Seyhan, E.; Atkinson, G.M. NGA-West2 equations for predicting PGA, PGV, and 5% damped PSA for shallow crustal earthquakes. Earthq. Spectra 2014, 30, 1057–1085. [Google Scholar] [CrossRef]
- D’Ayala, D.; Speranza, E. Definition of collapse mechanisms and seismic vulnerability of historic masonry buildings. Earthq. Spectra 2003, 19, 479–509. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, C.; Yang, Q. Data preparation for data mining. Appl. Artif. Intell. 2003, 17, 375–381. [Google Scholar] [CrossRef]
- Peterson, L.E. K-nearest neighbor. Scholarpedia 2009, 4, 1883. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Weisberg, S. Applied Linear Regression; John Wiley & Sons: Hoboken, NJ, USA, 2005; Volume 528. [Google Scholar]
- Tian, Y.; Zhang, Y.; Zhang, H. Recent advances in stochastic gradient descent in deep learning. Mathematics 2023, 11, 682. [Google Scholar] [CrossRef]
- Amari, S.i. Backpropagation and stochastic gradient descent method. Neurocomputing 1993, 5, 185–196. [Google Scholar] [CrossRef]
- Kingsford, C.; Salzberg, S.L. What are decision trees? Nat. Biotechnol. 2008, 26, 1011–1013. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Le, X.H.; Ho, H.V.; Lee, G.; Jung, S. Application of long short-term memory (LSTM) neural network for flood forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef]
- Cherif, I.L.; Kortebi, A. On using extreme gradient boosting (XGBoost) machine learning algorithm for home network traffic classification. In Proceedings of the 2019 Wireless Days (WD), Manchester, UK, 24–26 April 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Kavzoglu, T.; Teke, A. Predictive performances of ensemble machine learning algorithms in landslide susceptibility mapping using random forest, extreme gradient boosting (XGBoost) and natural gradient boosting (NGBoost). Arab. J. Sci. Eng. 2022, 47, 7367–7385. [Google Scholar] [CrossRef]
- Han, K.; Xiao, A.; Wu, E.; Guo, J.; Xu, C.; Wang, Y. Transformer in transformer. Adv. Neural Inf. Process. Syst. 2021, 34, 15908–15919. [Google Scholar]
- Thoyyibah, T.; Haryono, W.; Zailani, A.U.; Djaksana, Y.M.; Rosmawarni, N.; Arianti, N.D. Transformers in machine learning: Literature review. J. Penelit. Pendidik. IPA 2023, 9, 604–610. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef] [PubMed]



| No. | Description | Unit/Type |
|---|---|---|
| 1 | Structural fundamental period | s |
| 2 | Right wall connection quality | good/bad (categorical) |
| 3 | Left wall connection quality | good/bad (categorical) |
| 4 | Total area of openings (windows/doors) | m2 |
| 5 | Wall thickness | mm |
| 6 | Wall length | m |
| 7 | Wall height | m |
| 8 | Type of masonry used | fired/unfired (categorical) |
| 9 | Height of bricks | mm |
| 10 | Length of bricks | mm |
| 11 | Brick staggering (overlap) | mm |
| 12 | Type of mortar used | concrete/mud (categorical) |
| 13 | Length of wall perpendicular to inspected wall | m |
| 14 | No. of internal walls perpendicular to inspected wall | number |
| 15 | No. of internal walls parallel to inspected wall | number |
| 16 | No. of internal walls perpendicular to back & parallel to inspected wall | number |
| 17 | Type of roof | thatched/metallic (categorical) |
| 18 | Orientation of roof | parallel/orthogonal |
| 19 | Presence of gable | yes/no (binary) |
| 20 | Height of gable | m |
| 21 | Spandrel height | m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harirchian, E.; Novelli, V.I. Leveraging Transformer Models for Seismic Fragility Assessment of Non-Engineered Masonry Structures in Malawi. Infrastructures 2025, 10, 279. https://doi.org/10.3390/infrastructures10110279
Harirchian E, Novelli VI. Leveraging Transformer Models for Seismic Fragility Assessment of Non-Engineered Masonry Structures in Malawi. Infrastructures. 2025; 10(11):279. https://doi.org/10.3390/infrastructures10110279
Chicago/Turabian StyleHarirchian, Ehsan, and Viviana Iris Novelli. 2025. "Leveraging Transformer Models for Seismic Fragility Assessment of Non-Engineered Masonry Structures in Malawi" Infrastructures 10, no. 11: 279. https://doi.org/10.3390/infrastructures10110279
APA StyleHarirchian, E., & Novelli, V. I. (2025). Leveraging Transformer Models for Seismic Fragility Assessment of Non-Engineered Masonry Structures in Malawi. Infrastructures, 10(11), 279. https://doi.org/10.3390/infrastructures10110279







