Impact of Physical and Material Parameters on the Threshold Voltage and the Channel Resistance of Nanowire Field-Effect Transistors for Advanced Nanoscale Devices
Abstract
1. Introduction
2. Device Modeling
3. Contact Resistance in NWFETs
4. Results and Discussion
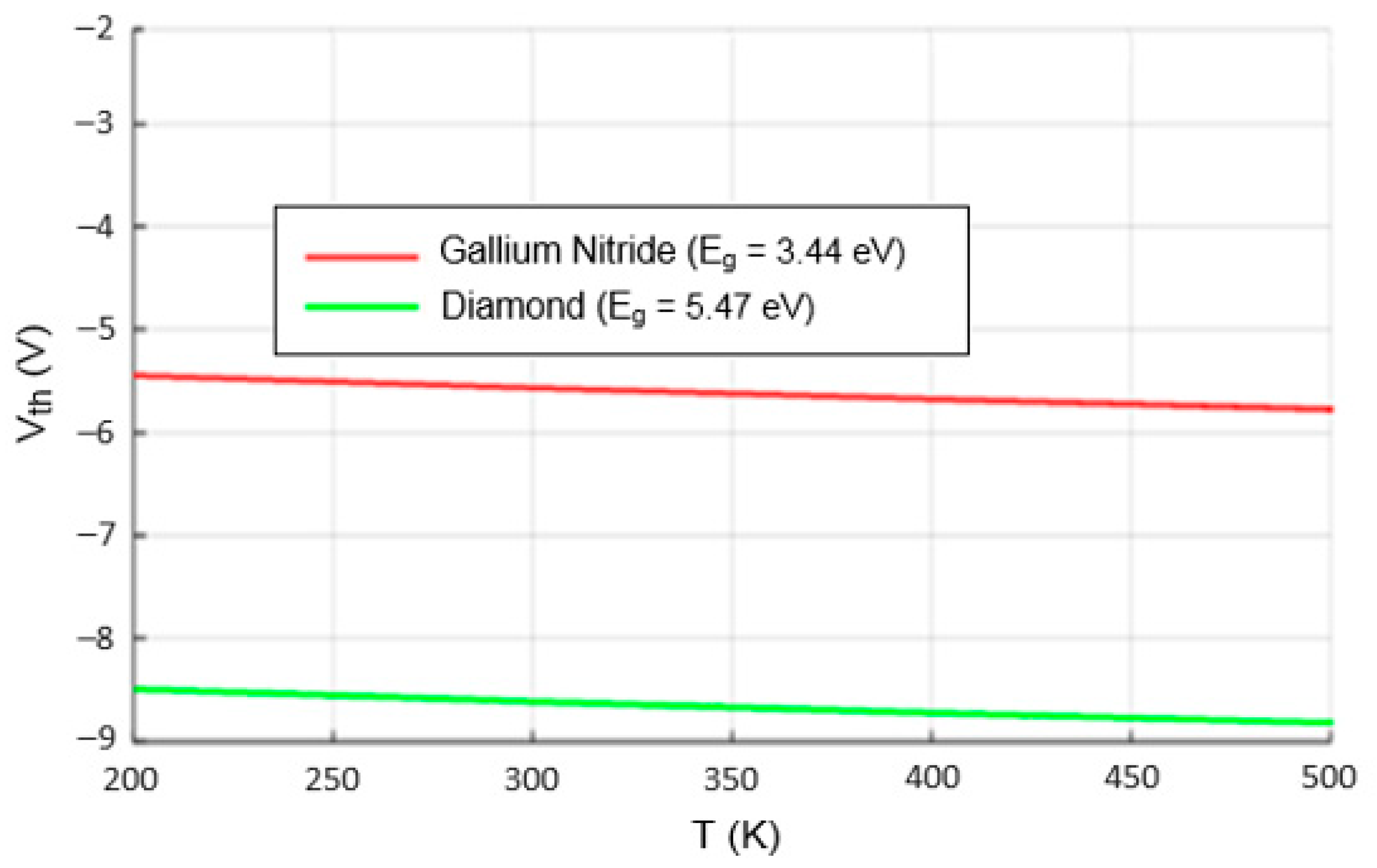
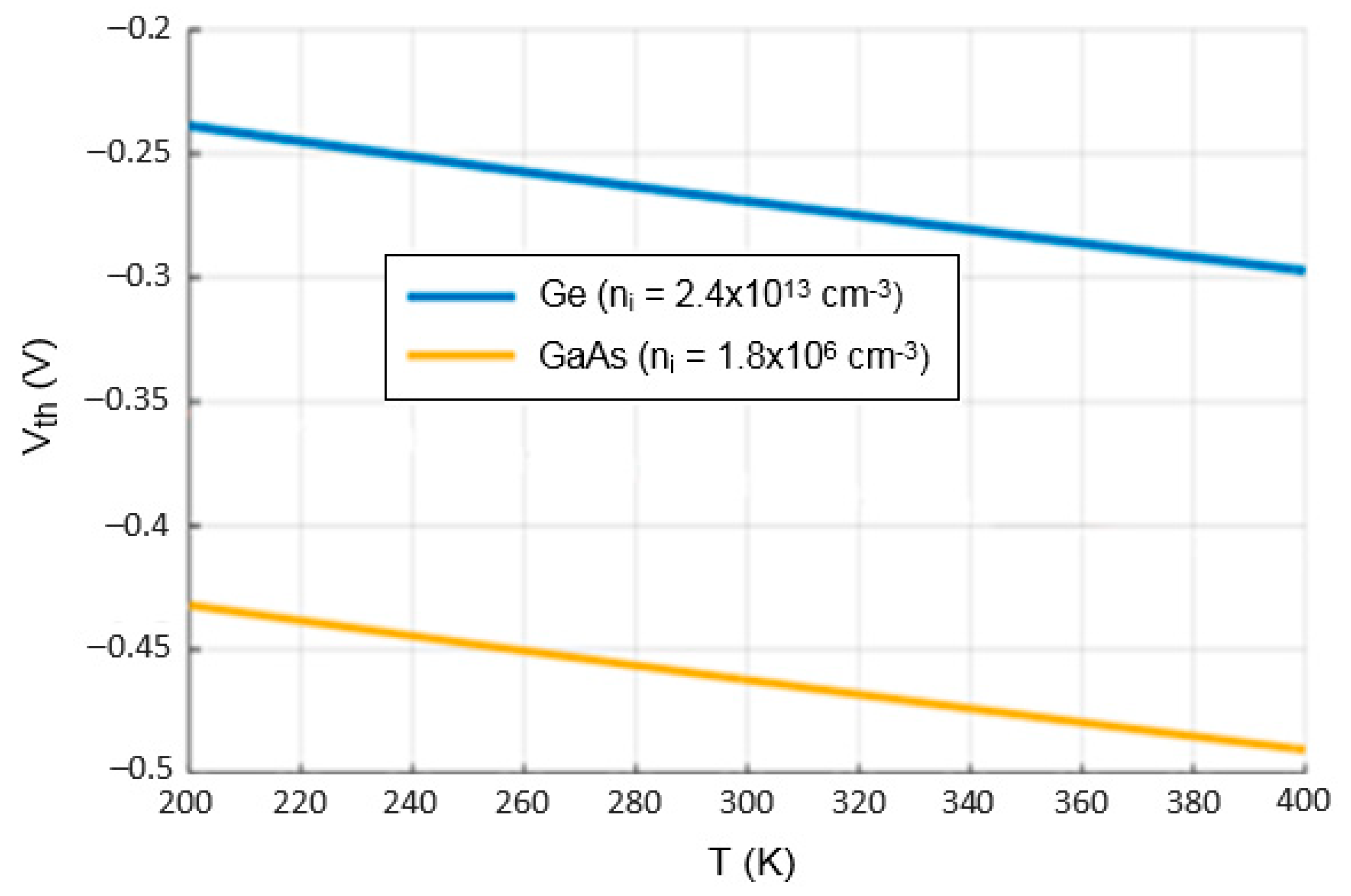
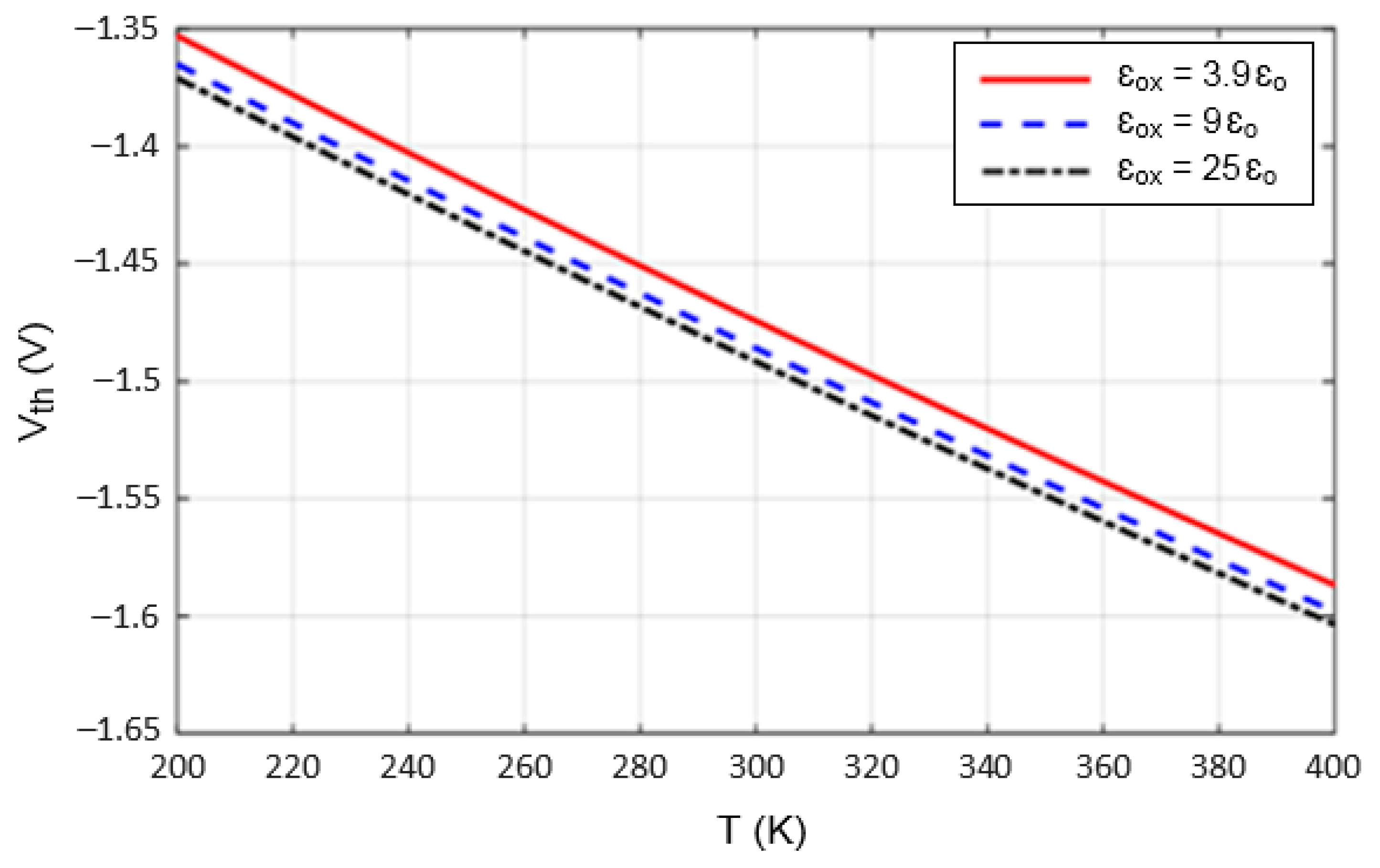
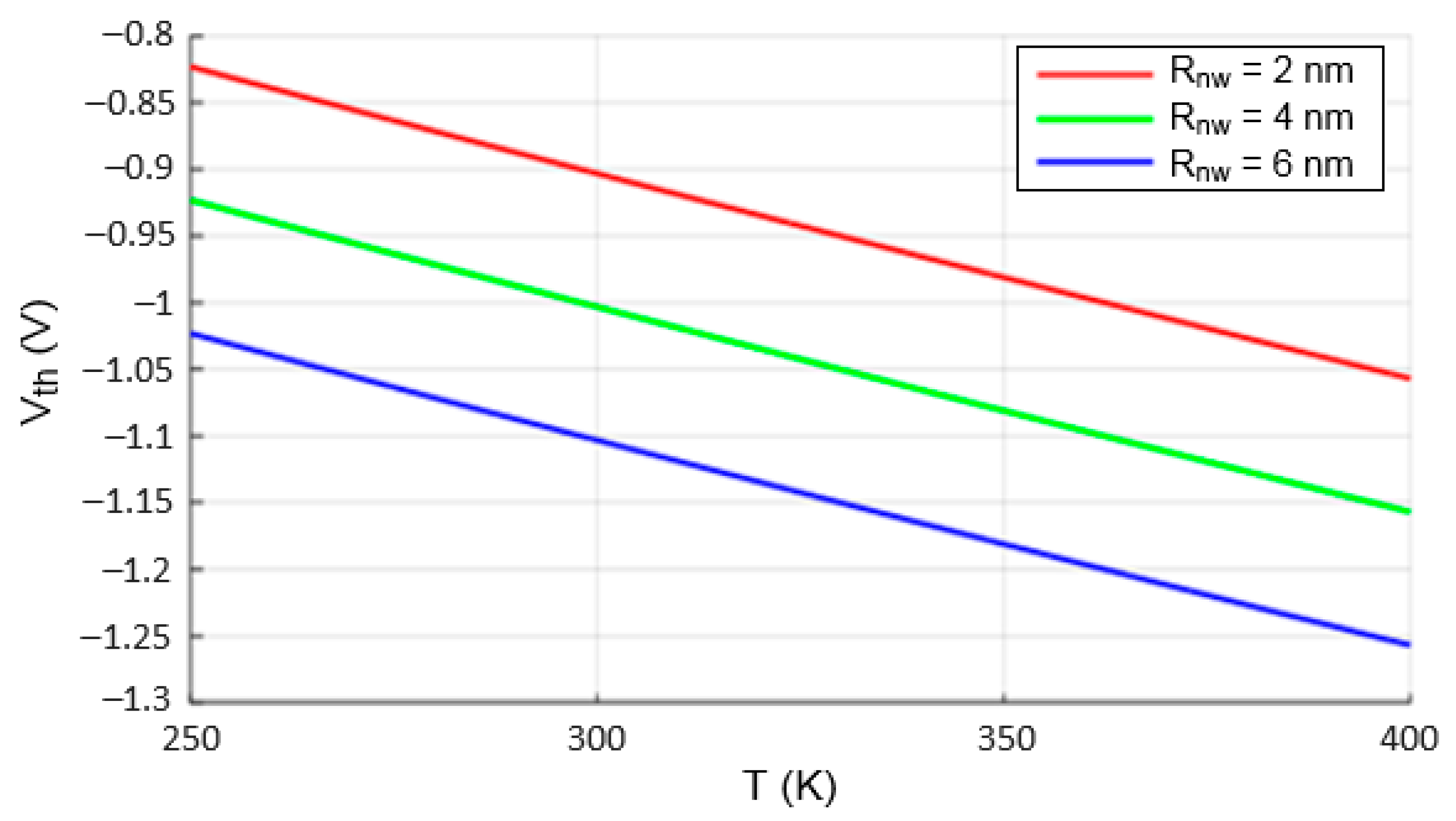
4.1. Threshold Voltage Analysis
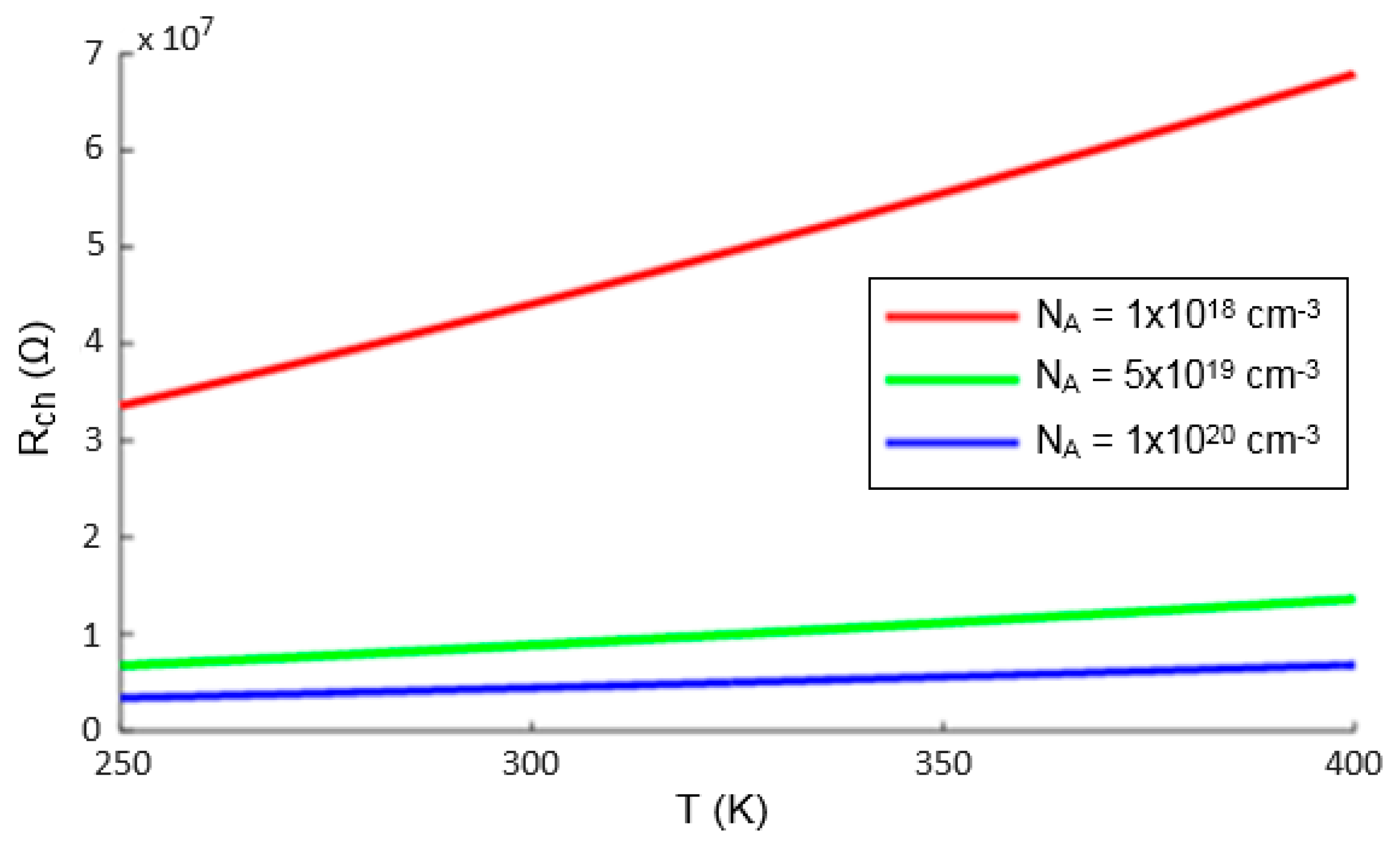
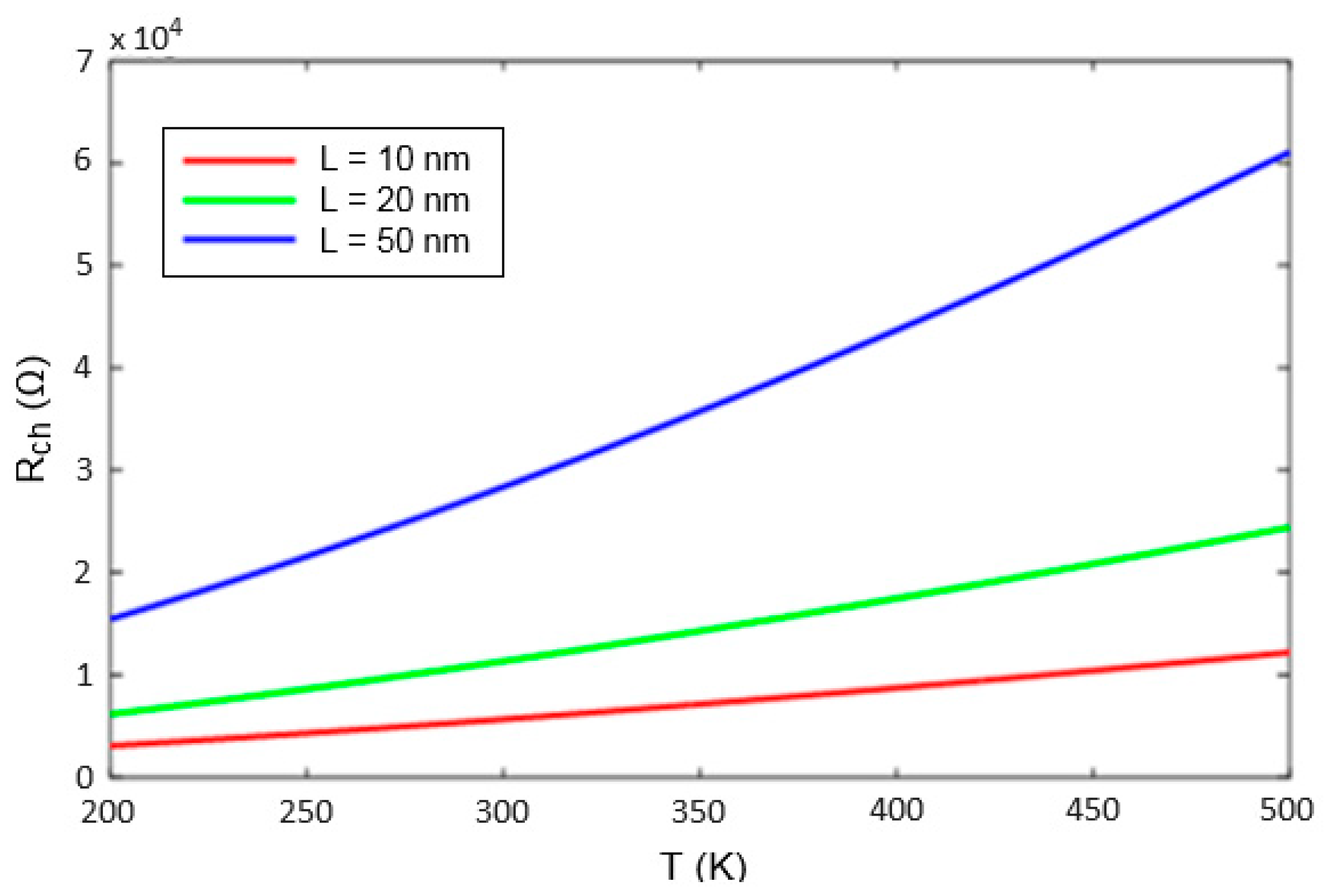
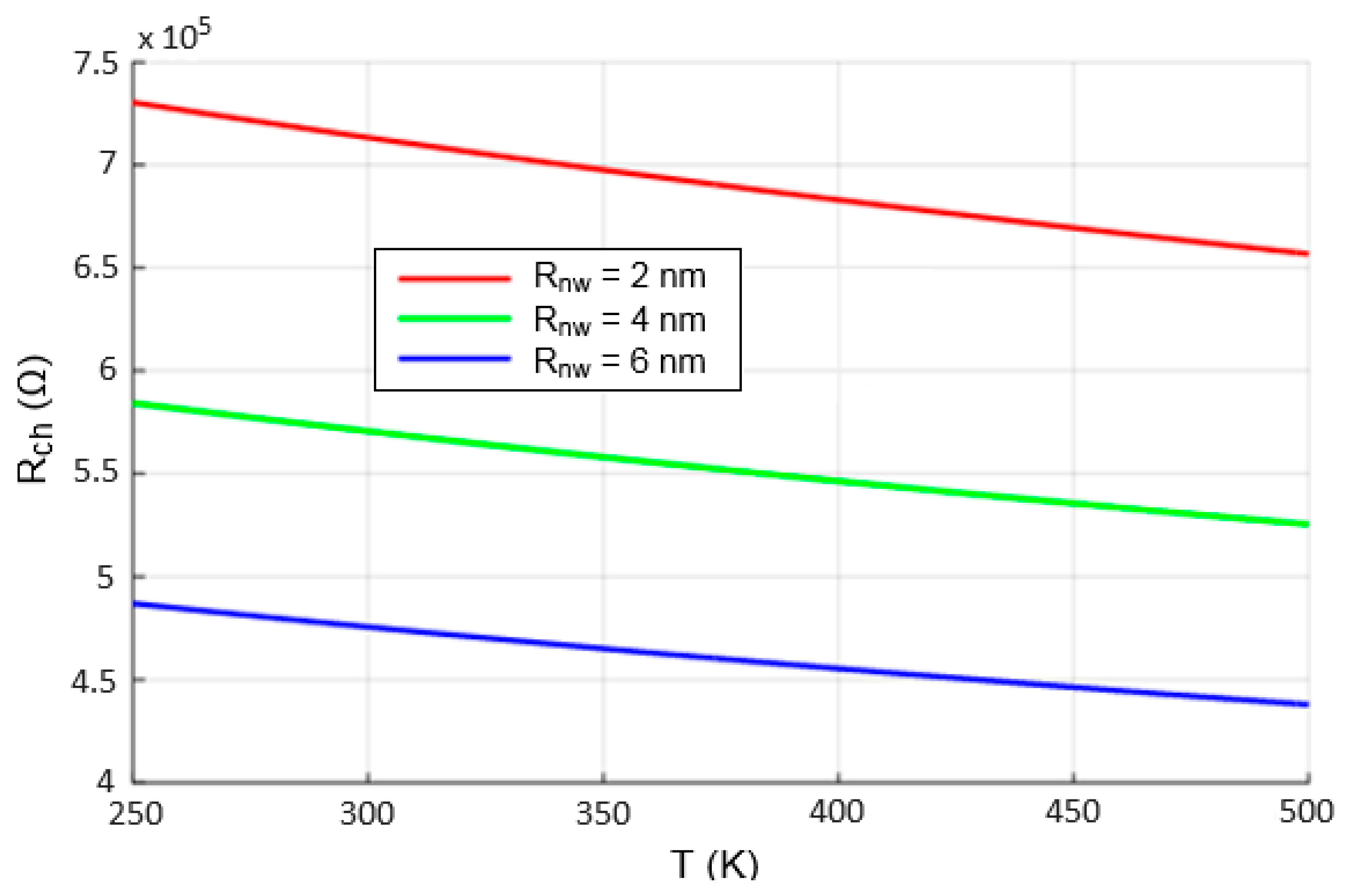
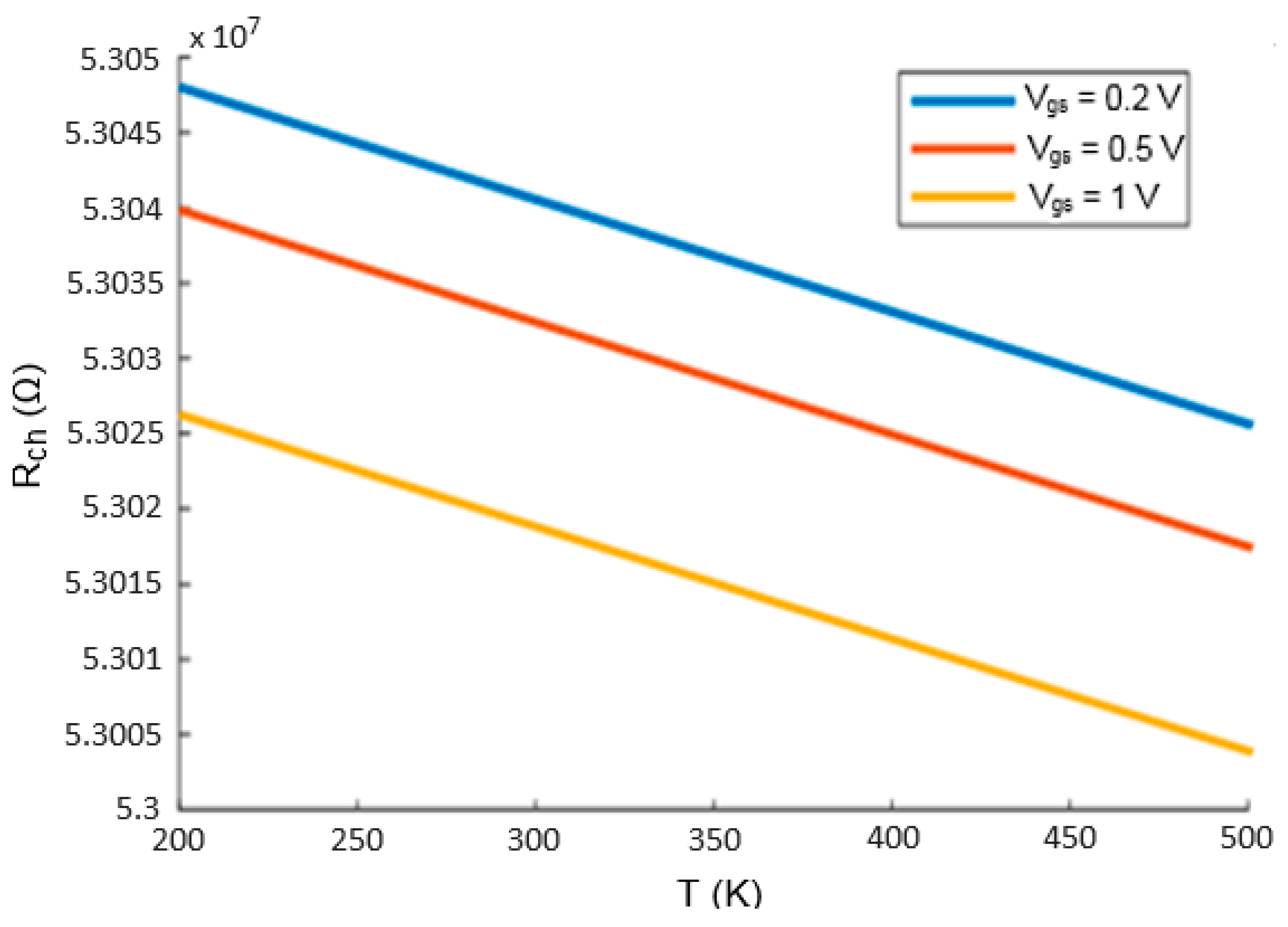
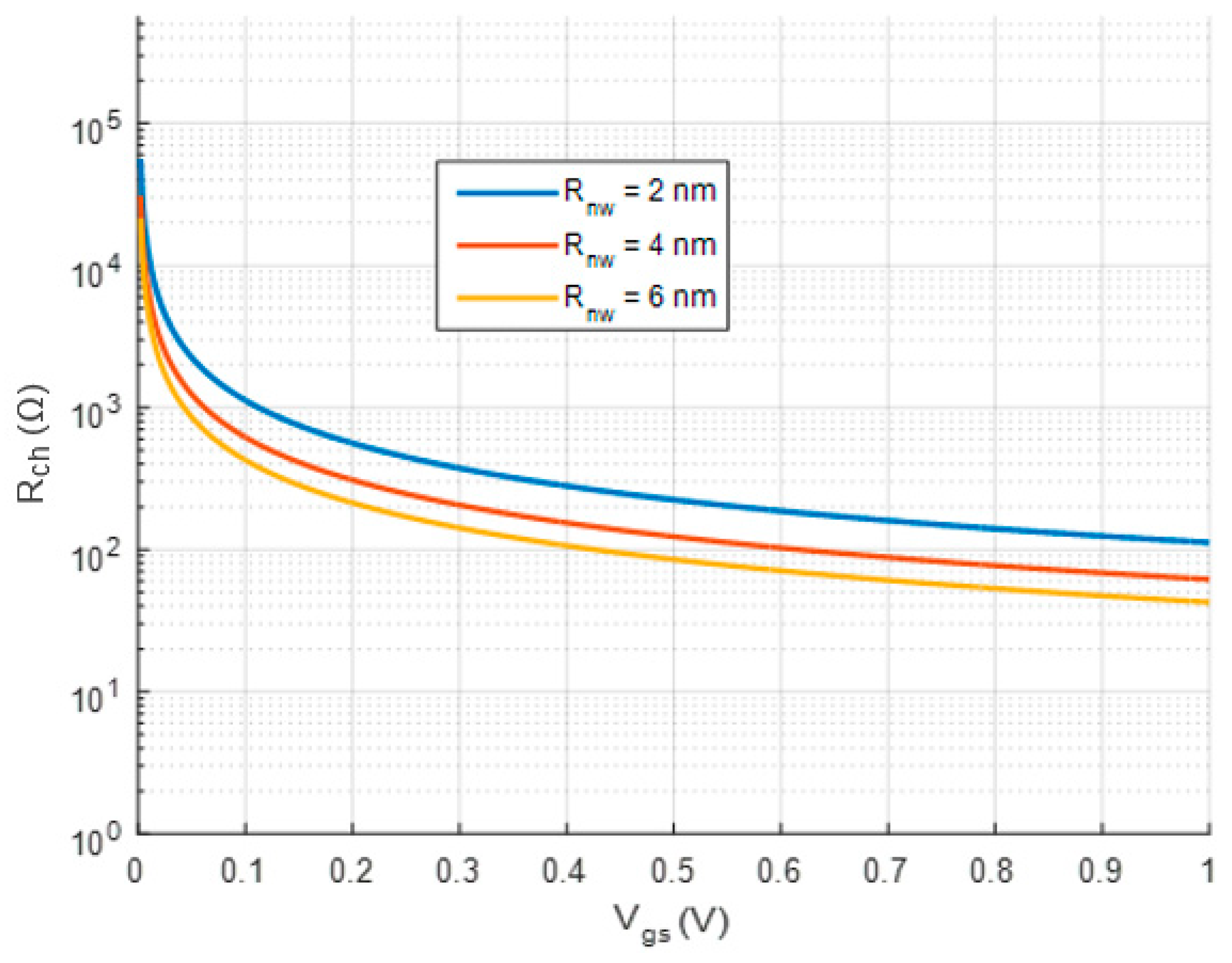
4.2. Channel Resistance Analysis
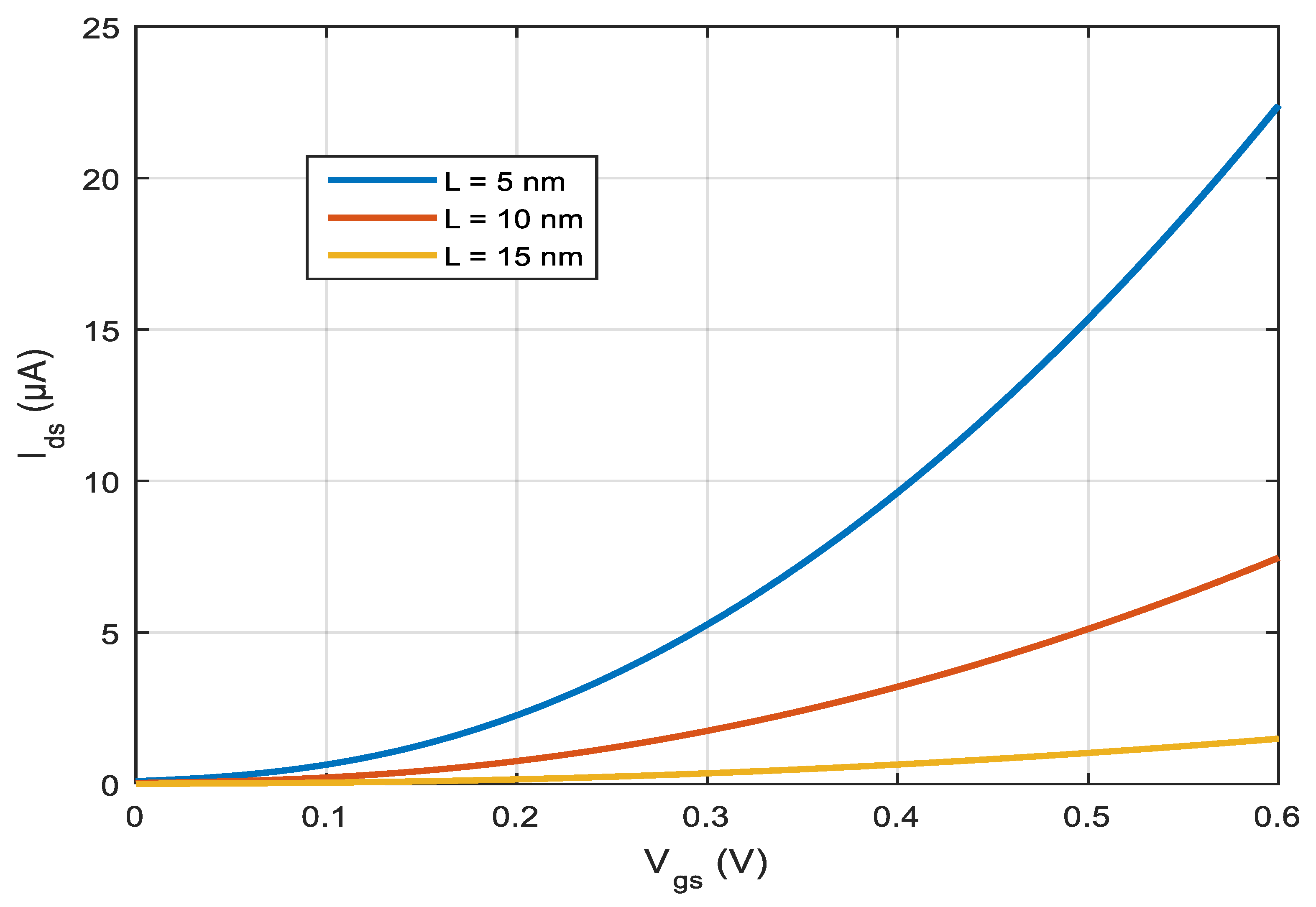
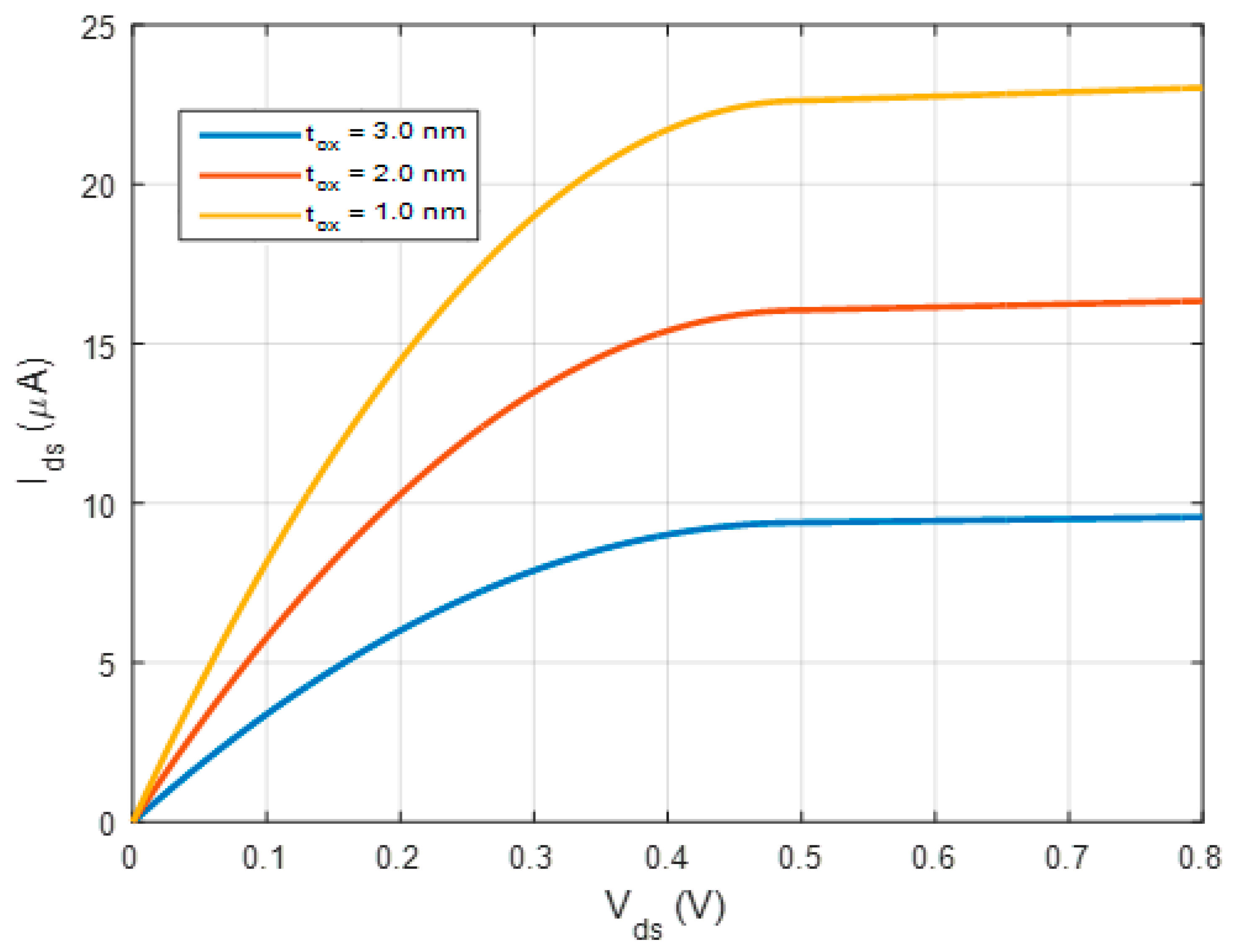
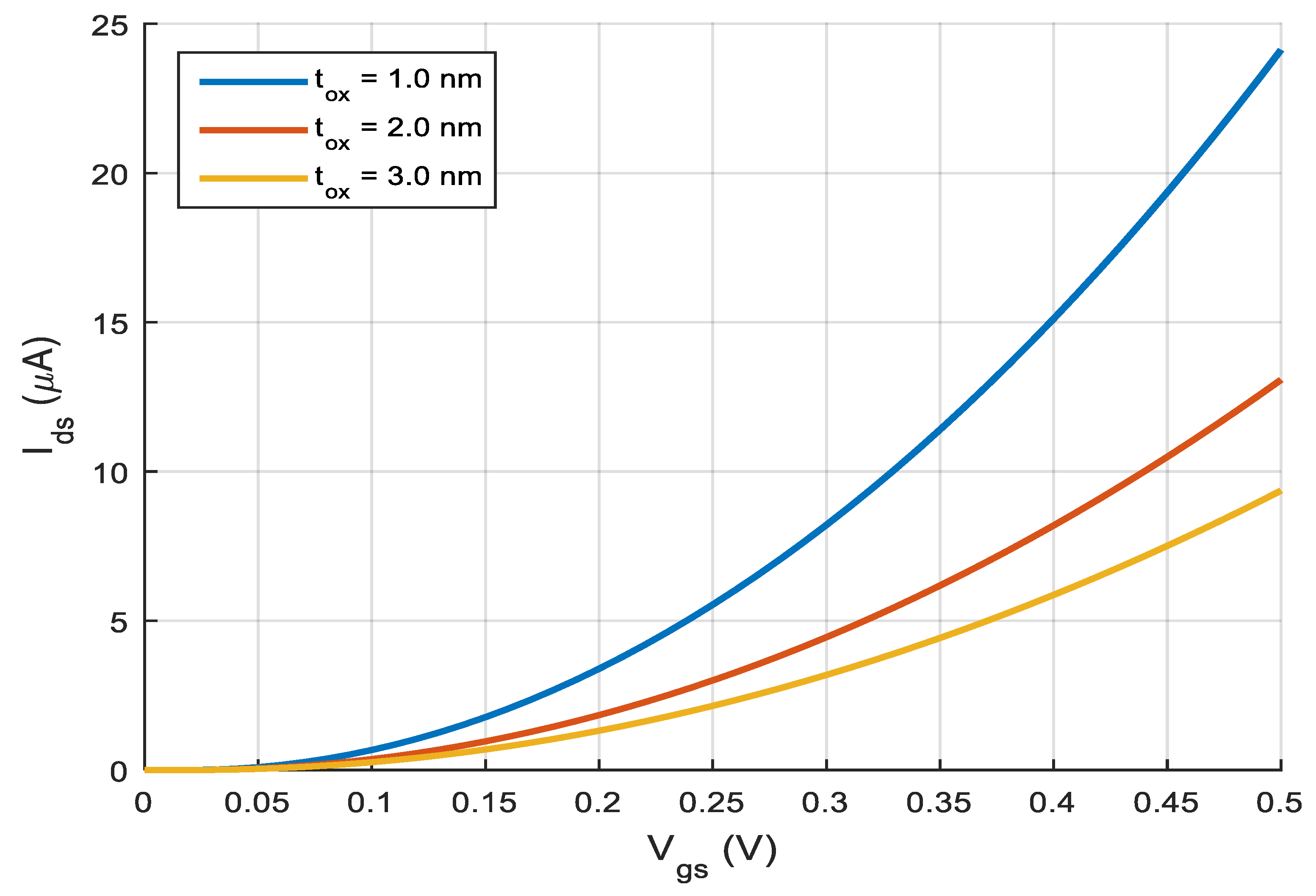
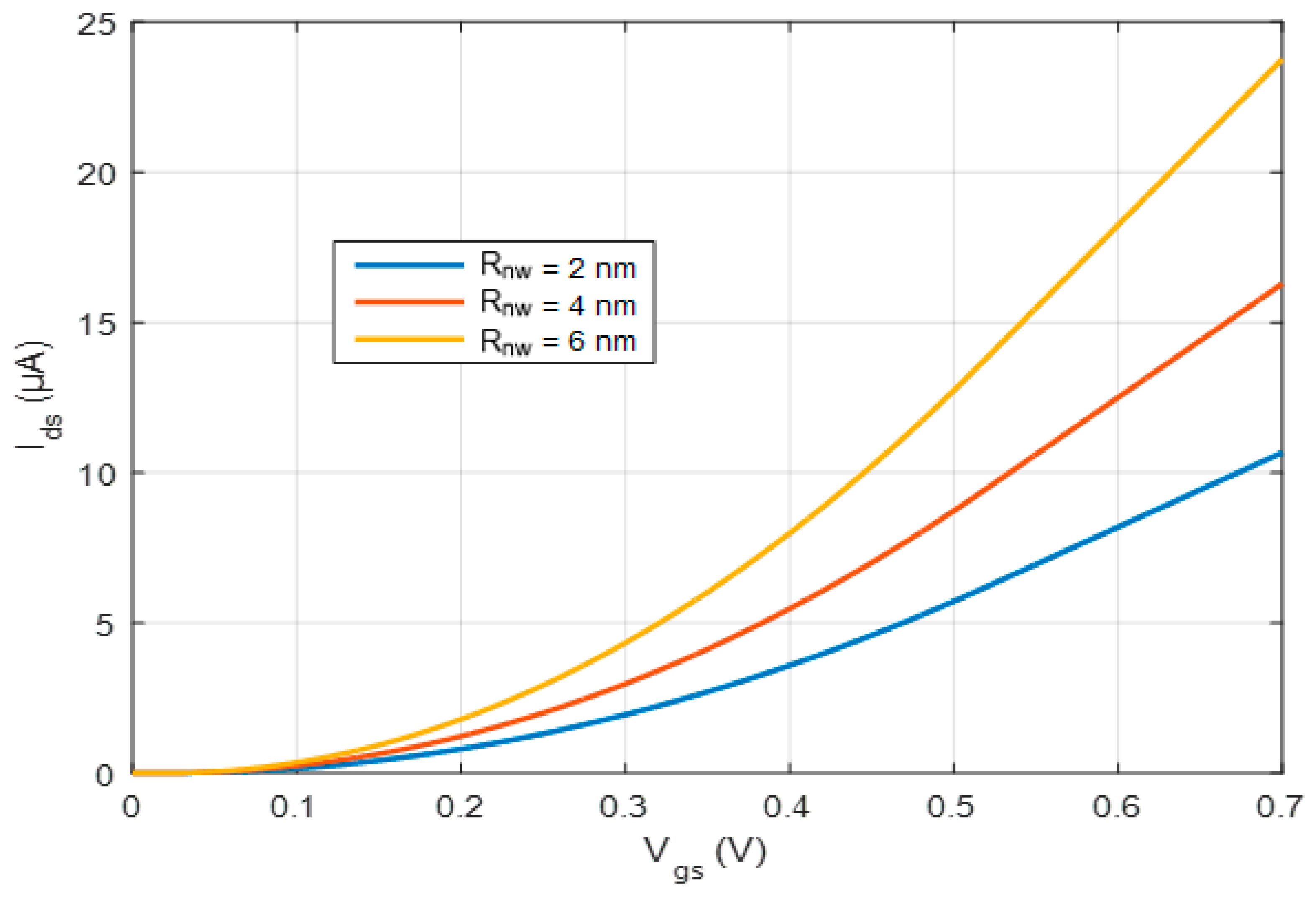
4.3. Current–Voltage Characteristics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, S.H.; Lee, T.I.; Lee, S.J.; Lee, S.M.; Yun, I.; Myoung, J.M. Electrical Characteristics of Metal Catalyst-Assisted Etched Rough Silicon Nanowire Depending on the Diameter Size. ACS Appl. Mater. Interfaces 2015, 7, 929–934. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Debnath, P.C.; Park, D.-H.; Kim, S.; Lee, S.Y. Controllability of Threshold Voltage in Ag-Doped ZnO Nanowire Field Effect Transistors by Adjusting the Diameter of Active Channel Nanowire. Appl. Phys. Lett. 2010, 96, 083103. [Google Scholar] [CrossRef]
- Lee, S.; Yoon, J.-S.; Lee, J.; Jeong, J.; Yun, H.; Lim, J.; Lee, S.; Baek, R.-H. Novel Modeling Approach to Analyze Threshold Voltage Variability in Short Gate-Length (15–22 nm) Nanowire FETs with Various Channel Diameters. Nanomaterials 2022, 12, 1721. [Google Scholar] [CrossRef]
- Ayvazian, T.; Xing, W.; Yan, W.; Penner, R.M. Field-Effect Transistors from Lithographically Patterned Cadmium Selenide Nanowire Arrays. ACS Appl. Mater. Interfaces 2012, 4, 4445–4452. [Google Scholar] [CrossRef] [PubMed]
- Van, N.H.; Lee, J.-H.; Sohn, J.I.; Cha, S.N.; Whang, D.; Kim, J.M.; Kang, D.J. High Performance Si Nanowire Field-Effect-Transistors Based on a CMOS Inverter with Tunable Threshold Voltage. Nanoscale 2014, 6, 5479. [Google Scholar] [CrossRef]
- Singh, P.; Miao, J.; Park, W.-T.; Kwong, D.-L. Minimum Detectable Strain Improvement in Junctionless Nanowire FET Sensors. In Proceedings of the 2012 IEEE 25th International Conference on Micro Electro Mechanical Systems (MEMS), Paris, France, 29 January–2 February 2012; pp. 1328–1331. [Google Scholar] [CrossRef]
- Zessin, J.; Xu, Z.; Shin, N.; Hambsch, M.; Mannsfeld, S.C.B. Threshold Voltage Control in Organic Field-Effect Transistors by Surface Doping with a Fluorinated Alkylsilane. ACS Appl. Mater. Interfaces 2019, 11, 2177–2188. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; Wu, P.; Guo, M.; Xu, X.; Xi, X.; Gao, J.; Rao, G.; Wang, S. Room Temperature Threshold Switching Behaviors of Bi0.9Nd0.1Fe1−xCoxO3 Nanoparticles. J. Mater. Chem. C 2015, 3, 4141–4147. [Google Scholar] [CrossRef]
- Lee, J.; Badami, O.; Carrillo-Nuñez, H.; Berrada, S.; Medina-Bailon, C.; Dutta, T.; Adamu-Lema, F.; Georgiev, V.P.; Asenov, A. Variability Predictions for the Next Technology Generations of n-type SixGe1−x Nanowire MOSFETs. Micromachines 2018, 9, 643. [Google Scholar] [CrossRef]
- Aldegunde, M.; Martinez, A.; Asenov, A. Non-equilibrium Green’s Function Analysis of Cross Section and Channel Length Dependence of Phonon Scattering and Its Impact on the Performance of Si Nanowire Field Effect Transistors. J. Appl. Phys. 2011, 110, 094518. [Google Scholar] [CrossRef]
- Vardhan, P.H.; Mittal, S.; Ganguly, S.; Ganguly, U. Analytical Modeling of Metal Gate Granularity Based Threshold Voltage Variability in NWFET. Solid-State Electron. 2018, 147, 26–34. [Google Scholar] [CrossRef]
- Nayak, K.; Agarwal, S.; Bajaj, M.; Oldiges, P.J.; Murali, K.V.R.M.; Ramgopal, V. Metal-Gate Granularity-Induced Threshold Voltage Variability and Mismatch in Si Gate-All-Around Nanowire n-MOSFETs. IEEE Trans. Electron Devices 2014, 61, 3892–3895. [Google Scholar] [CrossRef]
- Wu, C.-C.; Ko, F.-H.; Yang, Y.-S.; Hsia, D.-L.; Lee, B.-S.; Su, T.-S. Label-Free Biosensing of a Gene Mutation Using a Silicon Nanowire Field-Effect Transistor. Biosens. Bioelectron. 2009, 25, 820–825. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Debnath, P.C.; Kim, S.; Lee, S.Y. Temperature Stress on Pristine ZnO Nanowire Field Effect Transistor. Appl. Phys. Lett. 2011, 98, 113109. [Google Scholar] [CrossRef]
- Ghedira, S.; Fargi, A.; Besbes, K. Temperature Dependent Analytical Model for the Threshold Voltage of the SiC VJFET with a Lateral Asymmetric Channel. Electronics 2021, 10, 1494. [Google Scholar] [CrossRef]
- Sakuna, N.; Muanghlua, R.; Niemcharoen, S.; Ruangphanit, A.; Poyai, A. Temperature and Devices Dimension Dependence on Threshold Voltage, the Low Field Mobility and the Series Parasitic Resistance of PMOSFET. In Proceedings of the 2013 10th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Krabi, Thailand, 15–17 May 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Morioka, N.; Yoshioka, H.; Suda, J.; Kimoto, T. Quantum-Confinement Effect on Holes in Silicon Nanowires: Relationship between Wave Function and Band Structure. J. Appl. Phys. 2011, 109, 064318. [Google Scholar] [CrossRef]
- Yang, G.; Jang, S.; Ren, F.; Pearton, S.J.; Kim, J. Influence of High-Energy Proton Irradiation on β-Ga2O3 Nanobelt Field-Effect Transistors. ACS Appl. Mater. Interfaces 2017, 9, 40471–40476. [Google Scholar] [CrossRef]
- Minhaj, E.H.; Esha, S.R.; Adnan, M.M.R.; Dey, T. Impact of Channel Length Reduction and Doping Variation on Multigate FinFETs. In Proceedings of the 2018 International Conference on Advancement in Electrical and Electronic Engineering (ICAEEE), Gazipur, Bangladesh, 22–24 November 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Awadhiya, B.; Kondekar, P.N.; Yadav, S.; Upadhyay, P. Insight into Threshold Voltage and Drain Induced Barrier Lowering in Negative Capacitance Field Effect Transistor. Trans. Electr. Electron. Mater. 2021, 22, 267–273. [Google Scholar] [CrossRef]
- Choe, M.; Park, W.; Kang, J.-W.; Jeong, S.; Hong, W.-K.; Lee, B.H.; Park, S.-J.; Lee, T. Investigation of Threshold Voltage Instability Induced by Gate Bias Stress in ZnO Nanowire Field Effect Transistors. Nanotechnology 2012, 23, 485201. [Google Scholar] [CrossRef]
- Fan, J.-C.; Lee, S.-F. Giant Magnetoresistance Effect in Ni-Fe-Mo Alloys. MATEC Web Conf. 2016, 67, 02023. [Google Scholar] [CrossRef]
- Price, A.; Martinez, A. Impact of Oxide Thickness on the Performance of a GaAs NWFET. J. Phys. Conf. Ser. 2015, 609, 012004. [Google Scholar] [CrossRef]
- Jamwal, D.; Dass, D.; Prasher, R.; Vaid, R. Impact of Scaling Gate Oxide Thickness on the Performance of Silicon Based Triple Gate Rectangular NWFET. In Physics of Semiconductor Devices; Springer: Cham, Switzerland, 2014; pp. 581–584. [Google Scholar] [CrossRef]
- Wu, L.; Xu, J.; Li, Q.; Fan, Z.; Mei, F.; Zhou, Y.; Yan, J.; Chen, Y. Enhanced Performance of In2O3 Nanowire Field Effect Transistors with Controllable Surface Functionalization of Ag Nanoparticles. Nanotechnology 2020, 31, 355703. [Google Scholar] [CrossRef] [PubMed]
- Vardhan, P.H.; Ganguly, S.; Ganguly, U. An Accurate Expression to Estimate the Metal Gate Granularity Induced Threshold Voltage Variability in NWFETs. Solid-State Electron. 2019, 152, 65–71. [Google Scholar] [CrossRef]
- Dobrescu, D.; Cretu, B.; Simoen, E.; Veloso, A.; Voicu-Spineanu, A.; Dobrescu, L. Si GAA NW FETs Threshold Voltage Evaluation. Solid-State Electron. 2022, 194, 108317. [Google Scholar] [CrossRef]
- Bahador, S.N.; Tan, M.L.P.; Ismail, R. Performance Evaluation of Silicon Nanowire Gate-All-Around Field-Effect Transistors and Their Dependence of Channel Length and Diameter. Sci. Adv. Mater. 2015, 7, 190–198. [Google Scholar] [CrossRef]
- Bahador, N.; Tan, M.L.P.; Ahmadi, M.T.; Ismail, R. A Unified Drain–Current Model of Silicon Nanowire Field-Effect Transistor (SiNWFET) for Performance Metric Evaluation. Sci. Adv. Mater. 2014, 6, 354–360. [Google Scholar] [CrossRef]
- Yadav, D.; Nair, D.R. Performance Evaluation of Germanium-Tin Nanowire PFETs: Impact of Mole Fraction, Orientation and Doping. In Proceedings of the 2018 4th IEEE International Conference on Emerging Electronics (ICEE), Bengaluru, India, 17–19 December 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Patel, J.; Suman, P.; Lemtur, A.; Sharma, D. Performance Booster Electrical Drain SiGe Nanowire TFET (EDD-SiGe-NW-TFET) with DC Analysis and Optimization. In Information and Communication Technology for Intelligent Systems; Smart Innovation, Systems and Technologies; Springer: Singapore, 2019; pp. 567–574. [Google Scholar] [CrossRef]
- Irfan, M.; Sattar, A.; Iqbal, A.; Khan, M.F.; Amjad, R.J.; Mahmood, H.; Latif, H.; Akbar, N.; Alvi, F.; Sultana, I. Investigation of Effects of Diameter, Doping and Vacancy Defects on the Band Structure and Transport Properties of Silicon Nanowires for Potential Applications in Field-Effect Transistors. J. Electron. Mater. 2019, 48, 2761–2769. [Google Scholar] [CrossRef]
- Chaujar, R.; Yirak, M.G. Sensitivity Investigation of Junctionless Gate-All-Around Silicon Nanowire Field-Effect Transistor-Based Hydrogen Gas Sensor. Silicon 2023, 15, 609–621. [Google Scholar] [CrossRef]
- Zhou, X.; Waldron, N.; Boccardi, G.; Sebaai, F.; Merckling, C.; Eneman, G.; Sioncke, S.; Nyns, L.; Opdebeeck, A.; Maes, J.W.; et al. Scalability of InGaAs Gate-All-Around FET Integrated on 300 mm Si Platform: Demonstration of Channel Width down to 7 nm and Lg down to 36 nm. In Proceedings of the 2016 IEEE Symposium on VLSI Technology, Honolulu, HI, USA, 14–16 June 2016; pp. 1–2. [Google Scholar] [CrossRef]
- Blank, T.V.; Gol’dberg, Y.A. Mechanisms of current flow in metal-semiconductor ohmic contacts. Semiconductors 2007, 41, 1263–1292. [Google Scholar] [CrossRef]
- Lin, J.C.; Yu, S.Y.; Mohney, S.E. Characterization of Low-Resistance Ohmic Contacts to n- and p-Type InGaAs. J. Appl. Phys. 2013, 114, 044504. [Google Scholar] [CrossRef]
- Jo, G.; Maeng, J.; Kim, T.-W.; Hong, W.-K.; Choi, B.-S.; Lee, T. Channel-Length and Gate-Bias Dependence of Contact Resistance and Mobility for In2O3 Nanowire Field Effect Transistors. J. Appl. Phys. 2007, 102, 084508. [Google Scholar] [CrossRef]










| NWFET Parameters | Reference Values |
|---|---|
| Channel length (nm) | 5, 10, 15, 20, 50 |
| Nanowire radius (nm) | 2, 4, 6 |
| Oxide thickness (nm) | 1, 2, 3 |
| NWFET Parameters | Reference Values |
|---|---|
| Doping concentration (cm−3) | 1 × 1018–1 × 1020 |
| Energy bandgap for Si, Ge, GaAs, GaN, diamond (eV) | 1.12, 0.66, 1.43, 3.44, 5.47 |
| Relative permittivity for Si, Ge, GaAs | 11.7, 16, 12.9 |
| Intrinsic carrier concentrations for Ge, Si, GaAs (cm−3) | 2.4 × 1013, 1.5 × 1010, 1.8 × 106 |
| Dielectric constant for HfO2, Al2O3, SiO2 | 25ɛ0, 9ɛ0, 3.9ɛ0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marki, R.; Dehimi, L.; Zeghdar, K.; Pezzimenti, F.; Messina, G.; Della Corte, F.G. Impact of Physical and Material Parameters on the Threshold Voltage and the Channel Resistance of Nanowire Field-Effect Transistors for Advanced Nanoscale Devices. Electronics 2025, 14, 4279. https://doi.org/10.3390/electronics14214279
Marki R, Dehimi L, Zeghdar K, Pezzimenti F, Messina G, Della Corte FG. Impact of Physical and Material Parameters on the Threshold Voltage and the Channel Resistance of Nanowire Field-Effect Transistors for Advanced Nanoscale Devices. Electronics. 2025; 14(21):4279. https://doi.org/10.3390/electronics14214279
Chicago/Turabian StyleMarki, Rebiha, Lakhdar Dehimi, Kamal Zeghdar, Fortunato Pezzimenti, Giacomo Messina, and Francesco G. Della Corte. 2025. "Impact of Physical and Material Parameters on the Threshold Voltage and the Channel Resistance of Nanowire Field-Effect Transistors for Advanced Nanoscale Devices" Electronics 14, no. 21: 4279. https://doi.org/10.3390/electronics14214279
APA StyleMarki, R., Dehimi, L., Zeghdar, K., Pezzimenti, F., Messina, G., & Della Corte, F. G. (2025). Impact of Physical and Material Parameters on the Threshold Voltage and the Channel Resistance of Nanowire Field-Effect Transistors for Advanced Nanoscale Devices. Electronics, 14(21), 4279. https://doi.org/10.3390/electronics14214279







