Assessment of the Effective Flange Width for Cold-Formed Steel-Timber Composite Beams: A Finite Element Study
Abstract
1. Introduction and Literature Review
2. Shear Lag and Effective Flange Width
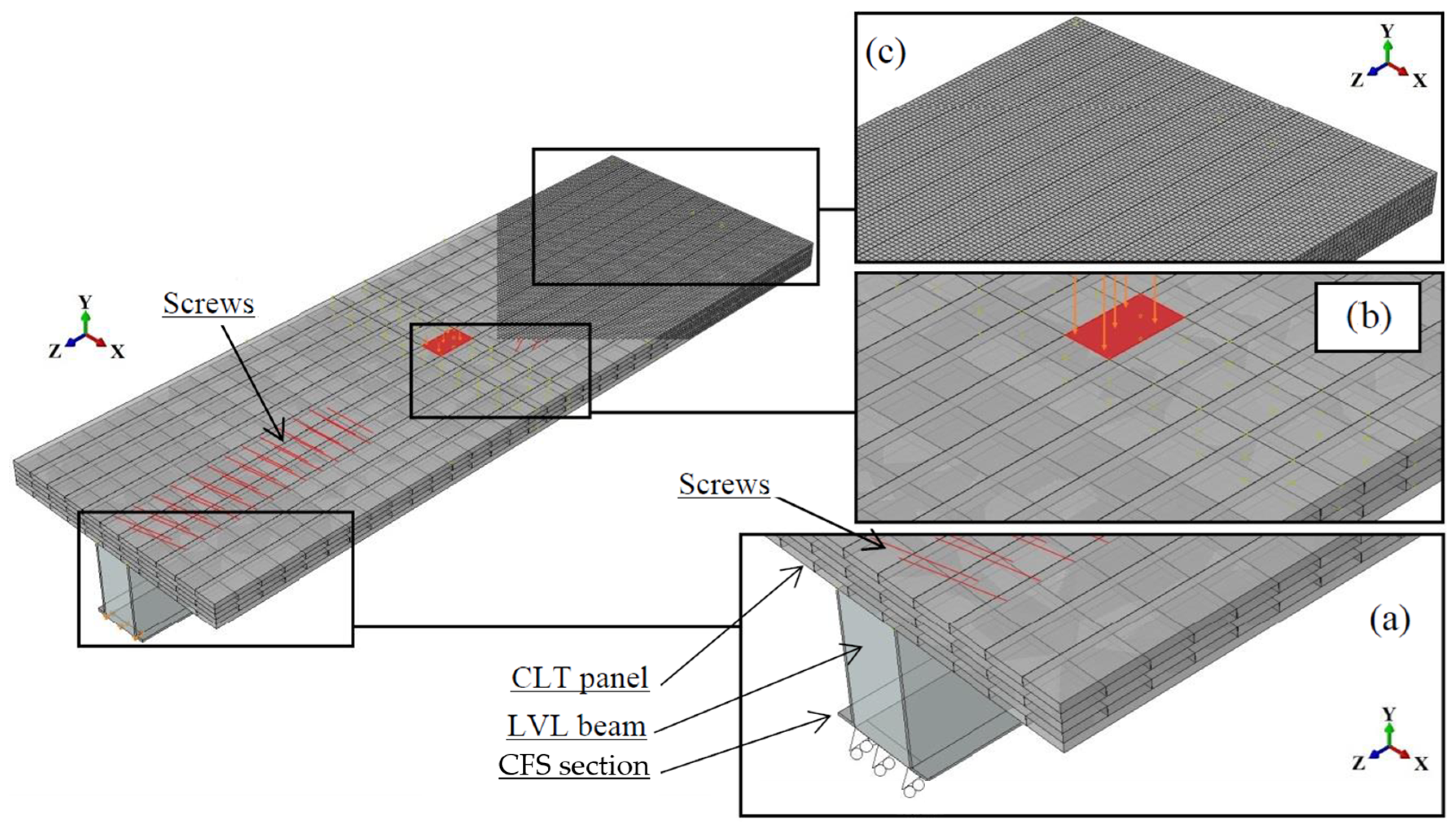
3. Test Setup and Finite Element Simulation
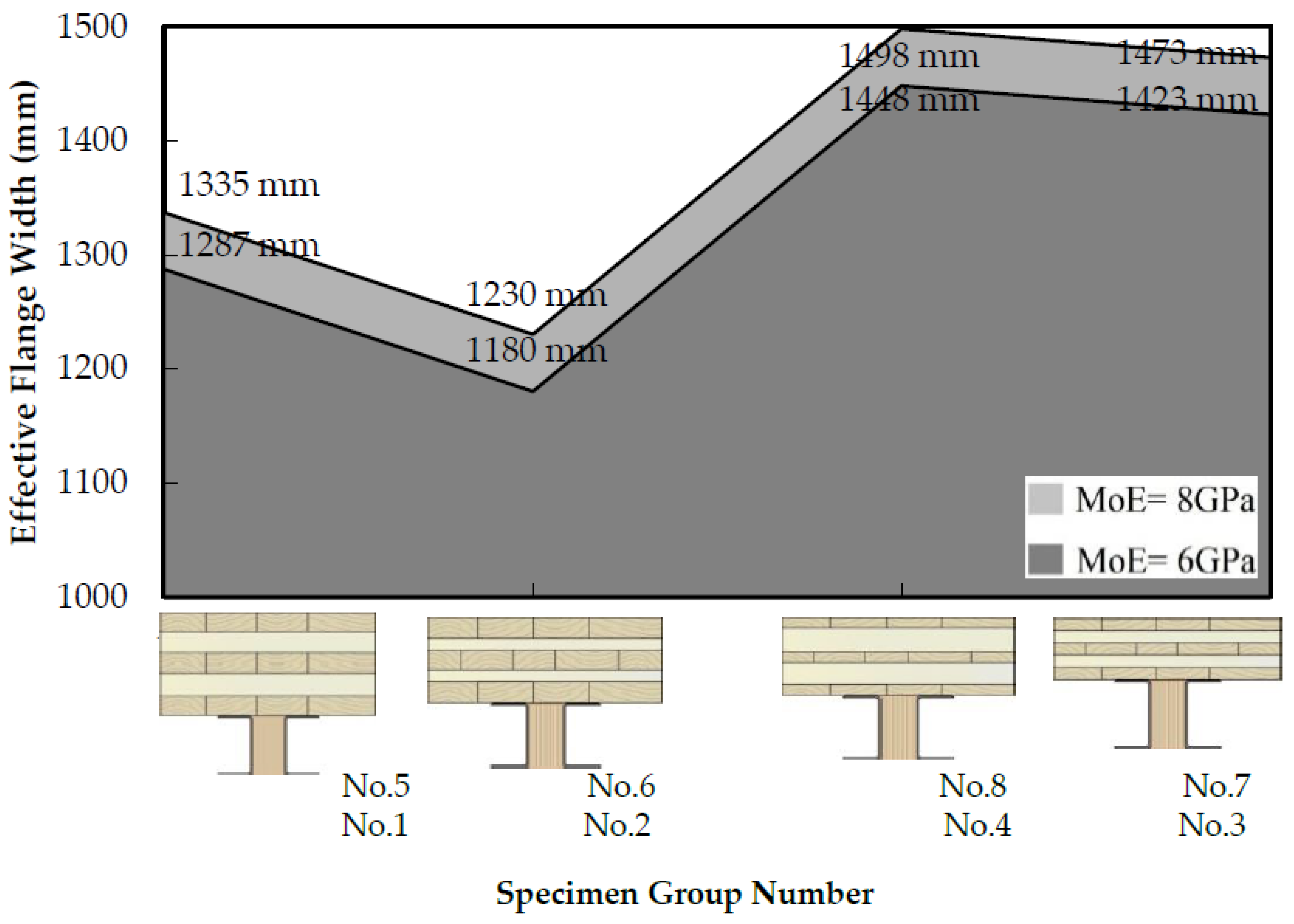
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kyvelou, P.; Gardner, L.; Nethercot, D.A. Composite Action Between Cold-Formed Steel Beams and Wood-Based Floorboards. Int. J. Struct. Stab. Dyn. 2015, 15, 1540029. [Google Scholar] [CrossRef]
- Masoudnia, R.; Quenneville, P. Stub girder flooring system for timber construction. In Proceedings of the World Conference on Timber Engineering, Quebec City, QC, Canada, 10–14 August 2014. [Google Scholar]
- Popovski, M.; Karacabeyli, E. Seismic behaviour of cross-laminated timber structures. In Proceedings of the World Conference on Timber Engineering, Auckland, New Zealand, 15–19 July 2012. [Google Scholar]
- Pearson, H.; Evernden, M.; Harris, R. Analysis of engineered timber panels using a strut and tie model for use in folded plate structures and deep beams. Eng. Struct. 2012, 9, 344–353. [Google Scholar]
- Masoudnia, R.; Quenneville, P. Stub Girder Flooring System for Timber Construction; Provisional Report; The University of Auckland: Auckland, New Zealand, 2013. [Google Scholar]
- Masoudnia, R.; Hashemi, A.; Quenneville, P. Evaluation of effective flange width in the CLT composite T.-beams. In Proceedings of the World Conference on Timber Engineering (WCTE 2016), Vienna, Austria, 22–25 August 2016. [Google Scholar]
- Dias, A.M.P.G.; Skinner, J.; Crews, K.; Riggio, M. Mechanical performance of timber–steel hybrid connections. Eng. Struct. 2016, 112, 196–207. [Google Scholar]
- Fragiacomo, M.; Lukaszewska, E. Design model for steel–timber composite beams. J. Struct. Eng. 2011, 137, 785–794. [Google Scholar]
- Chen, Z.; Yeoh, D.; Guan, Z.W. Finite element analysis of composite steel–timber beams with screw connections. Constr. Build. Mater. 2019, 208, 187–198. [Google Scholar]
- Chiewanichakorn, M.; Aref, A.J.; Chen, S.S.; Ahn, I. Effective flange width definition for steel-concrete composite bridge girder. J. Struct. Eng. 2014, 130, 2016–2031. [Google Scholar] [CrossRef]
- Chen, S.S.; Aref, A.J.; Chiewanichakorn, M.; Ahn, I. Proposed effective width criteria for composite bridge girders. J. Bridge Eng. 2007, 12, 325–338. [Google Scholar] [CrossRef]
- Masoudnia, R.; Hashemi, A.; Quenneville, P. Predicting the Effective Flange Width of a CLT Slab in Timber Composite Beams. J. Struct. Eng. 2018, 144, 04018084. [Google Scholar] [CrossRef]
- Alsarraf, M.A.; El Din, H.S. Effects of Web Openings on the Effective Slab Widths in Composite Steel Beams. In Proceedings of the ICCAE, Paris, France, 21–22 July 2014; pp. 27–28. [Google Scholar]
- Winter, G. Stress Distribution in the Equivalent Width of Flanges of Wide, Thin-Wall Steel Beams; National Advisory Committee for Aeronautics: Hampton, VA, USA, 1940. [Google Scholar]
- Schade, H.A. The Effective Breadth of Stiffened Plating Under Bending Loads; Society of Naval Architects and Marine Engineers: Alexandria, VA, USA, 1951. [Google Scholar]
- Timoshenko, S.; Goodier, J.; Abramson, H.N. Theory of elasticity. J. Appl. Mech. 1970, 37, 888. [Google Scholar] [CrossRef]
- Heins, C.P.; Fan, H.M. Effective composite beam width at ultimate load. J. Struct. Div. 1976, 102, 2163–2179. [Google Scholar] [CrossRef]
- Adekola, I. Effective widths of composite beams of steel and concrete. Struct. Eng. 1968, 46, 285–289. [Google Scholar]
- Aref, A.J.; Chiewanichakorn, M.; Chen, S.S.; Ahn, I. Effective slab width definition for negative moment regions of composite bridges. J. Bridge Eng. 2007, 12, 339–349. [Google Scholar] [CrossRef]
- Moffatt, K.R.; Dowling, P.J. British shear lag rules for composite girders. J. Struct. Div. 1978, 104, 1123–1130. [Google Scholar] [CrossRef]
- Nassif, H.; Abu-Amra, T.; El-Tawil, S. Effective flange width criteria for composite steel girder bridges. In Proceedings of the Transportation Research Board 84th Annual Meeting, Washington, DC, USA, 9–13 January 2005. No. 05-2477. [Google Scholar]
- Ahn, I.; Chiewanichakorn, M.; Chen, S.S.; Aref, A.J. Effective flange width provisions for composite steel bridges. Eng. Struct. 2004, 26, 1843–1851. [Google Scholar] [CrossRef]
- Castro, J.; Elghazouli, A.; Izzuddin, B. Assessment of effective slab widths in composite beams. J. Constr. Steel Res. 2007, 63, 1317–1327. [Google Scholar] [CrossRef]
- Masoudnia, R. Feasibility of Cross Laminated Timber Panel for Bridges Application: Preliminary Experimental, Numerical and Analytical Study. In Proceedings of the World Conference on Timber Engineering, Brisbane, Australia, 22–26 June 2025. [Google Scholar]
- Masoudnia, R.; Masoudnia, S.; Hashemi, A.; Quenneville, P. Numerical Investigation of CLT Composite Double T-Beams. In Proceedings of the World Conference on Timber Engineering, Brisbane, Australia, 22–26 June 2025. [Google Scholar]
- Gagnon, S.; Pirvu, C. CLT Handbook: Cross-Laminated Timber; FPInnovations: Montréal, QC, Canada, 2011. [Google Scholar]
- Buchanan, A.H.; New Zealand Timber Industry Federation. Timber Design Guide; New Zealand Timber Industry Federation: Wellington, New Zealand, 1999. [Google Scholar]
- Masoudnia, R. Improvements to Timber Composite Beams. Provisional Patent No. 731,716, 2017.












| Source | Formulas | Definitions |
|---|---|---|
| AISCE-LRFD:13.1 | be is least of: (1) Beam span/4 (2) bs (3) Two times distance to edge of slab. |  |
| Canadian CSA: SS17.4 Euro Code 2000 | be is least of: (1) Beam span/4 (2) bs | |
| ACI | be is least of: (1) Beam span/4 (2) bw + 16hf (3) Center to center spacing of beams |
| Formula | Scholars | Year | |
|---|---|---|---|
| beff = | Equation (1) | Miller and Metzer | 1929 |
| beff = 2 = | Equation (2) | Timoshenko and Goodier | 1970 |
| beff = = | Equation (3) | Methee Chiewanchakorn | 2004 |
| Component | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| CLT | 6 | 18 | 8000 | 363 | 363 | 0.2 | 0.018 | 0.15 | 0.018 | 0.21 | 0.18 |
| CLT | 4 | 15 | 6000 | 272 | 272 | 0.15 | 0.013 | 0.11 | 0.013 | 0.09 | 0.13 |
| LVL | 33 | 45 | 13,200 | 600 | 600 | 0.35 | 0.03 | 0.35 | 0.03 | 0.35 | 0.35 |
| Test Specimen | W × T × L (mm) × (mm) × (mm) | Deflection | |
|---|---|---|---|
| Experimental (mm) | Numerical (mm) | ||
| CLT | 2030 × 200 × 6000 | 17.9 * | 17.9 |
| LVL | 300 × 605 × 6000 | 3.1 * | 3.1 |
| Timber Composite Beam | CLT + LVL (connected by screws) | 1.8 ** | 1.7 |
| LVDT | Position of the LVDT | Slip (mm) (Experimental) * | Slip (mm) (Numerical) * |
|---|---|---|---|
| 1 | At mid-span | 0 | 0 |
| 2 | 1 m from mid-span | 0.056 | 0.055 |
| 3 | 2 m from mid-span | 0.084 | 0.085 |
| 4 | 3 m from mid-span | 0.121 | 0.122 |
| Config. | CLT (mm) W × T 1 × L | CLT (GPa) EL1, EL2, EL3, EL4, EL5 2 | LVL (mm) W × T × L | LVL (GPa) MoE | Predicted Effective Width Flange (mm) |
|---|---|---|---|---|---|
| 1 | 2000 × 200 × 6000 2000 × (40 + 40 + 40 + 40 + 40) 1 × 6000 | 8, 8, 8, 8, 8 2 | 150 × 200 × 6000 3 | 300 × 600 × 6000 | 1335 mm |
| 2 | 2000 × 160 × 6000 2000 × (40 + 20 + 40 + 20 + 40) × 6000 | 8, 8, 8, 8, 8 | 150 × 200 × 6000 3 | 300 × 600 × 6000 | 1230 mm |
| 3 | 2000 × 100 × 6000 2000 × (20 + 20 + 20 + 20 + 20) × 6000 | 8, 8, 8, 8, 8 | 150 × 200 × 6000 3 | 300 × 600 × 6000 | 1470 mm |
| 4 | 2000 × 140 × 6000 2000 × (20 + 40 + 20 + 40 + 20) × 6000 | 8, 8, 8, 8, 8 | 150 × 200 × 6000 3 | 300 × 600 × 6000 | 1498 mm |
| 5 | 2000 × 200 × 6000 2000 × (40 + 40 + 40 + 40 + 40) × 6000 | 6, 6, 6, 6, 6 | 150 × 200 × 6000 3 | 300 × 600 × 6000 | 1287 mm |
| 6 | 2000 × 160 × 6000 2000 × (40 + 20 + 40 + 20 + 40) × 6000 | 6, 6, 6, 6, 6 | 150 × 200 × 6000 3 | 300 × 600 × 6000 | 1180 mm |
| 7 | 2000 × 100 × 6000 2000 × (20 + 20 + 20 + 20 + 20) × 6000 | 6, 6, 6, 6, 6 | 150 × 200 × 6000 3 | 300 × 600 × 6000 | 1423 mm |
| 8 | 2000 × 140 × 6000 2000 × (20 + 40 + 20 + 40 + 20) × 6000 | 6, 6, 6, 6, 6 | 150 × 200 × 6000 3 | 300 × 600 × 6000 | 1448 mm |
| 9 | 2000 × 200 × 8000 2000 × (40 + 40 + 40 + 40 + 40) × 8000 | 8, 8, 8, 8, 8 | 150 × 200 × 8000 3 | 300 × 600 × 8000 | 1333 mm |
| 10 | 2000 × 160 × 8000 2000 × (40 + 20 + 40 + 20 + 40) × 8000 | 8, 8, 8, 8, 8 | 150 × 200 × 8000 3 | 300 × 600 × 8000 | 1234 mm |
| 11 | 2000 × 100 × 8000 2000 × (20 + 20 + 20 + 20 + 20) × 8000 | 8, 8, 8, 8, 8 | 150 × 200 × 8000 3 | 300 × 600 × 8000 | 1473 mm |
| 12 | 2000 × 140 × 8000 2000 × (20 + 40 + 20 + 40 + 20) × 8000 | 8, 8, 8, 8, 8 | 150 × 200 × 8000 3 | 300 × 600 × 8000 | 1503 mm |
| 13 | 2000 × 200 × 6000 2000 × (40 + 40 + 40 + 40 + 40) × 6000 | 8, 8, 8, 8, 8 | 150 × 200 × 6000 4 | 300 × 600 × 6000 | 1330 mm |
| 14 | 2000 × 200 × 6000 2000 × (40 + 40 + 40 + 40 + 40) × 6000 | 6, 6, 6, 6, 6 | 150 × 200 × 6000 5 | 300 × 600 × 6000 | 1328 mm |
| 15 | 2000 × 200 × 6000 2000 × (40 + 40 + 40 + 40 + 40) × 6000 | 6, 8, 6, 8, 6 | 150 × 200 × 6000 4 | 300 × 600 × 6000 | 1350 mm |
| 16 | 2000 × 200 × 6000 2000 × (40 + 40 + 40 + 40 + 40) × 6000 | 8, 6, 8, 6, 8 | 150 × 200 × 6000 4 | 300 × 600 × 6000 | 1245 mm |
| 17 | 2000 × 200 × 6000 2000 × (40 + 40 + 40 + 40 + 40) ×6000 | 8, 8, 8, 8, 8 | 150 × 200 × 6000 4 | 150 × 600 × 6000 | 1185 mm |
| 18 | 2000 × 200 × 6000 2000 × (20 + 40 + 20 + 40 + 20) × 6000 | 8, 8, 8, 8, 8 | 150 × 200 × 6000 4 | 150 × 600 × 6000 | 1350 mm |
| 19 | 2000 × 160 × 6000 2000 × (40 + 20 + 40 + 20 + 40) × 10,000 | 8, 8, 8, 8, 8 | 150 × 200 × 10,000 3 | 300 × 600 × 10,000 | 1237 mm |
| 20 | 2000 × 200 × 6000 2000 × (40 + 40 + 40 + 40 + 40) × 10,000 | 8, 8, 8, 8, 8 | 150 × 200 × 10,000 3 | 300 × 600 × 10,000 | 1337 mm |
| 21 | 2000 × 200 × 6000 2000 × (20 + 20 + 20 + 20 + 20) × 10,000 | 8, 8, 8, 8, 8 | 150 × 200 × 10,000 3 | 300 × 600 × 10,000 | 1477 mm |
| 22 | 2000 × 200 × 6000 2000 × (20 + 40 + 20 + 40 + 20) × 10,000 | 8, 8, 8, 8, 8 | 150 × 200 × 10,000 3 | 300 × 600 × 10,000 | 1510 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Masoudnia, R.; Fang, Z.; Hashemi, A.; Masoudnia, S.; Lim, J.B.P. Assessment of the Effective Flange Width for Cold-Formed Steel-Timber Composite Beams: A Finite Element Study. Buildings 2026, 16, 245. https://doi.org/10.3390/buildings16020245
Masoudnia R, Fang Z, Hashemi A, Masoudnia S, Lim JBP. Assessment of the Effective Flange Width for Cold-Formed Steel-Timber Composite Beams: A Finite Element Study. Buildings. 2026; 16(2):245. https://doi.org/10.3390/buildings16020245
Chicago/Turabian StyleMasoudnia, Reza, Zhiyuan Fang, Ashkan Hashemi, Saber Masoudnia, and James B. P. Lim. 2026. "Assessment of the Effective Flange Width for Cold-Formed Steel-Timber Composite Beams: A Finite Element Study" Buildings 16, no. 2: 245. https://doi.org/10.3390/buildings16020245
APA StyleMasoudnia, R., Fang, Z., Hashemi, A., Masoudnia, S., & Lim, J. B. P. (2026). Assessment of the Effective Flange Width for Cold-Formed Steel-Timber Composite Beams: A Finite Element Study. Buildings, 16(2), 245. https://doi.org/10.3390/buildings16020245






