Evolutionary Game Theory in Architectural Design: Optimizing Usable Area Coefficient for Qingdao Primary Schools

Abstract

Amidst the surge of high-density urban development and the growing demand for high-quality spaces, the Usable Area Coefficient (UAC) has emerged as a pivotal metric in the architectural planning. The rational calibration of the UAC for primary school buildings is key to balancing intensive land use, educational demands, and the well-being of children. Taking primary schools in a district of Qingdao as the research subject, this research rationally optimizes the range of UAC by constructing an evolutionary game model, based on quantitatively analyzing the divergent perspectives and requirements of three stakeholders: the government, school administrators, and students. After further identifying the key factors that influence the ultimate decision, the study yields the following insights: (1) The incremental comprehensive benefit emerges as the linchpin influencing the UAC. (2) The government’s risk compensation to schools and the benefit-sharing coefficient between schools and students exert significant impacts on system evolution. (3) Effective control of construction and land costs, coupled with enhanced availability of open activity spaces, paves the way for consensus on low UAC. This research not only furnishes a theoretical framework and practical guidance for harmonizing land use efficiency with educational excellence but also steers the design of salubrious primary school environments and informs pertinent policy-making.

1. Introduction

Under the dual background of the deepening global concept of healthy living environments and the rapid development of high-density cities, “well-being spaces” in educational settings have become the core medium for ensuring the comprehensive development of children in physiology, mentality, and emotion [1,2]. The creation of healthy spaces must be centered on user needs, while employing data science and technology to enhance spatial efficiency and adaptability [3]. With the continuous decline in the number of school-age children in China, the pursuit of spatial quality in basic education buildings is placing greater emphasis on improving overall quality [1]. However, constrained by practical issues such as limited funding for basic education and the scarcity of land in high-density urban areas, the current determination of the Usable Area Coefficient (the ratio of functional room area to total building area) in the architectural planning stage has already restricted the evolution of educational models [4,5,6,7,8]. Flexible space remains difficult to achieve, hindering the creation of an open and modern environment conducive to talent cultivation [9]. Particularly in developed, intensive cities where land resources are extremely scarce, primary school buildings generally face an inherent contradiction between “land scarcity” and the “need for open spaces”. On one hand, limited land availability compels governments to prefer higher UAC values in order to control construction costs. On the other hand, children’s healthy growth and the transformation of modern educational models require ample open activity spaces [10,11,12], which necessitates lowering the UAC to reserve more flexible spatial resources.

The essence of this contradiction lies in the decision-making conflicts among multiple stakeholders: the government focuses on cost control and intensive land use; schools emphasize teaching quality and spatial flexibility, while students and parents prioritize the assurance of a healthy and active environment. The traditional standards for determining the UAC of primary school buildings are outdated—neither incorporating the new requirements for children’s healthy spaces nor accounting for the dynamic game relationships among multiple actors. As a result, design outcomes often fall into a dilemma between “high UAC that compress open spaces” and “low UAC that exceed fiscal budgets”. Although technologies such as artificial intelligence and machine learning have been gradually applied to the simulation and optimization of healthy spaces, contraposing key design parameters like the UAC, there is still no quantitative decision-making framework for balancing the interests of all stakeholders in primary school buildings.

This research takes public primary schools in a district of Qingdao as the research object and introduces evolutionary game theory to depict the dynamic strategic adjustment processes of governments, schools, students and parents, approaching the actual decision-making logic comprehensively. This paper quantitatively analyzes the interests and interaction mechanisms among the three parties in determining the UAC, by integrating field survey data with MATLAB R2023b simulation modeling. Stable strategic combinations are identified, which can balance cost efficiency with the demand for healthy spaces, thereby providing theoretical support and practical guidance for the scientific design of healthy spaces in primary school buildings.

The principal contributions of this paper are summarized as follows:

• It fills the research gap in the architectural planning field regarding the multi-stakeholder game phenomenon in the determination of the UAC. For the first time, evolutionary game theory is applied to the optimization of the UAC in primary school buildings, thus expanding interdisciplinary methodologies within architectural planning.
• By constructing a government–school–student three-party evolutionary game model, the study identifies stable evolutionary strategy points and clarifies that the increment of overall benefits under low UAC and government risk compensation are key factors influencing the adoption of lower UAC in primary school buildings.
• Based on the stability conditions, the study proposes practical design strategies such as controlling construction and land-use costs and enhancing the usability of open activity spaces. These strategies not only ensure sufficient open activity spaces necessary for children’s education and learning but also balance fiscal budget constraints, thereby contributing to the creation of a healthy and comfortable educational environment.

2. Literature Review

2.1. Architectural Programming

Post-occupancy evaluation serves as an effective strategy for guiding architectural programming. A series of novel studies have been conducted in the field of post-utilization evaluation. For POI post-occupancy evaluation, an integrated AHP-Fuzzy Integrals approach is proposed to estimate factor weights and subfactor importance, enhancing accuracy via AHP’s hierarchical rigor and Fuzzy Integrals’ uncertainty handling [12]. Post-occupancy evaluations in the thermal-performance domain also deploy combined in situ environmental monitoring with regression analytics—a transferable method that can benchmark primary-school floor-area coefficients [13]. Fine-grained POE of an open-office shows that a Space-Utilization Index fusing spatial scale, occupancy dots and dwell time raises evaluation accuracy, suggesting primary-school stakeholders could likewise adopt this high-resolution metric to quantify and bargain over the use-area coefficient [14]. These cross-disciplinary advances collectively indicate that the application of POE in primary-school building programming is shifting from rough compliance checks to data-rich, stakeholder-negotiated scientific evaluations.

Participatory design also proves to be highly beneficial for architectural programming. By shifting to a user-participatory pre-planning process, Korean school-renovation cases show that pupils, teachers and facility managers can jointly convert “left-over” circulation zones into quantifiable floor-area credits, providing a negotiation template for fine-tuning primary-school use-area coefficients [15]. By embedding online surveys, living-lab VR trials and post-session focus groups into the sensory-square project, the study turns children into data-driven co-planners in the building program [16]. Evidence-Based Design (EBD) is an important source of scientific knowledge that can be applied to the design process, and the pattern language has long led the way in turning that evidence into a reusable, design-method toolkit [17].

In the architectural programming process, the Usable Area Coefficient (UAC), is an important concept, significantly contributing to enhancing the rationality of functional planning and assessing the economy and practicality of architectural spaces. Current research on UAC rarely focuses specifically on educational buildings, concentrating instead on residential and office building types. Several scholars have explored compact designs for school buildings in slums or unplanned urban areas, demonstrating the feasibility of such approaches. Their findings provide useful references for optimizing UAC under conditions of limited land resources [18]. Other researchers have analyzed the influencing factors of UAC through case studies of university teaching buildings, proposing optimization strategies that offer methodological support for quantitative analyses of these factors [19]. Nevertheless, existing standards for determining UAC do not fully reflect contemporary educational demands and changing trends. Although each stakeholder benefits from feedback obtained during the design and construction phases, the concept of “continuous improvement,” prevalent in business management, has not yet been widely adopted in architectural planning or UAC determination. Adopting this mindset and summarizing stakeholders’ feedback benefits could play a positive role in optimizing UAC methodologies [20]. Additionally, conducting multidisciplinary design reviews, especially incorporating the perspectives of building users, prior to construction helps identify design shortcomings [21]. Unfortunately, many users and organizations find it challenging to visualize a building’s functionality and user experience based solely on architectural drawings and renderings; users typically provide accurate feedback only after occupying the building for a certain period [22]. Thus, multidisciplinary design reviews should be integrated during the architectural planning stage to prevent iterative redesigns at their source.

Although these studies provide a theoretical foundation for understanding UAC, there remains significant research potential in primary educational buildings, particularly regarding multi-stakeholder decision-making interactions and investment costs. This study draws on existing quantitative analytical methods and combines them with the unique characteristics of primary school buildings to comprehensively investigate the rational determination of UAC.

2.2. Evolutionary Game Theory

Evolutionary game theory relaxes the assumption of complete rationality found in classical game theory, allowing agents to make incremental decisions under conditions of incomplete information and cognitive constraints. Through the replicator dynamics mechanism, strategy adjustment is viewed as a continuous and observable process. Furthermore, by introducing the evolutionarily stable strategy (ESS) concept, evolutionary game theory provides verifiable mathematical conditions for analyzing the long-term behavioral stability of groups [23].

Applying evolutionary game theory to this study offers significant advantages. First, it can simulate multi-stakeholder interactions; for instance, by constructing a tripartite game model involving government, schools, and students, the approach analyzes strategic interactions such as government implementation, school requirements, and student (or parental) requests for optimizing the UAC, thus addressing the shortcomings of traditional research that overlooks stakeholder interaction [24,25]. Second, evolutionary game theory does not require extensive data, allowing the analysis of strategy evolution trends through parameter settings and numerical simulations (e.g., MATLAB), which is particularly suitable for primary school buildings lacking systematic UAC data. Cost, benefits, and subsidies parameters can thus be rationally determined [26]. Third, it enables the analysis of equilibrium stability via the Jacobian matrix, identifying stable conditions for stakeholder strategy combinations (e.g., proactive government guidance, school supervision, student applications for lower UAC), thereby providing clear guidance for policy formulation [27]. Fourth, external environmental uncertainties (e.g., policy adjustments, changes in educational requirements) can be incorporated, enhancing the model’s adaptability to real-world scenarios [23,28,29].

2.3. Primary School Architecture

Educational research treats the school environment as a “third teacher” that shapes pupils’ cognition, affect and behavior, conditions their well-being and learning, and fosters inclusion without segregating. [30]. The classification of school environments is influenced by a variety of factors. Ahmed (2023) implicitly classifies Cairo primary schools into two spatial archetypes: large-plot campuses (>1200 m²) that accommodate the standard multi-block layout, and small-footprint sites (≤1200 m²) embedded in informal settlements where a single, five-story compact block with zero-lot-line setbacks is advanced as the only viable typology [18].

Relevant literature on primary school architectural design provides critical references for the construction and analysis of game theory models, addressing dimensions such as spatial demand characteristics, stakeholder requirements, parameter setting criteria, and verification methods. A study on spatial interactions in primary schools in Ho Chi Minh City, Vietnam, observed children’s interactions within classroom and playground spaces (“space-social-nature”) and found that shading conditions, seating arrangements, and the distribution of natural elements significantly influence spatial usage efficiency [31]. Research on personalized learning in Indian primary schools emphasized the importance of flexible spatial designs to accommodate diverse student learning needs, underscoring the principle of aligning spatial configurations with educational demands [32]. A review of natural learning spaces in Maltese primary schools confirmed that natural elements positively affect student learning and identified the proportion of natural space as a core spatial requirement from the school’s perspective [33]. Additionally, research on playful learning landscapes in American primary schools highlighted that school spatial design must match users’ practical needs, reinforcing the logic of aligning spatial functions with usage requirements [34]. A study examining the impact of the school environment on teachers’ commitment to educational quality indicated that teachers’ spatial needs affect educational quality, highlighting the correlation between teachers’ spatial requirements and educational environment design [35]. These studies collectively reflect the usage demands of schools and students from various perspectives. Research on school renovations in Nalchik, Russia, revealed conflicts between government planning standards and actual school demands, noting cases where existing schools needed expansions due to insufficient functional spaces [36]. A study on multi-grade teaching in Caowo Primary School, Gansu, China, demonstrated how small-scale schools adapt teaching activities through spatial reconfiguration, exemplifying specific scenarios of spatial adaptation under resource constraints [37].

In summary, the above studies provide multidimensional support for the evolutionary game analysis of primary school building usable area coefficient, covering aspects such as quantitative spatial demand, identification of stakeholder interests, parameter-setting references, and verification methods. This body of research helps clarify the core parameters, stakeholder strategies, and constraints within the game model, thereby enhancing the practical relevance and feasibility of the present study.

3. Methodology

Determining the Usable Area Coefficient (UAC) is a crucial step in architectural planning. However, this process often involves strategic conflicts that arise from neglecting the differing objectives among stakeholders. Evolutionary game theory provides a suitable approach to addressing this issue. It is founded on the principle of bounded rationality, acknowledging the decision-making characteristics of stakeholders (government, schools, and students) under information asymmetry. By using replicator dynamics equations to describe the dynamic evolution of strategy proportions and defining conditions for long-term strategic stability through the evolutionarily stable strategy (ESS), evolutionary game theory effectively characterizes stakeholder interactions during the determination of the UAC.

Constructing an evolutionary game model involves four key steps. First, the interest relationships and strategy set must be clearly defined. Second, a payoff matrix is established to quantify the payoffs of different strategy combinations. Third, a replicator dynamic equation is formulated to describe the dynamic changes in the proportions of each party’s strategies over time. Fourth, the stability of equilibrium points is analyzed using the Jacobian matrix. If all eigenvalues of the matrix are less than zero, the corresponding strategy combination is considered an evolutionarily stable equilibrium, which can serve as an optimal direction for determining the UAC of primary school buildings.

3.1. Data Collection

In the process of determining the usable area coefficient, each stakeholder has distinct motivations and objectives, which form the basis for constructing the game model. The stakeholders include three main groups. First, governmental departments responsible for policy formulation, resource allocation, and project construction, which have strategies of ”active implementation” or “inactive implementation”. Second, schools responsible for management and operation after project completion, specifically the “teaching” component, which may choose between “request” and “no request”. Third, students and their guardians (parents), representing the “learning” component, which may choose between “assert demands” and “not assert demands” (Figure 1). Additionally, the architectural design unit, which is distinct from the direct stakeholders, assists in planning and implementing specific designs. However, considering that the design unit primarily executes planning decisions and has limited influence on the game’s outcomes due to its weak ties to the building’s strategic decisions, it is excluded from participation in the game analysis.

Data collection focused on stakeholders’ interests, benefit parameters, and strategic costs related to UAC decisions for primary school buildings. The following two sections detail the methodology used to gather and analyze relevant data.

• Determination of benefit and cost parameters
• Benefits and cost parameters for each stakeholder were established through case studies and comparative policy analysis. Nine public primary schools in a district of Qingdao, characterized by floor area ratios of at least 1.9 and land compliance rates of no more than 0.5, were selected as samples. Architectural drawings and construction cost reports were collected, extracting key indicators such as total construction area, functional room areas (teaching, administrative, and logistical spaces), open activity spaces, and auxiliary circulation areas. These data formed a database correlating actual UAC with spatial configurations. Additionally, 11 national, provincial and municipal regulations were collated to extract constraint parameters, such as per-student land area, per-student building area, functional space ratios, and maximum floor area ratios. This process defined the policy-based range of UAC (e.g., provincial recommendation of UAC = 0.6). Cost parameters and investment data from the sample projects were systematically compared with corresponding standards, enabling accurate determination of government benefit parameters and costs.
• Stakeholder interests and survey data
• Two types of surveys were conducted to gather data on stakeholder interests. First, interviews were held with government officials, focusing on “UAC requirements” and the “distribution ratio of comprehensive benefits from low UAC between government and schools,” These interviews yielded 28 valid records. Second, questionnaires were distributed to schools (principals and academic staff) and students in grades 4–6, addressing “satisfaction with open spaces and spatial utilization issues” and the “distribution ratio of comprehensive benefits from low UAC between schools and students.” Out of 200 questionnaires distributed, 163 valid responses were received. Both survey instruments primarily collected quantitative data. Satisfaction and spatial utilization issues were analyzed using Likert scales, while distribution ratios were evaluated using a two-round Delphi method. This approach enabled comprehensive insight into stakeholder preferences and cost acceptance, offering robust data support for subsequent analyses and decision-making.

3.2. Data Processing

• Processing benefit and cost parameters
  Collected benefit and cost parameters were screened for outliers and standardized. Grubbs’ test was employed to exclude anomalous UAC (e.g., K > 0.85 or K < 0.35) arising from special policies (such as renovations of historical buildings), retaining nine valid samples for model parameter calibration. Data from primary schools of varying sizes (24, 36, and 48 classes) were converted to per-student indicators (m²/student) to eliminate interference from class-size differences. Additionally, various area types from schools of different scales were proportionally converted to eliminate project-scale disparities, using area proportion as a unified comparison dimension. Monetary and quasi-monetary data, including government subsidies, school costs, and parental expenditures, were uniformly adjusted to constant 2024 prices, removing inflationary influences and ensuring data comparability.

• Validation of stakeholder interest data
  Survey data consistency was validated using cross-analysis to examine correlations between questionnaire satisfaction ratings and actual proportions of open space, ensuring alignment between survey results and case data. A group-comparison validation strategy was employed, dividing the nine schools into three categories based on actual open space proportions: high (>10%), medium (5–10%), and low (<5%). Mean satisfaction scores across these groups were compared using ANOVA (p < 0.05). Significantly higher satisfaction scores among high-proportion schools compared to medium and low groups confirmed the congruence of survey data with case data, ensuring satisfaction ratings reliably reflected differences in spatial indicators related to UAC and preventing survey findings from diverging from actual spatial conditions.

4. Model Construction and Simulation Analysis

4.1. Model Construction

4.1.1. Stakeholder Analysis

This study develops an evolutionary game model involving three stakeholders, the government, schools, and students, to analyze the decision-making process for the usable area coefficient (UAC) during the architectural planning stage of primary schools. Considering information and power asymmetries, the model assumes that stakeholders are bounded-rational individuals who cannot initially identify a globally optimal strategy. Instead, they adjust their strategies through repeated interactions by observing the average payoffs of the group.

Identifying stakeholders’ unique motivations and goals provides a foundational basis for constructing the game model. The key stakeholders are classified as follows: First, government departments (construction authorities) aim primarily to ensure compliance with educational policies and standards, enhance educational quality, optimize resource allocation, control budgets, and ensure construction progress and quality. Second, schools are motivated to meet teaching and learning requirements, ensure buildings are safe, comfortable, and efficient, and minimize long-term operating costs. Their feasible strategies include articulating functional requirements, participating in design and planning, supervising construction quality, and providing usage feedback. Third, the actual users, students and their guardians (parents), are motivated primarily by educational needs and promoting healthy development. Their actionable strategies include school selection, providing suggestions on functional requirements, offering feedback, and actively disseminating opinions [38,39,40,41,42].

Based on stakeholder analysis, in response to the low UAC, the strategies for the three stakeholders are defined as follows: the government’s strategies are “actively implementation” or “passively implementation,” schools’ strategies are “request” or “not request,” and students’ strategies are “assert demands” or “not assert demands.”

4.1.2. Model Assumptions

Different choices by the stakeholders directly impact the overall decision-making system, influencing the determination of UAC. To simulate these dynamic interactions, the study follows the core evolutionary game theory premises of “bounded rationality” and “incremental learning,” proposing the following assumptions:

Assumption 1: Students and Parents’ Assertion of Demands

Students and parents, as direct beneficiaries of educational services, choose between “assert demands” and “not assert demands.” Asserting demands involves a fixed cost C₃ (e.g., information collection, attending meetings) but provides incremental benefits from increased open activity space, calculated as abΔR, where a and b are benefit-sharing coefficients between schools and students, and government and schools, respectively. Here, ΔR represents the incremental comprehensive benefit resulting from low UAC, including land-use fee savings and net present value of energy consumption savings (unit: 10,000 yuan/class). Specifically, G₄ represents the supportive benefit that school-built space confers on students when the government, the school, and the students themselves are all in their most proactive state. If demands are not expressed, no costs are incurred, but benefits are not shared. The government’s general subsidy G₂ is independent of demand expression behavior. This assumption reflects parents’ “cost–benefit” considerations under limited information and participation capabilities.

Assumption 2: Schools’ Decision-Making on Demands

Schools must choose between “requesting low UAC” and “not requesting low UAC.” Requesting low UAC requires a fixed cost C₂, but yields government incentives G₁, and direct incremental benefits from additional open space (1-a)bΔR. If the government passively implements the policy, and students and parents assert demands, schools must also bear a risk compensation cost W₂. If schools do not request a low UAC, they save C₂, but they forfeit all rewards and savings related to the low UAC. This assumption captures schools’ trade-offs between teaching quality, operational efficiency, and policy risks.

Assumption 3: Government’s Implementation Strategy

As the resource allocator and policymaker, the government chooses between “actively implementing low UAC” and “passively implementing low UAC.” Active implementation necessitates additional construction investments C₁, government incentives to schools G₁, government incentives to students G₂, and reputation benefits G₃. Passive implementation saves C₁, G₁ and G₂, gaining construction cost savings D; however, if schools persistently request a low UAC, the government faces communication and compliance pressures quantified as W₁. This assumption reflects the government’s balancing act among fiscal constraints, educational equity, and public reputation.

Assumption 4: Information Structure and Evolutionary Mechanism

All stakeholders simultaneously select strategies at each decision point, with binary strategy sets. Game information is public knowledge, but stakeholders exhibit bounded rationality and thus cannot immediately identify optimal solutions. Instead, they gradually adjust their strategies based on replicator dynamics by observing average group payoffs from previous rounds. Each decision round corresponds to an “evaluation-feedback-re-evaluation” cycle during the planning phase, with discrete time steps of 0.5 and a total duration of 20, aligning with simulation settings in Section 4.2.2. Initial values and parameter intervals for all exogenous parameters follow specifications in

Table 1. Overview of Model Parameters.

No.	Symbol	Description	Recommended Initial Value	Sensitivity Interval	Data Source/Calibration Method	Remarks
Benefits
1	ΔR	Incremental comprehensive benefit of low UAC	20	[5, 40]	Mean of 9 public school cases	★ Key control variable
2	a	Benefit-sharing coefficient (schools-students)	0.65	[0.45, 0.85]	Two-round Delphi survey	★
3	b	Benefit-sharing coefficient (government-schools)	0.60	[0.50, 0.75]	Same as above	★
4	D	Construction cost savings	5	—	Cost audit reports	Fixed
5	G1	Government incentives to schools	2	—	Policy documents	Fixed
6	G2	Government incentives to students	1	—	Same as above	Fixed
7	G3	Social reputation benefit	2	—	Converted from social benefits	Fixed
8	G4	Supportive Benefit of Campus Space	7	_	Academic-return valuation	Fixed
Costs
9	W1	Government risk compensation to schools	8	[1, 15]	Provincial financial audits	★ Policy lever
10	W2	School risk compensation to students	8	—	School internal regulations	Fixed
11	C1	Government’s active implementation cost	4	[2, 10]	Administrative cost surveys	★
12	C2	Schools’ active demand cost	3	[1, 8]	Expert Delphi survey	★
13	C3	Cost of students expressing demands	1	—	Questionnaire statistics	Fixed
14	S1	Schools’ opportunity loss	4	—	School surveys	Fixed
15	S2	Students’ opportunity loss	3	—	Same as above	Fixed

★: Key control variable.

, and subsequent sensitivity analyses will systematically explore parameter spaces through Monte Carlo simulations.

4.1.3. Parameter Assumptions

This study systematically calibrated all parameters of the evolutionary game model through literature review, field surveys, and expert consultations. The specific steps were as follows:

First, baseline values and variation ranges for economic variables were established. Completion settlement reports, financial audits, and school operation data from nine public primary schools in a District, Qingdao, were selected as samples. Baseline values and reasonable ranges for each economic variable were determined by combining descriptive statistics and two-round Delphi surveys.

Second, policy-related parameters (such as risk compensation levels and reward amounts) were identified through supplementary semi-structured interviews with representatives from provincial finance departments, construction units, and school principals.

Third, data sources were cross-validated using construction cost audit reports, current educational finance documents, and questionnaire results, ensuring the diversity and reliability of data.

Table 1 summarizes parameter symbols, economic meanings, recommended initial values, sensitivity analysis intervals, and data sources after the above calibration process. Critical variables, including ΔR, W1, a, and b, were identified as “key control variables” for the Monte Carlo sensitivity analysis in Section 4.2.2. Remaining parameters were held constant during simulations to reduce dimensional complexity and highlight the effects of policy levers. All parameters were uniformly measured in “10,000 yuan/class,” consistent with benefit measurement assumptions in Section 4.1.2.

4.1.4. Payoff Matrix

Based on the previously defined strategy sets and parameter system, this study quantified the payoffs (U_G, U_S, U_P) for government, schools, and students (including parents) under various strategic combinations, following the cost–benefit assumptions from Section 4.1.2. When a stakeholder chooses a passive strategy, their payoff may include saved construction or management costs; conversely, choosing an active strategy involves subtracting corresponding costs but adding incremental benefits from a low UAC, government rewards, or reputation gains. If stakeholder strategies lack coordination, risk compensation items are triggered, reflecting real-world policy constraints and opportunity losses. Thus, the following payoff matrix (

Table 2. Payoff Triplets (U_G, U_S, U_P) for Eight Pure Strategy Combinations.

Combination (G, S, P)	Government (UG)	Schools (US)	Students (UP)
(Active, Request, Assert)	(1 − b)ΔR + G3 + D − C1 − G1 − G2	(1 − a)bΔR + G1 − C2	abΔR + G2 + G4 − C3
(Active, Request, Not Assert)	(1 − b)ΔR + G3 + D − C1 − G1	(1 − a)bΔR + G1 − C2	abΔR + G2
(Active, Not Request, Assert)	(1 − b)ΔR − C1 − G2	−S1	G2 − C3
(Active, Not Request, Not Assert)	(1 − b)ΔR − C1	−S1	G2
(Passive, Request, Assert)	D − W1	G1 − W2 − C2	abΔR − C3
(Passive, Request, Not Assert)	D − W1	G1 − C2	abΔR
(Passive, Not Request, Assert)	0	0	−C3
(Passive, Not Request, Not Assert)	0	0	0

) was constructed, providing a numerical basis for replicator dynamics equations and equilibrium analyses in subsequent sections.

4.2. Model Simulation Analysis

4.2.1. Stability Analysis

To calculate the evolution of strategies over time for the government, schools, and students (including parents), the Taylor & Jonker replicator dynamics framework was adopted. The strategy growth rate is primarily driven by the difference between expected individual payoffs and average group payoffs. Let the probabilities of the government selecting “actively implementing low UAC,” schools “requesting low UAC,” and students (and parents) “assert demands” be denoted as z, y, and x, respectively. Complementary probabilities are thus 1 − z, 1 − y, and 1 − x.

(1)

Fundamental Derivation

The general form of replicator dynamics equations:

$${\displaystyle \frac{\mathrm{d}{x}_i}{\mathrm{d}t}}=x_i\left[{\mathrm{U}}_i-{\overline{U}}_i\right],i\in \left\{ \mathrm{strategies} \right\},$$

(1)

U_i represents the expected payoff for selecting strategy i, and Ū is the average payoff of the group. Expected and average payoffs for each stakeholder were obtained by weighting the payoffs of the eight pure-strategy combinations (Table 2) according to their probabilities.

(2)

Expected and Average Payoffs for the Government (G)

Let U_G1 and U_G0 represent the expected payoffs for the government choosing “active” and “passive” strategies, respectively:

$$\begin{array}{c}{U}_{\mathrm{G}1}=yx\left[\left(1-b\right)\mathsf{\Delta }R+G_3+D-C_1-G_1-G_2\right]\hfill \\ +y\left(1-x\right)\left[\left(1-b\right)\mathsf{\Delta }R+G_3+D-C_1-G_1\right]\hfill \\ +\left(1-y\right)x\left[\left(1-b\right)\Delta R-C_1-G_2\right]\hfill \\ +\left(1-y\right)\left(1-x\right)\left[\left(1-b\right)\Delta R-C_1\right]=U\_\left\{G1\right\}\hfill \\ =(1-b)\mathsf{\Delta }R-C_1+y(G_3+D-G_1)-x G_2\hfill \\ {\mathrm{U}}_{\mathrm{G}0}=\mathrm{y}\mathrm{x}\left(D-W_1\right)+\mathrm{y}\left(1-\mathrm{x}\right)\left(D-W_1\right)\hfill \\ =\mathrm{y}\left(D-W_1\right)\hfill \end{array}$$

(2)

The average payoff for the government group:

$${\overline{U}}_G=z{U}_{G1}+\left(1-z\right)U_{G0}$$

(3)

Substituting U_G1 and Ū_G0 into the replicator dynamics equation yields the evolutionary equation for the government’s strategy:

$$\begin{array}{c}{\displaystyle \frac{dz}{dt}}=z\left(1-z\right)\left[U_{G1}-U_{G0}\right]\hfill \\ =z\left(1-z\right)\left[\left(1-b\right)\Delta R-C_1+y\left(G_3-G_1+W_1\right)-x{G}_2\right]\hfill \end{array}$$

(4)

(3)

Expected and Average Payoffs for Schools (S)

Similarly, the expected payoffs for schools selecting “request” U_S1 and “not request” U_S0 strategies are:

$$\begin{array}{c}{U}_{S1}=xz\left[(1-a)b\Delta R+G_1-C_2\right]+x\left(1-z\right)\left({\mathrm{G}}_1-W_2-C_2\right)\hfill \\ +\left(1-x\right)z\left[(1-a)b\Delta R+G_1-C_2\right]+\left(1-x\right)\left(1-z\right)\left({\mathrm{G}}_1-C_2\right)\hfill \\ =z(1-a)b\Delta R+G_1-x\left(1-z\right)W_2-C_2\hfill \\ U_{S0}=xz\left(-S_1\right)+\left(1-x\right)z\left(-S_1\right)=-z{S}_1\end{array}$$

(5)

The average payoff for the school group is:

$${\overline{U}}_S=y{U}_{S1}+\left(1-y\right)U_{S0}$$

(6)

Thus, the evolutionary equation for the school’s strategy is:

$$\begin{gathered} {\displaystyle \frac{dy}{dt}}=y\left(1-y\right)\left[U_{S1}-U_{S0}\right] \\ =y\left(1-y\right)\left[z\left(1-a\right)b\Delta R+G_1+z{S}_1+zx{W}_2-C_2-x{W}_2\right] \end{gathered}$$

(7)

(4)

Expected and Average Payoffs for Students and Parents (P)

The expected payoffs for students and parents choosing “assert” U_P1 and “not assert” U_P0 strategies:

$$\begin{array}{c}{U}_{P1}=zy\left[ab\Delta R+G_2+G_4-C_3\right]+z\left(1-y\right)\left(G_2-C_3\right)+\left(1-z\right)y\left(ab\Delta R-C_3\right)\hfill \\ +\left(1-z\right)\left(1-y\right)\left(-C_3\right)\hfill \\ =\mathrm{a}b\Delta Ry+{zG}_2+zy{G}_4-C_3\hfill \\ U_{P0}=zy\left[ab\Delta R+G_2\right]+z\left(1-y\right)\left(G_2\right)+\left(1-z\right)yab\Delta R=yab\Delta R+{zG}_2\hfill \end{array}$$

(8)

The average payoff for students and parents is

$${\overline{U}}_P=x{U}_{P1}+\left(1-x\right)U_{P0}$$

(9)

Consequently, their strategy evolution equation is

$${\displaystyle \frac{dx}{dt}}=x\left(1-x\right)\left[U_{P1}-U_{P0}\right]=-x\left(1-x\right)(zy{G}_4-C_3)$$

(10)

Summarizing the above, the system of replicator dynamics equations for government, schools, and students (including parents) is:

$$\begin{array}{c}{\displaystyle \frac{dx}{dt}}=x\left(1-x\right)\left[-G_3\right]\hfill \\ {\displaystyle \frac{dy}{dt}}=y\left(1-y\right)\left[z\left(1-a\right)b\Delta R+z{G}_1+z{S}_1+zx{W}_2-C_2-x{W}_2\right]\hfill \\ {\displaystyle \frac{dz}{dt}}=z\left(1-z\right)\left[\left(1-b\right)\Delta R-C_1+y\left(G_3-G_1+W_1\right)-x{G}_2\right]\hfill \end{array}$$

(11)

Setting this system of equations to zero yields eight pure-strategy equilibrium points, E₁(0,0,0)~E₈(1,1,1).

The Jacobian matrix is derived as:

$$J=\left[\begin{array}{ccc}{\displaystyle \frac{\partial f}{\partial x}}& {\displaystyle \frac{\partial f}{\partial y}}& {\displaystyle \frac{\partial f}{\partial z}}\\ {\displaystyle \frac{\partial g}{\partial x}}& {\displaystyle \frac{\partial g}{\partial y}}& {\displaystyle \frac{\partial g}{\partial z}}\\ {\displaystyle \frac{\partial h}{\partial x}}& {\displaystyle \frac{\partial h}{\partial y}}& {\displaystyle \frac{\partial h}{\partial z}}\end{array}\right]$$

(12)

By substituting each equilibrium point, an ESS is identified when all eigenvalues are negative. The derivation shows that this occurs only when:

$$\begin{array}{c}{C}_3-zy{G}_4>0\hfill \\ (1-b)\Delta R+G_3+W_1>c_2+G_1+G_2\hfill \\ (1-a)b\Delta R+G_1+S_1+W_2>C_2\hfill \end{array}$$

(13)

When all conditions are simultaneously satisfied, E₈(1,1,1) represents the unique evolutionarily stable strategy. Under this equilibrium, the government actively implements the low UAC, schools choose to request a low UAC, and students and parents opt to express their demands, thereby ultimately achieving the goal of adopting and maintaining a low UAC.

4.2.2. Scenario Simulation

The parameterized MATLAB simulation was employed to validate the model through a three-step procedure: parameter configuration, simulation execution, and result output. According to research requirements, two scenarios were defined: a positive scenario (high ΔR and W₁, controllable C₁) and a negative scenario (low ΔR and W1, high C₁) (

Table 3. Parameters for Positive and Negative Scenarios.

Scenario	ΔR	W1	C1	Expected ESS
Positive	20	8	4	(1,1,1)
Negative	5	2	8	(0,0,0)

).

MATLAB R2023b was utilized as the simulation tool. Initial strategy probabilities x₀, y₀, z₀ were randomly generated within the interval [0.1, 0.9], creating 50 datasets covering diverse initial states. Simulation parameters were configured as follows: step size = 0.5, total duration = 20 steps, and the numerical solver ode45 was used to record, in real-time, the strategy probabilities of the government, schools, and students (including parents) at each step (t = 1 to t = 20). The resulting datasets from these two scenarios were plotted to illustrate dynamic evolution trajectories.

Figure 2 (positive scenario) demonstrates that when ΔR and W₁ are high and C₁ is relatively controllable, the probabilities that the government, schools, and students (including parents) select “active/request/express” strategies exhibit monotonic increases. These probabilities surpass 0.8 at approximately t = 6, subsequently converging smoothly toward (1,1,1). This trajectory confirms the unique evolutionarily stable equilibrium of the low-UAC strategy combination, indicating that under conditions of significant incremental benefits, adequate risk compensation, and manageable implementation costs, stakeholders rapidly reach consensus.

In contrast, Figure 3 (negative scenario) illustrates an opposite trend: the three probability curves rapidly decline below 0.2 around t = 4 and eventually stabilize at (0,0,0). This outcome clearly suggests that when incremental benefits are insufficient, risk compensation is inadequate, and implementation costs are excessively high, the high-UAC strategy becomes the stable attractor for the system.

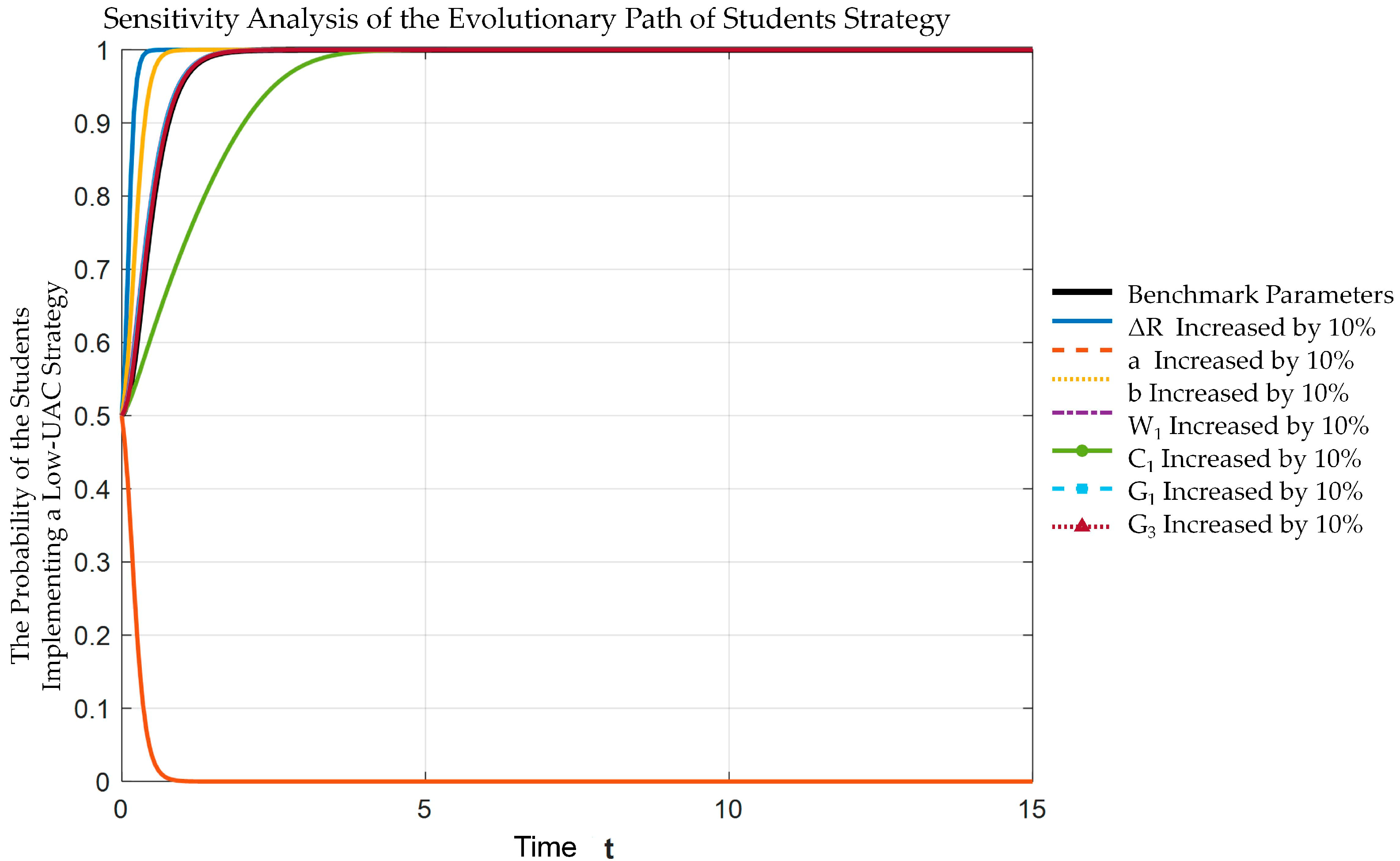
4.2.3. Sensitivity Analysis

This section employed MATLAB-based simulations and single-factor sensitivity analyses to evaluate the model’s stability and reliability. By repeatedly executing the simulation process outlined in Section 4.2.2 and comparing the consistency of results across multiple runs, the robustness of the model’s outputs was validated. Subsequently, a single-factor sensitivity analysis was conducted by adjusting key parameters individually (ΔR, benefit-sharing coefficients a and b, risk compensation W₁, etc.) while keeping other parameters constant.

For each adjusted parameter, simulations were conducted to record variations in the evolutionary trajectories of stakeholder strategies(Figure 4, Figure 5, Figure 6). By comparing the magnitude of fluctuations in these trajectories, the influence of each parameter on the system’s evolution was quantified. The sensitivity results allowed the identification of parameters with significant impacts and the determination of critical threshold values (e.g., W₁ ≥ 8, a within the range 0.6–0.7), providing methodological support for subsequent strategic recommendations.

The sensitivity analysis of the stakeholders’ evolutionary paths indicated notable differences in parameter sensitivity. The incremental comprehensive benefit (ΔR) emerged as the most influential parameter for all stakeholders, with increases in ΔR promoting a simultaneous shift toward proactive strategies. The benefit-sharing coefficient b strongly influenced school behavior by directly determining their cooperative benefits, while the coefficient a primarily impacted student strategies. An optimal range of 0.6–0.7 for a effectively motivated students and parents to express their demands. Government strategy was highly responsive to variations in risk compensation (W₁), with governmental willingness markedly increasing when W₁ ≥ 8.

Thus, ΔR, as a core economic lever, demonstrated a far greater regulatory effect than other parameters, serving as the most critical driver toward achieving a low UAC.

5. Discussion

5.1. Practical Implications

This study connects the identified game equilibrium directly with primary school architectural design practices. All monetary thresholds are expressed in 10,000-yuan per class (1 unit = CNY 10,000/class) to facilitate direct comparison with Table 1 and the scenario parameters. The core finding “when ΔR > 150,000 yuan/class and W₁ > 80,000 yuan/class, the system converges toward a low usable area coefficient (UAC) (0.48–0.53)” provides a quantitative decision-making basis for primary school designs, thereby overcoming traditional reliance on empirical standards. By examining practical scenarios in a District, Qingdao, this conclusion accurately addresses the inherent conflict between “land intensification” and “well-being spaces.” When incremental comprehensive benefits of a low UAC (such as land use savings and reduced operational energy consumption) and government risk compensation meet critical thresholds, the demands of the government (cost control), schools (educational space assurance), and students and parents (healthy environment) can be simultaneously met. This aligns strongly with demographic trends and design principles promoting “both spatial efficiency and educational needs.”

For instance, given the sensitivity of incremental comprehensive benefits (ΔR), strategies such as “optimizing circulation layouts” and “modular functional design” could be adopted to lower construction costs, thus enhancing the economic feasibility of low UAC. Concerning the threshold effect of government risk compensation (W₁), local governments might introduce targeted subsidies for “low-UAC campuses” to alleviate school concerns about budget overruns. Additionally, the optimal benefit-sharing coefficient (a = 0.6–0.7) suggests integrating “parent-participatory design workshops” and “student space-usage surveys” into decision-making, ensuring that increased open spaces align effectively with children’s developmental needs. This deeply resonates with the “user-centered” philosophy inherent in “well-being spaces.”

5.2. Theoretical Significance

• Advancing UAC research within primary school architecture:

The novelty of this research lies in its focus on the unique context of primary education. Previous UAC studies typically emphasized residential, office [43], or university buildings [44], concentrating primarily on spatial efficiency calculations. In contrast, this study integrates variables specific to primary education, including “children’s well-being space needs” and “school operational costs,” making parameter settings more aligned with the practical demands of basic educational facilities. For example, incorporating “maintenance costs for open spaces” into cost parameters and “student physical and mental health benefits” into benefit parameters underscores the fundamental differences between primary school buildings and other architectural types.

• Innovation from a multi-stakeholder dynamic equilibrium perspective:

The application of evolutionary game theory to primary school UAC decisions breaks from conventional approaches that focus solely on the physical properties of open spaces. It advocates balancing stakeholder interests during architectural planning. The identified equilibrium strategy, “E₈(1,1,1),” demonstrates that a stable increase in open spaces via low UAC requires positive interaction among government, schools, and families. Furthermore, the quantified parameter thresholds provide generalizable evaluation standards for designing healthy school environments. For instance, a threshold of ΔR ≥ 150,000 yuan/class serves as a baseline criterion for assessing the economic viability of implementing low UAC. In suburban areas with limited financial resources, incremental implementations of low-UAC designs could progressively meet this threshold. Compared to uniform, one-size-fits-all standards, differentiated strategies derived from game-theoretic equilibria offer greater practical adaptability, providing new methodological support for “data-driven applications in healthy built environments.”

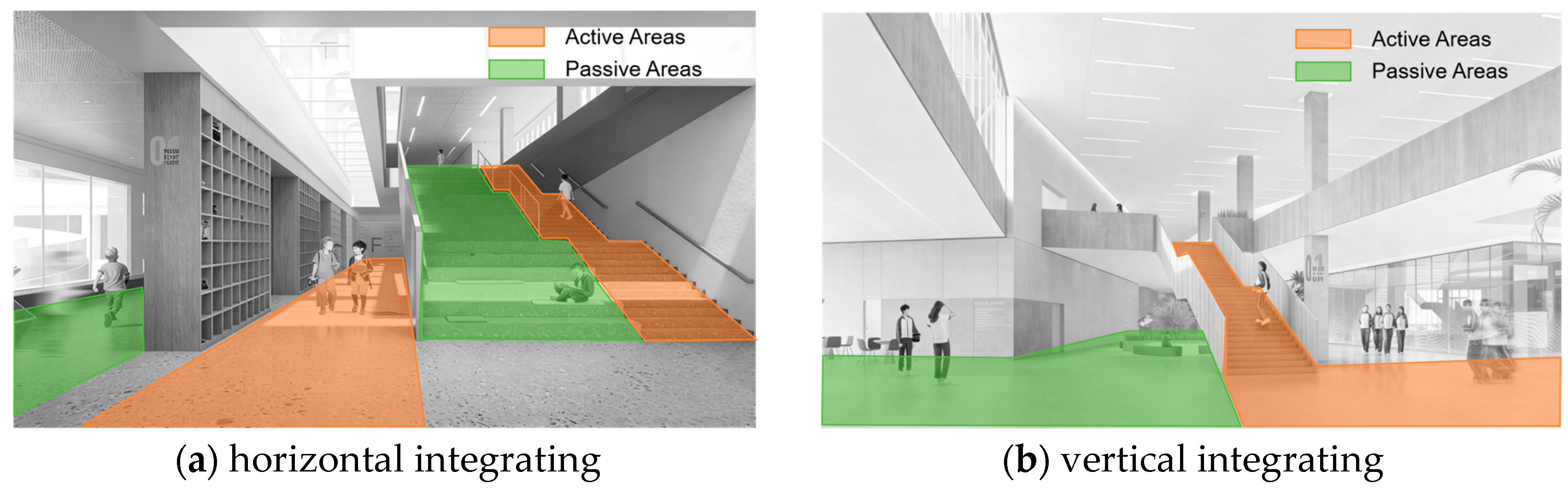
5.3. Primary School Design Suggestions

To translate the simulated ESS into practice, three mutually reinforcing design directives are advanced from an architectural standpoint, each explicitly tied to the key parameters that drive the low-UAC attractor.

Compact Site Layout: Adopt an intensive, horizontally or vertically consolidated massing that eliminates redundant circulation area and the associated construction-cost waste, thereby enlarging D (construction-cost saving).

Diverse Configuration Approaches for Open Space Planning: Deploy a rich yet code-compliant portfolio of permeable open-space configurations—semi-covered nodes, widened corridors, and locally enlarged bays—that remain classified as ancillary area yet elevate the perceived campus quality(Figure 7), pushing the supportive-benefit coefficient G₄ upward without raising the UAC denominator.

Activity Zones: Dynamic–Static Coupling: Calibrate location, area, and dimensional hierarchies between active and quiet spaces—clustering high-activity zones while embedding scaled-down quiet spaces along circulation spines—so that the resultant dynamic–static gradient delivers an immediately perceived spatial value increment to pupils(Figure 8); this secures the benefit-share coefficient a within the 0.6–0.7 interval that stabilizes the “student-assert” strategy in the replicator dynamics.

Together, these directives satisfy the fiscal, spatial, and behavioral conditions derived in Section 3 and Section 4, guiding land-constrained primary-school projects into the evolutionarily stable low-UAC band (0.48–0.53) while remaining fully aligned with everyday educational and regulatory requirements.

5.4. Policy Optimization Suggestions

Drawing from Williamson’s institutional analysis framework and the model’s findings, policy recommendations can be proposed at informal institutional, formal institutional, and governance levels to ensure the sustainable implementation of low-UAC campuses:

At the informal institutional level:

A social consensus emphasizing that “low-UAC campuses benefit children’s learning and health” should be strengthened. Public dissemination efforts, such as issuing “White Papers on the Benefits of Low-UAC Campuses” and organizing “Healthy Campus Design Exhibitions,” would raise awareness of the positive impacts that open space configurations associated with low UAC have on children’s learning efficiency and well-being. Additionally, creating a “Parent–School–Government” communication platform to integrate user demands into preliminary design surveys can enhance societal acceptance of low-UAC designs, indirectly reducing the difficulty of realizing incremental comprehensive benefits (ΔR).

At the formal institutional level:

Supporting policies and standards require improvement. Firstly, developing “Technical Guidelines for Low UAC Design in Primary Schools” to specify spatial requirements (e.g., open space ratio ≥ 10%) within the recommended UAC range (0.48–0.53) is essential. Secondly, establishing a “Cost-Sharing Mechanism for Low-UAC Campus Construction” to clearly define cost-sharing responsibilities between government and schools would prevent schools from resisting low-UAC schemes due to financial concerns. Thirdly, creating “Incentive Mechanisms for Low-UAC Designs” that reward schools adopting low-UAC schemes and achieving healthy campus certification could enhance schools’ motivation for requesting low UAC.

At the governance mechanism level:

Optimizing collaborative decision-making processes is critical. During architectural planning, the government should lead the formation of joint “Design–School–Parent” working groups to concurrently undertake technical assessments and stakeholder negotiations. During implementation, adopting a phased acceptance model that adjusts subsidies according to actual achievement of incremental comprehensive benefits (ΔR) would mitigate budgetary risks. Finally, during the operational phase, introducing “post-occupancy evaluation feedback mechanisms” to integrate satisfaction with open-space utilization into school performance assessments could form a comprehensive “decision–implementation–feedback” management cycle.

6. Conclusions and Limitations

This study systematically explored the determination of the usable area coefficient (UAC) for primary school buildings by constructing an evolutionary game model involving government, schools, students, and parents in a District, Qingdao. Using MATLAB simulations and sensitivity analysis, the primary conclusions are summarized as follows:

• Conditions for Evolutionarily Stable Strategies: When the incremental comprehensive benefit of a low UAC (ΔR) exceeds 150,000 yuan/class and the government’s risk compensation to schools (W1) surpasses 80,000 yuan/class, the system converges with a probability of no less than 0.8 to a low UAC range (0.48–0.53). Under these conditions, the stakeholder strategy combination (E₈(1,1,1)), namely, “active government implementation–schools requesting low UAC–students and parents expressing demands,” emerges as the unique evolutionarily stable strategy, enabling a synergy between intensive land use and well-being spaces.
• Key Influencing Parameters: Sensitivity analysis indicates that ΔR serves as the central driver influencing system evolution, with its increase positively aligning stakeholder strategies. The benefit-sharing coefficient a (0.6–0.7) significantly impacts the willingness of students and parents to express their demands. Additionally, when W1 ≥ 80,000 yuan/class, governmental willingness for active implementation notably increases, while school strategies demonstrate greater sensitivity to the benefit-sharing coefficient b.
• Design Strategies: A combined strategy of centralized compact planning, functionally hybridized circulation, dynamically static zoned activity areas, and modular unit construction enables primary-school projects to achieve simultaneous gains in land efficiency, floor-area utilization, child well-being and construction quality without increasing either site area or overall cost.

This study addresses existing gaps by integrating multi-stakeholder game theory with UAC determination during educational architectural planning, providing an interdisciplinary research perspective. By quantifying critical parameter thresholds for primary school UAC decisions, the study provides explicit guidance for architectural planning. The identified low UAC range (0.48–0.53) and accompanying strategies, such as cost control and risk compensation, can be directly applied to planning new constructions or renovations of primary schools in land-scarce urban areas. This ensures an increase in open space and enhances the educational environment, thereby improving students’ overall learning efficiency and promoting children’s healthy development.

However, due to limitations in the available literature and data, this study could not comprehensively analyze all potential influencing factors. Moreover, simplifications within the model’s assumptions might limit its applicability to complex real-world scenarios. Future research will incorporate additional practical factors into the evolutionary game model and conduct more extensive case studies to provide a more comprehensive analysis.