Seismic Performance of a Hybrid Structural Steel–Reinforced Concrete Coupled Wall Building: Preliminary Response Estimates from an NCREE–QuakeCoRE Joint Study

Abstract

In the field of earthquake-resistant design, there is an increasing emphasis on evaluating buildings as integrated systems rather than as assemblies of independent components. Hybrid wall systems based on structural steel and reinforced concrete offer a promising alternative to existing approaches by combining the stiffness and toughness of concrete with the ductility and flexibility of steel, which enhances resilience and seismic performance. The objective of this scientific study is to obtain preliminary analytical estimates of the earthquake response of a prototype hybrid steel RC coupled wall building that is being developed as part of a joint research program between the National Center for Research on Earthquake Engineering (NCREE) and New Zealand’s Centre for Earthquake Resilience (QuakeCoRE). Nonlinear response history analyses were carried out on the prototype building, using scaled ground motions and nonlinear hinge properties assigned to the primary lateral force resisting elements to replicate the expected inelastic behavior of the hybrid system. The results were used to evaluate story drift demands, deformation patterns, coupling beam behavior, and buckling restrained brace behavior, providing a system-level perspective on the expected earthquake performance of the proposed hybrid wall system. To deepen the current experimental understanding of the seismic behavior of the proposed hybrid structural system, a large-scale shaking table test is planned at NCREE as the next stage of this collaborative research.

1. Introduction

The demand for ever taller and more complex buildings has prompted a shift from building structures made exclusively of reinforced concrete (RC) or structural steel toward hybrid structural solutions that combine multiple materials. Although RC has long served as the basis for high-rise construction in many countries, its limitations become more evident as the height of a building increases: oversized member sections reduce usable floor area, excessive self-weight amplifies seismic demand, and foundations must be designed to resist larger loads. Hybrid configurations have been developed to address these challenges, in which RC core walls are typically used for stiffness and strength and are combined with steel or composite members [1]. This combination of materials reduces overall weight, accelerates construction, and enhances adaptability for future modifications while maintaining cost advantages over single-material systems [2]. From a theoretical perspective, the reliable application of such systems depends on advances in analytical and numerical methodologies capable of efficiently capturing dynamic processes in complex, heterogeneous structural systems, particularly under seismic loading. A recent study has proposed improved computational strategies for dynamic analysis of elastic elements in complex engineering constructions [3]. In parallel, increasing attention to environmental protection and sustainability, shaped by national legal frameworks and international policy discourse, has further encouraged the adoption of hybrid solutions that balance structural performance with reduced material consumption and environmental impact [4].

In practice, buildings that make use of RC and steel are becoming increasingly common. However, the design of a hybrid structure based on these materials is often governed by engineering judgment rather than codified standards, and systematic investigations into the seismic performance of such constructions remain limited [5,6,7,8]. Zhang et al. [9] carried out shaking table tests to demonstrate that confined masonry components in hybrid masonry–RC buildings tend to fail earlier than RC members, and may trigger progressive collapse. Their findings highlight the need to reassess design assumptions that often lead to underestimates of the structural contributions of masonry. Complementary studies of hybrid masonry–RC systems conducted by Abrams et al. [10] revealed that connection detailing, anchorage configuration, and force transfer mechanisms are essential aspects of stable seismic performance; if properly designed, hybrid systems of this type can achieve resilience comparable to that of conventional structures. Zheng et al. [11] extended this work by examining RC–masonry horizontal hybrids, which are common in rural China, and by showing that torsional irregularities and uneven stiffness distributions can exacerbate seismic vulnerability. Their combined shaking table and finite element analyses provided valuable insight into story drift patterns and stress concentrations at beam–column interfaces.

Subsequent studies have broadened the scope of investigations into hybrid or mixed-material structures. Kiani et al. [12,13] evaluated how the height and position of the transition story in buildings with RC bases and steel tops affect the fragility of mixed multistory frames, while Ghanbari et al. [14] examined its performance under sequential mainshock–aftershock excitations, and evaluated the possibility of cumulative damage effects. Askouni and Papagiannopoulos [15,16,17,18] explored the dynamic response of three-dimensional mixed frames subjected to strong near-fault ground motions. Askouni [2] carried out further investigations of hybrid buildings exposed to recurrent earthquakes, which included models of the lower RC portion of an existing structure supporting an upper steel framework, an arrangement that is often used in retrofit or vertical extension projects. Li et al. [19] proposed a simplified analytical approach for estimating the lateral demand in mixed systems, whereas Kaveh and Ardebili [20] introduced an optimization-based framework for enhanced cost efficiency. Building on these efforts, Kiani et al. [21] recommended seismic factors for concrete–steel composite buildings, and Pnevmatikos et al. [22] applied wavelet analysis to detect damage to planar mixed frames. Similarly, Maley et al. [23] confirmed that conventional design methods can be applied to frames with vertical material transitions, despite such configurations not being explicitly covered in existing codes. Fanaie and Shamlou [24] assessed response modification factors for various mixed frames, while Bhattarai and Shakya [25] investigated response reduction factors for steel–RC systems.

Recent research has commenced to explore hybrid mechanics–data-driven modeling strategies to enhance response prediction while preserving physical interpretability. Shahmansouri et al. [26] introduced a scaling-based integrated machine learning–mechanics framework for assessing the lateral response of self-centering RC walls. This study, while concentrating on self-centering wall systems instead of mixed-material buildings, illustrates an emerging class of hybrid modeling approaches that may complement physics-based numerical simulations and motivate future extensions in modeling frameworks for complex hybrid structural systems.

Taken together, these studies represent a growing research effort to define analytical tools, design methodologies, and performance assessment frameworks for hybrid structures, and highlight the need for physical evidence on the dynamic responses of such frameworks. Of the various hybrid configurations that have been developed, wall-dominated systems have gained prominence for their ability to combine control deformation and damage in seismic buildings [27]. In these systems, RC or steel–RC core walls act as the primary lateral-resisting elements, creating a concentration of stiffness and strength near the center of the building. The surrounding steel frames, typically with simple or moment connections, primarily act to support gravitational loads, while floor diaphragms act as collectors that unify the global structural response. For taller buildings, belt trusses or outriggers are often introduced to enhance the interaction between the steel framing and the core wall, in order to further reduce lateral deformation.

Although hybrid wall systems have been shown to yield reliable seismic performance, they continue to pose challenges in terms of both design and analysis. Careful detailing is essential to accommodate inelastic deformation in critical regions, as is a consideration of how coupling beams, floor slabs, and steel frame components influence the stiffness, strength, drift, and failure mechanisms. In steel–RC walls, special attention must be paid to anchorage, the interaction between steel and concrete, and local confinement in order to prevent premature failure. The behavior of the coupling beams, whether composed of RC or structural steel, strongly governs the lateral stiffness and the transfer of shear and axial forces between wall segments, meaning that proper configuration and connection detailing are important. The connections between structural steel and RC elements also require special attention, and evidence is needed in order to judge the current ability of designers to estimate drift, damage, and repairability. Nevertheless, seismic design provisions are primarily focused on single-material systems, such as RC, timber, or steel, and provide limited guidance for hybrid configurations [28].

As hybrid structural systems become increasingly prevalent in contemporary construction, the lack of dedicated design provisions highlights the need for systematic, system-level investigations that clarify their seismic behavior and support damage-control and resilience-oriented design strategies. To address this need, the present study focuses on a wall-dominated hybrid structural steel–RC coupled wall system, a configuration that has received comparatively limited experimental and analytical attention in prior research, which has largely emphasized vertically transitioned hybrid buildings. Through a comprehensive nonlinear analytical investigation of a full building system, this study examines how global seismic response, force-sharing mechanisms, and deformation demands develop at the system level, providing preliminary yet essential insight into these behaviors. The research was conducted through an international collaboration between the National Center for Research on Earthquake Engineering (NCREE) at the National Institutes of Applied Research (NIAR), Taiwan, and the New Zealand Centre for Earthquake Resilience Te Riranga Rū QuakeCoRE, with support from National Taiwan University (NTU), National Cheng Kung University (NCKU), the University of Canterbury, and the University of Auckland.

The study described the selection and scaling of input ground motions and included nonlinear dynamic simulation results obtained using ETABS. Nonlinear hinge properties followed TEASPA and ASCE guidelines, and appropriate boundary conditions were used to represent the expected deformation behavior of the hybrid system. The aim of this investigation was to produce tangible data on the measured seismic response of hybrid structures, in order to support design methods with a focus on the control of seismic drift and damage, to expedite building reuse. In addition, the paper outlines a large-scale experimental program that is planned to verify the analytical findings introduced here. By documenting both numerical modeling results and test planning for a hybrid steel–RC coupled wall system, this study will provide the research and engineering communities with a valuable reference to support the implementation of resilient hybrid structures.

2. Methodology

2.1. Steel–RC Hybrid System Under Study

Collaborative initiatives between the NCREE in Taiwan and New Zealand’s Te Hiranga Rū QuakeCoRE have laid important groundwork for extending the current knowledge of the seismic performance of whole buildings. Earlier joint studies focused on mid-rise RC frame buildings with torsional irregularities, which are typical of existing structures in Taiwan and New Zealand [29]. Subsequent programs under QuakeCoRE extended this exploration to low-damage systems, and included a two-story concrete-wall building and an ongoing investigation of a three-story steel structure incorporating a friction-based energy dissipation system. Complementary efforts by E-Defense in Japan and the University of California San Diego (UCSD) have further enriched the state of the art through large-scale shaking table tests of concrete, steel, and timber buildings [30]. Together, these projects have provided significant insight into how entire structures respond to seismic excitation, but further investigation remains essential to evaluate the performance of emerging hybrid systems that combine multiple materials and lateral force mechanisms.

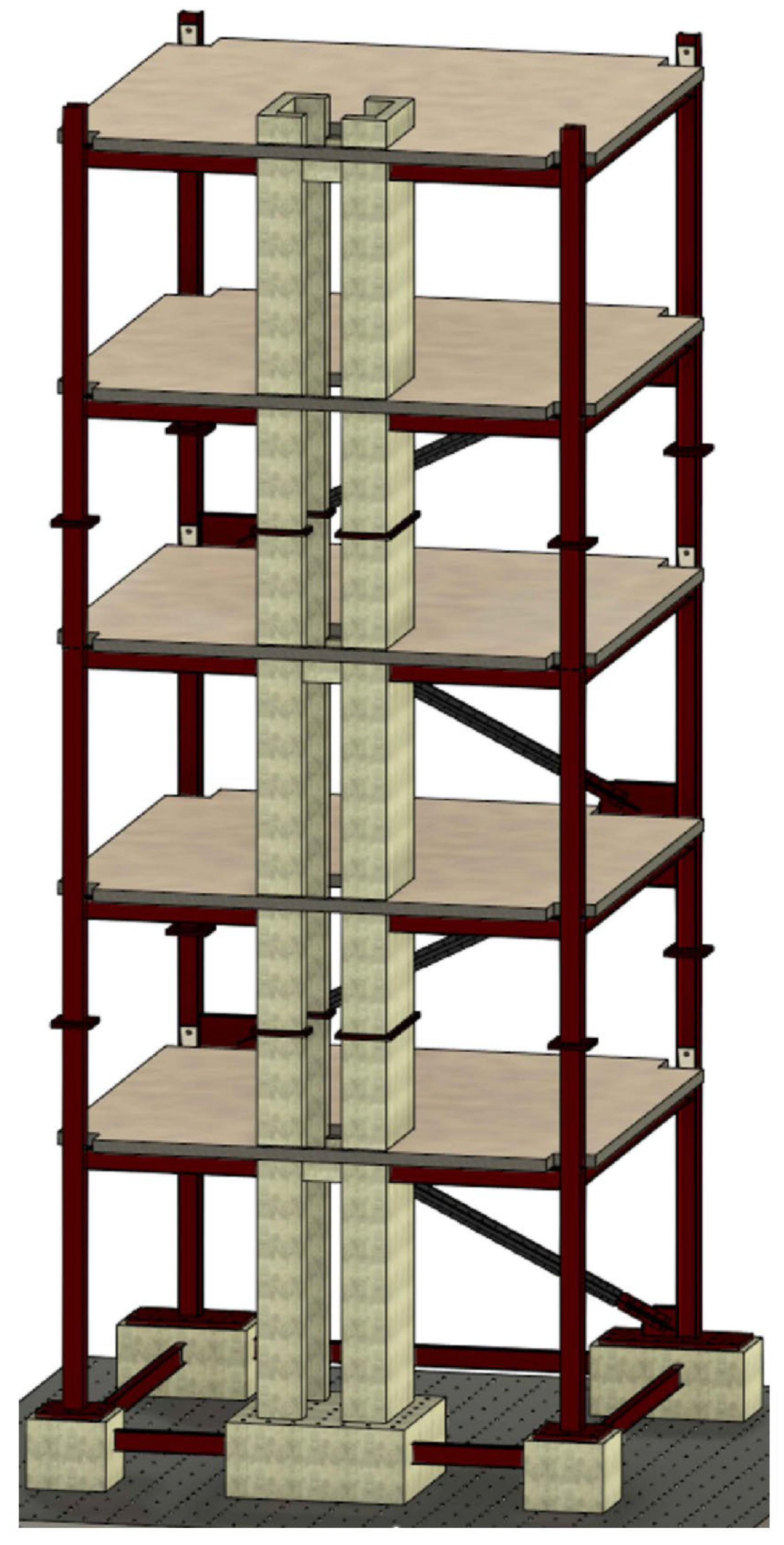
Building upon this international foundation, the present NCREE–QuakeCoRE collaboration developed a hybrid structural steel–RC coupled wall system that represents current practice in New Zealand and can be adapted to Taiwan’s high-seismic environment. The proposed prototype, shown in Figure 1, integrates structural steel framing with RC coupled-core walls to form a composite lateral resisting system. In this design, there is an emphasis on drift control, ductility, and post-earthquake repairability, in order to meet the broader objective of enhancing seismic resilience and “functional recovery”. In conceptual terms, the prototype represents a mid-rise five-story office building located in Christchurch, which was chosen as a reference for structures in regions of moderate to high seismic hazard.

The test structure features a 5 × 5 m floor plan, defined by centerline-to-centerline dimensions, with an overall height of 12.7 m. It includes two coupled walls that form a core offset from the center of mass. The ratio of the cross-sectional area of the wall to a typical gross floor plan area is 0.023. Coupling beams are located at three (out of five) levels above the foundation, to limit the base shear strength within the capacity of the earthquake simulator.

To allow the torsional response to be explored, buckling-restrained braces can be installed or removed from a frame that is located opposite to the wall and furnished with moment connections placed on alternate floor levels. In the direction perpendicular to the braces, there are steel frames that feature slotted, bolted shear tabs that connect beams to columns and wall segments. Concrete slabs cast on steel-deck panels serve as floors and diaphragms. Depending on the friction at the bolted steel connections, the coupling between the slabs and shear tabs can induce moment transfer at connections that are often assumed not to resist moments.

The structure was built in three modules, which were connected by two splices consisting of pairs of bolted plates, as illustrated in the three-dimensional model in Figure 2. Steel reinforcing bars and structural steel shapes were welded with full-penetration welds to the splice plates. The specified concrete compressive strength was 40 MPa, and ASTM 706 Grade 60 (f_y = 410 MPa) was selected for all concrete reinforcements. SS400A steel was selected for all structural steel components, including BRBs and gusset plates. The specified yield stress was 205 MPa, and the specified tensile strength was 400 MPa.

The building included nonstructural elements (office furniture, partitions, veneer, library shelves, sprinklers, and a curtain wall, amounting to approximately 1 kPa of added weight per floor except at roof level). The testing program included three phases: (i) without the buckling-restrained braces; (ii) with the braces installed to control torsion; and (iii) without the braces again. In the last phase, a partial curtain wall was installed along the facade accommodating the braces in Phase II. The total building weight, excluding footings, ranged between 730 and 750 kN depending on the configuration (i.e., testing phase). The distribution of building weights for each phase, including nonstructural components, is presented in

Table 1. Distribution of building weights in each testing phase.

Floor	No Braces, No Facade (kN)	Braces, No Facade (kN)	No Braces, Facade (kN)
1	156	160	156
2	154	158	163
3	155	158	163
4	154	156	154
5	112	112	112

.

Estimated initial periods associated with the first translational modes ranged between 2/5 and 2/3 s, depending on the direction, configuration, and assumptions about the ability of the connections to resist moments. Again, the proportions of the structure were adjusted to keep the demand on the shaking table within its specifications. In the configuration with braces, the prototype was designed to reach a roof drift ratio that did not exceed approximately 1%. The reference (or design) earthquake was represented by a displacement spectrum reaching 200 mm for a period of 1 s and a damping ratio of 2%. At a damping ratio of 5%, the spectrum reaches approximately 150 mm at 1 s. These ordinates correspond to spectral accelerations of approximately 0.8 g and 0.6 g at 1 s, and a peak ground velocity approaching 0.4 m/s. The minimum design base-shear strength coefficients ranged between 1/8 and 1/4, depending on the configuration.

2.1.1. Design of Sandwiched Buckling-Restrained Brace

The braces incorporated into the building were sandwiched buckling-restrained braces (SBRBs), as illustrated in Figure 3. Their design followed procedures outlined in previous studies [31,32], and consisted of a rectangular core plate and two identical restraining members, which were built by welding a steel channel to a rectangular face plate. Cross-sectional dimensions for each SBRB are summarized in Table 1. The restraining members were bolted together using M14 S10 high-strength bolts, where the distance between bolts was selected to avoid local and global buckling along the yielding length of the core plates. A silicone layer 2 mm thick was installed around the core plate to avoid friction with the restraining members.

To achieve the desired deformation performance, additional refinement was applied to the core plate and restraining components. The dimensions of the stiffener and the slit spacing on the face plates were adjusted to ensure that the core could undergo axial deformation without premature buckling. This tuning process enabled the braces to reach the target strain capacity while maintaining stable hysteretic behavior under cyclic loading. In this study, all four SBRBs were designed to sustain axial core strains exceeding 4.5%, in order to confirm their ability to provide reliable energy dissipation and consistent mechanical performance under simulated seismic demand. In this design approach, the SBRBs were expected to exhibit stable load–deformation characteristics and to contribute significantly to the overall seismic resilience of the hybrid structural system. Once these requirements had been met, the SBRB design was finalized, and the corresponding geometric and mechanical properties are summarized in

Table 2. Cross-sectional dimensions of the SBRBs.

Location	Core Plate			Restraining Member
	${\mathit{b}}_{\mathit{c}}$ (mm)	${\mathit{h}}_{\mathit{c}}$ (mm)	${\mathit{L}}_{\mathit{y}}$ (mm)	Face Plate (mm)	C-Channel Restrainer (mm)	Gross Second Moment of Area (mm)
1F	55	8	3095	164 × 15	50 × 55 × 10 × 10	9.75 × 106
2F	55	8	2615	164 × 15	50 × 55 × 10 × 10	9.75 × 106
3F	44	8	2615	164 × 15	40 × 35	5.43 × 106
4F	42	6	2615	164 × 15	40 × 35	5.08 × 106

Note: b_c and h_c represent the width and thickness of the core plate, respectively; L_y is the length of core plate shown in Figure 3a.

and

Table 3. Section properties of the SBRBs.

Location	Core Plate						Bolt (S10T)
	${\mathit{P}}_{\mathit{n}\mathit{y}}$ (kN)	${\mathit{P}}_{\mathit{m}\mathit{a}\mathit{x},\mathit{d}}$ (kN)	${\mathit{L}}_{\mathit{w}}$ (mm)	$\frac{{\mathit{P}}_{\mathit{e}}}{{\mathit{P}}_{\mathit{n}\mathit{y}}}$	$\frac{{\mathit{P}}_{\mathit{m}\mathit{a}\mathit{x},\mathit{g}}}{{\mathit{P}}_{\mathit{n}\mathit{y}}}$	$\frac{{\mathit{P}}_{\mathit{m}\mathit{a}\mathit{x},\mathit{l}}}{{\mathit{P}}_{\mathit{n}\mathit{y}}}$	${\mathit{P}}_{\mathit{n}\mathit{b}}$ (kN)	$\frac{{\mathit{L}}_{\mathit{b}}}{{\mathit{L}}_{\mathit{w}}}$
1F	140.00	242.00	82.00	10.00	8.60	22.10	40.00	1.80
2F	140.00	242.00	82.00	13.10	11.00	22.00	40.00	1.80
3F	112.00	193.00	82.00	9.10	7.90	15.90	36.00	1.80
4F	80.00	138.00	61.00	12.00	10.40	22.80	44.00	1.80

Note: P_ny is the nominal yield strength; P_max,d is the maximum design strength; L_w is the high-mode buckling wavelength; P_e is the elastic critical buckling strength; and the subscripts g, l, and b represent global, local, and bolt values, respectively.

.

2.1.2. Design of the Coupled Wall

The RC coupled wall consisted of two opposing C-shaped walls linked by coupling beams at three levels, as illustrated in Figure 4. Each C-shaped wall was based on a combination of a web and two flange panels, as shown in Figure 5a.

The core wall was designed to yield in flexure, without shear or bond failures. For anchorage, longitudinal wall bars were welded to plates placed at the bottom of the wall footing. The maximum shear demand was estimated using the likely properties of the material to enable an estimate of the moment capacities. An effective lever arm equal to 50% of the wall height was used to estimate the peak wall shear demand. The peak nominal unit shear stress estimated for the product of net wall length and web thickness was kept below 2 MPa. To estimate the peak shear in the direction of the coupling beams, a mechanism with plastic hinges was assumed to occur at all beam faces and wall bases, whereas in the perpendicular direction, hinging was assumed to occur exclusively at wall bases.

The boundary element (BE) regions, identified as Zones 1 through 4 in Figure 5b, were confined to enhance the deformation capacity of the concrete. The volumetric reinforcement ratios calculated for the concrete within confining hoop centerlines ranged from 1.11% to 1.98%. Excluding the hoop reinforcement, the continuous transverse reinforcement placed in the coupling wall web (CW web) and flange panels provided transverse reinforcement ratios between 0.89% to 1.58%. Ties were expected to be able to resist the entire shear force, without contributions attributable to the concrete. The total longitudinal reinforcement ratio was 1.60%. In the boundary elements, the longitudinal reinforcement ratios were 2.02% on the long-web side (BE₁ and BE₃) and 2.21% on the short-web side (BE₂ and BE₄).

2.1.3. Design of the Coupling Beams

Each coupling beam had a span of 400 mm, an overall depth of 240 mm, and a span-to-depth ratio of 1.67, as illustrated in Figure 6. The beam width was 200 mm, matching the width of the adjacent wall segments. The diagonal reinforcement consisted of #4 bars placed at an inclination of 20°, allowing the strength of the steel bars to be mobilized under diagonal tension. The diagonal bars were provided with headed anchors and embedment lengths of 30 times the bar diameter. The horizontal longitudinal reinforcement was not intended to yield under tension, and consisted of a total of six #6 bars with short embedment lengths of 15 times the bar diameter. The transverse reinforcement ratio provided by the stirrups was approximately 0.7%.

The coupling beams were confined with closed hoops and cross-ties made from #3 bars. The spacing of the ties (80 mm) did not exceed one-quarter of the beam depth or six times the diameter of the longitudinal bars, and one hoop was positioned within 50 mm from the wall face to improve confinement near the interface. The reinforcement detailing and member dimensions were chosen to ensure that the expected chord rotation under the reference (or design) earthquake does not surpass 3.5% or the rotational capacity observed in tests of similar beams, noting that a greater span-to-height ratio may result in increased beam chord rotation [33].

2.2. Selection of Input Ground Motion

The primary objective of this analytical model was to investigate the torsional behavior of a hybrid lateral-resisting system composed of steel and RC elements. To achieve this, the principal direction of seismic excitation was defined as the direction parallel to the SBRBs. The ground motion records were scaled to match the design spectra over the range of periods relevant to the system (0.4 to 1.5 s). The ground motion was further scaled to represent multiple seismic hazard levels, where R = 0.25 corresponds to serviceability-level shaking, R = 0.5 to the repairable level, R = 1.0 to the design-basis earthquake (DBE), and R = 1.5 or higher to the maximum considered earthquake (MCE). This multi-level scaling approach enabled a comprehensive evaluation of the structural response under a wide range of seismic demand, including both elastic behavior and highly nonlinear deformation regimes.

Three components of recorded ground motions were considered for reference: the EW component of the 1995 Hyogo-ken Nanbu (Kobe) earthquake recorded at the JMA station, the EW component of the 1940 Imperial Valley earthquake recorded at Array #6, and the EW component of the 1999 Chi-Chi earthquake recorded at the CHY006 station. Of these, the Chi-Chi CHY006 record was selected as the primary input motion for the nonlinear dynamic analyses, while the Kobe and Imperial Valley records were retained for comparative purposes to highlight differences in spectral shape and frequency content. 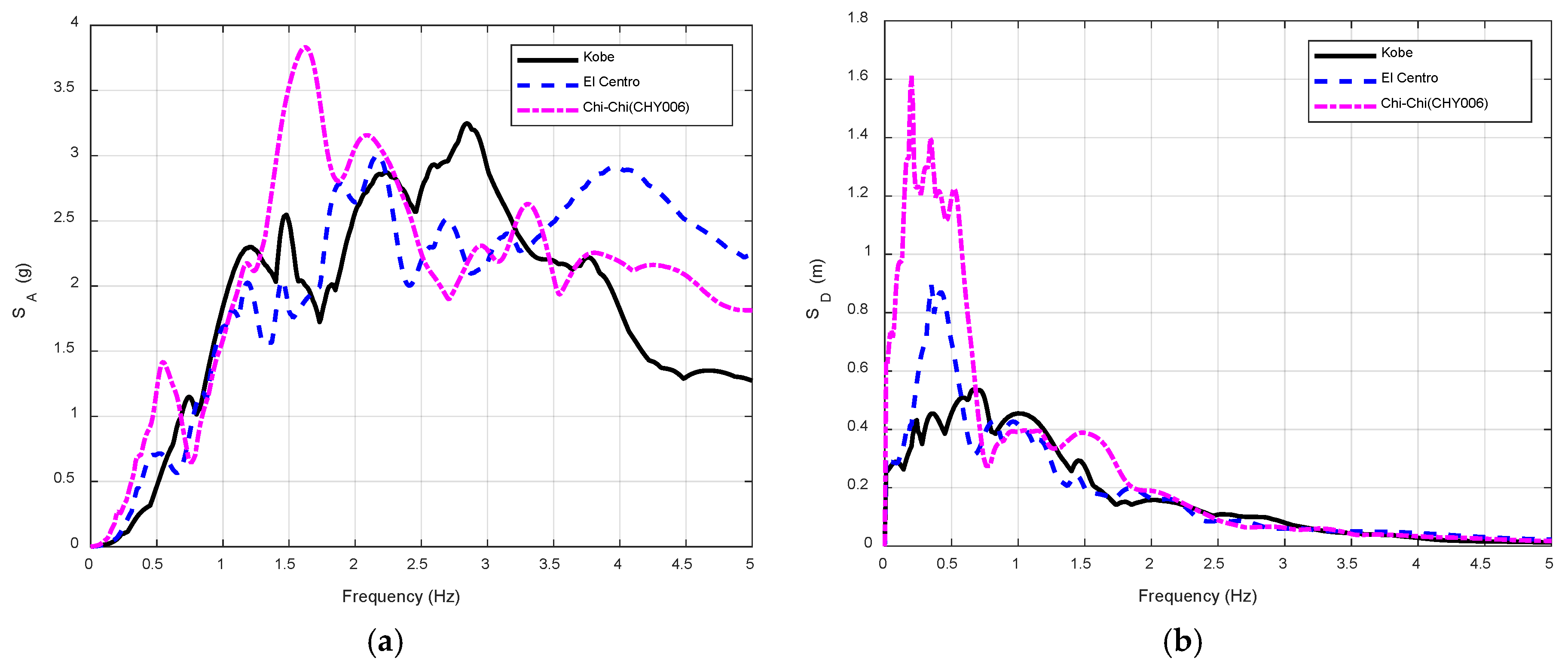Figure 7a–c present the corresponding acceleration time histories, and Figure 8 shows the 5%-damped response spectra after scaling. In particular, the scaled Chi-Chi CHY006 spectrum exhibits close agreement with the target design spectrum prescribed by NZS 1170.5 [34] over the period range of interest for the prototype structure (approximately 0.4–1.5 s), with spectral ordinates generally within an acceptable deviation for nonlinear time-history analysis. This range encompasses the fundamental and higher-mode periods of the hybrid coupled wall system, ensuring consistency between the selected input motion and the governing seismic hazard.

The Chi-Chi CHY006 motion is characterized by pronounced long-period pulse-like features, as reflected by its relatively high spectral displacement in the low-frequency range (approximately 0.2–0.5 Hz), which makes it particularly suitable for evaluating wall-dominated hybrid systems. Such pulse-like motions are known to impose large displacement and rotation demands and are therefore critical for assessing torsional response, force redistribution between RC walls and steel framing, and coupling-beam deformation demands. The EW component was selected because it produces the most significant structural response relative to the principal horizontal axes of the building, consistent with standard practice in performance-based seismic assessment. The applied scaling factors of 0.5, 1.0, 1.5, and 2.0 represent increasing intensity levels that may be interpreted as serviceability, design-basis, and beyond–design-basis to near-collapse conditions for the considered site and structural system, enabling a systematic evaluation of response progression under escalating seismic demand.

2.3. Numerical Modeling

To verify that the analytical model could accurately reproduce the intended structural behavior, a series of nonlinear dynamic analyses were performed, with a focus on evaluating the global and torsional responses of the proposed hybrid structural system under near-fault excitation. As described above, the ground motion recorded during the 1999 Chi-Chi earthquake (station CHY006) was used for the dynamic analysis.

Furthermore, as a preliminary investigation of the system response, the model used the design material properties. The concrete in the wall and the coupling beams used a design compressive strength $\left(f_c^{\prime }\right)$ of 30 MPa, while the reinforcing bars in these members used a design yield strength $\left(f_y\right)$of 420 MPa, values that were representative of common construction practice in New Zealand. The steel columns and beams were modeled using the standard structural steel grade SN400 [35], with a minimum design yield stress $\left(f_y\right)$ and tensile strength $\left(f_u\right)$ of 205 MPa and 400 MPa, respectively. The elastic moduli adopted for concrete $\left(E_c\right)$ and steel $\left(E_s\right)$ were 20.8 GPa and 200 GPa, respectively. Nonlinear behavior was represented by hinge properties assigned to the structural elements, and the detailed definitions of these hinges are presented in the following subsection. The outline of the modeling assumptions and setup, including material properties, section dimensions, and the configuration of the buckling-restrained braces, as summarized in

Table 4. Section sizes and materials used in the model.

Member		Section (mm)	Material	Properties
Column		H200 × 200 × 8 × 12	SN400	$f_y:$ 205 MPa; $f_u:400 \mathrm{M}\mathrm{P}\mathrm{a}$; $E_s:$ 200 GPa
Steel beam		H194 × 150 × 6 × 9	SN400
Coupling beam		200 × 240	RC	$f_c:$ 30 MPa; $f_y:420 \mathrm{M}\mathrm{P}\mathrm{a};$ $E_s:$ 20.8 GPa
Wall Flanges		200 × 450	RC
SBRB (core section)	4F	42 × 6	SS400	(see Table 3)
	3F	44 × 8
	2F	55 × 8
	1F	55 × 8

.

2.3.1. Basic Modeling Settings

In the analytical model, the X-direction was defined as the axis of the SBRB, and corresponded to the short direction of the RC core wall, while the Y-direction represented the long direction of the wall. Beam and column elements were modeled using their actual cross-sectional dimensions, to ensure accurate representation of the stiffness. The RC core wall was idealized using the equivalent wide-column approach described in TEASPA 4.0, in which the wall is represented by two boundary columns connected by a cross-shaped linking member. The equivalent wide columns were assigned their actual dimensions with a web and coupling beam width of 200 mm, and elastic end regions were defined at both ends of the wall columns, as shown in Figure 9.

To simulate realistic boundary conditions, pinned connections (representing hinged behavior) were used at the interfaces where the steel beam ends meet the RC-wall joints, reflecting the absence of fully connected top and bottom flanges. Meanwhile, the steel columns and the RC wall boundary elements were constrained using fixed joints at the base, as shown in Figure 9c,d. The panel zones at these joints were modeled as rotational springs, with values for the elastic shear stiffness derived from the geometry and material properties of the actual joint section. The applied loads followed the planned testing conditions: in addition to the self-weight of the structural members, all other vertical loads (representing nonstructural components such as equipment and furnishings) were applied as uniformly distributed loads on each floor slab. For the modal analysis, both the self-weights of the members and the additional vertical loads were treated as static loads, and were incorporated into the mass matrix of the analytical model.

2.3.2. Nonlinear Hinge Settings

Nonlinear hinge properties were incorporated into the analytical model for each primary structural component, in order to represent the expected inelastic response under seismic loading. To simplify the analysis and to reduce the computational effort involved, the number of hinges was minimized as far as possible without compromising the accuracy of the global response. The steel columns were assigned axial-flexural hinges, although in reduced quantity compared with a fully detailed model, while the steel beams were provided with flexural hinges in the regions of the SBRB beam ends to capture plastic rotations under lateral loading. The RC wall, which was primarily designed to resist shear rather than moment-frame action, was modeled as a single vertical element with a shear hinge located at its base. The RC coupling beams were equipped with flexural hinges at both ends, and the SBRBs were modeled with axial hinges at their ends to represent inelastic tensile and compressive behavior.

The mechanical properties of these hinges were defined following established standards. For the steel members, the hinge properties were specified in accordance with ASCE 41-17 [36], as illustrated in Figure 10a,b. The flexural and shear hinges of the RC wall were defined using TEASPA 4.0, which incorporates key backbone parameters such as cracking and yield strengths, post-yield stiffness ratio, and strength degradation, as shown in Figure 10c,d. Moreover, the plastic hinge length could be more accurately evaluated by considering the axial stress ratio and the coupling ratio of the coupled RC walls [37]. The hinge characteristics of the RC coupling beam and SBRB also followed ASCE 41-17 provisions [36], with backbone curves and rotation capacities appropriate for shear-dominated and axial-dominated members, respectively, as shown in Figure 10e,f. To capture cyclic degradation and energy dissipation behavior, the Takeda hysteresis model was applied to RC members, whereas the kinematic hardening model was used for steel members. In summary, flexural hinges were assigned at the ends of members to represent plastic rotations, while shear or axial hinges were introduced at critical locations corresponding to the expected inelastic mechanisms.

3. Results and Discussion

3.1. Modal Analysis

To gain an initial understanding of the global dynamic behavior of the hybrid structural system, a modal analysis was performed prior to the nonlinear time-history evaluation. This analysis focused on identifying the dominant vibration modes, their corresponding natural periods, and the associated modal mass participation ratios, which collectively describe the fundamental response characteristics of the building. The first three modes, which govern the overall dynamic behavior, are illustrated in Figure 11. Mode 1 involved a translation in the X-direction combined with a significant torsional component, with a fundamental period of 0.626 s. This mode reflected the interaction between the BRB frame and the RC wall, indicating that the torsional behavior is influenced by the asymmetric stiffness distribution of the lateral-force-resisting system. The mass participation ratios showed that approximately 42% of the total mass participated in this mode along the X-direction, thus confirming its dominance in the initial lateral-torsional response.

Mode 2 corresponded primarily to translational motion in the Y-direction, with a period of 0.569 s. The higher stiffness of the RC wall in this direction resulted in a shorter period compared with Mode 1. The mass participation ratio in the Y-direction reached approximately 75%, indicating that this mode effectively represented the primary lateral response perpendicular to the SBRB system. Mode 3 combined torsional rotation with additional translation in the X-direction, with a period of 0.418 s. The higher frequency and mode shape characteristics indicated advanced torsional coupling between the RC wall and the surrounding steel frame. The cumulative mass participation ratios showed that about 75% of the total mass participated in the X-direction, 70% in the Y-direction, and roughly 76% in torsional rotation, thus confirming that the first three modes capture the majority of the building’s dynamic response and provide a reliable foundation for subsequent nonlinear analyses.

3.2. Pushover Analysis

A pushover analysis was performed to assess the global lateral resistance and nonlinear deformation characteristics of the hybrid structural system. The applied lateral load pattern was determined by multiplying the mass of each floor by the corresponding first-mode displacement component in the direction of loading, with the forces applied at the centroids of the stories along the positive X-direction. The resulting base shear–roof displacement relationship is shown in Figure 12, and the progression of nonlinear hinge formation at representative response points is illustrated in Figure 13.

The base shear–roof displacement curve shows a gradual reduction in stiffness as lateral displacement increases, indicating the sequential yielding of key structural components. At Point A, the first nonlinear hinge formed in the SBRB on the fourth floor, corresponding to a base shear of 248 kN and a roof displacement of 37 mm, and marking the onset of yielding. At Point B, where the base shear reached 283 kN and the roof displacement increased to 44 mm, additional hinges developed in the SBRBs on the second and third floors, and flexural hinges formed at both ends of the RC coupling beam on the fourth floor. By Point C, with a base shear of 360 kN and a roof displacement of 75 mm, all SBRBs had yielded axially, and the RC walls at the first and second floors began to develop shear hinges, signaling the initiation of wall cracking and stiffness degradation. Flexural hinges also appeared at the base of the RC wall and within the coupling beam on the second floor, illustrating the progressive spread of inelastic behavior throughout the system.

As loading progressed to Point D (464 kN, 148 mm), the structure reached an advanced inelastic state, with all SBRBs, coupling beams, and the RC wall base forming nonlinear hinges, while the RC walls on the first to third floors exhibited additional shear hinging. In the last stage, represented as Point E (564 kN, 250 mm), a new shear hinge appeared at the fourth-floor RC wall, and the widespread development of hinges across all primary components indicated a well-distributed plastic mechanism. This progression of hinge formation, shown in Figure 13, indicates a stable and ductile global response rather than a localized failure pattern.

The results of the pushover analysis showed that the roof displacement at initial yielding was approximately 37 mm, while the ultimate roof displacement reached 250 mm, equivalent to about 6.7 times the yield displacement. The structure, which was designed for a ductility capacity corresponding to R = 4.0, exhibited interstory drift angles well below the limit set in the Taiwan building code [38] (maximum drift angle = 0.0037 < 0.005). This analysis therefore confirms that the hybrid system possesses substantial deformation capacity and ductile performance, with an overall ductility demand that exceeds the target design level specified by the code.

3.3. Nonlinear Time History Analysis

A series of nonlinear time-history analyses were conducted to investigate the seismic response of the hybrid structural system under near-fault ground motion. The record of the Chi-Chi CHY006 earthquake, characterized by a long-period pulse, was adopted as the input motion. The original record, with a peak ground acceleration of 0.36 g, was scaled to 0.3 g following the procedure recommended in NZS 1170.5 [34] to align with the design level of seismic motion. The input time history used in the analyses had a total duration of 80 s and consisted of the scaled record applied sequentially at 0.5, 1.0, 1.5, and 2.0 times its baseline amplitude to simulate progressively increasing levels of ground shaking.

3.3.1. Roof Displacement

The corresponding time histories for the roof displacement are presented in Figure 14. Under 0.5 EQ, the structure remained essentially elastic, with a maximum roof displacement of 41 mm and no residual deformation after shaking. At 1.0 EQ, the response began to exhibit nonlinear behavior, with a maximum displacement of 82 mm and a small residual deformation of about 6 mm.

As the input intensity increased to 1.5 EQ, nonlinear effects became more pronounced, with a peak roof displacement of 133 mm and a residual deformation of approximately 11 mm, indicating progressive stiffness degradation and energy dissipation. At the highest intensity level of 2.0 EQ, the structure underwent significant nonlinear deformation, with a maximum roof displacement of 193 mm and a residual deformation of around 13 mm. From the displacement histories, a gradual transition can be observed from an elastic to an inelastic response, consistent with the expected performance of the hybrid system under increasing seismic demand.

3.3.2. Interstory Drift Response

Figure 15 shows the distribution of maximum interstory drift ratios along the height of the building under different intensity levels of the ground motion. In all cases, the largest drift occurred at the third floor (3FL), indicating that this level experienced the most significant flexural and shear deformation due to its relative stiffness transition within the structural system. As the input intensity increased from 0.5 EQ to 2.0 EQ, the maximum interstory drift ratios increased to 0.45%, 0.87%, 1.39%, and 1.93%, respectively, indicating a gradual and well-controlled growth in deformation demand. At the design-level excitation of 1.0 EQ, the maximum interstory drift remained below 1.0% (DBE) [39], satisfying the displacement-based design target adopted for this hybrid system. Moreover, even at 2.0 EQ, the maximum drift remained below the commonly accepted drift limit of 2.5%, confirming that the structure maintained adequate deformation capacity and lateral stiffness under increasing earthquake intensity [34,40].

3.3.3. Global Hysteretic Response

The overall seismic response of the analytical model is presented in Figure 16, which shows the hysteretic relationship between the base shear and roof displacement under various intensity levels of the ground motion. Under an input of 0.5 EQ, the response remained almost elastic, as indicated by the narrow hysteresis loops and minimal energy dissipation. When the excitation increased to 1.0 EQ, the loops began to widen, signaling the onset of nonlinear behavior and the activation of energy-dissipating mechanisms within the SBRBs and RC members.

As the input intensity rose further, the effects of stiffness degradation and enhanced energy dissipation capacity became increasingly apparent, as reflected in the progressive expansion of the loops. At 2.0 EQ, the maximum base shear reached 529 kN, and was accompanied by a roof displacement of 193 mm. Compared with the ultimate capacity obtained from the pushover analysis, where the base shear was 564 kN and the roof displacement was 250 mm, the response under 2.0 EQ indicated that the structure had not yet reached its full strength and ductility limits. The hysteretic behavior confirmed that the system maintained stable cyclic performance, achieving an equivalent ductility ratio of approximately 5.2, which exceeded the initial design expectation.

3.3.4. Response of the RC Wall Base

The flexural response of the RC wall base is presented in Figure 17, which shows the moment–interstory displacement relationship at the first floor. Under an input of 0.5 EQ, the wall base behaved elastically, exhibiting a nearly linear response throughout the loading duration. When the excitation increased to 1.0 EQ, a flexural hinge formed at the base of the wall, marking the onset of nonlinear behavior.

As the ground-motion intensity rose, the wall experienced a steady increase in plastic deformation; the hysteresis loops show progressive expansion, indicating the development of a stable inelastic flexural mechanism. At higher excitation levels, the loops become broader and more consistent, confirming that the RC wall base underwent controlled plastic rotation while maintaining its load-carrying capacity. This response reflects the intended nonlinear mechanism of the hybrid structural system, in which the RC wall provides the dominant flexural resistance and significantly contributes to energy dissipation under strong seismic excitation.

3.3.5. Response of the RC Coupling Beam

Figure 18 shows the flexural response of the RC coupling beams, representing the relationship between the beam-end moment and the interstory displacement at the second floor (2FL), fourth floor (4FL), and roof level (RFL).

Of these, the 4FL coupling beam was the first to exhibit nonlinear behavior; once yielding occurred, its plastic deformation became more pronounced, making it the primary focus of analysis. Under an input of 0.5 EQ, the 4FL beam began to show slight yielding, while at higher excitation levels, the extent of inelastic deformation gradually increased. At a value of 2.0 EQ, the hysteresis loops significantly expanded, forming a distinct energy-dissipation area that represents stable cyclic plasticity. In contrast, the 2FL and RFL coupling beams displayed smaller plastic responses, indicating that the flexural demand in these regions was less critical compared with the mid-height coupling beam. This observation is consistent with the prior study conducted by Jafari et al. [41], which reported that the damage indices for RC coupling beams tend to peak at mid-story levels. This distribution of nonlinear behavior suggests that energy dissipation within the hybrid system was concentrated at intermediate stories, where the bending moments and deformation demand were greatest.

3.3.6. Axial Response of SBRBs

The axial response of the SBRBs provides valuable insight into how the hybrid structural system accommodated seismic deformation through controlled yielding mechanisms. Of all the levels of the building, the third-floor level (3FL) brace exhibited the most pronounced nonlinear behavior, corresponding to the largest interstory displacement observed in the structure. At an intensity of 1.0 EQ, the maximum core deformation reached approximately 8 mm, corresponding to a strain of about 0.3%, indicating the onset of mild yielding within the core. As the excitation increased to 1.5 EQ, the deformation rose to 14 mm, equivalent to a strain of about 0.5%, reflecting a progressive expansion of the plastic region and stable hysteretic energy dissipation. Under an input of 2.0 EQ, the maximum deformation increased further to 23 mm, corresponding to a strain of about 0.9%, which remained well below the maximum core strain limit of 2.5% specified for buckling-restrained braces in ASCE/SEI 41-17 [36], confirming that the brace cores operated within the allowable deformation range even under severe excitation. These results confirm that the braces functioned effectively within their intended performance range, providing reliable lateral stiffness and energy dissipation without excessive strain accumulation or strength degradation. The corresponding axial force–core deformation relationships for the SBRBs at the different floor levels are shown in Figure 19.

3.3.7. Cumulative Ductility Capacity of SBRBs

The cumulative ductility capacity of the SBRBs provides an important measure of their ability to sustain repeated inelastic cycles without loss of strength or fracture. The results for the cumulative ductility capacities obtained from the nonlinear analysis are shown in Figure 20. At the design-level excitation of 1.0 EQ, the cumulative ductility demands at all floor levels remained below the maximum plastic deformation limit of 10 specified for buckling-restrained braces in ASCE/SEI 41-17 [36]. These low cumulative ductility indices reflect the limited number of significant inelastic cycles imposed by the adopted ground-motion histories and therefore should not be interpreted as a limitation of brace capacity; brace fracture is not expected for the analyzed excitation sequences. In addition, the braces used in the present study have been previously investigated by Chou and Chen [31], who demonstrated that individual SBRBs can achieve cumulative ductility capacities exceeding 500 without fracture, indicating that the inherent deformation capacity of the SBRB itself far exceeds the minimum qualification requirement of 200 specified in ANSI/AISC 341-22 [42]. This cumulative ductility is associated with standardized individual component qualification protocols involving substantially larger numbers of inelastic cycles. The results show that braces were able to maintain stable cyclic behavior throughout the loading process while still satisfying requirements, thereby preventing premature brace failure during large inelastic deformation demands.

3.3.8. Torsional Response of the Structure

The values for the torsional rotation at each floor obtained from successive nonlinear analyses are shown in Figure 21. These results represent the rotational response about the vertical (Z) axis of the center of mass of each floor. The data indicate that the torsional demand progressively increases with the height of the building, reflecting the influence of the eccentric stiffness distribution between the RC core wall and the surrounding steel frame. At the second floor (2FL), the rotation angles under 0.5 EQ, 1.0 EQ, 1.5 EQ, and 2.0 EQ were approximately 0.002, 0.003, 0.004, and 0.005 rad, respectively. At the roof level (RFL), the corresponding values rose to 0.018, 0.025, 0.035, and 0.044 rad, representing a clear amplification of torsional rotation toward the upper stories. This trend demonstrates a nearly linear amplification of torsional deformation toward the upper stories, with the maximum demand concentrated at the roof, where the combined effects of global drift and stiffness asymmetry are most pronounced.

From a damage and design perspective, the amplified torsional response at higher intensity levels implies increased differential deformation demands in coupled wall segments and coupling beams. At elevated excitation levels, the interaction between torsional rotation and lateral drift is expected to intensify cracking and potential spalling in wall boundary regions, while increasing chord rotation demands in coupling beams. The results highlight the importance of adequate confinement detailing in wall boundary elements and sufficient rotational capacity in coupling beams to accommodate combined flexural–torsional demands.

The findings further demonstrate the role of the SBRB configuration in mitigating torsional effects by redistributing lateral stiffness and reducing torsional imbalance induced by the eccentric core wall. For the design of similar hybrid steel–RC buildings, these results underscore the need for an appropriate stiffness balance between the wall system and surrounding steel frames, as well as careful consideration of brace layout and symmetry. Explicit evaluation of torsional response at the system level is therefore essential for ensuring reliable seismic performance and informing effective detailing strategies in wall-dominated hybrid structures.

3.3.9. Distribution of Story Shear at the Base

The shear distribution at the first floor (1FL) provides important insight into how the components of the hybrid system are mobilized under increasing seismic intensity. The corresponding shear distributions at 1FL obtained from the nonlinear analyses are shown in Figure 22. At this level, the total story shear is resisted by four H-shaped steel columns, one set of SBRBs, and the RC wall, with the RC wall carrying the largest share. In the elastic stage represented by 0.5 EQ, the RC wall resisted approximately 72% of the total story shear, the SBRBs contributed about 22%, and the steel columns accounted for roughly 6%, values that are closely aligned with the initial design assumptions.

As the earthquake intensity increased and the RC wall reached its yield strength, its contribution gradually decreased, while that of the steel components increased. At 2.0 EQ, the RC wall carried around 60% of the total story shear, the SBRB contributed 24%, and the proportion borne by the steel columns increased to 16%. This redistribution of shear demand demonstrates the progressive participation of the steel framing elements as the RC wall transitioned into the inelastic range, enhancing the ductility and overall energy dissipation capacity of the hybrid system.

3.4. Model Verification

To assess the credibility of the adopted numerical modeling assumptions, a parameter-level verification was conducted by benchmarking key component models and selected global response characteristics against published experimental evidence and previously reported studies. This verification was intended to confirm that the numerical parameters used in the analytical model are consistent with experimentally validated behaviors at both the component and system levels. A summary of the component-level and system-level verification benchmarks is provided in

Table 5. Parameter-level and system-level verification of the adopted numerical model.

Component	Parameter	Adopted in This Study	Typical Experimental/ Reported Range	References	Verification
SBRB	Yield force	140 kN	Specimen-dependent; comparable SBRB tests	[31]	Consistent
	Yield displacement	4.9 mm	Elastic–plastic transition range	[31]	Consistent
	Post-yield strength ratio	1.5	≥1.4 (compressive-to-tensile load ratio)	[31]	Consistent
	Maximum axial strain capacity	Not exceeded in analyses	2.1–2.6% sustained without fracture	[31]	Consistent
	Hysteretic behavior	Stable, symmetric, isotropic	Stable, symmetrical hysteresis	[31]	Consistent
Coupling beam	Hinge formulation	Moment–rotation hinge with Takeda hysteresis	RC coupling-beam cyclic hinge models	[33]	Consistent
	Plastic rotation (IO)	0.003 rad	Capacity up to 0.035 rad	[33]	Conservative
	Plastic rotation (LS)	0.012 rad	Capacity up to 0.035 rad	[33]	Conservative
	Plastic rotation (CP)	0.015 rad	Capacity up to 0.035 rad	[33]	Conservative
	Cyclic Response characterization	Takeda-type degradation	Stable cyclic behavior reported	[33]	Consistent
Global system	Fundamental period (T1)	0.626 s	0.93 s (RC wall system validated by hybrid testing)	[43]	Same order of magnitude
	Story shear distribution	Concentrated at lower stories, decreasing with height	Similar lower-story shear concentration observed	[43]	Consistent trend

, which consolidates the adopted numerical parameters, corresponding experimental or literature-based reference values, and the resulting verification outcomes.

For the SBRBs, verification was performed by comparing the adopted backbone and hysteretic parameters with available experimental results. The SBRB model adopted a symmetric bilinear backbone with a yield force of 140 kN, a yield displacement of 4.9 mm, and a post-yield strength ratio of 1.5, together with isotropic hysteretic behavior. These modeling choices are consistent with the experimental observations reported by Chou and Chen [31], in which full-scale SBRBs exhibited stable and symmetric hysteretic responses under axial strains of approximately 2.1–2.6%, cumulative ductility demands on the order of 20, and maximum compressive-to-tensile load ratios exceeding 1.4, without strength degradation or fracture. The close correspondence between the adopted numerical parameters and these experimentally validated response characteristics supports the suitability of the SBRB model for representing stable inelastic behavior under the seismic demand levels considered in this study.

For the coupling beams, parameter-level verification was conducted by benchmarking the adopted nonlinear hinge properties against published experimental and analytical evidence. The coupling beams were modeled using a moment–rotation hinge formulation with Takeda hysteresis, which is widely used to represent reinforced concrete members under cyclic loading. The plastic rotation limits embedded in the hinge definition were 0.003 rad for Immediate Occupancy, 0.012 rad for Life Safety, and 0.015 rad for Collapse Prevention. Experimental results reported by Jafari et al. [33] indicate that reinforced concrete coupling beams can sustain chord rotations of up to approximately 3.5% (0.035 rad) while maintaining stable cyclic behavior. Accordingly, the adopted hinge limits are conservative relative to reported coupling-beam rotation capacities, supporting the suitability of the coupling-beam model for the seismic demand levels considered in this study.

At the global system level, verification was performed by benchmarking the fundamental dynamic characteristics and force distribution patterns of the present hybrid steel–RC coupled wall model against published hybrid testing results for reinforced concrete structures of comparable height. The modal analysis yielded a fundamental period of 0.626 s, which is of the same order of magnitude as the fundamental period of 0.93 s reported by Hsiao et al. [43] for a multi-story RC wall structure validated through large-scale shaking-table testing and hybrid simulation. Although differences in structural configuration, material composition, and mass distribution exist between the two systems, this comparison indicates that the modeled global stiffness and inertia representation are reasonable. In addition, the nonlinear analyses show that maximum story shear demands are concentrated in the lower stories and progressively decrease toward the upper levels, a trend that is qualitatively consistent with the system-level response observed by Hsiao et al. [43]. This trend-based agreement supports the plausibility of the predicted global force distribution and indicates that the numerical model captures the dominant system-level seismic response characteristics without exhibiting unrealistic stiffness or force concentration artifacts.

4. Limitations of the Numerical Model and Future Experimental Work

Table 6. Comparison between simulated structural response demands and allowable acceptance criteria for the proposed hybrid structural system.

Parameter	Demand				Allowable Criteria
	0.5 EQ	1.0 EQ	1.5 EQ	2.0 EQ
Maximum interstory drift (3FL)	0.45%	0.87%	1.39%	1.93%	≤2.5% [34] ≤2.5% (Category I and II) [40]
Wall base rotation/curvature	Not explicitly extracted				Acceptance inferred from ASCE-41/TEASPA hinge definitions
Coupling beam chord rotation	Not explicitly extracted				Hinge limits adopted from literature/ASCE-41
SBRB core axial strain (3FL)	<0.3%	0.3%	0.5%	0.9%	≤2.5% [36]
Cumulative ductility index		<10			≤10 (Life safety category) [36] single BRB test

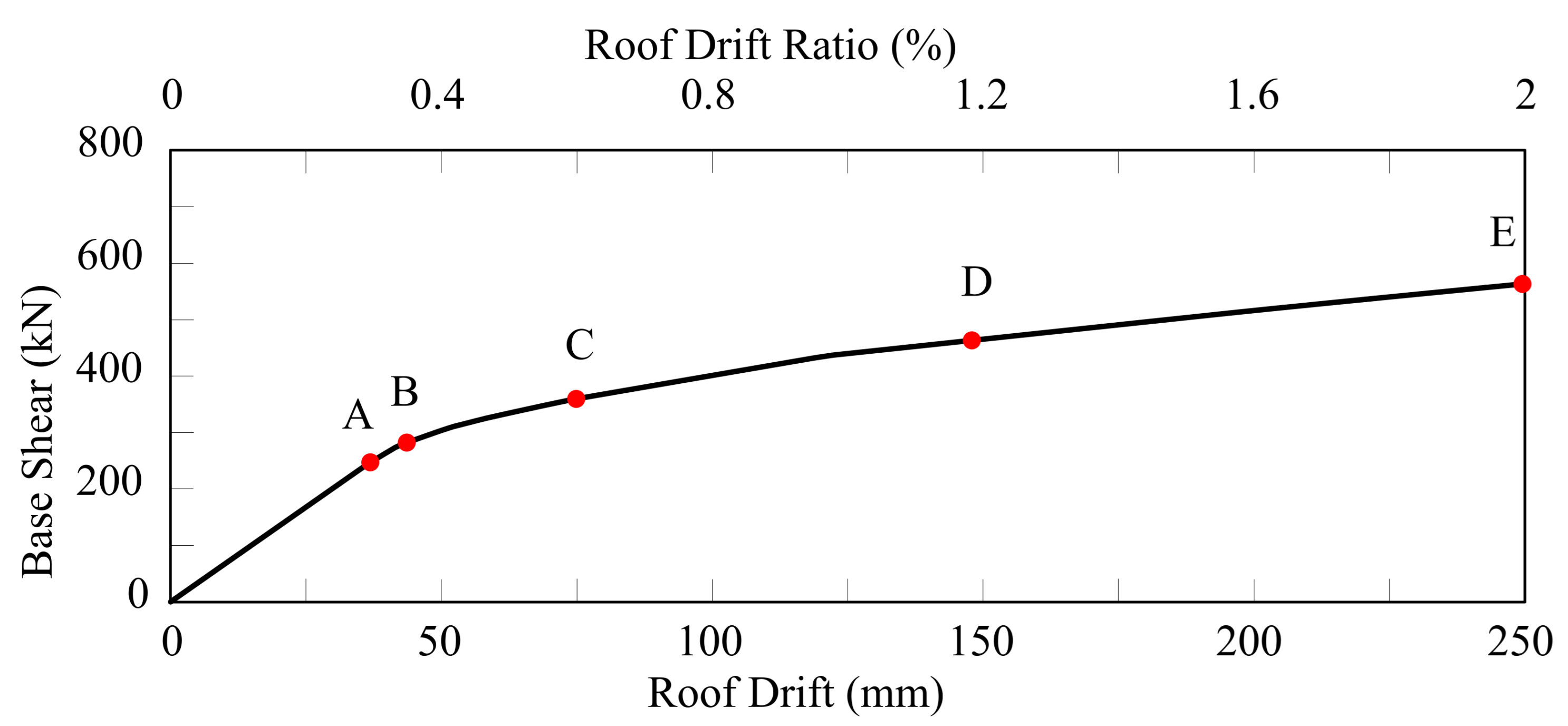
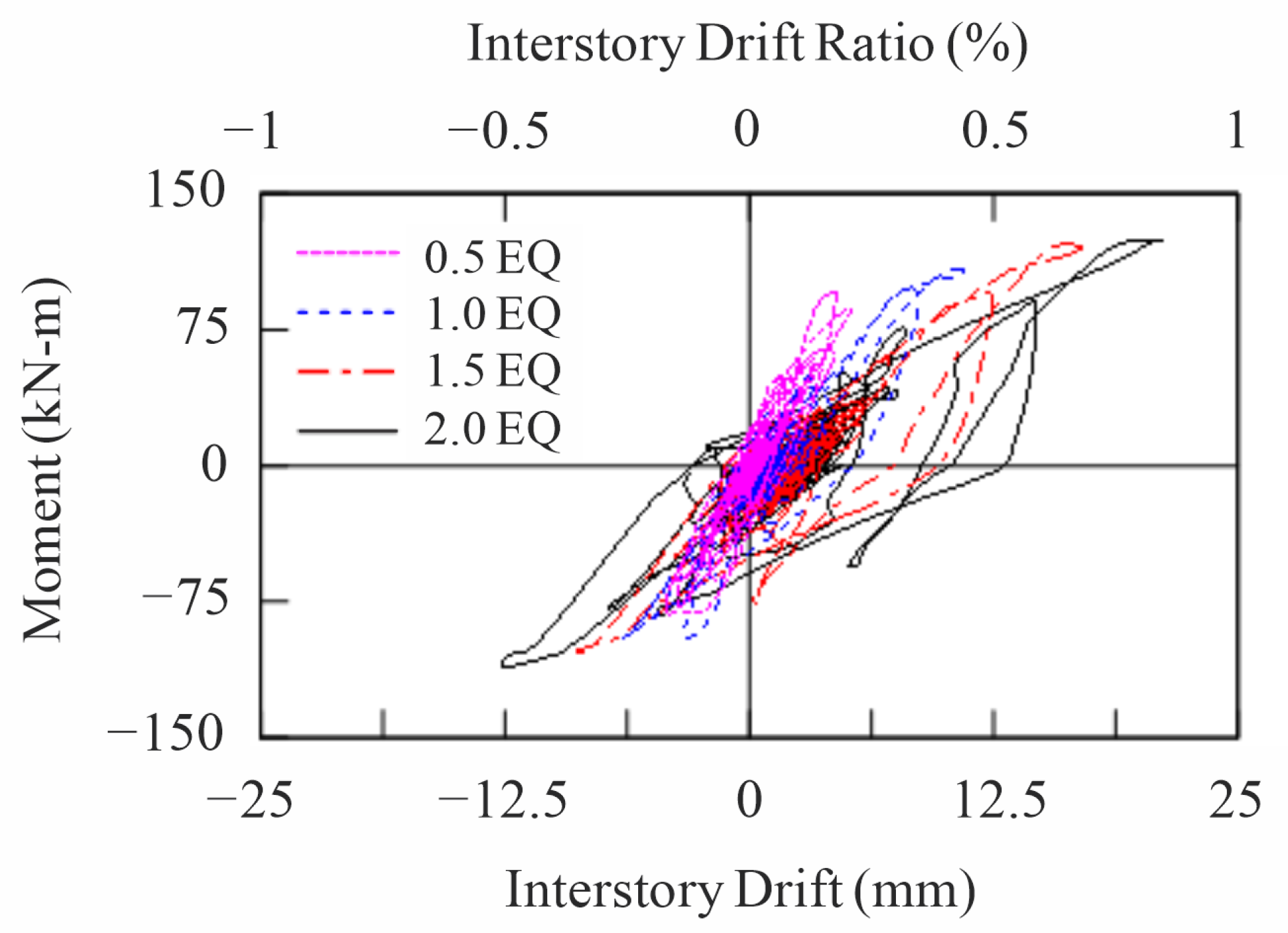
Note: Global response measures were verified directly from the numerical outputs; local component acceptance for the RC wall base and coupling beams was ensured through calibrated nonlinear hinge definitions, as explicit rotation or curvature demands were not extracted in the present scope.

presents a comparison between the numerical results and the corresponding allowable acceptance criteria specified in relevant design standards, providing a concise verification of the overall performance of the proposed hybrid structural system. While the analytical model captures the dominant global response characteristics and force-sharing mechanisms of the building, several simplifying assumptions were adopted to maintain computational efficiency and focus on system-level behavior.

Despite the satisfactory agreement with acceptance criteria shown in Table 6, the RC walls were idealized using an equivalent wide-column representation, which may lead to localized underestimation or overestimation of stiffness and deformation demands, especially near regions of stress concentration. The use of a reduced number of nonlinear hinges, concentrated at predefined critical locations, limits the ability of the model to fully represent the spread of plasticity along members under severe seismic excitation. Panel zones and beam–column joints were modeled using simplified rotational springs, and the floor slabs were assumed to behave as rigid or very stiff diaphragms; these assumptions may influence the predicted torsional response and the distribution of interstory drift, particularly in configurations with asymmetric stiffness. Consequently, the sensitivity of drift demand and torsional behavior to joint stiffness and diaphragm flexibility is not explicitly resolved in the present numerical framework. These limitations highlight the need for complementary experimental investigation to validate the modeling assumptions and to capture local deformation mechanisms that are not fully represented in the analytical model.

A large-scale shaking table program will be undertaken at the NCREE Tainan Laboratory, Taiwan. This program has been designed to capture both the global and local response mechanisms of the hybrid steel–RC coupled wall structure when subjected to design-level excitations with strong motion. A total of 42 ground motion simulations will be performed. The input motions, derived from recorded earthquake data, will be carefully scaled to match the design response spectrum over the target period range of 0.4 to 1.0 s, corresponding to the fundamental vibration modes of the structure. The baseline design intensity is a ground motion characterized by a peak ground velocity (PGV) of 40 cm/s and a peak ground acceleration of 0.4 g. The selection criteria for the applied ground motion are based on two primary considerations: (i) the scaled peak ground acceleration, velocity, and displacement must remain within the operational capacity of the shaking table, and (ii) the spectral displacement should increase proportionally with the period, within the designated range of interest. Based on these requirements, the 1940 El Centro, California, earthquake record has been chosen as the principal input motion for most test sequences, complemented by three additional records representing different spectral characteristics. To explore varying levels of seismic demand, the amplitude of each motion will be scaled to intensity levels ranging from 25% to 150%, in 25% increments.

The experimental program will use the long-stroke, high-velocity earthquake simulator housed at the NCREE Tainan Laboratory, as shown in Figure 23. This advanced facility features an 8 × 8 m shaking table with a 250-ton payload capacity, and is capable of generating three-dimensional broadband ground motions with high accuracy and control. The system can achieve horizontal and vertical strokes of ±1.0 and ±0.4 m, maximum velocities of 2 and 1 m/s, and peak accelerations of up to ±2.5 g horizontally and ±3.0 g vertically. These capabilities enable the realistic reproduction of design-level seismic demand, including both high-frequency acceleration pulses and long-period displacement components, thus ensuring that the structure experiences loading conditions consistent with those assumed in the numerical analyses.

For the experimental specimen, a modular construction system will be adopted that was specifically developed to facilitate transportation, assembly, and lifting operations within the laboratory. As illustrated in Figure 24, this structure is divided into three detachable modules representing lower, middle, and upper segments, each of which is designed to represent a distinct structural zone while maintaining full continuity when assembled on the shaking table.

This modular approach allows the specimen to be transported efficiently from the fabrication area to the test platform, and then reassembled with precise alignment and minimal on-site adjustments. The modular joints are designed to ensure sufficient stiffness and continuity, thereby reproducing the intended global behavior while also simplifying the handling process during setup. Furthermore, this configuration offers the potential for reuse of the individual modules in future experimental phases, such as parametric studies or retrofit investigations, thus significantly improving research efficiency and resource utilization.

To ensure a comprehensive evaluation of the structural response, a detailed instrumentation system will be distributed across the specimen. Five accelerometers, as shown in Figure 25, will be installed at each floor to capture both translational and rotational accelerations during shaking. These sensors will provide essential data for evaluations of the floor accelerations, interstory drift ratios, and dynamic amplification effects, which together describe the global seismic behavior of the hybrid structural system. In addition to the conventional accelerometers, a motion capture (MoCap) system will be incorporated to record the three-dimensional displacement field and torsional rotations with high precision. This enhanced instrumentation strategy will also enable direct measurement of critical local deformation parameters that were not explicitly resolved in the numerical analysis, including wall base curvature or rotation and coupling beam chord rotation, which are essential for detailed component-level performance assessment. This system will allow for continuous tracking of the absolute motion at critical points across the structure, offering an accurate visualization of its dynamic deformation patterns and enabling detailed comparison with analytical predictions.

The motion capture (MoCap) system will play an important role in achieving a detailed and reliable understanding of the dynamic behavior of the system. The overall configuration of the infrared cameras and marker layout that has been designed to achieve this objective is illustrated in Figure 26 and Figure 27.

Multiple infrared cameras will be used in conjunction with reflective markers mounted at key structural locations, such as the floor slabs, wall surfaces, and beam–column junctions. This arrangement will allow for continuous tracking of the three-dimensional displacements and rotations with high spatial accuracy, thus providing direct measurements of the structure’s absolute motion under seismic excitation. The data obtained from this system will be synchronized with accelerometer records to reconstruct the complete dynamic response of the structure, which will enable precise assessments of the modes of deformation, torsional effects, and overall stability. Capture of the full-field motion without physical contact will minimize measurement interference and significantly improve the fidelity of the experimental results.

The forthcoming shaking table experiment is expected to serve as an essential step in validating the numerical predictions presented in this study and advancing the current understanding of the seismic performance of the hybrid steel–RC wall system. The experimental results will enable a direct comparison between the analytical and measured responses, thus helping to verify the modeling assumptions and assess the accuracy of the nonlinear simulation techniques. In addition to confirming the predicted global response, this test will also provide valuable insight into the mechanisms governing energy dissipation, torsional interaction, and deformation concentration within the coupled wall and frame components. These findings are expected to deepen the understanding of how hybrid systems respond under strong earthquake excitations and to support the refinement of design parameters related to strength, ductility, and stiffness balance. Ultimately, the experiment will contribute to the development of more reliable performance-based seismic design methodologies and will promote the broader practical implementation of hybrid structural systems in regions of high seismic risk.

5. Conclusions

In this study, advanced numerical simulations were combined with experimental planning in order to evaluate the seismic performance of a hybrid structural steel–RC coupled wall system. An analytical investigation clarified the fundamental response characteristics of the system and confirmed its potential to achieve high strength, ductility, and stable energy dissipation. Preliminary analyses of the prototype structure designed for testing at the NCREE in Tainan suggest that seismic design for hybrid systems can be streamlined into three essential steps: (i) controlling drift through period regulation; (ii) verifying base shear strength using mechanism-based or nonlinear static analysis; and (iii) detailing structural elements to ensure adequate ductility. These principles provide a clear framework for developing hybrid structures with a balance between strength, stiffness, and deformability. A forthcoming large-scale shaking table test at NCREE will further validate these findings and provide full-scale insight into the dynamic behavior of the proposed system. The main conclusions of this work are as follows:

• The hybrid steel–RC wall system effectively combines the stiffness and strength of RC with the ductility of steel framing, resulting in balanced lateral resistance and improved seismic resilience.
• A modal analysis confirmed that the first three vibration modes captured most of the structural mass, with noticeable torsional participation due to the asymmetric stiffness distribution between the RC wall and the steel frame.
• Pushover analysis confirmed a stable and well-distributed inelastic mechanism, with initial yielding at a roof displacement of about 37 mm and an ultimate displacement of approximately 250 mm, corresponding to a global ductility ratio of about 6.7, which exceeds the design target while maintaining interstory drift within code limits.
• Time-history results indicate a progressive and well-controlled deformation response, with peak interstory drift ratios of about 0.87% at the design-level excitation (1.0 EQ), increasing gradually to approximately 1.93% at 2.0 EQ, and remaining within commonly accepted drift limits under all considered seismic intensities.
• The RC wall base exhibited controlled flexural yielding, while the coupling beams and SBRBs provided complementary energy-dissipating mechanisms that ensured sustained strength and stiffness during cyclic loading.
• Torsional rotation increased nearly linearly with height, rising from approximately 0.002–0.005 rad at the second floor to about 0.044 rad at the roof under 2.0 EQ, while the increased shear transfer from the RC wall to the surrounding steel frame at higher intensities highlighted the redundancy and adaptability of the hybrid structural system.
• Even in torsionally irregular configurations, the seismic displacements and story drift ratios varied almost linearly with intensity in ductile systems exhibiting stable hysteresis, indicating that linear analysis may be sufficient for drift control at the design stage.
• First-floor shear demand was progressively redistributed, with the RC wall contribution decreasing from about 72% at 0.5 EQ to 60% at 2.0 EQ, while steel components increased their share—SBRBs from approximately 22% to 24% and steel columns from 6% to 16%—demonstrating effective force sharing and ductile system behavior.
• The analytical findings offer practical design insights for hybrid steel–RC systems, showing that distributed yielding is achieved when the RC wall governs lateral resistance at low demand while steel components progressively engage at higher intensities, with inelastic action concentrated in SBRBs and coupling beams. Drift and torsion can be controlled by minimizing stiffness eccentricity and using symmetric brace layouts.