Abstract
The multiphase induction motor is considered to be the promising alternative to the conventional three-phase induction motor, especially in safety-critical applications because of its inherent fault-tolerant feature. Therefore, the attention of many researchers has been paid to develop different techniques for detecting various fault types of multiphase induction motors, to securely switch the control mode of the multiphase drive system to its post-fault operation mode. Therefore, several fault detection methods have been researched and adapted; one of these methods is the indices-based fault detection technique. This technique was firstly introduced to detect open-phase fault of multiphase induction motors. The main advantage of this technique is that its mathematical formulation is straightforward and can easily be understood and implemented. In this paper, the study of the indices-based fault detection technique has been extended to test its applicability in detecting some other stator and rotor fault types of multiphase induction motors, namely, open-phase, open-switch, bad connection and broken rotor bar faults. Experimental and simulation validations of this technique are also introduced using a 1 kW prototype symmetrical six-phase induction motor.
1. Introduction
The technological progress made in power converters and semiconductor switches helps in growing the interest in studying multiphase-based drive systems. Multiphase machine drives present several advantages over the conventional three-phase ones. Some of these advantages are lower torque pulsation with higher frequency, less DC-link current harmonics, and lower power per phase [1]. Since the motor input power is divided into a larger number of phases, the stator power per phase is reduced, leading to a reduction in the current and voltage ratings of the semiconductor switches. This will remove the need for connecting the switches in series or in parallel to achieve the required voltage or current ratings. However, the most important advantage is their higher reliability and fault-tolerant feature. In particular, if one stator phase is lost in a three-phase machine, it cannot be started and run. However, in multiphase machine case, it can continue running with (n − 3) disconnected phases with some reconfigurations to the control scheme to operate in a post-fault mode.
There are many fault types that may occur in induction motor drive systems, and they are categorized into two main categories: motor faults and converter faults [2]. Motor faults might be classified as electrical and mechanical faults. The electrical faults could be a short-circuited phase, an open-phase fault, inter-turn short circuit and broken rotor bar. Some examples of the motor mechanical faults could be bearing damage and rotor eccentricity, whereas main converter faults are switch short-circuit and open-circuit faults.
Among the various types of faults, the open-phase and open switch faults are the most investigated faults, because the protection against short-circuited phase or switch is a standard protection which should be inherently provided [3]. The three main stages of any multiphase motor fault-tolerant drive are fault detection and localization, isolation of the faulted part, and switching the control to the post-fault operation mode. As can be seen, the fault detection and localization is the first necessary step of a fault-tolerant drive, so that, many researchers have investigated different fault detection techniques aiming to reach a simple, fast and robust technique. In [4], the symmetrical components theory has been used to detect open-phase faults of a five-phase permanent magnet synchronous reluctance motor; the magnitudes and phase angles of the phase currents’ symmetrical components were analyzed under different open-phase faults and used to calculate two indices for the detection scheme. Other diagnostic indices for open circuit faults of a three-phase voltage source inverters were derived in [5] based on the errors between the average absolute values of the normalized phase currents under healthy and open-phase fault conditions. Similarly, the average values of the errors between the three-phase currents and their corresponding reference values were used as the diagnostic variables [6]. The derivative of the Park’s vector phase was chosen to be the open-phase fault detection variable in [7]. Adaptive and observer-based fault detection methods are proposed in [8,9] for detecting open-switch and open-phase faults. Despite the advantages of most of the above-mentioned fault detection techniques, they have some problems; such as a relatively low detection speed, more sophisticated algorithms and the dependency on parameter variations which may lead to false fault alarms.
A proposed idea of a passive or natural fault tolerance has been presented in [10,11,12,13]. It is demonstrated that it is possible to develop a drive control algorithm which should not be re-configured after a fault occurs (i.e., the current reference values will be automatically adjusted in the post-fault operation mode). Therefore, the fault detection and localization may not be necessary. However, as stated before, fault detection and localization is an important and necessary step even for the troubleshooting and maintenance of the multi-phase induction motor drives.
Recently, neural networks algorithms have been introduced to the fault diagnosis of induction and synchronous motors [14,15,16,17,18]. A neural network is considered as a classifier which is able to classify different faults through a well-trained network. The most popular structure of the neural networks is the multilayer perceptron (MLP) neural network [19,20]. The back propagation training algorithm is one of the most effective training algorithms; it is simple, easy to implement, and does not need parameter adjustment except some inputs.
In [21,22,23,24], open-phase fault indices have been derived based on the vector space decomposition (VSD) variables of five-phase and six-phase induction motors. The Clarke’s transformation matrix of phase currents is used to define the fault indices in the case of open-phase faults for each phase. Therefore, there are five indices in the five-phase machine case and six indices in the six-phase machine case. Various variations of open-phase faults (one-phase, two adjacent phases and two non-adjacent phases fault) under different operating conditions are tested, and it is proved through simulation and experimental results that a robust and fast detection performance can be achieved either in open-loop or closed-loop drive control.
The recognition that this fault detection technique could be used to detect various types of faults is necessary to widen its applicability and make use of its simplicity, reliability and robustness. Therefore, in this paper, the application of the indices-based fault detection technique is extended to detect other various faults such as open-switch, bad connection, and broken rotor bar faults. Some modifications are proposed to adapt the fault detection technique to be able to detect other faults rather than standard open-phase fault. Additionally, experimental results are introduced to validate the proposed detection technique.
The rest of the paper is organized as follows: Section 2 presents the mathematical modeling of the six-phase induction motor, whereas Section 3 introduces the mathematical formulation of the indices-based fault detection technique. In Section 4, an explanation of the application of indices-based fault detection technique to various faults along with the proposed modifications is presented. Section 5 shows the experimental and simulation results of this study, and the conclusion is drawn in Section 6.
2. Six-Phase Induction Motor Model
The stator windings of the six-phase induction motor might be considered to be constructed from two three-phase windings (a1b1c1 and a2b2c2) and it could be built in one of three configurations, namely, symmetrical, asymmetrical and dual configuration. In a symmetrical motor, the spatial displacement (g) between the two three-phase windings equals 60°, whereas in an asymmetrical motor this spatial displacement is 30° and the spatial displacement in a dual three-phase motor is 0°.
Figure 1 shows the schematic diagram of the six-phase symmetrical induction motor drive, where S1 to S12 are the power switches of the inverter and each switch has its own antiparallel diode. Additionally, Va1, Vb1, Vc1, Va2, Vb2, and Vc2 are the phase voltages of the six-phase induction motor, whereas Vdc is the DC link voltage. The vector space decomposition (VSD) technique is applied here for the case of six-phase induction motor in order to perform a co-ordinate transformation from the physical a1b1c1-a2b2c2 reference frame to an arbitrary reference frame. The machine will have six sequence components in the new reference frame, namely α-β, x-y, and 0+-0−. Since the air-gap flux is assumed sinusoidally distributed, the α-β components are completely decoupled from the x-y components, also there is no stator-rotor coupling in the x-y subspace [25]. Additionally, since the two neutrals of the six-phase motor are isolated, the 0+-0− current components are zero and will not be present in the further analysis. In order to develop a model for the six-phase induction motor, the following usual assumptions are made; the air-gap is uniform and the flux is sinusoidally distributed around the air-gap, and magnetic saturation and core losses are neglected.
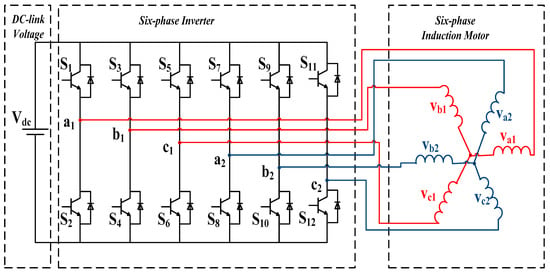
Figure 1.
Six-phase induction motor drive.
The generalized Clarke’s coordinate transformation matrix used to transform the machine stator variables from the physical a1b1c1-a2b2c2 reference frame into an arbitrary reference frame is [26],
where a = 2π/3 and g is the spatial displacement between the two three-phase stator winding sets. The machine equations represented in the VSD variables are as follows:
where and . Additionally,, , and are the stator voltages, , , and are the stator currents, and and are the rotor currents. Furthermore, and are the stator and rotor resistances, respectively, whereas is the stator self-inductance and is the stator leakage inductance, is the rotor self-inductance, is the mutual inductance, and is the stator inductance for the x-y subspace. Finally, is the electromagnetic torque, is the rotor electrical speed, and is the number of pole pairs.
3. Indices-Based Fault Detection Technique
The indices-based fault detection technique described here is the same as that elaborated in [21,22,23,24]. Each index is calculated by applying the inverse of the Clarke’s transformation matrix (1) and setting the corresponding open-phase current to zero. For example, if there is an open-phase fault in phase a1, then the phase current of that phase will be zero (iα1 = 0). Hence, by applying this condition to the first row of the inverse of the Clarke’s transformation matrix (1), the result that will be found. This result could be used to define the following ratio,
This ratio equals to one whenever there is an open-phase fault in phase a1, and it equals to zero in the healthy condition as ix is zero in this condition. By following the same approach to the other phases, the following indices can be found.
Each subscript of the above indices is used to indicate an open-phase fault in its corresponding phase. Furthermore, some more stages are required to filter out and perform a signal conditioning to the indices, as indicated in the flowchart of Figure 2. These signal conditioning stages are described below.
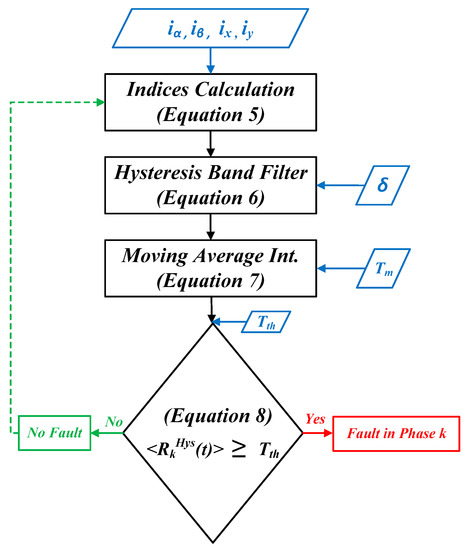
Figure 2.
Flowchart of the indices-based fault detection technique.
3.1. Hysteresis Band Filtering
All the indices will be subjected to a hysteresis band to filter out the noise. The hysteresis band filter is defined as follows.
where is the index resulted from the hysteresis filter and is the band of the hysteresis filter. The value of should be chosen to ensure low ripples in the indices; a typical value of 0.1 could be used to achieve a good filtering of noise (see Section 5).
3.2. Moving Average Integration
The second stage in the signal conditioning of the obtained indices is to apply a moving average integration as below.
where is the period of the moving average which should not be the same as the fundamental period . Moreover, the selection of the value is a tradeoff selection between the indices ripples and the detection speed. That is, the lower the value, the higher the indices ripples will be, nevertheless, the fault detection will be faster, and vice versa.
3.3. Comparison to A Threshold Value
This is the last stage in the indices signal conditioning, in which, each index will be compared to a threshold value to prevent false fault detection and ensure a real fault case. The mathematical formulation of this stage is as follows.
As can be seen from the above discussion, the indices-based fault detection technique has a fast detection response due to its simplicity, and it consumes low computation power as the α-β and x-y current components are already calculated to be used in the drive control, and no added input variables are required. Additionally, the fault indices are calculated based on the normalized x-y currents, so the dependency of the technique on the motor operating conditions does not exist.
4. Application of the Indices-Based Fault Detection Technique to Various Faults
In this section, the indices-based fault detection technique was tested against various types of stator and rotor faults in order to determine its applicability in detecting these faults. The fault indices in (5) were used after applying the signal conditioning stages described in the last section to detect the open-phase fault. Next, this technique was applied to detect an open-switch fault, a bad connection fault, and a broken rotor bar fault.
4.1. Open-Switch Fault
Open-circuit faults could be an open-phase fault (OPF) or an open-switch fault (OSF). Moreover, open-switch fault could be open-upper switch fault (OUSF) or open-lower switch fault (OLSF). Figure 3a shows the OPF phase current. In OUSF case, the upper switch has an open-circuit fault and the negative half cycle of the phase current flows through the lower switch, while the positive half cycles is clipped, see Figure 3b. Whereas, in OLSF case, the lower switch is open-circuited; thus, the phase current flows through the upper switch, and the negative half cycles of the current is clipped, see Figure 3c. Note, also, that if there is an open-circuit fault in both upper and lower switches, this situation could be considered to be the same as the OPF.
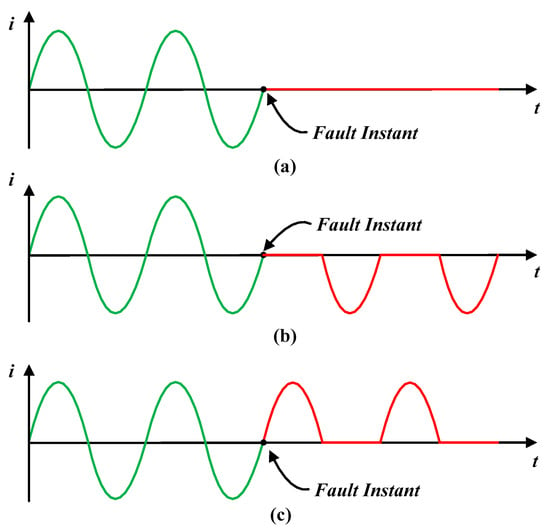
Figure 3.
(a) OPF or OSF with both upper and lower faulted switches phase current; (b) OUSF phase current; and (c) OLSF phase current.
In [23], the procedure which was described in the previous section is used to detect an OSF. Since an OSF has a zero-phase current during one half-cycle, OSF could be considered to be the same as OPF during that half-cycle. Thus, it is concluded that this procedure could be applied without any modification to detect an OSF.
However, there are two important points which could be discussed in this conclusion. First, using indices-based fault detection technique without any modification does not differentiate between the OPF and OSF. That is, if for example, value was above its threshold value, this indicates that there is an open-circuit fault in phase a1 which could be an OPF, OUSF or OLSF. Second, in the case of an OSF, the fault localization feature of this technique does not exist. That is, there is nothing that could determine whether the OSF is in the upper switch or in the lower switch.
Therefore, to overcome these two drawbacks, an additional index is proposed. This index is simply the average value of the phase current. Actually, six average values of the six phase currents are required in addition to the six indices which are previously illustrated in (5). The average value of each phase current is calculated by
This average value is calculated over the fundamental period (one complete cycle). In the case of an open-circuit fault, there is no problem to wait one cycle to localize the fault because this period is too short to yield a considerable damage to any component in the drive system.
As an illustrative example, if value was above its threshold value, this indicates that there is an open-circuit fault in phase a1, and the average value of phase a1 current will be checked. If is positive (above zero), this means that there is an OLSF, and if is negative (below zero), this means that there is an OUSF. In addition, if is zero, this means that there is an OPF, see Equation (10). However, if there are both OUSF and OLSF, this modified fault detection technique could not differentiate this case from the case of an OPF, as, in these two cases, the phase current of the faulted phase is zero in both positive and negative half cycles.
Finally, the employment of this proposed index is a trade-off between the fault localization feature and the detection speed of this technique. Moreover, this added index affects the detection speed of the technique as one complete fundamental cycle is required to calculate the average values of the phase currents. However, as mentioned earlier, this small delay in open-circuit fault detection will not affect any of the drive system components.
4.2. Bad Connection Fault
Bad connection faults, also known as high-resistance connection, can cause a severe damage to the drive components if kept undetected and unrectified for a long period. A bad connection at any joint in the drive system leads to a localized high temperature at that joint, which causes a failure; this failure may be an open-circuit fault due to a complete disconnection of that joint because of melting, a short-circuit fault due to insulation deterioration because of the joint high temperature, or a voltage-unbalance due to the high voltage drop across that bad-connected joint.
Bad connection faults could be detected by some traditional ways such as visual inspection, resistance imbalance measurement, and infrared thermography. However, there are many other researched techniques which are based on the existence of the negative sequence current and zero sequence voltage, due to the voltage and current unbalance caused by the high-resistance connection [27].
It is proposed in this paper to apply the indices-based fault detection technique to detect the bad-connection fault. As described earlier, in the healthy case, all the indices have a zero value, but if there is an open-circuit fault in any phase, the index value of that phase will evolve until reaching a value of one. Thus, it could be concluded that the index value equals either zero in the healthy case or one in the open-circuit fault (complete phase disconnection situation). Furthermore, since the bad connection fault introduces a high resistance value in the faulted phase, so it could be considered that the bad connection fault leads to a partial phase disconnection situation. Therefore, the index of that faulted phase has a value between zero and one, and it depends on the severity of the bad connection fault.
In conclusion, the indices-based fault detection technique could be used to detect the bad connection fault. However, some attention should be paid to the indices threshold values in order to differentiate between the open-circuit fault and the bad-connection fault.
4.3. Broken Rotor Bar Fault
The broken-rotor bar (BRB) fault is one of the common rotor faults in induction motors; however, its percentage of occurrence is only 5% [28]. Since the consequences of the BRB fault could be a severe damage to the motor, the BRB fault should be detected early. The BRB failure could mainly occur due to thermal or mechanical stresses on the rotor. Starting a high-inertia mechanical load may lead to a rotor bar failure if there is a crack in the joint between the rotor bar and the end ring of the rotor cage. Additionally, the thermal stresses on the rotor at motor start-up could be a cause of a BRB failure. Furthermore, if there is a BRB fault in one bar, higher currents will flow in the adjacent bars which may result in more damage to the rotor [29].
If there is a BRB fault in one bar, a backward rotating magnetic field will appear at a frequency of (where the rotor slip and is the system frequency) due to the asymmetry of the rotor [30]. As a consequence, the stator current frequency spectrum is distorted because of the stator-current component, which appears due to the induced voltages in the stator from the backward rotating magnetic field. This distortion appears in the frequency spectrum of the stator current as side-band frequencies at (where, = 1, 2, 3…), and the magnitude of these side-bands increases with the broken bars number. Therefore, this information is used in the motor current signature analysis (MCSA) detection method to detect that there is a BRB fault in the motor.
In this paper, the indices-based fault detection technique is applied to a BRB fault to test its possibility of detecting this type of fault. Note that this fault type will be tested based on simulations while the test of the other fault types is based on experimentation. Hence, in order to model the BRB fault accurately, the phase-variable model of the six-phase induction motor, which can easily model the rotor bars and end-rings, is firstly introduced. In this model, the m-bar squirrel-cage rotor is modeled as m rotor loops, and each loop consists of two adjacent bars and the connecting portion of the end-ring between these two adjacent bars from both sides [31]. The equivalent circuit of the squirrel cage rotor is shown in Figure 4, where and are rotor bar resistance and self-inductance, respectively, whereas and are end-ring resistance and self-inductance, respectively, and is the rotor bar current.
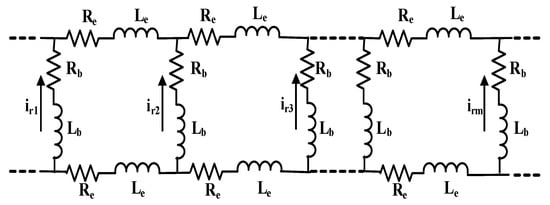
Figure 4.
Squirrel-cage rotor equivalent circuit.
The voltage equation of the stator winding in the matrix form is shown below.
where is the stator flux linkage matrix and is defined by:
where and are the stator phase voltages and currents, respectively, is the matrix of the rotor loop currents, and are the stator winding resistance and self-inductance matrices, respectively, and is the matrix of the mutual inductance between the stator phases and rotor loops.
The voltage equation of the rotor loops in the matrix form is defined as follows.
where is the rotor loop voltages which equals zero, as the rotor is short-circuited, and is the rotor flux linkage matrix and is calculated by:
where and are the rotor loop resistance and self-inductance matrices, respectively, and is the transpose of the matrix. Note that the inductance matrices are calculated based on the winding function approach as in [31].
Finally, the developed torque equation is calculated by:
where is the electrical angular displacement of the rotor. The mechanical equation is defined in (16).
where is the load torque, is the mechanical rotor speed, is the inertia, and is the friction coefficient.
Now, based on the previous discussion about the indices-based fault detection technique, it can be stated that stator current unbalance is the trigger for the indices to evolve and initiate a fault signal. Therefore, as the BRB fault does not introduce a significant unbalance in the stator current, the indices-based fault detection technique could not be adopted to detect this type of fault.
5. Experimental and Simulation Results
In this section, the experimental and simulation results of the various cases which have been discussed in this paper are described. An experimental setup was built to validate the proposed conclusions in the cases of the open-circuit (OPF and OSF) and the bad connection faults. The experimental setup was composed of a six-phase induction motor fed from a six-phase sinusoidal pulse-width modulated voltage source inverter with a 300 V programmable DC power supply. Additionally, a DSP controller (TMS320F28379D) along with some interface and signal-conditioning circuits was used to control the inverter. The electrical, mechanical, and geometrical parameters of the six-phase induction motor are listed in Table 1. The system prototype is given in Figure 5.

Table 1.
Symmetrical six-phase induction motor parameters.

Figure 5.
Experimental six-phase setup.
However, in the case of the BRB fault, MATLAB/SIMULINK was used to model and simulate the six-phase drive system along with the fault detection technique. Now, the results of each case are shown and investigated in the following sections.
5.1. Open-Phase Fault (OPF)
The experimental results of the OPF fault are presented in this section. In this test, the threshold value is determined based on the trial and error method and is set to 0.4, while the hysteresis band is adjusted to be 0.1. The moving average period is 20 percent the fundamental period (). The step time of the algorithm is 50 μsec. Figure 6 shows the phase current and the fault indices in the case of an open a1 fault. In order to indicate the changes in the fault indices, an open phase fault in a1 phase is introduced and cleared again as shown in Figure 6b. The a1 fault index rises as a consequence of the unbalance of the phase currents, whereas the remaining indices are close to zero.
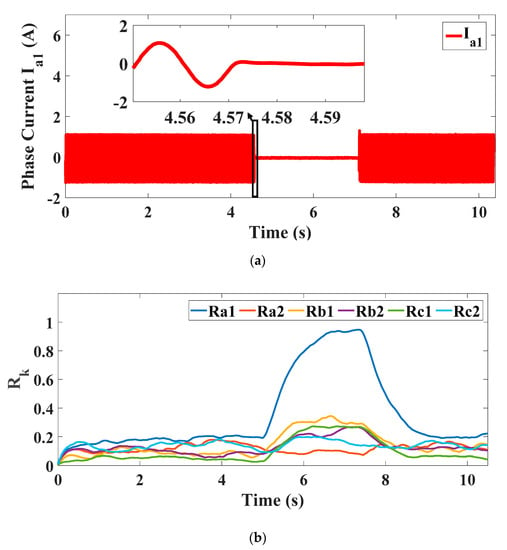
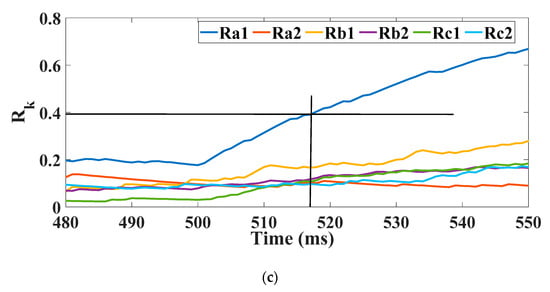
Figure 6.
OPF test: (a) Phase current (a1); (b) Fault indices; (c) Detection time (zoom in of the fault indices).
It is also shown in Figure 6c that the detection time is almost 17 msec; however, this value depends mainly on the threshold and the moving average period adjustments. For faster fault detection, lower threshold value and moving average period could be adjusted, but this will also increase the indices ripples.
Another test was performed to indicate the effect of varying the value of the moving average period . Figure 7 shows the index at three different values of the moving average period ; when and . Faster fault detection is observed at = 0.2 but the index ripples are higher. Whereas lower index ripples are noticed at = but the detection speed is also lower in this case.
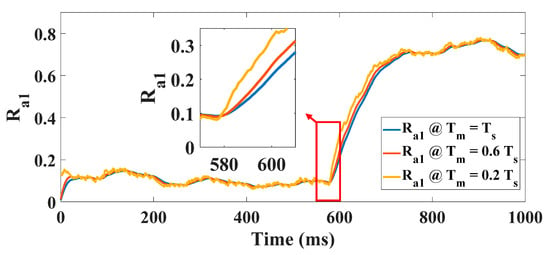
Figure 7.
Effect of changing the moving average period ().
Note also that, in this OPF case, the average value of the phase a1 current () should remain zero, in other words, has a zero value in the healthy case and in the case of an open-phase fault.
The results show the simplicity and effectiveness of this fault detection technique. Fast detection is achieved due to the low calculations burden of this technique, as compared to the other more complicated methods which require heavy calculations, such as neural network-based methods and frequency spectrum-based methods. Furthermore, robustness to load variation and operating conditions is guaranteed because the indices are inherently normalized as they are ratios of the VSD current variables. This ensures that the indices remain at a value of zero in the healthy situation and one in the case of a fault.
5.2. Open-Switch Fault (OSF)
Here, one test is presented to investigate the OUSF fault. In this test, the upper switch of phase a1 is opened at t = 3.75 s through disconnecting the gate signal of that switch. Figure 8a shows OUSF phase current. Thus, ideally, the a1 fault index evolves to one during the positive half cycle and returns back to zero during the negative half cycle. However, practically, it does not have enough time to reach zero because of the high supply frequency, as shown in Figure 8b. Moreover, Figure 8c presents a zoomed-in view of the fault index, and it is demonstrated that the detection time is about 9 msec.
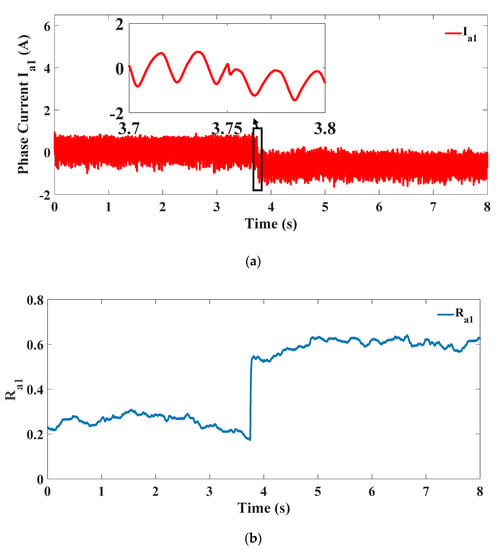
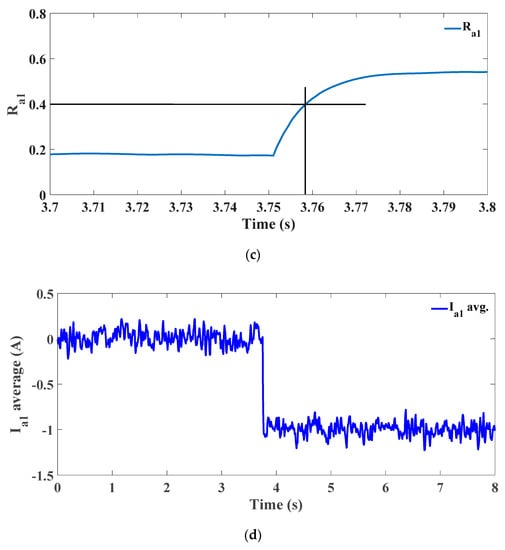
Figure 8.
OSF test: (a) Phase current (a1); (b) Ra1 index; (c) Ra1 index (zoom-in); (d) Iph_avg.
As discussed earlier, this is not enough to detect an OSF and deduce that the fault is in the upper switch. Therefore, the of phase a1 should be checked to be negative, as shown in Figure 8d, and that means that there is an OUSF.
Furthermore, the indices-based fault detection technique does not recognize an OPF case from the case of having both OUSF and OLSF at the same time. This is because, in these both cases, the fault index of the faulted phase will evolve and the index will be zero, as shown in Figure 6 and Figure 8.
Regarding the detection time, without considering the second index (), the detection time depends on the fault instant, and the maximum possible detection time equals the detection time of the OPF case plus a half fundamental cycle. This happens whenever the OSF occurs at the beginning of the half cycle of the healthy switch, for example, the maximum possible detection time for an OUSF occurs when the fault instant is at the beginning of the negative half cycle. However, by considering the index, the detection time will not be less than one complete fundamental cycle, which is the minimum required period to calculate the index .
5.3. Bad Connection Fault
The bad connection fault is experimentally represented by adding a variable resistance in series with the a1 phase connection. The severity of the bad connection fault is determined by the value of the added resistance (i.e., increasing the resistance value increases the bad connection fault severity and vice versa). In this test, the resistance has increased in two steps to visualize the change of the fault index. At the beginning, there was no bad connection fault; however, at t = 4 s, a 35 Ohms resistance (the first step) is added to simulate a bad connection fault with a moderate severity. Then, at t = 6.5 s, the resistance was increased to be 60 Ohms (the second step) to demonstrate a high severity bad connection fault. At this resistance value, the phase current was zero and the fault index reached to approximately one, so this is the worst bad connection fault case, as these results are similar to that of the open-circuit fault. Finally, the resistance was removed at t = 17.5 s and the current returned to its normal value.
Figure 9a shows the decay in a1 phase current to approximately zero due to the added resistances, whereas Figure 9b,c show the evolution of the fault index of phase a1 as a consequence of increasing the bad connection fault severity.
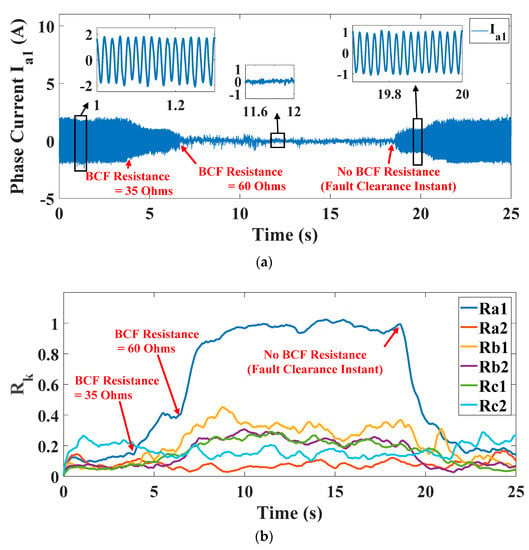
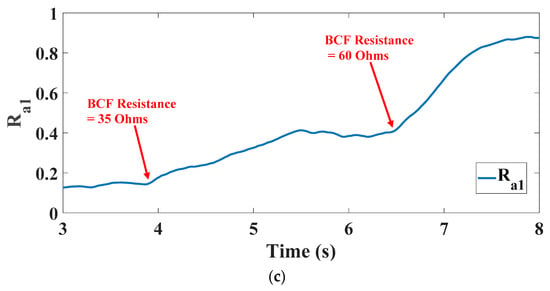
Figure 9.
Bad connection test: (a) Phase current (a1); (b) Fault indices; (c) Ra1 (zoom-in view).
Here, the set value of the index threshold value determines at which severity level the fault could be detected. That is, if the threshold value is low, the detection severity level is low, and if the threshold value is high, the detection severity level will be high. However, if the threshold value is set to be a high value, this may lead to a misinterpretation of the fault to be an open-phase or open-switch fault. Therefore, it is necessary to note that the index threshold value in bad connection fault detection should be lower than the index threshold value in open-phase and open-switch fault detection. This is important to differentiate between these types of fault.
5.4. Broken-Rotor Bar (BRB) Fault
The phase variable model of the six-phase induction motor is built using MATLAB/SIMULINK. The motor equations were implemented using the function blocks of the SIMULINK in addition to an S-Function, whereas a MATLAB Function was used to implement the fault detection algorithm. The fixed-step solver (ode3) was used with a step size value = 1 × 10−3. The stator phase currents and rotor loop currents are shown in Figure 10 and Figure 11, a zoomed view of one of the rotor loop currents is presented also in Figure 11 for better visualization. Additionally, the mechanical performance of the motor is shown in Figure 12, where the motor started at no load, then at t = 0.6 s, a 4 N.m load torque was applied.
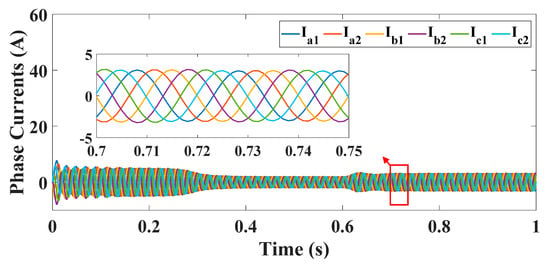
Figure 10.
Stator phase currents.
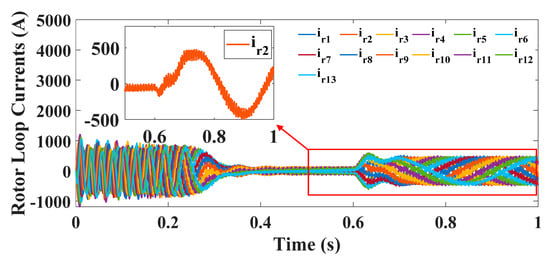
Figure 11.
Rotor loop currents.
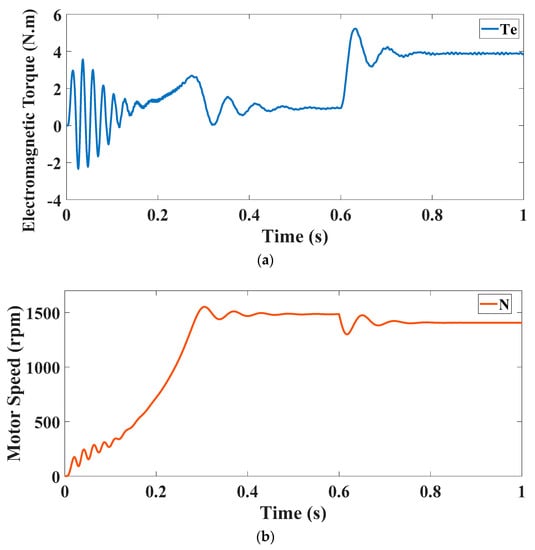
Figure 12.
(a) Electromagnetic torque; (b) Rotor speed.
A broken rotor-bar fault was simulated by increasing the value of one rotor-bar resistance to be 0.001 Ohms, so the number of the broken rotor bars in this test is one. In this test, the motor started with one broken rotor bar fault at no load, then the motor was impacted by a load torque of 4 N.m at t = 0.6 s. Figure 13 shows the rotor-bar currents and indicates that the current of the first rotor-bar is reduced to zero (BRB fault). The frequency spectrum of the stator phase a1 current in both the healthy case and the one BRB fault case is provided in Figure 14. It can be shown that the amplitudes at about 42 and 58 Hz are increased in the BRB fault case; these side-band frequencies are consistent with equation, where in this case and.
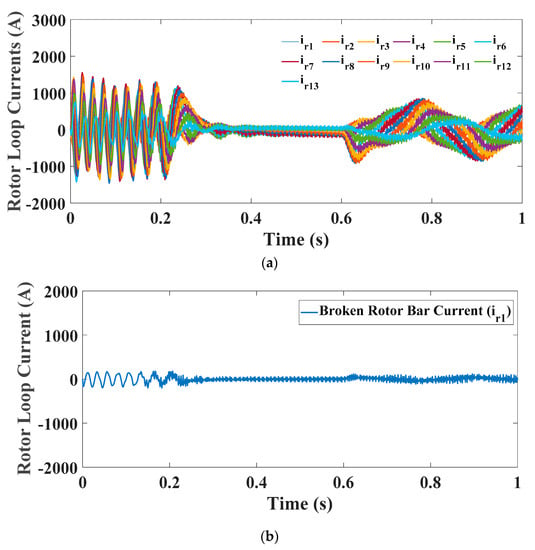
Figure 13.
(a) BRB-rotor loop currents; (b) Broken rotor bar current.
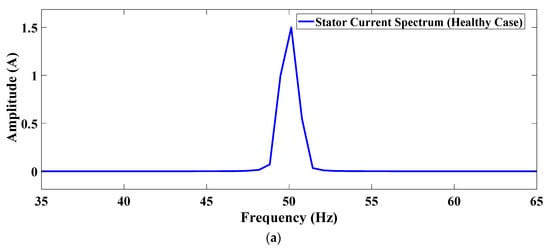
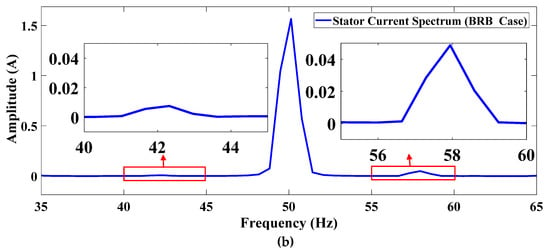
Figure 14.
Stator current spectrum: (a) Healthy case; (b) BRB fault case.
However, unbalance in the stator phase currents was not observed in Figure 15. Additionally, Figure 16 and Figure 17 present the α-β and x-y current components of the phase currents, and it is explicitly shown that the x-y components are approximately zero. Therefore, as expected, there will be no effect on the indices, as presented in Figure 18. All the filtered indices are zero; however, there are small notches in the values which could be filtered out through a proper filter. In Figure 18b, there are some notches, specifically at the zero-crossing instants; therefore, a hysteresis-band filter is used to filter out these notches, along with the comparison to a threshold value stage which was described earlier.
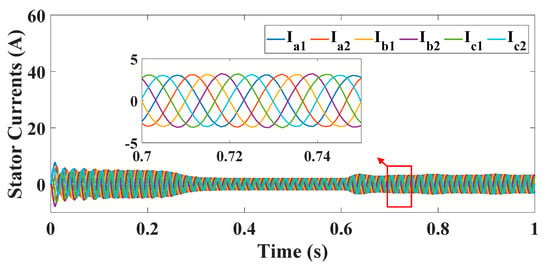
Figure 15.
BRB-stator phase currents.
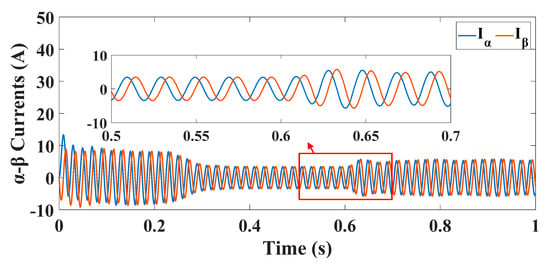
Figure 16.
BRB-αβ currents.
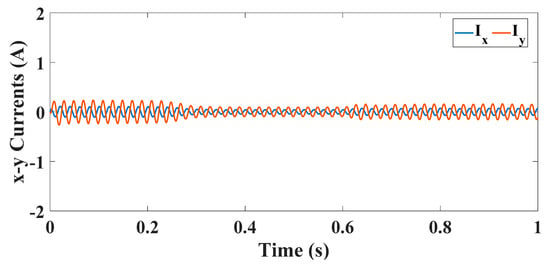
Figure 17.
BRB-xy currents.
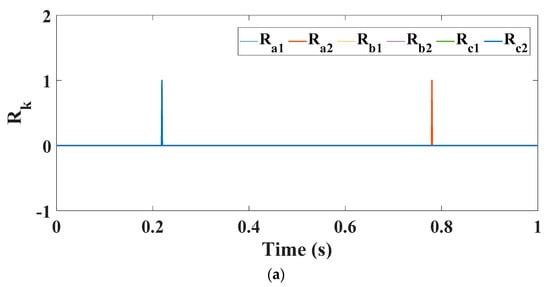
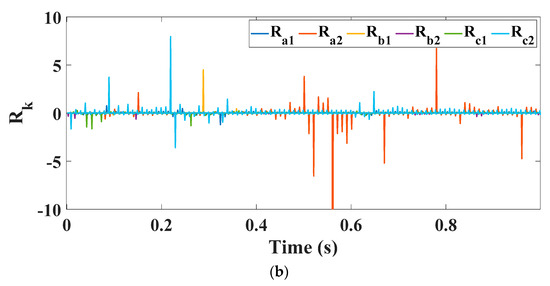
Figure 18.
(a) Filtered indices; (b) Unfiltered indices.
Furthermore, more tests were conducted to validate this conclusion. Since the fault indices were calculated from the α-β and x-y sequence currents, Table 2 introduces the rms values of these sequence currents in various BRB fault conditions, namely, in one, two adjacent, two non-adjacent, three adjacent, and three non-adjacent BRB faults. All these cases were tested under rated torque condition. It can be shown that there is no considerable variation in the x-y sequence current rms values, which indicates that the phase currents have a small unbalance component at these various fault conditions. Thus the fault indices will not evolve to detect this fault type.

Table 2.
Sequence rms currents in various BRB fault conditions.
6. Conclusions
In this study the indices-based fault detection technique was investigated against various types of faults. This fault detection technique has the advantages of being reliable and robust to varying operating conditions. In addition, it is quite simple as it requires no heavy calculations. However, some signal filtering and conditioning are required due to the inherit notches and ripples which are present in the indices signals. Four types of faults were tested, namely, open-phase, open-switch, bad connection, and broken rotor bar faults. As described in other previous studies, the open-phase faults could be successfully detected using this technique without any modification. However, in the case of the open-switch faults, an additional index, which is the average value of the phase current, is proposed to differentiate between the open-phase and open-switch faults. Although this added index will increase the detection time to be at least one complete fundamental cycle, an advantage of localizing the open-switch fault will be gained. Furthermore, the fault detection technique was tested against the bad connection fault, and it is shown that this fault could also be detected, but with a proper choice of the fault threshold value, in order not to misinterpret the fault with the open phase or open switch faults. Moreover, a six-phase induction motor model based on the phase variables was implemented to adequately simulate the broken rotor bar fault. In this case, it is concluded that the indices-based fault detection technique could not be able to detect the broken rotor bar fault, as there is a small unbalance in the stator phase currents. Finally, experimental and simulation results validate all the above conclusions.
Author Contributions
Conceptualization and methodology, K.F. and A.S.A.-K.; software, K.F., A.S. and S.A.; validation, K.F., A.S. and A.S.A.-K.; formal analysis and investigation, all authors; resources, all authors; data curation, all authors; writing—original draft preparation, K.F.; writing—review and editing, all authors; visualization, all authors; supervision, A.S.A.-K. and M.M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Renukadevi, G.; Rajambal, K. Modeling and Analysis of Multi-Phase Inverter Fed Induction Motor Drive with Different Phase Numbers. WSEAS Trans. Syst. Control 2013, 8, 73–80. [Google Scholar]
- Meinguet, F.; Semail, E.; Gyselinck, J. An on-line method for stator fault detection in multi-phase PMSM drives. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Salas-Biedma, P.; González-Prieto, I.; Durán, M.J.; Bermúdez, M.; Barrero, F. Multiphase Current Imbalance Localization Method Applied to Natural Fault-Tolerant Strategies. IET Elect. Power Appl. 2020, 14, 1421–1429. [Google Scholar] [CrossRef]
- Choi, A.S.; Baek, J. Open-Phase Fault Detection of a Five-Phase Permanent Magnet Assisted Synchronous Reluctance Motor Based on Symmetrical Components Theory. IEEE Trans. Ind. Elect. 2017, 64, 6465–6474. [Google Scholar] [CrossRef]
- Estima, J.O.; Cardoso, A.J.M. A New Approach for Real-Time Multiple Open-Circuit Fault Diagnosis in Voltage-Source Inverters. IEEE Trans. Ind. App. 2011, 47, 2487–2494. [Google Scholar] [CrossRef]
- Estima, J.O.; Cardoso, A.J.M. A New Algorithm for Real-Time Multiple Open-Circuit Fault Diagnosis in Voltage-Fed PWM Motor Drives by the Reference Current Errors. IEEE Trans. Ind. Electron. 2013, 60, 3496–3505. [Google Scholar] [CrossRef]
- Freire, N.; Estima, J.O.; Cardoso, A.J.M. Open-Circuit Fault Diagnosis in PMSG Drives for Wind Turbine Applications. IEEE Trans. Ind. Electron. 2013, 60, 3957–3967. [Google Scholar] [CrossRef]
- Salehifar, M.; Arashloo, R.S.; Moreno-Equilaz, J.M.; Sala, V.; Romeral, L. Fault Detection and Fault Tolerant Operation of a Five Phase PM Motor Drive Using Adaptive Model Identification Approach. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 212–223. [Google Scholar] [CrossRef]
- Salehifar, M.; Arashloo, R.S.; Moreno-Eguilaz, M.; Sala, V.; Romeral, L. Observer-based open transistor fault diagnosis and fault-tolerant control of five-phase permanent magnet motor drive for application in electric vehicles. IET Power Electron. 2015, 8, 76–87. [Google Scholar] [CrossRef]
- Barrero, F.; Bermudez, M.; Duran, M.J.; Salas, P.; Gonzalez-Prieto, I. Assessment of a Universal Reconfiguration-Less Control Approach in Open-Phase Fault Operation for Multiphase Drives. Energies 2019, 12, 4698. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Prieto, A.; Aciego, J.J.; Gonzalez-Prieto, I.; Duran, M.J. Automatic Fault-Tolerant Control of Multiphase Induction Machines: A Game Changer. Electronics 2020, 9, 938. [Google Scholar] [CrossRef]
- Garcia-Entrambasaguas, P.; Gonzalez-Prieto, I.; Duran, M.J. Single-Index Open-Phase Fault Detection Method for Six-Phase Electric Drives. IEEE Trans. Ind. Electron. 2020, 67, 10233–10242. [Google Scholar] [CrossRef]
- Prieto, G.; Duran, M.J.; Entrambasaguas, P.; Bermudez, M. Field Oriented Control of Multiphase Drives with Passive Fault-Tolerance. IEEE Tran. Ind. Elect. 2020, 67, 7228–7238. [Google Scholar] [CrossRef]
- Skowron, M.; Wolkiewicz, M.; Orlowska-Kowalska, T.; Kowalski, C.T. Application of Self-Organizing Neural Networks to Electrical Fault Classification in Induction Motors. Appl. Sci. 2019, 9, 616. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.-H.; Pack, J.-H.; Lee, I.-S. Fault Diagnosis of Induction Motor Using Convolutional Neural Network. Appl. Sci. 2019, 9, 2950. [Google Scholar] [CrossRef] [Green Version]
- Torabi, N.; Sundaram, V.M.; Toliyat, H.A. On-line fault diagnosis of multi-phase drives using self-recurrent wavelet neural networks with adaptive learning rates. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 18 May 2017; pp. 570–577. [Google Scholar] [CrossRef]
- Annamalai, B.; Swaminathan, S.T. Fault Diagnosis in Multi-Phase Induction Machine Using Mind Evolution Computation Algorithm Optimized Neural Network. Int. J. Eng. Adv. Technol. 2020, 9, 1722–1726. [Google Scholar]
- Annamalai, B.; Swaminathan, S.T. Neural Network Based Fault Diagnosis in Multi-Phase Induction Machine. Int. J. Innov. Technol. Explor. Eng. 2020, 9, 2278–3075. [Google Scholar]
- Skowron, M.; Orlowska-Kowalska, T.; Wolkiewicz, M.; Kowalski, C.T. Convolutional Neural Network-Based Stator Current Data-Driven Incipient Stator Fault Diagnosis of Inverter-Fed Induction Motor. Energies 2020, 13, 1475. [Google Scholar] [CrossRef] [Green Version]
- Hsueh, Y.-M.; Ittangihal, V.R.; Wu, W.-B.; Chang, H.-C.; Kuo, C.-C. Fault Diagnosis System for Induction Motors by CNN Using Empirical Wavelet Transform. Symmetry 2019, 11, 1212. [Google Scholar] [CrossRef] [Green Version]
- Duran, M.J.; Gonzalez-Prieto, I.; Rios-Garcia, N.; Barrero, F. A Simple, Fast, and Robust Open-Phase Fault Detection Technique for Six-Phase Induction Motor Drives. IEEE Trans. Power Electron. 2018, 33, 547–557. [Google Scholar] [CrossRef]
- Rios-Garcia, N.; Duran, M.; Prieto, I.G.; Martin, C.; Barrero, F. An Open-Phase Fault Detection Method for Six-Phase Induction Motor Drives. Renew. Energy Power Qual. J. 2017, 1, 473–478. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Prieto, I.; Duran, M.J.; Rios-Garcia, N.; Barrero, F.; Martin, C. Open-Switch Fault Detection in Five-Phase Induction Motor Drives Using Model Predictive Control. IEEE Trans. Ind. Elect. 2018, 65, 3045–3055. [Google Scholar] [CrossRef]
- Hammad, R.; Dabour, S.M.; Rashad, E.M. Open-Circuit Fault Detection of Asymmetrical Six-phase Induction Motor Fed from Z-Source Inverter. In Proceedings of the 2019 21st International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 27 February 2020. [Google Scholar] [CrossRef]
- Renukadevi, G.; Rajambal, K. Generalized d-q Model of n-Phase Induction Motor Drive. Int. J. Electr. Comp. Elect. Comm. Eng. 2012, 6, 62–71. [Google Scholar]
- Munim, W.N.W.A.; Duran, M.J.; Che, H.S.; Bermúdez, M.; Gonzalez-Prieto, I.; Rahim, N.A. A Unified Analysis of the Fault Tolerance Capability in Six-Phase Induction Motor Drives. IEEE Trans. Power Electron. 2017, 32, 7824–7836. [Google Scholar] [CrossRef]
- Yun, J.; Cho, J.; Lee, S.B.; Yoo, J. Online Detection of High-Resistance Connections in the Incoming Electrical Circuit for Induction Motors. IEEE Trans. Ind. Appl. 2009, 45, 694–702. [Google Scholar] [CrossRef]
- Pezzani, C.; Donolo, P.D.; Bossio, G.; Donolo, M.; Guzman, A.; Zocholl, S.E. Detecting Broken Rotor Bars with Zero-Setting Protection. IEEE Trans. Ind. Appl. 2014, 50, 1373–1384. [Google Scholar] [CrossRef]
- Drakaki, M.; Karnavas, Y.L.; Karlis, A.D.; Chasiotis, I.D.; Tzionas, P. Study on fault diagnosis of broken rotor bars in squirrel cage induction motors: A multi-agent system approach using intelligent classifiers. IET Electr. Power Appl. 2020, 14, 245–255. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, J.; Li, H.; Zhen, D.; Xu, Y.; Gu, F. Fault Identification of Broken Rotor Bars in Induction Motors Using an Improved Cyclic Modulation Spectral Analysis. Energies 2019, 12, 3279. [Google Scholar] [CrossRef] [Green Version]
- Toliyat, H.; Lipo, T.; White, J. Analysis of A Concentrated Winding Induction Machine for Adjustable Speed Drive Applications: Part 1 (Motor Analysis). IEEE Trans. Energy Convers. 1991, 6, 679–683. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).