Abstract
The viscosity models for concentrated suspensions of unimodal hard spheres published in the twenty-first century are reviewed, compared, and evaluated using a large pool of available experimental data. The Pal viscosity model for unimodal suspensions is the best available model in that the predictions of this model agree very well with the low (zero)-shear experimental relative viscosity data for coarse suspensions, nanosuspensions, and coarse suspensions thickened by starch nanoparticles. The average percentage error in model predictions is less than 6.5%. Finally, the viscous behavior of concentrated multimodal suspensions is simulated using the Pal model for unimodal suspensions.
1. Introduction
Suspensions of solid particles in a liquid medium are ubiquitous. They form a large group of materials of industrial importance. Both aqueous and non-aqueous suspensions are encountered in industrial applications. Some examples of suspensions are blood, drilling fluid, paint, ink, and a mixture of flour and water. Some of the industries wherein suspensions play a vital role are food, paints, pharmaceutical, mineral processing, coal, ceramics, pulp and paper, polymers, construction, petroleum, agriculture, cosmetics and toiletries, biotechnology, and nanotechnology [1,2,3,4,5,6,7,8,9,10,11].
Understanding the rheological behavior of suspensions is important from both theoretical and practical points of view. The key rheological property of a suspension is its shear viscosity. Knowledge of the shear viscosity of suspensions as a function of particle concentration is required for the design, selection, and operation of the equipment involved in the formulation, mixing, processing, storage, and pipeline transportation of suspensions.
In this article, the recent progress made in the viscosity modeling of concentrated suspensions is reviewed. The key viscosity models for suspensions published in the twenty-first century are discussed and compared. The available models are also evaluated using a large pool of low (zero)-shear experimental viscosity data available on coarse suspensions, nanosuspensions, and coarse suspensions thickened by starch nanoparticles (SNPs).
2. Theoretical Background
2.1. Dilute Suspensions of Hard Spheres
For a dilute suspension of identical hard-sphere-type particles, the rheological constitutive equation is given as follows [1,12]:
where is the dipole strength of a single hard-sphere particle located in an infinite matrix fluid, is the volume fraction of particles, is the particle radius, is the bulk rate of the strain tensor, is the matrix viscosity, is the average pressure, is a unit tensor, and is the bulk (average) stress tensor.
The dipole strength of a single hard-sphere particle located in an infinite matrix fluid, , is given as follows:
where is the rate of the strain tensor far away from the sphere. The rate of the strain tensor, , far away from the particles in dilute suspensions can be equated to the bulk or imposed rate of the strain tensor, , on the suspension. Upon substitution of from Equation (2) into Equation (1), we obtain the following:
For a homogeneous incompressible Newtonian fluid possessing a shear viscosity, , the constitutive equation is given as follows:
Upon comparison of Equations (3) and (4), the following expression for the viscosity of a dilute suspension of solid hard-sphere-type particles is obtained:
This is the celebrated Einstein equation [13,14] for the viscosity of a dilute suspension of hard-sphere-type solid particles. The Einstein equation was published in 1906 (erratum published in 1911).
Batchelor [15] extended the Einstein relationship, as in Equation (5), to the second order as follows:
where for Brownian suspensions at a low Peclet number. However, this equation gives reasonable predictions of suspension viscosity only at particle concentrations lower than about 15 vol%. At higher particle concentrations, the experimental values of viscosity generally fall well above the predictions of this equation, and the gap increases with an increase in particle concentration.
A number of numerical simulation studies have been published to extend the work of Einstein to higher concentrations by taking into account the hydrodynamic and nonhydrodynamic interactions between particles [16,17,18]. For example, Ladd [17] determined the relative viscosity of random suspensions of hard spheres from a multipole-moment expansion of force density on the surface of solid particles. Based on his numerical simulation results, Ladd developed the following expression for the high-frequency relative viscosity of a suspension:
In the limit , the Ladd expression reduces to the Einstein equation. Although the Ladd expression is applicable over a somewhat broader range of , as compared with the Einstein equation, it too fails to give accurate predictions of relative viscosity at particle concentrations larger than about 15 vol%. Also, note that this equation is restricted to suspensions subject to only hydrodynamic interactions.
2.2. Concentrated Suspensions of Hard Spheres
The publication of the Einstein equation triggered a lot of long-lasting activity on the rheology of dilute and concentrated suspensions [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72]. In this section, two well-known models for the viscosity of concentrated suspensions are discussed, namely, the Mooney model [24] and the Krieger–Dougherty model [34]. These models are applicable over the full range of particle concentrations, ranging from zero to packed-bed concentrations.
Consider a suspension with a volume fraction of particles, . The relative viscosity of this suspension can be expressed as follows:
where is the relative viscosity function. In the limit , is given by the Einstein equation, as in Equation (5), as follows:
We now add more particles to the existing suspension of a concentration such that the new concentration of the suspension is . Treating the previous suspension as a continuous phase (matrix) with respect to the new particles, we can write the following:
Thus:
This functional relationship does not consider the crowding effect of particles. Mooney proposed the following functional relation for concentrated suspensions taking into consideration the crowding effect of particles:
where is the maximum packing volume fraction of particles. This functional relationship gives the following solution for the relative viscosity of a concentrated suspension with any volume fraction, , which also satisfies the Einstein equation in the limit :
This is the celebrated Mooney equation for the viscosity of unimodal concentrated suspensions of spherical particles. The Mooney equation was published in 1951 [24].
According to Krieger and Dougherty [34], Equation (13) over-corrects the crowding and packing of particles. They proposed a modified version of the functional relationship, as in Equation (12), as follows:
This equation considers the crowding effect for only the second fraction of particles added to the suspension. The solution of Equation (14), which also satisfies the Einstein equation in the limit , is given as follows:
This is the celebrated Krieger–Dougherty equation for the viscosity of unimodal concentrated suspensions of spherical particles. The Krieger–Dougherty equation was published in 1959 [34].
The Mooney and Krieger–Dougherty equations are used extensively in the literature to describe the viscosity data of concentrated suspensions subject to hydrodynamic and Brownian interactions. They both diverge in the limit . The maximum packing volume fraction of unimodal suspensions usually falls in a range of . A of 0.58 corresponds to the glass transition (GT) point of a suspension, and a of 0.64 corresponds to random close packing (RCP) of uniform spherical particles.
3. Recent Progress in the Viscosity Modeling of Concentrated Suspensions
Many articles have been published on the development of viscosity models for concentrated suspensions in the twentieth century [20,23,24,25,26,27,28,31,32,34,35,36,37,38,39,40,41,44,45,50]. A good number of review articles have also been published on the subject [35,43]. Among the most popular models published in the twentieth century for the viscosity of concentrated suspensions are the Mooney and Krieger–Dougherty models discussed in the preceding section. In what follows, the relative viscosity models for concentrated suspensions published recently, in the past decade or so, are reviewed, compared, and evaluated using a large pool of experimental viscosity data available for concentrated suspensions.
3.1. Cheng et al. Model (2002)
Cheng et al. [73] proposed the following theoretical model for the low-shear viscosity of concentrated colloidal suspensions of hard spheres:
where is the high-frequency hydrodynamic contribution and is the non-hydrodynamic contribution to the relative viscosity of a suspension. The high-frequency relative viscosity is given by the following equations:
The non-hydrodynamic contribution to the relative viscosity of the suspension is given as follows:
3.2. Mendoza and Santamaria-Holek Model (2009)
Mendoza and Santamaria-Holek [63] modified the following Roscoe–Brinkman model for the viscosity of moderately concentrated suspensions of hard-sphere-type particles:
where is the relative viscosity–concentration function of a suspension. They replaced the actual volume fraction of particles, , with an effective volume fraction, , defined as follow:
where is given as follows:
Thus, the viscosity model of Mendoza and Santamaria-Holek is given as follows:
In the limit , this model reduces to the Einstein equation; in the limit , the viscosity diverges.
3.3. Brouwers Model (2010)
Based on geometrical considerations, Brouwers [64] developed the following differential equation for the relative viscosity of a concentrated suspension of unimodal hard spheres:
Upon integration and application of the boundary condition, , the differential equation, as in Equation (24), gives the following solution:
This equation, referred to as Brouwers model, can also be rearranged as follows:
The Brouwers model reduces to the Einstein equation in the limit . Also, it diverges in the limit .
3.4. Faroughi–Huber Model (2015)
Faroughi and Huber [70] used a differential effective medium approach similar to that used by Pal [60,69] to obtain the following differential equation:
where , and Ω is a self-crowding parameter given as follows:
Note that Ω is equal to c of the Mendoza and Santamaria-Holek model (see Equation (22)).
Upon integration, Equation (27) yields the following expression:
It is important to note that this model proposed in the Faroughi and Huber [70] article is not original. It is identical to the Brouwers model, as shown in Equation (26). Upon substitution of from Equation (28) into Equation (29), Equation (29) reduces to the following Brouwers model:
Surprisingly, the authors claim this to be their own model, not recognizing that it is an exact replica of the Brouwers model.
3.5. Pal Model (2015)
Pal [69] proposed a model for the viscosity of concentrated suspensions considering the clustering of particles. The clustering of particles is expected with an increase in particle concentration. Due to Brownian motion, particles encounter each other and form clusters. Even in the absence of Brownian motion, the clustering of particles is expected under the application of shearing motion. Particles are known to form clusters that are continually created and destroyed in shearing motion [46]. At low concentrations of particles, clusters may consist of just doublets. The size of clusters grows progressively from doublets to triplets, from triplets to quartets, from quartets to quintets, and so on. The clustering process is shown schematically in Figure 1 as the concentration of particles is increased. Due to the clustering of particles, a significant amount of the continuous phase is immobilized within the clusters, resulting in an increase in the effective volume fraction of the dispersed phase. Based on the general characteristics of suspensions of solid particles, Pal proposed the following relationship between the effective dispersed-phase concentration () of a suspension and the actual dispersed-phase concentration () [69]:
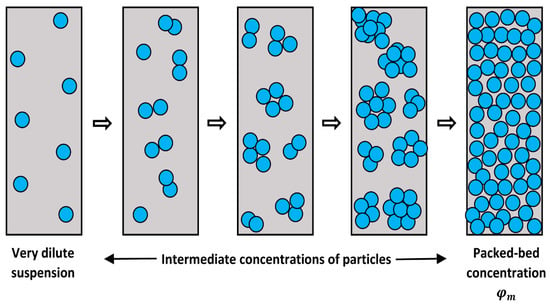
Figure 1.
Clustering of particles with an increase in particle concentration.
The important features of this expression are as follows:
(a) In the dilute limit , ;
(b) In the limit , ;
(c) The slope of the ratio, , with respect to , is always positive, that is, . The ratio, , is expected to only increase with an increase in due to an increase in the size of clusters.
(d) The ratio, , becomes constant at high values of . This ratio does not continue to increase with an increase in the number of particles in clusters. When the number of particles in a cluster has reached a certain value, the ratio, , is expected to become constant. For clusters with a large number of particles, the ratio, , depends only on the type of particle packing (random close packing, hexagonal close packing, etc.).
Thus, in the limit .
Figure 2 shows the plots of versus generated from Equation (30) for two different types of particle packing clusters, namely, random close packing (RCP) and glass transition (GT) packing of particles. Note that for random close packing and for glass transition packing of uniform spheres. The ratio, , increases initially with an increase in but levels off at high values of . The ratio, , becomes equal to 1/, that is, reaches a value of unity.
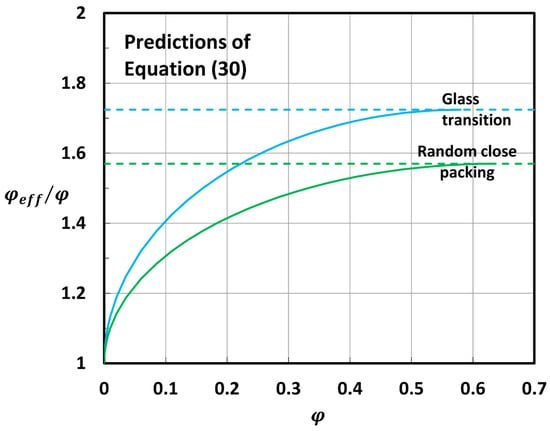
Figure 2.
Increase in with an increase in for two different types of particle packing clusters.
The viscosity model for concentrated suspensions was derived using a differential effective medium approach. In this approach, it is visualized that a concentrated suspension can be obtained from the starting suspending medium by successively adding differential quantities of particles to the suspension until the final concentration of particles is obtained. Let, at any stage (i) in the process of particle addition, the total volume of the suspension be , the effective dispersed-phase volume be , and the viscosity of suspension be . Upon addition of of the dispersed phase to the stage (i) suspension, the stage (i + 1) is reached where the effective dispersed-phase volume is , the total volume of the suspension is , and the viscosity of the suspension is . Treating the stage (i) suspension as an effective medium of viscosity, η, with respect to the stage (i + 1) suspension of viscosity, , the application of the Einstein equation gives the following:
It can be readily shown that:
From Equations (31) and (32), it follows that:
The integration of Equation (33) yields the following expression:
Upon substitution of Equation (30) into Equation (34), the following model for the viscosity of concentrated suspensions of unimodal spherical particles is obtained:
This model is referred to as Pal model P1 in the remainder of this article.
3.6. Pal Model (2017)
Starting from the Einstein equation, as in Equation (5), Pal [71] proposed a new model for the viscosity of concentrated suspensions of hard spheres. According to the Einstein equation, as in Equation (5):
In analogy with real gas behavior, Pal [71] modified the Einstein equation as follows:
Pal contended that the volume of particles should be excluded from the total volume of the suspension in the calculation of the particle concentration.
Let be the total volume of suspension and be the volume fraction of particles. Thus, the following can be expressed:
From Equations (37) and (38), we obtain:
Pal [71] further modified this equation taking into consideration the clustering of particles. Thus, the actual volume fraction of particles in Equation (39) was replaced by an effective volume fraction, , given as follows (see Equation (30)):
Consequently, the viscosity model for a concentrated suspension of hard spheres as proposed by Pal [71] is as follows:
where is given by Equation (40). This model is referred to as Pal model P2 in the remainder of this article.
3.7. Pal Model (2020)
Pal [72] recently developed another suspension viscosity model for non-dilute suspensions. Considering the clustering of particles in shear flow, he proposed a linear relationship between the aggregation coefficient and volume fraction of particles:
where is the aggregation coefficient defined as follows:
Applying the following conditions: when and when (note that when ), the constants and can be determined as follows: and . Thus, the aggregation coefficient and in shear flow can be expressed as:
This expression for is simpler than the one developed earlier for Pal model P2 (see Equation (40)). Using the effective medium approach discussed in Section 3.5 and the above expression for , the following model for concentrated suspensions of unimodal spherical particles was derived:
This model is referred to as Pal model P3 in the remainder of this article.
4. Comparisons of Model Predictions
Figure 3 compares the predictions of various models for two different values of the maximum packing concentration: and . The comparisons reveal the following information:
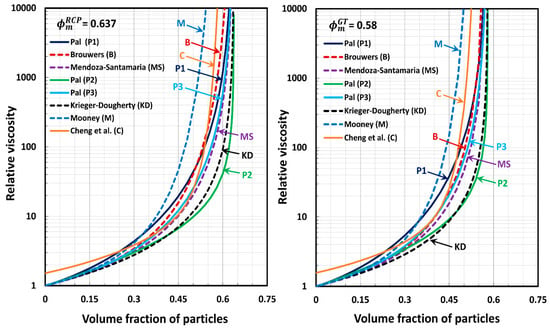
Figure 3.
Comparisons of model predictions for two different values of maximum packing concentrations: and . M refers to Mooney model (Equation (13)), C refers to Cheng et al. model (Equation (16)), B refers to Brouwers model (Equation (26)), P1 refers to Pal model P1 (Equation (35)), P2 refers to Pal model P2 (Equation (41)), P3 refers to Pal model P3 (Equation (46)), MS refers to Mendoza and Santamaria-Holek model (Equation (23)), and KD refers to Krieger–Dougherty model (Equation (15)).
- The Mooney model (M) generally predicts the highest values of relative viscosities.
- Pal model P2 generally predicts the lowest values of relative viscosities.
- The Krieger–Dougherty model (KD) and Pal model P2 predict similar values of relative viscosities.
- The Mendoza and Santamaria-Holek model (MS) generally predicts relative viscosities lower than that of Pal model P3.
- The Cheng et al. (C) model predicts unrealistically high values of relative viscosities when . Also, the relative viscosity is greater than unity at
- For large values of particle volume fractions , the predictions of the models are generally in the following order: .
5. Comparisons of Model Predictions with Experimental Data
5.1. Experimental Data
The models were evaluated using three groups of low-shear experimental data: coarse suspensions (22 sets of data), nanosuspensions (16 sets of data), and coarse suspensions thickened by starch nanoparticles (6 sets of data). Table 1, Table 2 and Table 3 give details of these suspensions. The suspensions were unimodal, and the matrix phase of the suspensions was Newtonian. Both Newtonian and non-Newtonian suspensions were considered. For non-Newtonian suspensions, the viscosity data at low-shear rates were used. For some non-Newtonian suspensions that followed power law behavior, a consistency index was used instead of viscosity. Note that a consistency index is equal to viscosity at a low shear rate of 1 s−1. While coarse suspensions were subject to mainly hydrodynamic interactions, nanosuspensions were subject to both hydrodynamic and Brownian interactions.

Table 1.
Details of coarse suspensions (22 sets).

Table 2.
Details of nanosuspensions (16 sets).

Table 3.
Details of the SNP-thickened coarse suspensions (6 sets).
The relative viscosity versus particle volume fraction data for the coarse suspensions (22 sets) are shown in Figure 4. The data for all the suspensions in this group tend to fall on the same curve. The relative viscosity versus particle volume fraction data for the sixteen sets of nanosuspensions, as shown in Figure 5, also fall on the same curve. The six sets of data for the coarse suspensions thickened by starch nanoparticles (SNPs), as shown in Figure 6, generally tend to fall on the same curve, regardless of the SNP concentration of the matrix phase. However, some scattering of data can be observed for low-volume fractions of solid particles.
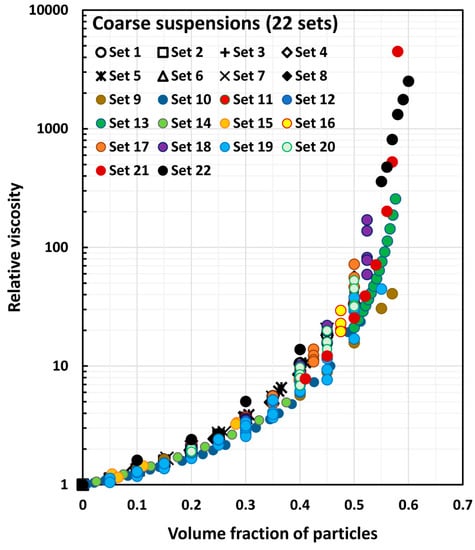
Figure 4.
Experimental relative viscosity versus particle volume fraction data for twenty-two sets of coarse suspensions.
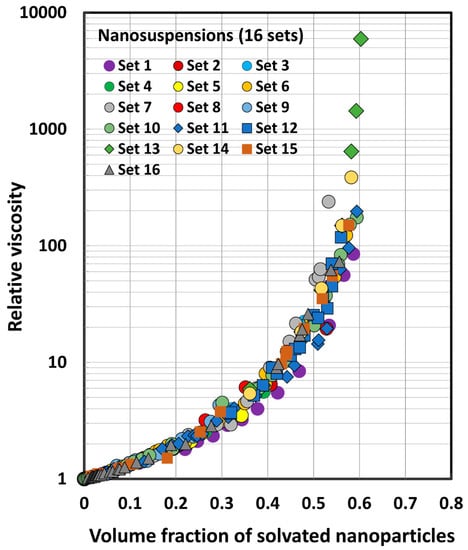
Figure 5.
Experimental relative viscosity versus particle volume fraction data for sixteen sets of nanosuspensions.
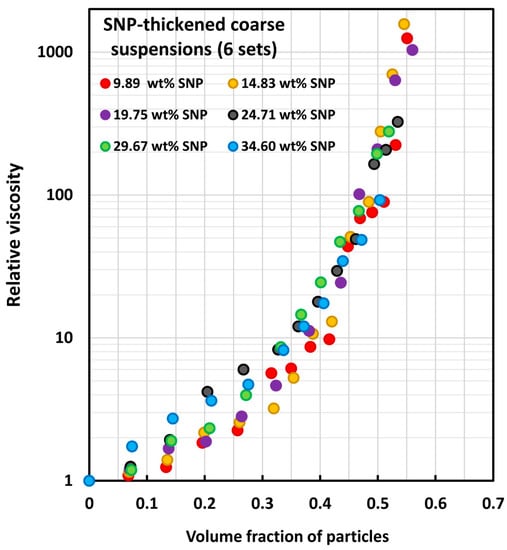
Figure 6.
Experimental relative viscosity versus particle volume fraction data for six sets of SNP-thickened coarse suspensions.
Figure 7 shows all the experimental data (44 sets) together for coarse suspensions, nanosuspensions, and SNP-thickened coarse suspensions. The data for different groups of suspensions do not seem to overlap with each other. The reason for this observation is that the packing structure, and, hence, the maximum packing volume fraction, of suspensions is not the same for these different groups of suspensions.
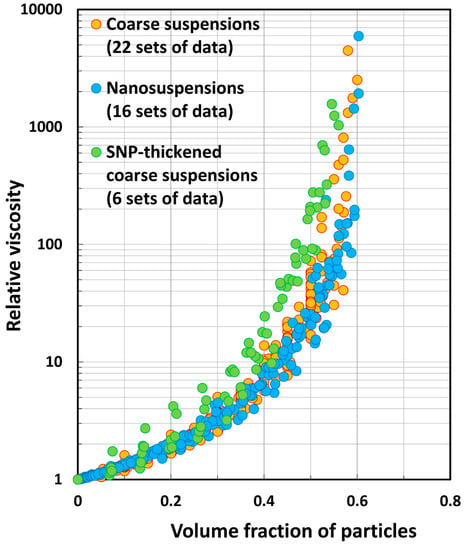
Figure 7.
Experimental relative viscosity versus particle volume fraction data for all the suspensions (44 sets), including coarse suspensions, nanosuspensions, and SNP-thickened coarse suspensions.
5.2. Estimation of Maximum Packing Volume Fraction of Suspensions
The maximum packing volume fraction of suspensions is estimated from the relative viscosity versus particle concentration data at high particle concentrations (. A linear relationship can be observed when the data are plotted as versus . This linear relationship can be extended to to estimate . A similar approach was used by Tanner [83] to estimate for suspensions.
Figure 8, Figure 9 and Figure 10 show the plots of versus for the three group of suspensions: coarse suspensions (Figure 8), nanosuspensions (Figure 9), and SNP-thickened coarse suspensions (Figure 10). The estimated values of are as follows: coarse suspensions, ; nanosuspensions, ; SNP-thickened coarse suspensions, . Note that the maximum packing volume fraction is 0.637 for random close packing of hard spheres. The packing volume fraction of particles is 0.58 at glass transition of hard spheres. Thus, the values for the coarse suspensions and nanosuspensions are close to the random packing of hard spheres, whereas the value for SNP-thickened coarse suspensions is almost equal to the glass transition volume fraction of hard spheres corresponding to .
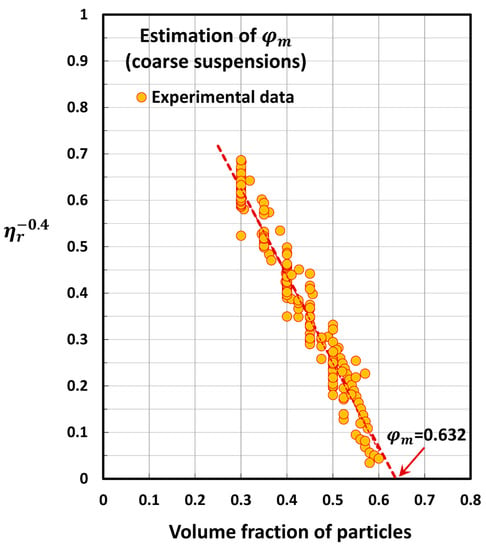
Figure 8.
Estimation of the maximum packing volume fraction for coarse suspensions.
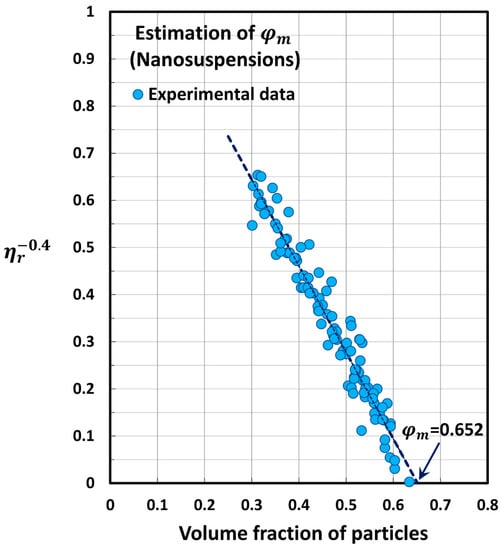
Figure 9.
Estimation of the maximum packing volume fraction for nanosuspensions.
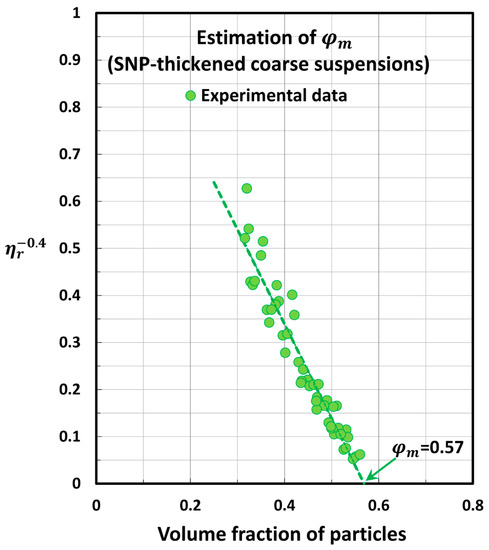
Figure 10.
Estimation of the maximum packing volume fraction for SNP-thickened coarse suspensions.
5.3. Model Predictions Versus Experimental Data
Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 compare the predictions of the viscosity models (eight models) with the experimental data. Figure 11 compares the predictions of the Mooney model with the three groups of experimental data (coarse suspensions, nanosuspensions, and SNP-thickened coarse suspensions). The values estimated in the preceding section are used in the model. Likewise, Krieger–Dougherty model comparisons are shown in Figure 12, Cheng et al. model comparisons are shown in Figure 13, Mendoza and Santamaria-Holek model comparisons are shown in Figure 14, Brouwers model comparisons are shown in Figure 15, Pal model P1 comparisons are shown in Figure 16, Pal model P2 comparisons are shown in Figure 17, and Pal model P3 comparisons are shown in Figure 18.
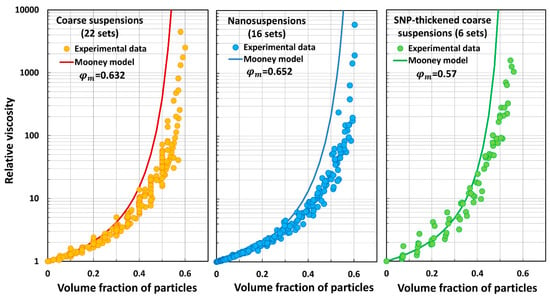
Figure 11.
Comparisons of Mooney model predictions with experimental data.
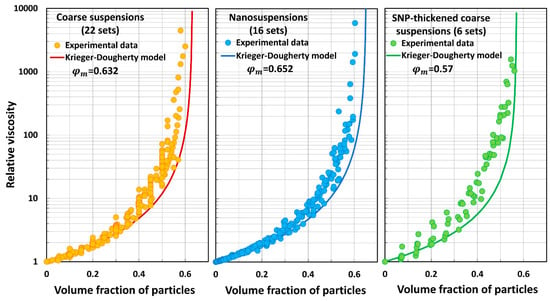
Figure 12.
Comparisons of Krieger–Dougherty model predictions with experimental data.
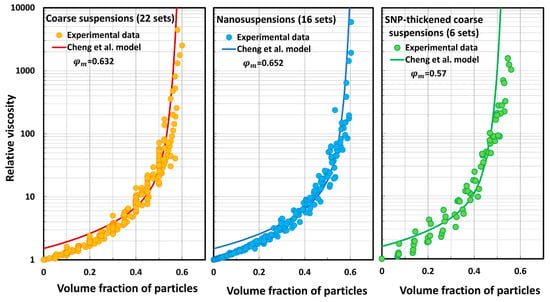
Figure 13.
Comparisons of Cheng et al. model predictions with experimental data.
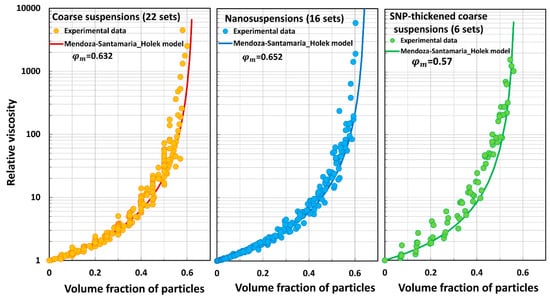
Figure 14.
Comparisons of Mendoza and Santamaria-Holek model predictions with experimental data.
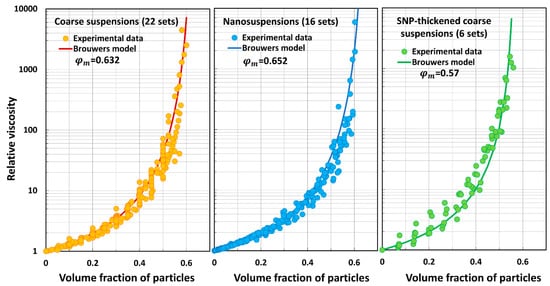
Figure 15.
Comparisons of Brouwers model predictions with experimental data.
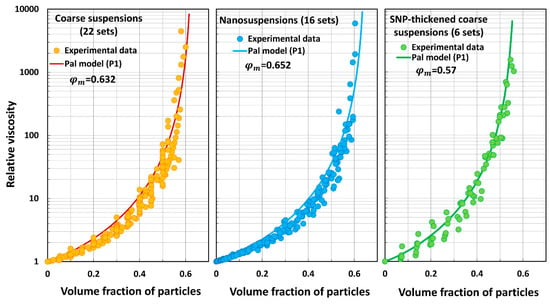
Figure 16.
Comparisons of Pal model P1 predictions with experimental data.
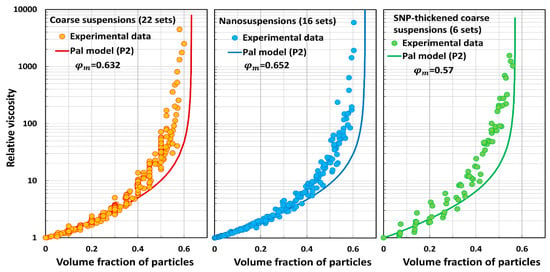
Figure 17.
Comparisons of Pal model P2 predictions with experimental data.
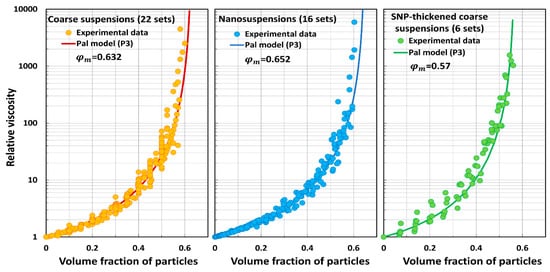
Figure 18.
Comparisons of Pal model P3 predictions with experimental data.
The comparisons of the model predictions with the experimental data shown in Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 reveal the following information:
- The Mooney model (M) overpredicts the relative viscosity of suspensions.
- The Krieger–Dougherty model (KD) underpredicts the relative viscosity of suspensions.
- The Cheng et al. model (C) overpredicts the relative viscosity at low and high particle concentrations.
- The Mendoza and Santamaria-Holek model (MS) underpredicts the relative viscosity of suspensions.
- The Brouwers model (B) overpredicts the relative viscosity of suspensions.
- Pal model P1 overpredicts the relative viscosity of suspensions.
- Pal model P2 underpredicts the relative viscosity of suspensions.
- Pal model P3 predictions are close to experimental values.
Table 4 summarizes the average percentage relative error (APRE) values calculated for each model. The APRE is defined as follows:
where the subscripts “exp” and “mod” refer to experimental value and model predicted value, and n is the number of data points. Based on the average percent error, the deviations of model predictions are grouped into five categories as indicated below:

Table 4.
APRE values for different models.
Magnitude of APRE 5%: deviation in model prediction: Slight;
Magnitude of APRE 10%: deviation in model prediction: Moderate;
Magnitude of APRE 30%: deviation in model prediction: Substantial;
Magnitude of APRE 100%: deviation in model prediction: Severe;
Magnitude of APRE 100%: deviation in model prediction: Extreme.
The Mooney and Cheng et al. models overpredict the relative viscosity values of coarse suspensions, nanosuspensions, and SNP-thickened coarse suspensions in an extreme way. The average percentage error is very large (. These models are clearly not suitable for the prediction of the relative viscosities of suspensions. The Krieger–Dougherty model underpredicts the relative viscosities of suspensions substantially to severely. The Mendoza and Santamaria-Holek model underpredicts the relative viscosities substantially. The Brouwers model overpredicts the relative viscosities substantially to severely. Pal model P1 overpredicts the relative viscosities severely. Pal model P2 underpredicts the relative viscosities substantially to severely. Pal model P3 is the best model in that it deviates from the experimental data only slightly to moderately.
As Pal model P3 shows relatively small deviations from the experimental data, a master curve for the relative viscosity of coarse suspensions, nanosuspensions, and SNP-thickened coarse suspensions was developed based on this model. Figure 19 shows the master curve based on Pal model P3. The data are plotted as relative viscosity versus effective volume fraction of particles (, where is given by Equation (45). The experimental data for all the suspensions fall on the master curve generated by Pal model P3. Some scatter in the experimental data observed around the master curve could probably be explained in terms of friction between the particles of the suspensions. We have assumed that the suspension particles are smooth with negligible friction. Several recent studies [83,84] have indicated that the role of friction between particles is important in determining the viscosity of suspensions.
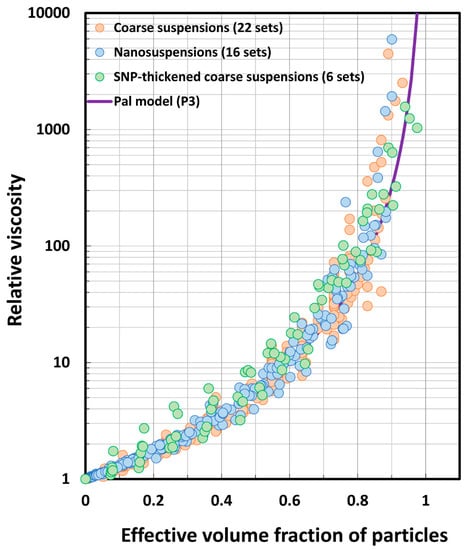
Figure 19.
Master curve generated by Pal model P3 (Equation (46)). The experimental data for all the suspensions (coarse suspensions, nanosuspensions, and SNP-thickened coarse suspensions) overlap with each other, which is in agreement with Pal model P3.
6. Simulation of the Viscous Behavior of Concentrated Multimodal Suspensions
From a practical point of view, it is important to formulate suspensions with as high a concentration of particles as possible while keeping the viscosity reasonable. As can be observed in the preceding sections, the viscosity of unimodal suspensions becomes infinite when the particle concentration, , reaches the maximum packing volume fraction, . For random packing of uniform hard spheres, the value of is 0.637. Thus, it is impossible to load a suspension with particles above a particle concentration (volume fraction) of 0.637. Interestingly, the loading of suspensions with particles exceeding a concentration of 0.637 can be readily achieved by making the suspension multimodal while keeping the viscosity of the suspension reasonable at the same time. Alternatively, the viscosity of the suspension can be reduced substantially at a fixed particle concentration by making the suspension multimodal.
Consider the formulation of a multimodal suspension consisting of N different-size particles. Let be the volume of the initial suspending medium liquid (matrix phase without any particles). Let , , , …, , ……, be the volumes of different-size particles added successively to the initial liquid of volume . We assume that each new set of particles added is much larger in size than the previous set of particles. Thus, is the volume of smallest-size particles in the suspension, and is the volume of largest-size particles. Let the apparent concentrations of different-size particles be defined as follows:
where is the apparent concentration of any set of particles, and could be any number from 1 to N. Note that is not the actual concentration (volume fraction) of the set of particles. The actual concentration of any set of particles is given as follows:
The denominator on the right-hand side of Equation (50) is the total volume of the suspension.
The actual total concentration of particles is given as follows:
It can be readily shown that [85]:
where ∏ is the product sign.
Now consider two successive stages, (i) and (i + 1), in the process of the addition of different-size particles to formulate a multimodal suspension of N particle sizes. Following the effective medium approach, the suspension of stage (i) can be treated as an effective medium that is homogeneous with respect to the new set of particles added to reach stage (i + 1). For the effective medium approach to be valid, it is assumed that the new set of particles added at stage (i + 1) is much larger (ten times) than the set of particles added in the previous stage (i). Consequently, the relative viscosity of the multimodal suspension can be expressed as follows:
where is the relative viscosity function of a suspension. We use Pal model P3 (Equation (46)) for the relative viscosity function:
where is taken to be 0.637, corresponding to random close packing of hard spheres. From Equations (53) and (54), it follows that:
Equation (55) can be used to predict the relative viscosity of multimodal suspensions.
6.1. Relative Viscosity of Bimodal Suspensions
For bimodal suspensions, Equation (55) simplifies to the following:
Given the total concentration of particles, , and fraction of coarse particles in the mixture of fine and coarse particles, we can estimate the relative viscosity of bimodal suspensions from Equation (56). If the fraction of coarse particles in the mixture of fine and coarse particles is , it can be readily shown that:
Equation (58) follows from the simplification of Equation (52) for a bimodal system.
Figure 20 shows the relative viscosities of bimodal suspensions calculated from Equations (56)–(58) for different values of total particle concentration,. As already noted, we used in the calculations. Interestingly, the relative viscosity of a suspension decreases substantially by changing a monomodal suspension to a bimodal suspension while keeping the total particle concentration, , constant. The effect of the bimodality of suspension on the relative viscosity is especially strong at high values of . As an example, the relative viscosity of a unimodal suspension at a total particle concentration, , of 0.63 is 36,696. A sharp reduction in the relative viscosity of suspension from 36,696 to 43 can be observed when the single-size (uniform) particles of a unimodal suspension are replaced by a mixture of large and small particles with a large particle fraction of 0.60. Note that the relative viscosity of the suspension is minimum (see Figure 20) at a coarse particle fraction of 0.60 when = 0.63.
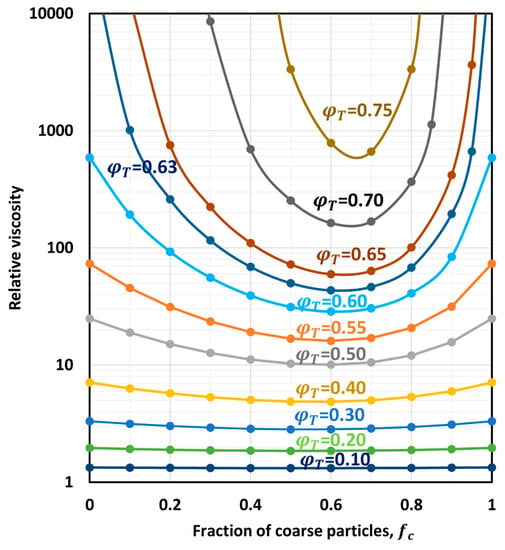
Figure 20.
Relative viscosity of bimodal suspensions as a function of coarse particle fraction of the particle mixture.
6.2. Minimum Relative Viscosity of Multimodal Suspensions
Figure 20 reveals that the relative viscosity of a bimodal suspension at a fixed becomes minimum at a certain fraction of coarse particles in a mixture of fine and coarse particles. This observation is not restricted to bimodal suspensions. It is true for any multimodal suspension.
Farris [85] has shown that a minimum in the relative viscosity of a multimodal suspension occurs when:
Equation (59) indicates that the minimum in the relative viscosity of multimodal suspensions occurs when the apparent concentrations, , of all particle sizes are equal. The apparent concentrations of different particle-size fractions are defined in Equations (48) and (49). The common value of , denoted as , where minimum relative viscosity occurs can be calculated from Equation (52) as follows:
Thus, the minimum viscosity of a multimodal suspension can be calculated from Equation (55) as follows:
Figure 21 shows the plots of relative viscosity of different multimodal suspensions (unimodal, bimodal, trimodal, octamodal, and decamodal) as a function of total particle concentration, . The plots are generated from Equation (62); therefore, they represent the minimum relative viscosity plots for different multimodal suspensions. Interestingly, a large drop in relative viscosity can be observed when the modality of the suspension is increased at any given . However, the decrease in relative viscosity reaches a limit. The limiting relative viscosity plot corresponding to an infinitely multimodal suspension is given by the following Roscoe–Brinkman equation:
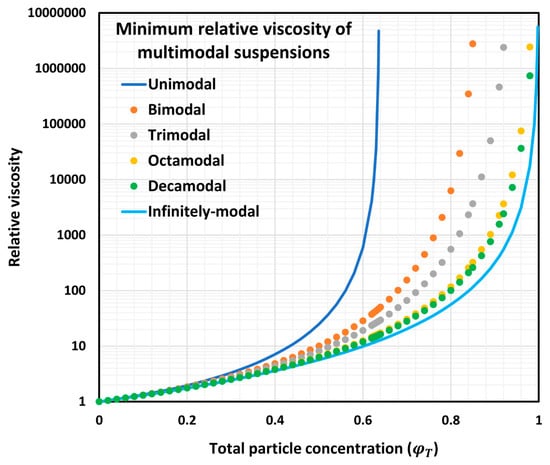
Figure 21.
Minimum relative viscosity of multimodal suspensions as a function of total particle concentration, .
This equation was originally derived by Roscoe [25] and Brinkman [26] independently to describe the relative viscosities of an infinitely multimodal suspension. Note that in this equation is the total particle concentration, .
6.3. Composition of Multimodal Suspensions at Minimum Relative Viscosity
Equation (62) allows the calculation of the minimum relative viscosity at a given for a multimodal suspension of any modality N. However, it does not give the composition of the multimodal suspension. For example, consider a trimodal suspension consisting of three different particle-size fractions: coarse, medium, and fine particles. For an engineer to formulate this trimodal suspension with a minimum viscosity at a given , it is important to know the composition in terms of the fractions of coarse, medium, and fine particles in the total mixture of particles.
The calculation of the composition of a suspension is complicated. We will consider only a trimodal suspension and develop equations to calculate the composition where the relative viscosity is minimum. A similar approach can be used for any other multimodal suspension. Let the total particle concentration be , the fraction of coarse particles in the particle mixture be , the fraction of medium-size particles be , and the fraction of fine particles be . From Equation (48), we can express the volumes of different fractions of particles as follows:
The fractions of different particle sizes in the mixture of particles are as follows:
By definition,
Thus, the fraction of coarse particles can be expressed as follows:
Using Equation (63), the fraction of medium-size particles in the particle mixture can be expressed as follows:
As at the minimum relative viscosity, the fractions , and can be expressed in terms of the known values of (Equation (61)) and as follows:
Table 5 summarizes the calculations for trimodal suspensions giving minimum relative viscosities and the corresponding compositions for different values of total particle concentration.

Table 5.
Minimum relative viscosity and corresponding composition of trimodal suspensions.
7. Conclusions
The relative viscosity models for suspensions of hard spheres proposed in the 21st century, along with the classical models of Mooney and Krieger–Dougherty, published in the 1950s, were reviewed, compared, and evaluated using a large pool of experimental data available on coarse suspensions, nanosuspensions, and coarse suspensions thickened by starch nanoparticles. The Mooney model (Equation (13)) gives the worst performance in that the magnitude of the average percentage error is extremely large (APRE > ), the Cheng et al. model (Equation (16)) is the second worst performer with APRE > 3531, the Krieger–Dougherty model (Equation (15)) underpredicts the relative viscosities of suspensions substantially to severely (23% < APRE < 48%), the Mendoza and Santamaria-Holek model (Equation (23)) underpredicts the relative viscosities substantially (10% < APRE < 25%), the Brouwers model (Equation (26)) overpredicts the relative viscosities substantially to severely (21% < APRE < 44%), Pal model P1 (Equation (35)) overpredicts the relative viscosities severely (26% < APRE < 57%), and Pal model P2 (Equation (41)) underpredicts the relative viscosities substantially to severely (23% < APRE < 43%).
Clearly, the best available model in terms of the predictability of the relative viscosity of suspensions is Pal model P3 (Equation (46)). It gives reasonably good predictions of relative viscosities. The average percentage error for this model is in the range of 3 to 6.5 (3% < APRE < 6.5%).
Finally, the viscous behavior of multimodal suspensions was simulated using the Pal model P3 of unimodal suspensions. The influence of increasing the modality of particle sizes on the viscosity of suspensions was discussed, and the relationships for the minimum viscosity and the corresponding compositions for multimodal suspensions were developed.
Funding
This research was funded by the Discovery Grant awarded to R.P. by the Natural Sciences and Engineering Research Council of Canada.
Data Availability Statement
The data presented in this study are available on request from the author.
Conflicts of Interest
The author declares no conflict of interest.
Nomenclature
| Greek Symbols | |
| Unit tensor | |
| Viscosity | |
| Viscosity of matrix phase (suspending medium) | |
| Relative viscosity | |
| High-frequency relative viscosity | |
| Experimental value of relative viscosity | |
| Relative viscosity predicted by the model | |
| Non-hydrodynamic contribution to relative viscosity (see Equation (16)) | |
| Bulk stress tensor | |
| Volume fraction of particles | |
| Effective volume fraction of particles | |
| Volume fraction of ith set of particles in a multimodal suspension, defined in Equations (48) and (49) | |
| Maximum packing volume fraction of particles where the viscosity of suspension diverges | |
| Volume fraction of nth set of particles in a multimodal suspension, defined in Equations (48) and (49) | |
| Volume fraction of different-size particles in a multimodal suspension corresponding to minimum relative viscosity of suspension (see Equation (61)) | |
| Total volume fraction of particles in a multimodal suspension, defined in Equation (51) | |
| Self-crowding parameter, defined in Equation (28) | |
| Latin Symbols | |
| a | Constant in Equation (42) |
| APRE | Average percentage relative error |
| b | Constant in Equation (42) |
| c | Self-crowding parameter (see Equation (22)) |
| Bulk rate of strain tensor | |
| Rate of strain tensor far away from the particle | |
| Fraction (volume basis) of coarse particles in a bimodal or trimodal mixture of particles | |
| Fraction (volume basis) of fine particles in a bimodal or trimodal mixture of particles | |
| Fraction (volume basis) of medium-sized particles in a trimodal mixture of particles | |
| GT | Glass transition point |
| H | Relative viscosity function |
| k | Aggregation coefficient (see Equation (42)) |
| n | Number of data points or nth set of particles in a multimodal suspension |
| N | Number of different-size particle fractions in a multimodal suspension, same as modality |
| P | Pressure |
| R | Radius of particle |
| RCP | Random close packing |
| Dipole strength of a single particle in an infinite matrix | |
| Volume of smallest-size particles in a multimodal suspension | |
| Volume of ith set of particles in a multimodal suspension | |
| Volume of suspending medium of a multimodal suspension | |
| Volume of nth set of particles in a multimodal suspension | |
| Volume of largest-size particles in a multimodal suspension | |
References
- Pal, R. Rheology of Particulate Dispersions and Composites; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Pal, R. Electromagnetic, Mechanical, and Transport Properties of Composite Materials; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Stickel, J.J.; Powell, R.L. Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 2005, 37, 127–149. [Google Scholar] [CrossRef]
- Denn, M.M.; Morris, J.F. Rheology of non-Brownian suspensions. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 203–228. [Google Scholar] [CrossRef] [PubMed]
- Guazzelli, E.; Pouliquen, O. Rheology of dense granular suspensions. J. Fluid. Mech. 2018, 852, P1. [Google Scholar] [CrossRef]
- Tadros, T.F. Suspension Concentrates: Preparation, Stability and Industrial Applications; De Gruyter: Berlin, Germany; Boston, MA, USA, 2017. [Google Scholar]
- Schramm, L.L. Emulsions, Foams, Suspensions, and Aerosols: Microscience and Applications; Wiley-VCH Verlag: Weinheim, Germany, 2014. [Google Scholar]
- Kulshreshtha, A.; Wall, M. Pharmaceutical Suspensions: From Formulation Development to Manufacturing; Springer: London, UK, 2010. [Google Scholar]
- Halloran, J.W.; Tomeckova, V. Flow behavior of polymerizable ceramic suspensions as function of ceramic volume fraction and temperature. J. Eur. Ceram. Soc. 2011, 31, 2535–2542. [Google Scholar]
- Camargo, I.L.; Morais, M.M.; Fortulan, C.A.; Branciforti, M.C. A review on the rheological behavior and formulations of ceramic suspensions for vat polymerization. Ceram. Int. 2021, 47, 11906–11921. [Google Scholar] [CrossRef]
- Zhou, W.; Li, D.; Wang, H. A novel aqueous ceramic suspension for ceramic stereolithography. Rapid Prototyp. J. 2010, 16, 29–35. [Google Scholar] [CrossRef]
- Pal, R. Modeling the viscosity of concentrated nanoemulsions and nanosuspensions. Fluids 2016, 1, 11. [Google Scholar] [CrossRef]
- Einstein, A. Eine neue Bestimmung der Molekuldimension. Ann. Phys. 1906, 19, 289–306. [Google Scholar] [CrossRef]
- Einstein, A. Berichtigung zumeiner Arbeit: Eine neue Bestimmung derMolekuldimension. Ann. Phys. 1911, 34, 591–592. [Google Scholar] [CrossRef]
- Batchelor, G.K. Effect of Brownian motion on bulk stress in a suspension of spherical particles. J. Fluid Mech. 1977, 83, 97–117. [Google Scholar] [CrossRef]
- Brady, J.F.; Bossis, G. Stokesian dynamics. Ann. Rev. Fluid Mech. 1988, 20, 111–157. [Google Scholar] [CrossRef]
- Ladd, A.J.C. Hydrodynamic transport coefficients of random dispersions of hard spheres. J. Chem. Phys. 1990, 93, 3483–3494. [Google Scholar] [CrossRef]
- Wang, G.; Fiore, A.M.; Swan, J.W. On the viscosity of adhesive hard sphere dispersions: Critical scaling and the role of rigid contacts. J. Rheol. 2019, 63, 229–245. [Google Scholar] [CrossRef]
- Taylor, G.I. The viscosity of a fluid containing small drops of another liquid. Proc. R. Soc. Lond. A 1932, 138, 41–48. [Google Scholar]
- Vand, V. Viscosity of solutions and suspensions. 1. Theory. J. Phys. Colloid Chem. 1948, 52, 277–299. [Google Scholar] [CrossRef]
- Vand, V. Viscosity of solutions and suspensions. II. Experimental determination of the viscosity-concentration function of spherical inclusions. J. Phys. Colloid Chem. 1948, 52, 300–314. [Google Scholar] [CrossRef]
- Ward, S.G.; Whitmore, R.L. Studies of the viscosity and sedimentation of suspensions Part 1.—The viscosity of suspension of spherical particles. Br. J. Appl. Phys. 1950, 1, 286–290. [Google Scholar] [CrossRef]
- Saito, N. Concentration dependence of the viscosity of high polymer solutions. J. Phys. Soc. 1950, 5, 4–8. [Google Scholar] [CrossRef]
- Mooney, M. The viscosity of a concentrated suspension of spherical particles. J. Colloid Sci. 1951, 6, 162–170. [Google Scholar] [CrossRef]
- Roscoe, R. The viscosity of suspensions of rigid spheres. Br. J. Appl. Phys. 1952, 3, 267–269. [Google Scholar] [CrossRef]
- Brinkman, H.C. The viscosity of concentrated suspensions and solutions. J. Chem. Phys. 1952, 20, 571–581. [Google Scholar] [CrossRef]
- Simha, R. A treatment of the viscosity of concentrated suspensions. J. Appl. Phys. 1952, 23, 1020–1024. [Google Scholar] [CrossRef]
- Oldroyd, J.G. The elastic and viscous properties of emulsions and suspensions. Proc. R. Soc. Lond. A 1953, 218, 122–132. [Google Scholar]
- Manley, R.S.J.; Mason, S.G. The viscosity of suspensions of spheres: A note on the particle interaction coefficient. Can. J. Chem. 1954, 32, 763–767. [Google Scholar] [CrossRef]
- Van der Waarden, M. Viscosity and electroviscous effect of emulsions. J. Colloid Sci. 1954, 9, 215–222. [Google Scholar] [CrossRef]
- Maron, S.H.; Pierce, P.E. Application of Ree-Eyring generalized flow theory to suspensions of spherical particles. J. Colloid Sci. 1956, 11, 80–95. [Google Scholar] [CrossRef]
- Happel, J. Viscosity of suspensions of uniform spheres. J. Appl. Phys. 1957, 28, 1288–1292. [Google Scholar] [CrossRef]
- Ting, A.P.; Luebbers, R.H. Viscosity of suspensions of spherical and other isodimensional particles in liquids. AIChE J. 1957, 3, 111–116. [Google Scholar] [CrossRef]
- Krieger, I.M.; Dougherty, T.J. Mechanism for non-Newtonian flow in suspensions of rigid particles. Trans. Soc. Rheol. 1959, 3, 137–152. [Google Scholar] [CrossRef]
- Rutgers, R. Relative viscosity of suspensions of rigid spheres in Newtonian liquids. Rheol. Acta 1962, 2, 202–210. [Google Scholar] [CrossRef]
- Thomas, D.G. Transport characteristics of suspensions: VIII. A note on the viscosity of Newtonian suspensions of uniform spherical particles. J. Colloid Sci. 1965, 20, 267–277. [Google Scholar]
- Frankel, N.A.; Acrivos, A. On the viscosity of a concentrated suspension of solid spheres. Chem. Eng. Sci. 1967, 22, 847–853. [Google Scholar] [CrossRef]
- Chong, J.S.; Christiansen, E.B.; Baer, A.D. Rheology of concentrated suspensions. Trans. Soc. Rheol. 1968, 12, 281–301. [Google Scholar] [CrossRef]
- Lewis, T.B.; Nielsen, L.E. Viscosity of dispersed and aggregated suspensions of spheres. J. Rheol. 1968, 12, 421–443. [Google Scholar] [CrossRef]
- Batchelor, G.K.; Green, J.T. The determination of the bulk stress in a suspension of spherical particles to order c2. J. Fluid Mech. 1972, 56, 401–427. [Google Scholar] [CrossRef]
- Yaron, I.; Gal-Or, B. On viscous flow and effective viscosity of concentrated suspensions and emulsions. Rheol. Acta 1972, 11, 241–252. [Google Scholar] [CrossRef]
- Smith, J.H. Rheology of Concentrated Suspensions of Spheres. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1972. [Google Scholar]
- Jeffrey, D.J.; Acrivos, A. The rheological properties of suspensions of rigid particles. AIChE J. 1976, 22, 417–432. [Google Scholar] [CrossRef]
- Quemada, D. Rheology of concentrated disperse systems and minimum energy dissipation principle: 1. Viscosity-concentration relationship. Rheol. Acta 1977, 16, 82–94. [Google Scholar] [CrossRef]
- Graham, A.L. On the viscosity of suspensions of solid spheres. Appl. Sci. Res. 1981, 37, 275–286. [Google Scholar] [CrossRef]
- Graham, A.L.; Bird, R.B. Particle clusters in concentrated suspensions. 1. Experimental observations of particle clusters. Ind. Eng. Chem. Fundam. 1984, 23, 406–410. [Google Scholar] [CrossRef]
- Metzner, A.B. Rheology of Suspensions in Polymeric Liquids. J. Rheol. 1985, 29, 739–775. [Google Scholar] [CrossRef]
- Poslinski, A.J.; Ryan, M.E.; Gupta, R.K.; Seshadri, S.G.; Frechette, F.J. Rheological behavior of filled polymeric systems I. Yield stress and shear-thinning effects. J. Rheol. 1988, 32, 703–735. [Google Scholar] [CrossRef]
- Poslinski, A.J.; Ryan, M.E.; Gupta, R.K.; Seshadri, S.G.; Frechette, F.J. Rheological behavior of filled polymeric systems II. The effect of a bimodal size distribution of particulates. J. Rheol. 1988, 32, 751–771. [Google Scholar]
- Pal, R.; Rhodes, E. Viscosity/concentration relationships for emulsions. J. Rheol. 1989, 33, 1021–1045. [Google Scholar] [CrossRef]
- Park, M.; Gandhi, K.; Sun, L.; Salovey, R. Model-filled polymers. III: Rheological behavior of polystyrene containing cross-linked polystyrene beads. Polym. Sci. Eng. 1990, 30, 1158–1164. [Google Scholar]
- Jones, A.A.R.; Leary, B.; Boger, D.V. The rheology of a concentrated colloidal suspension of hard spheres. J. Colloid Interface Sci. 1991, 147, 479–495. [Google Scholar] [CrossRef]
- Jones, A.A.R.; Leary, B.; Boger, D.V. The rheology of a sterically stabilized suspension at high concentration. J. Colloid Interface Sci. 1992, 150, 84–96. [Google Scholar] [CrossRef]
- Ilic, V.; Phan-Thien, N. Viscosity of concentrated suspensions of spheres. Rheol. Acta 1994, 33, 283–291. [Google Scholar] [CrossRef]
- Pal, R. Rheology of emulsions containing polymeric liquids. In Encyclopedia of Emulsion Technology; Chapter, 3, Becher, P., Eds.; Dekker: New York, NY, USA, 1996; Volume 4. [Google Scholar]
- Weiss, A.; Dingenouts, N.; Ballaquff, M.; Senf, H.; Richtering, W. Comparison of the effective radius of sterically stabilized latex particles determined by small angle X-ray scattering and by zero shear viscosity. Langmuir 1998, 14, 5083–5087. [Google Scholar] [CrossRef]
- Pal, R. Linear viscoelastic behavior of multiphase dispersions. J. Colloid Interface Sci. 2000, 232, 50–63. [Google Scholar] [CrossRef]
- Zarraga, I.E.; Hill, D.A.; Leighton, D.T. The characterization of the total stress of concentrated suspensions of noncolloidal spheres in Newtonian fluids. J. Rheol. 2000, 44, 185–220. [Google Scholar] [CrossRef]
- Pal, R. Evaluation of theoretical viscosity models for concentrated emulsions at low capillary numbers. Chem. Eng. J. 2001, 81, 15–21. [Google Scholar] [CrossRef]
- Pal, R. Novel viscosity equations for emulsions of two immiscible liquids. J. Rheol. 2001, 45, 509–520. [Google Scholar] [CrossRef]
- Pal, R. Complex shear modulus of concentrated suspensions of solid spherical particles. J. Colloid Interface Sci. 2002, 245, 171–177. [Google Scholar] [CrossRef] [PubMed]
- Pal, R. A new linear viscoelastic model for emulsions and suspensions. Poly. Eng. Sci. 2008, 48, 1250–1253. [Google Scholar] [CrossRef]
- Mendoza, C.I.; Santamaria-Holek, I. The rheology of hard sphere suspensions at arbitrary volume fractions: An improved differential viscosity model. J. Chem. Phys. 2009, 130, 044904. [Google Scholar]
- Brouwers, H.J.H. Viscosity of a concentrated suspension of rigid monosized particles. Phys. Rev. E 2010, 81, 051402. [Google Scholar] [CrossRef]
- Pal, R. Rheology of simple and multiple emulsions. Curr. Opin. Coll. Interface Sci. 2011, 16, 41–60. [Google Scholar] [CrossRef]
- Tanner, R.I.; Qi, F.; Dai, S. Scaling the normal stresses in concentrated non-colloidal suspensions of spheres. Rheol. Acta 2013, 52, 291–295. [Google Scholar] [CrossRef]
- Pal, R. New models for the viscosity of nanofluids. J. Nanofluids 2014, 3, 260–266. [Google Scholar] [CrossRef]
- Pal, R. Rheology of suspensions of solid particles in power-law fluids. Can. J. Chem. Eng. 2015, 93, 166–173. [Google Scholar] [CrossRef]
- Pal, R. A new model for the viscosity of asphaltene solutions. Can. J. Chem. Eng. 2015, 93, 747–755. [Google Scholar] [CrossRef]
- Faroughi, S.A.; Huber, C. A generalized equation for rheology of emulsions and suspensions of deformable particles subjected to simple shear at low Reynolds number. Rheol. Acta 2015, 54, 85–108. [Google Scholar] [CrossRef]
- Pal, R. Viscosity-concentration relationships for nanodispersions based on glass transition point. Can. J. Chem. Eng. 2017, 95, 1605–1614. [Google Scholar] [CrossRef]
- Pal, R. New generalized viscosity model for non-colloidal suspensions and emulsions. Fluids 2020, 5, 150. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhu, J.; Chaikin, P.M.; Phan, S.E.; Russel, W.B. Nature of dicergence in low shear viscosity of colloidal hard-sphere dispersions. Phys. Rev. E 2002, 65, 041405. [Google Scholar] [CrossRef]
- Boyer, F.; Guazzelli, E.; Pouliquen, O. Unifying suspension and granular rheology. Phys. Rev. Lett. 2011, 107, 188301. [Google Scholar] [CrossRef]
- Wilms, P.; Hinrichs, J.; Kohlus, R. Macroscopic rheology of non-Brownian suspensions at high shear rates: The influence of solid volume fraction and non-Newtonian behaviour of the liquid phase. Rheol. Acta 2022, 61, 123–138. [Google Scholar]
- De Kruif, C.G.; Van Lersel, E.M.F.; Vrij, A.; Russel, W.B. Hard sphere colloidal dispersions: Viscosity as a function of shear rate and volume fraction. J. Chem. Phys. 1985, 83, 4717–4725. [Google Scholar]
- Van der Werff, J.C.; De Kruif, C.J. Hard-sphere colloidal dispersions: The scaling of rheological properties with particle size, volume fraction, and shear rate. J. Rheol. 1989, 33, 421–454. [Google Scholar]
- Rodriguez, B.E.; Kaler, E.W.; Wolfe, M.S. Binary mixtures of monodisperse latex dispersions. Viscosity. Langmuir 1992, 8, 2382–2389. [Google Scholar] [CrossRef]
- Shikata, T.; Pearson, D.S. Viscoelastic behavior of concentrated spherical suspensions. J. Rheol. 1994, 38, 601–616. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Desgranges, F.; Roy, G.; Galanis, N.; Mare, T.; Boucher, S.; Angue Mintsa, H. Temperature and particle-size dependent viscosity data for water-based nanofluids-hysteresis phenomenon. Int. J. Heat Fluid Flow 2007, 28, 1492–1506. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Desgranges, F.; Galanis, N.; Roy, G.; Mare, T.; Boucher, S.; Angue Mintsa, H. Viscosity data for Al2O3 nanofluid-hysteresis: Is heat transfer enhancement using nanofluids reliable? Int. J. Therm. Sci. 2008, 47, 103–111. [Google Scholar]
- Ghanaatpishehsanaei, G.; Pal, R. Rheology of suspensions of solid particles in liquids thickened by starch nanoparticles. Colloids Interfaces 2023, 7, 52. [Google Scholar] [CrossRef]
- Tanner, R.I. Review Article: Aspects of non-colloidal suspension rheology. Phys. Fluids 2018, 30, 101301. [Google Scholar]
- Morris, J.F. Shear thickening of concentrated suspensions: Recent developments and relation to other phenomenon. Ann. Rev. Fluid Mech. 2020, 52, 121–144. [Google Scholar]
- Farris, R.J. Prediction of the viscosity of multimodal suspensions from unimodal viscosity data. J. Rheol. 1968, 12, 281–301. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).