Effects of Temperature and Axial Strain on Four-Wave Mixing Parametric Frequencies in Microstructured Optical Fibers Pumped in the Normal Dispersion Regime

Abstract

A study of the effect of temperature and axial strain on the parametric wavelengths produced by four-wave mixing in microstructured optical fibers is presented. Degenerate four-wave mixing was generated in the fibers by pumping at normal dispersion, near the zero-dispersion wavelength, causing the appearance of two widely-spaced four-wave mixing spectral bands. Temperature changes, and/or axial strain applied to the fiber, affects the dispersion characteristics of the fiber, which can result in the shift of the parametric wavelengths. We show that the increase of temperature causes the signal and idler wavelengths to shift linearly towards shorter and longer wavelengths, respectively. For the specific fiber of the experiment, the band shift at rates –0.04 nm/ºC and 0.3 nm/ºC, respectively. Strain causes the parametric bands to shift in the opposite way. The signal band shifted 2.8 nm/mε and the idler −5.4 nm/mε. Experimental observations are backed by numerical simulations.

1. Introduction

Four-wave mixing (FWM) is a third-order nonlinear parametric effect [1], where two photons of the pump are annihilated and two new photons are created at different frequencies. In the frequency domain, FWM leads to the generation of two sidebands about the pump. The parametric wavelengths of the signal and idler waves are determined by the conservation of energy and momentum. In the context of optical fibers, FWM has been extensively studied over the last decades. Wavelength converters and fiber optical parametric oscillators based on FWM have been successfully developed in the past [2,3]. Recently, degenerated FWM has been proposed as an efficient method for the generation of correlated photon pairs [4]. When the chromatic dispersion of the fiber is anomalous at the pump wavelength, the parametric wavelength of signal and idler waves are close to the pump wavelength, and they depend strongly on the pump power. This regime is also known as modulation instability. When the dispersion of the fiber at the pump wavelength is normal, and the pump wavelength is relatively close to a zero dispersion wavelength (ZDW), two widely-spaced parametric bands can be generated.

Microstructured optical fibers (MOF) exhibit unique guidance properties, which makes the generation of nonlinear effects, and more specifically FWM processes, more efficient [5]. MOFs can be fabricated with engineered dispersion properties and very small modal area, which leads to a very efficient nonlinear response, despite the low nonlinearity of silica. The experimental generation of widely spaced FWM bands in MOFs pumped at normal dispersion has also been reported [6,7].

The parametric wavelengths of the signal and idler waves generated by FWM in an optical fiber depend strongly on the dispersion properties of the fiber [1]. Any change of the fiber dispersion characteristics caused by any external factor leads to the shift of the parametric bands. As mentioned before, phase-matching can be found in both, anomalous and normal dispersion regimes. However, it is worth to note that the sensitivity of the parametric frequencies to changes of the fiber dispersion properties is much larger when the dispersion of the fiber at the pump wavelength is normal and, consequently, widely spaced FWM bands are generated. In this work, we report an experimental investigation on the effects of temperature and axial strain on the FWM parametric wavelengths generated in MOFs pumped at normal dispersion. Numerical simulations that support the experimental observations are also included.

2. Experimental Setup and Characteristics of the MOFs

FWM was produced in normal dispersion MOFs using a compact Q-switched Nd:YAG microchip laser emitting 0.72 ns pulses at 1064 nm wavelength. The repetition rate of the microchip laser was 19.9 kHz and it provides an average output power of 160 mW. Aspheric lenses were used to launch the laser beam into the core of the fibers. A half-wave plate was used to rotate the polarization axes of the beam with respect to the polarization axes of the MOFs. The light at the output of the MOFs was collected with a multimode fiber and the spectrum was recorded with an optical spectrum analyzer.

Figure 1 shows an image taken with a scanning electronic microscope (SEM) of the cross-section of a MOF used in the experiments. The fibers were fabricated in our laboratory following the stack-and-draw technique. The central region of the core is doped with GeO₂ (Δn = 0.025). Table 1 gives the structural parameters of the fibers. The transmission loss of the fibers at 1064 nm was below 0.05 dB/m (detection limit of our setup). The chromatic dispersion characteristics of the fibers were measured experimentally using an interferometric method similarly as it is described in [8]. Figure 2a shows the dispersion of the MOFs as a function of wavelength. Within the experimental wavelength range, the dispersion of both fibers show a unique zero-dispersion wavelength (λ_Z), at 1100 nm and 1080 nm, respectively. Figure 2b shows an example of a typical spectrum obtained in the experiments, where optical parametric generation in the normal dispersion regime is clearly observed. Along with the residual 1064 nm pump, signal and idler bands can be observed. The experiments were done with fiber sections of about 2 m long.

Figure 1. SEM image of the cross section of one of the MOFs used in the experiments.

Figure 1. SEM image of the cross section of one of the MOFs used in the experiments.

Table 1. Structural parameters of the two fibers used in the experiments. Λ: pitch; d: hole diameter; D_n: diameter of the GeO₂ area.

	Λ (μm)	d/Λ (μm)	Dn (μm)	λZ (nm)
Fiber I	3.0	0.56	1.3	1100
Fiber II	2.5	0.52	1.2	1080

Table 1. Structural parameters of the two fibers used in the experiments. Λ: pitch; d: hole diameter; D_n: diameter of the GeO₂ area.

	Λ (μm)	d/Λ (μm)	Dn (μm)	λZ (nm)
Fiber I	3.0	0.56	1.3	1100
Fiber II	2.5	0.52	1.2	1080

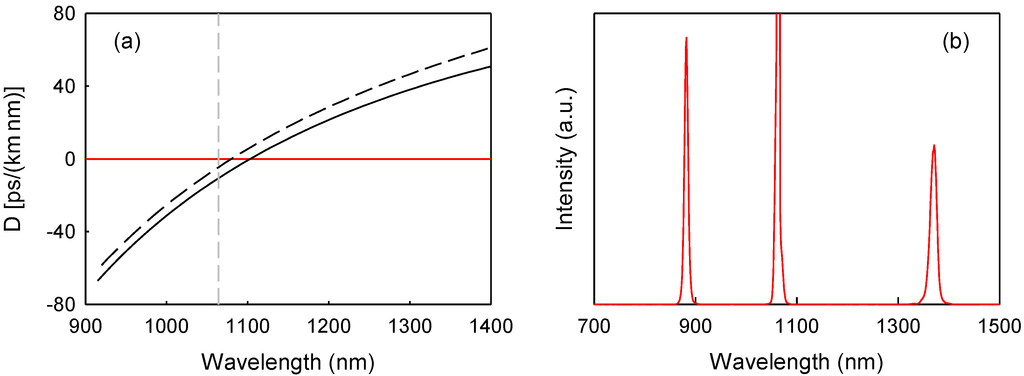
Figure 2. (a) Measured chromatic dispersion as a function of wavelength of fiber I (solid line) and fiber II (dashed line). The vertical dashed line indicates the wavelength of the pump laser used in the experiments, 1064 nm. (b) An example of the spectrum recorded in the experiments using fiber-II.

Figure 2. (a) Measured chromatic dispersion as a function of wavelength of fiber I (solid line) and fiber II (dashed line). The vertical dashed line indicates the wavelength of the pump laser used in the experiments, 1064 nm. (b) An example of the spectrum recorded in the experiments using fiber-II.

3. Experimental Results

3.1. Parametric Wavelengths vs. Temperature

In a first experiment, we investigated the effect of temperature on the FWM parametric wavelengths using fiber-I. The temperature of the MOF was varied from 10 ºC to 70 ºC by immersion of the fiber in a thermal bath. Special care was taken to keep as short as possible the section of fiber between the input end face and the immersed section, to avoid the generation of FWM in that fiber section. Figure 3a,b shows the shift of the signal and idler parametric bands as a function of temperature. Both parametric wavelengths show a rather linear response to temperature. The signal band shifts towards shorter wavelengths while the idler band shifts towards longer wavelengths, thus, increasing the wavelength gap between them. The shift rates are –0.04 nm/ºC for the signal wavelength and 0.3 nm/ºC for the idler band.

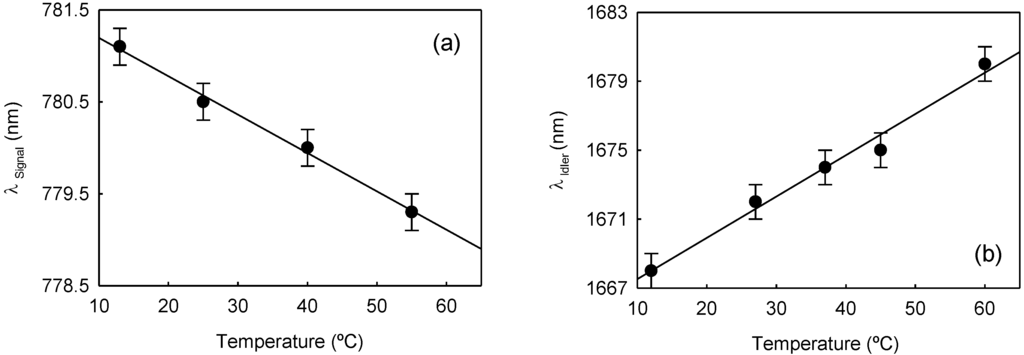
Figure 3. Signal (a) and idler (b) wavelengths as a function of the fiber temperature.

Figure 3. Signal (a) and idler (b) wavelengths as a function of the fiber temperature.

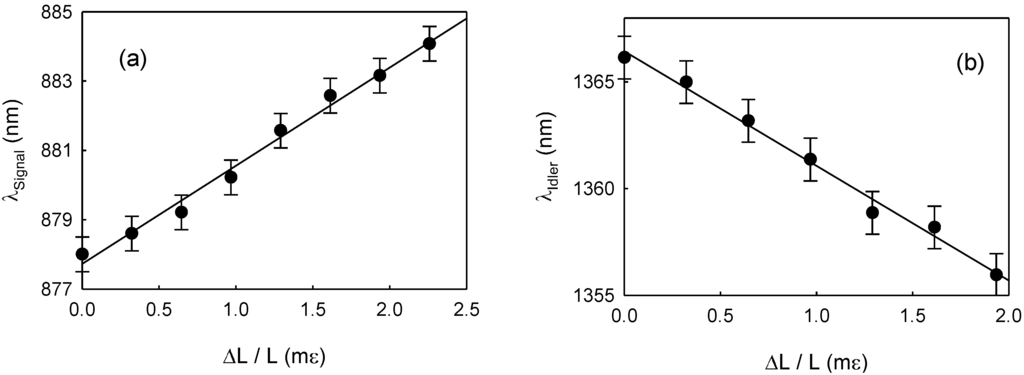
Figure 4. Signal (a) and idler (b) wavelengths as a function of the axial strain.

Figure 4. Signal (a) and idler (b) wavelengths as a function of the axial strain.

3.2. Parametric Wavelengths vs. Axial Strain

In a second experiment, we analyzed the shift of the parametric FWM bands with axial strain using fiber-II. Axial strain was applied to the fiber by fixing one end to a fixed post and the other end to a linear translation stage. As in the previous experiment, care was taken to keep as short as possible the unstrained fiber section at the input fiber end. Figure 4a,b shows the shift of the signal and idler parametric bands generated in fiber II as a function of the axial strain applied to the fiber. A linear response is observed again. The increase of axial strain causes the reduction of the wavelength gap between signal and idler waves. The signal band shifts towards longer wavelengths at a rate of 2.8 nm/mε, while the idler band shifts towards shorter wavelengths at a rate of −5.4 nm/ mε. It is worth to note that the sensitivity to axial strain reported here is more than one order of magnitude larger than in a previous report [9] where a strain sensor based on four-wave mixing generated in a microstructured optical fiber pumped in the anomalous dispersion regime is demonstrated.

4. Discussion

For quasi-continuous pump, degenerate FWM is governed by the dispersion properties of the fiber through the phase matching condition [1]:

$$2\cdot \beta ({\omega }_p)=\beta ({\omega }_i)+\beta ({\omega }_s)+2\cdot \gamma \cdot P$$

(1)

where β(ω) is the propagation factor of the fiber, ω_p, ω_s, and ω_i are the angular frequencies of the pump, signal, and idler fields, γ is the nonlinear coefficient, and P is the pump power. Equation (1) together with the conservation of energy determines the frequencies of the parametric bands.

The aim of the numerical calculations included in the following sections is to provide just a qualitative description of the effects observed experimentally. The simulations presented were done for a representative all-silica MOF with Λ = 4.0 μm, d/Λ = 0.5. A quantitative analysis of the experimental results would require a more accurate modeling of the fibers taking into account the content of GeO₂ at the core.

4.1. The Effect of Temperature

Changes of temperature of the MOF affects the refractive index through the thermo-optic effect, and it also affects the cross-sectional dimensions because of thermal expansion. This results in the shift of λ_Z towards longer wavelengths as the temperature of the fiber was increased, and consequently, the wavelengths of the signal and idler waves shift towards shorter and longer wavelengths, respectively. Numerical calculations of the effect of temperature on the fiber chromatic dispersion, and on the idler and signal wavelengths were carried out. For each temperature, the linear guiding properties were calculated using the method described in [10]. The thermo-optic properties of silica were taken from [11], and the typical thermal expansion coefficient of 0.5 × 10^–6 ºC^–1 was assumed. It was assumed that thermal expansion of the fiber because of a temperature change causes a change of Λ proportional to the fiber diameter variation, but the air-filling fraction is preserved. Inset of Figure 5a shows the chromatic dispersion vs. wavelength for two fiber temperatures. We found that, within the temperature variation range of the experiments, λ_Z shifts linearly with temperature towards longer wavelengths. For these specific fiber parameters, the shift rate is 23 pm/ºC.

The parametric wavelengths were obtained by imposing the conservation of energy and momentum Equation (1). Figure 5b shows the parametric wavelengths as a function of pump wavelength around 1064 nm, at room temperature and when the temperature was increased in 50 ºC. As it was observed experimentally, the wavelength gap between the signal and idler waves increases with temperature. Figure 5c,d shows the shift of the parametric wavelengths as a function of temperature. For both waves, the corresponding wavelengths show a linear dependency on temperature. The slopes are –0.09 nm/ºC and 0.29 nm/ºC, respectively, which agree qualitatively with the experimental results.

4.2. The Effect of Axial Strain

Axial strain affects the refractive index of the fiber through the elasto-optic effect. The change of refractive index can be calculated by [12]:

$$\Delta n=-\frac{1}{2}{n}^3((1-\mu )P_{12}-\mu \cdot P_{11})\frac{\Delta L}{L}$$

(2)

where μ is the Poisson coefficient, P₁₁ and P₁₂ are elements of the elasto-optic tensor and ΔL/L is the strain. Additionally, the cross-sectional structural parameters of the fiber, in particular the pitch Λ, change with strain since the fiber diameter decreases when a given amount of axial strain is applied. The change of Λ is determined by the change of the fiber radius R, which can be calculated by:

$$\frac{\Delta \text{Λ}}{\text{Λ}}=\frac{\Delta R}{R}\approx -\mu \frac{\Delta L}{L}$$

(3)

We analyzed numerically the effect of axial strain on the chromatic dispersion, and on the idler and signal wavelengths. The elasto-optic coefficients and the Poisson ratio used in the calculations were the typical for silica (P₁₁ = 0.121, P₁₂ = 0.270, μ = 0.16). Figure 6a shows the chromatic dispersion for two strain values in the vicinity of λ_Z. The calculations show that λ_Z shifts towards shorter wavelengths as the strain is increased. For small strain values, λ_Z shifts linearly with the strain. For this specific fiber, the λ_Z shift is –0.15 nm/mε.

Figure 6b shows the parametric wavelengths as a function of pump wavelength around 1064 nm, in two cases: ΔL/L = 0 and ΔL/L = 2 mε. Signal and idler bands shift towards longer and shorter wavelengths, respectively, in accordance with λ_Z. Figure 6c,d shows the shift of the signal and idler wavelengths, respectively, as a function of strain. Again, the wavelength shift shows a linear dependence on strain as it was observed experimentally. The slopes are 0.7 nm/mε and ‒2.3 nm/mε, respectively.

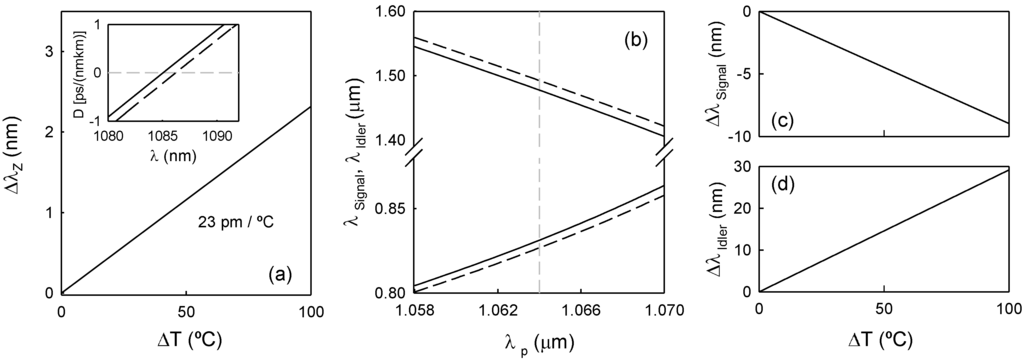
Figure 5. (a) Numerical calculation of the zero-dispersion wavelength shift as a function of temperature. Inset shows the dispersion around λ_Z, for ΔT = 0 ºC (solid line) and ΔT = 50 ºC (dashed line). (b) Calculation of signal and idler wavelengths as a function of pump wavelength, for ΔT = 0 ºC (solid line) and ΔT = 50 ºC (dashed line). The dashed vertical line indicates the experimental pump wavelength of 1064 nm. The shift of signal and idler wavelengths with temperature, for 1064 nm pump wavelength, is shown in (c) and (d), respectively. The fiber structural parameters used for calculations are Λ = 4.0 μm, d/Λ = 0.5.

Figure 5. (a) Numerical calculation of the zero-dispersion wavelength shift as a function of temperature. Inset shows the dispersion around λ_Z, for ΔT = 0 ºC (solid line) and ΔT = 50 ºC (dashed line). (b) Calculation of signal and idler wavelengths as a function of pump wavelength, for ΔT = 0 ºC (solid line) and ΔT = 50 ºC (dashed line). The dashed vertical line indicates the experimental pump wavelength of 1064 nm. The shift of signal and idler wavelengths with temperature, for 1064 nm pump wavelength, is shown in (c) and (d), respectively. The fiber structural parameters used for calculations are Λ = 4.0 μm, d/Λ = 0.5.

Figure 6. (a) Numerical calculation of the zero-dispersion wavelength shift as a function of axial strain. Inset shows the dispersion around λ_Z, for ΔL/L = 0 (solid line) and ΔL/L = 2 mε (dashed line). (b) Calculation of signal and idler wavelengths as a function of pump wavelength, for ΔL/L = 0 (solid line) and ΔL/L = 2 mε (dashed line). The dashed vertical line indicates the experimental pump wavelength of 1064 nm. The shift of signal and idler wavelengths with axial strain, for 1064 nm pump wavelength, is shown in (c) and (d), respectively. The fiber structural parameters used for calculations are Λ = 4.0 μm, d/Λ = 0.5.

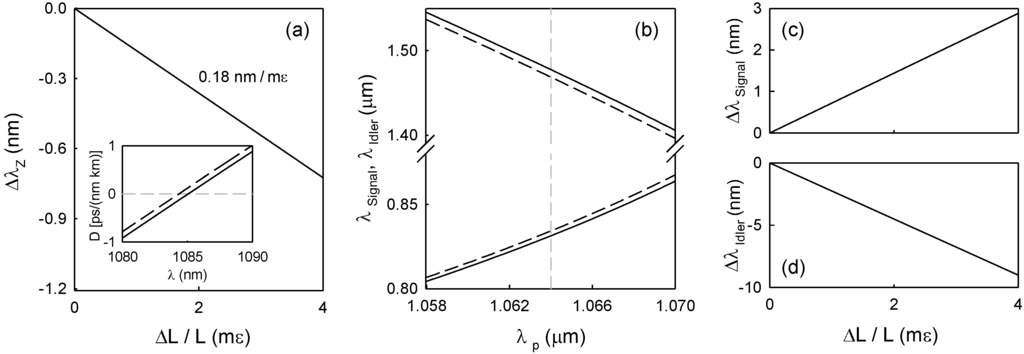
Figure 6. (a) Numerical calculation of the zero-dispersion wavelength shift as a function of axial strain. Inset shows the dispersion around λ_Z, for ΔL/L = 0 (solid line) and ΔL/L = 2 mε (dashed line). (b) Calculation of signal and idler wavelengths as a function of pump wavelength, for ΔL/L = 0 (solid line) and ΔL/L = 2 mε (dashed line). The dashed vertical line indicates the experimental pump wavelength of 1064 nm. The shift of signal and idler wavelengths with axial strain, for 1064 nm pump wavelength, is shown in (c) and (d), respectively. The fiber structural parameters used for calculations are Λ = 4.0 μm, d/Λ = 0.5.

5. Conclusions

We have studied experimentally the shift with temperature and strain of the FWM parametric bands generated in MOFs pumped at normal dispersion near the ZDW. With temperature, the signal and idler wavelengths shift linearly towards shorter and longer wavelengths, respectively. For the specific fiber of the experiment, the bands’ shift rates are –0.04 nm/ºC and 0.3 nm/ºC, respectively. Strain causes the FWM bands to shift in the opposite way. The signal band shifted 2.8 nm/mε and the idler −5.4 nm/mε. Numerical simulations are in good agreement with experimental results.