Variable-Step-Size Efficient Proportionate Affine Projection Sign Algorithms

Abstract

For sparse system identification, a memory-improved proportionate affine projection sign algorithm with a simplified, generalized correntropy induced metric (SGCI-M-IPAPSA) has good filtering performance. However, the SGCI-M-IPAPSA is based on a fixed step size and is not always the best choice. To overcome the limitation of a fixed step size in filtering precision and convergence speed under non-Gaussian impulsive interferences, in this paper, we apply the combined-step-size idea and a variable-step-size method based on the mean-square deviation to the SGCI-M-IPAPSA, respectively, and propose two new robust algorithms to enhance the filtering performance of the SGCI-M-IPAPSA. In addition, by combining the combined-step-size and proposed variable-step-size methods, we propose a fresh combined variable-step-size way and apply it to the SGCI-M-IPAPSA. The convergence of the proposed algorithms is also elaborated, and a conditional decision on the mean-square error is used to cope with abrupt changes. The better performances of the proposed algorithms than the conventional SGCI-M-IPAPSA in terms of the filtering accuracy and convergence rate are demonstrated with non-Gaussian impulsive interferences for sparse system identification, abrupt changes and colored inputs.

1. Introduction

Sparse adaptive filtering algorithms (AFAs) have attracted a lot of attention in the past few years because of their ability to echo a cancellation application or efficiently identify systems that are sparse and unrecognized [1]. Additionally, the characterized impulse response is composed of many coefficients close to zero [2,3]. A (improved) proportionate method was applied to the NLMS (normalized least mean-square), yielding (I)PNLMS, which obtains better performance in terms of filtering accuracy and convergence rate in comparison to the NLMS in sparse systems. Furthermore, with the developed proportionate idea, the affine projection (AP) algorithm was proposed to reduce the steady-state misadjustment and improve the convergence rate of (I)PNLMS for colored inputs [4,5].

Regrettably, based on the ${\mathsf{\ell }}_2$ minimization criterion, the above-mentioned algorithms result in a degradation of performance when the signals are disturbed in the presence of non-Gaussian noise [5]. To overcome the interference of impulse noise, some algorithms using the mixed p-norm optimization [6,7] and the affine projection sign algorithm (APSA) composed of the AP and sign algorithm (SA) with the ${\mathsf{\ell }}_1$ minimization criterion have been proposed [8,9]. Thus, based on efficient proportionate ways, some sparse APSA-type algorithms including the (improved) proportionate APSA ((I)PAPSA), generalized correntropy induced metric (GCIM) memory IPAPSA (GCI-M-IPAPSA) and the simplified GCI-M-IPAPSA (SGCI-M-IPAPSA) are proposed [10,11,12,13]. Generally, a proper step size is needed when choosing for the SGCI-M-IPAPSA to meet the demand of a high filtering accuracy and a fast convergence rate. The tradeoff between the filtering accuracy and convergence rate is obvious with the fixed-step-size SGCI-M-IPAPSA. For addressing this issue, a weight transfer method of two SGCI-M-IPAPSA (CSGCI-M-IPAPSA) is proposed in [11], which enhances the filtering performance of the SGCI-M-IPAPSA and adopts a convex combination or variable-step-size (VSS) strategy. The diversity of the varying step size affects the performance of algorithms. Therefore, two classes of the VSS-type algorithms (VSS-APSA and combined-step-size (CSS) APSA) are proposed [14,15]. Additionally, these two VSS methods are the better choice than a convex combination, which is used in [11,16].

In this paper, applying the efficient combined-step-size method to the algorithm SGCI-M-IPAPSA yields the CSS-SGCI-M-IPAPSA. Here, we rewrite the CSS method and reduce the operation of variables associated with two different step sizes in comparison with the conventional combined step size. Additionally, a VSS way based on the mean-square deviation is proposed and applied to the SGCI-M-IPAPSA. In addition, we combine the CSS and VSS ways and propose a new combined variable-step-size (CVSS) method. This new derived CVSS method is an extension of the CSS or VSS way and has much greater potential. Thus, the SGCI-M-IPAPSA based on the CVSS method named as the CVSS-SGCI-M-IPAPSA is proposed. To further improve the proposed algorithms’ tracking capabilities, a conditional decision on mean-square error (MSE) [14] is used. Furthermore, the convergence of the proposed algorithms is elaborated. For colored inputs, simulation results demonstrate the excellent filtering performance with respect to filtering accuracy, convergence rate and tracking performance of the proposed algorithms in sparse system identifications and abrupt changes with non-Gaussian impulsive interferences.

2. Review of the GCI-M-IPAPSA

We consider the desired output signal (DOS) $d\left(k_{\tau }\right)$ as

$$d\left(k_{\tau }\right)={\mathit{w}}_{ot}^T\mathit{u}\left(k_{\tau }\right)+{\mathit{v}}_M\left(k_{\tau }\right),$$

(1)

where $k_{\tau }$ represents the instant time, ${\mathit{w}}_{ot}\in {\mathbb{R}}^{M\times 1}$ needs to be estimated and denotes an unrecognized weight column vector (CV), an input CV is written as $\mathit{u}\left(k_{\tau }\right)=[u\left(k_{\tau }\right),u(k_{\tau }-1),$$\dots ,u(k_{\tau }-M+1){]}^T\in {\mathbb{R}}^{M\times 1}$, superscript T transposes a vector or matrix and ${\mathit{v}}_M\left(k_{\tau }\right)\in {\mathbb{R}}^{M\times 1}$ is the measurement noise.

We define the DOS $\mathit{d}\left(k_{\tau }\right)$, the input matrix $\mathit{U}\left(k_{\tau }\right)$ and the output error CV $\mathit{e}\left(k_{\tau }\right)$ as $\mathit{d}\left(k_{\tau }\right)={[d\left(k_{\tau }\right),d(k_{\tau }-1),\dots ,d(k_{\tau }-K+1)]}^T\in {\mathbb{R}}^{K\times 1}$, $\mathit{U}\left(k_{\tau }\right)=[\mathit{u}\left(k_{\tau }\right),\mathit{u}(k_{\tau }-1),\dots ,\mathit{u}(k_{\tau }-K+1)]\in {\mathbb{R}}^{M\times K}$, $\mathit{e}\left(k_{\tau }\right)=\mathit{d}\left(k_{\tau }\right)-{\mathit{U}}^T\left(k_{\tau }\right)\mathit{w}\left(k_{\tau }\right)\in {\mathbb{R}}^{K\times 1}$, where K is the AP order, and ${\mathit{w}}_{ot}$ is estimated by the $\mathit{w}\left(k_{\tau }\right)$ at instant $k_{\tau }$. In addition, the updated $\mathit{w}\left(k_{\tau }\right)$ of GCI-M-IPAPSA is expressed as follows:

$$\begin{array}{cc}\hfill {\mathit{P}}_g\left(k_{\tau }\right)& =\left[\begin{array}{cccc}& u\left(k_{\tau }\right)g_0\left(k_{\tau }\right),& \cdots ,& u(k_{\tau }-K+1)g_0(k_{\tau }-K+1)\\ & u(k_{\tau }-1)g_1(k_{\tau }-1),& \cdots ,& u(k_{\tau }-K)g_1(k_{\tau }-K)\\ & ⋮& \ddots & \cdots \\ & u(k_{\tau }-M+1)g_{M-1}(k_{\tau }-M+1),& \cdots ,& u\left(k_{\tau }^{\prime }\right)g_{M-1}\left(k_{\tau }^{\prime }\right)\end{array}\right]\hfill \\ \hfill & =\left[\mathit{u}\left(k_{\tau }\right)\circ {\mathit{g}}_g\left(k_{\tau }\right),\mathit{u}(k_{\tau }-1)\circ {\mathit{g}}_g(k_{\tau }-1),\dots ,\mathit{u}(k_{\tau }-K+1)\circ {\mathit{g}}_g(k_{\tau }-K+1)\right]\hfill \\ \hfill & =\left[{\mathit{g}}_g\left(k_{\tau }\right)\circ \mathit{u}\left(k_{\tau }\right),{\mathit{P}}_{g-1}\left(k_{\tau }\right)\right],\hfill \end{array}$$

(2)

$$\mathit{w}\left(k_{\tau }\right)=\mathit{w}(k_{\tau }-1)+\mu \frac{{\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right)}{\sqrt{{\xi }_1+{\parallel {\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right)\parallel }_2^2}},$$

(3)

where $k_{\tau }^{\prime }=k_{\tau }-K-M+2$, the operation ∘ is regarded as the Hadamard product, ${\mathit{P}}_{g-1}\left(k_{\tau }\right)$ includes the first $K-1$ columns of ${\mathit{P}}_g(k_{\tau }-1)$, $\mathrm{sgn}(·)$ performs sign operations on each element in a vector, $0<{\xi }_1\ll 1$ to avoid possible division by zero, ${\parallel ·\parallel }_2$ is a symbol of ${\mathsf{\ell }}_2$-norm, $\mu$ is a step size and ${\mathit{g}}_g\left(k_{\tau }\right)$ denotes a CV with elements expressed as

$$g_m\left(k_{\tau }\right)=\frac{1-{\phi }_g}{2M}+\frac{(1+{\phi }_g)f\left(w_m\left(k_{\tau }\right)\right)}{2{\sum }_{m\in IB}f\left(w_m\left(k_{\tau }\right)\right)+{\xi }_2},$$

(4)

$$f\left(w_m\left(k_{\tau }\right)\right)=1-exp\left(-\frac{|w_m\left(k_{\tau }\right){|}^{{\alpha }_g}}{{{\beta }_g}^{{\alpha }_g}}\right),m\in IB,$$

(5)

where $-1\le {\phi }_g<1$, the typical value is $-0.5$ or 0, $|·|$ denotes the absolute value, $0<{\xi }_2\ll 1$ can be treated as ${\xi }_1$, $IB=\{0,1,\cdots ,M-1\}$, ${\alpha }_g$ denotes the shape parameter, ${\alpha }_g\in (0,2]$ ensures that the kernel is positive definite and ${\beta }_g>0$ is the scale factor. Furthermore, a simplified way can be applied to (5), which is written as

$$f\left(w_m\left(k_{\tau }\right)\right)=\left\{\begin{array}{c}\frac{|w_m\left(k_{\tau }\right){|}^{{\alpha }_g}}{{{\beta }_g}^{{\alpha }_g}},{\left|w_m\left(k_{\tau }\right)\right|}^{{\alpha }_g}<{{\beta }_g}^{{\alpha }_g}\hfill \\ 1,\mathrm{otherwise}.\hfill \end{array}\right.$$

(6)

The algorithms’ updates are shown in Algorithm 1.

Algorithm 1 The algorithms’ updates.

Initialization: Choose $\mu$ and $\mathit{w}\left(0\right)=\mathbf{0}$ Computation: while ${\{\mathit{U}\left(k_{\tau }\right),d\left(k_{\tau }\right)\}}_{k_{\tau }\ge 1}$, do     1: $\mathit{e}\left(k_{\tau }\right)=\mathit{d}\left(k_{\tau }\right)-{\mathit{U}}^T\left(k_{\tau }\right)\mathit{w}\left(k_{\tau }\right)$     2: $\mathit{w}\left(k_{\tau }\right)=\mathit{w}(k_{\tau }-1)+\mu \times \frac{{\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right)}{\sqrt{{\xi }_1+{\parallel {\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right)\parallel }_2^2}}$     3: ${\mathit{P}}_g\left(k_{\tau }\right)=\left[{\mathit{g}}_g\left(k_{\tau }\right)\circ \mathit{u}\left(k_{\tau }\right),{\mathit{P}}_{g-1}\left(k_{\tau }\right)\right]$     4: $g_m\left(k_{\tau }\right)=\frac{1-{\phi }_g}{2M}+\frac{(1+{\phi }_g)f\left(w_m\left(k_{\tau }\right)\right)}{2{\sum }_{m\in IB}f\left(w_m\left(k_{\tau }\right)\right)+{\xi }_2}$ for the GCI-M-IPAPSA:     5: $f\left(w_m\left(k_{\tau }\right)\right)=1-exp\left(-\frac{|w_m\left(k_{\tau }\right){|}^{{\alpha }_g}}{{{\beta }_g}^{{\alpha }_g}}\right)$ for the SGCI-M-IPAPSA:     5: $f\left(w_m\left(k_{\tau }\right)\right)=\left\{\begin{array}{cc}\frac{|w_m\left(k_{\tau }\right){|}^{{\alpha }_g}}{{{\beta }_g}^{{\alpha }_g}},\hfill & {\left|w_m\left(k_{\tau }\right)\right|}^{{\alpha }_g}<{{\beta }_g}^{{\alpha }_g}\hfill \\ 1,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$ end while

3. Improved GCI-M-IPAPSA

3.1. Proposed Algorithms

We propose a combined-step-size GCI-M-IPAPSA (CSS-GCI-M-IPAPSA), which obtains a good convergence rate in the sparse system in this brief. The updated weight CV $\mathit{w}\left(k_{\tau }\right)$ is based on the combination of ${\mathit{w}}_l\left(k_{\tau }\right)$ and ${\mathit{w}}_s\left(k_{\tau }\right)$ controlled by two different step sizes $\tilde{\mu }$, $\mu$ (in which $\tilde{\mu }>\mu$). The combined-step-size (CSS) weight coefficient CV is written as

$$\begin{array}{c}\hfill \mathit{w}\left(k_{\tau }\right)={\lambda }_s\left(k_{\tau }\right){\mathit{w}}_l\left(k_{\tau }\right)+(1-{\lambda }_s\left(k_{\tau }\right)){\mathit{w}}_s\left(k_{\tau }\right),\end{array}$$

(7)

where ${\lambda }_s\left(k_{\tau }\right)\in [0,1]$ is a mixing factor, ${\mathit{w}}_l\left(k_{\tau }\right)={\mathit{w}}_l(k_{\tau }-1)+\tilde{\mu }\frac{{\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right)}{\sqrt{{\xi }_1+{\parallel {\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right)\parallel }_2^2}}$ and ${\mathit{w}}_s\left(k_{\tau }\right)={\mathit{w}}_s(k_{\tau }-1)+\mu \frac{{\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right)}{\sqrt{{\xi }_1+{\parallel {\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right)\parallel }_2^2}}$. Substituting (3) into (7), the combination form (7) is changed as

$$\begin{array}{cc}\hfill \mathit{w}\left(k_{\tau }\right)=& \mathit{w}(k_{\tau }-1)+[{\lambda }_s\left(k_{\tau }\right)\tilde{\mu }+(1-{\lambda }_s\left(k_{\tau }\right))\mu ]\hfill \\ \hfill & \times \frac{{\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right)}{\sqrt{{\xi }_1+{\parallel {\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right)\parallel }_2^2}}.\hfill \end{array}$$

(8)

Compared with (3), the variable-step-size update formula is expressed clearly as

$$\begin{array}{cc}{\mu }_v=\hfill & {\lambda }_s\left(k_{\tau }\right)\tilde{\mu }+(1-{\lambda }_s\left(k_{\tau }\right))\mu =[{\lambda }_s\left(k_{\tau }\right)(\tilde{N}-1)+1]\mu \hfill \\ =\hfill & ({\lambda }_s\left(k_{\tau }\right)N+1)\mu ={\lambda }_s\left(k_{\tau }\right)N\mu +\mu ,\hfill \end{array}$$

(9)

where $\tilde{\mu }=\tilde{N}\mu$, $\tilde{N}$ denotes a constant and $N=\tilde{N}-1$.

Observing (9), one can find that ${\mu }_v$ is only associated with the small $\mu$ rather than $\tilde{\mu }$ and $\mu$, which is simpler than the old CSS way [15,17] and means that the proposed CSS method is only needed with one filter to run the whole time in comparison with the conventional combination method (CGCI-M-IPAPSA) [11,18,19]. The modified (9) is the step size of the proposed CSS-GCI-M-IPAPSA, which can be viewed as a new variable-step-size (VSS) GCI-M-IPAPSA.

For (9), we hope that ${\lambda }_s\left(k_{\tau }\right)=1,{\mu }_v=\tilde{N}\mu$ related to the faster convergence in the beginning of adaptation, ${\lambda }_s\left(k_{\tau }\right)=0,{\mu }_v=\mu$ related to the smaller steady-state error at steady state, and the corresponding shift operation (the learning rate factor of faster filter leaks to the slower one) from $\tilde{N}\mu$ to $\mu$ can be realized adaptively. Additionally, ${\lambda }_s\left(k_{\tau }\right)$ is updated based on a sigmoidal activation with a variable $s\left(k_{\tau }\right)$, where $s\left(k_{\tau }\right)$ based on a gradient descent method with minimization of the ${\mathsf{\ell }}_1$-norm can be robust against impulsive noise, i.e.,

$${\lambda }_s\left(k_{\tau }\right)=\frac{C}{1+exp(-{\beta }_{m}s\left(k_{\tau }\right))}-\left(\frac{C}{2}-\frac{1}{2}\right),$$

(10)

where $C>1$, ${\beta }_m>0$ is a proportional parameter and $-ln\left(\frac{C+1}{C-1}\right)/{\beta }_m<s\left(k_{\tau }\right)<ln\left(\frac{C+1}{C-1}\right)/{\beta }_m$.

Combining (3) and (9), we can obtain

$$\begin{array}{cc}\hfill s\left(k_{\tau }\right)=& s(k_{\tau }-1)-{\mu }_s\frac{\partial \left|e\right(k_{\tau }\left)\right|}{\partial s(k_{\tau }-1)}\hfill \\ \hfill =& s(k_{\tau }-1)+{\mu }_s{\mathit{u}}^T\left(k_{\tau }\right)\frac{\partial \mathit{w}(k_{\tau }-1)}{\partial s(k_{\tau }-1)}\mathrm{sgn}\left(e\left(k_{\tau }\right)\right)\hfill \\ \hfill =& s(k_{\tau }-1)+{\mu }_s(\tilde{\mu }-\mu ){\lambda }_s(k_{\tau }-1)(1-{\lambda }_s(k_{\tau }-1))\hfill \\ \hfill & \times \frac{{\mathit{u}}^T\left(k_{\tau }\right){\mathit{P}}_g(k_{\tau }-1)\mathrm{sgn}\left(\mathit{e}(k_{\tau }-1)\right)\mathrm{sgn}\left(e\left(k_{\tau }\right)\right)}{\sqrt{{\xi }_1+{\parallel {\mathit{P}}_g(k_{\tau }-1)\mathrm{sgn}\left(\mathit{e}(k_{\tau }-1)\right)\parallel }_2^2}}\hfill \\ \hfill =& s(k_{\tau }-1)+{\mu }_{s}N\mu [{\lambda }_s(k_{\tau }-1)(1-{\lambda }_s(k_{\tau }-1))+{\xi }_3]\hfill \\ \hfill & \times \frac{{\mathit{u}}^T\left(k_{\tau }\right){\mathit{P}}_g(k_{\tau }-1)\mathrm{sgn}\left(\mathit{e}(k_{\tau }-1)\right)\mathrm{sgn}\left(e\left(k_{\tau }\right)\right)}{\sqrt{{\xi }_1+{\parallel {\mathit{P}}_g(k_{\tau }-1)\mathrm{sgn}\left(\mathit{e}(k_{\tau }-1)\right)\parallel }_2^2}},\hfill \end{array}$$

(11)

where ${\xi }_3$ is a positive number that approaches zero, which is used to avoid the updates (11) of $s\left(k_{\tau }\right)$ from halting.

Remark 1. 

In fact, the range of parameter $\tilde{N}$ can be $\tilde{N}>0$. When $\tilde{N}>1$, the two step sizes $\tilde{\mu }>\mu$ are set in this paper. If $\tilde{N}=1$, the two step sizes $\tilde{\mu }=\mu$, the Formula (10) will become ${\mu }_v=\mu$, which means that the various step size ${\mu }_v$ is a constant during the entire process of the experiment, and the proposed CSS-GCI-M-IPAPSA will degenerate into the GCI-M-IPAPSA. If $0<\tilde{N}<1$, the step size μ is lager than $\tilde{\mu }$, the Formula (9) can become ${\mu }_v={\lambda }_s\left(k_{\tau }\right)\mu +(1-{\lambda }_s\left(k_{\tau }\right))\tilde{\mu }$ or remain unchanged, ${\mu }_v={\lambda }_s\left(k_{\tau }\right)\tilde{\mu }+(1-{\lambda }_s\left(k_{\tau }\right))\mu$ (which is also an efficient CSS way), according to the symmetry of ${\lambda }_s\left(k_{\tau }\right)$.

Then, applying the first-order Taylor series expansion to the exponential function of (12), we obtain

$${\lambda }_s\left(k_{\tau }\right)=\frac{C}{2-{\beta }_{m}s\left(k_{\tau }\right)}-\left(\frac{C}{2}-\frac{1}{2}\right),$$

(12)

where $\frac{-2}{(C-1){\beta }_m}\le s\left(k_{\tau }\right)\le \frac{2}{(C+1){\beta }_m}$. This efficient algorithm is named as the simplified CSS-GCI-M-IPAPSA (SCSS-GCI-M-IPAPSA), in which ${\beta }_{m}s\left(k_{\tau }\right)$ is not equal to 2.

Additionally, on the basis of (6), we propose the algorithms CSS-SGCI-M-IPAPSA and SCSS-SGCI-M-IPAPSA. The filtering performance of the SGCI-M-IPAPSA and GCI-M-IPAPSA algorithms are comparable from [11], so we only focus on the algorithm SGCI-M-IPAPSA and propose SGCI-M-IPAPSA-type algorithms in this paper.

Furthermore, we consider a new VSS method based on the mean-square deviation (MSD) and apply it to the SGCI-M-IPAPSA. Note that it is not a direct extension of conventional VSS ways because we need to deal with several special issues caused by the operation of ${\mathit{g}}_g\left(k_{\tau }\right)$ and impulsive noise. We set ${\mathit{w}}_{es}\left(k_{\tau }\right)={\mathit{w}}_{ot}-\mathit{w}\left(k_{\tau }\right)$; the optimum step size ${\mu }^{*}\left(k_{\tau }\right)$ of the SGCI-M-IPAPSA is generated by minimising $E(\Vert {\mathit{w}}_{es}(k_{\tau }+1){\Vert }_2^2)$ [14] as follows:

$$\begin{array}{cc}\hfill E(\Vert {\mathit{w}}_{es}(k_{\tau }+1){\Vert }_2^2)=& E(\Vert {\mathit{w}}_{es}\left(k_{\tau }\right){\Vert }_2^2)+{\mu }^2\left(k_{\tau }\right)-2\mu \left(k_{\tau }\right)\hfill \\ \hfill & \times E(\frac{\mathrm{sgn}\left({\mathit{e}}^T\left(k_{\tau }\right)\right){\mathit{P}}_g^T\left(k_{\tau }\right){\mathit{w}}_{es}\left(k_{\tau }\right)}{\sqrt{\parallel {\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right){\parallel }_2^2}})\hfill \end{array}$$

(13)

and

$$\begin{array}{cc}\hfill {\mu }^{*}\left(k_{\tau }\right)& =E(\frac{\mathrm{sgn}\left({\mathit{e}}^T\left(k_{\tau }\right)\right){\mathit{P}}_g^T\left(k_{\tau }\right){\mathit{w}}_{es}\left(k_{\tau }\right)}{\sqrt{\parallel {\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right){\parallel }_2^2}})\hfill \\ \hfill & \approx E(\frac{\mathrm{sgn}\left({\mathit{e}}^T\left(k_{\tau }\right)\right)\mathit{g}\left(k_{\tau }\right)\circ (\mathit{e}\left(k_{\tau }\right)-{\mathit{v}}_K\left(k_{\tau }\right))}{\sqrt{\parallel {\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right){\parallel }_2^2}})\hfill \\ \hfill & \approx \frac{\Vert \mathit{g}\left(k_{\tau }\right)\circ \mathit{e}\left(k_{\tau }\right){\Vert }_1-{\xi }_{4}K\left|e\left(k_{\tau }\right)\right|}{\sqrt{\parallel {\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right){\parallel }_2^2}},\hfill \end{array}$$

(14)

where $E(·)$ denotes expectation, $\mathit{g}\left(k_{\tau }\right)={[g_1\left(k_{\tau }\right),g_1(k_{\tau }-1),\cdots ,g_1(k_{\tau }-K+1)]}^T$, ${\xi }_4$ is a constant and ${\parallel ·\parallel }_1$ is a symbol of ${\mathsf{\ell }}_1$-norm. To improve the filtering accuracy of the SGCI-M-IPAPSA, by means of the convex combination, we obtain

$$\begin{array}{c}\hfill {\mu }^{*}\left(k_{\tau }\right)={\xi }_5{\mu }^{*}(k_{\tau }-1)+(1-{\xi }_5)\min \left(\right|{\mu }^{*}\left(k_{\tau }\right)|,{\mu }^{*}(k_{\tau }-1)),\end{array}$$

(15)

where ${\xi }_5$ is a smoothing factor. The SGCI-M-IPAPSA updating the weight CV with (15) is called the VSS-SGCI-M-IPAPSA.

The tracking performance of these proposed algorithms can be reduced in nonstationary situations (for example, an abrupt change). To improve the tracking performance (in abrupt change scenarios) of proposed algorithms, we apply the CSS (9) and a constraint way based on the mean-square error (MSE) [14] to them. Then, (15) can be written as

$$\begin{array}{cc}\hfill {\mu }^{*}\left(k_{\tau }\right)=& {\lambda }_s\left(k_{\tau }\right){\mu }^{*}\left(0\right)+(1-{\lambda }_s\left(k_{\tau }\right)){\mu }^{*}\left(k_{\tau }\right)\hfill \\ \hfill =& {\lambda }_s\left(k_{\tau }\right){\mu }^{*}\left(0\right)+(1-{\lambda }_s\left(k_{\tau }\right))[{\xi }_5{\mu }^{*}(k_{\tau }-1)\hfill \\ \hfill & +(1-{\xi }_5)\min \left(\right|{\mu }^{*}\left(k_{\tau }\right)|,{\mu }^{*}(k_{\tau }-1)\left)\right].\hfill \end{array}$$

(16)

Making use of (3), (14) and (16), we obtain a novel algorithm named the combined variable-step-size (CVSS) SGCI-M-IPAPSA (CVSS-SGCI-M-IPAPSA).

Remark 2. 

The CVSS method combining the variable-step-size means and combined-step-size tactic is firstly mentioned to offer a possible solution for the improvement of the algorithms’ performance. Additionally, the CVSS method can be seen as an extension of the VSS way from (16): (1) if ${\lambda }_s\left(k_{\tau }\right)=0$, the CVSS method will become the VSS way; (2) if $0<{\mu }^{*}\left(k_{\tau }\right)\ll 1$ is a constant, the CVSS method will be the CSS mode.

A condition determination is set as [14] (please see Equations (23)–(26)), and the different points are the setting of the initial conditions

$$\begin{array}{c}\hfill \mathrm{if}({\mathrm{ctrl}}_{\mathrm{new}}-{\mathrm{ctrl}}_{\mathrm{old}})/{\mu }^{*}(k_{\tau }-1)>L_1\\ \hfill \mathrm{For}\mathrm{proposed}\mathrm{CVSS}\text{-}\mathrm{type}\mathrm{algorithms}:\\ \hfill s\left(k_{\tau }\right)=s\left(0\right),{\mu }^{*}\left(k_{\tau }\right)={\mu }^{*}\left(0\right);\\ \hfill \mathrm{For}\mathrm{proposed}\mathrm{VSS}\text{-}\mathrm{type}\mathrm{algorithm}:\\ \hfill {\mu }^{*}\left(k_{\tau }\right)={\mu }^{*}\left(0\right);\\ \hfill \mathrm{else}\\ \hfill \mathrm{Proposed}\mathrm{algorithms}’\mathrm{update}\\ \hfill {\mathrm{ctrl}}_{\mathrm{new}}={\mathrm{ctrl}}_{\mathrm{old}},\end{array}$$

(17)

where $L_1=25$ is a threshold value. This condition determination (17) is for determining whether a mutation has occurred. The Algorithms 2 and 3 summarize the proposed algorithms’ updates for convenience.

Algorithm 2 Proposed algorithms’ updates.

Initialization: Choose C, ${\beta }_m$, N, $\mu$, ${\mu }^{*}\left(0\right)$, $s\left(0\right)$ and $\mathit{w}\left(0\right)=\mathbf{0}$ Computation: while ${\{\mathit{U}\left(k_{\tau }\right),d\left(k_{\tau }\right)\}}_{k_{\tau }\ge 1}$, do     1: $\mathit{e}\left(k_{\tau }\right)=\mathit{d}\left(k_{\tau }\right)-{\mathit{U}}^T\left(k_{\tau }\right)\mathit{w}\left(k_{\tau }\right)$     2: $\mathit{w}\left(k_{\tau }\right)=\mathit{w}(k_{\tau }-1)+{\mu }_v\times \frac{{\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right)}{\sqrt{{\xi }_1+{\parallel {\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right)\parallel }_2^2}}$     3: ${\mathit{P}}_g\left(k_{\tau }\right)=\left[{\mathit{g}}_g\left(k_{\tau }\right)\circ \mathit{u}\left(k_{\tau }\right),{\mathit{P}}_{g-1}\left(k_{\tau }\right)\right]$     4: $g_m\left(k_{\tau }\right)=\frac{1-{\phi }_g}{2M}+\frac{(1+{\phi }_g)f\left(w_m\left(k_{\tau }\right)\right)}{2{\sum }_{m\in IB}f\left(w_m\left(k_{\tau }\right)\right)+{\xi }_2}$ for the proposed CSS-GCI-M-IPAPSA:     5: $f\left(w_m\left(k_{\tau }\right)\right)=1-exp\left(-\frac{|w_m\left(k_{\tau }\right){|}^{{\alpha }_g}}{{{\beta }_g}^{{\alpha }_g}}\right)$     6: $s\left(k_{\tau }\right)=s(k_{\tau }-1)-{\mu }_s\frac{\partial \left|e\right(k_{\tau }\left)\right|}{\partial s(k_{\tau }-1)}$     7: ${\lambda }_s\left(k_{\tau }\right)=\frac{C}{1+exp(-{\beta }_{m}s\left(k_{\tau }\right))}-\left(\frac{C}{2}-\frac{1}{2}\right)$     8: ${\mu }_v={\lambda }_s\left(k_{\tau }\right)N\mu +\mu$ for the proposed CSS-SGCI-M-IPAPSA:     5: $f\left(w_m\left(k_{\tau }\right)\right)=\left\{\begin{array}{cc}\frac{|w_m\left(k_{\tau }\right){|}^{{\alpha }_g}}{{{\beta }_g}^{{\alpha }_g}},\hfill & {\left|w_m\left(k_{\tau }\right)\right|}^{{\alpha }_g}<{{\beta }_g}^{{\alpha }_g}\hfill \\ 1,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$     6: $s\left(k_{\tau }\right)=s(k_{\tau }-1)-{\mu }_s\frac{\partial \left|e\right(k_{\tau }\left)\right|}{\partial s(k_{\tau }-1)}$     7: ${\lambda }_s\left(k_{\tau }\right)=\frac{C}{1+exp(-{\beta }_{m}s\left(k_{\tau }\right))}-\left(\frac{C}{2}-\frac{1}{2}\right)$     8: ${\mu }_v={\lambda }_s\left(k_{\tau }\right)N\mu +\mu$ for the proposed SCSS-SGCI-M-IPAPSA:     5: $f\left(w_m\left(k_{\tau }\right)\right)=\left\{\begin{array}{cc}\frac{|w_m\left(k_{\tau }\right){|}^{{\alpha }_g}}{{{\beta }_g}^{{\alpha }_g}},\hfill & {\left|w_m\left(k_{\tau }\right)\right|}^{{\alpha }_g}<{{\beta }_g}^{{\alpha }_g}\hfill \\ 1,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$     6: $s\left(k_{\tau }\right)=s(k_{\tau }-1)-{\mu }_s\frac{\partial \left|e\right(k_{\tau }\left)\right|}{\partial s(k_{\tau }-1)}$     7: ${\lambda }_s\left(k_{\tau }\right)=\frac{C}{2-{\beta }_{m}s\left(k_{\tau }\right)}-\left(\frac{C}{2}-\frac{1}{2}\right)$     8: ${\mu }_v={\lambda }_s\left(k_{\tau }\right)N\mu +\mu$ end while

Algorithm 3 Proposed algorithms’ updates.

Initialization: Choose C, ${\beta }_m$, ${\mu }^{*}\left(0\right)$, $s\left(0\right)$ and $\mathit{w}\left(0\right)=\mathbf{0}$ Computation: while ${\{\mathit{U}\left(k_{\tau }\right),d\left(k_{\tau }\right)\}}_{k_{\tau }\ge 1}$, do     1: $\mathit{e}\left(k_{\tau }\right)=\mathit{d}\left(k_{\tau }\right)-{\mathit{U}}^T\left(k_{\tau }\right)\mathit{w}\left(k_{\tau }\right)$     2: $\mathit{w}\left(k_{\tau }\right)=\mathit{w}(k_{\tau }-1)+{\mu }_v\times \frac{{\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right)}{\sqrt{{\xi }_1+{\parallel {\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right)\parallel }_2^2}}$     3: ${\mathit{P}}_g\left(k_{\tau }\right)=\left[{\mathit{g}}_g\left(k_{\tau }\right)\circ \mathit{u}\left(k_{\tau }\right),{\mathit{P}}_{g-1}\left(k_{\tau }\right)\right]$     4: $g_m\left(k_{\tau }\right)=\frac{1-{\phi }_g}{2M}+\frac{(1+{\phi }_g)f\left(w_m\left(k_{\tau }\right)\right)}{2{\sum }_{m\in IB}f\left(w_m\left(k_{\tau }\right)\right)+{\xi }_2}$     5: $f\left(w_m\left(k_{\tau }\right)\right)=\left\{\begin{array}{cc}\frac{|w_m\left(k_{\tau }\right){|}^{{\alpha }_g}}{{{\beta }_g}^{{\alpha }_g}},\hfill & {\left|w_m\left(k_{\tau }\right)\right|}^{{\alpha }_g}<{{\beta }_g}^{{\alpha }_g}\hfill \\ 1,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$ for the proposed VSS-SGCI-M-IPAPSA:     6: ${\mu }^{*}\left(k_{\tau }\right)=\frac{\Vert \mathit{g}\left(k_{\tau }\right)\circ \mathit{e}\left(k_{\tau }\right){\Vert }_1-{\xi }_{4}K\left|e\left(k_{\tau }\right)\right|}{\sqrt{\parallel {\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right){\parallel }_2^2}}$     7: ${\mu }_v={\mu }^{*}\left(k_{\tau }\right)={\xi }_5{\mu }^{*}(k_{\tau }-1)+(1-{\xi }_5)\min \left(\right|{\mu }^{*}\left(k_{\tau }\right)|,{\mu }^{*}(k_{\tau }-1))$ for the proposed CVSS-SGCI-M-IPAPSA:     6: ${\mu }^{*}\left(k_{\tau }\right)=\frac{\Vert \mathit{g}\left(k_{\tau }\right)\circ \mathit{e}\left(k_{\tau }\right){\Vert }_1-{\xi }_{4}K\left|e\left(k_{\tau }\right)\right|}{\sqrt{\parallel {\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right){\parallel }_2^2}}$     7: ${\mu }^{*}\left(k_{\tau }\right)={\xi }_5{\mu }^{*}(k_{\tau }-1)+(1-{\xi }_5)\min \left(\right|{\mu }^{*}\left(k_{\tau }\right)|,{\mu }^{*}(k_{\tau }-1))$     8: $s\left(k_{\tau }\right)=s(k_{\tau }-1)-{\mu }_s\frac{\partial \left|e\right(k_{\tau }\left)\right|}{\partial s(k_{\tau }-1)}$     9: ${\lambda }_s\left(k_{\tau }\right)=\frac{C}{1+exp(-{\beta }_{m}s\left(k_{\tau }\right))}-\left(\frac{C}{2}-\frac{1}{2}\right)$     10: ${\mu }_v={\mu }^{*}\left(k_{\tau }\right)={\lambda }_s\left(k_{\tau }\right){\mu }^{*}\left(0\right)+(1-{\lambda }_s\left(k_{\tau }\right)){\mu }^{*}\left(k_{\tau }\right)$ end while

3.2. Convergence of Proposed Algorithms

The SGCI-M-IPAPSA algorithm has good performance in sparse systems due to an efficient method (4). Based on (3), we obtain

$$\begin{array}{c}\hfill \Vert \Delta \mathit{w}\left(k_{\tau }\right){\Vert }_2^2={\mu }^2{\Vert \mathit{P}\left(k_{\tau }\right)\Vert }_2^2,\end{array}$$

(18)

where $\mathit{P}\left(k_{\tau }\right)=\frac{{\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right)}{\sqrt{{\xi }_1+{\parallel {\mathit{P}}_g\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right)\parallel }_2^2}}$, $\Delta \mathit{w}\left(k_{\tau }\right)=\mathit{w}\left(k_{\tau }\right)-\mathit{w}(k_{\tau }-1)$, and we set

$$\begin{array}{c}\hfill \Vert \mathit{P}\left(k_{\tau }\right){\Vert }_2^2=\delta \left(k_{\tau }\right)\Vert \frac{\mathit{U}\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right)}{\sqrt{{\xi }_1+{\parallel \mathit{U}\left(k_{\tau }\right)\mathrm{sgn}\left(\mathit{e}\left(k_{\tau }\right)\right)\parallel }_2^2}}{\Vert }_2^2,\end{array}$$

(19)

where $\delta \left(k_{\tau }\right)$ is a proportionality coefficient. Making use of (4), we know $0<g_m\left(k_{\tau }\right)\le 1$ and obtain $0<\delta \left(k_{\tau }\right)\le 1$.

According to Formula (19) and [8], it is clear that the SGCI-M-IPAPSA is an extension of the APSA, which indicates that the cost function of the SGCI-M-IPAPSA is the same as the APSA, and the SGCI-M-IPAPSA has extra operations on the input signal $\mathit{u}\left(k_{\tau }\right)$. To ensure the stability of the APSA, $\Vert \Delta \mathit{w}\left(k_{\tau }\right){\Vert }_2^2\le {\mu }^2\ll 1$ from [8]. Combining (18) and (19), the step size $\mu$ of the SGCI-M-IPAPSA needs to satisfy the condition of $0<\mu \ll 1$. For the proposed algorithms, the variable step size ${\mu }_v$ also satisfies

$$\begin{array}{c}\hfill 0<{\mu }_v\ll 1.\end{array}$$

(20)

4. Numerical Simulation Results

In this section, the proposed algorithms’ performance is demonstrated by computer simulations to identify a sparse system. $\frac{\sqrt{M}}{\sqrt{M}-1}\left(1-\frac{\parallel {\mathit{w}}_{ot}{\parallel }_1}{\sqrt{M}{\parallel {\mathit{w}}_{ot}\parallel }_2}\right)\in [0,1]$ is the sparse level and set to 0.953. We set ${\xi }_1={\xi }_2={\xi }_3=0.001$, ${\phi }_g=0$, ${\mu }_s=0.1$, $K=15$, $s\left(0\right)=1/K$, ${\alpha }_g=2$, ${\beta }_g=0.1$ in the following experiments. The unknown weight CV ${\mathit{w}}_{ot}$ (with $M=256$ taps) is randomly generated and suddenly changed to $-{\mathit{w}}_{ot}$ halfway through iterations, and the NMSD is defined as

$$\begin{array}{c}\hfill \mathrm{NMSD}\left(k_{\tau }\right)=10{log}_{10}\left(\frac{\parallel {\mathit{w}}_{es}\left(k_{\tau }\right){\parallel }_2}{\parallel {\mathit{w}}_{ot}{\parallel }_2}\right).\end{array}$$

(21)

The input signal is generated by filtering a zero-mean white Gaussian signal with a power of one through the following system $F\left(z\right)=\frac{1}{1-0.7z^{-1}}$. The impulsive noise obeys the alpha-stable distribution ($\alpha$-SD) (in practical environments such as low-frequency atmospheric noises, underwater acoustic signals and various types of man-made noises, it is common to encounter a class of signals or noises with the pulse amplitude. Moreover, the pulse characteristics of these signals or noises (as severe external interferences or outliers) will affect the systems or algorithms based on the Gaussian model assumptions and even cause the Gaussian model systems or algorithms to not work properly. A large number of studies have shown that the reason is the probability density distribution of these signals or noises has a thicker trailing phenomenon than the Gaussian model, which means the probability of outliers appearing is larger than the Gaussian model. Through relevant studies, it is proved that the non-Gaussian distribution model satisfying the above characteristics belongs to a family of distribution functions with stable characteristics, which is called the alpha-stable distribution model [20,21].) and is expressed as

$$\begin{array}{c}\hfill \varphi \left(k_{\tau }\right)=exp\left[i(\delta k_{\tau }+\beta tan(\frac{\pi \alpha }{2})|\gamma k_{\tau }{|}^{\alpha }\mathrm{sgn}(k_{\tau }))-|\gamma k_{\tau }{|}^{\alpha }\right],\end{array}$$

(22)

where $-1\le \beta \le 1$ is the symmetry factor, $\alpha \in (0,1)\cup (1,2]$ denotes the characteristic parameter, $\overline{\gamma }>0$ is the dispersion factor and $-\infty <\delta <+\infty$ denotes the location parameter [21]. Let ${\mathit{P}}_{\alpha }=[\alpha ,\beta ,\gamma ,\delta ]$ be the $\alpha$-SD parameter vector, and the parameter vector is set as ${\mathit{P}}_{\alpha }=[1.8,0,0.01,0]$ for all the experiments (unless otherwise stated). The NMSD already mentioned is used for measuring the corresponding algorithms’ filtering performance in this paper, and 100 independent trials were averaged in all simulation results (The running environment: (1) Windows 7, Intel(R) Core(TM) i7-4770K CPU @ 3.50 GHz; (2) Matlab R2014a).

In the first experiment, we evaluate the effectiveness of the proposed algorithm CSS-SGCI-M-IPAPSA with different $C\in \{2,4,6,8,10\}$, as shown in Figure 1, where $\mu =0.001$, ${\beta }_m=1$ and $N=9$ are set to constants for the proposed algorithm. It is clearly shown from Figure 1 that: (1) the appropriate value of C (such as 6 or 8) results in preferable filtering accuracy compared with other values, and the proposed algorithm (with $C=6$) achieves the fastest convergence rate than others; (2) with the increase of the C value ($C\in (1,6]$), the performance of the proposed CSS-SGCI-M-IPAPSA can also be improved; (3) the value of C (such as 2) that is too small degrades the convergence speed and steady-state misalignment of the proposed CSS-GCI-M-IPAPSA; (4) the proposed CSS-SGCI-M-IPAPSA (with a proper C value) achieves the same steady-state misalignment as SGCI-M-IPAPSA and better performance with respect to the convergence rate than SGCI-M-IPAPSA.

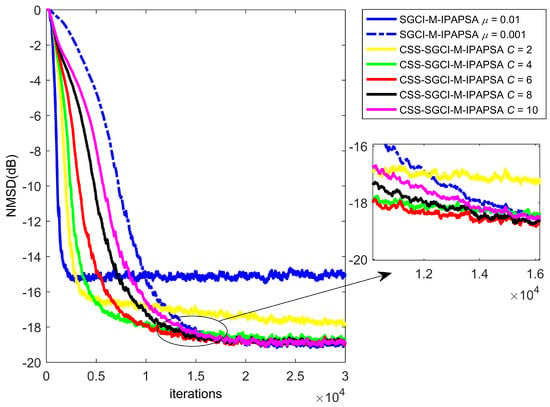
Figure 1. Learning curves of SGCI-M-IPAPSA and CSS-SGCI-M-IPAPSA with $\mu =0.001$, ${\beta }_m=1$, $N=9$ and various $C\in \{2,4,6,8,10\}$ for non-Gaussian impulsive interferences ${\mathit{P}}_{\alpha }=[1.8,0,0.01,0]$, sparse system identification and colored inputs in $F\left(z\right)$.

In the second experiment, Figure 2 mainly shows the NMSD learning curves of the CSS-SGCI-M-IPAPSA with various ${\beta }_m\in \{1,2,4,6,8\}$; we fix $C=6$, and other parameters are the same as those in Figure 2. As can be seen from Figure 2, we know that: (1) as the parameter ${\beta }_m$ decreases (from 8 to 4) properly, the filtering convergence rate of the proposed CSS-SGCI-M-IPAPSA can be improved; (2) the proposed CSS-SGCI-M-IPAPSA with ${\beta }_m=4$ and ${\beta }_m=1$ achieves better performance than others; (3) the proposed CSS-SGCI-M-IPAPSA with ${\beta }_m=4$ has a faster convergence rate than that with ${\beta }_m=1$.

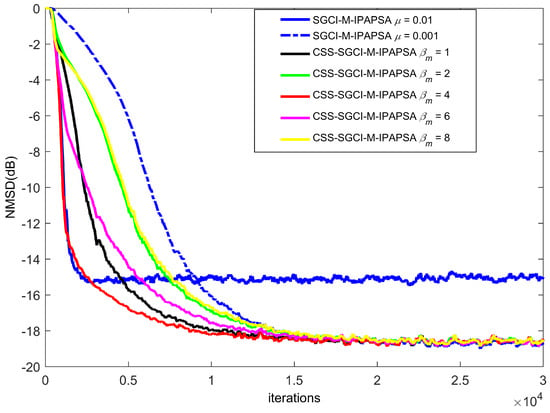
Figure 2. Learning curves of SGCI-M-IPAPSA and CSS-SGCI-M-IPAPSA with $\mu =0.001$, $C=6$, $N=9$ and various ${\beta }_m\in \{1,2,4,6,8\}$ for sparse system identification, non-Gaussian impulsive interferences ${\mathit{P}}_{\alpha }=[1.8,0,0.01,0]$ and colored inputs in $F\left(z\right)$.

In the third experiment, we demonstrate the effectiveness of the proposed algorithm SCSS-SGCI-M-IPAPSA based on CSS-SGCI-M-IPAPSA. The $\mu =0.001,N=9,C=6$ are basic parameters for these two algorithms, and we choose ${\beta }_m$ from $\{1,4,6\}$ (from Figure 2, the CSS-SGCI-M-IPAPSA has good performance and is representative with ${\beta }_m\in \{1,4,6\}$). The corresponding NMSD learning curves of these proposed algorithms are plotted in Figure 3. From this figure, we know SCSS-SGCI-M-IPAPSA (which needs less computational complexity) has the equivalent filter accuracy and convergence rate as those of CSS-SGCI-M-IPAPSA.

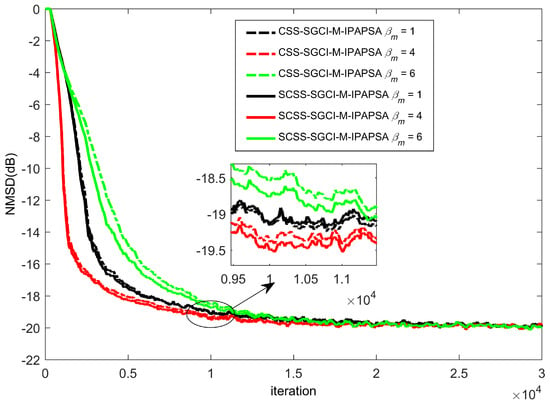
Figure 3. Learning curves of CSS-SGCI-M-IPAPSA and SCSS-SGCI-M-IPAPSA with $\mu =0.001$, $C=6$, $N=9$ and various ${\beta }_m\in \{1,4,6\}$ for sparse system identification, non-Gaussian impulsive interferences ${\mathit{P}}_{\alpha }=[1.8,0,0.01,0]$ and colored inputs in $F\left(z\right)$.

In the fourth experiment, the proposed algorithms are applied in an abrupt system with impulsive interferences to test the tracking performance of corresponding algorithms in $F\left(z\right)$. We set $\mu =0.001$ for all algorithms and fix $N=9$ for all combined algorithms. Corresponding NMSD learning curves are plotted in Figure 4, and the performance comparisons of different AFAs are shown in Table 1. The initial value $\mu \left(0\right)$ is 0.01 for VSS-APSA; for CSS-APSA, $C=5$; for SCSS-SGCI-M-IPAPSA, $C=6$, ${\beta }_m\in \{1,4\}$; for VSS-SGCI-M-IPAPSA, ${\mu }^{*}\left(0\right)=0.1$, ${\xi }_4=0.1$, ${\xi }_5=0.9$; for CVSS-SGCI-M-IPAPSA, $C=8$, ${\beta }_m\in \{1,2\}$, ${\mu }^{*}\left(0\right)=0.1$, ${\xi }_4=0.1$, ${\xi }_5=0.9$. Compared with APSA, CAPSA, VSS-APSA, CSS-APSA, the proposed SCSS-SGCI-M-IPAPSA achieves a faster convergence rate. Also compared with SGCI-M-IPAPSA and CSGCI-M-IPAPSA, the proposed SCSS-SGCI-M-IPAPSA realizes better tracking performance and a faster convergence rate. The proposed VSS-SGCI-M-IPAPSA and CVSS-SGCI-M-IPAPSA achieve the best performance, including the tracking performance, filtering accuracy and convergence rate in Figure 5. For the proposed SCSS-SGCI-M-IPAPSA, the reason we choose the two values of the parameter ${\beta }_m$ (${\beta }_m\in \{1,4\}$) is to prove that the CSS way (${\beta }_m=1$) is a good measure to improve the performance of CSGCI-M-IPAPSA, and the SCSS method (${\beta }_m=4$) is a better way to enhance the tracking performance of the proposed algorithms.

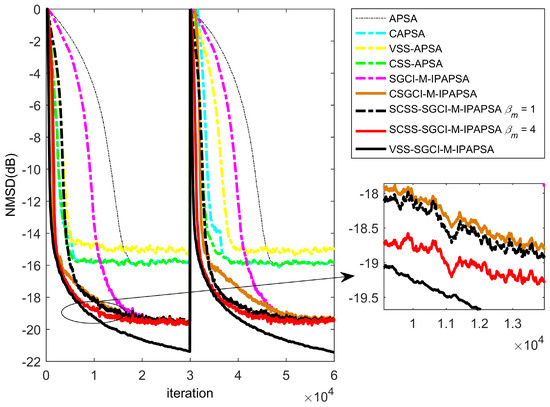
Figure 4. Learning curves of related APSA-type algorithms for sparse system identification, non-Gaussian impulsive interferences ${\mathit{P}}_{\alpha }=[1.8,0,0.01,0]$, an abrupt change (at an iteration of $3\times {10}^4$) and colored inputs in $F\left(z\right)$.

Table 1. Performance comparisons of different AFAs.

Algorithms	NMSD (dB)
APSA	−15.95
CAPSA	−15.95
VSS-APSA	−15.16
CSS-APSA	−15.95
SGCI-M-IPAPSA	−19.53
CSGCI-M-IPAPSA	−19.53
proposed SCSS-SGCI-M-IPAPSA	−19.54
proposed VSS-SGCI-M-IPAPSA	<−19.54

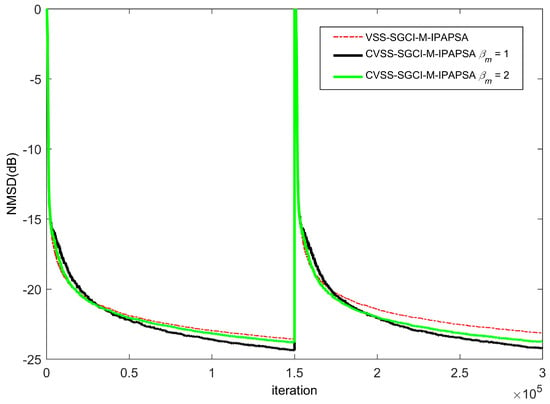
Figure 5. Learning curves of VSS-SGCI-M-IPAPSA and CVSS-SGCI-M-IPAPSA for sparse system identification, non-Gaussian impulsive interferences ${\mathit{P}}_{\alpha }=[1.8,0,0.01,0]$, an abrupt change (at an iteration of $1.5\times {10}^5$) and colored inputs in $F\left(z\right)$.

In the fifth experiment, we use a sparse acoustic echo path and real speech signals to verify the system identification performance of related algorithms. A typical sparse network echo path and speech input are shown in Figure 6 and Figure 7, respectively. The main parameters are set as ${\mu }^{*}\left(0\right)=0.01$, $C=7$, $K=2$ and ${\mathit{P}}_{\alpha }=[1.8,0,0.001,0]$. The other parameters are the same as in Figure 4. One can see that the proposed algorithms outperform other algorithms, such as the CSGCI-M-IPAPSA, SGCI-M-IPAPSA, CSS-APSA, CAPSA and APSA, in terms of convergence speed from Figure 8.

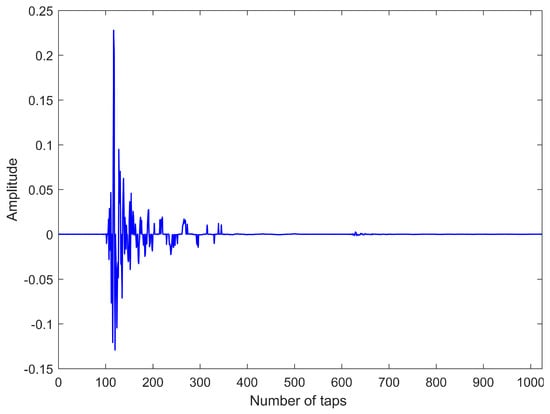
Figure 6. A typical sparse network echo path $M=1024$.

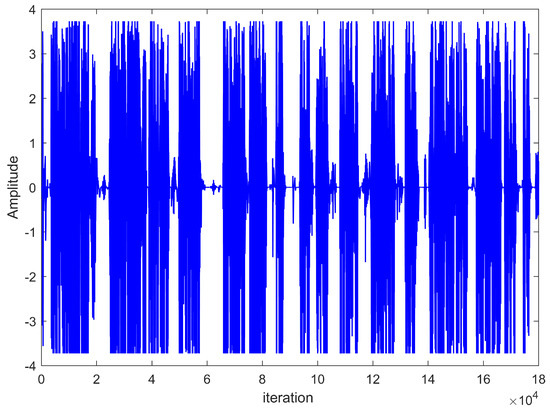
Figure 7. Speech input.

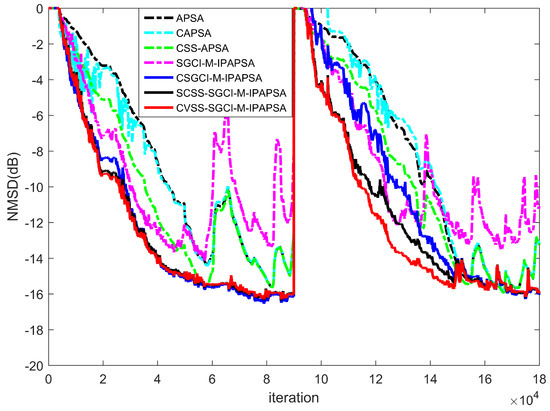
Figure 8. Learning curves of related algorithms with speech signals.

5. Conclusions

Based on efficient variable-step-size ways, the algorithms CSS-SGCI-M-IPAPSA and VSS-SGCI-M-IPAPSA are proposed to improve the convergence rate of the previous SGCI-M-IPAPSA for sparse system identification in this paper. Additionally, the proposed CVSS-SGCI-M-IPAPSA using the combination of the CSS and VSS methods has the best performance rather than the SGCI-M-IPAPSA, CSGCI-M-IPAPSA, CSS-SGCI-M-IPAPSA and VSS-SGCI-M-IPAPSA in terms of the filtering accuracy and convergence rate. To improve the tracking performance of proposed algorithms in an abrupt system, a conditional decision on MSE is applied to the proposed algorithms. Numerical simulation results confirm that our proposed algorithms have better filtering performance as compared to the existing SGCI-M-IPAPSA-type algorithms, with respect to the convergence rate with non-Gaussian impulsive interferences for sparse system identification, abrupt changes and colored inputs. Certainly, the core ideas of the proposed VSS ways not only enrich adaptive filter theory, but can also be applied to other algorithms and domains, such as echo cancellation application, machine learning and so on [1,12,18,22,23,24,25,26,27,28,29,30].