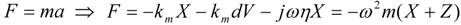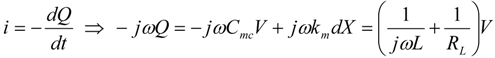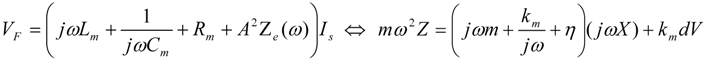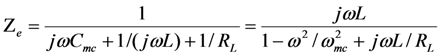Abstract
Devices that harvest electrical energy from mechanical vibrations have the problem that the frequency of the source vibration is often not matched to the resonant frequency of the energy harvesting device. Manufacturing tolerances make it difficult to match the Energy Harvesting Device (EHD) resonant frequency to the source vibration frequency, and the source vibration frequency may vary with time. Previous work has recognized that it is possible to tune the resonant frequency of an EHD using a tunable, reactive impedance at the output of the device. The present paper develops the theory of electrical tuning, and proposes the Bias-Flip (BF) technique, to implement this tunable, reactive impedance.
1. Introduction
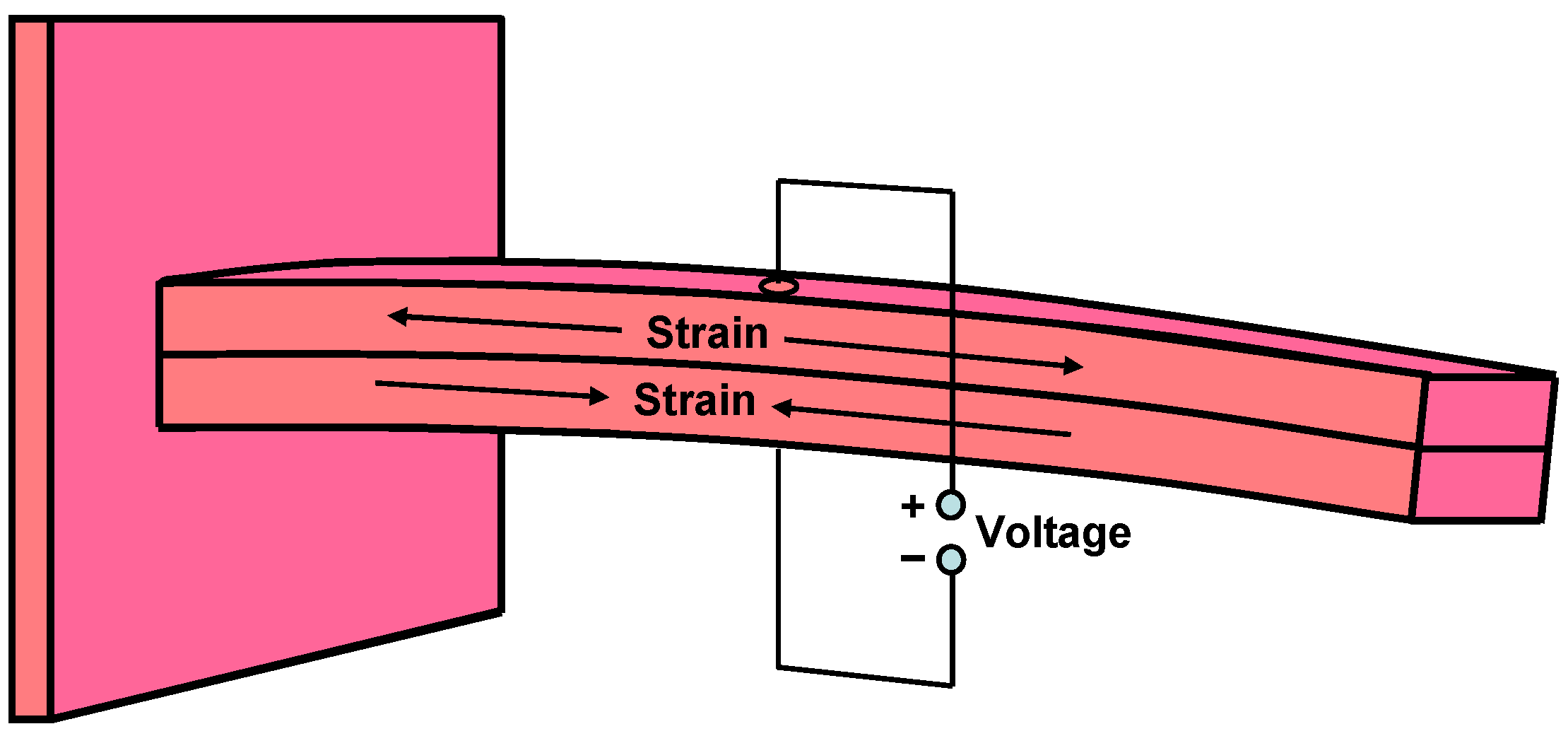
Figure 1 shows a schematic of a Piezoelectric (PZ) Energy Harvesting Device (EHD) that is the subject of this research. This structure is referred to as a cantilever structure, and is used to amplify the amplitude of the source vibration [1]. Previous work has shown that maximum output power is achieved when the cantilever has a high Q resonance at the frequency of the source vibration. However, the frequency of the source vibration is not usually matched to the resonant frequency of the EHD. The source vibration may vary with time. This paper addresses the problem of electronically tuning the PZ EHD to achieve maximum power in situations where the source vibration is not a stable frequency matched to the mechanical resonant frequency of the EHD.
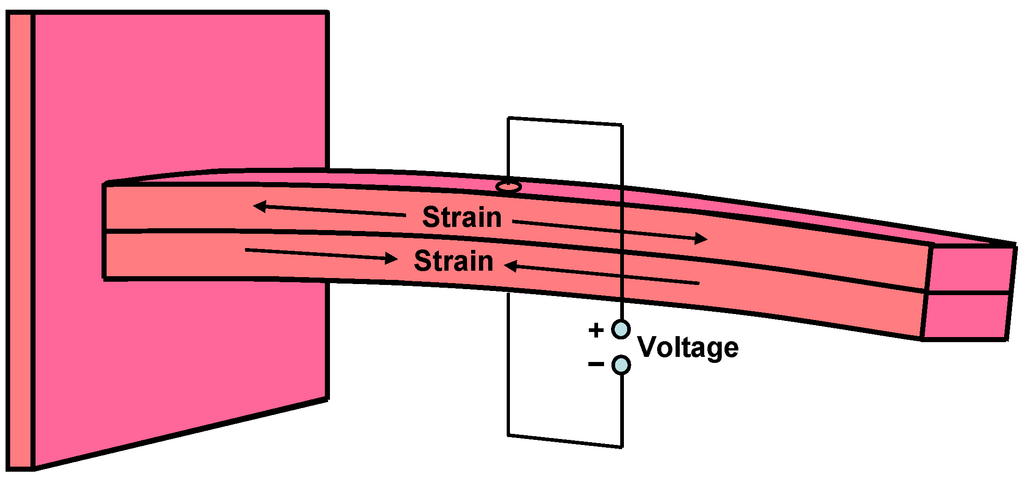
Figure 1.
Schematic of a Piezo-Electric (PZ) Energy Harvesting Device (EHD) based on the Cantilever Beam structure.
Figure 1.
Schematic of a Piezo-Electric (PZ) Energy Harvesting Device (EHD) based on the Cantilever Beam structure.
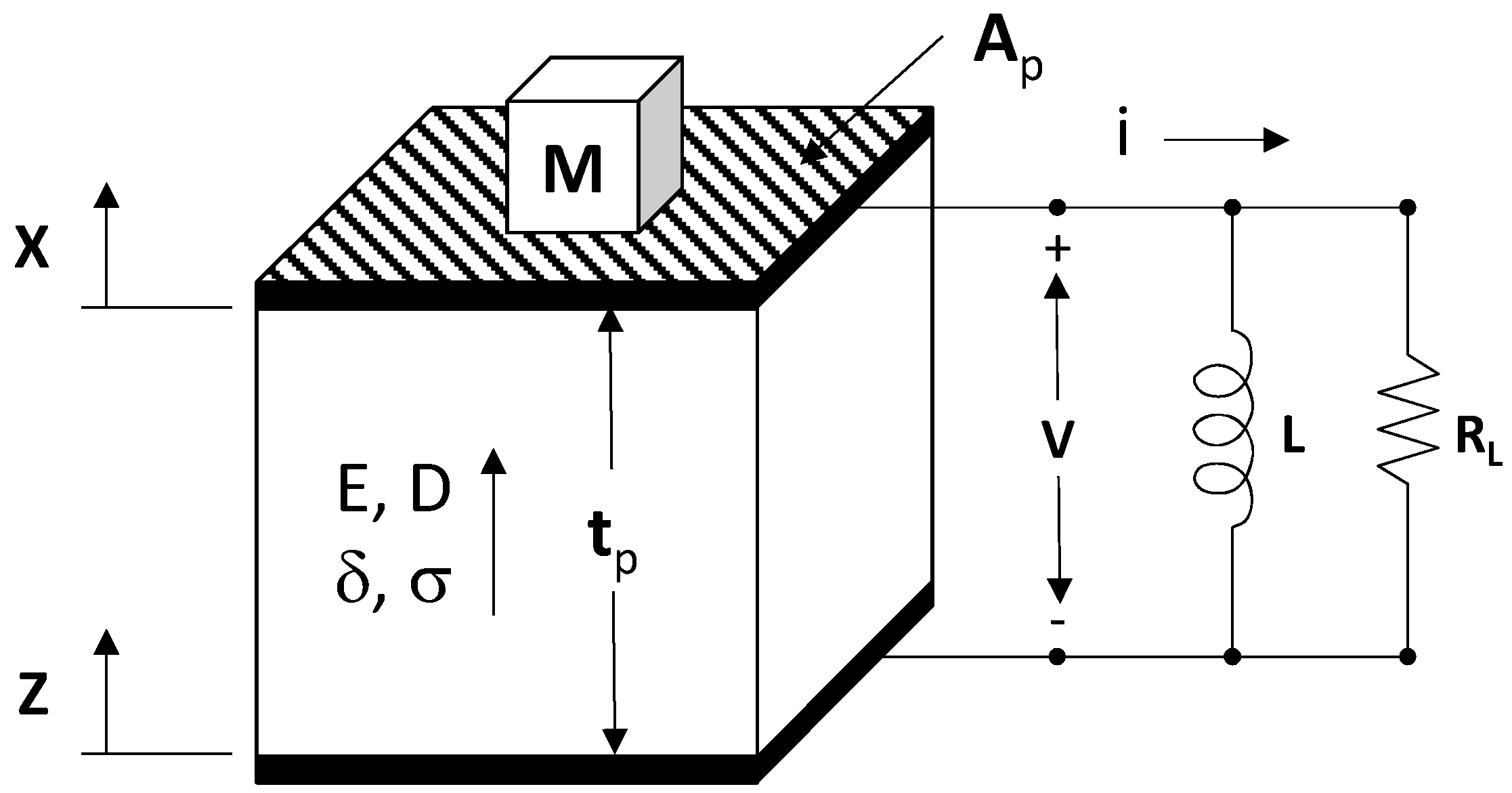
In the interest of simplicity, we will analyze the structure in Figure 2. The results achieved through analysis of this structure can be generalized to the cantilever structure through the addition of geometrical constants.
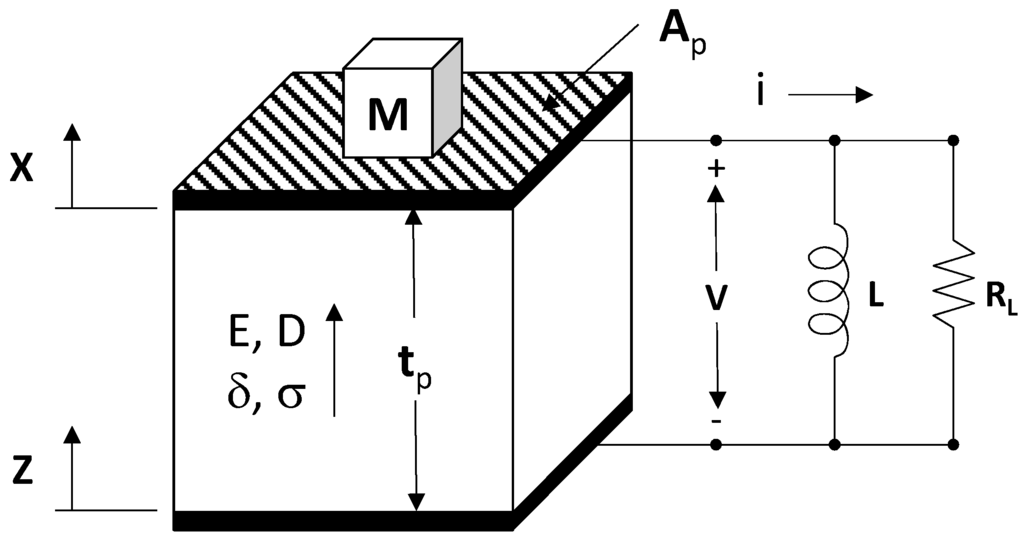
Figure 2.
Schematic of the simplified EHD that is analyzed in this paper. Ap is the area of the PZ capacitor, and tp is the thickness. Z is the complex amplitude of the source vibration, and X is the complex amplitude of the mechanical displacement of the mass M. This simplified model illustrates the concepts of electronic tuning that apply to the cantilever structure of Figure 1.
Figure 2.
Schematic of the simplified EHD that is analyzed in this paper. Ap is the area of the PZ capacitor, and tp is the thickness. Z is the complex amplitude of the source vibration, and X is the complex amplitude of the mechanical displacement of the mass M. This simplified model illustrates the concepts of electronic tuning that apply to the cantilever structure of Figure 1.
This paper describes three concepts for electrically tuning of PZ EHDs.
- Use of voltage amplitude to tune the mechanical stiffness of the EHD;
- Coupling of the mechanical resonator to an electrical RLC tank circuit;
- Bias-Flip (BF) technique to emulate the large tunable inductor that is required for the RLC tank circuit.
These three concepts were introduced in summary form in [2]. In the succeeding sections of this paper, these concepts will be presented in more detail. Section 6 shows that BF can be used to effectively optimize the power output from a PZ EHD. In this paper, we have changed some of the notation that we used in [2], in order to conform to generally accepted usage.
In this paper, we will analyze the PZ EHD. However, many of the results and conclusions are equally applicable to electromagnetic and electrostatic EHDs. Cammarano et al. [3] have described concepts very similar to #1 and #2 above in the context of electro-magnetic EHDs.
2. Frequency Tuning by Voltage
The material equations for PZ material can be written as follows [1].
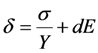
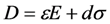
The parameters are defined below.
- δ = mechanical strain (displacement/length)
- σ = mechanical stress (force/area)
- Y = Young’s Modulus (force/area)
- d = piezo-electric (PZ) coefficient (m/volt)
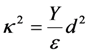
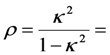 PZ coupling constant
PZ coupling constant- E = electric field (volt/m)
- D = electrical displacement (coulomb/m2)
- ε = dielectric constant (coul/volt-m)
- km = mechanical (short-circuit) spring constant
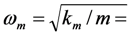 mechanical (short-circuit) resonant frequency
mechanical (short-circuit) resonant frequency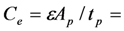 electrical (σ = 0) capacitance
electrical (σ = 0) capacitance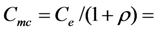 motion constrained (δ = 0) capacitance.
motion constrained (δ = 0) capacitance.- L = inductance
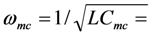 motion constrained resonant frequency
motion constrained resonant frequency- η = mechanical damping factor (force/velocity)
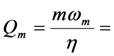 mechanical Q-factor
mechanical Q-factor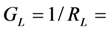 load conductance
load conductance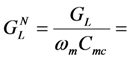 normalized load conductance
normalized load conductance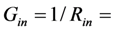 internal conductance
internal conductance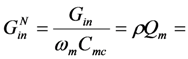 normalized internal conductance
normalized internal conductance
Refer to the device of Figure 2. When the output is shorted, E = 0, and the mechanical stiffness is given by Young’s modulus, 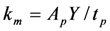 . The short-circuit, resonance frequency is given by
. The short-circuit, resonance frequency is given by 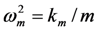 . However, when the output is in the open circuit condition, D = 0; the open-circuit stiffness is given by
. However, when the output is in the open circuit condition, D = 0; the open-circuit stiffness is given by 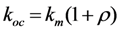 , where ρ is the dimensionless PZ coupling constant, defined in Table 1. From this, it can be shown that the open-circuit and short-circuit resonant frequencies ωoc and ωm are related by the equation
, where ρ is the dimensionless PZ coupling constant, defined in Table 1. From this, it can be shown that the open-circuit and short-circuit resonant frequencies ωoc and ωm are related by the equation 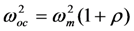 . This relationship is well-known, and has been used to experimentally determine the coupling constant ρ [1].
. This relationship is well-known, and has been used to experimentally determine the coupling constant ρ [1].
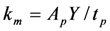 . The short-circuit, resonance frequency is given by
. The short-circuit, resonance frequency is given by 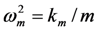 . However, when the output is in the open circuit condition, D = 0; the open-circuit stiffness is given by
. However, when the output is in the open circuit condition, D = 0; the open-circuit stiffness is given by 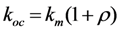 , where ρ is the dimensionless PZ coupling constant, defined in Table 1. From this, it can be shown that the open-circuit and short-circuit resonant frequencies ωoc and ωm are related by the equation
, where ρ is the dimensionless PZ coupling constant, defined in Table 1. From this, it can be shown that the open-circuit and short-circuit resonant frequencies ωoc and ωm are related by the equation 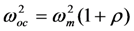 . This relationship is well-known, and has been used to experimentally determine the coupling constant ρ [1].
. This relationship is well-known, and has been used to experimentally determine the coupling constant ρ [1].Similarly, we define the electrical capacitance 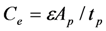 for the case when there is no stress (σ = 0); and we define the motion constrained capacitance
for the case when there is no stress (σ = 0); and we define the motion constrained capacitance 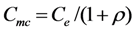 for the case when δ = 0.
for the case when δ = 0.
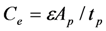 for the case when there is no stress (σ = 0); and we define the motion constrained capacitance
for the case when there is no stress (σ = 0); and we define the motion constrained capacitance 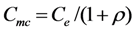 for the case when δ = 0.
for the case when δ = 0.These equations can be solved for V(ω) and X(ω) as shown below.
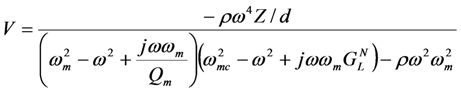
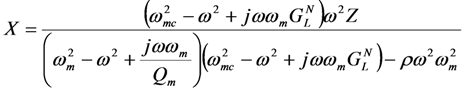
When the source vibration frequency ω equals the mechanical resonant frequency ωm, Equation (5) for output voltage reduces to a familiar form.
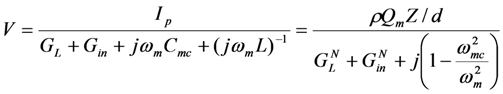
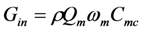 and
and 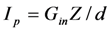 .
.This results in the familiar circuit model for the PZ EHD, shown at the left of Figure 3.
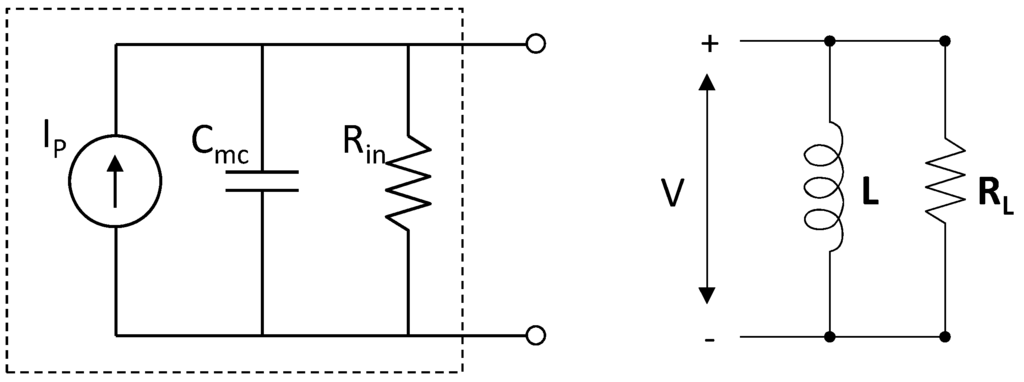
Figure 3.
The circuit within the dashed box is the equivalent circuit that applies to a PZ EHD when ω=ωm. At this frequency, the PZ current Ip is independent of the load. For ω ≠ ωm this equivalent circuit does not accurately model device behavior, because the PZ current Ip changes as the load changes. The circuit at the right includes an inductor to cancel the capacitive reactance of the EHD.
Figure 3.
The circuit within the dashed box is the equivalent circuit that applies to a PZ EHD when ω=ωm. At this frequency, the PZ current Ip is independent of the load. For ω ≠ ωm this equivalent circuit does not accurately model device behavior, because the PZ current Ip changes as the load changes. The circuit at the right includes an inductor to cancel the capacitive reactance of the EHD.
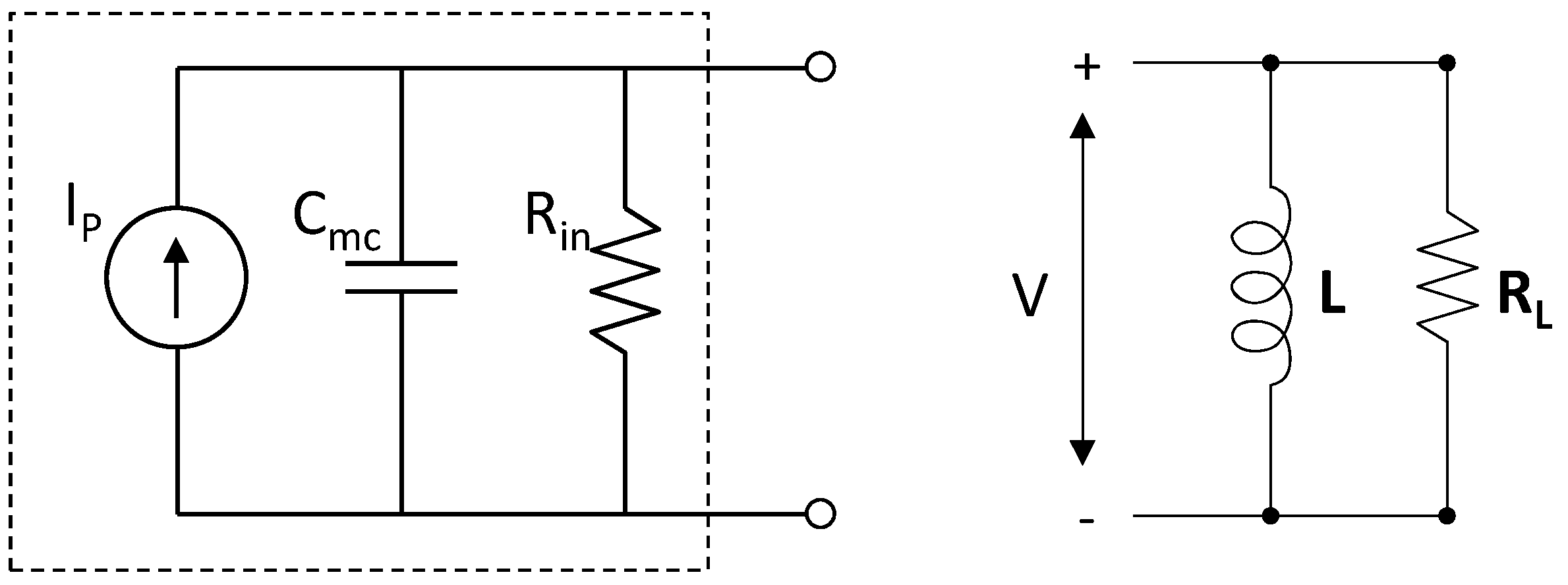
If a purely resistive load is connected to the EHD, the device capacitance Cmc degrades output power. As a result, an inductor (or an effective inductor) is added to the output circuit for the purpose of cancelling the capacitive admittance and achieving maximum average power to the load.
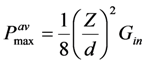
In succeeding sections, simulations of voltage and output power are shown as a function of frequency. In [2] simulations were shown for ρ = 0.2; Qm = 50; and 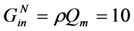 . Throughout this paper, simulations are shown for ρ = 0.05; Qm = 20; and
. Throughout this paper, simulations are shown for ρ = 0.05; Qm = 20; and 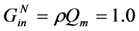 . These values are more representative of today’s commercial devices.
. These values are more representative of today’s commercial devices.
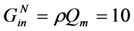 . Throughout this paper, simulations are shown for ρ = 0.05; Qm = 20; and
. Throughout this paper, simulations are shown for ρ = 0.05; Qm = 20; and 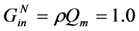 . These values are more representative of today’s commercial devices.
. These values are more representative of today’s commercial devices.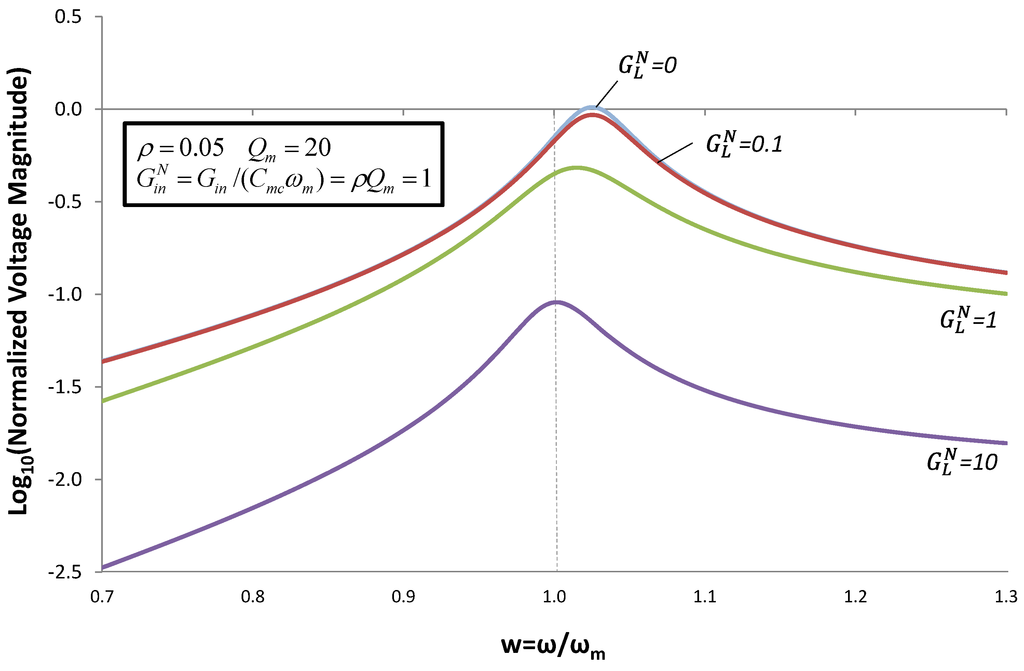
Figure 4.
Voltage magnitude for the case of no inductor. Voltage is normalized to Z / d, the open-circuit voltage at w = 1.
Figure 4.
Voltage magnitude for the case of no inductor. Voltage is normalized to Z / d, the open-circuit voltage at w = 1.
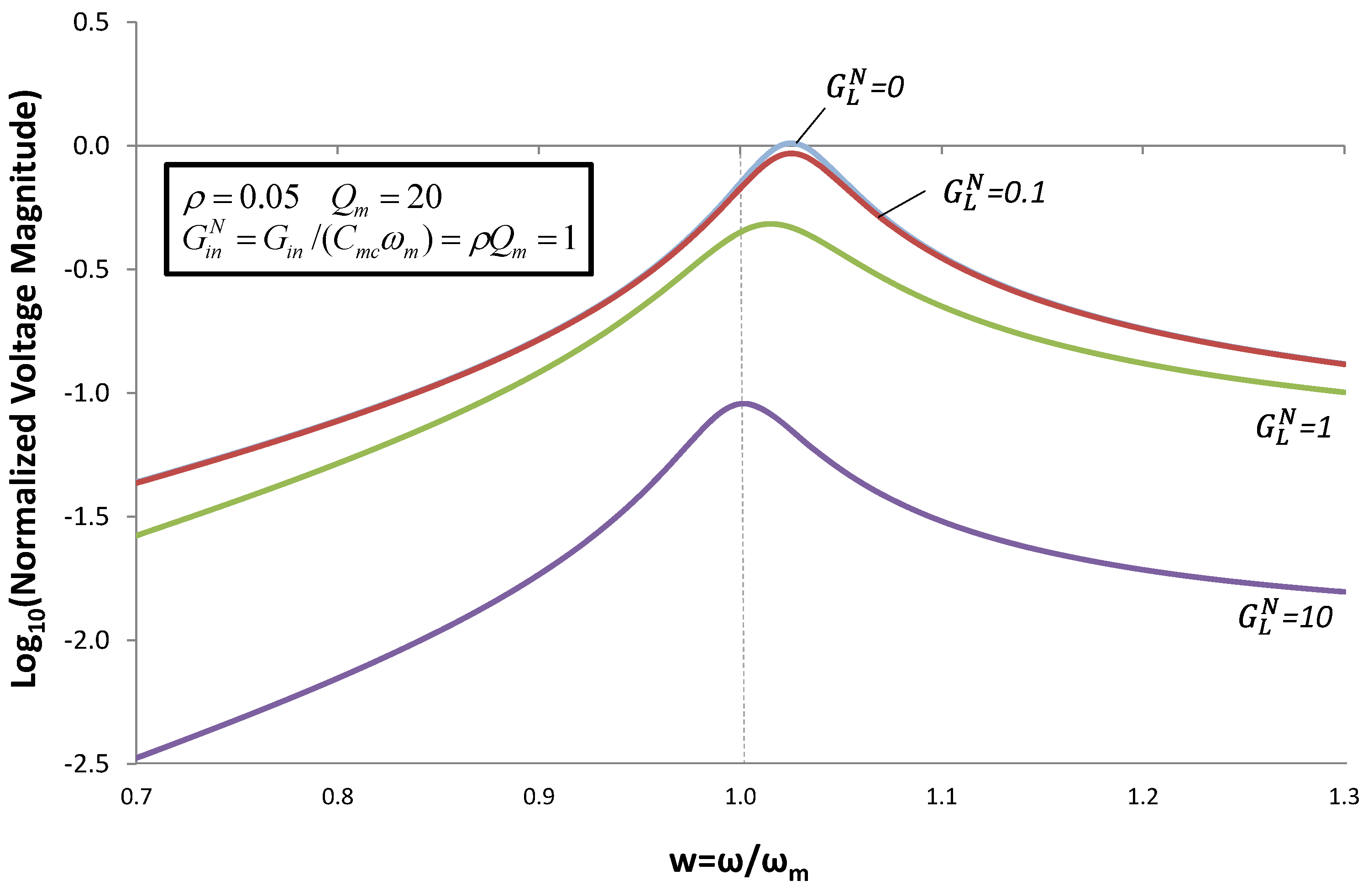
Figure 4 shows the magnitude of the output voltage as a function of frequency, calculated using Equation (5), for the case of no inductor (ωmc = 0). On the vertical axis, voltage is normalized to the maximum open-circuit voltage at the mechanical resonant frequency 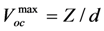 . Frequency, on the horizontal axis, is normalized to ωm. For
. Frequency, on the horizontal axis, is normalized to ωm. For 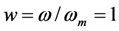 , Figure 4 confirms the predictions of Equation (7). For
, Figure 4 confirms the predictions of Equation (7). For 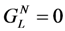 , the normalized voltage magnitude is 0.707; and for
, the normalized voltage magnitude is 0.707; and for 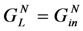 , the normalized voltage magnitude is 0.447. However, for w ≠ 1, Figure 4 shows interesting behavior, especially for
, the normalized voltage magnitude is 0.447. However, for w ≠ 1, Figure 4 shows interesting behavior, especially for 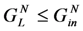 . For
. For 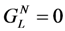 , the voltage shows a resonance at
, the voltage shows a resonance at 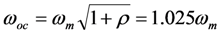 .
.
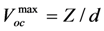 . Frequency, on the horizontal axis, is normalized to ωm. For
. Frequency, on the horizontal axis, is normalized to ωm. For 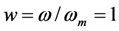 , Figure 4 confirms the predictions of Equation (7). For
, Figure 4 confirms the predictions of Equation (7). For 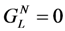 , the normalized voltage magnitude is 0.707; and for
, the normalized voltage magnitude is 0.707; and for 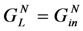 , the normalized voltage magnitude is 0.447. However, for w ≠ 1, Figure 4 shows interesting behavior, especially for
, the normalized voltage magnitude is 0.447. However, for w ≠ 1, Figure 4 shows interesting behavior, especially for 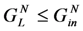 . For
. For 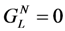 , the voltage shows a resonance at
, the voltage shows a resonance at 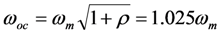 .
.Figure 4 shows that, for large  , the voltage peaks at the mechanical or short-circuit resonance frequency ωm. However, for small
, the voltage peaks at the mechanical or short-circuit resonance frequency ωm. However, for small  , the device characteristics change. When
, the device characteristics change. When 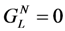 , the peak voltage occurs at
, the peak voltage occurs at 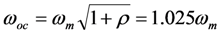 . This can be understood as follows. For large
. This can be understood as follows. For large  , the electric field is effectively shorted. As
, the electric field is effectively shorted. As  decreases, the electric field in the EHD increases, and alters the effective spring constant of the cantilever beam.
decreases, the electric field in the EHD increases, and alters the effective spring constant of the cantilever beam.
 , the voltage peaks at the mechanical or short-circuit resonance frequency ωm. However, for small
, the voltage peaks at the mechanical or short-circuit resonance frequency ωm. However, for small  , the device characteristics change. When
, the device characteristics change. When 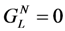 , the peak voltage occurs at
, the peak voltage occurs at 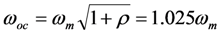 . This can be understood as follows. For large
. This can be understood as follows. For large  , the electric field is effectively shorted. As
, the electric field is effectively shorted. As  decreases, the electric field in the EHD increases, and alters the effective spring constant of the cantilever beam.
decreases, the electric field in the EHD increases, and alters the effective spring constant of the cantilever beam.It is tempting to assume from the above that frequency tuning is possible only in the narrow range 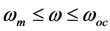 [4]. However, as we will see below, the addition of a resonant electrical circuit allows the voltage to swing below zero and above Voc, thereby enabling a wider tuning range.
[4]. However, as we will see below, the addition of a resonant electrical circuit allows the voltage to swing below zero and above Voc, thereby enabling a wider tuning range.
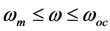 [4]. However, as we will see below, the addition of a resonant electrical circuit allows the voltage to swing below zero and above Voc, thereby enabling a wider tuning range.
[4]. However, as we will see below, the addition of a resonant electrical circuit allows the voltage to swing below zero and above Voc, thereby enabling a wider tuning range. 3. Coupled Oscillators
In the simulations in the previous section, we did not attempt to cancel the reactive admittance of the PZ capacitor, and we observed the degradation in output voltage. Since 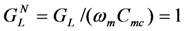 in the simulations above, the degradation is not large. However, in some cases, the PZ EHD has a large capacitance, which can substantially degrade output power at ω = ωm. In Figure 5, we simulate Equation (5) for the case ωmc = ωm. This is equivalent to adding an inductor that cancels the reactive admittance of the capacitor at ω = ωm. The inductor performs as expected at ω = ωm. The output voltage equals
in the simulations above, the degradation is not large. However, in some cases, the PZ EHD has a large capacitance, which can substantially degrade output power at ω = ωm. In Figure 5, we simulate Equation (5) for the case ωmc = ωm. This is equivalent to adding an inductor that cancels the reactive admittance of the capacitor at ω = ωm. The inductor performs as expected at ω = ωm. The output voltage equals 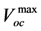 . Moreover, for large
. Moreover, for large  , the output voltage continues to show a resonant peak at ω = ωm; and the voltage falls away sharply away from ω = ωm.
, the output voltage continues to show a resonant peak at ω = ωm; and the voltage falls away sharply away from ω = ωm.
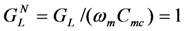 in the simulations above, the degradation is not large. However, in some cases, the PZ EHD has a large capacitance, which can substantially degrade output power at ω = ωm. In Figure 5, we simulate Equation (5) for the case ωmc = ωm. This is equivalent to adding an inductor that cancels the reactive admittance of the capacitor at ω = ωm. The inductor performs as expected at ω = ωm. The output voltage equals
in the simulations above, the degradation is not large. However, in some cases, the PZ EHD has a large capacitance, which can substantially degrade output power at ω = ωm. In Figure 5, we simulate Equation (5) for the case ωmc = ωm. This is equivalent to adding an inductor that cancels the reactive admittance of the capacitor at ω = ωm. The inductor performs as expected at ω = ωm. The output voltage equals 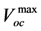 . Moreover, for large
. Moreover, for large  , the output voltage continues to show a resonant peak at ω = ωm; and the voltage falls away sharply away from ω = ωm.
, the output voltage continues to show a resonant peak at ω = ωm; and the voltage falls away sharply away from ω = ωm.However, for ω ≠ ωm, Figure 5 shows a surprising result when  is small. Two peaks occur at
is small. Two peaks occur at 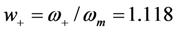 and
and 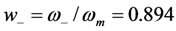 . These resonances result from the poles in the denominator of Equation (5) when
. These resonances result from the poles in the denominator of Equation (5) when 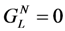 .
.
 is small. Two peaks occur at
is small. Two peaks occur at 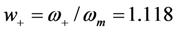 and
and 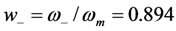 . These resonances result from the poles in the denominator of Equation (5) when
. These resonances result from the poles in the denominator of Equation (5) when 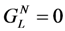 .
.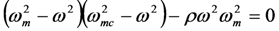
Solution to the pole-splitting equation above, for the case ωmc = ωm and ρ = 0.05 gives the values of w+ and w− above. Note that, when ωmc = 0 (case of no inductor), the solutions of Equation (9) are w− = 0 and 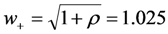 . Pole splitting, which describes coupled modes of the mechanical and electrical resonators, occurs only for small
. Pole splitting, which describes coupled modes of the mechanical and electrical resonators, occurs only for small  . When
. When  is large, the electric field in the PZ material is screened, and coupling is suppressed.
is large, the electric field in the PZ material is screened, and coupling is suppressed.
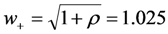 . Pole splitting, which describes coupled modes of the mechanical and electrical resonators, occurs only for small
. Pole splitting, which describes coupled modes of the mechanical and electrical resonators, occurs only for small  . When
. When  is large, the electric field in the PZ material is screened, and coupling is suppressed.
is large, the electric field in the PZ material is screened, and coupling is suppressed.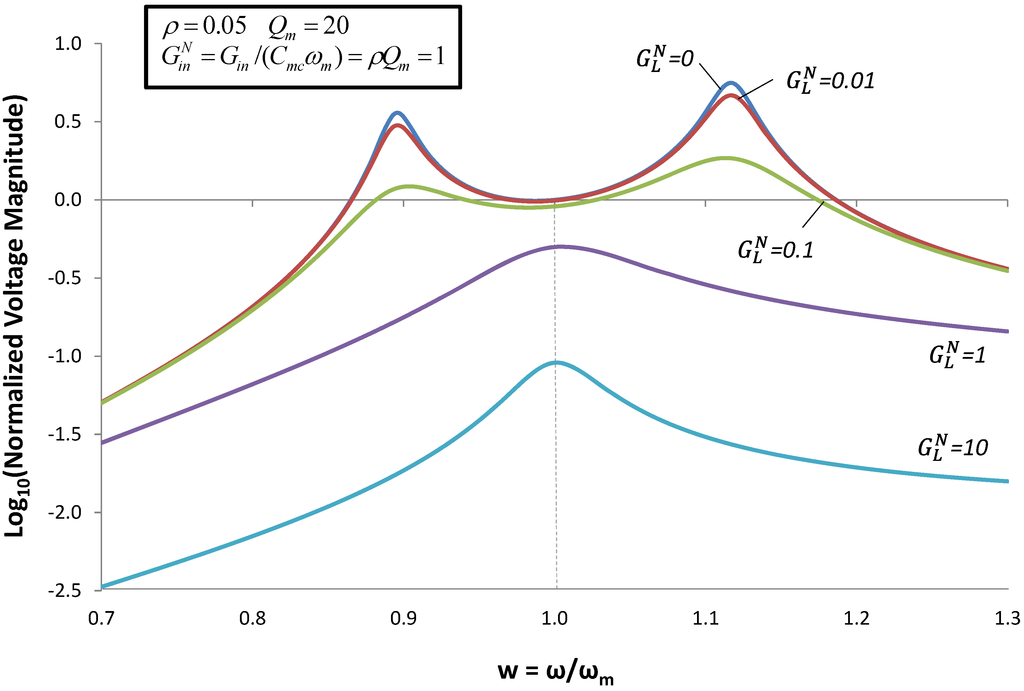
Figure 5.
Voltage magnitude for the case when an inductor of value 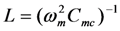 is added to the circuit. Voltage is normalized as in Figure 4.
is added to the circuit. Voltage is normalized as in Figure 4.
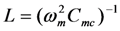 is added to the circuit. Voltage is normalized as in Figure 4.
is added to the circuit. Voltage is normalized as in Figure 4.
Figure 5.
Voltage magnitude for the case when an inductor of value 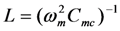 is added to the circuit. Voltage is normalized as in Figure 4.
is added to the circuit. Voltage is normalized as in Figure 4.
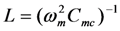 is added to the circuit. Voltage is normalized as in Figure 4.
is added to the circuit. Voltage is normalized as in Figure 4.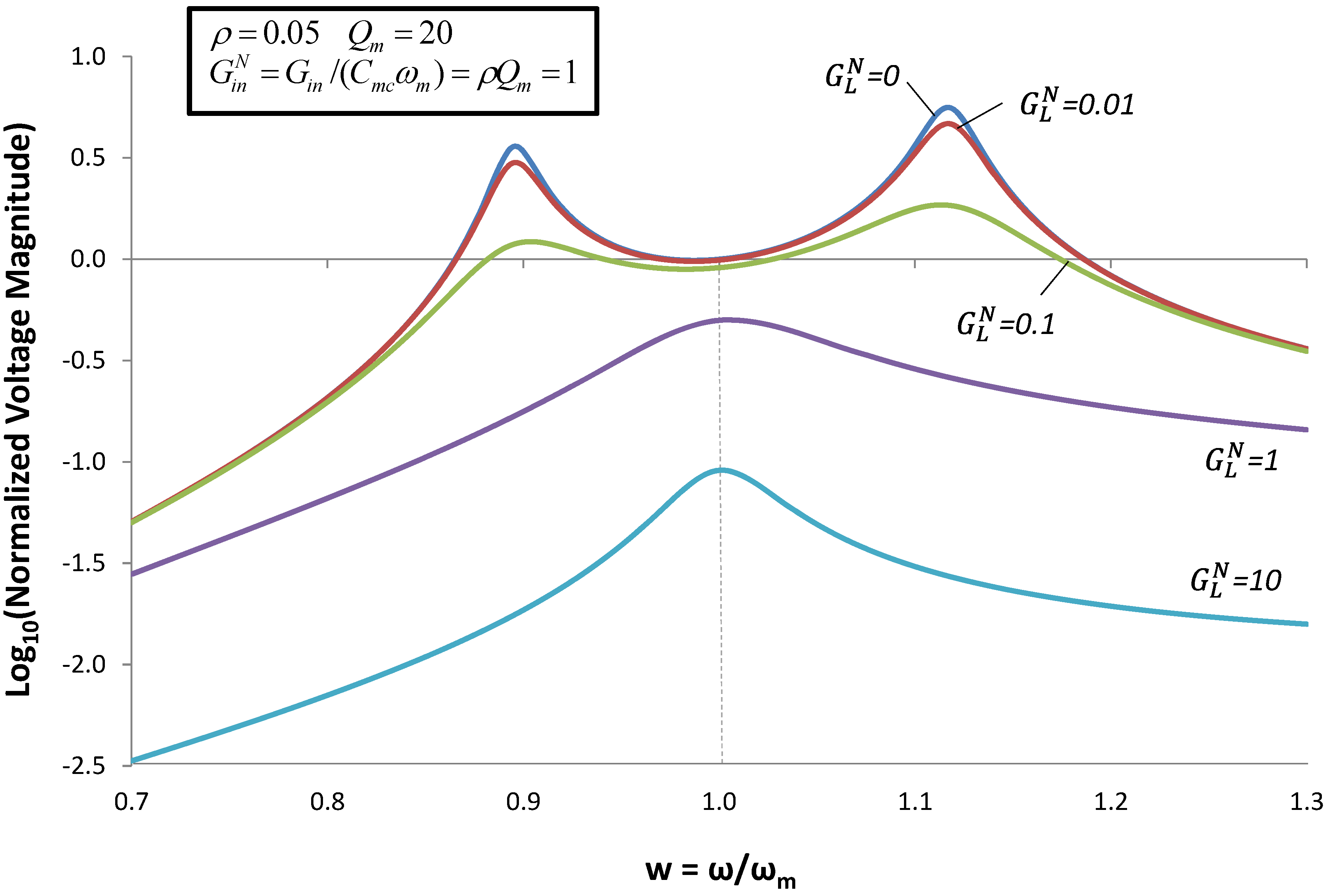
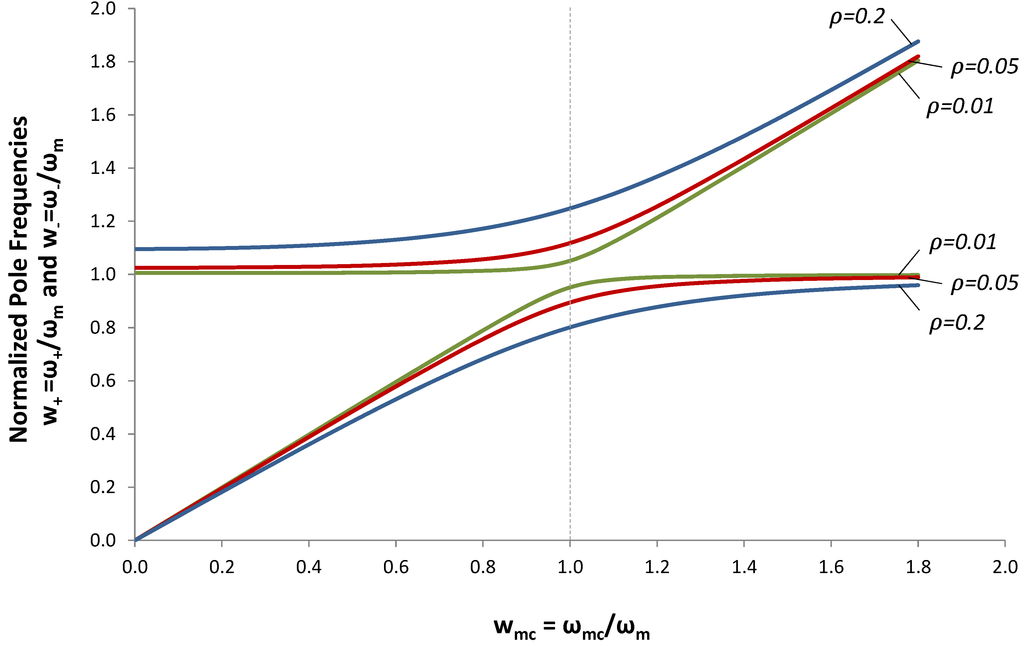
Figure 6.
Roots of the Pole-splitting Equation (9). The normalized pole frequencies 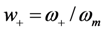 and
and 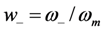 are plotted vs.
are plotted vs. 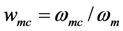 .
.
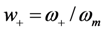 and
and 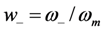 are plotted vs.
are plotted vs. 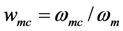 .
.
Figure 6.
Roots of the Pole-splitting Equation (9). The normalized pole frequencies 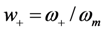 and
and 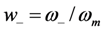 are plotted vs.
are plotted vs. 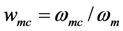 .
.
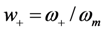 and
and 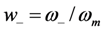 are plotted vs.
are plotted vs. 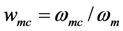 .
.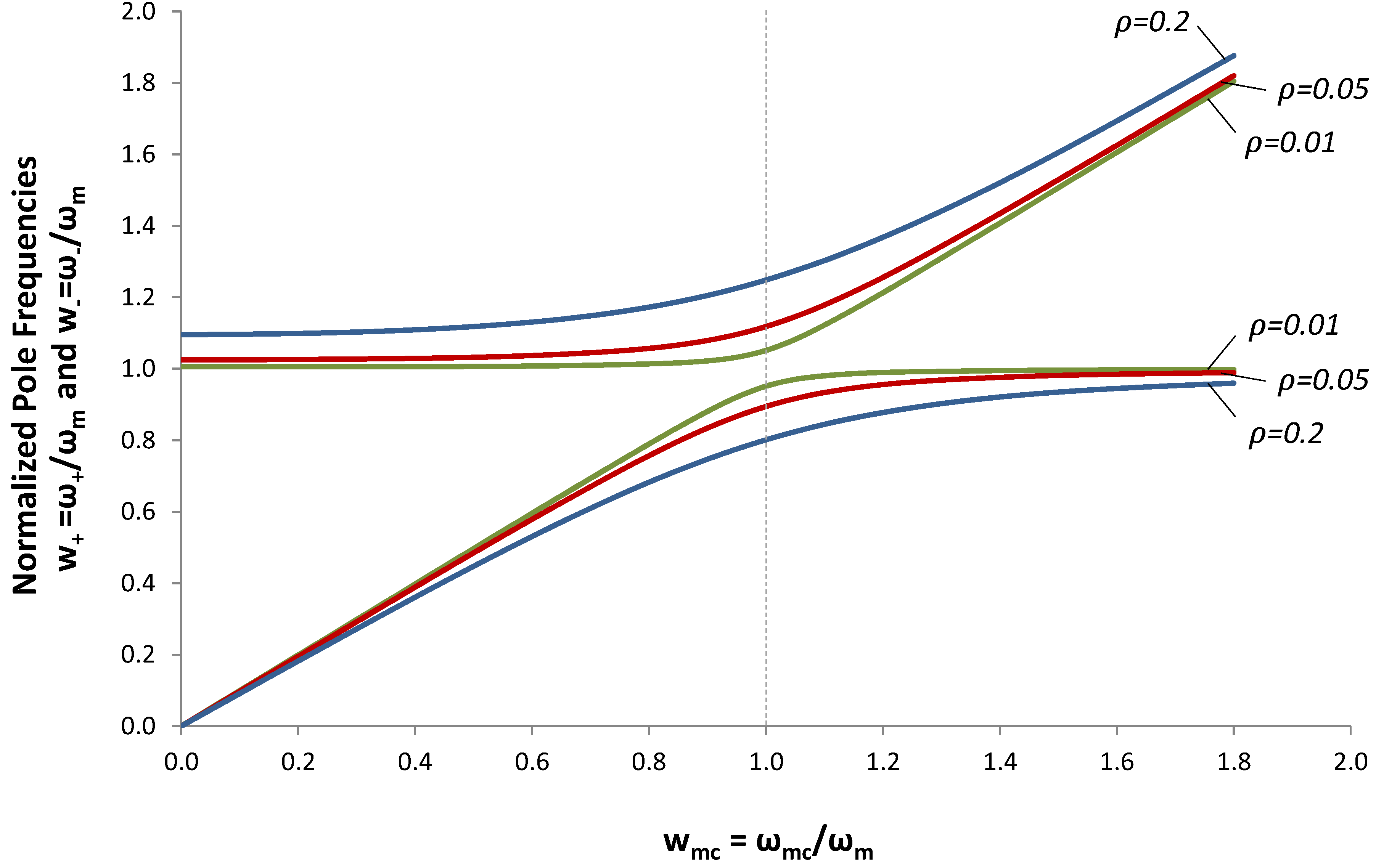
The roots of the pole-splitting equation are shown in Figure 6 for several values of coupling constant ρ. In Figure 5, we selected ωmc = ωm, in order to optimize output power at ω = ωm. But, we discovered that, if we increased the load resistance, we could also optimize output voltage at w+ and w−. (We will show in the next section that output power is also optimized at these frequencies). This analysis suggests that we can tune the EHD resonant frequency by varying ωmc.
We can gain further insight into the pole-splitting by returning to Equations (5) and (6). For small  , the following relationship holds between X(ω) and V(ω).
, the following relationship holds between X(ω) and V(ω).
 , the following relationship holds between X(ω) and V(ω).
, the following relationship holds between X(ω) and V(ω).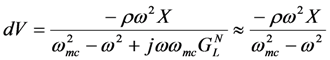
Using Equation (10) the force of the spring can be written as
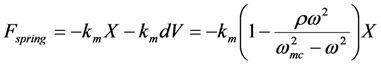
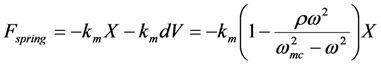
The above equation shows that, by tuning L, we can vary ωmc and vary the effective spring constant. When ω < ωmc, V(ω) has a phase of 180° relative to X(ω); and the voltage reduces the effective spring constant. When ω > ωmc, V(ω) has a phase of 0° relative to X(ω); and the voltage increases the effective spring constant. When ω = ωmc, the magnitude of X(ω) is zero. If we adjust ωmc such that the corresponding root of Equation (9) equals the source vibration frequency, then Equation (11) reduces to
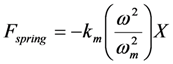
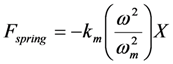
Equation (12) shows that the effective spring constant can be tuned over a wide range.
It is also somewhat surprising that the peak voltages at ω− and ω+ are 3.5× to 5.5× higher than 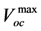 . The simulations in this paper assume that the source magnitude Z is held constant as the frequency changes. As a result, the input acceleration increases in proportion to ω2, and
. The simulations in this paper assume that the source magnitude Z is held constant as the frequency changes. As a result, the input acceleration increases in proportion to ω2, and 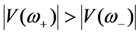 . The important result is that the peak voltages away from resonance can be somewhat higher than
. The important result is that the peak voltages away from resonance can be somewhat higher than 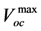 , and the higher voltage enables frequency tuning.
, and the higher voltage enables frequency tuning.
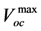 . The simulations in this paper assume that the source magnitude Z is held constant as the frequency changes. As a result, the input acceleration increases in proportion to ω2, and
. The simulations in this paper assume that the source magnitude Z is held constant as the frequency changes. As a result, the input acceleration increases in proportion to ω2, and 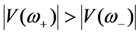 . The important result is that the peak voltages away from resonance can be somewhat higher than
. The important result is that the peak voltages away from resonance can be somewhat higher than 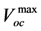 , and the higher voltage enables frequency tuning.
, and the higher voltage enables frequency tuning.4. Optimizing Output Power
In the previous section, we showed that voltage can be made to peak at frequencies ω− and ω+, which are different from ωm. Figure 7 shows that power is also maximized at these frequencies. The curve for 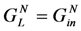 indicates that output power peaks at ω = ωm, at the power
indicates that output power peaks at ω = ωm, at the power 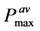 given by Equation (8). The curve for
given by Equation (8). The curve for 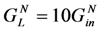 shows a peak at ω = ωm at a degraded power level. The curve for
shows a peak at ω = ωm at a degraded power level. The curve for 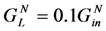 shows two peaks at ω− and ω+ that have output power comparable to
shows two peaks at ω− and ω+ that have output power comparable to 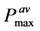 . When
. When  is further reduced to
is further reduced to 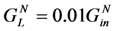 , the output power at ω− and ω+ decreases.
, the output power at ω− and ω+ decreases.
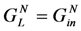 indicates that output power peaks at ω = ωm, at the power
indicates that output power peaks at ω = ωm, at the power 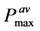 given by Equation (8). The curve for
given by Equation (8). The curve for 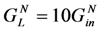 shows a peak at ω = ωm at a degraded power level. The curve for
shows a peak at ω = ωm at a degraded power level. The curve for 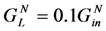 shows two peaks at ω− and ω+ that have output power comparable to
shows two peaks at ω− and ω+ that have output power comparable to 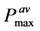 . When
. When  is further reduced to
is further reduced to 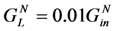 , the output power at ω− and ω+ decreases.
, the output power at ω− and ω+ decreases.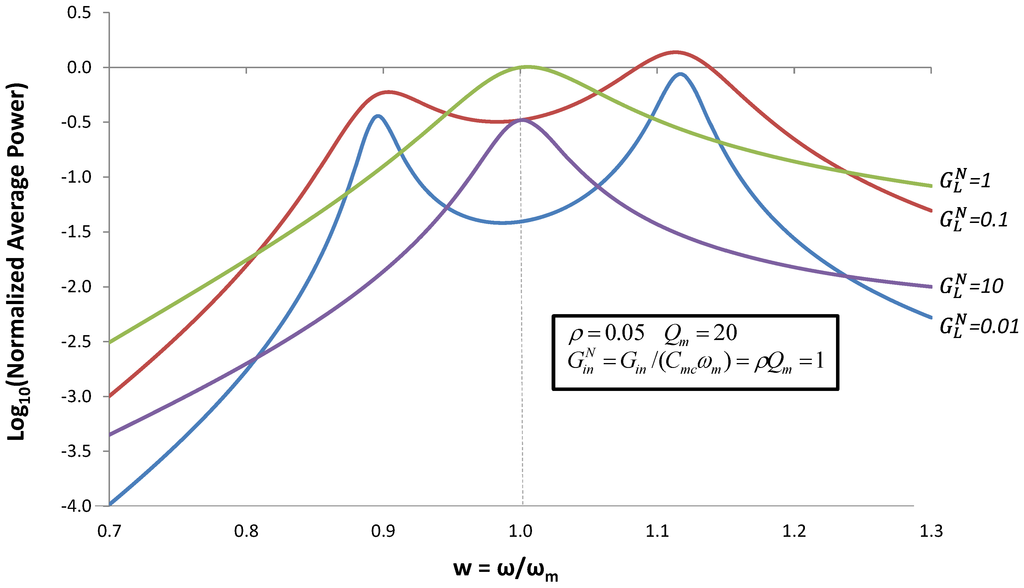
Figure 7.
Normalized average output power for the case when an inductor of value 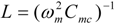 is added to the circuit. Average power is normalized by
is added to the circuit. Average power is normalized by 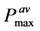 Equation (8).
Equation (8).
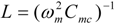 is added to the circuit. Average power is normalized by
is added to the circuit. Average power is normalized by 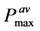 Equation (8).
Equation (8).
Figure 7.
Normalized average output power for the case when an inductor of value 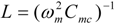 is added to the circuit. Average power is normalized by
is added to the circuit. Average power is normalized by 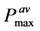 Equation (8).
Equation (8).
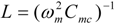 is added to the circuit. Average power is normalized by
is added to the circuit. Average power is normalized by 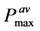 Equation (8).
Equation (8).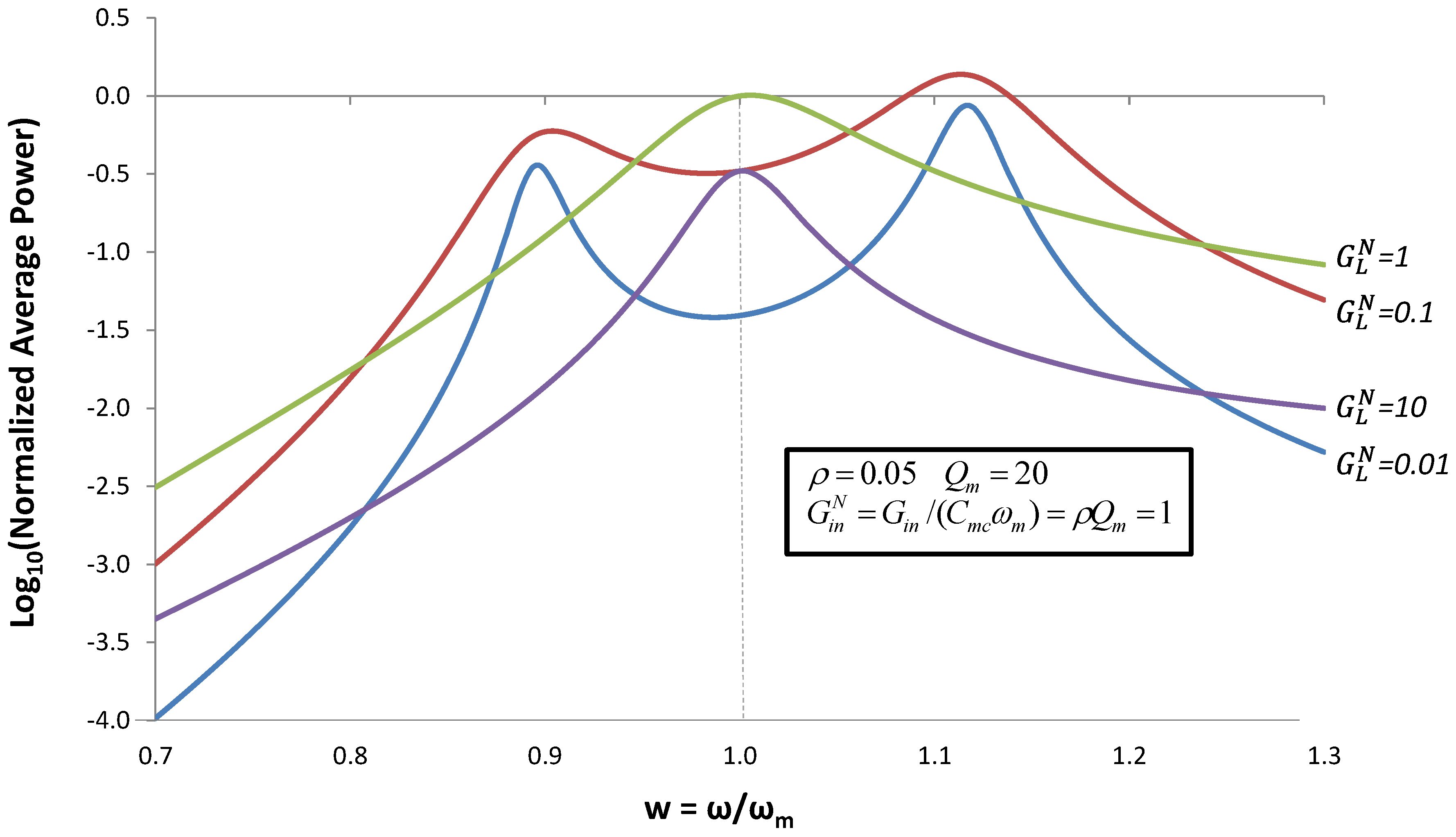
Figure 7 suggests that output power can be optimized at frequencies different from ωm by adjusting the external inductor (or effective inductor). Equation (5) provides a general expression for V(ω). Varying the parameter 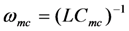 in Equation (5) is equivalent to varying the inductor. Maximizing power with respect to ωmc gives the expression
in Equation (5) is equivalent to varying the inductor. Maximizing power with respect to ωmc gives the expression
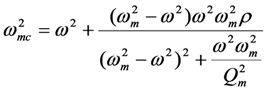
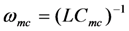 in Equation (5) is equivalent to varying the inductor. Maximizing power with respect to ωmc gives the expression
in Equation (5) is equivalent to varying the inductor. Maximizing power with respect to ωmc gives the expression
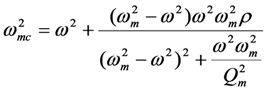
When we use Equation (13) to determine the value of ωmc that optimizes power at each frequency, the resulting voltage and power are shown in Figure 8, Figure 9.
Equation (13) suggests that we need two strategies for optimizing power, depending on the source frequency ω. For frequencies near ωm, (Region 2), Equation (13) reduces to
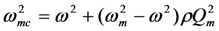
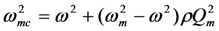
Note that, when ω = ωm, Equation (14) reduces further to ωmc = ωm, which is equivalent to matching the capacitive admittance (refer to Figure 3). When ω is above or below ωm (Regions 1 and 3), Equation (13) reduces to the pole-splitting Equation (9). Far from ωm, output power is maximized at the pole frequencies [roots of Equation (9)]. However, as ω approaches ωm, interaction between the poles shifts the max-power frequency [given by Equation (13)] slightly away from the pole frequency.
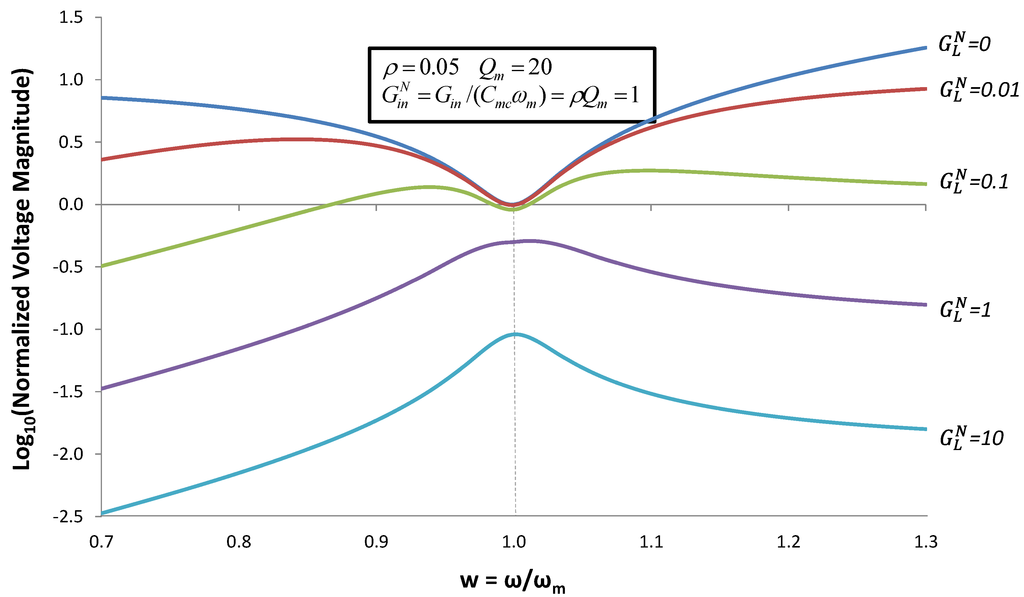
Figure 8.
Normalized voltage magnitude for the case when the reactive admittance is optimized to give maximum output power using Equation (13). Plots of Voltage vs. frequency are given for different values of normalized load conductance  . These plots can be thought of as envelopes of curves such as Figure 5 for different values of ωmc.
. These plots can be thought of as envelopes of curves such as Figure 5 for different values of ωmc.
 . These plots can be thought of as envelopes of curves such as Figure 5 for different values of ωmc.
. These plots can be thought of as envelopes of curves such as Figure 5 for different values of ωmc.
Figure 8.
Normalized voltage magnitude for the case when the reactive admittance is optimized to give maximum output power using Equation (13). Plots of Voltage vs. frequency are given for different values of normalized load conductance  . These plots can be thought of as envelopes of curves such as Figure 5 for different values of ωmc.
. These plots can be thought of as envelopes of curves such as Figure 5 for different values of ωmc.
 . These plots can be thought of as envelopes of curves such as Figure 5 for different values of ωmc.
. These plots can be thought of as envelopes of curves such as Figure 5 for different values of ωmc.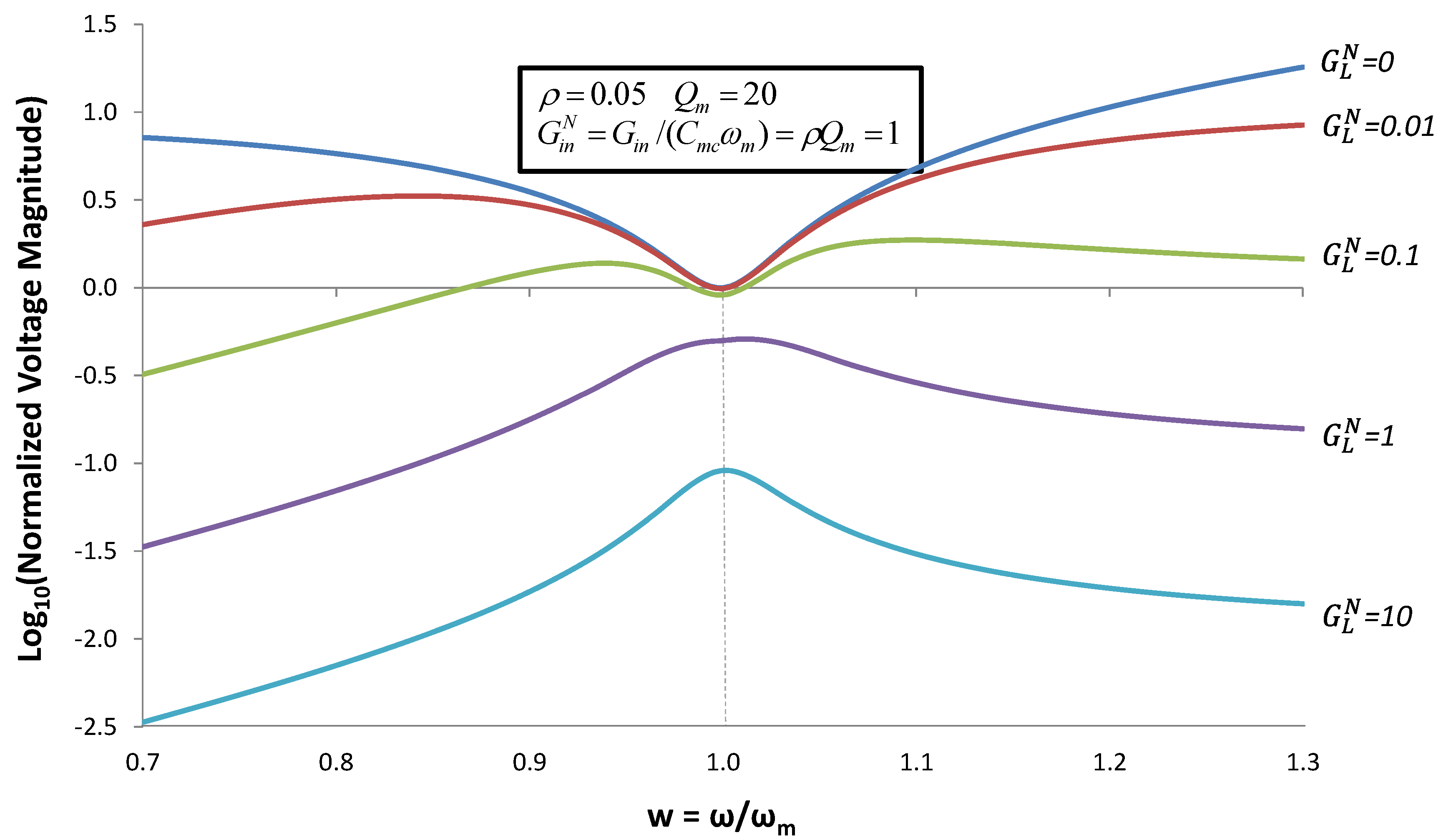
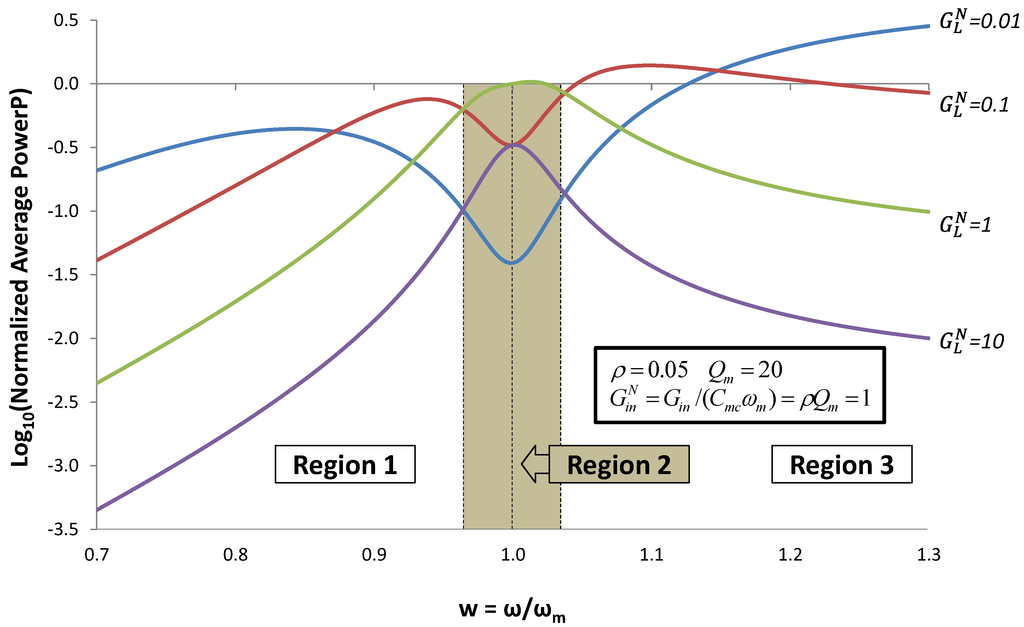
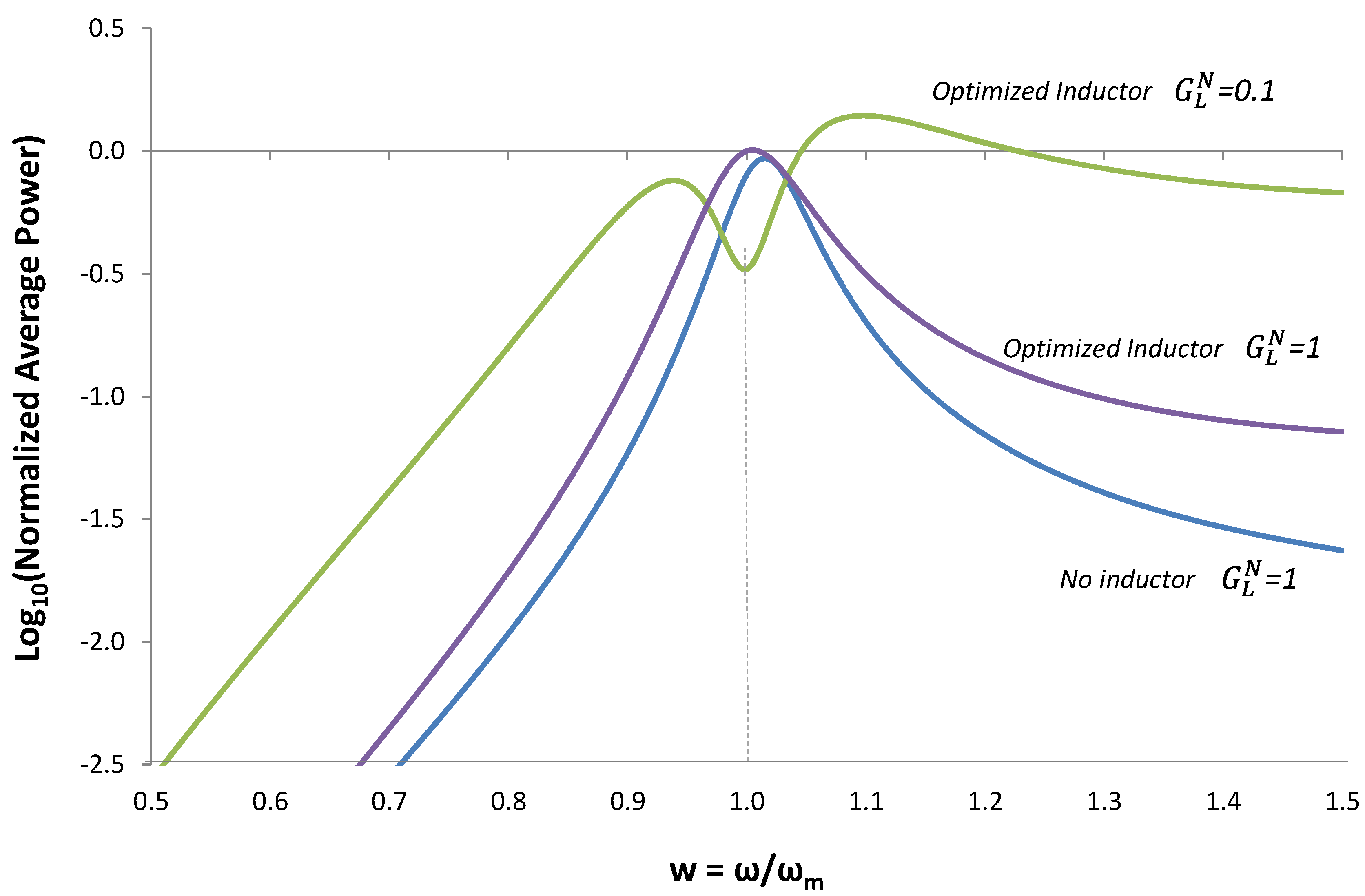
Figure 9.
Normalized average power for the case when the reactive admittance is optimized to give maximum output power using Equation (13). Plots of power vs. frequency are given for different values of normalized load conductance  . Power increases with increasing ω because source acceleration increases, thereby increasing input power.
. Power increases with increasing ω because source acceleration increases, thereby increasing input power.
 . Power increases with increasing ω because source acceleration increases, thereby increasing input power.
. Power increases with increasing ω because source acceleration increases, thereby increasing input power.
Figure 9.
Normalized average power for the case when the reactive admittance is optimized to give maximum output power using Equation (13). Plots of power vs. frequency are given for different values of normalized load conductance  . Power increases with increasing ω because source acceleration increases, thereby increasing input power.
. Power increases with increasing ω because source acceleration increases, thereby increasing input power.
 . Power increases with increasing ω because source acceleration increases, thereby increasing input power.
. Power increases with increasing ω because source acceleration increases, thereby increasing input power.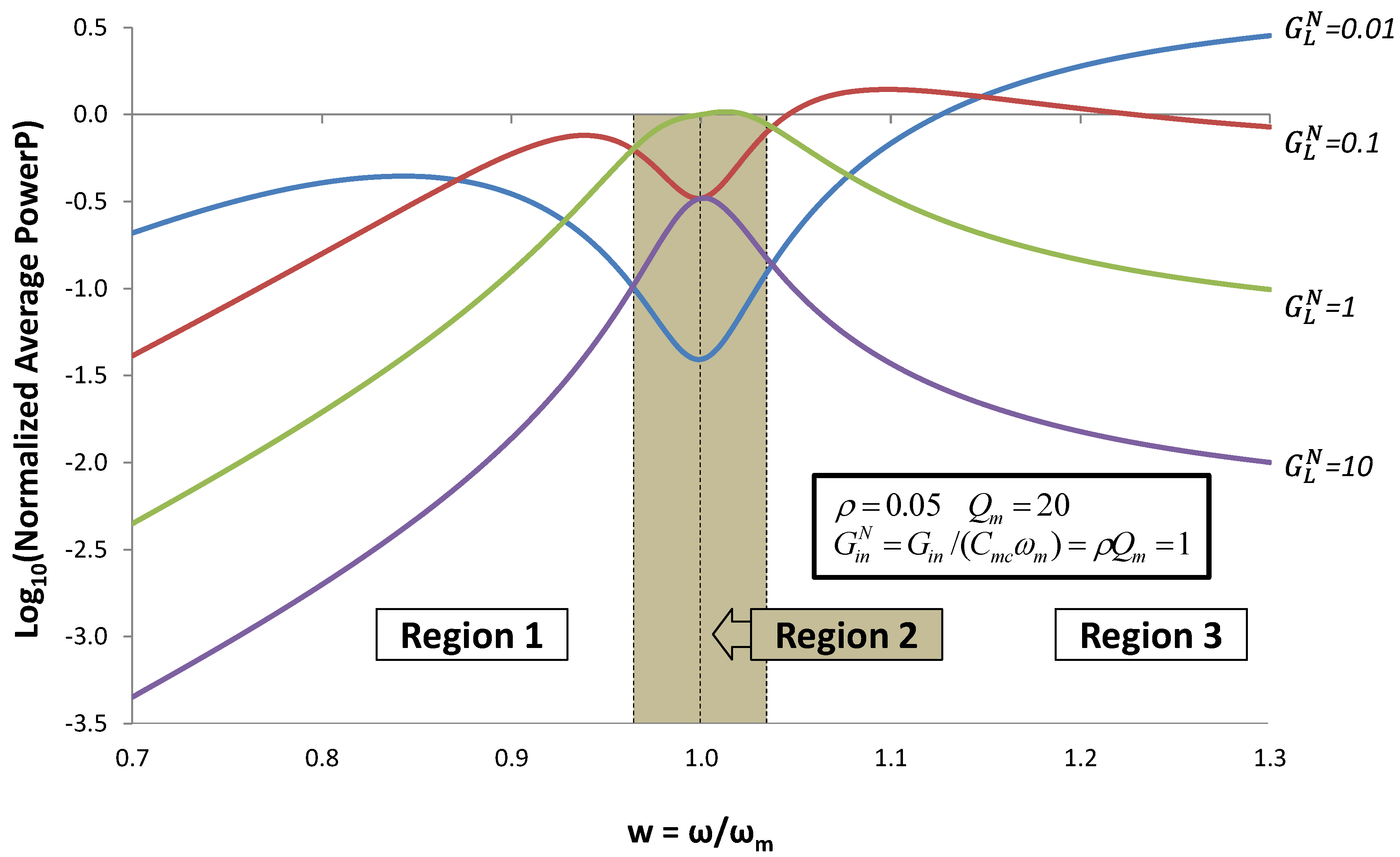
Within the region 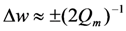 around the mechanical resonant frequency (Region 2), output power can be optimized by using (14) for reactive admittance and
around the mechanical resonant frequency (Region 2), output power can be optimized by using (14) for reactive admittance and 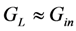 . In Regions 1 and 3, power is optimized by using the pole splitting Equation (9) for reactive admittance and
. In Regions 1 and 3, power is optimized by using the pole splitting Equation (9) for reactive admittance and 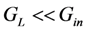 . For the parameters used in this example (Qm = 20), Δw ≈ 0.025.
. For the parameters used in this example (Qm = 20), Δw ≈ 0.025.
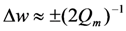 around the mechanical resonant frequency (Region 2), output power can be optimized by using (14) for reactive admittance and
around the mechanical resonant frequency (Region 2), output power can be optimized by using (14) for reactive admittance and 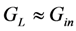 . In Regions 1 and 3, power is optimized by using the pole splitting Equation (9) for reactive admittance and
. In Regions 1 and 3, power is optimized by using the pole splitting Equation (9) for reactive admittance and 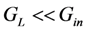 . For the parameters used in this example (Qm = 20), Δw ≈ 0.025.
. For the parameters used in this example (Qm = 20), Δw ≈ 0.025.Cammarano et al. [3] have derived an equation very similar to Equation (13): Equation (8) in [3]. They observe that the power conditioning system at the output of the EHD can be used to synthesize the complex load impedance required by Equation (13), and they comment on the challenge of reducing the power of such systems. Chang et al. [5] have implemented a switch-mode power conditioning system to the output of a PZ EHD, and have demonstrated the ability to harvest energy from two sources simultaneously: ω = ωm and ω = 1.2ωm.
5. Bias-Flip Technique
For a typical, discrete EHD, Cmc ≈ 100nF, and the inductor required to match this reactance at 100 Hz is impractically large: L ≈ 25H. However, it has been shown that the Bias-Flip technique can be used to synthesize a reactive impedance for effective impedance matching [6,7]. This technique is suitable to ULP miniaturization. It utilizes a very small inductor together with ULP microelectronics to emulate an inductor that is large and tunable. The BF technique has been shown to be effective in maximizing the output power of PZ EHDs at ω = ωm [7]. In this section, we will describe the Bias-Flip technique in the context of the equivalent circuit of Figure 3 describing a PZ EHD operating at the mechanical resonance frequency.
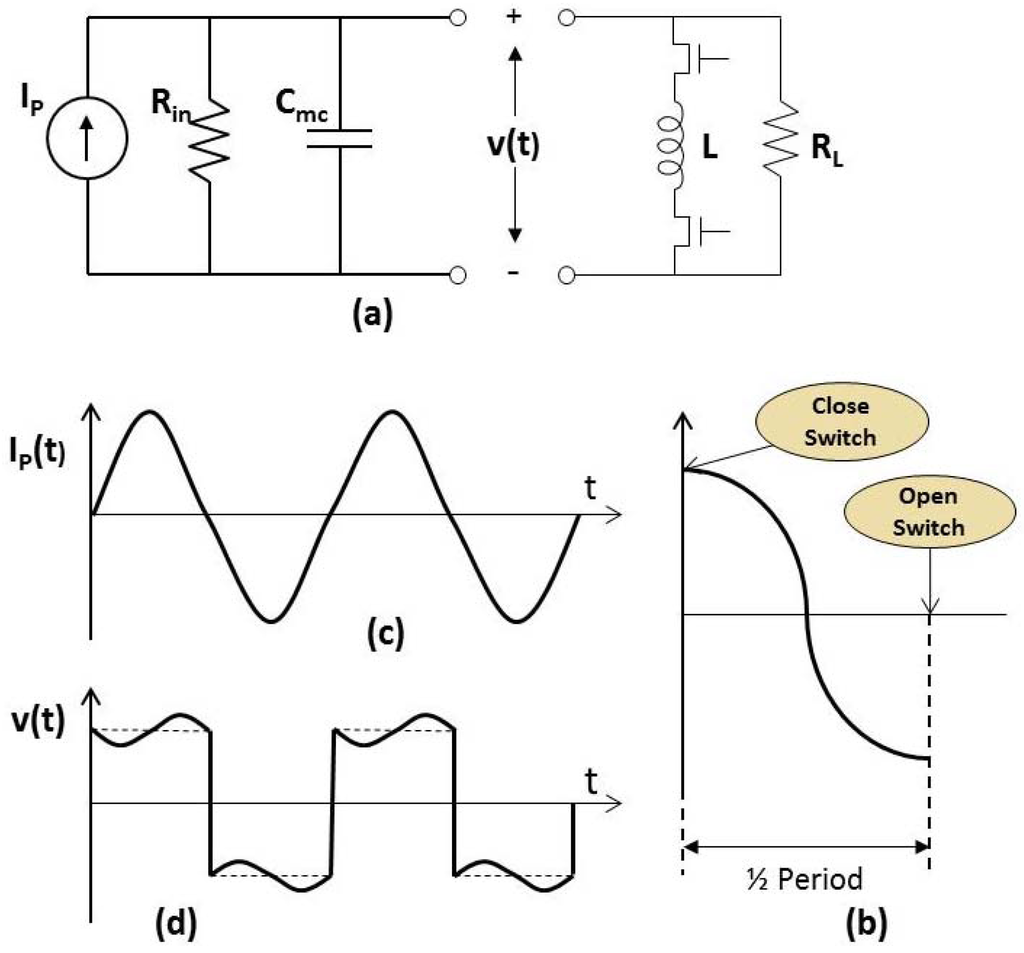
Figure 10.
Operation of a Bias Flip (BF) Inductor. (a) A small inductor is connected to the output through ideal switches; (b) When the switchers are closed, the LC tank circuit begins to oscillate, when the switches are opened, half a period later, the sign of the voltage has been adiabatically “flipped”; (c) To achieve maximum power to the load, the bias is flipped when Ip changes sign; (d) The resulting voltage waveform is “in-phase” with the current.
Figure 10.
Operation of a Bias Flip (BF) Inductor. (a) A small inductor is connected to the output through ideal switches; (b) When the switchers are closed, the LC tank circuit begins to oscillate, when the switches are opened, half a period later, the sign of the voltage has been adiabatically “flipped”; (c) To achieve maximum power to the load, the bias is flipped when Ip changes sign; (d) The resulting voltage waveform is “in-phase” with the current.
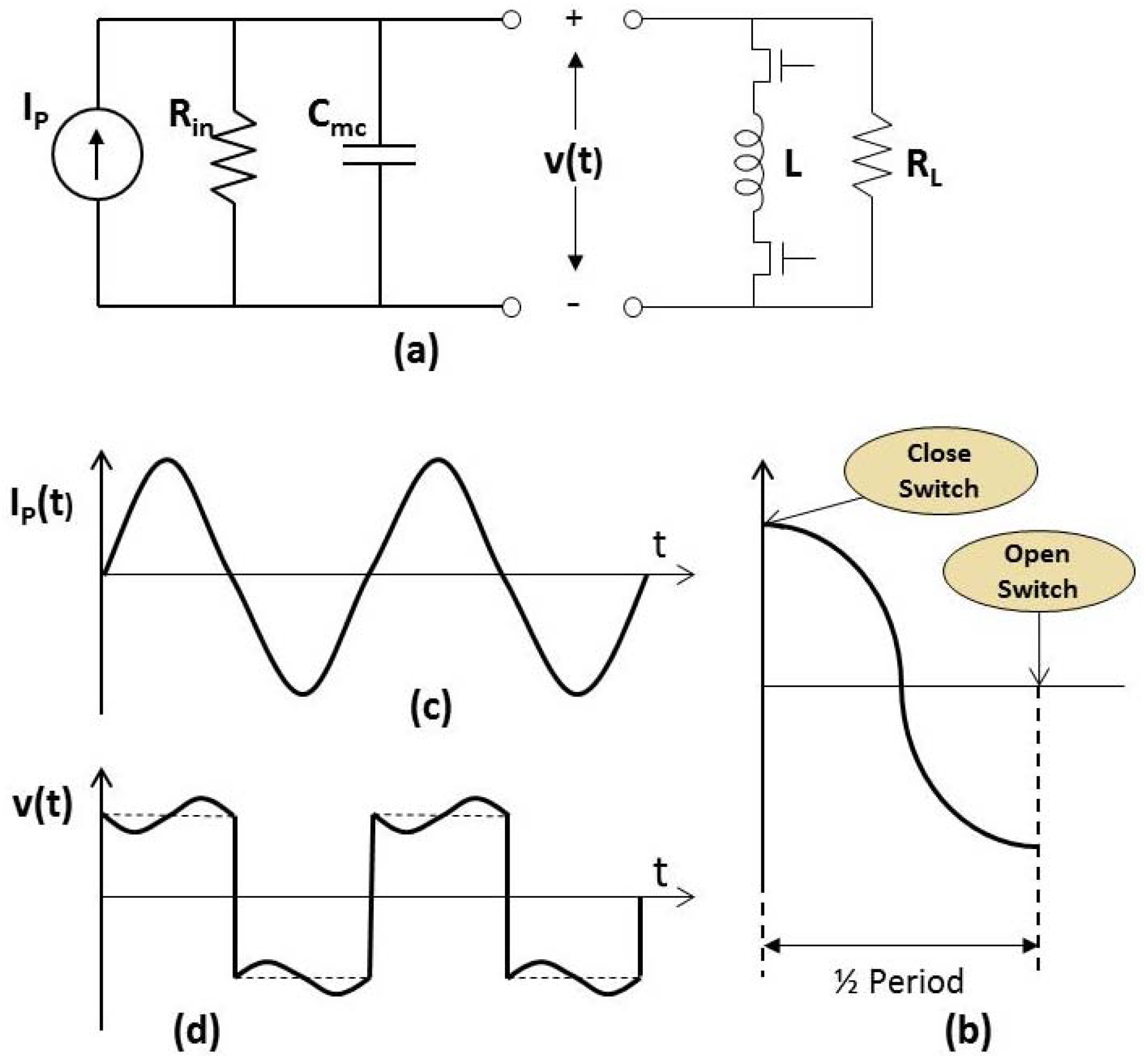
The BF technique is illustrated in Figure 10. In the BF circuit, the large inductor is replaced by a small inductor, connected by MOS switches. When the switches are closed, a high frequency tank circuit is formed. After ½ period of oscillation of this tank circuit, the switches are opened, and the voltage on the capacitor has “flipped” adiabatically from +V to −V. In this paper, the switches are assumed to be ideal and lossless.
Refer to Figure 3. When an ideal inductor is used together with a matched resistive load RL = Rin, the maximum average output power is given by 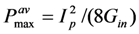 . [See Equation (8)] In Figure 11, we show how effective the ideal Bias-Flip circuit is in achieving maximum power.
. [See Equation (8)] In Figure 11, we show how effective the ideal Bias-Flip circuit is in achieving maximum power.
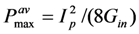 . [See Equation (8)] In Figure 11, we show how effective the ideal Bias-Flip circuit is in achieving maximum power.
. [See Equation (8)] In Figure 11, we show how effective the ideal Bias-Flip circuit is in achieving maximum power. 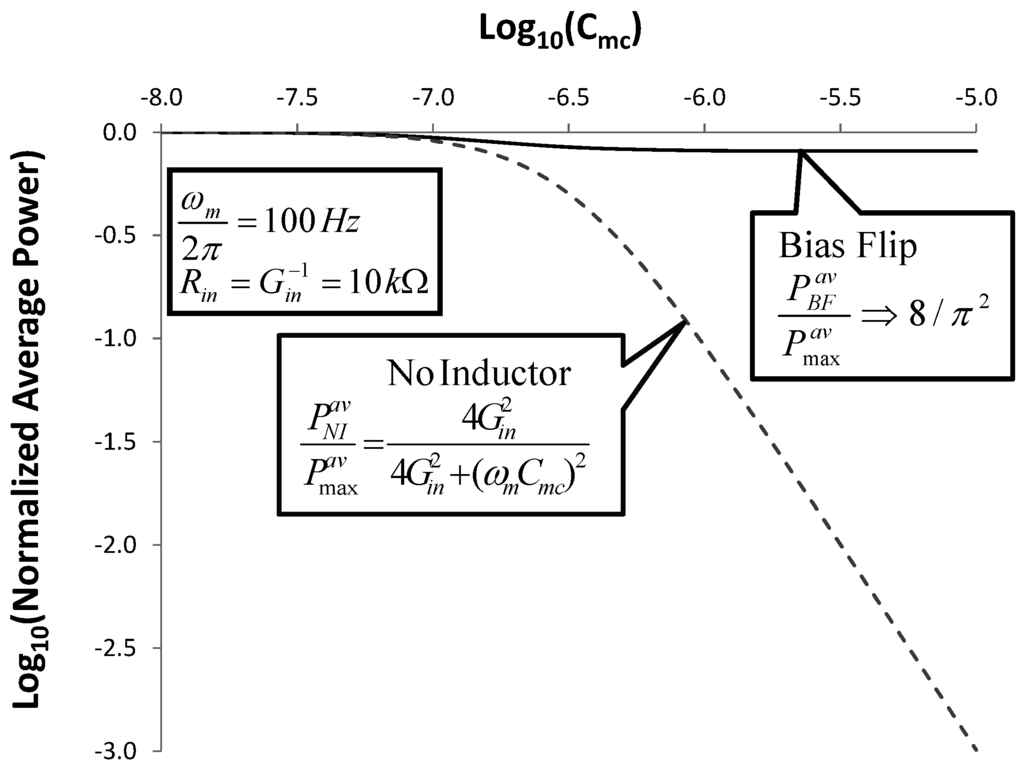
Figure 11.
Normalized Average Power delivered to the load at ω = ωm. The equivalent circuit of Fig 3 is used with RL = Rin. The dashed line shows the case of no inductor. The solid line shows the improvement in output power that is achievable using the Bias-Flip inductor. Both curves are normalized to the average power obtained using an ideal tuned inductor 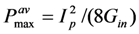 .
.
 .
.
Figure 11.
Normalized Average Power delivered to the load at ω = ωm. The equivalent circuit of Fig 3 is used with RL = Rin. The dashed line shows the case of no inductor. The solid line shows the improvement in output power that is achievable using the Bias-Flip inductor. Both curves are normalized to the average power obtained using an ideal tuned inductor 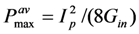 .
.
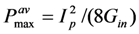 .
.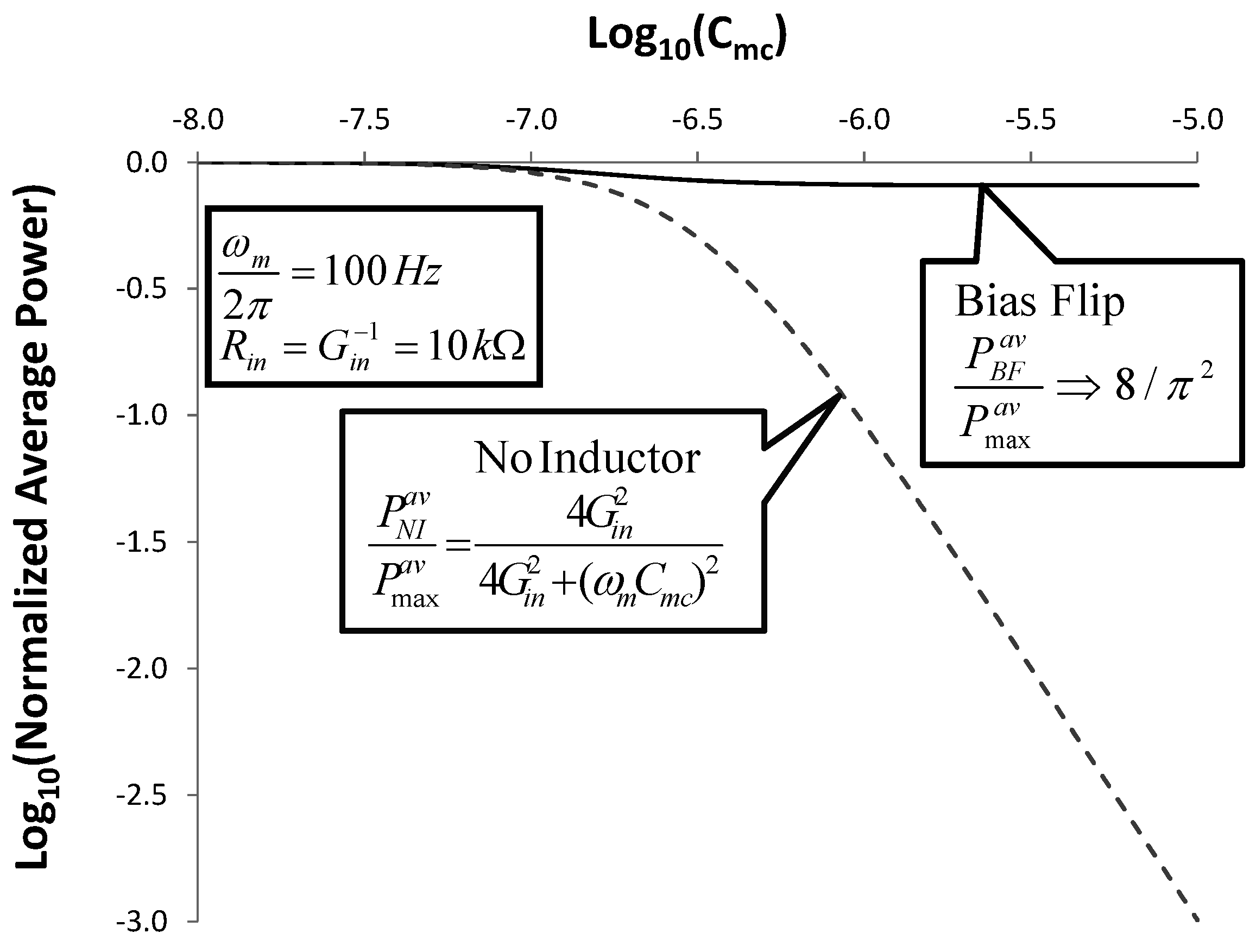
In the worst case of very large Cmc, the output power is degraded by several orders of magnitude, when no inductor is used. However, the Bias-Flip approach delivers power 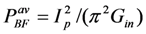 , which is 8 / π2 = 81% of the max power obtained using an ideal inductor. This illustrates the effectiveness of Bias-Flip circuits to achieve high output power when Cmc is large [7].
, which is 8 / π2 = 81% of the max power obtained using an ideal inductor. This illustrates the effectiveness of Bias-Flip circuits to achieve high output power when Cmc is large [7].
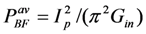 , which is 8 / π2 = 81% of the max power obtained using an ideal inductor. This illustrates the effectiveness of Bias-Flip circuits to achieve high output power when Cmc is large [7].
, which is 8 / π2 = 81% of the max power obtained using an ideal inductor. This illustrates the effectiveness of Bias-Flip circuits to achieve high output power when Cmc is large [7].So far in this paper, we have discussed the case in which AC power is delivered to a resistive load. We have done this because the analysis can be performed in closed form. However, in many energy harvesting applications, it is necessary to rectify the AC power and store it in a battery or super-capacitor. The Bias-Flip technique is especially applicable to this case, as shown in [7].
The rectification circuit analyzed in [7] is shown in Figure 12. For simplicity, we assumed that the EHD is operating at the mechanical resonance frequency, and we use the equivalent circuit of Figure 3. The output AC voltage v(t) is rectified in the diode bridge and stored on the capacitor CRECT that is maintained at voltage VRECT by the Energy Management Circuit. The analysis below assumes ideal diodes.
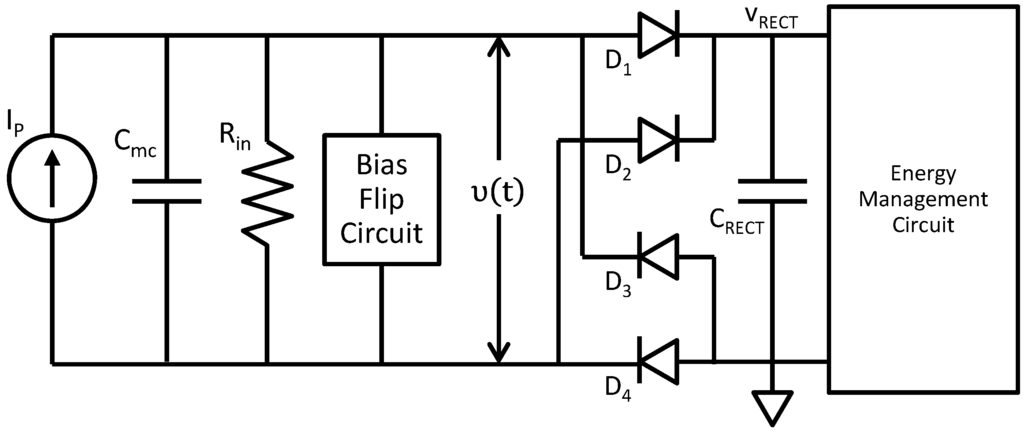
Figure 12.
Circuit to rectify and store the AC power being generated by the EHD. It is assumed that the EHD is operating at the mechanical resonance frequency.
Figure 12.
Circuit to rectify and store the AC power being generated by the EHD. It is assumed that the EHD is operating at the mechanical resonance frequency.
Operation of the Bias-Flip rectifier is described with reference to Figure 13.
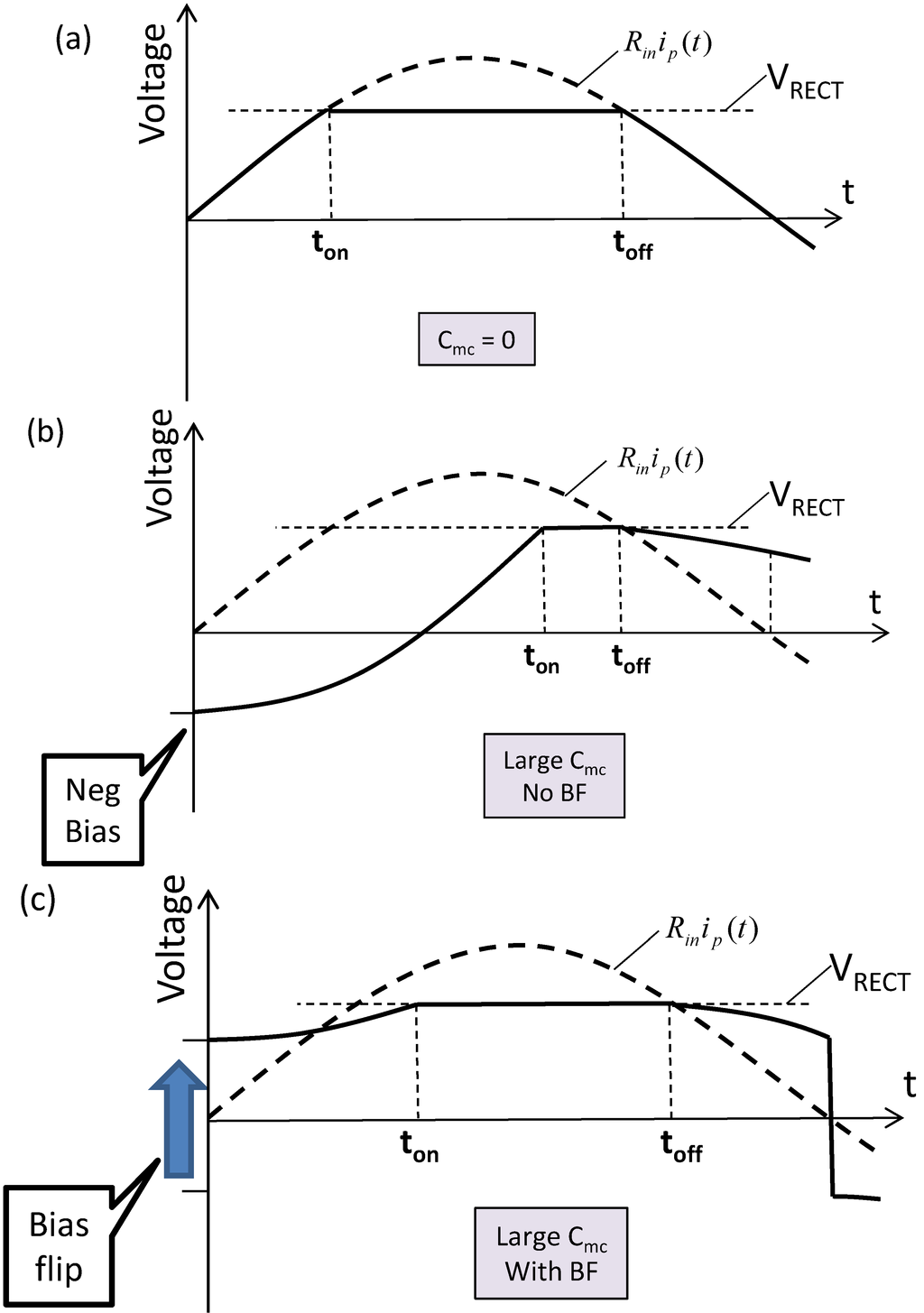
Figure 13.
(a) Voltage waveform v(t) in Figure 12 for the case Cmc = 0; in this case, the Bias-Flip circuit is not required; (b) Voltage waveform for the case of large Cmc without Bias-Flip compensation; when the current becomes positive, there is a large negative voltage on the capacitor Cmc, this must be discharged before the voltage can swing positive; (c) When the current becomes positive, the polarity of the voltage v(t) is “flipped”. This reduces the time to diode turn-on and increases power transferred to CRECT.
Figure 13.
(a) Voltage waveform v(t) in Figure 12 for the case Cmc = 0; in this case, the Bias-Flip circuit is not required; (b) Voltage waveform for the case of large Cmc without Bias-Flip compensation; when the current becomes positive, there is a large negative voltage on the capacitor Cmc, this must be discharged before the voltage can swing positive; (c) When the current becomes positive, the polarity of the voltage v(t) is “flipped”. This reduces the time to diode turn-on and increases power transferred to CRECT.
When the capacitance is zero, as shown in Figure 13a, Bias-Flip is not required.  until t = ton; at which time, v(t) becomes clamped at VRECT. Between ton and toff power is supplied to the storage unit. At t = toff, the diodes turn off, and v(t) returns to zero following the curve
until t = ton; at which time, v(t) becomes clamped at VRECT. Between ton and toff power is supplied to the storage unit. At t = toff, the diodes turn off, and v(t) returns to zero following the curve  . The presence of non-zero Cmc degrades transferred power: Figure 13b. When the current turns positive, there is a negative bias on Cmc that must be discharged before the voltage can swing positive. This delays diode turn-on, and forces a reduction in VRECT, both of which degrade transferred power. This degradation can be corrected by adiabatically flipping the bias on Cmc when the current changes sign, as illustrated in Figure 13c.
. The presence of non-zero Cmc degrades transferred power: Figure 13b. When the current turns positive, there is a negative bias on Cmc that must be discharged before the voltage can swing positive. This delays diode turn-on, and forces a reduction in VRECT, both of which degrade transferred power. This degradation can be corrected by adiabatically flipping the bias on Cmc when the current changes sign, as illustrated in Figure 13c.
 until t = ton; at which time, v(t) becomes clamped at VRECT. Between ton and toff power is supplied to the storage unit. At t = toff, the diodes turn off, and v(t) returns to zero following the curve
until t = ton; at which time, v(t) becomes clamped at VRECT. Between ton and toff power is supplied to the storage unit. At t = toff, the diodes turn off, and v(t) returns to zero following the curve 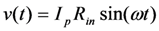 . The presence of non-zero Cmc degrades transferred power: Figure 13b. When the current turns positive, there is a negative bias on Cmc that must be discharged before the voltage can swing positive. This delays diode turn-on, and forces a reduction in VRECT, both of which degrade transferred power. This degradation can be corrected by adiabatically flipping the bias on Cmc when the current changes sign, as illustrated in Figure 13c.
. The presence of non-zero Cmc degrades transferred power: Figure 13b. When the current turns positive, there is a negative bias on Cmc that must be discharged before the voltage can swing positive. This delays diode turn-on, and forces a reduction in VRECT, both of which degrade transferred power. This degradation can be corrected by adiabatically flipping the bias on Cmc when the current changes sign, as illustrated in Figure 13c.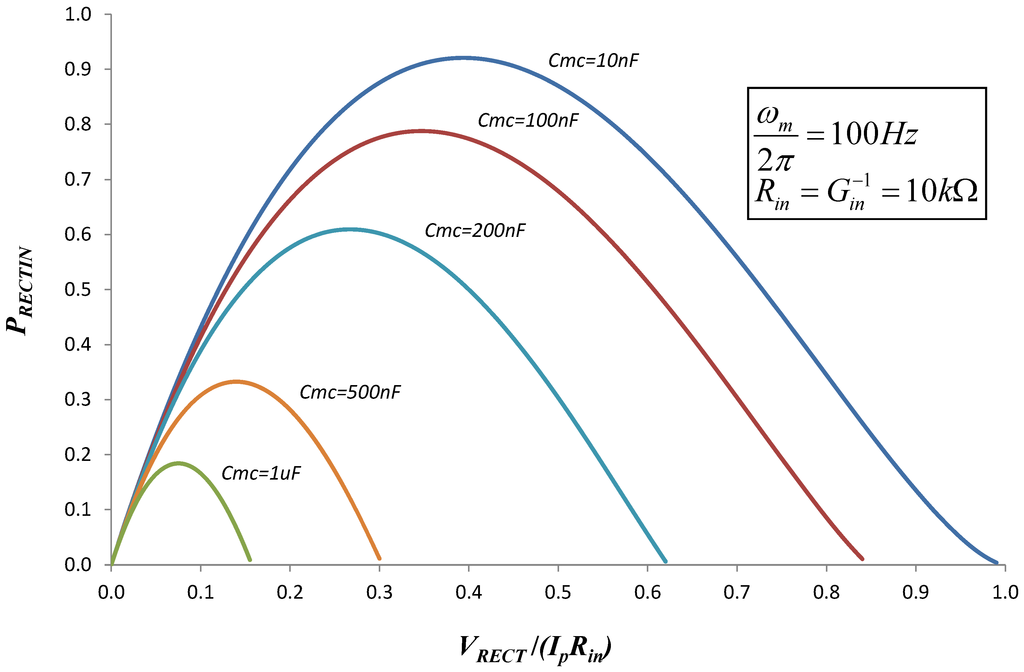
Figure 14.
Power transferred to the storage capacitor CRECT as a function of VRECT for different values of Cmc. Power is normalized to 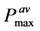 (see Equation (8)). The curve for Cmc = 0 is negligibly different from the curve for Cmc = 10nF, and is not shown. For the case of no capacitor, the max power transfer of 0.92 occurs at
(see Equation (8)). The curve for Cmc = 0 is negligibly different from the curve for Cmc = 10nF, and is not shown. For the case of no capacitor, the max power transfer of 0.92 occurs at 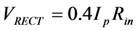 .
.
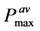 (see Equation (8)). The curve for Cmc = 0 is negligibly different from the curve for Cmc = 10nF, and is not shown. For the case of no capacitor, the max power transfer of 0.92 occurs at
(see Equation (8)). The curve for Cmc = 0 is negligibly different from the curve for Cmc = 10nF, and is not shown. For the case of no capacitor, the max power transfer of 0.92 occurs at 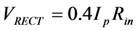 .
.
Figure 14.
Power transferred to the storage capacitor CRECT as a function of VRECT for different values of Cmc. Power is normalized to 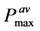 (see Equation (8)). The curve for Cmc = 0 is negligibly different from the curve for Cmc = 10nF, and is not shown. For the case of no capacitor, the max power transfer of 0.92 occurs at
(see Equation (8)). The curve for Cmc = 0 is negligibly different from the curve for Cmc = 10nF, and is not shown. For the case of no capacitor, the max power transfer of 0.92 occurs at 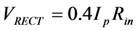 .
.
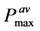 (see Equation (8)). The curve for Cmc = 0 is negligibly different from the curve for Cmc = 10nF, and is not shown. For the case of no capacitor, the max power transfer of 0.92 occurs at
(see Equation (8)). The curve for Cmc = 0 is negligibly different from the curve for Cmc = 10nF, and is not shown. For the case of no capacitor, the max power transfer of 0.92 occurs at 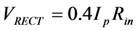 .
.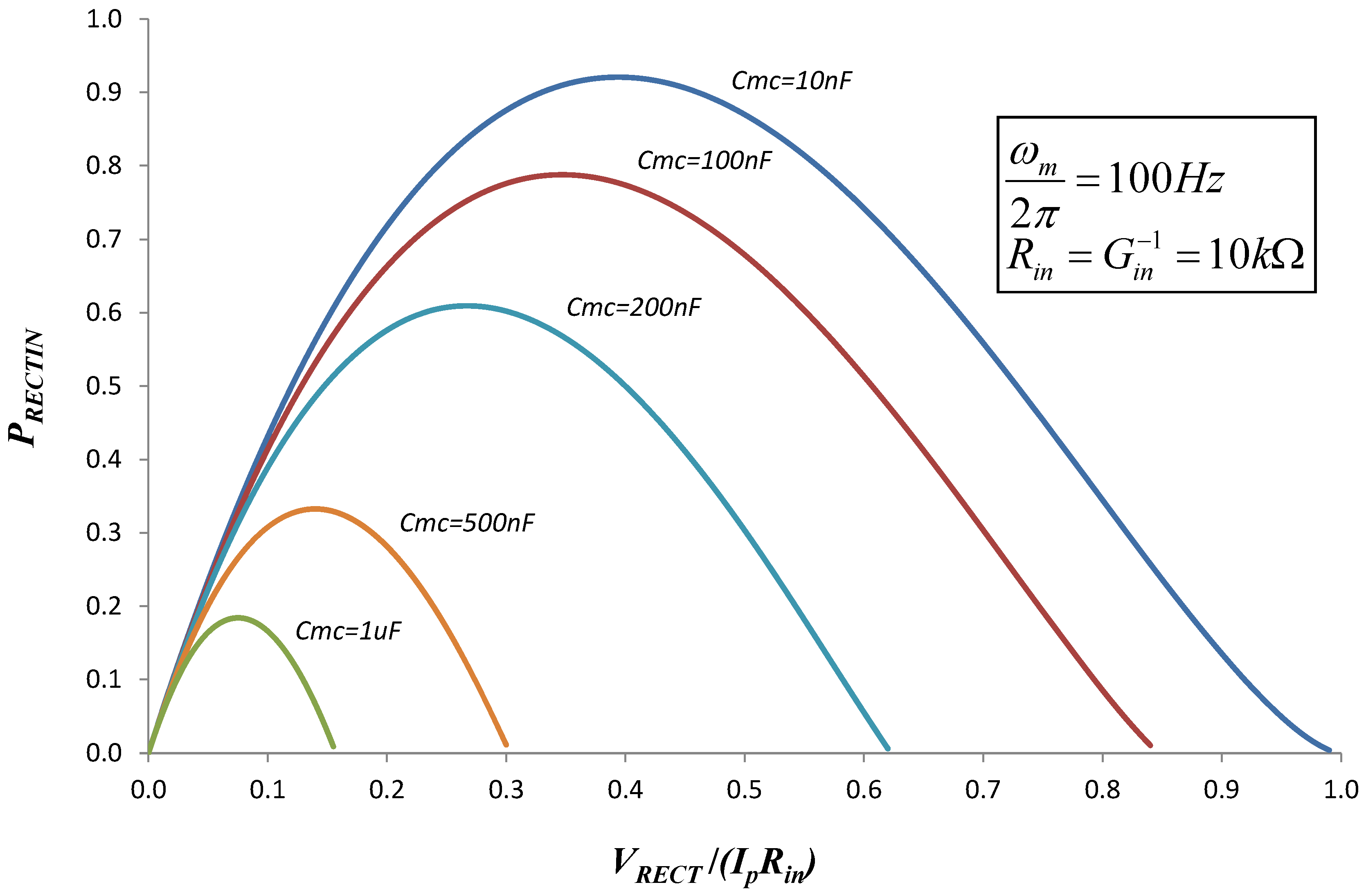
The energy transferred per cycle depends on VRECT. When VRECT is low, the power transfer interval toff − ton is long, but the power is low. When VRECT is high, the power transfer is high, but the transfer interval is short. In fact, for VRECT above a maximum value the diodes do not turn on, and no power is transferred. Figure 14 shows the power transfer as a function of VRECT, for various values of Cmc. This simulation is made using the values 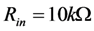 and
and 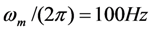 .
.
 and
and  .
.
Figure 15.
Shows the rectified power as a function of Cmc. For each point on the curve, VRECT was selected to give the max power transfer. Power is normalized to 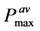 , and capacitance has units Farads.
, and capacitance has units Farads.
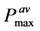 , and capacitance has units Farads.
, and capacitance has units Farads.
Figure 15.
Shows the rectified power as a function of Cmc. For each point on the curve, VRECT was selected to give the max power transfer. Power is normalized to 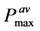 , and capacitance has units Farads.
, and capacitance has units Farads.
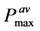 , and capacitance has units Farads.
, and capacitance has units Farads.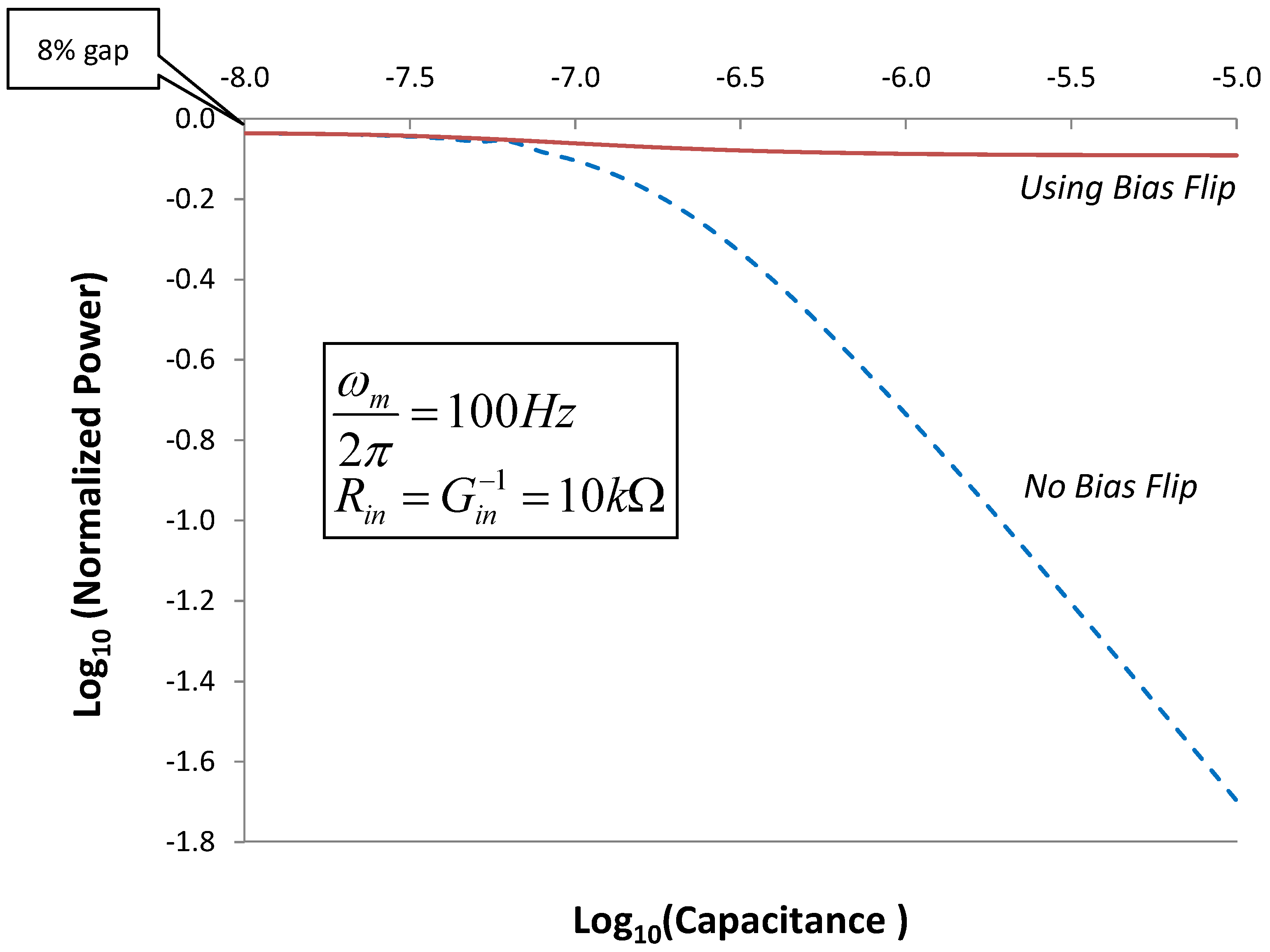
Figure 15 shows that, for large Cmc, output is severely degraded. However, the Bias-Flip circuit is effective in recovering most of the lost output power. This analysis confirms the conclusions of Ramadass and Chandrakasan [7] that for an EHD, operating at resonance, the Bias-Flip circuit is effective in canceling the reactive impedance of the device, and achieving near-optimum output power. In the next section, we will demonstrate that the Bias-Flip technique can be used to form an effective LC tank circuit that, when coupled to the EHD can tune the resonant frequency.
6. Bias Flip for Frequency Tuning
In Section 5, we confirmed the effectiveness of the BF technique for power optimization at the mechanical resonant frequency. When ω = ωm, and the equivalent circuit of Figure 3 applies, we can optimize power to the load by “canceling” or “matching” the reactive admittance of the capacitor with an inductor. We select an inductor value such that 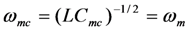 . Matching the reactive admittance aligns the phase of the voltage across the load with the phase of the current. This works because the current source is assumed to be ideal. Varying the reactive load does not change the current from the source. We confirmed the finding of [7] that the BF inductor is effective in canceling capacitive admittance at ωm. In this section, we will demonstrate that the BF inductor can also be used to tune the resonant frequency of the EHD and optimize power at frequencies substantially different from ωm.
. Matching the reactive admittance aligns the phase of the voltage across the load with the phase of the current. This works because the current source is assumed to be ideal. Varying the reactive load does not change the current from the source. We confirmed the finding of [7] that the BF inductor is effective in canceling capacitive admittance at ωm. In this section, we will demonstrate that the BF inductor can also be used to tune the resonant frequency of the EHD and optimize power at frequencies substantially different from ωm.
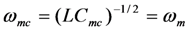 . Matching the reactive admittance aligns the phase of the voltage across the load with the phase of the current. This works because the current source is assumed to be ideal. Varying the reactive load does not change the current from the source. We confirmed the finding of [7] that the BF inductor is effective in canceling capacitive admittance at ωm. In this section, we will demonstrate that the BF inductor can also be used to tune the resonant frequency of the EHD and optimize power at frequencies substantially different from ωm.
. Matching the reactive admittance aligns the phase of the voltage across the load with the phase of the current. This works because the current source is assumed to be ideal. Varying the reactive load does not change the current from the source. We confirmed the finding of [7] that the BF inductor is effective in canceling capacitive admittance at ωm. In this section, we will demonstrate that the BF inductor can also be used to tune the resonant frequency of the EHD and optimize power at frequencies substantially different from ωm.In order to maximize output power at any frequency, we need to maximize the input power delivered from the mechanical source to the EHD. In other words, we need to align the phase of the force with the phase of the source velocity.
In the following analysis, we assume the phase of z(t) to be zero. 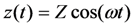 , and the velocity of the source is
, and the velocity of the source is 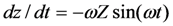 . The source velocity has a phase of +90o. The force acting on the EHD is given by Equation (3). Our goal is to maximize.
. The source velocity has a phase of +90o. The force acting on the EHD is given by Equation (3). Our goal is to maximize.
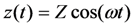 , and the velocity of the source is
, and the velocity of the source is 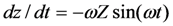 . The source velocity has a phase of +90o. The force acting on the EHD is given by Equation (3). Our goal is to maximize.
. The source velocity has a phase of +90o. The force acting on the EHD is given by Equation (3). Our goal is to maximize.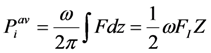
Where FI is the imaginary part of F. 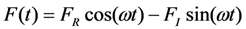 . From this, we conclude that input average power is maximized when F has phase +90°, matched to source velocity, and X has phase −90°.
. From this, we conclude that input average power is maximized when F has phase +90°, matched to source velocity, and X has phase −90°.
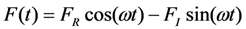 . From this, we conclude that input average power is maximized when F has phase +90°, matched to source velocity, and X has phase −90°.
. From this, we conclude that input average power is maximized when F has phase +90°, matched to source velocity, and X has phase −90°.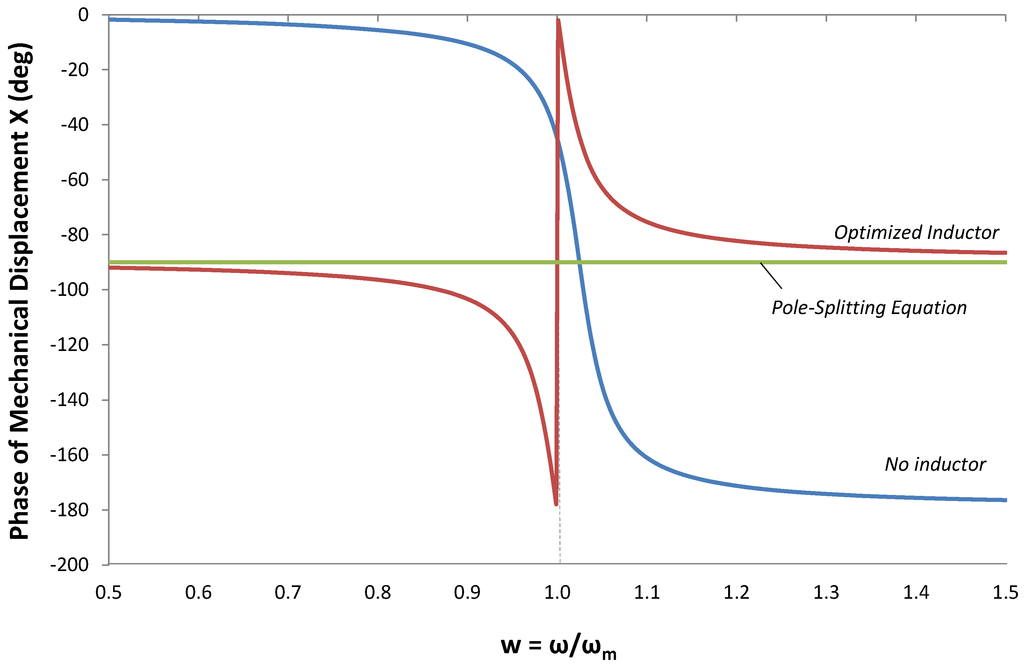
Figure 16.
Phase of mechanical displacement X(ω) for three cases: (1) No inductor; (2) Inductor optimized using (13) and (3) Inductor optimized using the pole-splitting Equation (9). In all three cases, GL = 0.
Figure 16.
Phase of mechanical displacement X(ω) for three cases: (1) No inductor; (2) Inductor optimized using (13) and (3) Inductor optimized using the pole-splitting Equation (9). In all three cases, GL = 0.
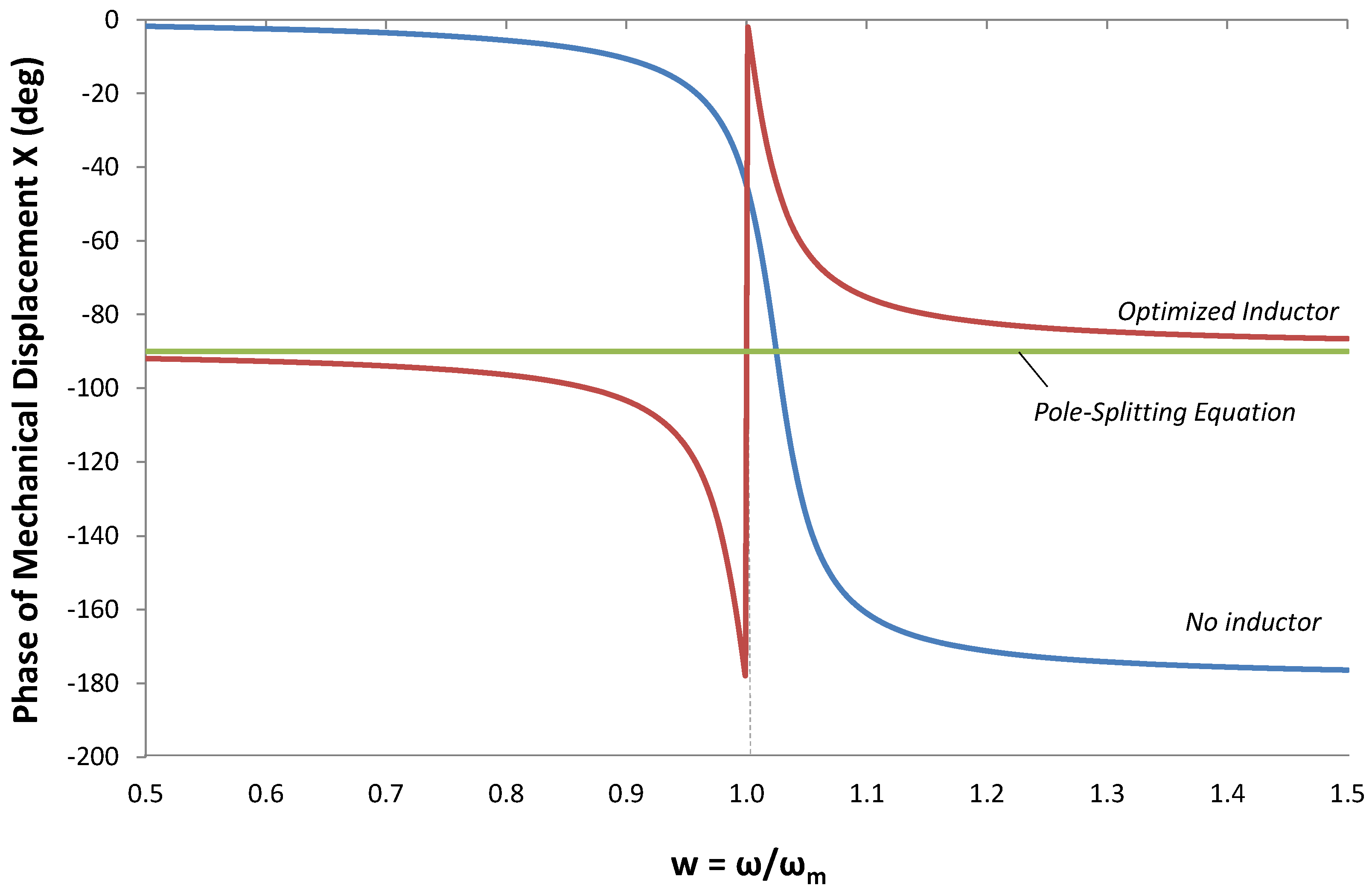
Additional insight into maximization of output power is seen in Figure 16. Here, we compare the phase of mechanical displacement X(ω) for three conditions
- No inductor. The phase is −90° only at
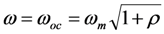 . Below ωm, the phase is ≈0°, and above ωm, the phase is ≈ −180°. Only at ω = ωoc is the force in phase with the source velocity;
. Below ωm, the phase is ≈0°, and above ωm, the phase is ≈ −180°. Only at ω = ωoc is the force in phase with the source velocity; - Inductor, optimized using Equation (13). Note that the phase approaches −90° above and below ω = ωm;
- Inductor optimized using the pole-splitting Equation (9). The phase is −90° for all frequencies.
The improvement in power at frequencies above and below ωm results from phase alignment between force and source velocity.
Figure 17 shows output power for 3 conditions.
- No inductor:
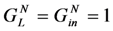 ;
; - Inductor optimized using Equation (13):
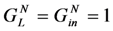 ;
; - Inductor optimized using Equation (13):
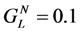 .
.
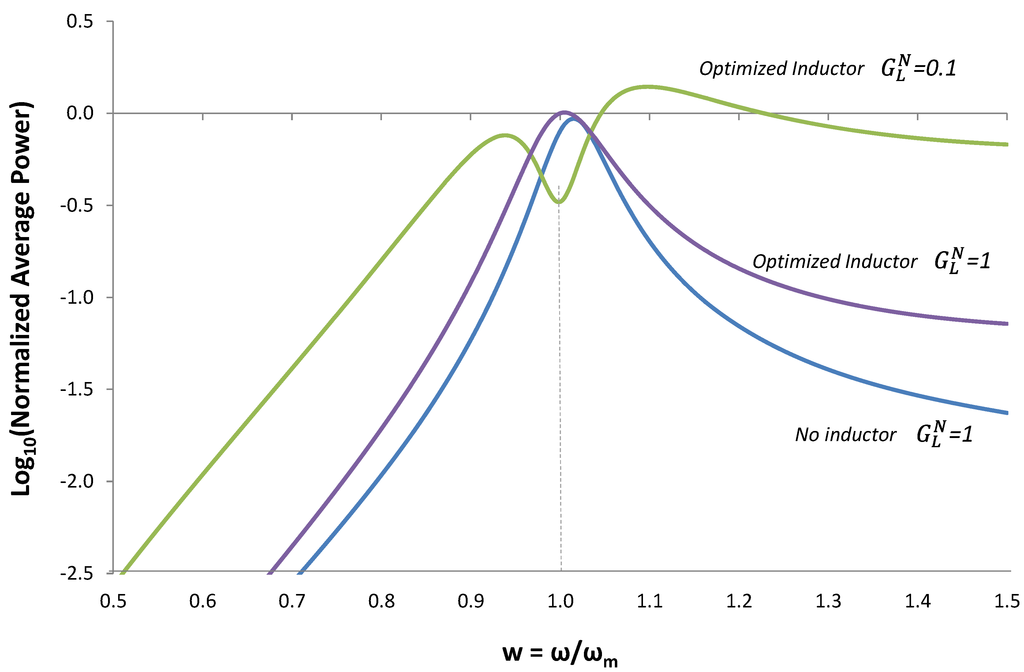
Figure 17.
Normalized Average Output Power for three cases. (1) No inductor & 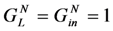 ; (2) Inductor optimized using Equation (13) &
; (2) Inductor optimized using Equation (13) & 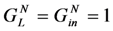 ; (3) Inductor optimized using Equation (13) &
; (3) Inductor optimized using Equation (13) & 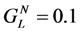 .
.
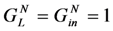 ; (2) Inductor optimized using Equation (13) &
; (2) Inductor optimized using Equation (13) & 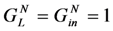 ; (3) Inductor optimized using Equation (13) &
; (3) Inductor optimized using Equation (13) & 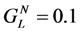 .
.
Figure 17.
Normalized Average Output Power for three cases. (1) No inductor & 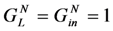 ; (2) Inductor optimized using Equation (13) &
; (2) Inductor optimized using Equation (13) & 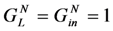 ; (3) Inductor optimized using Equation (13) &
; (3) Inductor optimized using Equation (13) & 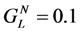 .
.
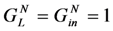 ; (2) Inductor optimized using Equation (13) &
; (2) Inductor optimized using Equation (13) & 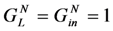 ; (3) Inductor optimized using Equation (13) &
; (3) Inductor optimized using Equation (13) & 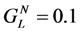 .
.
Case #2 illustrates the case where the reactive admittance is chosen to optimize output power, but the load conductance  is kept at
is kept at 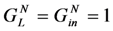 . Very little improvement is achieved, because the voltage is kept low by the high load conductance, and the voltage is ineffective in modulating the cantilever spring constant. Case #3 shows power improvement of ~50X compared to case #1. When we compensate for the increase in acceleration with frequency, case #3 demonstrates that it is possible to achieve output power at ω ≠ ωm that is comparable to the maximum power at ωm.
. Very little improvement is achieved, because the voltage is kept low by the high load conductance, and the voltage is ineffective in modulating the cantilever spring constant. Case #3 shows power improvement of ~50X compared to case #1. When we compensate for the increase in acceleration with frequency, case #3 demonstrates that it is possible to achieve output power at ω ≠ ωm that is comparable to the maximum power at ωm.
 is kept at
is kept at 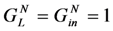 . Very little improvement is achieved, because the voltage is kept low by the high load conductance, and the voltage is ineffective in modulating the cantilever spring constant. Case #3 shows power improvement of ~50X compared to case #1. When we compensate for the increase in acceleration with frequency, case #3 demonstrates that it is possible to achieve output power at ω ≠ ωm that is comparable to the maximum power at ωm.
. Very little improvement is achieved, because the voltage is kept low by the high load conductance, and the voltage is ineffective in modulating the cantilever spring constant. Case #3 shows power improvement of ~50X compared to case #1. When we compensate for the increase in acceleration with frequency, case #3 demonstrates that it is possible to achieve output power at ω ≠ ωm that is comparable to the maximum power at ωm.Additional insight into the mechanism of frequency tuning can be obtained by transforming the mechanical equations of motion to an equivalent circuit [1,8,9], as shown in Figure 18.
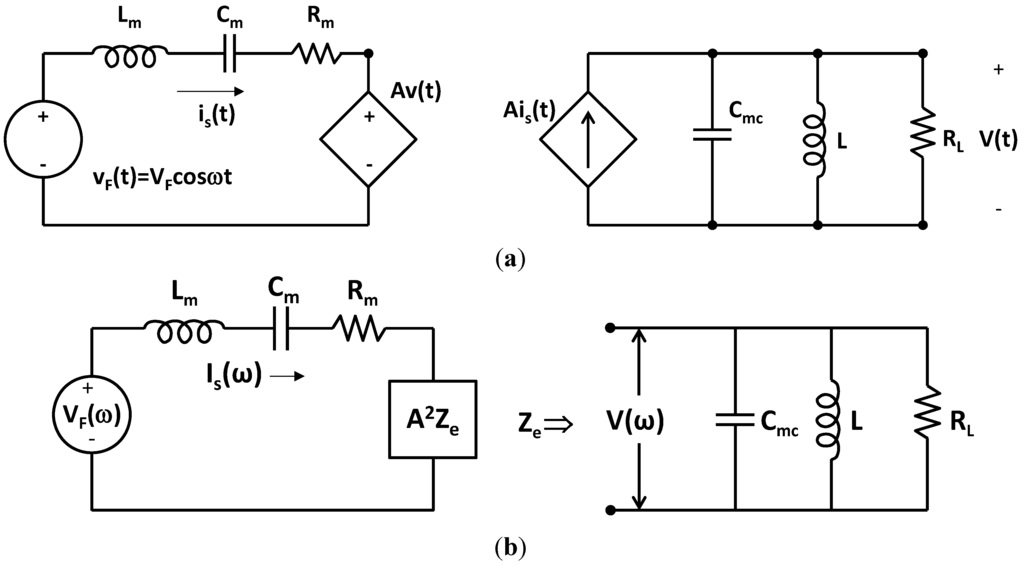
Figure 18.
(a) Equivalent circuit model for a PZ EHD in which 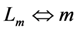 ,
, 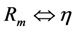 ,
, 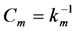 ,
, 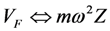 ,
, 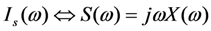 , and
, and 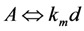 The subscript m denotes the mechanical circuit. S(ω) is used for velocity to avoid confusion with voltage; (b) Equivalent circuit model of Figure 18a, in which the electronic circuit is replaced by an electrical impedance Ze.
The subscript m denotes the mechanical circuit. S(ω) is used for velocity to avoid confusion with voltage; (b) Equivalent circuit model of Figure 18a, in which the electronic circuit is replaced by an electrical impedance Ze.
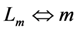 ,
, 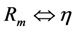 ,
, 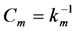 ,
, 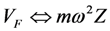 ,
, 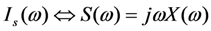 , and
, and 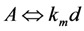 The subscript m denotes the mechanical circuit. S(ω) is used for velocity to avoid confusion with voltage; (b) Equivalent circuit model of Figure 18a, in which the electronic circuit is replaced by an electrical impedance Ze.
The subscript m denotes the mechanical circuit. S(ω) is used for velocity to avoid confusion with voltage; (b) Equivalent circuit model of Figure 18a, in which the electronic circuit is replaced by an electrical impedance Ze.
Figure 18.
(a) Equivalent circuit model for a PZ EHD in which 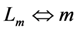 ,
, 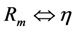 ,
, 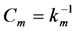 ,
, 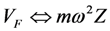 ,
, 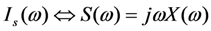 , and
, and 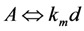 The subscript m denotes the mechanical circuit. S(ω) is used for velocity to avoid confusion with voltage; (b) Equivalent circuit model of Figure 18a, in which the electronic circuit is replaced by an electrical impedance Ze.
The subscript m denotes the mechanical circuit. S(ω) is used for velocity to avoid confusion with voltage; (b) Equivalent circuit model of Figure 18a, in which the electronic circuit is replaced by an electrical impedance Ze.
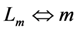 ,
, 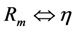 ,
, 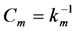 ,
, 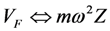 ,
, 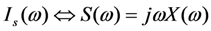 , and
, and 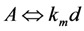 The subscript m denotes the mechanical circuit. S(ω) is used for velocity to avoid confusion with voltage; (b) Equivalent circuit model of Figure 18a, in which the electronic circuit is replaced by an electrical impedance Ze.
The subscript m denotes the mechanical circuit. S(ω) is used for velocity to avoid confusion with voltage; (b) Equivalent circuit model of Figure 18a, in which the electronic circuit is replaced by an electrical impedance Ze.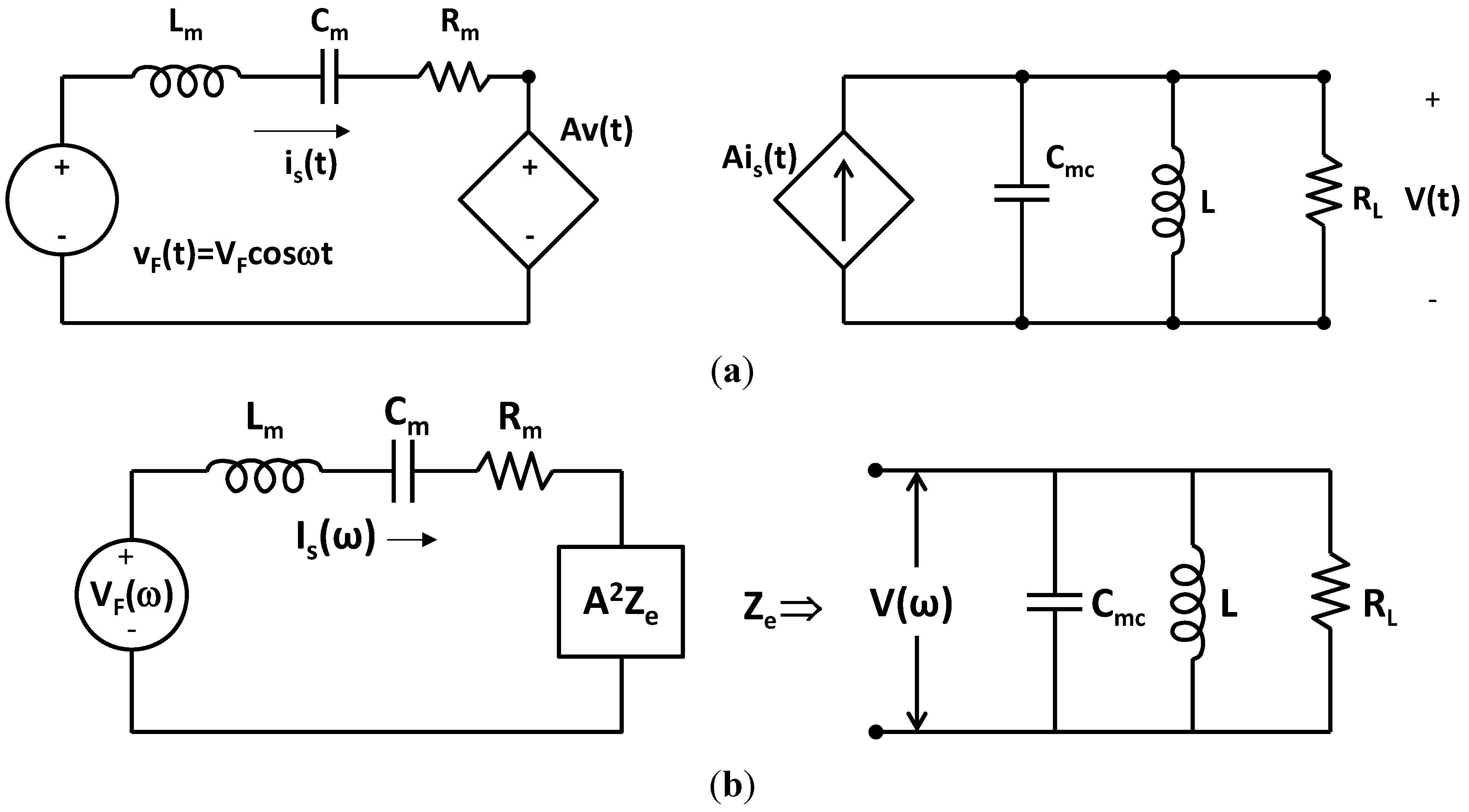
The equations for the mechanical portion of the equivalent circuit are shown below.
Define Zm to be the impedance seen by the voltage source VF(ω) in Figure 18b. Setting Im(Zm) = 0 gives the pole-splitting equation, equivalent to Equation (9), in the limit 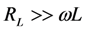 .
.
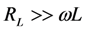 .
.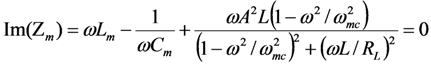
The last term in the above equation can be used to tune the resonance frequency above or below the mechanical resonance frequency. The last term takes the form
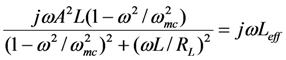 where Leff can be made positive or negative to add or subtract from Lm. At the mechanical resonance frequency ω = ωm,
where Leff can be made positive or negative to add or subtract from Lm. At the mechanical resonance frequency ω = ωm, 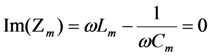 , and output power is optimized by setting ω = ωmc. When ω < ωm the resonant frequency ω− must be reduced. This can be achieved by increasing the effective inductance, which can be achieved by setting ωmc > ω. When ω > ωm, the resonant frequency ω+ must be increased. This can be achieved by decreasing the effective inductance, which can be achieved by setting ωmc < ω.
, and output power is optimized by setting ω = ωmc. When ω < ωm the resonant frequency ω− must be reduced. This can be achieved by increasing the effective inductance, which can be achieved by setting ωmc > ω. When ω > ωm, the resonant frequency ω+ must be increased. This can be achieved by decreasing the effective inductance, which can be achieved by setting ωmc < ω.
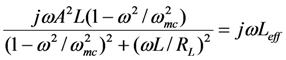
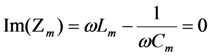 , and output power is optimized by setting ω = ωmc. When ω < ωm the resonant frequency ω− must be reduced. This can be achieved by increasing the effective inductance, which can be achieved by setting ωmc > ω. When ω > ωm, the resonant frequency ω+ must be increased. This can be achieved by decreasing the effective inductance, which can be achieved by setting ωmc < ω.
, and output power is optimized by setting ω = ωmc. When ω < ωm the resonant frequency ω− must be reduced. This can be achieved by increasing the effective inductance, which can be achieved by setting ωmc > ω. When ω > ωm, the resonant frequency ω+ must be increased. This can be achieved by decreasing the effective inductance, which can be achieved by setting ωmc < ω. These results are summarized in Table 1.

Table 1.
Strategy For Power Optimization in the Three Frequency Regions of Operation.
| Frequency region | Leff | ωmc | Phase of voltage | Optimum power |
|---|---|---|---|---|
| Region 1: ω < ωm | >0 | ωmc > ω | ~ +90o | RL >> Rin |
| Region 2: ω ≈ ωm | ≈0 | ωmc = ω ≈ ωm | ~0o | RL = Rin |
| Region 3: ω > ωm | <0 | ωmc < ω | ~ −90o | RL >> Rin |
Maximizing power in the three regions can be envisioned in term of an effective inductor. Alternatively, it can be envisioned in terms of setting the phase of the voltage V(ω). The phase in each of the three regions is given in the table. In Region 2, the voltage across the load V(ω) is in phase with IS(ω), and output power is optimized by setting RL = Rin. However, in Regions 1 and 3, max power occurs when V(ω) has a phase of +90o (Region 1) and −90° (Region 3) relative to the phase of IS(ω), and optimum power is achieved by setting RL to be substantially larger than Rin.
The foregoing analysis suggests that the Bias-Flip technique can be used to synthesize an inductor, by flipping the polarity of the voltage in such a way that X(ω) has a phase of −90° in all three regions of operation. Recall from Equation (10) that, when  is small, the phase of X(ω) is related to the phase of V(ω) in a simple way. By adjusting the phase of V(ω) as shown in Table 1, we also adjust the phase of X(ω) to −90°.
is small, the phase of X(ω) is related to the phase of V(ω) in a simple way. By adjusting the phase of V(ω) as shown in Table 1, we also adjust the phase of X(ω) to −90°.
 is small, the phase of X(ω) is related to the phase of V(ω) in a simple way. By adjusting the phase of V(ω) as shown in Table 1, we also adjust the phase of X(ω) to −90°.
is small, the phase of X(ω) is related to the phase of V(ω) in a simple way. By adjusting the phase of V(ω) as shown in Table 1, we also adjust the phase of X(ω) to −90°.Simulations were performed starting from the differential equations for v(t) and x(t) that are comparable to Equations (3) and (4), for the case of no inductor. These equations were solved subject to the boundary conditions.
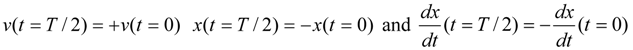
In the case of no Bias-Flip, 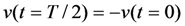 . The effect of the BF inductor is to change the phase of v(t) every half-period.
. The effect of the BF inductor is to change the phase of v(t) every half-period.
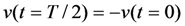 . The effect of the BF inductor is to change the phase of v(t) every half-period.
. The effect of the BF inductor is to change the phase of v(t) every half-period.Using the voltage waveform, we calculated average output power. This is shown normalized to 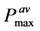 in Figure 19. These simulations show that the BF technique is capable of achieving output power, comparable to the optimum power achievable with an optimized inductor. Moreover, the BF technique is self-tuning. If the bias is flipped whenever the source velocity crosses zero (as assumed in this simulation), the desired phase is maintained as the source frequency changes. No calculation is required to solve Equation (13).
in Figure 19. These simulations show that the BF technique is capable of achieving output power, comparable to the optimum power achievable with an optimized inductor. Moreover, the BF technique is self-tuning. If the bias is flipped whenever the source velocity crosses zero (as assumed in this simulation), the desired phase is maintained as the source frequency changes. No calculation is required to solve Equation (13).
 in Figure 19. These simulations show that the BF technique is capable of achieving output power, comparable to the optimum power achievable with an optimized inductor. Moreover, the BF technique is self-tuning. If the bias is flipped whenever the source velocity crosses zero (as assumed in this simulation), the desired phase is maintained as the source frequency changes. No calculation is required to solve Equation (13).
in Figure 19. These simulations show that the BF technique is capable of achieving output power, comparable to the optimum power achievable with an optimized inductor. Moreover, the BF technique is self-tuning. If the bias is flipped whenever the source velocity crosses zero (as assumed in this simulation), the desired phase is maintained as the source frequency changes. No calculation is required to solve Equation (13).
Figure 19.
Normalized average power as a function of frequency. In Regions 1 and 3, the Bias-Flip technique (red and blue dashed lines) improves output power by ~100X compared to the case of no inductor and no BF (green line). Moreover, it gives output power that is comparable to the maximum power achievable with an optimized inductor (red and blue solid lines).
Figure 19.
Normalized average power as a function of frequency. In Regions 1 and 3, the Bias-Flip technique (red and blue dashed lines) improves output power by ~100X compared to the case of no inductor and no BF (green line). Moreover, it gives output power that is comparable to the maximum power achievable with an optimized inductor (red and blue solid lines).
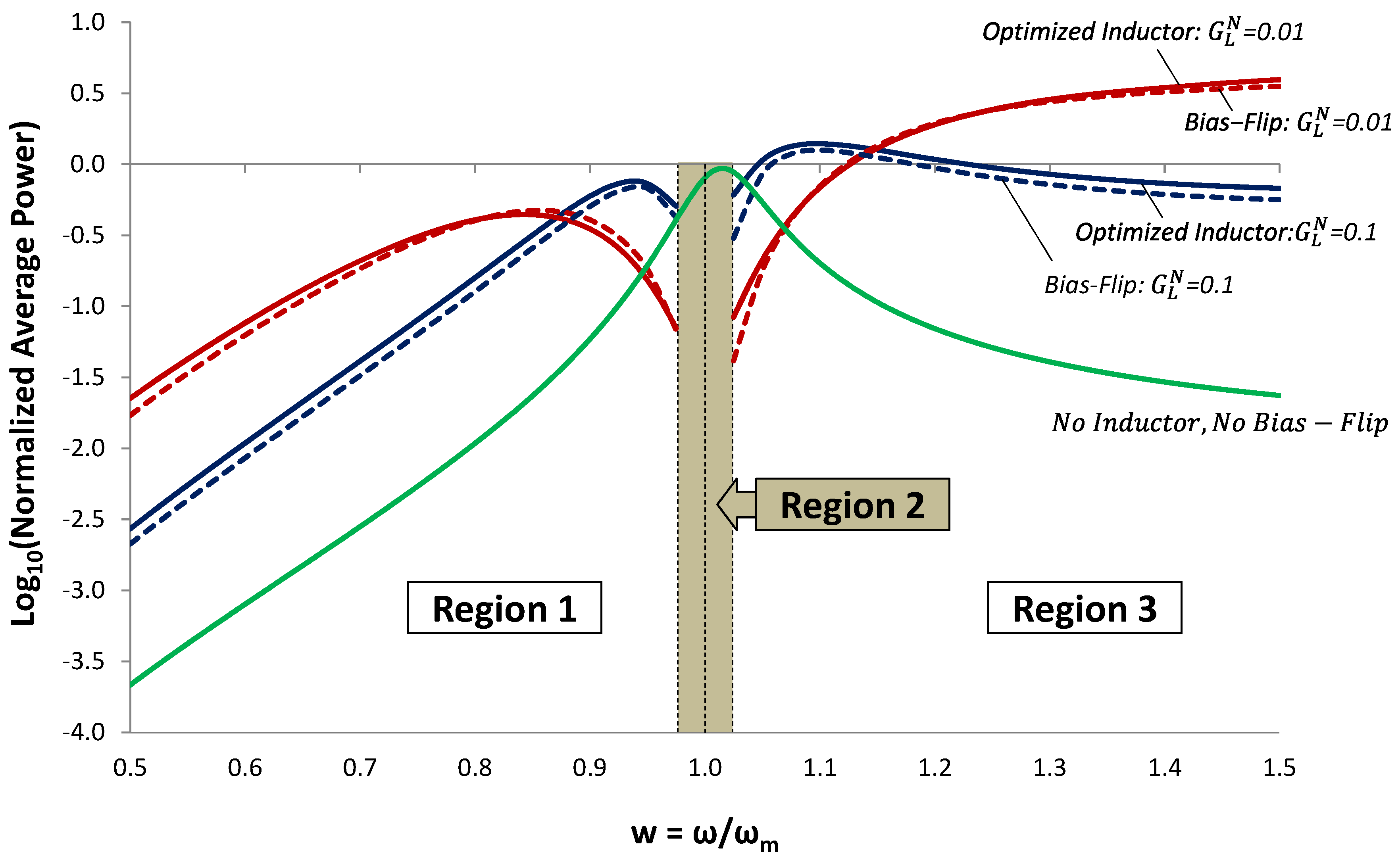
Analysis of the voltage waveforms reveals another aspect of self-tuning. In Region 1, the bias flips from negative to positive at t = 0 and from positive to negative at t = T / 2, thereby emulating a +90° phase shift. In Region 3, the reverse happens. The bias flips from positive to negative at t = 0 and from negative to positive at t = T / 2, thus emulating a −90° phase shift.
7. Conclusions
In the preceding sections, we have explained the principles for electrically tuning of PZ EHDs. These principles are summarized below.
Equation (11) shows that the effective spring constant of the mechanical resonator is a function of voltage. If the load conductance is large, the voltage is kept small, and the resonator responds only at the mechanical resonant frequency ωm. However, for small load conductance GL, the voltage can be used to tune the spring constant, and the resonant frequency of the mechanical oscillator.
In Regions 1 and 3, output power is maximized by maximizing input power (force x velocity), transferred from the source to the EHD. At frequencies below ωm (Region 1), this occurs when the phase of the voltage is +90° relative to the source vibration, and at frequencies above ωm (Region 3), output power is optimized when the phase of the voltage is -90o relative to the source vibration.
This optimum phase relationship can, in theory, be achieved using a tunable inductor, whose value can be obtained from Equation (13). A large tunable inductor is not generally practical. However, the Bias-Flip technique can be used to emulate a large, tunable inductor. Previous work has shown that the BF technique can be used to optimize the output power at ωm, by cancelling the capacitive admittance of the EHD. In this work, we have shown how the BF technique can be used to tune an EHD and harvest energy from frequencies other than the mechanical resonance frequency.
Acknowledgments
The authors acknowledge informative exchanges with Samuel Chang of MIT.
Conflict of Interest
The authors declare no conflict of interest.
References
- Roundy, S.; Wright, P.K.; Rabaey, J.M. Energy Scavenging for Wireless Sensor Networks, with Special Focus on Vibrations; Kluwer Academic Publishers: Norwell, MA, USA, 2004. [Google Scholar]
- Zhao, J.; Ramadass, Y.; Buss, D.; Ma, J. Microelectronic Techniques for Frequency Tuning of Piezo-Electric Energy Harvesting Devices. In Proceedings of the 2012 IEEE Subthreshold Microelectronics Conference (SubVt), Waltham, MA, USA, 9–10 October 2012.
- Cammarano, A.; Burrow, S.G.; Barton, D.A.; Carella, A.; Clare, L.R. Tuning a resonant energy harvester using a generalized electrical load. Smart Mater. Struct. 2010, 19, 1–7. [Google Scholar]
- Wu, W.-J.; Chen, Y.-Y.; Lee, B.-S.; He, J.-J.; Peng, Y.-T. Tunable Resonant Frequency Power Harvesting Devices. In Smart Structures and Materials: Damping and Isolation; Clark, W.W., Ahmadian, M., Lumsdaine, A., Eds.; SPIE: San Diego, CA, USA, 2006; Volume 6169, pp. 61690A-1–61690A-8. [Google Scholar]
- Chang, S.C.; Ocalan, M.; Pabon, J.; Lang, J.H. Harvesting Energy from Multi-Harmonic Vibrations with a Tunable Electric Load. In proceedings of PowerMEMS, Atlanta, GA, USA, 2–5 December 2012; pp. 72–75.
- Guyomar, D.; Badel, A.; Lefeuvre, E.; Richard, C. Toward energy harvesting using active materials and conversion improvement by nonlinear processing. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 584–595. [Google Scholar] [CrossRef]
- Ramadass, Y.; Chandrakasan, A. An Efficient Piezoelectric Energy Harvesting Interface Circuit Using a Bias-Flip Rectifier and Shared Inductor. In Proceedings of the IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 8–12 February 2009.
- Toh, T.T; Mitcheson, P.D.; Dussud, L.; Wright, S.W.; Holmes, A.S. Electronic Resonant Frequency Tuning of a Marine Energy Harvester. In Proceedings of the PowerMEMS, Seoul, Korea, 15–18 November, 2011; pp. 383–386.
- Chang, S.C. Harvesting Energy from Non-Ideal Vibration Sources. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, May 2013. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).