A Reliable Control Strategy for Dual Induction Motor Drive System Consisting of Five-Leg Inverter

Abstract

This paper proposes a reliable control strategy for dual induction motor drives using a five-leg inverter (FLI). Since the FLI has the structural characteristic where both motors share a common leg, the current of the common leg can flow at twice the magnitude of the other leg currents. To prevent this overcurrent, this paper proposes a reliable integrated control strategy for both normal and open-circuit fault conditions in the FLI. Under normal conditions, overcurrent can occur when the phase and frequency of the current for both motors are distinct; therefore, the angle controller and current limitation prevent overcurrent. In contrast, an open-circuit fault in the FLI can cause overcurrent due to altered current paths. To ensure a safe shutdown, identifying the specific location of the faulty switch is essential. Therefore, fault diagnosis is required using the stator currents. Once the fault is located, a fault-tolerant method is applied to safely stop the motors, considering both the fault location and the rated current of the common leg. Consequently, the proposed system enables reliable operation of dual induction motor drives under various conditions. The experimental results verify the effectiveness of the proposed system.

1. Introduction

As a representative AC motor, the induction motor (IM) has a robust structure, high durability, and cost-effectiveness. Thus, IM is widely used in various applications, such as compressors in home appliances, conveyor belts in industry, HVAC systems in railway vehicles, etc. In the past, IMs were directly connected to fixed-frequency power sources and operated at a constant speed. Precise speed control and efficient energy management were difficult. However, with advancements in power semiconductor technology, inverters capable of variable voltage variable frequency (VVVF) control have enabled variable-speed operation of IMs. Moreover, the development of vector control theory and advances in microprocessor technology have significantly improved the performance of IM drives. Recently, as the number of motors in systems continues to increase, research has focused on reducing system cost and volume by optimizing drive system configurations [1,2,3,4].

The five-leg inverter (FLI) is one of the topologies for driving dual IMs independently. Because of using ten switches and components, it has advantages of volume and cost compared to using two three-leg inverters. However, dual IMs are supplied from a shared voltage source, which limits the available voltage range to 0.577 V_dc [5]. By changing from a star connection to a delta connection of the IM, the range can be increased by approximately √3 times [6]. This means that the operating range of the FLI can be improved by changing the connection of the IM. The common leg, which is connected to the C-phase of dual IMs, may cause twice the current magnitude as that of the other legs [7]. This overcurrent reduces the efficiency and shortens the system lifespan. Refs. [8,9] propose an angle controller that minimizes the I_C when the speeds of each IM are the same. If the load torques are the same and the phase difference is 180 degrees, the I_C can be reduced to 0 A. Nevertheless, overcurrent may occur if the speeds are different.

The proposed system consists of a PFC and the FLI for the HVAC system in railway vehicles, as shown in Figure 1. Here, the PFC, such as the Vienna rectifier, is used to stably control the DC voltage used by the FLI [10,11,12]. In this paper, a control strategy to prevent the overcurrent for both normal and fault conditions is proposed. Under normal conditions, compressors in the HVAC can be driven in two cases, as shown in Figure 2: identical operation and distinct operation. When both IMs operate at identical speeds, the angle controller minimizes the I_C. However, when the speeds differ, the phase difference cannot be maintained. Overcurrent can occur due to the sum of C-phase currents with different magnitudes and frequencies. Most studies on FLIs focus on cases under identical operation or do not comprehensively address the common leg overcurrent issue during distinct operation [13,14,15,16,17]. Meanwhile, fault conditions can be divided into short-circuit faults and open-circuit faults. Short-circuit faults generate large currents within a very short time; therefore, it must be isolated as quickly as possible by protection devices (e.g., fast-acting fuse, solid-state CB) [8,9,18,19,20]. In contrast, open-circuit faults block current paths, causing current distortion and increased torque ripple, which degrade overall system performance, stability, and reliability. In particular, the overcurrent can occur because the common leg cannot be properly controlled by the angle controller.

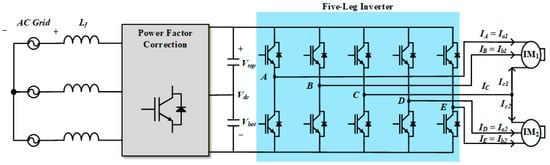
Figure 1. Circuit for dual induction motor drive systems with five-leg inverter.

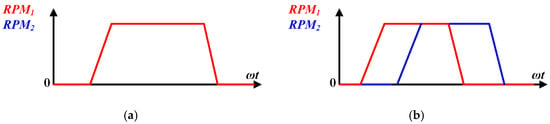
Figure 2. Operation profile under normal conditions: (a) identical operation, (b) distinct operation.

To enhance system reliability, this paper proposes a reliable control strategy for the FLI. The proposed strategy includes an overcurrent prevention control that considers both operation conditions and open-circuit fault. The main contributions are as follows: 1. sequence-based current limitation strategy; 2. switch fault diagnosis and mitigation methods. In the sequence-based current limitation strategy, the stator currents (I_sn, n = 1, 2) of both IMs are limited to less than half of its rated current (I_sn,rated, n = 1, 2) to ensure that I_C cannot exceed I_sn,rated. Under current-limiting conditions, both motors are controlled at the same speed. Once the speeds of both IMs become synchronized, the angle controller is activated to minimize I_C. In the switch fault diagnosis and mitigation methods, fault diagnosis is based on the fact that the current through a fault switch becomes zero. Consequently, the current magnitude in the stationary reference frame at the fault location becomes zero, allowing both fault diagnosis and location identification. Similarly, to prevent overcurrent after a fault, it is limited to less than half of I_sn,rated. If an open-circuit fault occurs on an independent leg, the IM connected to the fault switch stops while the other IM continues to operate. If a fault occurs on the common leg, both IMs stop.

This paper is structured as follows. The principle of operation for the FLI is expressed in Section 2. Section 3 explains the operation sequence with overcurrent prevention for the proposed system. In Section 4, fault diagnosis and mitigation methods for the FLI are proposed. Section 5 presents the experimental results to confirm the validity of the proposed method. Finally, the conclusions of this paper are provided in Section 6.

2. Principle of Operation

The FLI consists of five legs with upper and lower switches as shown in Figure 3. Four legs (A-leg, B-leg, D-leg, E-leg) are connected to the A-phase and B-phase of the IM. The common leg (C-leg) is connected to the C-phase of both IMs. This C-leg configuration makes it difficult to apply the conventional PWM method. To control each IM independently, [5] proposes a double zero sequence (DZS) modulation method. The zero-voltage component consists of two parts: one for modulation range expansion and the other for independent operation. The zero-voltage obtained by injecting the third harmonic extends the voltage modulation range from 0.5 V_dc to 0.577 V_dc. Furthermore, the C-phase reference voltage (V^*_cn, n = 1, 2) corresponds to the zero-voltage component. The V^*_cn is added to the reference voltages (V^*_an, V^*_bn, V^*_cn, n = 1, 2) of the other IM. As a result, both IMs can operate independently. Similar to the offset voltage, this component does not appear in the line-to-line voltages and therefore does not affect the actual output.

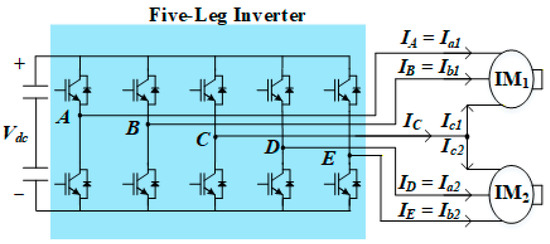
Figure 3. Circuit of five-leg inverter.

This paper employs the field-oriented control (FOC) method [21]. The synchronous reference frame d-axis current (I_den, n = 1, 2) represents the flux, and the synchronous reference frame q-axis current (I_qen, n = 1, 2) represents the torque component. The current PI controller minimizes the error between the reference and actual currents. A speed controller regulates the IM speed by generating the I^*_qen that drives the speed error to 0. Both speed and current controllers are required for each IM. Since the C-leg is connected to both IMs, I_C is the sum of I_c1 and I_c2. The magnitude of I_C (I_C,peak) can be expressed as

$$I_{C,peak}=\sqrt{{\left(I_{c1}\right)}^2+{\left(I_{c2}\right)}^2+2I_{c1}{I}_{c2}\cos (\delta )},$$

(1)

where δ represents the phase difference between I_c1 and I_c2. When δ = 0°, I_C has up to twice the current in the other legs. In contrast, when δ = 180°, I_C has its minimum. Therefore, I_C can be controlled to 0 if the torque and the speed are identical. The angle controller generates the I^*_qen to ensure that the δ is controlled to 180° by synchronizing the electrical angular velocities (ω_en, n = 1, 2) [7]. The resulting speed error is eliminated by the d-axis compensation current (I^*_den,comp). Figure 4 shows a control block diagram for the FLI. ω_rn represents the rotor angular speed; ω_sln represents the slip angular speed; θ_en represents the electrical angle; T_IMn the represents torque of the IM; V^*_A, V^*_B, V^*_C, V^*_D, and V^*_E represent modulation voltages; I_den,comp represents the compensation of speed error by angle controller; and σ represents the normalized phase difference between θ_e1 and θ_e2 + δ. The mathematical definition of σ is expressed as

$$\sigma =\sin \left({\theta }_{e1}-({\theta }_{e2}+\delta )\right)$$

(2)

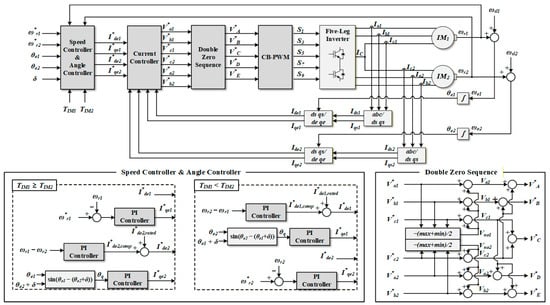
Figure 4. Control block diagram of five-leg inverter.

I_an, I_bn, and I_cn are transformed into the d-q reference frame using θ_en. I_den and I_qen are used as inputs to the current controller. The relationship in the angle controller varies depending on T_IMn. When T_IM1 is larger, I^*_qe1 is determined by the speed controller, whereas I^*_qe2 is determined such that ω_e1 and ω_e2 maintain δ = 180°. Although the ω_en values are the same, a difference in I^*_qen causes a speed error. The speed error is compensated by I_den,comp, which compensates for the slip and eliminates the speed error. V^*_an, V^*_bn, and V^*_cn from the current controller are applied to the DZS to produce V^*_A, V^*_B, V^*_C, V^*_D, and V^*_E. Finally, S₁, S₃, S₅, S₇, and S₉ are determined by comparing V^*_A, V^*_B, V^*_C, V^*_D, and V^*_E with the triangular carrier. Here, the switching state of the lower switches is the complementary operation of the upper switches.

3. Operation Sequence of FLI

In an HVAC system used in railway vehicles, the compressor normally accelerates to its rated speed (RPM_rated) for stable air compression. Depending on the instantaneous cooling demand and compressed air requirements, both IMs may operate simultaneously or only a single IM may be engaged. Therefore, the operation sequence is divided into two cases: identical-speed operation and distinct-speed operation. Figure 5 shows the mechanical speed (RPM₁, RPM₂), I_c1, I_c2, and I_C according to the operation profile. When both IMs operate identically as shown in Figure 5a, they have the same RPMs. In this case, the angle controller is activated immediately from the start because it is only effective when RPM₁ and RPM₂ are the same. The angle controller maintains δ = 180° between I_c1 and I_c2, thereby minimizing I_C. Unlike the identical operation, the angle controller cannot always be activated in the distinct operation as shown in Figure 5b. It is only activated within RPM_rated, where RPMs are identical. Specifically, the speed difference prevents a constant phase relationship between the two currents, making the angle controller ineffective. Consequently, the I_C becomes the sum of I_c1 and I_c2 with different frequencies, magnitudes, and time-varying phase angles. The worst-case scenario occurs when the peaks of I_c1 and I_c2 align, causing I_C,peak to reach up to twice the current in the other legs. This result often exceeds I_sn,rated, leading to thermal stress, junction degradation, or failure of the switch.

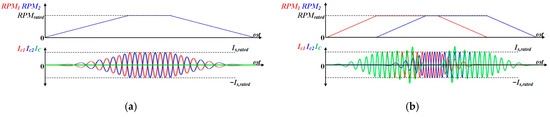
Figure 5. RPM₁, RPM₂, I_c1, I_c2, and I_C according to the operation profile: (a) identical operation; (b) distinct operation.

No method for minimizing I_C in the FLI under different speed conditions has been reported in the literature yet. Studies either assume identical operation or do not consider the overcurrent of the C-leg. This limitation requires a separate strategy to prevent overcurrent during asynchronous operation until speed synchronization is achieved. This paper proposes a sequence-based current limitation strategy that prioritizes hardware protection over dynamic response during these transient intervals. Specifically, since I_C is the sum of the I_c1 and I_c2 as expressed in Equation (1), I_C can reach up to twice I_sn,rated when δ = 0°. To ensure that I_C does not exceed I_sn,rated even in this worst case, I_sn is limited to half of I_sn,rated. This limitation serves two purposes. First, it prevents I_C,peak from exceeding I_sn,rated. Second, by limiting torque, the time to safely activate the angle controller is reduced. The q-axis current limit for operation (I^*_qen,lim) can be expressed as

$$I_{qen,lim}^{*}=0.5\sqrt{{\left(I_{sn,rated}\right)}^2-{\left(I_{den}^{*}\right)}^2},(n=1,2).$$

(3)

Figure 6 shows the three-step operation sequence for accelerating IM2 while IM1 is running, as follows:

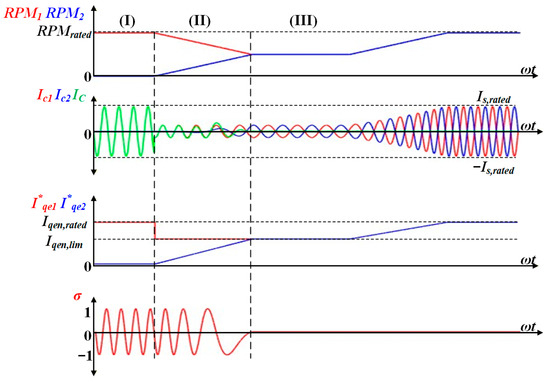
Figure 6. The proposed operation sequence for accelerating an IM₂ while the IM₁ is running.

(I)

Restriction of the current step: Upon receiving a start command for IM₂, I^*_qe1 and I^*_qe2 are limited to I^*_qe1,lim and I^*_qe2,lim, respectively. This limitation ensures that I_C does not exceed the switch current rating.

(II)

Speed convergence step: Under the limited torque by I^*_qen,lim, IM₂ accelerates and IM₁ decelerates at the same RPM gradient. RPMs converge at a specific RPM defined by the limited torque. The RPMs become equal, allowing the angle controller to be enabled.

(III)

Angle controller activation step: If σ is significantly distant from zero at the moment of the angle controller activation, the angle controller may generate a large I^*_qen in an attempt to force it to zero instantly. This can cause a sudden deceleration or acceleration of RPM. To prevent this sudden surge, σ must be adjusted sufficiently close to zero before the angle controller activation. Therefore, a slight deviation is applied between I^*_qe1 and I^*_qe2. Specifically, a small offset magnitude (∆I_qen), which is empirically determined to be approximately 1% to 3% of the rated q-axis current (I_qen,rated), is temporarily added to I^*_qe2 as shown in Figure 7. This range is sufficiently large to induce a phase alignment, yet small enough to prevent sudden acceleration or deceleration during the transition. Consequently, δ is gradually shifted by 180°, ensuring a smooth transition. Once the speeds match and σ crosses zero (within a tolerance of ±0.02), the angle controller is activated. The I_den,comp generated by the angle controller is applied after ∆I_qen returns to zero. Furthermore, since the variation of σ is very slow during this state, it can be treated as a DC component, making the PI control applicable for stable control [7]. At this point, I^*_qe2 returns to I^*_qe2,lim, and δ is fixed at 180°. The current limit is released to I_qen,rated, and I^*_qen ramps up to I_qen,rated. Consequently, both IMs reach RPM_rated synchronously without overcurrent.

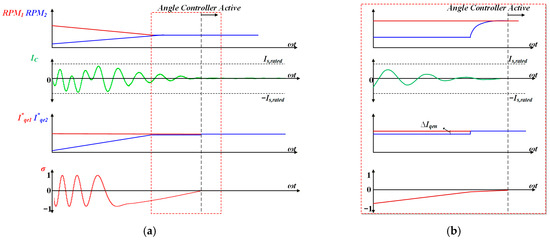Figure 7. The method for smoothly operating the angle controller in step II: (a) overall waveform (b) expanded waveform.

A similar operation sequence is applied for the transition from dual to single operation as shown in Figure 8, where IM₁ is decelerating while IM₂ is running.

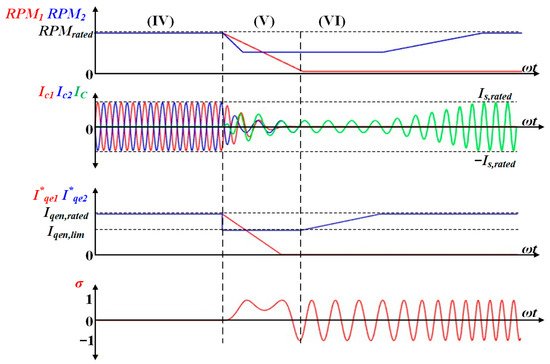
Figure 8. The proposed operation sequence for decelerating an IM₁ while the IM₂ is running.

(IV)

Angle controller deactivation: Upon receiving a stop command for IM₁, the angle controller is deactivated to allow independent control of each motor.

(V)

Restriction of the current step: I^*_qe,1 is controlled to zero to stop and I^*_qe2 is temporarily limited to I^*_qe2,lim. Here, IM₁ decelerates at twice the speed gradient of IM₂. These prevent overcurrent when RPM differences occur.

(VI)

Safe shutdown: IM₁ continues to decelerate to a standstill, and then I^*_qe2 returns to I_qe2,rated. Therefore, IM₂ is accelerated to RPM_rated.

This operation sequence ensures that the C-leg is protected against overcurrent throughout the entire operation state, regardless of load conditions.

4. Switch Fault Diagnosis and Mitigation Methods for FLI

Figure 9 shows the current path depending on the fault switch location in the A-leg. When an open fault occurs in the upper switch (S₁), negative current flows through the upper reverse diode (D₁) and the lower switch (S₂). On the other hand, positive current cannot flow through S₁ and flows only through the lower reverse diode (D₂). Conversely, when an open fault occurs in S₂, positive current flows through S₁ and D₂, while negative current cannot flow through S₂ and flows only through D₁. Therefore, the output voltage and current are different from normal conditions. This means that the I_sn decreases by fault, enabling fault diagnosis. The I_sn is expressed as the stationary reference frame d-q axis current (I_dsn, I_qsn, n = 1, 2).

$$\begin{array}{ll}{I}_{sn}& =\left|I_{sn}\right|\angle {\theta }_n\\ & = \sqrt{{\left(I_{dsn}\right)}^2+{\left(I_{qsn}\right)}^2}\angle {\tan }^{-1}\left(I_{qsn}/I_{dsn}\right), (n=1,2)\end{array}.$$

(4)

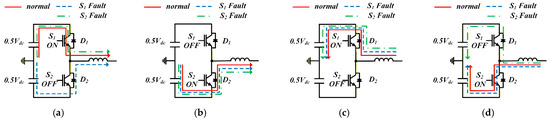
Figure 9. Current path depending on the fault switch location: (a) I > 0, S₁: ON, S₂: OFF; (b) I > 0, S₁: OFF, S₂: ON; (c) I < 0, S₁: ON, S₂: OFF; (d) I < 0, S₁: OFF, S₂: ON.

When open-circuit fault occurs, I_sn decreases compared to the reference stator current (I^*_sn). Therefore, the fault is diagnosed as follows.

$$f_{FDn}=\left\{\begin{array}{l}1 (\mathrm{fault}), \mathrm{for} I_{sn}<k{I}_{sn}^{*}\\ 0 (\mathrm{normal}), \mathrm{for} I_{sn}\ge k{I}_{sn}^{*}, \end{array}\right.(n=1,2),$$

(5)

where f_FDn is the fault diagnosis function, and k is a fault diagnosis coefficient with a value between 0 and 1. k is determined by hardware conditions and applications.

Figure 10 shows I_a1, I_b1, I_c1, I_s1, and I^*_s1 when the upper switch of the A-leg is faulty. For simplicity, it is assumed that the two IMs have identical torque and speed conditions. When the upper switch of the A-leg is faulty, no positive current path exists, and thus |I_a1| becomes zero. As a result, I_s1 decreases and a fault is diagnosed when I_s1 falls below k∙I^*_s1. In this case, I_a2, I_b2, and I_c2 are not affected. This is because each IM is driven independently by DZS.

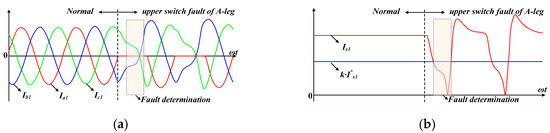
Figure 10. Waveforms for upper switch fault of A-leg: (a) waveforms of I_a1, I_b1, I_c1; (b) waveforms of I_s1, k∙I^*_s1.

The switch fault of the C-leg can be divided into two cases as shown in Figure 11: when δ = 0° and when δ = 180°. When δ = 0°, as shown in Figure 11a, no positive current path exists. Since the C-phase is shared by both IMs, the fault affects both. Thus, the fault diagnosis is possible on both sides using (5). When δ = 180°, as shown in Figure 11b, no positive current path exists either. However, since I_C is almost 0, the current distortion of I_c1 and I_c2 is minimized. In other words, the magnitude of I_sn does not decrease significantly; therefore, the fault cannot be easily diagnosed. In this specific condition, the switch fault of the C-leg has no impact on the system because there is no current flow to be interrupted. Consequently, although the open switch fault is not diagnosed, the system continues to operate normally without any performance degradation. When the speed or torque varies, I_C becomes non-zero. The fault current path leads to progressive distortion. This distortion naturally enables the fault diagnosis. Therefore, in all other actual scenarios, including different speed, torque, and δ, sufficient distortion occurs to diagnose the fault in the same manner as when δ = 0°.

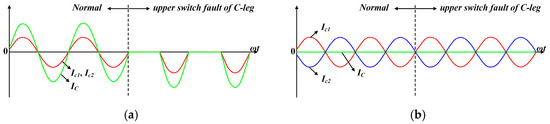
Figure 11. Waveforms when upper switch fault of C-leg: (a) δ = 0°; (b) δ = 180°.

Figure 12 shows the I_sn in the d-q axis reference frame for the fault switch location. Depending on the fault switch location, either the positive or the negative current cannot flow. Except for the case where δ = 180° and a fault switch of the C-leg occurs, I_sn appears in a semicircular pattern depending on the fault location (f_Ln, n = 1, 2). Therefore, the fault switch location can be identified using the θ^*_n and the phase current magnitude. θ^*_n can be calculated using I^*_den and I^*_qen.

$${\theta }_n^{*}={\tan }^{-1}\left(I_{qsn}^{*}/I_{dsn}^{*}\right), (n=1,2).$$

(6)

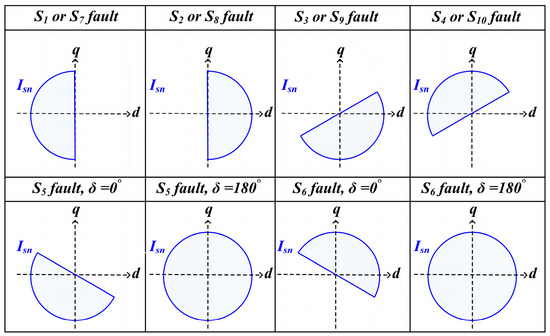
Figure 12. The I_sn in the d-q axis reference frame for the fault switch location.

The location is determined when the phase current corresponding to θ^*_n is 0. However, a sensing error by the hardware may occur. The phase current magnitude at f_Ln may not be sensed as exactly 0. Therefore, f_Ln is determined when the magnitude of the phase current is smaller than k₂. k₂ is the fault location coefficient, which is determined by hardware conditions and expressed as

$$f_{Ln}=\left\{\begin{array}{l}1, \mathrm{for} 330°\le {\theta }_n^{*}<30° \mathrm{and} \left|I_{an}\right|<k_2\\ 2, \mathrm{for} 150°\le {\theta }_n^{*}<210° \mathrm{and} \left|I_{an}\right|<k_2\\ 3, \mathrm{for} 90°\le {\theta }_n^{*}<150° \mathrm{and} \left|I_{bn}\right|<k_2\\ 4, \mathrm{for} 270°\le {\theta }_n^{*}<330° \mathrm{and} \left|I_{bn}\right|<k_2\\ 5, \mathrm{for} 210°\le {\theta }_n^{*}<270° \mathrm{and} \left|I_{cn}\right|<k_2\\ 6, \mathrm{for} 30°\le {\theta }_n^{*}<90° \mathrm{and} \left|I_{cn}\right|<k_2\\ 0 \left(\mathrm{normal}\right), \mathrm{for} \left|I_{sn}\right|\ge k_2\end{array}\right., (n=1,2).$$

(7)

In the FLI, an open-circuit fault can cause overcurrent, as shown in Figure 11a. This overcurrent can damage the hardware and the IMs. Therefore, this paper proposes a fault mitigation that prevents overcurrent and stops the IM. If an open-circuit fault occurs in one of the A-leg, B-leg, D-leg, and E-leg, it primarily affects the operation of the motor connected to the fault switch (IM^f). Therefore, the fault mitigation method focuses on stopping IM^f while simultaneously limiting the current of the motor connected to normal switches (IMⁿ) to prevent the overcurrent. The principle of limitation is similar to the method described in Section 3. The q-axis reference current limit for open-circuit fault (I^*_fn,lim) is the same value as in (3), and then expressed as

$$I_{fn,lim}^{*}=I_{qen,lim}^{*},(n=1,2)$$

(8)

The q-axis reference current of IM^f (I^*f_qen) is regulated to zero to stop this motor. The desired current does not flow by the open-circuit fault, so the angle controller does not operate. Simultaneously, q-axis reference current of IMⁿ (I^*n_qen) is constrained not to exceed that in (8). Consequently, IM^f is safely stopped, while IMⁿ has its current limit restored to I_qen,rated and continues operating.

If a switch of the C-leg has an open-circuit fault, the fault affects both IMs because of the shared current path. Unlike a fault in an independent leg, it is essential to note that normal operation cannot fundamentally be achieved without additional redundant circuits (e.g., isolation relays or additional legs) [22,23]. Therefore, only an immediate system shutdown occurs. When f_Ln latches at 5 or 6, both IMs are stopped by simultaneously setting I^*_qe1 and I^*_qe2 to zero. Figure 13 shows the flowchart described above for when f_L,n has a non-zero value.

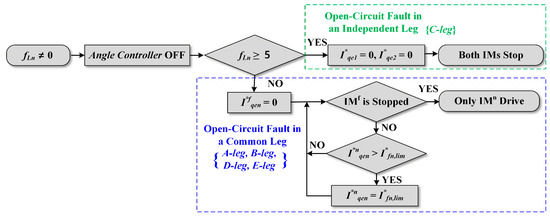
Figure 13. Flowchart of the fault mitigation when f_Ln has a non-zero value.

Figure 14 shows the entire block diagram for the proposed system with the operation sequence and the fault diagnosis, where E_AC, E_IM1, and E_IM2 are enable signals for the angle controller and drive command. When E_IM1 or E_IM2 is latched to 1 (ON), it operates up to RPM_rated. If both IMs are operated together, E_AC is latched to 1. Conversely, if operated separately or at different speeds, E_AC is latched to 0 (OFF). Accordingly, the currents are limited and the angle controller is activated when the speeds become equal. Fault diagnosis is always performed throughout the entire operation. I_dsn and I_qsn are calculated from three-phase currents and used to diagnose an open-circuit fault as in (5). When f_FDn is latched, I^*_dsn and I^*_qsn are used to locate the open-circuit as in (7). Then I^*_qen is regulated to I^*_fn,lim according to f_Ln, as shown in Figure 15.

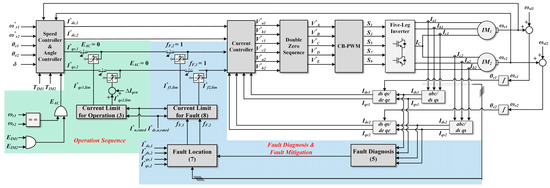
Figure 14. Entire block diagram for proposed system with the fault diagnosis.

Figure 15. Experimental setup: (a) prototype of the Vienna rectifier and FLI; (b) induction motors.

5. Experimental Results

The experiments have been implemented to verify the performance of the proposed system. To provide a stable V_dc supply, the PFC employed a Vienna rectifier. Figure 15 shows the experimental setup of the system and Table 1 shows the parameters of the system and IMs used for control. Both IMs have the same parameters. The IM was coupled to a servo motor that created variable load torque and speed conditions. The proposed system was implemented with the TMS320F28377D made by TI. The loads operated as fan loads proportional to the square of the speed.

Table 1. Experimental parameters.

Parameter	Value	Parameter	Value
Grid Voltage	220 [Vrms,pp]	Rs	1.9625 [Ω]
Grid Frequency	60 [Hz]	Rr	2.2103 [Ω]
Lf	4.06 [mH]	Lls, Llr	0.63 [H]
DC-Link Capacitor	1670 [µF]	Lm	0.186 [H]
V*dc	650 [V]	Pole	4
Rated Power of IM	2.2 [kW]	Rated RPM	900 [RPM]
Rated Current	7.7 [Apeak]	Switching Frequency	10 [kHz]
Deadtime	1 [µs]	Sampling Frequency	10 [kHz]

Figure 16 shows waveforms of line-to-line voltage V_UV, I_U, V_dc, RPM₁, RPM₂, I_c1, I_c2, and I_C for identical operation. The V_dc is charged to approximately 538 V through a diode rectifier at the start. At point I, both IMs are magnetized before the IM drive. Subsequently, IMs are driven at 450 rpm. During the drive, the Vienna rectifier operates to control V_dc to 650 V at point III. When the angle controller is activated at IV, the I_C is controlled to its minimum.

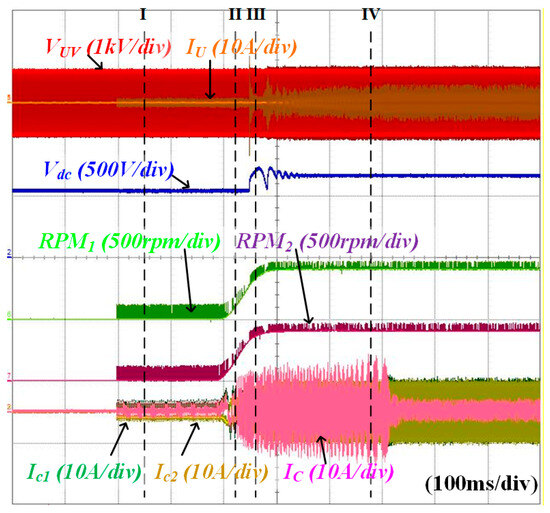
Figure 16. Waveforms of V_UV, I_U, V_dc, RPM₁, RPM₂, I_c1, I_c2, and I_C for identical operation.

Figure 17 shows waveforms of RPM₁, RPM₂, I_c1, I_c2, and I_C when applying the conventional current-limiting method. Each current is limited to I_sn,rated of 7.7 Apeak. While IM₁ operates at 450 rpm, IM₂ accelerated from 0 rpm to 450 rpm. Although the current flowing in each IM did not reach the limit, an overcurrent occurred in I_C, increasing to a maximum of 14 Apeak.

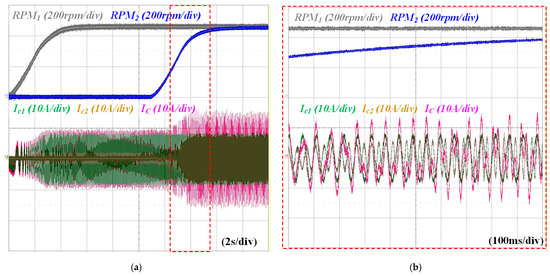
Figure 17. Waveforms of RPM₁, RPM₂, I_c1, I_c2, and I_C when applying conventional current-limiting method: (a) overall waveforms, (b) expanded waveforms.

Figure 18 shows waveforms of V_UV, I_U, V_dc, RPM₁, RPM₂, I_c1, I_c2, and I_C for distinct operation. First, when IM₁ is started from 0 rpm to 450 rpm, the Vienna rectifier operates. Since IM₂ is magnetized before driving, the average value of I_C increases by I_c1 as shown in Figure 18b. When IM₂ is started, I^*_qe1 is limited by (3), which decelerates its speed accordingly. The angle controller activates when the speed difference between both IMs is zero. Consequently, as shown in Figure 18c, I_c1 and I_c2 have a phase difference of 180°. Both IMs then accelerate together to 450 rpm while maintaining δ = 180°, as shown in Figure 18d, and the current magnitude increases accordingly. The same sequence applies when IM₁ stops during IM₂ operation. During this sequence, I_C increased only up to the rated current of 7.7 A maximum.

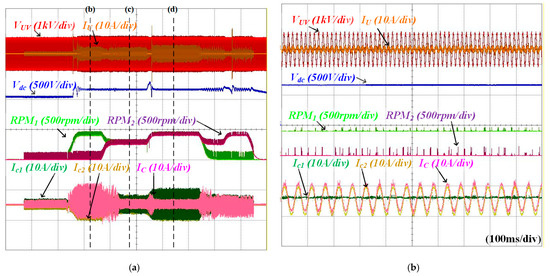
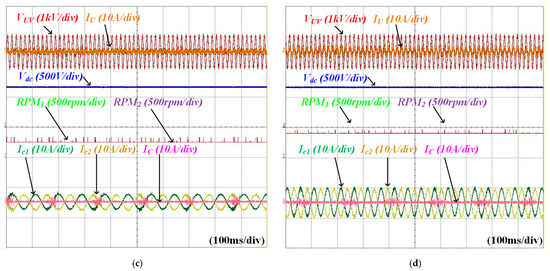
Figure 18. Waveforms of V_UV, I_U, V_dc, RPM₁, RPM₂, I_c1, I_c2, and I_C for distinct operation: (a) overall waveforms, (b) only IM₁ is operating, (c) angle controller is activated when both IMs are operating, (d) both IMs are operating at 450 rpm.

Figure 19 shows waveforms of I_A, I_B, I_C, I_D, I_E, I_s1, I^*_s1, θ₁, and f_L1 according to the fault switch and δ. k and k₂ were set to 0.5 and 0.1 for fault diagnosis. Figure 19a and Figure 19b show an open fault in the S₁ at δ = 180° and δ = 0°, respectively. The fault is diagnosed when I_s1 falls below k∙I^*_s1. The fault location can be determined by (7). Since f_L1 = 1, the fault in S₁ is recognized. Figure 19c and Figure 19d show an open fault in S₅ at δ = 180° and δ = 0°, respectively. As shown in Figure 19c, when I_C is minimum, I_s1 does not fall below k∙I^*_s1. Therefore, the fault is not diagnosed. Conversely, in Figure 19d, the fault can be diagnosed, and f_L1 = 5 indicates that S₅ is the fault. Consequently, except for the Figure 19c, all faults are diagnosed within half a cycle.

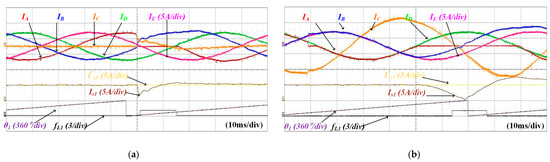
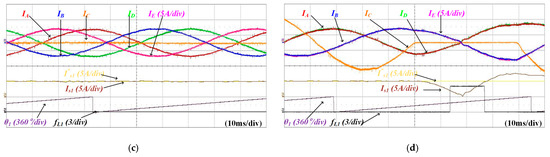
Figure 19. Waveforms of I_A, I_B, I_C, I_D, I_E, I_s1, I^*_s1, θ₁, f_L1 according to the fault switch and δ: (a) open fault in S₁ at δ is 180°, (b) open fault in S₁ at δ is 0°, (c) open fault in S₅ at δ is 180°, (d) open fault in S₅ at δ is 0°.

Figure 20 shows waveforms of current under an open-circuit fault in the upper switch of C-leg when a torque difference is 0.1 Nm. The coefficients were set k = 0.9, k₂ = 0.1. Since torque difference makes I_C to be non-zero, unlike in Figure 19c. As a results, the fault is successfully diagnosed within half of a cycle.

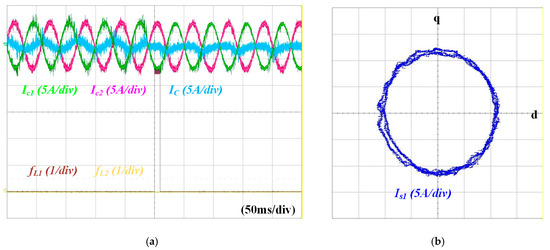
Figure 20. Waveforms of current under an open-circuit fault in the upper switch of C-leg when a torque difference is 0.1 Nm: (a) I_c1, I_c2, I_C, f_L1, and f_L2, (b) I_s1 in the stationary reference frame.

Figure 21 shows waveforms of I_A, I_B, I_C, I_D, I_E, RPM₁, RPM₂, f_L1, and f_L2 for the fault mitigation method when S₁ is fault. Both IMs are operating at 500 rpm. When S₁ is the fault, the fault is diagnosed by (5)–(7), and the angle controller is not activated. IM₁ is controlled to 0 rpm, while IM2 decelerates to a speed by (8). After IM₁ is stopped, IM₂ can be accelerated to 500 rpm. This operation sequence prevents overcurrent during an open-circuit fault as shown in Figure 21.

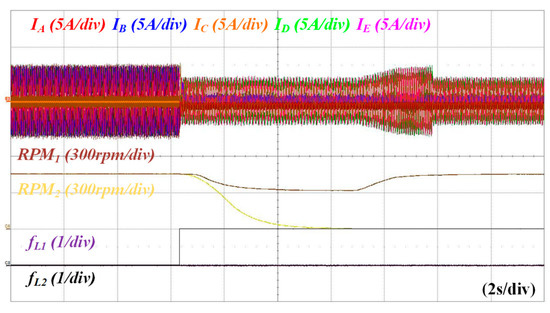
Figure 21. Waveforms of I_A, I_B, I_C, I_D, I_E, RPM₁, RPM₂, f_L1, and f_L1 for fault mitigation method when S₁ is fault.

6. Conclusions

This paper proposes a reliable control strategy for dual induction motor (IM) drives using a five-leg inverter (FLI). The structure of the FLI may cause overcurrent in the common leg when the two IMs operate asynchronously at different speeds. To prevent this overcurrent, an operation sequence that effectively utilizes current limitation and angle controller activation is applied. Furthermore, a fault diagnosis and mitigation method is proposed, ensuring safe shutdown without overcurrent during open-circuit fault conditions. As a result, the proposed strategy ensures reliable system operation under various operating conditions. The experimental results demonstrate that while the common leg current reached a peak of 14 A (180% of the rated current) using conventional methods, the proposed sequence-based current limitation successfully restricted it to 7.7 A (100% of the rated current), ensuring device safety during speed transitions. Furthermore, the fault diagnosis and mitigation method successfully detected open-circuit faults within half a fundamental cycle and enabled safe shutdown without overcurrent. The validity of the proposed system is verified using dual 2.2 kW IMs.