Reliability Modeling and Assessment of a Dual-Span Rotor System with Misalignment Fault and Shared Load

Abstract

To address the challenge of time-varying reliability assessment for double-span rotor systems under misalignment faults and load-sharing conditions, a time-varying reliability modeling method based on neural networks and reliability velocity mapping is proposed in this paper. By establishing a system dynamics model coupled with misalignment fault, a feedforward neural network surrogate model is constructed to efficiently predict stochastic stress responses, overcoming the limitations of high computational cost and difficulty in probabilistic analysis inherent in traditional finite element methods. Furthermore, by introducing the concept of reliability velocity, an intelligent mapping from independent systems to dependent systems is established, significantly enhancing the assessment accuracy of system time-varying reliability under small-sample conditions. Case study validation demonstrates that the proposed method can accurately capture the system degradation behavior under load-sharing and failure dependency mechanisms, providing a theoretical foundation for reliability analysis and intelligent operation and maintenance of rotor systems.

1. Introduction

Rotor systems, such as those in steam turbines, compressors, pumps, and generators, are core power equipment in major installations within the energy, chemical, aerospace, and other sectors [1,2,3]. Multi-span rotor systems, composed of multiple rotor systems connected via couplings, are widely used in the aforementioned applications to meet requirements such as long-axis transmission and load sharing. Time-varying reliability assessment of multi-span rotor systems is of significant importance.

Misalignment fault [4,5,6], one of the most common and severely detrimental faults in multi-span rotor systems, not only induces severe vibration and noise, accelerating wear on components like bearings and seals, but is also a primary cause of unplanned shutdowns. This fault mode has become a major cause of abnormal vibration and failure in machinery. Moreover, as each sub-rotor system (SRS) within a multi-span rotor system bears the same operational load or transmits loads from the same source, significant statistical correlation exists between SRSs due to the randomness of the operational loads. Misalignment faults originate from the connecting structures between different SRSs. This coupled structural fault, the failure dependency caused by load sharing and the dynamic operational characteristics of multi-span rotor systems pose severe challenges for time-varying reliability evaluation. Therefore, it is necessary to develop a quantitative system reliability model that can account for the aforementioned complex failure dependencies. This holds important theoretical value and engineering significance for accurately assessing the operational risk of multi-span rotor systems.

In recent years, researchers have conducted extensive study on the modeling, feature extraction, and diagnosis methods for rotor system misalignment faults [7,8,9]. Due to factors such as manufacturing errors, assembly deviations, and operational wear, the geometric parameters, support stiffness, damping characteristics, and external excitations of rotor systems always present significant uncertainty, making accurate prediction of their dynamic behavior difficult with traditional deterministic analysis. Consequently, researchers have undertaken dynamics studies of misaligned rotor systems considering uncertainties. These studies often employ uncertainty quantification methods like polynomial chaos expansion (PCE) and interval analysis to systematically analyze the nonlinear dynamic behavior of misaligned rotor systems under parameter and external excitation uncertainties, providing important theoretical basis for reliability design and fault diagnosis of rotor systems [10,11,12].

Currently, there is relatively little literature directly addressing the quantitative evaluation of time-varying reliability for multi-span rotor systems with misalignment faults. In fact, the various SRSs form a typical series system. In classical system reliability theory analysis, subsystems are always assumed to be independent and the series system structure function is used for easy calculation of system reliability. However, when analyzing the time-varying reliability of multi-span rotor systems, the structural connections between SRSs, common fault sources and the load-sharing mechanism make the time-varying failure dependency characteristics of the complex dynamic rotor system difficult to describe, posing significant challenges for time-varying reliability calculation. Simultaneously, the complex statistical correlations arising from the aforementioned structure and operating environment also cause correlations in the performance degradation of different SRSs, making stochastic characteristics hard to characterize. Meanwhile, as multi-span rotor systems are generally costly, obtaining extensive random failure statistics for all operational time periods (TP) is unrealistic. Therefore, it is necessary to provide a quantitative calculation method for the time-varying reliability of multi-span rotors under small-sample conditions that considers the system’s operational mechanisms and time-varying failure dependency characteristics. This could enable analysis of the dynamic impact of system structure, material parameters, etc., on time-varying reliability, providing a foundation for system fault diagnosis and intelligent operation and maintenance.

To address these difficulties, a neural network for a double-span system to construct a mapping relationship from the traditional independent failure model to the actual dependent failure model is utilized in this paper. Then, a time-varying reliability quantitative model based on a failure dependency mapping method is proposed for high-precision assessment of system reliability. The structure of this paper is arranged as follows: Dynamic analysis of the dual-cross rotor system is conducted in Section 2. Reliability models are established in Section 3. Numerical examples are provided in Section 4. The conclusions are listed in Section 5.

Unlike previous approaches that primarily focus on response prediction or independent failure models, this work introduces a novel reliability velocity mapping framework that enables accurate time-varying reliability assessment for dependent systems with limited data. The method specifically addresses the challenges of load-sharing and misalignment-induced failure coupling in rotor systems, which have not been adequately treated in existing literature.

2. Dynamics Analysis of Double-Span Rotor System

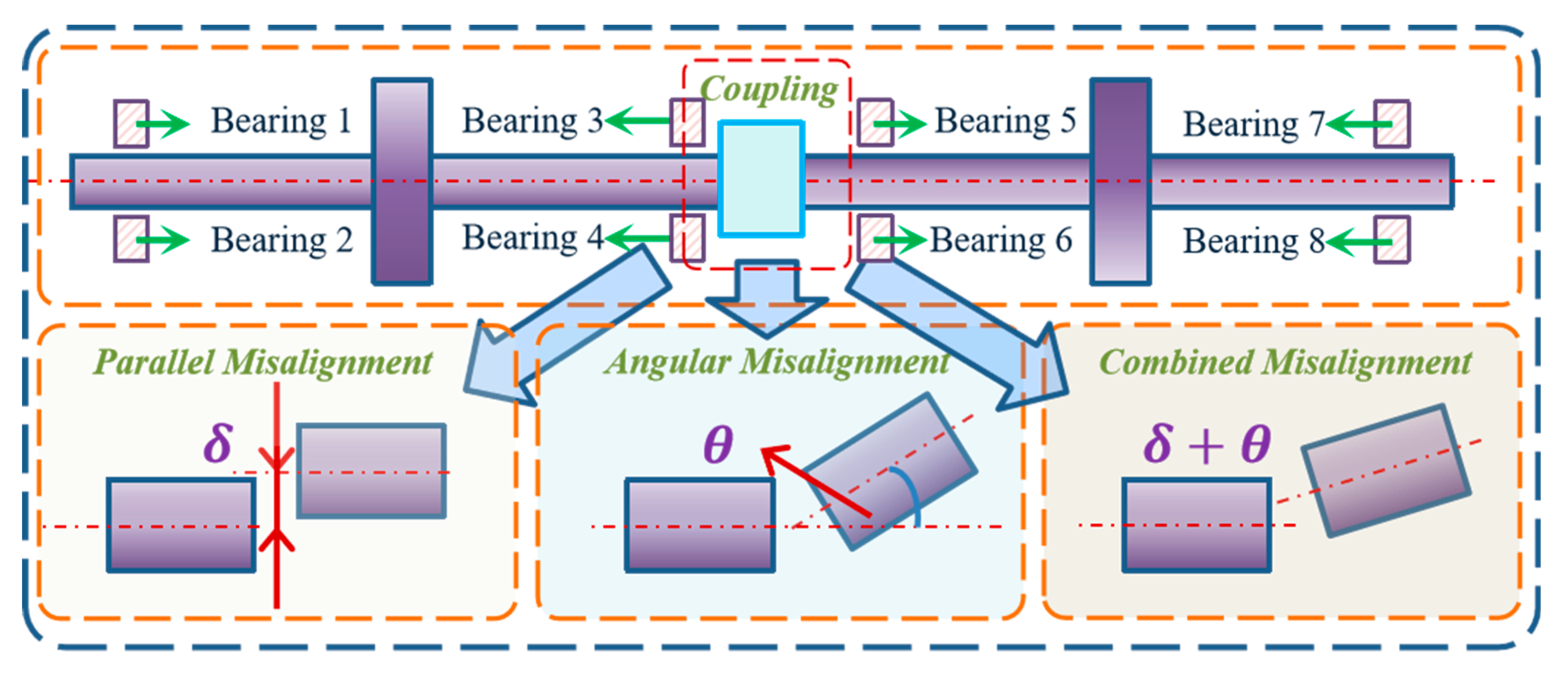
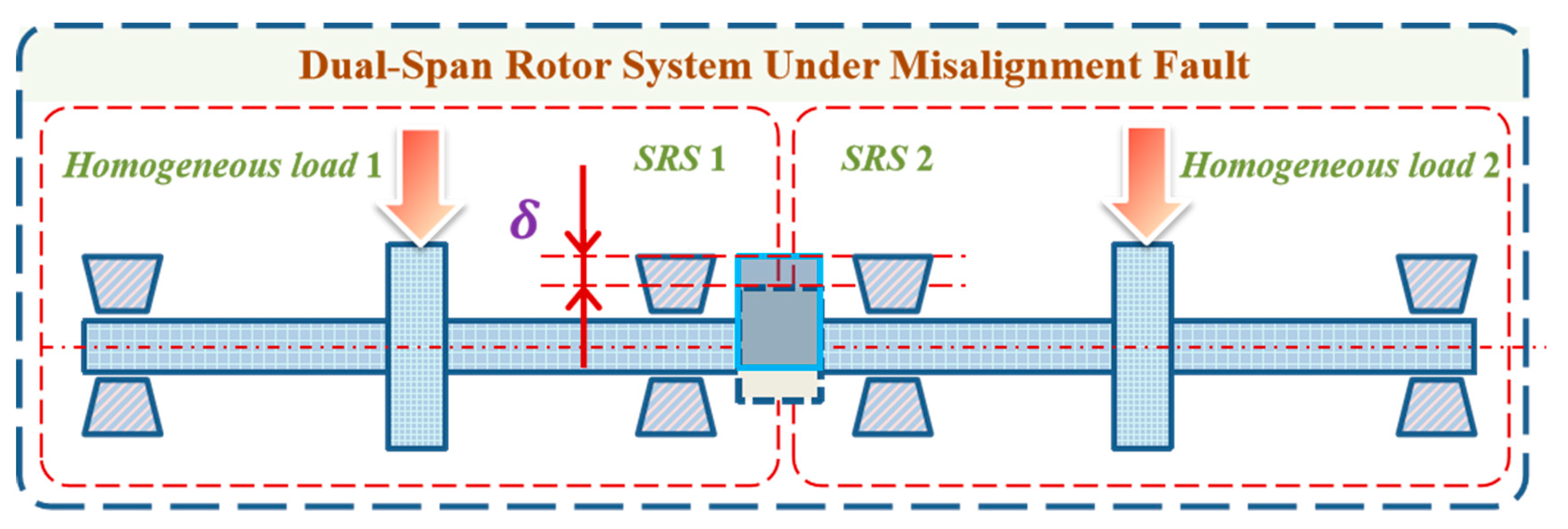
2.1. Misalignment Fault Analysis

Rotor misalignment fault refers to a condition where the rotational centerlines of various rotating components connected on the same shafting are not collinear, or where the deviation from the expected bearing centerline exceeds allowable limits. It is one of the most common faults in rotating machinery (e.g., pumps, fans, compressors, motors, gearboxes) and a major cause of equipment vibration faults. Installation errors, manufacturing errors, and operational wear can all cause rotor system misalignment. For example, failure to achieve precision alignment during installation, improper handling of foundation plates or base shims and loose anchor bolts can cause misalignment at the fixed end of the rotor system. In engineering equipment like steam turbines and gas turbines, differences in temperature rise and thermal expansion among components like rotors, cylinders and bearing pedestals due to operating temperatures and coefficients of thermal expansion can lead to misalignment during operation, even if the equipment was well-aligned during shutdown. The equipment foundation may undergo uneven settlement over time, due to geological changes or nearby construction, directly causing distortion of the entire equipment base and resulting in misalignment fault. Bearing wear, shaft bending, coupling wear or damage and frame deformation can all exacerbate the misalignment state.

Misalignment fault significantly impacts rotor system operation. Misalignment causes increased vibration and dynamic stress, leading to abnormal operational noise. It generates additional radial and axial forces, greatly increasing bearing load and wear, leading to bearing overheating, early fatigue, cage damage, spalling, or brinelling on races or rolling elements. The additional alternating dynamic stress may also cause fatigue cracks in the shaft, leading to fracture and fatigue failure. Typically, as shown in Figure 1, misalignment faults include [13,14,15]: (1) Parallel misalignment: The axes of the two rotors are parallel but have a center offset. This can be further divided into horizontal and vertical misalignment. In this fault mode, the coupling faces are parallel, but the centers are not coincident. During rotation, the coupling attempts to pull the shafts into alignment, generating a radial force. (2) Angular misalignment: The axes of the two rotors intersect at the coupling center point but form an angle. During rotation, the speed of the driven rotor fluctuates periodically for each revolution of the driving rotor, generating an axial force that tends to bend the rotor. (3) Combined misalignment: Simultaneous presence of parallel and angular misalignment.

2.2. System Dynamics Modeling

Due to the numerous and diverse mechanisms and structures causing misalignment faults, to more conveniently illustrate the proposed time-varying reliability calculation method, this paper studies a typical simplified double-span rotor system as shown in Figure 2. The system consists of two single-span rotors connected by a coupling. Both spans are driven by the same motor via a gearbox, bearing identical and fully synchronized operational loads. It should be noted that the proposed time-varying reliability analysis for double-span rotor systems is not limited to this specific dynamics model. The method can be extended by using dynamics modeling of misaligned rotor systems in different scenarios to obtain time-varying reliability under different misalignment fault modes. The shafting of each SRS is a continuous elastic body, simplified as an elastic shaft with rigid disks. According to vibration theory and finite element theory, using $X$ to represent the global displacement vector, the system dynamics equation for each SRS can be expressed as

$$M\ddot{X}+C\dot{X}+KX=F\left(t\right)$$

(1)

where $M$, $C$ and $K$ are the system mass, damping, and stiffness matrices, respectively, and $F\left(t\right)$ is the external operational load vector. To simulate the misalignment fault, known time-varying displacement constraints are applied at the coupling node connecting the two SRSs. The enforced displacement vector at this node is defined as

$$\delta \left(t\right)=\left[0,{\delta }_y\left(t\right),{\delta }_{\mathrm{z}}\left(t\right),\mathrm{0,0},0\right]$$

(2)

where ${\delta }_y\left(t\right)$ and ${\delta }_z\left(t\right)$ are the time-varying misalignment amounts described in the local coordinate system. By solving the system dynamics equation, the dynamic response of the system under the enforced displacement boundary condition can be obtained. The misalignment fault, through its coupling effect with the global stiffness matrix influences the displacement and stress fields of the entire system, thus simulating the misalignment fault at the dynamics level. Although Equation (1) is presented in a linear matrix form for notational simplicity, the actual finite element model accounts for nonlinear dynamic behavior induced by time-varying misalignment displacements. The enforced displacement boundary conditions at the coupling node (Equation (2)) vary periodically and introduce geometric nonlinearity and stress stiffening effects, which are captured in the full transient dynamic analysis.

The shaft modeling as an elastic body with rigid disks represents a simplification commonly adopted in rotor dynamics studies for computational efficiency. While this approach captures the essential dynamic characteristics, it neglects localized flexibility effects and distributed mass properties. However, for the purpose of system-level reliability assessment under misalignment faults, this simplification provides a reasonable balance between accuracy and computational cost. Future extensions could incorporate more detailed finite element modeling for specific component-level analyses.

2.3. Dynamic Stress and Neural Network

In the time-varying reliability analysis of the double-span rotor system, it is necessary to analyze the statistical distribution characteristics of the structural dynamic stress response under the combined action of random operational loads and misalignment faults. Although deterministic finite element methods are accurate, high computational cost makes them difficult to apply to large-scale reliability analysis based on Monte Carlo simulation (MCS). This section will use a Feedforward Neural Network (FNN) as a high-precision surrogate model to establish a direct mapping from the system’s stochastic input parameters to key stress responses, serving as the basis for stress distribution characterization and reliability calculation. To consider the influence of the operational load amplitude $F_{aj}$ and the misalignment amount ${\delta }_j$ on the structural stress within the $j\mathrm{t}\mathrm{h}$ (j = 1, 2, …, N) TP, the following input samples are obtained:

$$U_j=\left[F_j,{\delta }_j\right]$$

(3)

For a sample set containing $m$ different working conditions, the input matrix $U_j\left(m\right)$ has dimensions m × 2, specifically

$$U_j\left(m\right)=\left[\begin{array}{cc}{F}_{j1}& {\delta }_{j1}\\ F_{j2}& {\delta }_{j2}\\ ⋮& ⋮\\ F_{jm}& {\delta }_{jm}\end{array}\right]$$

(4)

The corresponding stress output is expressed as

$$Y_j\left(m\right)=\left[\begin{array}{c}{\sigma }_{j1}\\ {\sigma }_{j2}\\ ⋮\\ {\sigma }_{jm}\end{array}\right]$$

(5)

The dataset originates from finite element analysis. Through dynamic analysis based on the finite element method, the corresponding stress responses are obtained, ultimately forming the dataset for training and testing. After determining the input and output samples, a FNN is employed to learn the complex nonlinear mapping relationship between the input $U_j\left(m\right)$ and the output $Y_j\left(m\right)$ within each TP. The network’s topology and hyperparameter selection are determined through extensive trial calculations to ensure both excellent prediction accuracy and generalization capability [16,17,18]. The network topology consists of three parts: the input layer, hidden layers, and the output layer. The input layer contains 2 neurons for receiving the input vector. The hidden layers employ 2 fully connected hidden layers with the Hyperbolic Tangent Sigmoid activation function, which is symmetric about the origin and enables faster convergence during training. The output layer uses 1 neuron with a linear activation function to output the predicted stress value. The FNN training adopts the Bayesian regularization algorithm. This algorithm automatically balances the network’s fitting accuracy and model complexity by introducing a weight sum of squares term into the objective function, effectively preventing overfitting and demonstrating outstanding generalization performance even with limited training data. The FNN architecture is designed based on both theoretical considerations and empirical optimization. The selected configuration represents an optimal balance between model capacity and generalization performance for the specific application. The FNN provides sufficient nonlinear mapping capability to capture the complex relationship between input parameters and stress responses. The structure is particularly effective for learning the underlying physical relationships in rotor dynamics. The hyperbolic tangent activation functions in hidden layers are chosen for their smooth differentiability and zero-centered outputs, which facilitate stable gradient propagation during training.

For a FNN with $L$ hidden layers, its forward propagation process can be expressed as

$$\begin{gathered} z^{\left(l\right)}=W^{\left(l\right)}{a}^{(l-1)}+b^{\left(l\right)}\left(l=2,\dots ,L\right) \\ {a}^{\left(l\right)}={\varphi }^{\left(l\right)}\left(z^{\left(l\right)}\right) \\ {z}^{(L+1)}=W^{(L+1)}{a}^{\left(L\right)}+b^{(L+1)} \\ \widehat{y}={\varphi }^{(L+1)}\left(z^{(L+1)}\right) \end{gathered}$$

(6)

where $a^{(l-1)}$ is the output activation value of the $(l-1)\mathrm{t}\mathrm{h}$ layer, $W^{\left(l\right)}$ is the weight matrix of the lth layer, $b^{\left(l\right)}$ is the bias vector of the $l$th layer, and ${\varphi }^{\left(l\right)}$ is the activation function of the $l$th layer.

After obtaining the trained neural network, a large number of random samples under the joint probability distribution of working load and misalignment amount can be generated using the Monte Carlo method. These samples are used as inputs to the neural network, and the corresponding stresses are obtained using the trained network. Finally, the probability density function of the stress is derived from the predicted stress values. The data partitioning followed an 80%/20% split for training and validation when using the FNN. This partitioning strategy ensures sufficient data for model training while maintaining a robust validation set to prevent overfitting. The training employed Bayesian regularization as the training function, which automatically balances model complexity and prediction accuracy. The convergence was controlled by monitoring the validation error, with training proceeding for a maximum of 500 epochs while the algorithm automatically determined the optimal stopping point based on regularization parameters.

3. Reliability Analysis

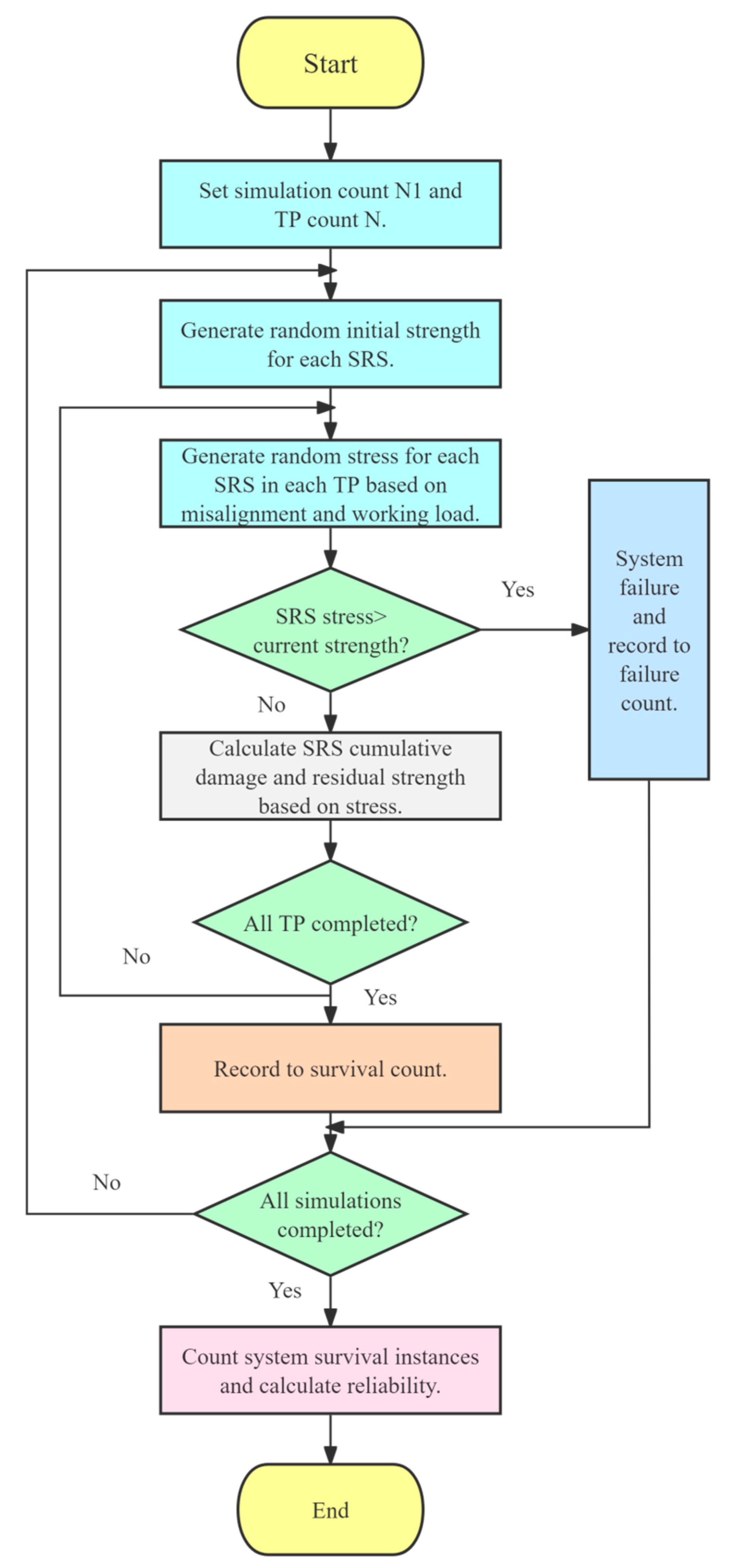
3.1. System Reliability Modeling

In a multi-span rotor system, each SRS shares the operational load from the same power source. This structure leads to significant load-sharing and failure dependency among the SRSs. Traditional reliability theory always assumes that component failures are independent, meaning the failure of one component does not affect the failure probability of others. However, in practical engineering, due to factors such as load-sharing, common environmental effects, and correlated material degradation, component failures are often dependent [19,20]. For a series system composed of n components, let $f\left({\sigma }_{ij}\right|F_j,{\delta }_j)$ denote the stress probability density function for the ith component within the jth TP of the system. The strength degradation law of a component can generally be expressed as follows [21]:

$${\psi }^{\left(i\right)}(j)={\psi }_0^{\left(i\right)}\left(1-{\sum }_{k=1}^{j-1}{D}_k^{\left(i\right)}\left({\sigma }_{ij}|F_j,{\delta }_j,{\omega }_i\right)\right),\hspace{1em}i=1,2,\dots ,n$$

(7)

where ${\omega }_i$ represents the material parameters of the ith component. Considering the randomness of the working load $F_j$ and the initial strength ${\psi }_0^{\left(i\right)}$ of the components, represented by the probability density functions $f_{F_j}\left(F_j\right)$ and $f_{{\psi }_0^{\left(i\right)}}\left({\psi }_0^{\left(i\right)}\right)$ respectively, the time-varying reliability of the ith component can be expressed as:

$$R_i\left(N\right)={\int }_{-\infty }^{\infty }{f}_{{\psi }_0^{\left(i\right)}}({\psi }_0^{\left(i\right)}){\prod }_{j=1}^N{\int }_{-\infty }^{{\psi }_0^{\left(i\right)}\left(1-{\sum }_{k=1}^{j-1}{D}_k^{\left(i\right)}\left({\sigma }_{ij}|F_j,{\delta }_j,{\omega }_i\right)\right)}f\left({\sigma }_{ij}\right|F_j,{\delta }_j)d{\sigma }_{ij}d{\psi }_0^{\left(i\right)}$$

(8)

The system reliability under the traditional independence assumption can then be expressed as:

$$R_{sys}\left(N\right)={\prod }_{i=1}^n{\int }_{-\infty }^{\infty }{f}_{{\psi }_0^{\left(i\right)}}({\psi }_0^{\left(i\right)}){\prod }_{j=1}^N{\int }_{-\infty }^{{\psi }_0^{\left(i\right)}\left(1-{\sum }_{k=1}^{j-1}{D}_k^{\left(i\right)}\left({\sigma }_{ij}|F_j,{\delta }_j,{\omega }_i\right)\right)}f\left({\sigma }_{ij}\right|F_j,{\delta }_j)d{\sigma }_{ij}d{\psi }_0^{\left(i\right)}$$

(9)

The corresponding failure rate can be expressed as:

$$\begin{gathered} {\xi }_{sys}\left(N\right)=\left\{{\prod }_{i=1}^n{\int }_{-\infty }^{\infty }{f}_{{\psi }_0^{\left(i\right)}}({\psi }_0^{\left(i\right)}){\prod }_{j=1}^N{\int }_{-\infty }^{{\psi }_0^{\left(i\right)}\left(1-{\sum }_{k=1}^{j-1}{D}_k^{\left(i\right)}\left({\sigma }_{ij}|F_j,{\delta }_j,{\omega }_i\right)\right)}f\left({\sigma }_{ij}\right|F_j,{\delta }_j)d{\sigma }_{ij}d{\psi }_0^{\left(i\right)}\right.- \\ \left.{\prod }_{i=1}^{n+1}{\int }_{-\infty }^{\infty }{f}_{{\psi }_0^{\left(i\right)}}({\psi }_0^{\left(i\right)}){\prod }_{j=1}^N{\int }_{-\infty }^{{\psi }_0^{\left(i\right)}\left(1-{\sum }_{k=1}^{j-1}{D}_k^{\left(i\right)}\left({\sigma }_{ij}|F_j,{\delta }_j,{\omega }_i\right)\right)}f\left({\sigma }_{ij}\right|F_j,{\delta }_j)d{\sigma }_{ij}d{\psi }_0^{\left(i\right)}\right\}/ \\ \left\{{\prod }_{i=1}^n{\int }_{-\infty }^{\infty }{f}_{{\psi }_0^{\left(i\right)}}({\psi }_0^{\left(i\right)}){\prod }_{j=1}^N{\int }_{-\infty }^{{\psi }_0^{\left(i\right)}\left(1-{\sum }_{k=1}^{j-1}{D}_k^{\left(i\right)}\left({\sigma }_{ij}|F_j,{\delta }_j,{\omega }_i\right)\right)}f\left({\sigma }_{ij}\right|F_j,{\delta }_j)d{\sigma }_{ij}d{\psi }_0^{\left(i\right)}\right\} \end{gathered}$$

(10)

In fact, the system reliability and failure rate calculated by the above formulas have advantages such as simple form, ease of understanding and convenient parameter statistics. Therefore, the system structure function under the independence assumption is widely used in engineering system reliability calculations. However, as indicated by previous analysis, due to load-sharing and failure correlation, the stress distribution and stochastic strength degradation history of different components within the system exhibit significant statistical correlation. This causes potential large errors in reliability calculations based on the traditional independence assumption. The system reliability model considering failure dependency should be expressed as:

$$R_{sys}^{dep}\left(N\right)=P\left({\bigcap }_{i=1}^n\left\{T_i>N\right\}\right)$$

(11)

where $T_i$ is the service time of the ith component.

To address the difficulty in system time-varying reliability assessment caused by the failure dependency issues arising from the combined effects of working loads, mechanical structure and material properties, a time-varying reliability calculation model for dual-span rotor systems under small-sample conditions based on reliability velocity mapping is proposed. To more finely describe the variation characteristics of system reliability, the concept of reliability velocity is introduced. Reliability velocity is defined as the negative derivative of the reliability function with respect to time:

$$v_s(t)=-{\displaystyle \frac{d{R}_s\left(t\right)}{dt}}$$

(12)

For each discretized TP, the above equation can be expressed as:

$$v_s\left(T\right)=R_s\left(T\right)-R_s(T+1)$$

(13)

Since the calculation of system reliability under both the independence assumption and the failure dependency assumption requires analysis based on the actual working mechanism, structural and material parameters and operating conditions of the system, the reliability velocities under both assumptions are highly similar and exhibit the following diffeomorphic relationship:

$$v_s^{dep}(t_1)=\mu \left({\displaystyle \frac{\partial R_s^{ind}}{\partial t_2}}\left(t_2\right)\right)$$

(14)

where $v_s^{dep}\left(t_1\right)$ is the system reliability velocity considering failure dependency and $R_s^{ind}$ is the system reliability under the independence assumption. Therefore, we can construct a mapping relationship between them using a neural network, convert the reliability velocity of the independent model to that of the dependent model and then calculate the system time-varying reliability considering failure dependency through numerical integration. The reliability velocity, defined as the negative derivative of reliability with respect to time, provides a more sensitive indicator of system degradation than reliability values alone. While reliability represents the probability of survival at a given time, reliability velocity captures the instantaneous rate of degradation, which is more responsive to changes in operating conditions and failure dependencies. This sensitivity enables the neural network to establish a more accurate mapping between independent and dependent system behaviors, particularly under small-sample conditions where traditional reliability indicators may be insufficient.

Mathematically, the reliability velocity amplifies the differences in degradation patterns between independent and dependent systems, making the mapping relationship more learnable for the neural network. This is especially crucial for capturing the complex interactions in misaligned rotor systems where failure dependencies evolve nonlinearly over time. Since the reliability decline periods of the independent system and the failure-dependent system do not coincide, the time variables for both are distinguished in the expression. In practical calculations, the following normalization model is needed to unify the time variable intervals of the two different systems.

To unify the time scales of the two models, a linear normalization method is introduced. Let the effective reliability interval be $\left[R_1,R_2\right]$ and extract the corresponding TPs for both models within this interval:

$$t^{ind}=\left\{j\mid R_s^{ind}(j)\in [R_1,R_2]\right\},\hspace{1em}{t}^{dep}=\left\{j\mid R_s^{dep}(j)\in [R_1,R_2]\right\}$$

(15)

Normalize them as follows:

$${\tau }^{ind}={\displaystyle \frac{t^{ind}-min\left(t^{ind}\right)}{max\left(t^{ind}\right)-min\left(t^{ind}\right)}},\hspace{1em}{\tau }^{dep}={\displaystyle \frac{t^{dep}-min\left(t^{dep}\right)}{max\left(t^{dep}\right)-min\left(t^{dep}\right)}}$$

(16)

Similarly, normalize the calculated system reliability velocity samples under the independence assumption and the actual system reliability velocity sample points as follows:

$${\epsilon }^{ind}={\displaystyle \frac{v_s^{ind}-min\left(v_s^{ind}\right)}{max\left(v_s^{ind}\right)-min\left(v_s^{ind}\right)}},\hspace{1em}{\epsilon }^{dep}={\displaystyle \frac{v_s^{dep}-min\left(v_s^{dep}\right)}{max\left(v_s^{dep}\right)-min\left(v_s^{dep}\right)}}$$

(17)

By interpolating ${\epsilon }^{ind}$ at the system reliability velocity sample TPs, the normalized system reliability velocity at these TPs suitable for neural network mapping is obtained. The FNN is then used to obtain the system reliability velocity considering failure dependency as follows:

$${\epsilon }^{dep}\left({\tau }^{dep}\right)=\mathcal{N}\mathcal{N}\left({\epsilon }^{ind}\left({\tau }^{dep}\right)\right)$$

(18)

Subsequently, the system reliability velocity $v_s^{dep}(t_1)$ is obtained through denormalization. The system reliability considering failure dependency can be calculated using the following iterative formula:

$$R_{sys}^{\mathrm{d}ep}(j+1)=R_{sys}^{\mathrm{d}ep}(j)-{\alpha }_j\cdot \widetilde{v_s^{\mathrm{d}ep}}(j)$$

(19)

where ${\alpha }_j$ is the iteration coefficient for the jth TP, used to adjust the step size of the reliability decrease. $\widetilde{v_s^{\mathrm{d}ep}}\left(j\right)$ is the estimated reliability velocity obtained through mapping. The introduction of the iteration coefficient ${\alpha }_j$ is to adapt to different TP lengths and nonlinear degradation characteristics.

To maximize computational accuracy, the iteration coefficients $\alpha =[{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_N]$ can be calibrated using an optimization algorithm. The optimization objective is to minimize the error between the predicted reliability and the sample reliability:

$${\underset{\alpha }{\min }{\sum }_{b=1}^M\left(R_{sys}^{\mathrm{d}\mathrm{e}\mathrm{p}}(b)-R_{sys}^{\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}}(b)\right)}^2$$

(20)

$${\alpha }_j>0\hspace{1em}\mathrm{for} \mathrm{all} b$$

Thus, the system time-varying reliability is obtained. The proposed reliability velocity mapping represents a departure from conventional reliability methods by establishing a diffeomorphic relationship between independent and dependent system behaviors, enabled by neural network learning of complex degradation patterns. Compared to PCE methods that primarily handle parameter uncertainty, our approach directly addresses system-level failure dependency. Unlike traditional MCS that require extensive sampling, our method achieves accurate reliability prediction with limited data through intelligent mapping. Furthermore, while interval analysis deals with parameter bounds, our model captures the actual statistical dependencies between component degradations, providing more realistic reliability estimates for engineering applications.

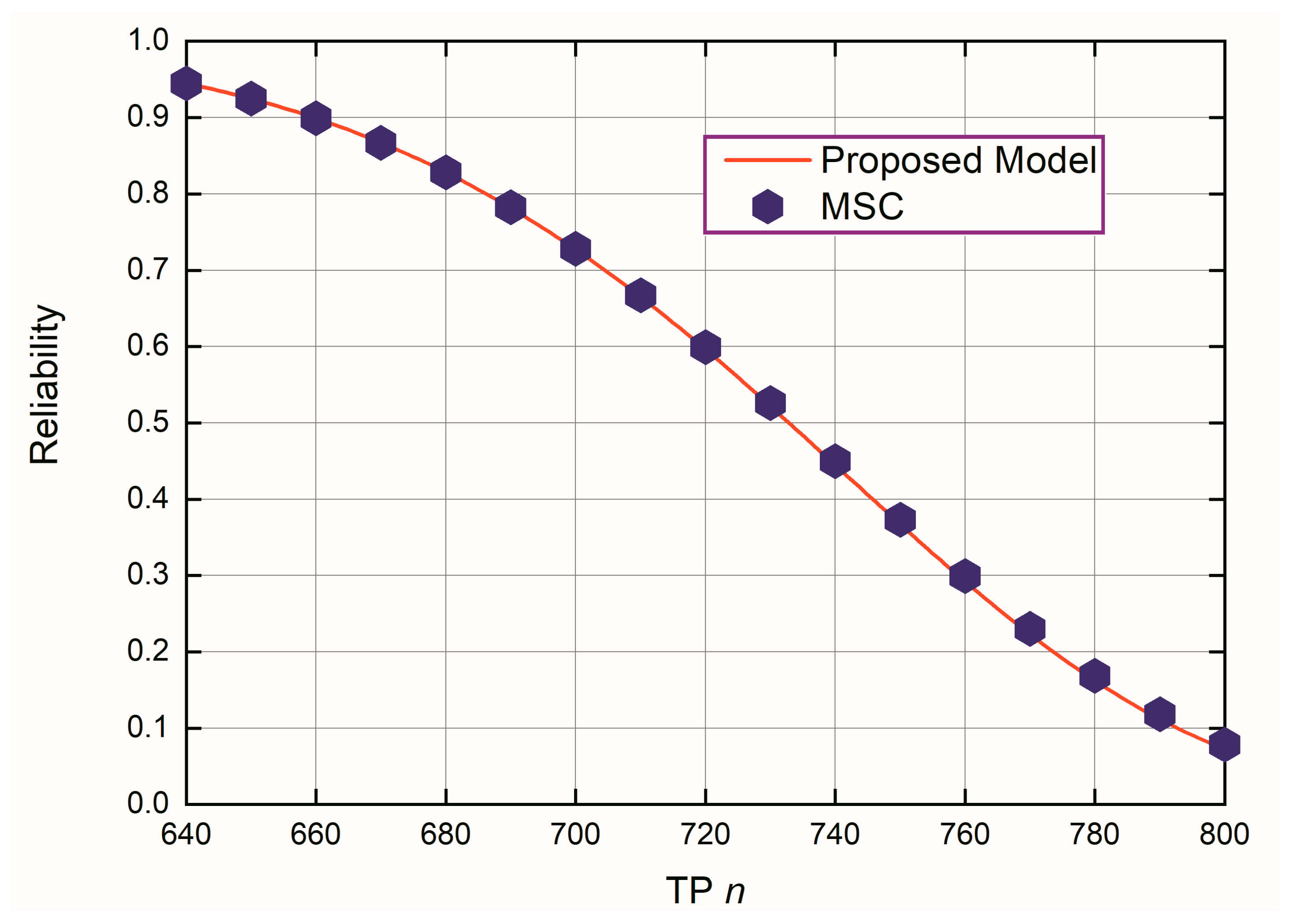
3.2. Reliability Validation

To validate the effectiveness and accuracy of the proposed time-varying reliability model based on reliability velocity mapping for dual-span rotor systems under misalignment faults, MCS is used as a benchmark method for comparative verification. MCS simulates the system’s failure process under the combined action of actual working loads and misalignment faults through a large number of random samples, which can more realistically reflect the system’s time-varying reliability behavior, especially suitable for system reliability assessment considering failure dependency and load-sharing mechanisms.

The basic idea of MCS is to statistically estimate the system’s time-varying reliability by repeatedly performing random sampling based on the system’s working mechanism and counting the number of survivals over multiple time periods. The specific MCS procedure adopted in this paper is shown in Figure 3 as follows:

4. Numerical Examples

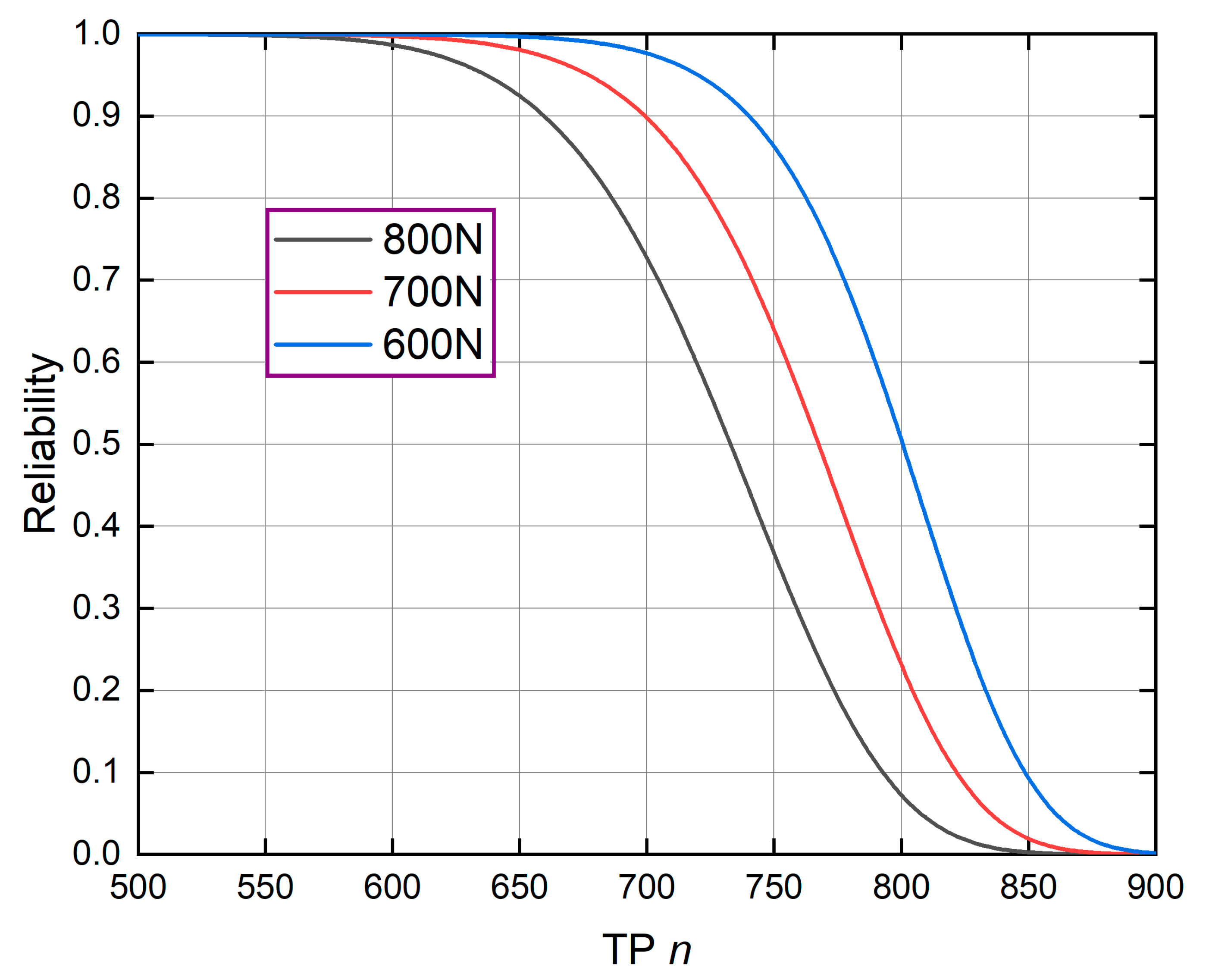
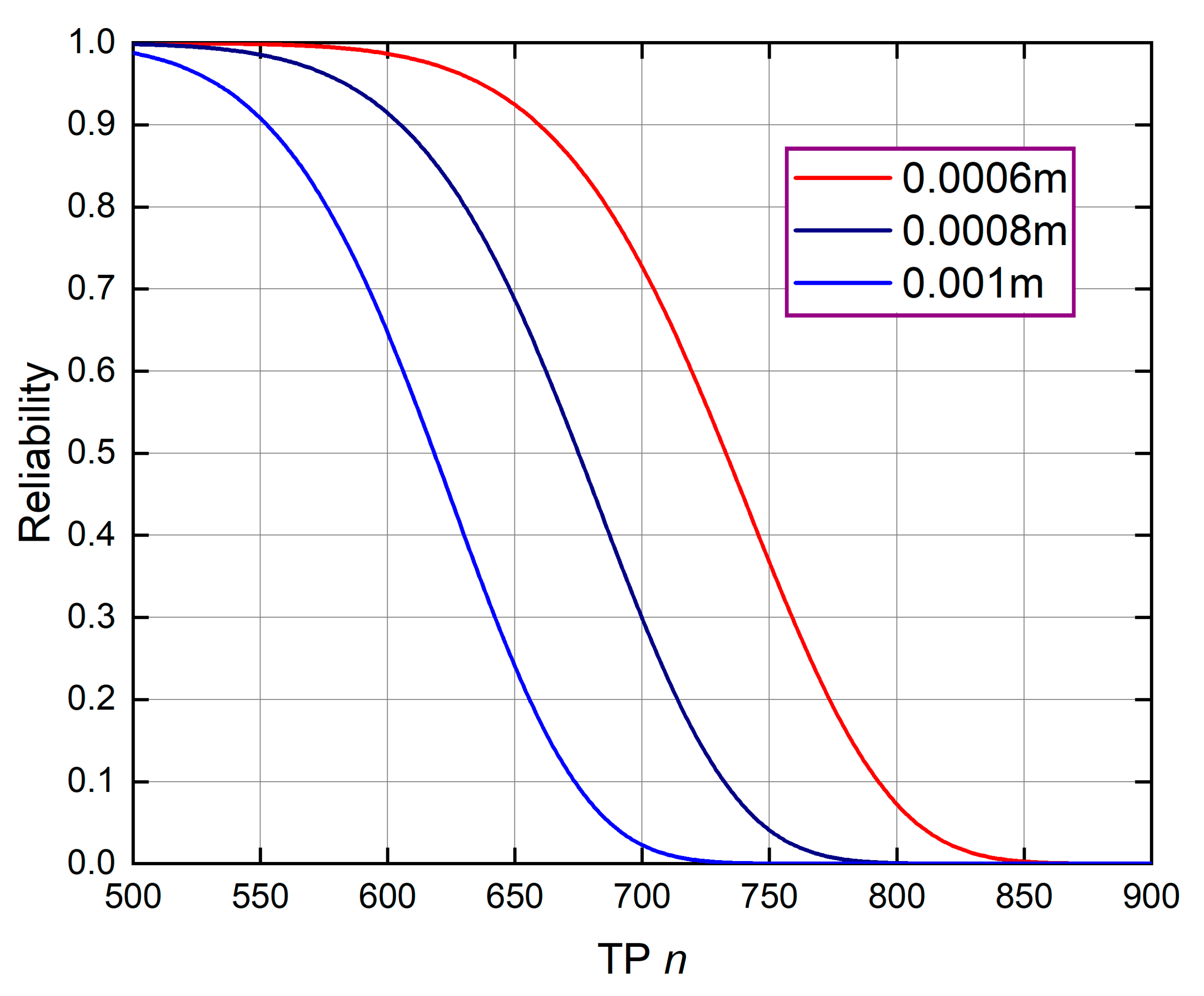
The effectiveness and applicability of the proposed time-varying reliability model for dual-span rotor systems is verified in this section through numerical examples. The examples mainly include four parts: (1) Model validation. (2) The influence of different working load statistical characteristics on system reliability. (3) The influence of different misalignment amounts on system reliability. 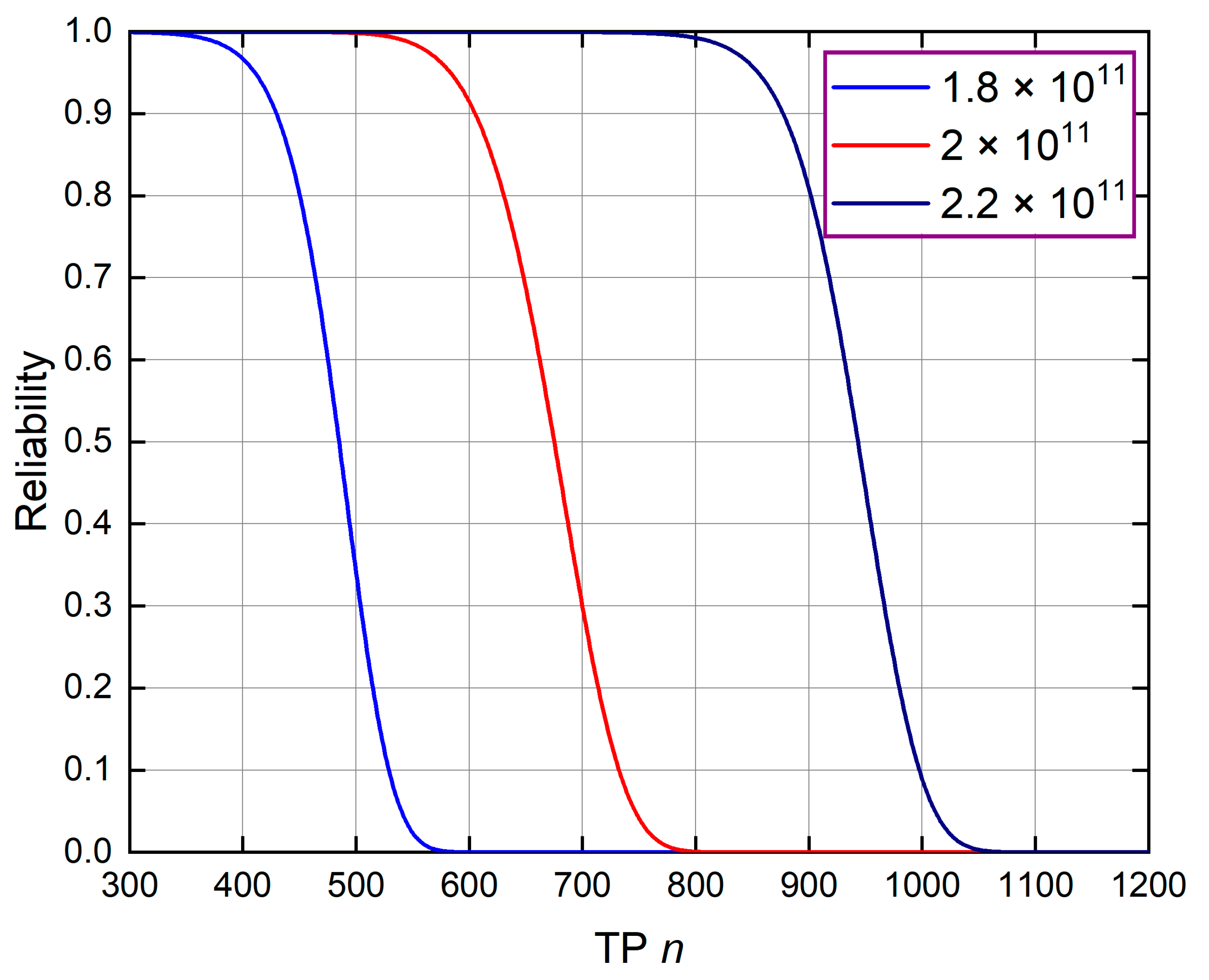(4) The influence of different elastic modulus on system reliability.

The dual-span rotor model considered in this study is representative of typical rotor systems found in industrial applications such as steam turbines, compressors, and pumps. In such systems, misalignment faults often occur due to thermal expansion, foundation settlement, or bearing wear. The proposed reliability model is applicable to these scenarios for predicting system degradation and planning maintenance.

4.1. Model Validation

To verify the accuracy of the proposed reliability model, the calculation results are compared with those of MCS in this section. MCS simulates the system’s failure process under actual operating conditions through extensive random sampling, capable of reflecting the time-varying behavior of system reliability. Other detailed system parameters are shown in

Table 1. System parameters.

Parameter	Value	Unit
Modulus of elasticity E	$2\times {10}^{11}$	Pa
Mean value of working load	12,000	N
Standard deviation of working load	800	N
Magnitude of misalignment	0.0006	m
Initial strength deviation	2	MPa
Mean value of initial strength	60	MPa
$l$	2	m
$r$	0.06	m
Density	7800	kg/m3
Angular velocity	62.83	Rad/s

. The comparison between the proposed time-varying reliability model and MCS is shown in Figure 4. Simultaneously, under the premise of selecting reliability values at every tenth TP as sample points, the system time-varying reliability curves under the independence assumption and considering failure dependency are shown in Figure 5.

Figure 4 shows the comparison of reliability curves between the proposed model and MCS results under the same system parameters. It can be seen that the two curves are highly consistent throughout the entire time range, especially in the middle stage where reliability begins to decline from high values. The model can still accurately capture the system’s failure behavior. In regions of very high and very low reliability, the two curves also show good agreement, indicating that the model has stable predictive capability at different reliability stages, verifying its applicability throughout the entire life cycle.

Figure 5 further compares the system reliability under the traditional independent failure assumption with the system reliability considering failure dependency. It can be seen that the independence assumption significantly underestimates the system reliability, especially in the middle and later stages, where the gap between the two gradually increases. The reliability calculated under both cases is high initially and decline gently. This is because the initial strength of the system is much higher than the stress and the misalignment amount is small, resulting in limited additional stress contribution and a slow accumulation of damage. In the middle and later stages of system operation, due to the continuous accumulation of damage and the continuous degradation of residual strength, the additional stress effect caused by misalignment becomes more significant and the statistical correlation effect of strength decline between the two SRSs becomes more obvious, leading to a larger difference in time-varying reliability between the two cases. The proposed model effectively corrects this deviation by constructing a reliability velocity mapping between the independent model and the dependent model using a neural network, more realistically reflecting the actual reliability characteristics of the system.

In summary, the proposed reliability model based on neural network mapping can effectively characterize the time-varying reliability characteristics of dual-span rotor systems under misalignment faults and shared loads, maintaining high prediction accuracy and robustness even under small-sample conditions, providing a theoretical tool for reliability analysis and intelligent maintenance of rotor systems in engineering practice.

4.2. Influence of Different Working Load Statistical Characteristics

The stochastic characteristics of the working load are one of the key factors affecting rotor system reliability. This section explores the impact of the dispersion of random working loads on the system’s time-varying reliability. Under the condition of a constant mean working load, the system time-varying reliability for three cases with standard deviations of 600 N, 700 N and 800 N is shown in Figure 6.

From Figure 6, it can be observed that as the dispersion of the working load increases, the system reliability decreases overall and the reliability curve becomes steeper, indicating an accelerated system degradation rate and a significantly shortened reliable life. When the standard deviation is 600 N, the system reliability drops to 0.5 at approximately TP 800. When the standard deviation increases to 700 N, the system reliability at the same TP has dropped below 0.3. This is because increased load dispersion leads to heavier tails in the stress distribution, i.e., an increased probability of high stress values, thereby accelerating material damage accumulation and strength degradation. Furthermore, load dispersion also affects the shape of the reliability curve. When dispersion is small, the curve declines more gently, indicating a more stable degradation process. When dispersion is large, the curve declines more sharply, indicating stronger randomness and uncertainty in the system. This suggests that in practical engineering, not only the average load level but also its fluctuation range should be strictly controlled to improve the long-term operational reliability of the system.

4.3. Influence of Different Misalignment Amounts on System Reliability

Misalignment is a typical fault in rotor systems. Its impact on system reliability by varying the misalignment amount is analyzed in this section. The system reliability for three cases with misalignment amounts of 0.0006 m, 0.0008 m and 0.001 m is shown in Figure 7.

From Figure 7, it can be seen that as the misalignment amount increases, the system reliability decreases significantly. It is shown that an increase in misalignment amount causes the entire reliability curve to shift leftwards, indicating that the system enters the degradation stage earlier. When the misalignment amount is 0.0006 m, the system reliability remains high for a long time throughout the time range. When the misalignment amount increases to 0.001 m, the system enters an accelerated degradation stage after 550 TPs and the reliability falls below 0.4 by TP 650. In fact, misalignment faults induce additional dynamic forces and moments, leading to local stress concentration and aggravated vibration, thereby accelerating material fatigue and damage accumulation. Therefore, in actual operation, misalignment faults should be detected and corrected promptly to delay system degradation and improve its service life. Time-varying reliability indicators can also serve as predictors and monitors of misalignment severity, providing a basis for maintenance.

4.4. Influence of Different Elastic Moduli on System Reliability

The elastic modulus is a measure of material stiffness and directly affects the dynamic characteristics and stress response of the rotor system. This section analyzes its impact on the system’s time-varying reliability by varying the elastic modulus, with the results shown in Figure 8.

From Figure 8, it can be seen that an increase in the elastic modulus improves the system reliability and delays the reliability decline process. When the elastic modulus is 2.2 × 10¹¹ Pa, the system reliability remains above 0.8 at TP 900. When the elastic modulus decreases to 1.8 × 10¹¹ Pa, the same reliability level can only be maintained until around TP 450. This is because a higher elastic modulus increases the system’s stiffness, reducing dynamic deformation and stress amplitude under the same load and misalignment conditions, thereby lowering the damage accumulation rate. Additionally, changes in the elastic modulus also affect the slope of the reliability curve. A higher modulus results in a slower decline in the curve, indicating stronger resistance to degradation. This suggests that selecting high-stiffness materials in rotor system design helps improve long-term operational reliability. The proposed reliability model can also serve as a theoretical basis for the optimal design of rotor systems.

Direct comparison with existing time-varying reliability models for rotor systems is challenging due to the scarcity of studies incorporating strength degradation and failure dependency. However, compared to the stochastic dynamics approaches in [10,11,12], which focus on response uncertainty, our model explicitly addresses reliability degradation under shared loads and misalignment faults. The proposed reliability velocity mapping provides a novel way to handle failure dependency with limited data, unlike traditional methods that require large failure statistics.

5. Conclusions

The modeling and assessment of time-varying reliability for dual-span rotor systems under misalignment faults and shared loads are systematically investigated in this paper. The main conclusions are listed as follows:

(1) A system reliability assessment framework integrating neural network surrogate and reliability velocity mapping considering failure dependency is proposed. Addressing the bottleneck of high computational complexity in traditional physical models which makes them difficult to use for probabilistic reliability analysis, a neural network surrogate model was constructed for stress prediction. Based on this, the concept of reliability velocity was introduced, and a nonlinear mapping between the independent failure rotor system model and the failure-dependent rotor system model was established via a neural network, breaking through the limitations of the traditional independence assumption and enabling the calculation of time-varying reliability for rotor systems under misalignment fault modes.

(2) The modeling challenges of failure dependency and load-sharing mechanisms under small-sample conditions are addressed. Existing methods often rely on extensive failure data or strong assumptions. The proposed mapping mechanism requires only a small number of samples to accurately capture the system’s true reliability behavior, making it particularly suitable for high-reliability, long-life rotor systems and providing a method for reliability analysis under small-sample conditions.

(3) The accuracy, robustness and engineering applicability of the model are verified. Through comparison with MCS, the predictive consistency of the proposed method throughout the entire life cycle was systematically validated. Parameter analysis shows that working load dispersion, misalignment amount and material stiffness have significant impacts on system reliability. The proposed time-varying reliability model provides a quantitative basis for the optimal design, fault diagnosis, and condition-based maintenance of rotor systems. The proposed model reduces the reliability prediction error by up to approximately 40% compared to the independence assumption model, as shown in Figure 5. Under a working load standard deviation of 800 N, the system’s reliable life (R = 0.5) is extended by approximately 9.5% when considering failure dependency.

(4) An extensible reliability modeling method is provided. The established time-varying reliability analysis model possesses good generality and extensibility and can be widely applied to the reliability assessment of complex mechanical systems where failure dependencies exist.

While the current study is based on numerical simulations due to the challenges of constructing a controlled dual-span rotor test rig, the proposed framework provides a theoretical foundation for future experimental validation. The reliability mapping method can be adapted to real rotor systems in turbines or compressors once operational data becomes available. The proposed time-varying reliability model can be directly applied to industrial rotor systems such as steam turbines, gas turbines, compressors, and pumps. In these applications, the model can serve as a digital twin for the following: (1) predicting remaining useful life under misalignment faults; (2) optimizing maintenance schedules based on real-time reliability indicators; (3) guiding alignment procedures during installation and operation; and (4) supporting design decisions for rotor stiffness and material selection. For example, in a compressor station, the model could be integrated with vibration monitoring systems to provide early warnings of misalignment-induced degradation, allowing for proactive maintenance before catastrophic failures occur.

Future work will include experimental validation on a dedicated rotor test rig to verify the model’s accuracy under real operating conditions. In addition, future research will also include more comparative studies as more models become available in the literature. In addition, the current study assumes small misalignment values and linear material behavior, which are valid for early-stage fault conditions but may not capture severe misalignment scenarios or material nonlinearities. In practical applications with large misalignments, geometric nonlinearities and material yielding may become significant. Future research will extend the model to include nonlinear material models and large deformation effects to address these scenarios.