An Improved PID Controller for the Compliant Constant-Force Actuator Based on BP Neural Network and Smith Predictor

Abstract

A compliant constant-force actuator based on the cylinder is an important tool for the contact operation of robots. Due to the nonlinearity and time delay of the pneumatic system, the traditional proportional–integral–derivative (PID) method for constant force control does not work so well. In this paper, an improved PID control method combining a backpropagation (BP) neural network and the Smith predictor is proposed. Through MATLAB simulation and experimental validation, the results show that the proposed method can shorten the maximum overshoot and the adjustment time compared with traditional the PID method.

1. Introduction

With the continuous development of industrial automation, the application of robots is becoming more extensive [1]. Robots are required to have the capabilities of precise force perception and force control in contact operations such as grinding, polishing and assembly, as subtle changes in the contact force will affect processing quality [2,3]. In recent years, a number of compliant constant-force actuators have been developed based on gasbag [4], voice coil motor [5], cylinder [6,7,8,9], artificial muscle [10,11] and special mechanical structures [12,13]. Among them, the pneumatic system based on the cylinder is the most widely used because air has good compliance. However, the pneumatic system is a complex nonlinear system, due to the compressibility of air and the inevitable static friction [14]. Therefore, achieving precise force control in the pneumatic system is both practical and challenging.

In recent years, intelligent control algorithms such as fuzzy logic, neural networks and expert systems have been developed rapidly, providing new ideas for the design of a pneumatic force control system [15,16,17,18,19,20,21]. The traditional proportional–integral–derivative (PID) method is a classic controller that was used for years because of its simplicity and effectiveness. However, with the requirement of low force control error in modern industry, it is difficult for a traditional PID controller to achieve the expected control quality indices in such complex nonlinear systems. Scholars made great efforts in the combination of intelligent control and traditional PID control, especially the combination of a backpropagation neural network (BPNN) and a PID controller. Kang et al. applied the BPNN-PID control method to the pneumatic force control system and demonstrated that the controller had better robustness and control performance [17,18,19].

These intelligent controllers have improved the performance of force control in the pneumatic nonlinear system to some extent. Nevertheless, besides the nonlinear property, there is a pure time delay link in the pneumatic systems based on pneumatic cylinders [22]. In the implementation of such stabilizing feedback control, even a small time delay may cause destabilization of the controller [23], because the time delay makes the controlled variables unable to reflect the disturbance of the system in time, which will produce a larger overshoot and longer adjustment time [24].

In some other control systems, such as chemical engineering, oil refining, metallurgy and heat engineering process control systems, the Smith predictor has been used effectively for compensating for the pure time delay [25,26]. For a given signal, the Smith predictor estimates the dynamic characteristics of the system under disturbance in advance and then compensates the time delay error to reduce the overshoot of the system and shorten the adjustment process [27]. However, the Smith predictor depends on the system model, so its performance is very sensitive to modeling errors. Pneumatic force control systems are usually complex and time-varying, so it is difficult to build accurate mathematical models. As a result, the Smith predictor is rarely used in such systems to the best of our knowledge.

In order to improve the modeling accuracy and make the Smith predictor suitable for use in a pneumatic force control system, this paper brings the neural network algorithm into the structure of the Smith predictor. Moreover, the improved Smith predictor is connected with the BPNN-PID controller to optimize the overall control performance. Therefore, the structure of this improved controller (backpropagation neural network-Smith predictor-proportional–integral–derivative (BPNN-SP-PID)) proposed in this paper is mainly divided into two parts. One part is to combine the artificial neural network (ANN) with the PID controller. An online learning backpropagation neural network ANN1 is taken to adjust the PID parameters adaptively to improve the dynamic performance of the controller. The other part is to combine the artificial neural network with the Smith predictor. A neural network ANN2 is used for identifying the nonlinear model of the controlled object to improve its modeling accuracy, so that the Smith predictor can compensate for the pure time delay well. The integration of a BPNN-PID controller and the Smith predictor improves the robustness and speed of the pneumatic force control system.

The rest of this paper is organized as follows. Section 2 introduces the system structure and model of the compliant constant-force actuator. Section 3 introduces the design of the BPNN-SP-PID controller. Section 4 shows the simulation and experimental results and gives a discussion. Section 5 gives the conclusive points.

2. System Description

As Figure 1 shows, the pneumatic constant force actuator mainly included a tilt sensor (KELAG Kabel variante kas90), a cylinder (SMC MGPM20-30Z), a force sensor (LH Z05A-200N), a base, a proportional pressure regulator (Festo VPPE-3-1-1/8-10-010-E1) and an electromagnetic valve (Parker A05PS25X-1s). Among them, the base was connected with the robot by bolts, and the force sensor had its thread for connecting the workpiece.

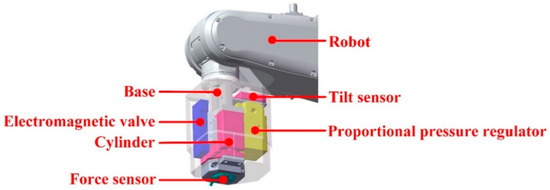
Figure 1. Compliant constant-force actuator structure diagram.

The pneumatic system control diagram is shown in Figure 2. The force sensor fed back the contact force F to the electrical signal Uf in real time, and the tilt sensor was used for obtaining the attitude signal Ut of the actuator. The signals were transmitted to the host computer through the data acquisition (DAQ) board. Then, the host computer ran the controller and adjusted the control voltage Uc of the proportional pressure regulator, making the output force F meet the set value. It also controlled the on and off state of the electromagnetic valve to change the direction of the force. As a result, the system had force perception and force control capabilities.

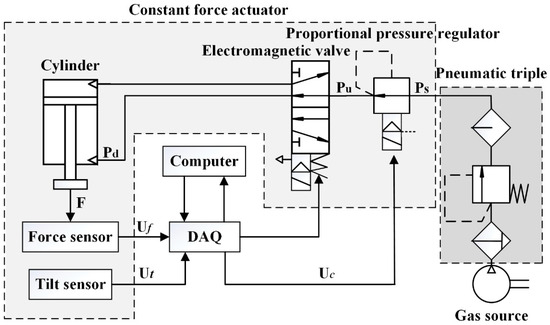
Figure 2. Pneumatic system control diagram.

The pneumatic system has nonlinear factors that are difficult to quantify [13]. To understand the characteristics of the system intuitively and to facilitate the following simulations, a linear approximate model of the system needed to be obtained first.

The mathematical model G(s) of the system represents the corresponding relationship between the control voltage of the proportional pressure regulator Uc(s) and the output force of the actuator F(s), including three links: the control voltage Uc(s) to the output pressure of the proportional pressure regulator Pu(s); the Pu(s) to the input pressure of the cylinder action chamber Pd(s); and the Pd(s) to the output force F(s).

According to the device structure above, it is divided into three parts to calculate the mathematical model. The first part is the proportional pressure regulator. The schematic diagram of its internal structure is shown in the Figure 3. The following equation is the force balance equation of the proportional pressure regulator spool:

$$P_{pv}{A}_1+P_{dv}{A}_2+mg-P_{dv}{A}_1-P_{sv}{A}_2-c{\dot{x}}_v-k_f\left(x_v+x_0\right)-F_c=0$$

(1)

where $P_{pv}$ is the air pressure in the pilot cavity; $P_{dv}$ is the output pressure of the proportional pressure regulator; $P_{sv}$ is the supply pressure of the proportional pressure regulator; $A_1$ is the effective area of the diaphragm; $A_2$ is the cross-sectional area of the valve chamber; m is the self-weight of the valve spool; $x_v$ is the displacement of the valve spool; $x_0$ is the initial deformation of the spring; $c$ is the viscous damping coefficient; $k_f$ is the equivalent spring stiffness; and $F_c$ is the Coulomb friction.

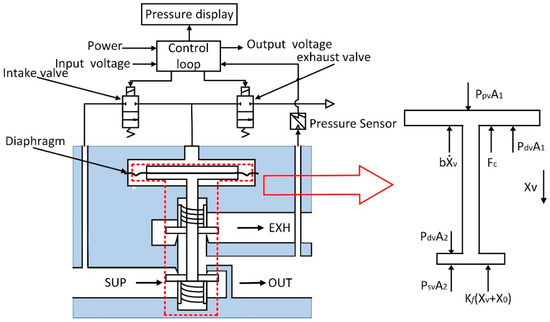
Figure 3. The internal structure of the proportional pressure regulator. (SUP = supply; EXH = exhaust; and OUT = output).

Ignoring the influence of the Coulomb friction, we can write Equation (1) in incremental form and perform a Laplace transform:

$$\left(cs+k_f\right)\Delta x_v\left(s\right)-\Delta P_{pv}\left(s\right)A_1+\Delta P_{dv}\left(s\right)\left(A_1-A_2\right)=0$$

(2)

According to the properties of the proportional pressure regulator, the spool displacement $x_v$ and the air pressure $P_{pv}$ of the pilot cavity can be approximated as proportional to the control voltage $U_c$.

$$\left(cs+k_f\right)K_1\Delta U_c\left(s\right)-K_2{A}_1\Delta U_c\left(s\right)+\Delta P_{dv}\left(s\right)\left(A_1-A_2\right)=0$$

(3)

Then, we can obtain the following relationship:

$$\frac{\Delta P_u\left(s\right)}{\Delta U_c\left(s\right)}=\frac{K_{1}cs+K_1{k}_f-K_2{A}_1}{A_1-A_2}=k_{1}s+k_2$$

(4)

where $K_n$, $k_n$ (n = 1, 2, 3…) are all undetermined coefficients.

The second part is the gas pipeline.

Assuming that the trachea is circular and the airflow movement is laminar, according to Anderson theory [28], we have

$$\Delta q_m\left(s\right)=K_3\left(\Delta P_u\left(s\right)-\Delta P_d\left(s\right)\right)$$

(5)

where $q_m$ is the mass flow rate.

The gas enters the cylinder through the proportional pressure regulator and the gas pipe. Assume that the gas in the cylinder is ideal and satisfies the ideal gas law:

$$P_d={\rho }_d{R}_c{T}_d$$

(6)

where $R_c$ is the proportionality coefficient; ${\rho }_d$ is the density; $T_d$ is the temperature; and $V_d$ is the volume of the gas.

Assuming that the temperature in the gas circulation process satisfies the adiabatic process, $q_m$ is equal to the rate of change of the gas mass m in the cavity. Combining the above, we get

$$q_m=\frac{1}{k}\frac{V_d}{R_c{T}_d}\frac{d{P}_d}{dt}$$

(7)

where $k$ is an undetermined coefficient.

Write Equation (7) in incremental form and perform a Laplace transformation:

$$\Delta q_m\left(s\right)=\frac{1}{k}\frac{V_d}{R_c{T}_d}s\Delta P_d\left(s\right)=K_{4}s\Delta P_d\left(s\right)$$

(8)

Combine Equations (5) and (8) to get

$$\frac{\Delta P_d\left(s\right)}{\Delta P_u\left(s\right)}=\frac{K_3}{K_{4}s+K_3}=\frac{1}{k_{3}s+1}$$

(9)

The third part is the cylinder.

The force analysis of the cylinder is carried out according to Newton’s second law, and the friction is ignored:

$$M{s}^2\Delta Y\left(s\right)+Cs\Delta Y\left(s\right)+\Delta F\left(s\right)=\Delta P_d\left(s\right)A_3$$

(10)

where $M$ is the total mass of the cylinder rod; $C$ is the viscous damping coefficient; $F$ is the output force; $A_3$ is the cylinder cross-section; and $Y$ is the displacement of the cylinder.

The force causes slight deformation of the workpiece, and the actuator passively generates displacement y. Set the equivalent stiffness coefficient to $K$:

$$\Delta F\left(s\right)=K\Delta Y\left(s\right)$$

(11)

Combine Equations (10) and (11) to get

$$\frac{\Delta F\left(s\right)}{\Delta P_d\left(s\right)}=\frac{K{A}_3}{M{s}^2+Cs+K}=\frac{k_7}{k_4{s}^2+k_{5}s+k_6}$$

(12)

According to the above derivation, the transfer function of each link is listed in Figure 4.

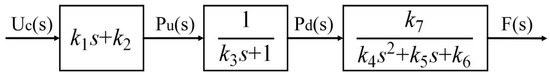
Figure 4. The transfer function of the system.

Therefore, the open-loop mathematical model G_o(s) of the system can be obtained as follows:

$$G_o\left(s\right)=\frac{k_7(k_{1}s+k_2)}{\left(k_{3}s+1\right)\left(k_4{s}^2+k_{5}s+k_6\right)}$$

(13)

where $k_n$ (n = 1, 2, …, 7) in Figure 4 and Equation (13) represents undetermined coefficients. It can be seen that the mathematical model of the system has three poles and one zero.

The undetermined coefficients are identified through the gray box experimental method. The system is loaded with an input signal, and the corresponding output signal is collected over time. When the loaded signal is a step signal, the output signal always takes ~70 ms before it starts to respond, as shown in Figure 5, so a time delay link needs to be added to the mathematical model. Afterward, the MATLAB system identification tool is used for analyzing the relationship between the collected input signal and output signal [29]. As a mathematical model with three poles, one zero and a pure time delay link are used for identification. The approximate mathematical model including the pure time-delay G(s) is obtained:

$$G\left(s\right)=\frac{2s+15.6}{s^3+15.8s^2+130.7s+350.7}{\mathrm{e}}^{-0.07s}$$

(14)

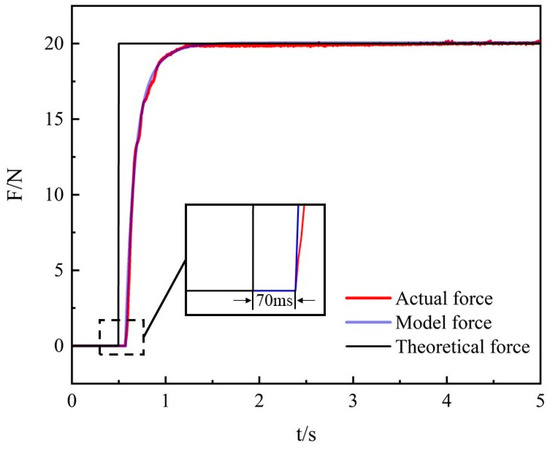
Figure 5. Comparison of the open-loop step response between the mathematical and actual models.

The step response curve of the mathematical model is calculated in MATLAB Simulink and compared with the actual curve for model validation. It can be seen from Figure 5 that the identified mathematical model matches the actual one well. The approximate mathematical model will be used in the simulation of Section 4.

3. Controller Design

The structure of the improved PID control method proposed in this paper is shown in Figure 6. The BP neural network-Smith predictor-PID (BPNN-SP-PID) controller was divided into two parts. One part was the BPNN-PID controller. ANN1 could realize self-optimization of the PID parameters and improve the control performance. The other part was the Smith predictor. The Smith predictor was used for reducing the influence of the pure time delay [27]. ANN2 was used for identifying the open-loop model of the controlled object Go(s), eliminating the pure time delay. Higher identification accuracy brought by ANN2 could make the Smith predictor compensate the time delay more effectively. The two parts are described in detail below.

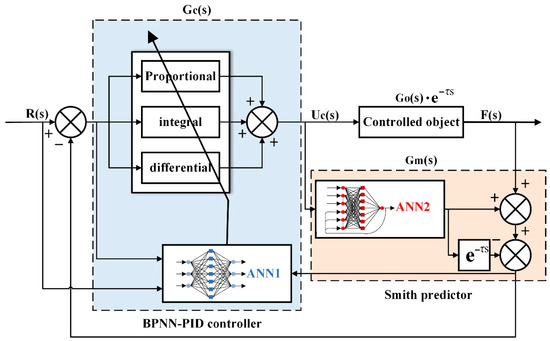
Figure 6. Backpropagation neural network-Smith predictor-proportional–integral–derivative (BPNN-SP-PID) controller structure diagram.

3.1. BPNN-PID

The neural network has a strong self-adaptive ability and can be combined well with other control methods [18]. On the basis of PID control, in order to optimize the performance of the controller, the online learning type BP neural network ANN1 was applied.

The BPNN-PID controller consisted of two parts: the PID controller and the BP network ANN1. The PID controller directly controlled the controlled object in the closed loop, and the BPNN adjusted the three parameters of the PID controller in real time according to the error function J.

The structure of the neural network ANN1 is shown in Figure 7.

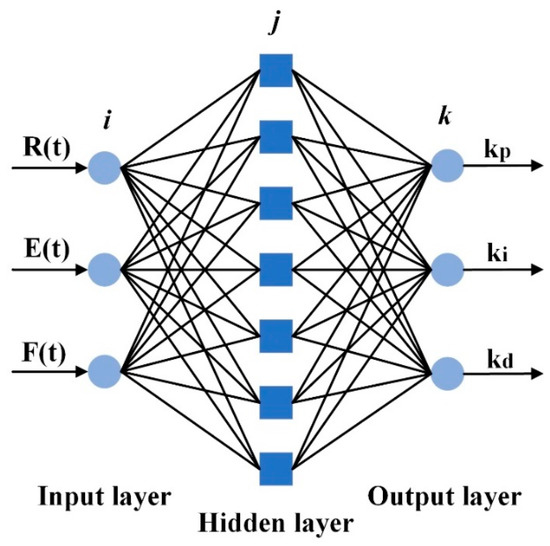
Figure 7. Schematic diagram of the neural network ANN1’s structure, part of the BPNN-PID controller depicted in Figure 6.

The input and output of the network are

$$\{\begin{array}{c}{O}_i\left(t\right)={\left[\begin{array}{ccc}R\left(t\right)& E\left(t\right)& F\left(t\right)\end{array}\right]}^T\\ ne{t}_k\left(t\right)={\left[\begin{array}{ccc}{k}_p& k_i& k_d\end{array}\right]}^T\end{array}$$

(15)

where t is the discrete time series (t = 1, 2, 3...); R(t) is the set force at time t; E(t) is the error at time t; F(t) is the actual output force at time t; and $k_p, k_i,k_d$ indicate the proportional, integral and differential parameters of the PID controller, respectively.

The activation function of the hidden layer was the tanh function. Since PID parameters cannot be negative, the activation function of the output layer was taken as a sigmoid function. Based on the previous paper [30], other parameters of the neural network were determined, as shown in Table 1.

Table 1. Parameters of neural network ANN1.

Type	Value
Learning type	Online
Learning rate ($\eta$)	0.3
Inertia index ($\mathsf{\alpha }$)	0.15
Number of hidden layer neurons	8
Hidden layer activation function	Tanh
Output layer activation function	Sigmoid
Initialization weight method	0.03rands(n, 1) 1

¹ rands(n, 1) returns an random matrix of n rows and one column, and the range of elements in the matrix is (−1, 1).

The incremental PID control algorithm is used for calculating the control voltage Uc(t):

$$U_c\left(t\right)=U_c\left(t-1\right)+\left[\begin{array}{ccc}E\left(t\right)-E\left(t-1\right)& E\left(t\right)& E\left(t\right)-2E\left(t-1\right)+E\left(t-2\right)\end{array}\right]·ne{t}_k\left(t\right)$$

(16)

The error function J [18,19] is expressed as

$$J=\frac{1}{2}{\left(R\left(t\right)-F\left(t\right)\right)}^2$$

(17)

According to the gradient descent method, the weights of the output layer and hidden layer of the network are adjusted in turn, and an inertia term $\mathsf{\alpha }\Delta \omega \left(t-1\right)$ is added to avoid falling into the local minimum:

$$\Delta \omega \left(t\right)=-\eta \frac{\partial J\left(t\right)}{\partial \omega }+\mathsf{\alpha }\mathsf{\Delta }\omega \left(t-1\right)$$

(18)

In Equation (18), $\Delta \omega \left(t\right)$ is the weights adjusting value; $\eta$ is the learning rate; and $\mathsf{\alpha }$ is the coefficient of inertia.

In application, this BPNN-PID control algorithm could be roughly divided into the following steps, as shown in Figure 8:

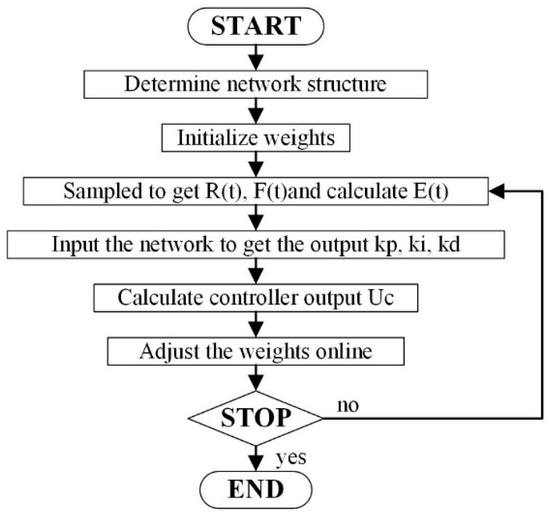
Figure 8. ANN1 training flowchart.

• Determine the structure of the BP neural network. The parameters of the neural network are listed in Table 1;
• Give the initial value of each layer’s weights;
• The input data R(t), F(t) is sampled, and the error E(t) is calculated;
• Calculate the input and output values of each layer of neurons, and the output values of the output layer are PID parameters $k_p, k_i,k_d$;
• Calculate the control voltage Uc(t) based on the incremental PID control algorithm;
• Perform online learning of neural networks, and adjust the weights of the hidden layers and the output layer;
• Return to Step 3 for the next round of training.

3.2. Smith Predictor

To optimize the response speed of the control system, the Smith predictor is added for predictive compensation. Its structure is shown in Figure 6, and the transfer function ${\mathrm{G}}_m\left(s\right)$ of the Smith predictor compensator is expressed as

$${\mathrm{G}}_m\left(s\right)={\mathrm{G}}_o\left(s\right)\left(1-e^{-\tau s}\right)$$

(19)

where ${\mathrm{G}}_o\left(s\right)·e^{-\tau s}$ is the open-loop transfer function of the controlled object considering the time delay.

When the Smith predictor is not added, the closed-loop transfer function of the system is

$$\mathrm{G}\left(s\right)=\frac{G_c\left(s\right)G_o\left(s\right)e^{-\tau s}}{1+G_c\left(s\right)G_o\left(s\right)e^{-\tau s}}$$

(20)

where $G_c\left(s\right)$ is the transfer function of the controller.

After adding the Smith predictor, the closed-loop transfer function of the system changes:

$$\mathrm{G}\left(s\right)=\frac{G_c\left(s\right)G_o\left(s\right)}{1+G_c\left(s\right)G_o\left(s\right)}{e}^{-\tau s}$$

(21)

By comparison of Equations (20) and (21), it can be found that the Smith predictor uses compensation to separate the pure time delay $e^{-\tau s}$ and G_o(s), which is equivalent to putting the pure time delay of the controlled object outside the control closed loop.

As the Smith predictor depends on the prior system model, a BP neural network shown in Figure 9 was used for identifying the system to improve modeling accuracy.

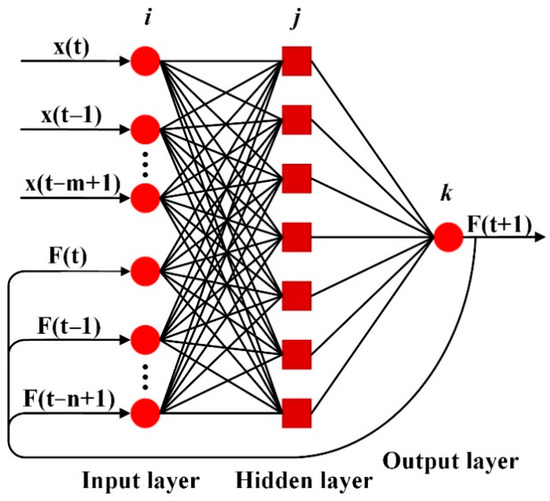
Figure 9. Schematic diagram of the neural network ANN2 structure, part of the BPNN-PID controller depicted in Figure 6.

The controlled object was a single-input single-output (SISO) nonlinear system, which can be described as follows:

$$F\left(t+1\right)=f\left[F\left(t\right),\dots ,F\left(t-n\right),U_c\left(t\right),\dots ,U_c\left(t-m\right)\right]$$

(22)

where F(t) and Uc(t) are the input and output of the object at time t, respectively; m and n mark the orders of F(t) and Uc (t), respectively; and $f[•]$ represents a nonlinear function.

The input $O_i^1\left(t\right)$ of the network is

$$O_i^1\left(t\right)=\{\begin{array}{c}{U}_c\left(t-i+1\right),0\le i\le m+1\\ F\left(t-i+m-2\right),m+2\le i\le m+n+2\end{array}$$

(23)

The output $ne{t}_k\left(t\right)$ is

$$ne{t}_k\left(t\right)=F\left(t+1\right)$$

(24)

The neural network ANN2 also used the BP algorithm, and its structural parameters were determined as shown in Table 2.

Table 2. Parameters of neural network ANN2.

Type	Value
learning type	Offline
Learning rate ($\eta$)	0.3
Inertia index ($\mathsf{\alpha }$)	0.15
Number of hidden layer neurons	15
Hidden layer activation function	tanh
Output layer activation function	tanh
Initialization weight method	0.03rands (n, 1)
Time orders m,n	4

The neural network ANN2 was trained offline. As Figure 10 shows, the main training steps of the neural network ANN2 are listed as follows:

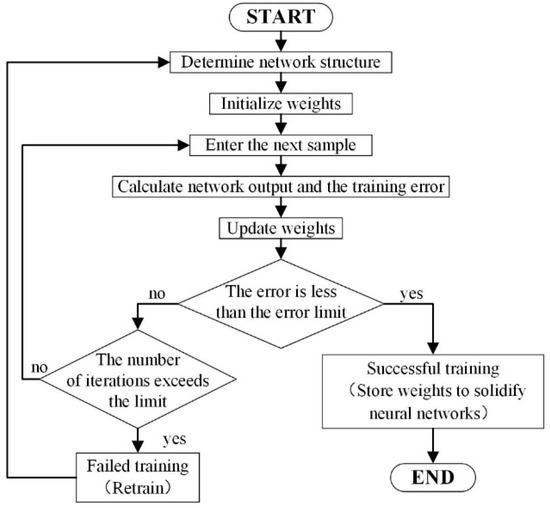
Figure 10. ANN2 training flowchart.

• Determine the structure of the neural network, including the number of hidden layers, neuron activation functions and training samples;
• Take a small initial value for the weight;
• Import samples for training;
• Calculate the input and output of each layer of neurons;
• For each iteration, calculate the weight adjustment of the hidden layer and the output layer;
• Check whether the network training error is less than the error tolerance. If it meets the requirements, go to Step 7, and if not, go to Step 8;
• Solidify and save each weight. The training is successful, and you can call it through Labview or MATLAB Simulink;
• Check whether the current iteration number exceeds the upper limit. If not, return to Step 3 for further training; otherwise, the training failed. Return to Step 1 to restart training.

4. Results and Discussion

In this section, the performance of the proposed BPNN-SP-PID method is validated through simulation and experiments. First, according to the mathematical model deduced in Section 2, a simulation block diagram of the system was built in MATLAB Simulink. Three types of controllers (PID, BPNN-PID and BPNN-SP-PID) were tested and compared. Then, an experimental prototype was built, and the force response curves under step input and sinusoid input were collected. Finally, a comprehensive discussion was made based on the results of the simulation and experiment.

4.1. Simulation Results

In the block diagram shown in Figure 11, ANN2 is a neural network that describes the controlled object. It was trained and solidified to generate a Simulink module and added to the block diagram. The inside of the BPNN-PID structure was the packed neural network ANN1 and a PID controller. The online learning neural network ANN1 was realized by using the S-function module. There were two kinds of input signals as the setting force: a step signal with an amplitude of 20 N and a sin signal with an amplitude of 20 N and frequency of 0.2 Hz. The simulation data of the three controllers were exported through the simout module.

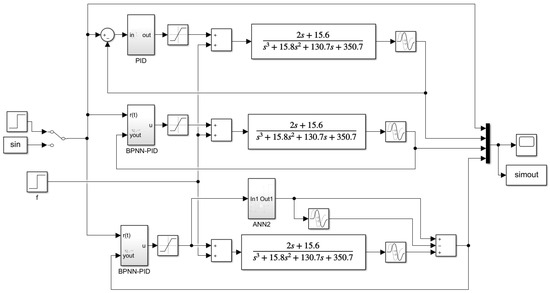
Figure 11. MATLAB Simulink simulation block diagram.

4.1.1. Step Response

The response curve under step signal input with an amplitude of 20 N is shown in Figure 12.

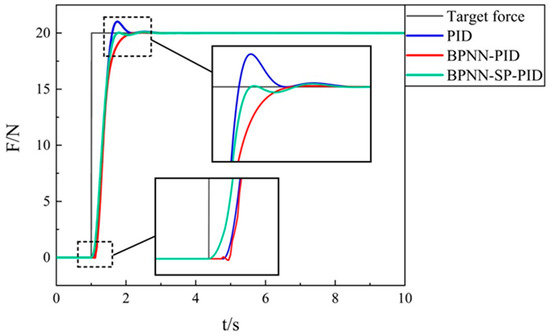
Figure 12. Comparison of step responses of the three controllers in the simulation.

All three controllers could make the output response meet the target values. However, there were differences at the beginning stage and the approaching stage. At the beginning stage, the BPNN-SP-PID controller acted first, and the reaction time was almost zero. The action time of BPNN-PID and PID was almost the same, taking ~80 ms to start the action. At the approaching stage, the PID method produced the largest overshoot of 6.1% among the three, and the overshoots of BPNN-PID and BPNN-SP-PID were 0.45% and 0.15%, respectively. At the stable stage, the residuals of the three were all close to zero due to the integral part of the PID controller.

By comparison of the three response curves, two phenomena could be observed. First, the use of a BPNN greatly enhanced the robustness of the system. Due to the self-adjusting ability of neural networks, the approaching processes of BPNN-PID and BPNN-SP-PID were more stable than PID, and there was almost no overshoot or oscillation. Second, the application of the Smith predictor could significantly improve the speed. Though BPNN-PID and BPNN-SP-PID showed good robustness, BPNN-SP-PID had a much faster reaction than BPNN-PID, especially at the beginning stage. This was mainly because the Smith predictor based on ANN2 could fit the system model precisely, resulting in a compensation for the inherent time delay of the system.

4.1.2. Sinusoid Track

A sinusoidal signal with an amplitude of 20 N and frequency of 0.2 Hz was set for the simulation, and the response curves of the three controllers were obtained, as shown in Figure 13.

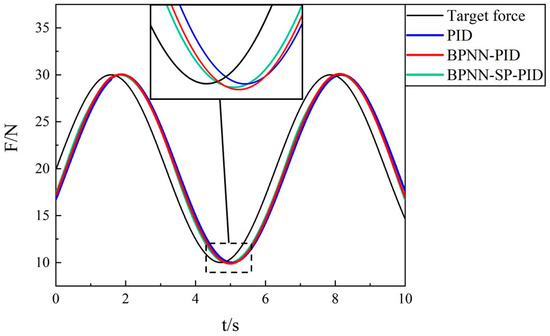
Figure 13. Comparison of sinusoid tracking response curves in the simulation.

All three controllers could smoothly follow the setting curve but had different degrees of lag. BPNN-SP-PID produced the smallest lag, followed by BPNN-PID, and the worst was from the PID method. The difference in response time also brought about a difference in control accuracy. The maximum force error of PID reached 3.22 N, and the average error reached 2.09 N. The maximum error of BPNN-PID was 2.65 N, and the average error was 1.68 N. The maximum error of BPNN-SP-PID was 2.63 N, and the average error was 1.59 N.

It can be seen that the BPNN-SP-PID controller had the best dynamic adjustment performance among the three controllers.

4.2. Experimental Validation

A prototype of the compliant constant-force actuator was built and mounted on the robot ABB 1200 for the experiment as shown in Figure 14. The whole experimental platform mainly included an air compressor, a control cabinet, a robot, a computer and the constant-force actuator prototype. The DAQ board (Zhongtai USB7660BD) in the control cabinet was used for signal input and output. The control and data acquisition program on the host computer was programmed through Labview, shown in Figure 15. The practical application of the BPNN-SP-PID controller in this system was completed by the joint compilation of Labview and MATLAB [31,32]. In order to reduce the influence of the posture and the surface shape of the workpiece, the posture of the robot arm was kept vertical during the entire experiment, and a flat steel plate was selected as the workpiece.

Figure 14. Schematic diagram of the experimental platform.

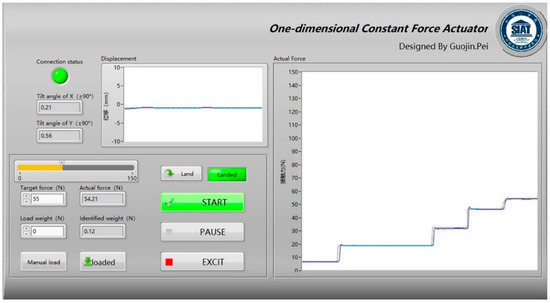
Figure 15. Software interface diagram in Labview.

4.2.1. Step Response

When the input was a step signal with an amplitude of 20 N, the response curve of the output force obtained was as shown in Figure 16.

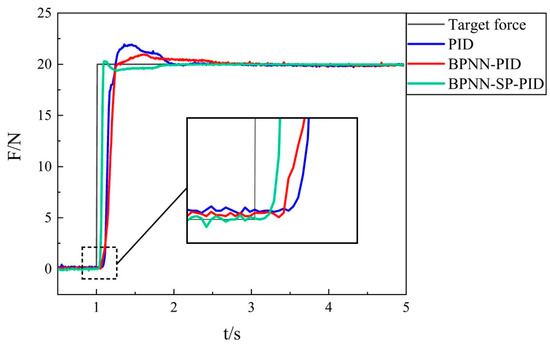
Figure 16. Comparison of the step responses of three controllers in the experiment.

The experimental results coincided with the simulation results. The BPNN-SP-PID controller was the fastest at the beginning stage, which needed ~30 ms of action time, while BPNN-PID and PID took ~70 ms and ~80 ms, respectively. At the approaching stage, BPNN-SP-PID was still the fastest to reach the set value of 20 N and to enter the ideal range. The adjustment times of the BPNN-SP-PID, BPNN-PID and PID were 0.16 s, 0.46 s and 0.48 s, respectively. The three controllers also presented different degrees of overshoot. The overshoot of BPNN-SP-PID was the smallest, being only 1.6%, while the overshoots of BPNN-PID and PID were 4.9% and 9.7%, respectively. At the stable stage, the residuals of the three were different from the ideal scenario in the simulation, but the steady state error could also be guaranteed to be within 0.2 N.

By comparison with Section 4.1.1, it can be found that the experimental results were a bit worse than the simulation due to the influence of uncontrollable nonlinear factors under the actual experiment. BPNN-SP-PID still presented the best performance among the three controllers in the experiment, which could significantly improve the reaction speed while maintaining stability.

4.2.2. Sinusoid Track

The input was then changed to the sinusoidal signal with an amplitude of 20 N and frequency of 0.2 Hz, and the response curve is shown in Figure 17. The data collection rate was 1 sampling/10 ms, and the total number of samples was 900 in 9 s. The error data between the set value and the actual value collected in Figure 17a was calculated and statistically analyzed, and the probability distribution of the 900 error data within ±3 N is shown in Figure 17b.

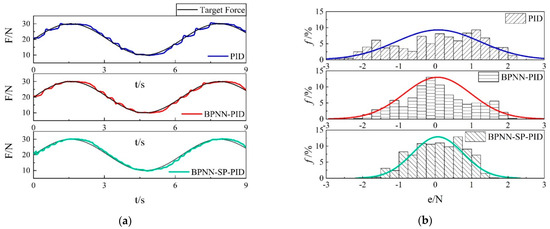
Figure 17. Comparison of actual sinusoid tracking response curves in the experiment. (a) Response curves of the three controllers. (b) Histogram of the tracking errors.

The sinusoid curve tracking in the experiment was not as smooth as that in the simulation (Figure 13), and the response curve fluctuated up and down around the target curve. Among the three controllers, the BPNN-SP-PID gave the smoothest response and the smallest fluctuation. The maximum error was 1.88 N, and the average error was only 0.68 N. Meanwhile, the maximum errors of the BPNN-PID and PID controllers were both above 2 N, and the average errors reached 0.74 N and 0.98 N, respectively. The force control accuracy was expected to be ±1 N in some robot contact operations, such as robot grinding, and BPNN-SP-PID could meet the requirements well.

According to the histogram of the tracking errors, it can be seen that the error distribution of BPNN-SP-PID was concentrated around zero, showing better precision than the other two controllers. The addition of the neural network and Smith predictor made the control system more robust and quicker, resulting in a reduction of the tracking error.

4.3. Discussion

The specific indicators [33] of the three controllers are listed in Table 3.

Table 3. Comparison of overall performance indicators of three controllers.

	Performance Indicators of Three Controllers
Type	PID	BPNN-PID	BPNN-SP-PID
Simulation
Step response
Steady-state error (N)	~0	~0	~0
Settling time1 (s)	0.76	0.76	0.59
Maximum overshoot (%)	6.10	0.45	0.15
Sinusoid track
Maximum error (N)	3.22	2.65	2.63
Average error (N)	2.09	1.68	1.59
Experiment
Step response
Steady-state error (N)	0.18	0.12	0.12
Settling time1 (s)	0.48	0.46	0.16
Maximum overshoot (%)	9.70	4.90	1.56
Sinusoid track
Maximum error (N)	2.70	2.06	1.88
Average error (N)	0.98	0.74	0.68

¹ The minimum time required for the system response to reach and maintain a value within 5% of the final value.

It can be learned that there were some gaps between the experiment and simulation results. First, the steady state error in the experiment could not be ignored like that in the simulation because of the environmental noise, the sensor error and other nonlinear factors (such as the motion of the robot, air source instability and cylinder friction). Second, some indicators in the experiment, such as the settling time and the errors of the sinusoid track, were even better than those in the simulation. This was mainly because the simulation started from the linear approximation model, while the experimental model was estimated through experimental data. Despite this, the simulation and experiment results both showed the same result: the BPNN-SP-PID had the best performance among the three controllers.

BPNN-SP-PID and BPNN-PID were obviously better than traditional PID, as the BPNN could adaptively adjust the PID parameters when dealing with the influence of nonlinear factors. The indicator of the maximum overshoot proved that BPNN-SP-PID had the best robustness. On the other hand, it is interesting to find that the performance gap between BPNN-SP-PID and BPNN-PID was different in the step response and sinusoid track. In the case of the step response, the BPNN-SP-PID showed a huge improvement compared with BPNN-PID. The maximum overshoot and settling time of BPNN-SP-PID were reduced by 68% and 65% in the experiment, respectively. In the case of the sinusoid track, however, the BPNN-SP-PID was just a litter better than the BPNN-PID controller. The maximum error and average error of the BPNN-SP-PID were only reduced by 9% and 8% in the experiment, respectively. The reason for this was probably that the setting force in the sinusoid track process was time-varying, which would partially affect the fitting precision of the Smith predictor and weaken the effect of it. A potential solution is adding a neural network identifier to update the ANN2 to further enhance the matching degree of the theoretical model and the actual one.

5. Conclusions

Aiming at the nonlinearity and time delay of pneumatic constant force actuators, this paper proposes an improved PID control method combining a BPNN and the Smith predictor. An on-line BPNN ANN1 is used for adjusting the PID coefficients intelligently, which can enhance the robustness of a nonlinear system. The Smith predictor, with the aid of off-line neutral network ANN2, compensates the pure time delay, which can improve the adjustment speed of the system. The simulation and experiment results both showed that the BPNN-SP-PID control method was feasible and superior compared with the traditional PID controller.

The matching error between the theoretical model and the actual model is concerned with the control performance. In a simulation, Smith predictor can compensate almost all of the time delay. In practical applications, the posture of the actuator is time-varying, and the system model will also change accordingly. As the offline ANN2 cannot fully fit the time-varying nonlinear system, the time delay compensation effect is not as good as that found in simulation. Adding a neural network identifier to update ANN2 will be beneficial for identifying the actual model in time so that the adaptability of the controller will be stronger. This will be the focus of future work.