Analysis of Volcanic Thermohaline Fluctuations of Tagoro Submarine Volcano (El Hierro Island, Canary Islands, Spain)
Abstract
:1. Introduction
2. Materials and Methods
- Construction of N/10 new time series each of length . The new time series, , contains the absolute change between two values of the original series that are set apart by Δ, so that for and for with m = 1, 2, ..., N/10 where and define the minimum and maximum time lags.
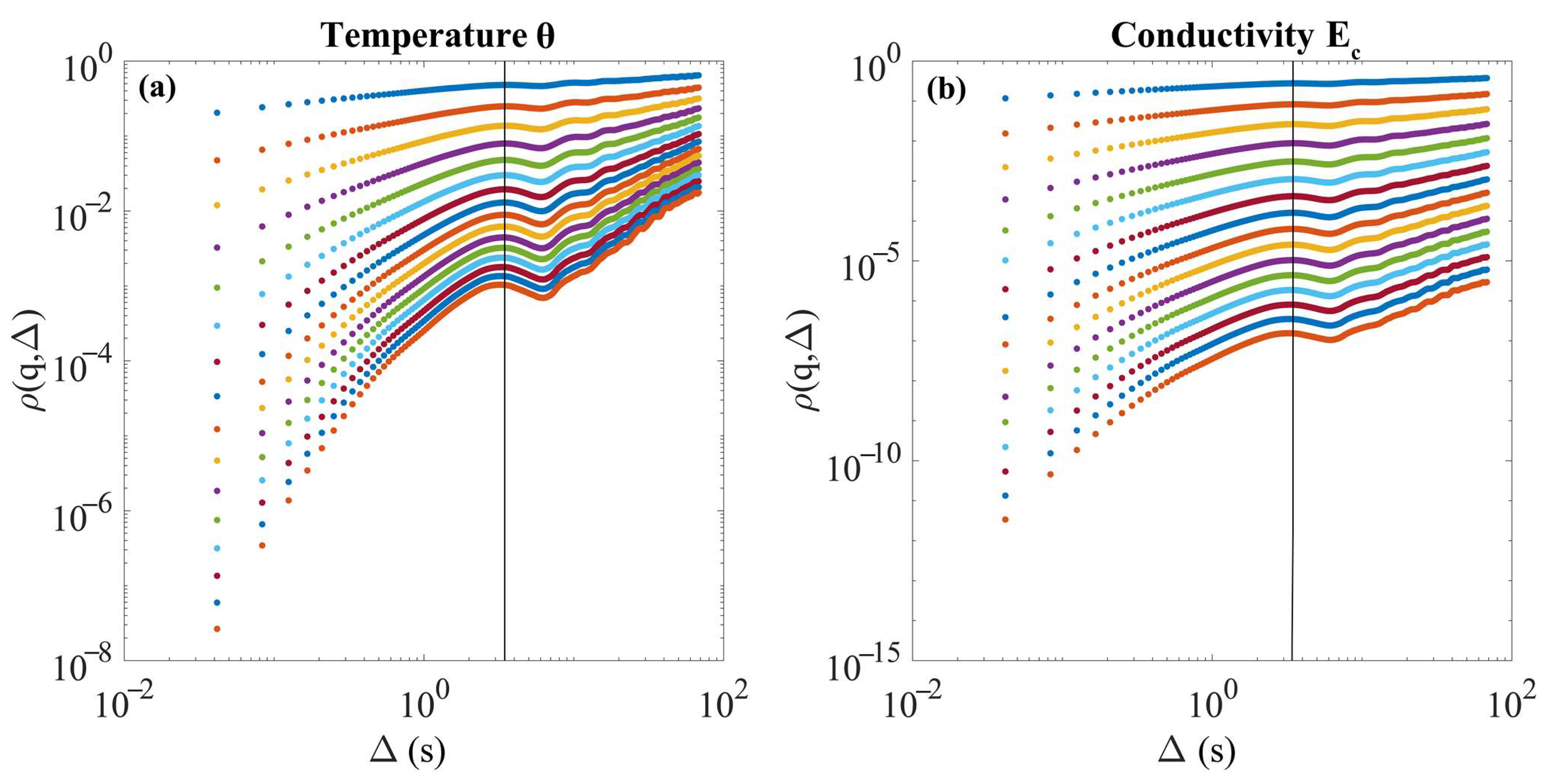
- Estimation of the statistical moments, order of q, for each one of the new time series, , is carried out according to:where only positive moments, are taken into account. Moments between 0 < q ≤ 2 are responsible for the core of the probability density function (pdf), while moments q > 2 contribute to the tails of the pdf (Bakalis et al., 2017 and the references therein).
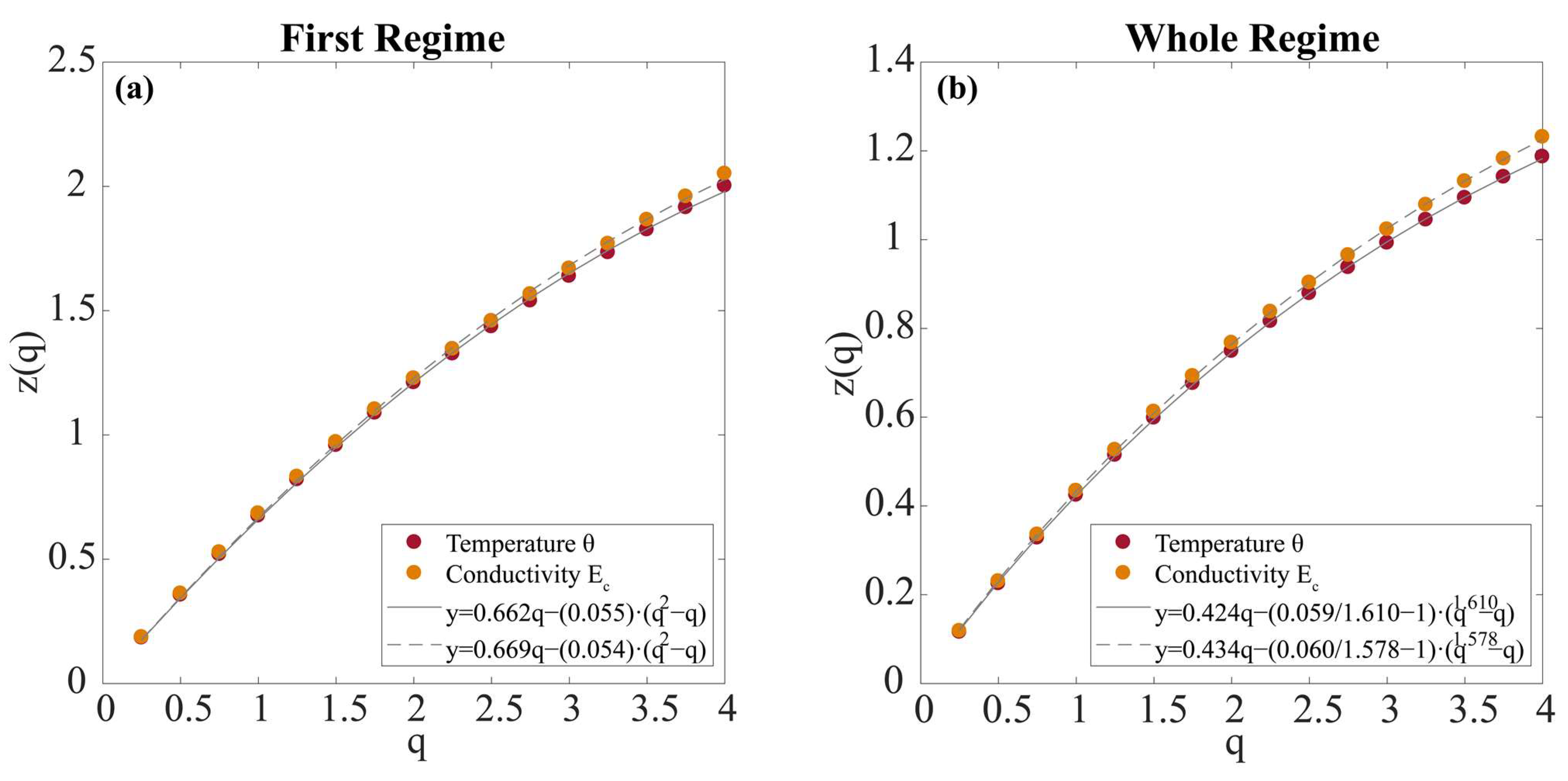
- The moments will scale according to:where is the structure function and its shape gives information about the stochastic mechanisms that govern the process. When the structure function fits a linear form, that is, , then there is a direct relation between the scaling exponent γ of Equation (1) and the Hurst exponent, H, , being the process characterised as monofractal. The parameter H is the mean fluctuating scaling exponent. For the process is anti-persistent (sub-normal), normal for , and super-normal or persistent for . If presents any convex shape, then the process is multifractal. Among multifractals, universal multifractals are ubiquitous, and their structure function reads [31]:where the Lévy index, , 0 ≤ ≤ 2, indicates the class to which the probability distribution belongs and shows how fast the inhomogeneity rises. Inhomogeneity refers to the degree of mixing of various stochastic mechanisms shaping the final process. For = 0, , the process is monofractal, and the field homogeneous. For = 1, , the process draws steps from a Cauchy–Lorentz distribution. For = 2, , the process is the multiplication of two random processes and is described by a log-normal or Kolmogorov distribution. For 1 < < 2, the multifractal character is the multiplicative result of more than two random processes. Finally, C is the intermittency parameter that measures the mean inhomogeneity of the field and always takes positive values.
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Edmond, J.M.; Von Damm, K.L.; McDuff, R.E.; Measures, C.I. Chemistry of hot springs on the East Pacific Rise and their effluent dispersal. Nat. Cell Biol. 1982, 297, 187–191. [Google Scholar] [CrossRef]
- Baker, E.T.; Massoth, G.J.; Walker, S.L.; Embley, R.W. A method for quantitatively estimating diffuse and discrete hydrothermal discharge. Earth Planet. Sci. Lett. 1993, 118, 235–249. [Google Scholar] [CrossRef]
- Speer, K.G.; Rona, P.A. A model of an Atlantic and Pacific hydrothermal plume. J. Geophys. Res. Space Phys. 1989, 94, 6213–6220. [Google Scholar] [CrossRef]
- Speer, K.G. A forced baroclinic vortex around a hydrothermal plume. Geophys. Res. Lett. 1989, 16, 461–464. [Google Scholar] [CrossRef]
- Fiasconaro, A.; Valenti, D.; Spagnolo, B. Noise in ecosystems: A short review. Math. Biosci. Eng. 2004, 1, 185–211. [Google Scholar] [CrossRef] [PubMed]
- Bakalis, E.; Mertzimekis, T.J.; Nomikou, P.; Zerbetto, F. Breathing modes of Kolumbo submarine volcano (Santorini, Greece). Sci. Rep. 2017, 7, 46515. [Google Scholar] [CrossRef] [Green Version]
- Bakalis, E.; Mertzimekis, T.J.; Nomikou, P.; Zerbetto, F. Temperature and Conductivity as Indicators of the Morphology and Activity of a Submarine Volcano: Avyssos (Nisyros) in the South Aegean Sea, Greece. Geosciences 2018, 8, 193. [Google Scholar] [CrossRef] [Green Version]
- Fraile-Nuez, E.; Santana-Casiano, J.M.; González-Dávila, M.; Vázquez, J.T.; Fernández-Salas, L.M.; Sánchez-Guillamón, O.; Palomino, D.; Presas-Navarro, C. Cyclic Behavior Associated with the Degassing Process at the Shallow Submarine Volcano Tagoro, Canary Islands, Spain. Geosciences 2018, 8, 457. [Google Scholar] [CrossRef] [Green Version]
- Carracedo, J.-C. The Canary Islands: An example of structural control on the growth of large oceanic-island volcanoes. J. Volcanol. Geotherm. Res. 1994, 60, 225–241. [Google Scholar] [CrossRef]
- Carracedo, J.C.; Day, S.; Guillou, H.; Badiola, E.R.; Canas, J.A.; Perez-Torrado, F.J. Hotspot volcanism close to a passive continental margin: The Canary Islands. Geol. Mag. 1998, 135, 591–604. [Google Scholar] [CrossRef] [Green Version]
- Nuez, E.F.; Gonzalez-Davila, M.; Casiano, J.M.S.; Arístegui, J.; Alonso-González, I.J.; Hernández-León, S.; Blanco, M.J.; Rodriguez-Santana, A.; Hernández-Guerra, A.; Gelado-Caballero, M.; et al. The submarine volcano eruption at the island of El Hierro: Physical-chemical perturbation and biological response. Sci. Rep. 2012, 2, 486. [Google Scholar] [CrossRef] [Green Version]
- Santana-Casiano, J.M.; Gonzalez-Davila, M.; Nuez, E.F.; De Armas, D.; González, A.G.; Domínguez-Yanes, J.F.; Escánez, J. The natural ocean acidification and fertilization event caused by the submarine eruption of El Hierro. Sci. Rep. 2013, 3, srep01140. [Google Scholar] [CrossRef]
- Resing, J.; Baker, E.T.; Lupton, J.E.; Walker, S.L.; Butterfield, D.; Massoth, G.J.; Nakamura, K.-I. Chemistry of hydrothermal plumes above submarine volcanoes of the Mariana Arc. Geochem. Geophys. Geosyst. 2009, 10, 1–23. [Google Scholar] [CrossRef]
- Hawkes, J.A.; Connelly, D.P.; Rijkenberg, M.J.A.; Achterberg, E.P. The importance of shallow hydrothermal island arc systems in ocean biogeochemistry. Geophys. Res. Lett. 2014, 41, 942–947. [Google Scholar] [CrossRef] [Green Version]
- Rivera, J.; Lastras, G.; Canals, M.; Acosta, J.; Arrese-González, B.; Hermida-Jiménez, N.; Micallef, A.; Tello-Antón, M.; Amblas, D. Construction of an oceanic island: Insights from the El Hierro (Canary Islands) 2011–2012 submarine volcanic eruption. Geology 2013, 41, 355–358. [Google Scholar] [CrossRef]
- Ariza, A.; Kaartvedt, S.; Røstad, A.; Garijo, J.C.; Arístegui, J.; Fraile-Nuez, E.; Hernández-León, S. The Submarine Volcano Eruption off El Hierro Island: Effects on the Scattering Migrant Biota and the Evolution of the Pelagic Communities. PLoS ONE 2014, 9, e102354. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coca, J.; Ohde, T.; Redondo, A.; García-Weil, L.; Santana-Casiano, M.; González-Dávila, M.; Arístegui, J.; Nuez, E.F.; Ramos, A.G. Remote sensing of the El Hierro submarine volcanic eruption plume. Int. J. Remote Sens. 2014, 35, 6573–6598. [Google Scholar] [CrossRef] [Green Version]
- Eugenio, F.; Martin, J.; Marcello, J.; Fraile-Nuez, E. Environmental monitoring of El Hierro Island submarine volcano, by combining low and high resolution satellite imagery. Int. J. Appl. Earth Obs. Geoinf. 2014, 29, 53–66. [Google Scholar] [CrossRef]
- Blanco, M.J.; Fraile-Nuez, E.; Felpeto, A.; Santana-Casiano, J.M.; Abella, R.; Fernández-Salas, L.M.; Almendros, J.; Díaz-del-Río, V.; Domínguez Cerdeña, I.; García-Cañada, L.; et al. Comment on “Evidence from acoustic imaging for submarine volcanic activity in 2012 off the west coast of El Hierro (Canary Islands, Spain)” by Pérez, N.M.; Somoza, L.; Hernández, P.A.; González de Vallejo, L.; León, R.; Sagiya, T.; Biain, A.; González, F.J.; Medialdea, T.; Barrancos, J.; Ibáñez, J.; Sumino, H.; Nogami, K.; Romero, C. (2014). Bull. Volcanol. 2015, 76, 882–896. [Google Scholar] [CrossRef]
- Ferrera, I.; Arístegui, J.; Gonzalez, J.; Montero, M.F.; Fraile-Nuez, E.; Gasol, J.M. Transient Changes in Bacterioplankton Communities Induced by the Submarine Volcanic Eruption of El Hierro (Canary Islands). PLoS ONE 2015, 10, e0118136. [Google Scholar] [CrossRef]
- Santana-Casiano, J.M.; Nuez, E.F.; Gonzalez-Davila, M.; Baker, E.T.; Resing, J.; Walker, S.L. Significant discharge of CO2 from hydrothermalism associated with the submarine volcano of El Hierro Island. Sci. Rep. 2016, 6, 25686. [Google Scholar] [CrossRef] [PubMed]
- Danovaro, R.; Canals, M.; Tangherlini, M.; Dell’Anno, A.; Gambi, C.; Lastras, G.; Amblas, D.; Sanchez-Vidal, A.; Frigola, J.; Calafat, A.; et al. A submarine volcanic eruption leads to a novel microbial habitat. Nat. Ecol. Evol. 2017, 1, 144. [Google Scholar] [CrossRef] [PubMed]
- Santana-González, C.; Santana-Casiano, J.M.; González-Dávila, M.; Fraile-Nuez, E. Emissions of Fe(II) and its kinetic of oxidation at Tagoro submarine volcano, El Hierro. Mar. Chem. 2017, 195, 129–137. [Google Scholar] [CrossRef]
- Álvarez-Valero, A.; Burgess, R.; Recio, C.; de Matos, V.; Guillamón, O.S.; Gómez-Ballesteros, M.; Recio, G.; Nuez, E.F.; Sumino, H.; Flores, J.; et al. Noble gas signals in corals predict submarine volcanic eruptions. Chem. Geol. 2018, 480, 28–34. [Google Scholar] [CrossRef] [Green Version]
- Santana-Casiano, J.M.; González-Dávila, M.; Fraile-Nuez, E. The Emissions of the Tagoro Submarine Volcano (Canary Islands, Atlantic Ocean): Effects on the Physical and Chemical Properties of the Seawater. In Volcanoes: Geological and Geophysical Setting, Theoretical Aspects and Numerical Modeling, Applications to Industry and Their Impact on the Human Health; IntechOpen: London, UK, 2018; Volume 53. [Google Scholar] [CrossRef] [Green Version]
- Sotomayor-García, A.; Rueda, J.L.; Sánchez-Guillamón, O.; Urra, J.; Vázquez, J.T.; Palomino, D.; Fernández-Salas, L.M.; López-González, N.; González-Porto, M.; Santana-Casiano, J.M.; et al. First Macro-Colonizers and Survivors Around Tagoro Submarine Volcano, Canary Islands, Spain. Geosciences 2019, 9, 52. [Google Scholar] [CrossRef] [Green Version]
- González-Vega, A.; Fraile-Nuez, E.; Santana-Casiano, J.M.; González-Dávila, M.; Escánez-Pérez, J.; Gómez-Ballesteros, M.; Tello, O.; Arrieta, J.M. Significant Release of Dissolved Inorganic Nutrients from the Shallow Submarine Volcano Tagoro (Canary Islands) Based on Seven-Year Monitoring. Front. Mar. Sci. 2020, 6, 829. [Google Scholar] [CrossRef] [Green Version]
- Sotomayor-Garcia, A.; Rueda, J.L.; Sánchez-Guillamón, O.; Vázquez, J.T.; Palomino, D.; Fernández-Salas, L.M.; Lopez-Gonzalez, N.; González-Porto, M.; Urra, J.; Santana-Casiano, J.M.; et al. Geomorphic features, main habitats and associated biota on and around the newly formed Tagoro submarine volcano, Canary Islands. In GeoHab Atlas of Seafloor Geomorphic Features and Benthic Habitats; Elsevier: Amsterdam, The Netherlands, 2020; Volume 51, pp. 835–846. [Google Scholar] [CrossRef]
- Wang, B.; Anthony, S.; Bae, S.C.; Granick, S. Anomalous yet Brownian. Proc. Natl. Acad. Sci. USA 2009, 106, 15160–15164. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Metzler, R.; Klafter, J. The restaurant at the end of the random walk: Recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A Math. Gen. 2004, 37, R161–R208. [Google Scholar] [CrossRef]
- Moss, M.E.; Bárdossy, A.; Kotwicki, V.; Strupczewski, W.G.; Mitosek, H.T.; Lian, G.S.; Kemblowski, M.W.; Wen, J.-C.; Lovejoy, S.; Schertzer, D.; et al. New Uncertainty Concepts in Hydrology and Water Resources; Cambridge University Press: Cambridge, UK, 1995; Volume 270, pp. 61–103. [Google Scholar]
- Spagnolo, B.; Dubkov, A.A.; Agudov, N.V. Enhancement of stability in randomly switching potential with metastable state. Eur. Phys. J. B 2004, 40, 273–281. [Google Scholar] [CrossRef] [Green Version]
- Giuffrida, A.; Valenti, D.; Ziino, G.; Spagnolo, B.; Panebianco, A. A stochastic interspecific competition model to predict the behaviour of Listeria monocytogenes in the fermentation process of a traditional Sicilian salami. Eur. Food Res. Technol. 2009, 228, 767–775. [Google Scholar] [CrossRef] [Green Version]
- Biro, T.; Jakovác, A. Power-Law Tails from Multiplicative Noise. Phys. Rev. Lett. 2005, 94, 132302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Caruso, A.; Gargano, M.E.; Valenti, D.; Fiasconaro, A.; Spagnolo, B. Cyclic fluctuations, climatic changes and role of noise in planktonic foraminifera in the mediterranean sea. Fluct. Noise Lett. 2005, 5, L349–L355. [Google Scholar] [CrossRef] [Green Version]
- Longpré, M.-A.; Stix, J.; Klügel, A.; Shimizu, N. Mantle to surface degassing of carbon- and sulphur-rich alkaline magma at El Hierro, Canary Islands. Earth Planet. Sci. Lett. 2017, 460, 268–280. [Google Scholar] [CrossRef] [Green Version]
- Anteneodo, C.; Riera, R. Additive-multiplicative stochastic models of financial mean-reverting processes. Phys. Rev. E 2005, 72, 026106. [Google Scholar] [CrossRef] [Green Version]
- West, B.J. Colloquium: Fractional calculus view of complexity: A tutorial. Rev. Mod. Phys. 2014, 86, 1169–1186. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Ciuchi, S.; de Pasquale, F.; Spagnolo, B. Nonlinear relaxation in the presence of an absorbing barrier. Phys. Rev. E 1993, 47, 3915–3926. [Google Scholar] [CrossRef]
- Ciuchi, S.; de Pasquale, F.; Spagnolo, B. Self-regulation mechanism of an ecosystem in a non-Gaussian fluctuation regime. Phys. Rev. E 1996, 54, 706–716. [Google Scholar] [CrossRef]
- Spagnolo, B.; La Barbera, A. Role of the noise on the transient dynamics of an ecosystem of interacting species. Phys. A Stat. Mech. Appl. 2002, 315, 114–124. [Google Scholar] [CrossRef]
- Peng, C.-K.; Buldyrev, S.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef] [Green Version]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef] [Green Version]
- Scafetta, N.; Grigolini, P. Scaling detection in time series: Diffusion entropy analysis. Phys. Rev. E 2002, 66, 036130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hurst, H.E. Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Hübscher, C.; Ruhnau, M.; Nomikou, P. Volcano-tectonic evolution of the polygenetic Kolumbo submarine volcano/Santorini (Aegean Sea). J. Volcanol. Geotherm. Res. 2015, 291, 101–111. [Google Scholar] [CrossRef]
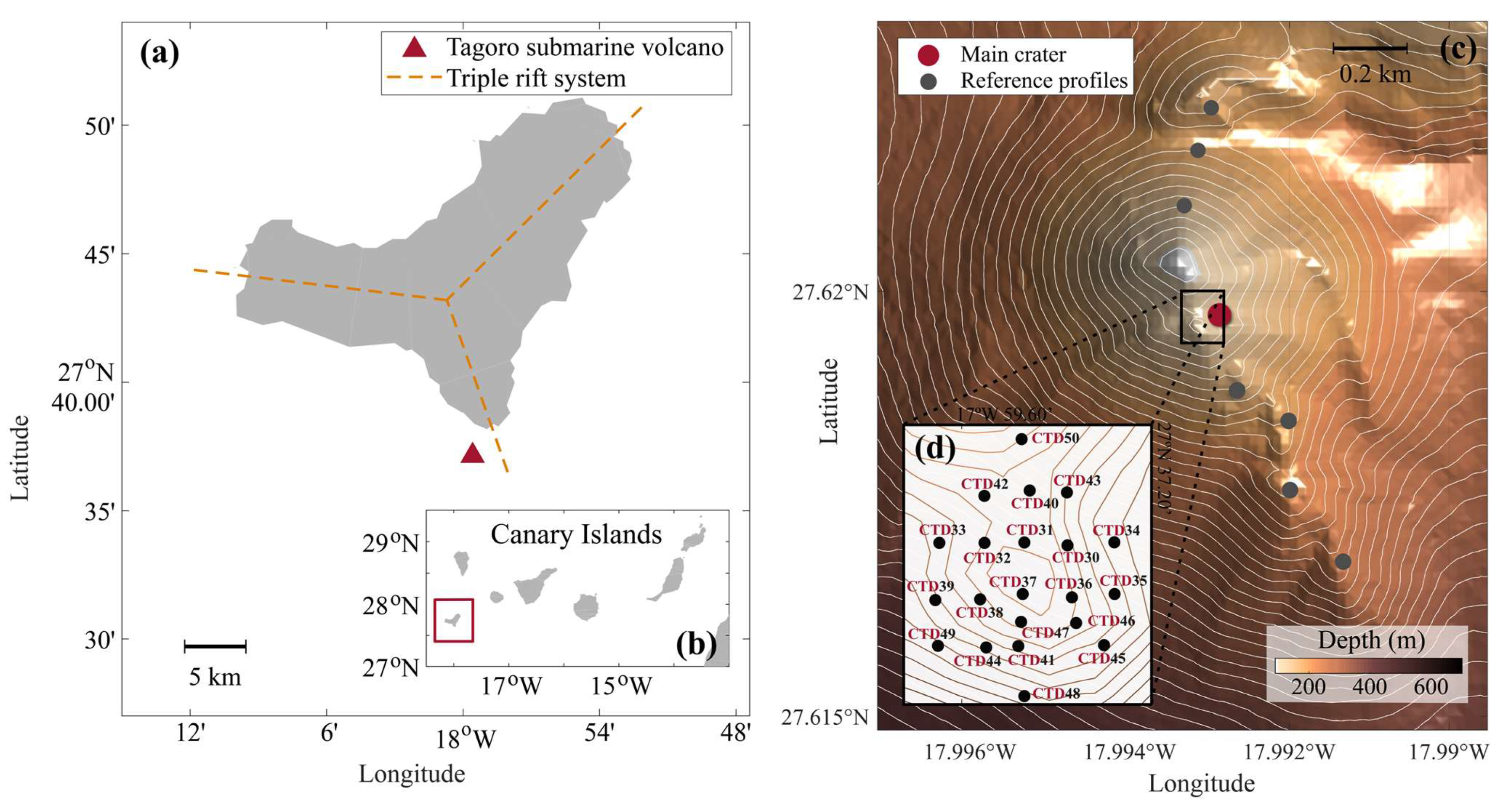
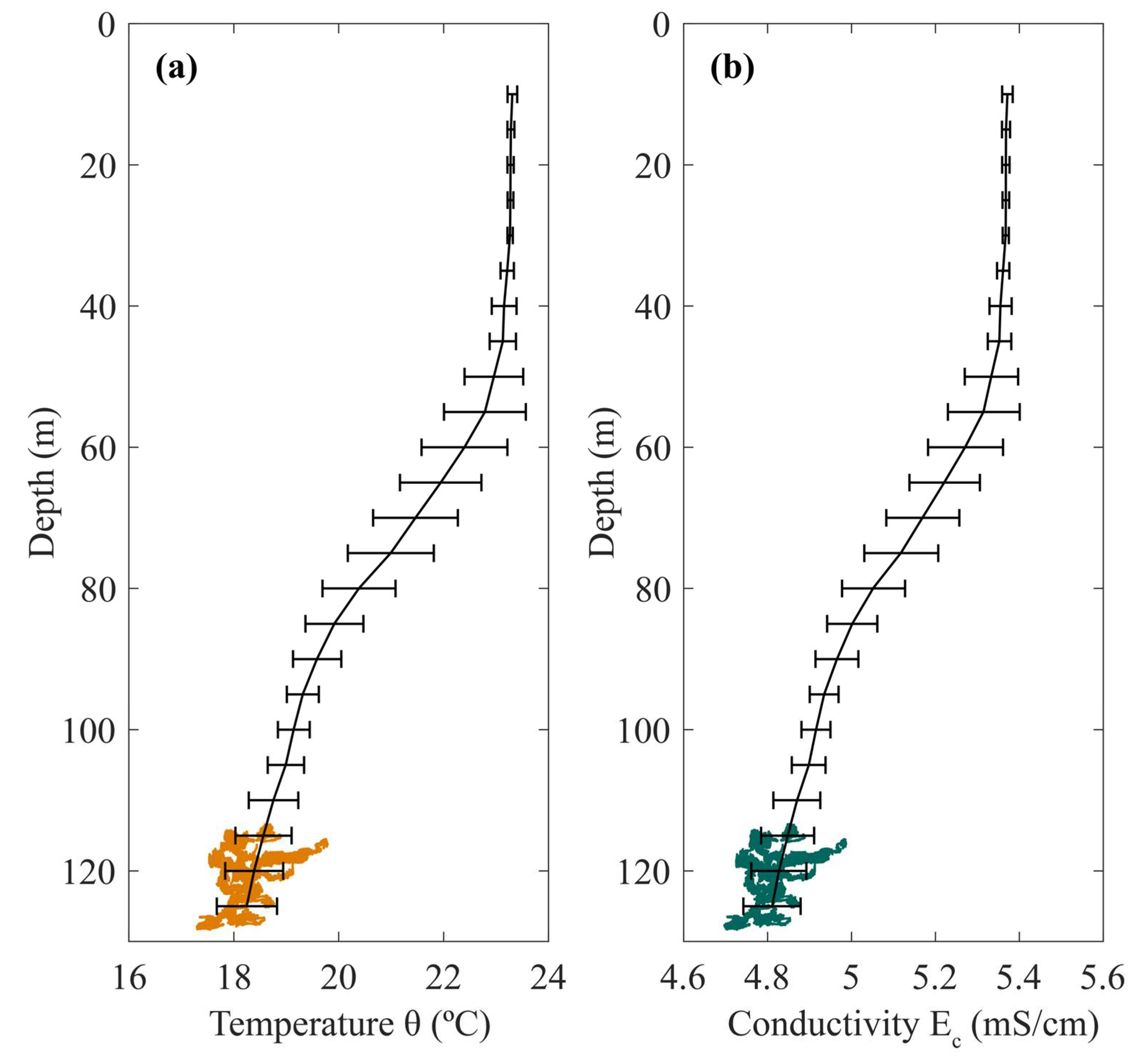
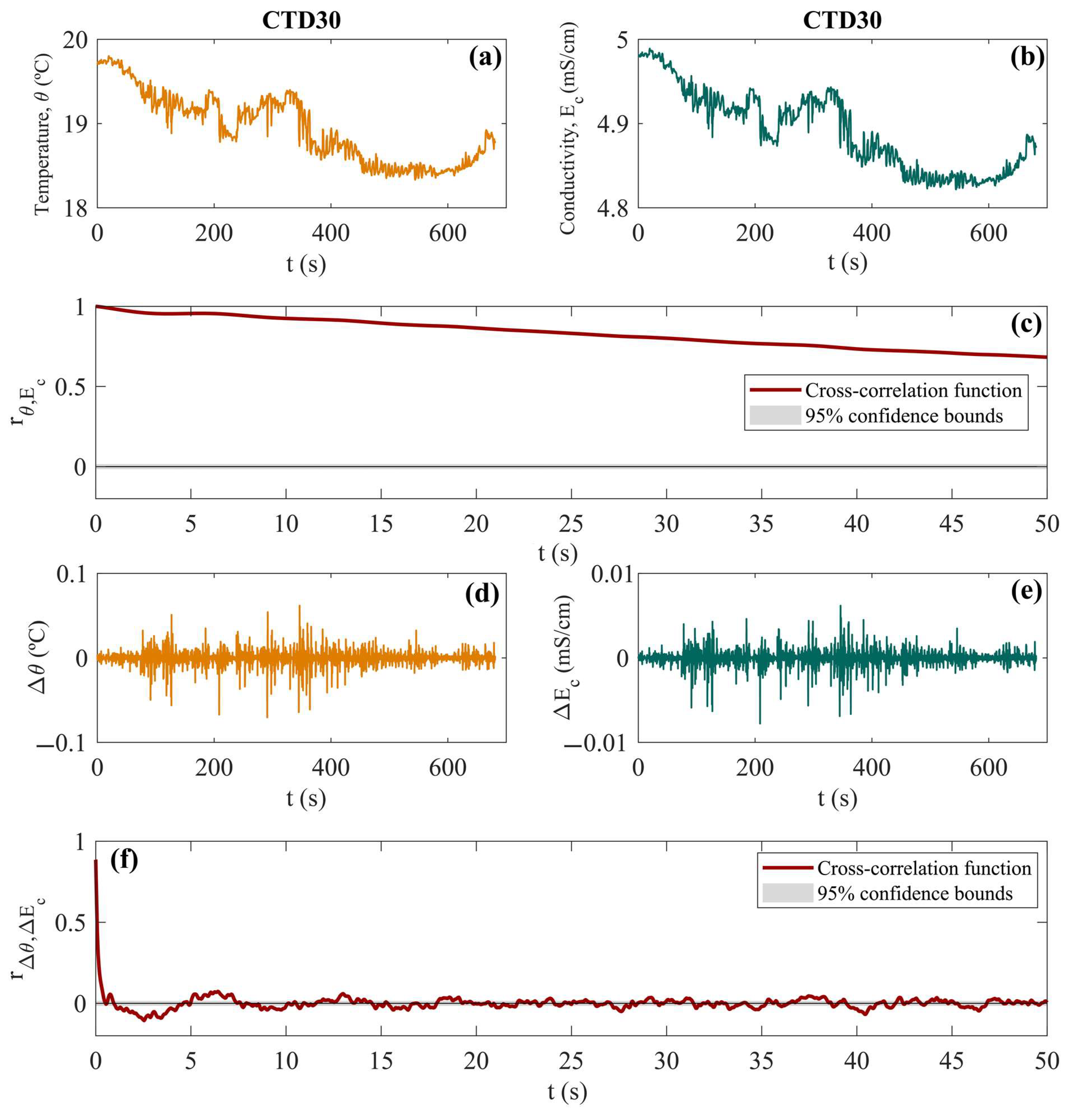
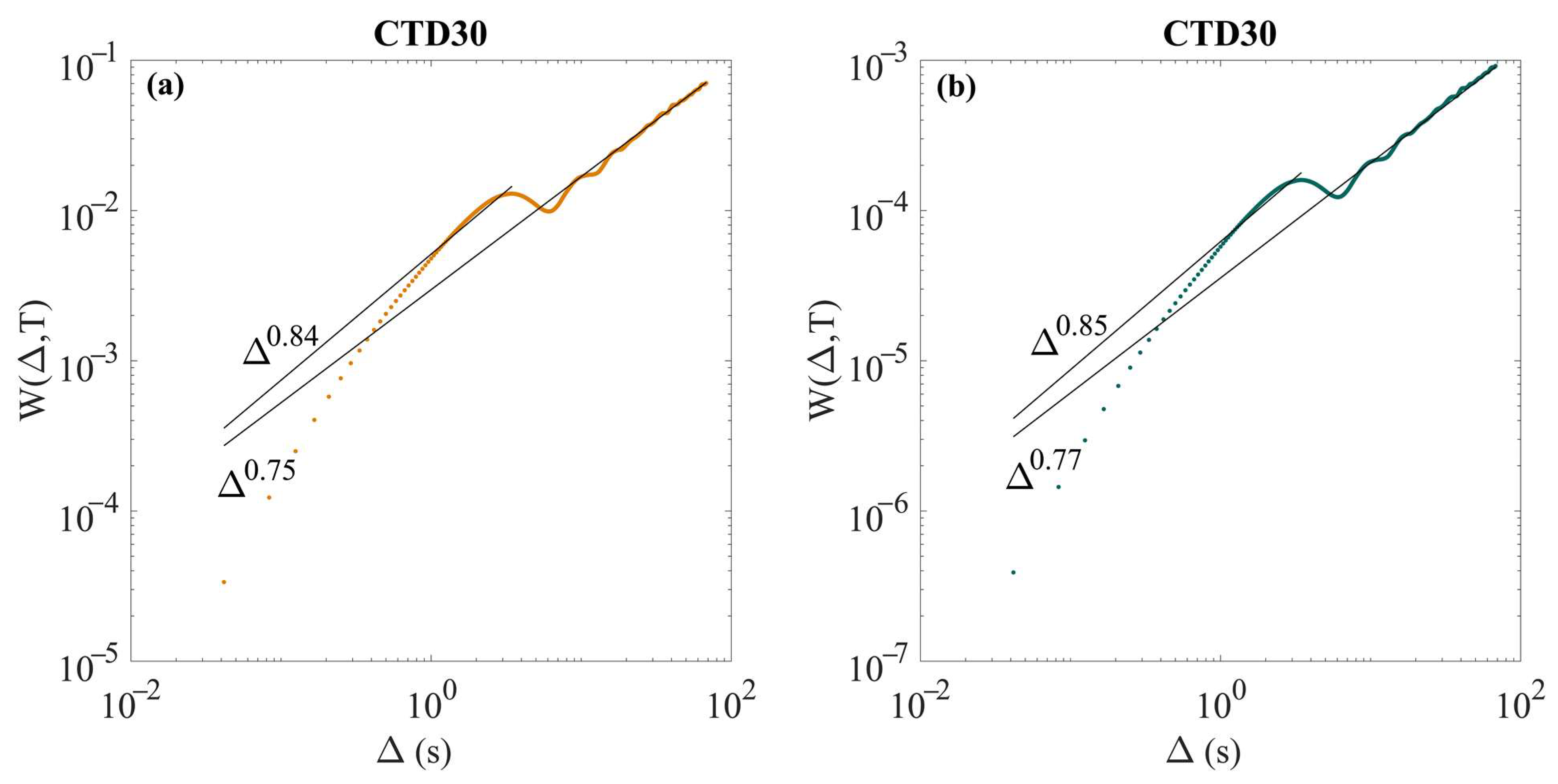
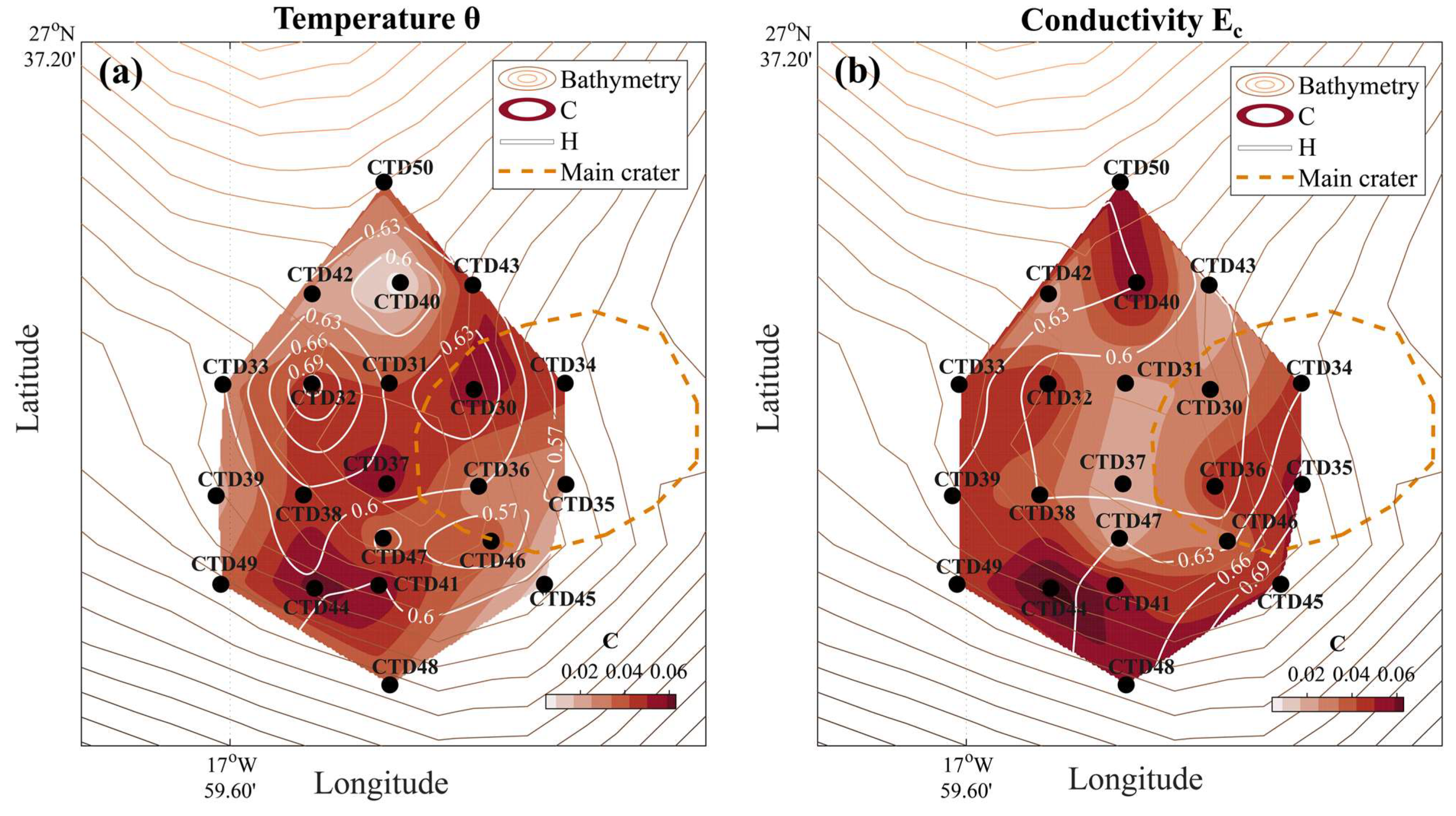
| Nº CTD | Latitude | Longitude | Initial Time | Final Time | Duration |
|---|---|---|---|---|---|
| CTD30 | 27°37.1788′ N | 17°59.5831′ W | 28 October 2016 12:59 | 28 October 2016 13:17 | 11 min. 21 s |
| CTD31 | 27°37.1793′ N | 17°59.5893′ W | 28 October 2016 13:38 | 28 October 2016 13:56 | 12 min. 20 s |
| CTD32 | 27°37.1793′ N | 17°59.5944′ W | 28 October 2016 14:36 | 28 October 2016 14:54 | 9 min. 37 s |
| CTD33 | 27°37.1788′ N | 17°59.6008′ W | 28 October 2016 15:14 | 28 October 2016 15:32 | 10 min. 44 s |
| CTD34 | 27°37.1795′ N | 17°59.5775′ W | 28 October 2016 15:57 | 28 October 2016 16:15 | 11 min. 40 s |
| CTD35 | 27°37.1725′ N | 17°59.5773′ W | 28 October 2016 16:36 | 28 October 2016 16:55 | 11 min. 49 s |
| CTD36 | 27°37.1732′ N | 17°59.5836′ W | 28 October 2016 17:18 | 28 October 2016 17:37 | 12 min. 32 s |
| CTD37 | 27°37.1729′ N | 17°59.5895′ W | 28 October 2016 17:57 | 28 October 2016 18:16 | 12 min. 17 s |
| CTD38 | 27°37.1729′ N | 17°59.5257′ W | 28 October 2016 18:28 | 28 October 2016 18:47 | 13 min. 19 s |
| CTD39 | 27°37.1731′ N | 17°59.6008′ W | 28 October 2016 19:42 | 28 October 2016 19:59 | 11 min. 25 s |
| CTD40 | 27°37.1849′ N | 17°59.5878′ W | 28 October 2016 20:16 | 28 October 2016 20:34 | 12 min. 1 s |
| CTD41 | 27°37.1670′ N | 17°59.5904′ W | 28 October 2016 20:55 | 28 October 2016 21:13 | 5 min. 0 s |
| CTD42 | 27°37.1848′ N | 17°59.5949′ W | 29 October 2016 07:10 | 29 October 2016 07:28 | 11 min. 35 s |
| CTD43 | 27°37.1849′ N | 17°59.5936′ W | 29 October 2016 07:56 | 29 October 2016 08:13 | 6 min. 6 s |
| CTD44 | 27°37.1674′ N | 17°59.5948′ W | 29 October 2016 08:42 | 29 October 2016 08:59 | 11 min. 28 s |
| CTD45 | 27°37.1680′ N | 17°59.5792′ W | 29 October 2016 09:33 | 29 October 2016 09:50 | 10 min. 45 s |
| CTD46 | 27°37.1704′ N | 17°59.5822′ W | 29 October 2016 10:51 | 29 October 2016 11:11 | 11 min. 25 s |
| CTD47 | 27°37.1701′ N | 17°59.5895′ W | 29 October 2016 11:33 | 29 October 2016 11:52 | 6 min. 38 s |
| CTD48 | 27°37.1616′ N | 17°59.5887′ W | 29 October 2016 12:23 | 29 October 2016 12:40 | 11 min. 28 s |
| CTD49 | 27°37.1674′ N | 17°59.6005′ W | 29 October 2016 13:01 | 29 October 2016 13:18 | 9 min. 53 s |
| CTD50 | 27°37.1909′ N | 17°59.5891′ W | 29 October 2016 13:48 | 29 October 2016 14:06 | 10 min. 46 s |
| Temperature θ | Conductivity Ec | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| First Regime | Whole Regime | First Regime | Whole Regime | |||||||||||||
| γ | α | H | C | γ | α | H | C | γ | α | H | C | γ | α | H | C | |
| CTD30 | 0.84 | 2 | 0.662 | 0.055 | 0.75 | 1.610 | 0.424 | 0.059 | 0.85 | 2 | 0.669 | 0.054 | 0.77 | 1.578 | 0.434 | 0.060 |
| CTD31 | 0.80 | 2 | 0.620 | 0.041 | 0.50 | 1.045 | 0.352 | 0.099 | 0.81 | 2 | 0.628 | 0.045 | 0.51 | 1.078 | 0.360 | 0.100 |
| CTD32 | 0.91 | 2 | 0.738 | 0.046 | 0.55 | 1.159 | 0.316 | 0.085 | 0.99 | 2 | 0.730 | 0.052 | 0.61 | 1.428 | 0.330 | 0.068 |
| CTD33 | 0.78 | 2 | 0.598 | 0.032 | 0.85 | 1.79 | 0.403 | 0.053 | 0.90 | 2 | 0.620 | 0.033 | 0.87 | 1.793 | 0.391 | 0.052 |
| CTD34 | 0.78 | 2 | 0.557 | 0.046 | 0.44 | 1.076 | 0.316 | 0.065 | 0.90 | 2 | 0.571 | 0.048 | 0.46 | 1.104 | 0.324 | 0.063 |
| CTD35 | 0.74 | 2 | 0.564 | 0.025 | 0.42 | 1.136 | 0.382 | 0.124 | 0.75 | 2 | 0.578 | 0.028 | 0.42 | 1.188 | 0.384 | 0.117 |
| CTD36 | 0.80 | 2 | 0.601 | 0.028 | 0.57 | 1.115 | 0.446 | 0.180 | 0.75 | 2 | 0.593 | 0.019 | 0.62 | 1.208 | 0.456 | 0.168 |
| CTD37 | 0.96 | 2 | 0.619 | 0.056 | 0.74 | 1.622 | 0.405 | 0.048 | 0.82 | 2 | 0.631 | 0.061 | 0.79 | 1.633 | 0.422 | 0.047 |
| CTD38 | 0.96 | 2 | 0.622 | 0.047 | 0.55 | 1.190 | 0.390 | 0.067 | 0.96 | 2 | 0.644 | 0.055 | 0.66 | 1.171 | 0.406 | 0.065 |
| CTD39 | 0.73 | 2 | 0.568 | 0.021 | 0.80 | 1.199 | 0.469 | 0.109 | 0.86 | 2 | 0.588 | 0.024 | 0.83 | 1.244 | 0.483 | 0.110 |
| CTD40 | 0.83 | 2 | 0.564 | 0.004 | 0.39 | 1.395 | 0.295 | 0.105 | 1.01 | 2 | 0.589 | 0.018 | 0.42 | 1.480 | 0.306 | 0.105 |
| CTD41 | 0.85 | 2 | 0.604 | 0.058 | 0.26 | 1.275 | 0.307 | 0.102 | 0.84 | 2 | 0.627 | 0.058 | 0.29 | 1.314 | 0.324 | 0.100 |
| CTD42 | 0.93 | 2 | 0.614 | 0.021 | 0.59 | 1.796 | 0.430 | 0.047 | 0.94 | 2 | 0.631 | 0.017 | 0.71 | 1.821 | 0.446 | 0.055 |
| CTD43 | 0.85 | 2 | 0.623 | 0.05 | 0.62 | 1.367 | 0.426 | 0.126 | 0.84 | 2 | 0.642 | 0.056 | 0.63 | 1.391 | 0.438 | 0.123 |
| CTD44 | 0.77 | 2 | 0.598 | 0.064 | 0.61 | 1.210 | 0.356 | 0.051 | 0.85 | 2 | 0.623 | 0.075 | 0.53 | 1.223 | 0.368 | 0.055 |
| CTD45 | 0.88 | 2 | 0.620 | 0.013 | 0.88 | 1.902 | 0.416 | 0.051 | 0.90 | 2 | 0.646 | 0.022 | 0.90 | 1.847 | 0.430 | 0.056 |
| CTD46 | 0.77 | 2 | 0.540 | 0.039 | 0.52 | 2.000 | 0.345 | 0.017 | 0.82 | 2 | 0.573 | 0.048 | 0.77 | 2.000 | 0.358 | 0.018 |
| CTD47 | 0.73 | 2 | 0.559 | 0.032 | 0.57 | 1.547 | 0.356 | 0.055 | 0.77 | 2 | 0.599 | 0.039 | 0.59 | 1.540 | 0.377 | 0.061 |
| CTD48 | 0.88 | 2 | 0.619 | 0.034 | 0.43 | 1.431 | 0.393 | 0.162 | 0.99 | 2 | 0.652 | 0.045 | 0.21 | 1.445 | 0.405 | 0.163 |
| CTD49 | 0.77 | 2 | 0.584 | 0.036 | 0.59 | 1.000 | 0.536 | 0.130 | 0.79 | 2 | 0.600 | 0.043 | 0.62 | 1.000 | 0.545 | 0.134 |
| CTD50 | 0.97 | 2 | 0.662 | 0.037 | 0.15 | 0.941 | 0.237 | 0.122 | 1.07 | 2 | 0.695 | 0.044 | 0.14 | 0.928 | 0.283 | 0.131 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olivé Abelló, A.; Vinha, B.; Machín, F.; Zerbetto, F.; Bakalis, E.; Fraile-Nuez, E. Analysis of Volcanic Thermohaline Fluctuations of Tagoro Submarine Volcano (El Hierro Island, Canary Islands, Spain). Geosciences 2021, 11, 374. https://doi.org/10.3390/geosciences11090374
Olivé Abelló A, Vinha B, Machín F, Zerbetto F, Bakalis E, Fraile-Nuez E. Analysis of Volcanic Thermohaline Fluctuations of Tagoro Submarine Volcano (El Hierro Island, Canary Islands, Spain). Geosciences. 2021; 11(9):374. https://doi.org/10.3390/geosciences11090374
Chicago/Turabian StyleOlivé Abelló, Anna, Beatriz Vinha, Francisco Machín, Francesco Zerbetto, Evangelos Bakalis, and Eugenio Fraile-Nuez. 2021. "Analysis of Volcanic Thermohaline Fluctuations of Tagoro Submarine Volcano (El Hierro Island, Canary Islands, Spain)" Geosciences 11, no. 9: 374. https://doi.org/10.3390/geosciences11090374
APA StyleOlivé Abelló, A., Vinha, B., Machín, F., Zerbetto, F., Bakalis, E., & Fraile-Nuez, E. (2021). Analysis of Volcanic Thermohaline Fluctuations of Tagoro Submarine Volcano (El Hierro Island, Canary Islands, Spain). Geosciences, 11(9), 374. https://doi.org/10.3390/geosciences11090374








