Rain, Snow and Frozen Soil: Open Questions from a Porescale Perspective with Implications for Geohazards

Abstract

Climate change is already affecting high mountain regions, such as the European Alps. Those regions will be confronted with a significant rise of temperatures above the global average, and more and heavier rain events, also during wintertime. The system response to the coincidence of rain, snow, and possibly frozen soil depends on the almost infinite number of possible combinations of thermo-hydraulic states of the involved phases. Landslides, snow avalanches, debris flows, or extensive surface runoff are just a few of the possible hazardous outcomes. With rising temperatures and increased precipitation, those hazardous outcomes are expected to occur even more frequently in the future, requiring a better understanding of those coupled processes for hazard mitigation strategies. The macroscopic phenomena are controlled by porescale processes, such as water freezing and ice grains blocking pores, which are only barely understood. The strong coupling between thermal state and hydraulic parameters, the possible phase change, and material heterogeneity pose great challenges for investigation. This work provides an overview of documented hazard events regarding rain, snow, and possibly frozen soil. The current state in theoretical and experimental research is presented before several knowledge gaps are derived and possible techniques to address those gaps are discussed.

1. Introduction

Climate change already affects Alpine Europe as changed weather conditions have arrived in local spots and confronted communities with increased precipitation patterns or frequent flood events [1,2]. Even though inhabitants of the Alpine region have always been confronted by natural hazard events, heavy precipitation, stormwater, flood event, torrential flow, or any kind of avalanche have had increasingly negative impacts on human health and material assets in recent years [2]. The changing hazard patterns and the increased vulnerability to alpine natural hazards, as well as the changing nature of the events, pose major challenges to alpine communities and their inhabitants. In high mountain areas, the snow starts melting during spring and summer, providing water and energy resources for whole regions. However, when the melting process accelerates or the snows thaws from temperatures above 10 $°$C, and additionally coincides with rain, the mobilised water masses can rapidly increase and pose a possible hazard. A variety of circumstances govern the location, timing, duration, and type of hazard events.

Several serious natural hazard events have beset the European Alps during the last 30 years [3] causing severe infrastructure damage and loss of life. However, the role of climatic factors in the initiation of hazard events might become even more significant [1]. In the context of climate change and accompanying atmospheric and soil heating, scientists expect that slight-constant variations of temperature will occur, especially in high latitude mountain regions, such as the European Alps, over the next years and decades that will have serious effects on hydrology [4,5,6,7]. It is predicted that temperatures increase considerably more in mountain areas compared to the global average [8]. This will also induce more and heavier rain events [4], in particular, during the winter months [9,10], as well as diminish the ice and snow coverage, melting alpine glaciers, thaw permafrost grounds, and initiate more rain-on-snow events (liquid precipitation falls on pre-existing snowpack) [3,8,11,12]. This might facilitate thawing and melting and enhance soil liquefaction and runoff, which could change the probability of hazard events.

Gravitational mass flows, such as landslides, debris flows, avalanches, or other fluvial events (torrential flow, river floods) can seriously threaten inhabited areas. Such events result from a multitude of climatic and hydrogeological factors, in particular, from soil composition and saturation, precipitation, or snow coverage, just to name a few. Among others, precipitation, groundwater, melting snow and ice, degradation of permafrost, or freeze-thaw weathering supply the essential water that poses a crucial driving factor for the mobilisation of gravitational mass flows. Enhanced localised liquefaction of the soil due to increased water presence could be enough to reduce slope stability of the former stable ground. In addition to the moment and quantity of the water supply into the ground (duration, intensity), the hydrogeological factors and the elevation of the snowfall limit are important [13]. The failures in residual and colluvial soils are usually initiated due to a relevant reduction of the mean effective stresses often because of an interstitial pore pressure increase. [14,15,16,17,18]. Or, as water from precipitation infiltrates along a slope and propagate further through the soils body (groundwater flow), the failure results from the reduction in the matrix suction [15].

One crucial condition for infiltration and runoff is the aggregate state of the water in the soil as well as a potential snow cover. Thick snow coverage can insulate the ground surface and diminish intense cooling [13]. Snow cover has some important positive effects in reducing the probability of enlarged runoff or soil mobilisation. The snowpack has a cooling effect on rainwater (heat transfer from rainwater to snow matrix) that tends to insulate and, thus, preserve soil frost [19]. Moreover, the snow cover dissipates raindrop energy and increase infiltration by serving as infiltration storage [20]. The water is incorporated into the snow matrix and is released steadily into the ground to contribute to the baseflow [13]. If the infiltration capacity is not exceeded, the precipitation does not contribute to runoff. In general, water can even be soaked into the frozen soil (ice in voids) [21,22], which is dominated by the thermal state of the multi-phase system. However, frozen soil reduces the infiltration ability into the soil because some voids are blocked by ice grains reducing hydraulic conductivity and storage capacity. Non-infiltrated water could significantly enhance the runoff volume during rain events and snowmelt [13,23]. Moreover, snow coverage can amplify the failure trigger by increasing the baseflow during melting [13]. That could be enhanced if ice needles and superficial ground freezing destroy soil aggregates and disperse the ground [13]. The situation is worsened when additional rain falls on an existing snow cover. The snowpack, as a porous composition, is able to incorporate some water volume from rain initially and serve as non-flowing water storage. That will reduce the quantity of runoff at first. However, prolonged and low-intensity rainfall will wet a shallow snow cover and often melt it entirely, which can cause sediment saturation and augment runoff [19], especially when the period of high precipitation and increased temperature is identical [24]. However, short but intense rainfall can also cause serious events [3].

The atmospheric warming and increased anthropogenic development, as well as an accelerated change of glacial and periglacial environments, necessitates proper hazard assessment [25]. Further research is required to study the interaction of rain, snow, and soil. Due to the specific role of microscale processes controlling the macroscopic natural hazard, research on microscale processes is essential to improving forecast and early-warning systems. Those outcomes are, in particular, required for the dense populated Central European Alps to predict and mitigate hazard events [26].

In this work, we start by describing representative past rain and snow events interacting with the soil (Section 2). In the next step, we evaluate in Section 3 which scenarios are generally conceivable according to the wide range of possible properties of the rain, snow, and soil and which of them may cause devastating threats. In Section 4, we identify potential upcoming research and discuss anticipating challenges for theoretical approaches, experimental investigations and numerical simulation. We conclude with a summary and discussion of open questions raised and possible solution strategies.

2. Documented Hazard Events Containing Precipitation, Snow, and Frozen Soil

Numerous serious natural hazard events occurred in the European Alps in recent years [3]. Some of these events are dedicated to the seasonal transition between winter and spring when a combination of rainfall and snow melting coincides or occur towards the end of the summer and the early fall [27,28,29]. Beniston and Stoffel [3] explains those events with synoptic weather patterns, which are favourable to substantial moisture convergence. When the humidity rises above a specific altitude, different precipitation intensities are possible: short intense rainfall up to and sometimes above 100 mm/day, or continuous-moderate precipitation over several days.

However, changing weather conditions and rising temperatures at high altitudes might facilitate hazardous events. This leads to amalgamated events where rain, snow and geohazards occur simultaneously. An altitude range between 1000 and 2500 m is particularly susceptible (Figure 1).

In the following, we itemise some important former events mainly from the alpine region.

• Several destructive massive floods happened, e.g., in 1987, in Switzerland [30,31,32] and in Austria [33], 2000, in the Central European Alps [13], in Central Europe in Spring, 2006, in the Danube River basin [12], or in November, 2019, in the south-eastern part of Austria. These are just some examples of the negatives impacts that have their starting point in high altitudes. The events in Switzerland, 1987, were attributable to a blockage of water beneath perennial snow patches. Melting snow was considered to be the main reason for several debris flow events. A following subsequent warm rainfall event intensified this situation and led to over 600 debris flows during summer, 1987 [31,32]. Bardou and Delaloye [13] showed that debris flow presence depended on ice formation in the ground before the event, or on the presence of snow coverage (from snow avalanche or snow precipitation).
• In 1999 and 2011, several floods were triggered on the Swiss plateau due to rain-on-snow events when intense rainfall fell on a pre-existing snowpack during elevated temperatures [34]. As a consequence, rivers flooded major cities in low altitude regions [35,36]. The event in 1999 also affected southern Germany and northern Austria in the first half of May [37]. The so-called Pentecost-flood resulted from the combination of high precipitation and snow melting, which both saturated the soils. The following heavy rain could not infiltrate and become runoff eventually. Moreover, high temperatures melted the snow cover in altitudes up to 2000 m asl. Among others, Bayerisches Landesamt für Wasserwirtschaft [37] reported that at the German mountain Wendelstein (1835 m asl) snow depth decreased by 35 cm from 19 May 1999 to the beginning of June. Amplifying precipitation caused massive floods in the rivers Isar, Amper, Ammer, Wertach, Lech, Iller, Vils, Inn, and Danube.
• A similar event happened in November, 2019. Heavy snowfall was followed by heavy rain events in the eastern and south-eastern parts of Austria, in particular, Salzburg, Styria, Carinthia. The rain fell onto an already wetted snow cover inducing wet snow avalanches, debris flows, and landslides (P. Wagner, Bavarian Environment Agency, personal communication, 9 March 2021). The pattern repeated at an earlier event in January, 2004, in the Valais Alps, where rain fell onto a snow-covered area at high altitude [13]. Beniston and Stoffel [3] reported that in May, 2015, an intense rainfall occurred under very mild conditions in the Mont-Blanc region and fell on an already existing thick snowpack. This event provoked highly exceeded discharges of the Arve River causing urban flooding in the City of Geneva (University district). Other communities, further to the east, suffered from multiple debris-flows resulting in high damage costs to infrastructure.
• Specific rain-on-snow events were reported for the south-western part of Bavaria in January 2018 [7]. Heavy rainfalls occurred after a phase of rich accumulation of snow. With air temperatures in the range −0.14 $°$C ≤ T ≤ 8.65 $°$C, rain intensities were roughly between 32 and 49 mm with a duration of 20 to 35 h. Moran-Tejeda et al. [38] analysed temporal and spatial patterns of rain-on-snow events between 1972 and 2012 in Switzerland. According to their results, the reported rain-on-snow events occurred mainly during the winter months at low elevations or during summer months at high elevations.
• Rain-on-snow events outside Europe have been reported, e.g., by Surfleet and Tullos [39] investigating the relationship between such specific precipitation events and peak daily flow events against the background of climate change within the Santiam River Basin, Oregon. Heavy winter precipitation and a sequence of snowfall and snowmelt in 2018 triggered several landslides in the Andean paraglacial environment (Yerba Loca landslide, central Chile) [40].

The documented events indicate the dramatic effects when rainfall and snow melting coincide with a possibly frozen soil. The fact that climate change is already promoting such events necessitates intensive scientific research on this topic in the future. Admittedly, numerous possible scenarios arise from altered properties of rain, snow, and soil. This will challenge theoretical approaches, experimental investigations, and numerical modelling.

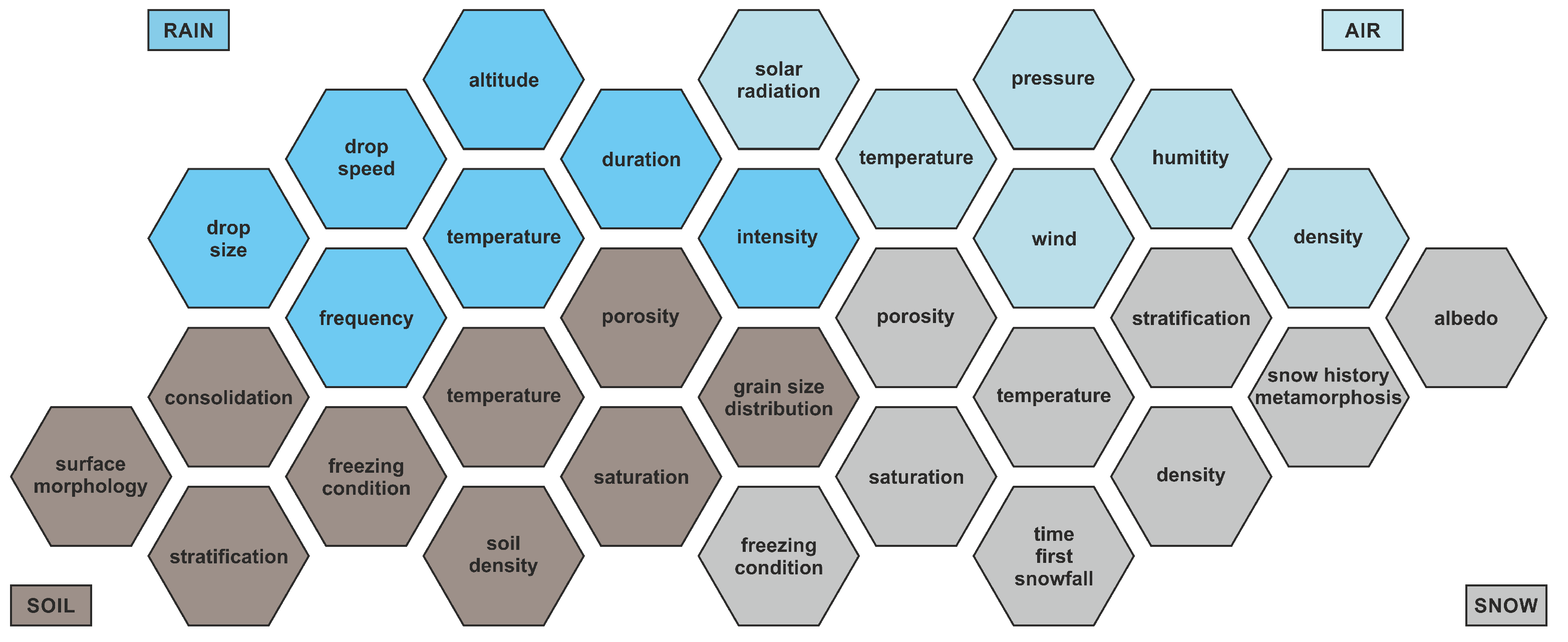
3. Possible Scenarios and Characteristics

The thermal-hydraulic interaction between rain, snow, and soil is complex and challenging because the thermal and hydraulic processes are strongly coupled. Snow and soil are mostly heterogeneous and anisotropic materials with a complex pore structure. Depending on the porosity and water saturation of snow and soil, as well as of the vertical temperature profile in snowpack and soil, many different responses of this multi-phase system are conceivable with respect to the phase transition between frozen and liquid water. Some of the possible responses may cause serious natural hazards but some might turn out innocuous. This depends additionally on the surrounding circumstances, e.g., topographic slope, vegetation, influences of infrastructures such as dams or reservoirs, as well as anthropologic activities. It seems that there is an unmanageable amount of possible responses of rain and snow in combination with soil. All three phases as well as the surrounding air crucially change their physical behaviour when their properties are varied due to environmental changes (Figure 2). The respective local and temporal characteristics of these multivariate properties ultimately determine whether, how and in what form a hazard event occurs.

The possible system responses for the relevant thermo-hydraulic states of rain, snow, and soil can result in (increased) surface runoff at various levels (surface runoff, interlayer runoff), snow avalanches, landslides, debris flow, or enhanced groundwater flow. Combinations of those results are possible and processes might develop along the downhill movement, as, e.g., surface runoff can develop into debris flow due to erosion. Those processes take place annually in mountainous regions and are usually not hazardous. However, with large amounts of water available at high altitudes through rain and snow, any surface process can become threatening.

We separate the system into four layers, each subject of possible internal as well as boundary processes with its adjacent layers (Figure 3). Beginning with the upper boundary layer, the rain, which can either infiltrate into the snowpack or drain on top of the snowpack. While the infiltration is the most likely scenario, runoff on top of the snowpack might occur if an ice layer exists on top of the snowpack, inhibiting further water infiltration. Such an ice layer can especially be generated through rain freezing at the top of the snowpack [41]. Once rainwater infiltrated into the snowpack, it can either freeze or stay liquid. In the case of freezing, the rainwater will remain in the snowpack and inhibit or reduce further infiltration of rainwater. Through the increased load of the additional water stored in the snowpack, snow avalanches might occur. However, this depends very much on amount and location of stored water within the snowpack. If the rainwater remains liquid, it will move relative to the snowpack, which acts as porous media. Depending on the inclination of the hillslope and possible ice layers in the snow inhibiting further downward movement, downhill internal flow of water can occur at various depths within the snowpack. As the water remains liquid, it might start melting the snow crystals forming the porous matrix. It is known that the heat stored in rainwater is usually too small to initiate a significant snowmelt [42] but as rainfall often comes with associated changes in air temperature, air pressure, and solar radiation, an increased melting can still occur during rain events [43]. In the case of snowmelt, the amount of mobilised liquid water will further increase. Depending on the thermal gradient within the snow, rain- or meltwater might (re-)freeze at deeper layers. Generally, several processes can simultaneously occur within the snowpack due to heterogeneity in thermal and hydraulic parameters and variables.

At the boundary of snow and soil, similarly, either infiltration or surface runoff, or a combination of both, can occur. Surface runoff might be inhibited through the existing snow layer but might also facilitate melting of the snowpack at the snow–soil interface. Infiltration into the soil can be inhibited due to a surface ice layer, or ice grains plugging the pores [44]. Depending on soil heterogeneity in its pore structure and the pore water distribution at freezing, some pores might remain open, so that water can infiltrate into the partly frozen soil but at a reduced capacity [45]. In such a case, the snow might act as water storage, slowly but steadily releasing the water into the soil [13]. Similar to the snowpack, the infiltrating water can freeze within the soil pores or facilitate thawing of the soil depending on the thermal conditions. In principle, the temperature difference between rainwater and soil temperature can be significant, but rain temperature is measured seldom and usually assumed to be equal with air temperature [46]. Depending on soil properties, the presence of ice and the slope inclination, the infiltrating water can travel significant distances in the vadose zone, prior to reaching the groundwater. Soil heterogeneity or ice layers in the soil body can cause slack water increasing the pore pressure at various depths in the soil layer. Open preferential pathways in a partly frozen layer can cause increasing pore pressures below the freezing front, possibly triggering slope failure. Through varying temperature conditions and a delayed heat conduction through the soil, complex temperature gradients can exist within the soil with freezing of water at a greater depth after infiltration causing complex patterns of frozen and unfrozen soil in the subsurface.

4. Thermo-Hydraulic Processes at Microscale

4.1. Theoretical Considerations

The thermal and hydraulic processes at porescale during rain, snowmelt and within a frozen soil are complex due to their strong coupling, their dynamics and the multi-phase nature of the problem. The porous soil matrix is a solid phase with a constant volume fraction $(1-\varphi )$, with porosity $\varphi$. Its parameters are usually well-known and it experiences comparably little dynamics. However, frost heave can occur, altering the soils pore structure during freeze and thaw cycles [47]. Typically, a soil incorporates a range of pore volumes, some of them forming preferential pathways consisting of so-called macropores with substantially larger pore radii than the majority of the porous soil matrix. Those macropores can have various sources, often arising from biological activity such as root growth or worms [48]. Further, soil heterogeneity will occur along a hill slope due to different soil types and different stages of compaction. Therefore, the soil is usually a heterogeneous, anisotropic medium with preferential pathways that in a saturated state can often hydraulically be described best using a dual-porosity approach [49]. For a partially saturated state, the Richard’s equation is the most common approach. Following well-known relationships such as vanGenuchten [50] or Brooks and Corey [51], the heterogeneity in pore radii can be incorporated into continuum mechanical parameters to account for the dependence of capillary forces on the pore radius.

It is well-known that freezing in soil has similarities to soil drying and to the respective equations [52]. The Clausius–Clapeyron equation describes the relationship between pressure and temperature in freezing/thawing soils under equilibrium conditions between the liquid and frozen water [53]. While thermal equilibrium between ice and liquid water has so far always be assumed, modifications of the Clausius–Clapeyron equations to account for pressure differences between phases have been formulated [54]. The Clausius–Clapeyron equation is able to reproduce the important experimental observations of water flowing towards the freezing front causing as well as a depression in the freezing point in the porous matrix [52,55]. The ice content can be empirically related to the hydraulic conductivity using an impedance factor [56]. It should be noted that, for simplicity, most theoretical approaches neglect the density difference between liquid and frozen water, which is often associated with frost heave and would affect the pressure in the pores. In addition to its various mathematical forms, the Clausius–Clapeyron equation does not provide any microscopic information, such as a separation between micro- and macropores or similar [57]. Using a capillary bundle model, ice in a pore can be represented by a cylindric body with water flow around it (Figure 4a) [58]. The size of the cylinder and the surrounding liquid water layer can be calculated based on the counteraction of van der Waals forces at the pore walls and the Gibbs–Thomson effect [59]. However, from experimental observations, it is known that in macropores, water freezes at the walls first and grows towards the inner circle of the capillary tube (Figure 4b) [60].

Most models and theoretical considerations in the past focused on freezing/thawing in a (partly) saturated porous media [52,61,62,63]. In those scenarios, the phases are in local thermal equilibrium (LTE) and can therefore be described by a single temperature equal for all phases. However, when considering rain- or meltwater infiltration into a frozen soil, the LTE assumption is violated as the soil is at temperatures below the freezing point while the infiltrating water is at temperatures above the freezing point. There is no experimental or theoretical evidence for how quickly phases approach thermal equilibrium, as measurements of separate phase temperatures at porescale have never been conducted and seem experimentally challenging—to say so the least. In the case of an absence of an LTE, phase temperatures have to be distinct, and the thermal evolution of each phase not only depends on the heat transport processes of each phase but its interaction with the other involved phases. Phases of different temperature with direct contact to each other exchange heat usually described by Newton’s law of cooling $Q=hA\Delta T$, with the transferred heat Q (W/m${}^3$), the heat transfer coefficient h (W/m${}^2$K), the specific contact area A (1/m) and the temperature difference between the phases $\Delta T$ (K) [64]. In this formulation, there is one transfer term for each interaction between phases. More phases in contact result in more heat transfer terms. This concept is well established in geothermal applications, e.g., [65,66,67] but less often applied in near-surface processes and aquifers [68,69]. There are a few discontinuous models describing heat and mass transport in frozen soil: A three-phase heat and mass transfer model is presented in Xu et al. [70] and implemented using the Lattice–Boltzmann method [71]. Their model describes the pre-melted film surrounding the soil grains and links film thickness to soil temperature. Interactive forces between soil, water, and ice are used to describe the moisture movement [70]. Peng et al. [72] introduced a thermal non-equilibrium between the ice and the liquid water. While the Richards equation is used to describe liquid water movement in frozen and unfrozen soil, it is modified with a sink term coupled to the freezing of liquid water.

The application of local thermal non-equilibrium (LTNE) models in frozen soil is complicated by a lack of empirical values for the heat transfer coefficient, its likely dynamics, and the changing heat transfer areas. Neither theoretical models, nor experimental findings constrain the heat transfer coefficient, e.g., between soil and ice, ice and water in porous media, or air and ice. From saturated porous media, it is widely accepted that the heat transfer coefficient is velocity dependent [69,73,74]. It might be reasonable to assume that this is also the case in a frozen soil but its degree is yet unknown. For fracture flow in a porous media, the heat transfer coefficient is different in value and has a different velocity dependence compared to porous media probably due to its different flow regime [75]. This might lead to different heat transfer coefficients in the preferential pathways compared to micropores of the soil matrix. Furthermore, the heat transfer area between phases is subjected to rapid changes as freezing or melting occurs. For determining the heat transfer area, the underlying freezing model is of special importance. Ice growing cylindrical inside the pores will not have a contact area with the solid soil matrix, and therefore, no heat will be transferred between those phases. In contrast, ice growing at the walls of macropores will isolate the water from the solid soil matrix. Consequently, relevant heat transfer processes might differ depending on the pore size.

Generally, similar concepts for soil can be applied for snow, e.g., [76]. Considering snow as a porous medium, flow and heat transfer models derived for general porous media can be adopted [77]. However, describing and parameterising processes in the snow is even more difficult as not only does it have similar complexity in terms of heterogeneity and anisotropy apply with respect to preferential pathways for flow apply, but the whole pore structure is continuously changing. Through freeze and thaw cycles, the snow grains change in size and shape also altering the pore space [12]. Ice layers can develop depending on air temperature, water movement, and compaction through additional snowfall [78]. Such ice layers might inhibit water infiltration completely, or limit to preferential flow along fractures and joints in the ice [79]. The consequences of the dynamics of the snow pore structure, as far as the vanishing of the snow, apply to all issues already discussed in the soil with respect to flow and heat transfer processes. This limits most kinds of porescale descriptions to a current snapshot of the snowpack. Even then, water infiltration or re-freezing of meltwater remains a complex task with many unknowns. For example, it remains unclear how (re-)freezing water relates to the snow crystal with respect to heat transfer. Similar to the soil, the snow matrix might be at substantially colder temperatures than the (just) frozen water. As both snow matrix and frozen water are ice in principle, heat conduction might occur or the previously used concept of heat transfer might be a more suitable description due to the different ice crystal structures. Additionally, there are no experimental observations of heat transfer processes during water infiltration into a snowpack required to help quantify the heat transfer coefficient.

4.2. Experimental Investigations and Field Measurements

Highly sophisticated, well-documented experimental investigations essentially fathom natural processes and represent an indispensable segment in attaining scientific knowledge. On the one hand, fundamental research questions are investigated initially by utilising experiments. The conclusions are generalised subsequently to physical laws after independent experimental repetitions confirmed the results several times (induction principle). On the other hand, experiments serve to verify, calibrate and validate both theoretical approaches and computational models. Consequently, reliable predictions can be applied for additional physical cases (principle of deduction), which permits a feasible engineering implementation of experimental investigations in the first place.

Experimental knowledge can be obtained from laboratory experiments or field measurements. Laboratory experiments have the distinct advantage that the physical processes are investigated under precisely controlled conditions, the initial and boundary conditions can be influenced, and measurement data are collected at previously defined points. This enables a high and qualitatively valuable density of measurement data. Despite tremendous efforts, however, laboratory experiments remain somehow influenced by artificial, possible anthropogenic, processes. In contrast, field measurements reflect the actual natural circumstances at a specific measurement location, either immediately during an event (e.g., measuring the water level at a gauging station) or subsequently (e.g., recording the dimensions of a deposition lobe after a landslide). For rather complex research questions, akin to this study’s topic, the scientific investigation might benefit from both laboratory experiments as well as field measurements.

Rain, snow, and frozen soil interact generally in manifold ways in nature and each varies locally and temporally. According to arising experimental challenges, these three phases have only been investigated experimentally independently of each other or at most in a combination of the two, so far. Essentially, three types of previous investigations can be distinguished: (1) freezing experiments in single soil columns, (2) field site infiltration measurements of precipitation into soil or a snow package, and (3) flume studies about geomorphological hazards induced by rainfall trigger or melting snow.

Jame and Norum [61] presented one of the first freezing experiments in single soil columns by measuring temperature profiles and total water content (frozen and liquid) in a one-sided sub-freezed soil sample. Fluid dye and digital image analysis on frozen soil columns visualised preferential pathways below the freezing zone [45]. At the time of freezing, unsaturated macropores formed the preferential pathways and remained open during further freezing and subsequent infiltration. However, this has only been observed in an undisturbed soil probe and not in packed sand [45], questioning the bias introduced through artificial homogeneous soil probes. Weigert and Schmidt [47] observed corresponding infiltration processes into frozen soil through macropores in soil column experiments and verified a significantly reduced infiltration capacity compared to unfrozen soil conditions. Their experiments also revealed cracking through frost heave in loamy samples while sandy soils were unaltered [47].

Nowadays, the soil column experiments’ results from Hansson et al. [52] are often utilised to calibrate and validate numerical models. In those experiments, soil columns filled with sandy loam were homogeneously saturated to some degree and then frozen. Liquid and frozen water content were determined for 1 cm thick slices for various times after freezing of the soil column at the top [52]. Although a general water movement towards the top was detected, no preferential flow due to the homogeneous character of the packed soil columns could be observed.

Watanabe and Kugisaki [60] prepared packed soil columns of sandy and silt loam to explicitly study the flow and freezing behaviour in added artificial cylindrical macropores. In those unique experiments, comparably warm water (4 $°$C) infiltrated into a frozen soil column (−6 $°$C). They further examined different freezing behaviours of macropores and micropores as well as the role of macropores during fluid infiltration into frozen soil.

As a second type of previous investigations, numerous infiltration measurements of precipitation into the soil or a snow package have been conducted in laboratories or on field sites over the years. Infiltration processes of precipitated water into a maritime snowpack during two midwinter rain on snow events have been studied by Conway and Benedict [80]. By tracking the wetting process and monitoring the zero-degree isotherm’s vertical variation, they observed that water infiltrated the snowpack non-uniformly through localised channels. Even though the snow stratigraphy strongly influenced the evolution of wetting, the majority of the precipitation remained liquid and wetted the snowpack or drained through it. That water movement towards the freezing front, as well as the refreezing of infiltrating snowmelt, is of particular importance as it reveal the outcomes of the lysimeter experiment in sandy soils with regular measurements of moisture content, soil temperatures, and groundwater levels over two winters [81].

Similar to those soil column experiments, dye tracers have been used efficaciously during field observations, highlighting preferential pathways in snow volumes [82]. Such experiments reveal that a shallow thin ice layer diminishes the infiltration noticeably and can force up to 25% of the snowmelt to surface runoff. Webb et al. [83] investigated preferential flow paths in snow during an entire snowmelt season. They examined how near-surface soil moisture varied on hillslopes relative to the according toes and flat areas. Consequently, snow acted as an extension of the vadose zone, and the hydrologic flow path development varied by aspect during spring snowmelt in complex subalpine terrain. Webb et al. [83] postulated that future hydrologic investigations would benefit from studying snow and soil collectively.

However, ground freezing and snow coverage can also influence the flow processes in snow and soil layers and can amplify or reduce slope instability caused by the precipitation event. Bardou and Delaloye [13] studied those effects by undertaking field survey analysis. They concluded from their results that both growth of ice needles and superficial ground freezing destroyed soil aggregates, and deep ground freezing decreased the infiltration rate, which in turn might have increased surface runoff. Snow coverage could have simultaneously amplified or reduced debris flow risk. Wright and Novakowski [84] performed field observations of midwinter melts and rain on snow events in a seasonally frozen bedrock aquifer. They instrumented a granitic outcrop to measure the atmosphere-subsurface interaction for a subsequently coupled modelling of snowpack and subsurface. The results indicated the occurrence of rapid recharge in the bedrock despite frozen conditions and limited infiltration through a shallow frozen soil layer.

The third type of previous investigations include studies about the initiation and the outcome of rainfall-triggered landslides and debris flows, or triggering effects of massive melting snow due to rapid temperature increase. Despite several surveys about natural events [22,24,26,85,86,87] and field studies [13,19,31], laboratory experiments in artificial flumes equipped with sprinklers have been conducted over the years [88,89,90,91,92,93,94,95,96]. However, the complex interaction between rain and snow (rain falls on already melting snowpack, rainfall cannot be stored in snowpack and is rapidly percolated downwards), in particular, in combination with frozen soil, has been observed [24,33] but has been studied experimentally only rudimentarily thus far.

Former studies, either under laboratory conditions or on field sites, reveal the enormous challenges of investigating the multivariate interaction of rain, snow, and frozen soil. In complex research questions, all three components could have only been examined independently of each other or at most in a combination of two. Some of the former experiments were performed under highly idealised conditions (single soil column samples, artificial macropores, rectangular flumes), which perhaps suppress dynamic interactions, such as intermittent melting and refreezing, blockage of preferential pathways, or interlayer runoff. Gatto et al. [23] highlight that more laboratory and field experiments should be performed to investigate the freeze–thaw processes in different compacted and undisturbed soil types with altered soil moistures, as well as changes in soil density, infiltration rate, and surface geometry. Furthermore, the effects of snow cover on soil freeze–thaw regimes on soil stability should be explored. That would extend the existing knowledge of the effects of seasonally dynamic soil processes, which is crucially needed for physics-based soil-erosion and landscape evolution models.

For a comprehensive experimental investigation of rain, snow, and frozen soil, however, some challenges cannot be neglected. A detailed experimental investigation on a porescale requires a very precise design of the experimental setup and minute control of the initial and boundary conditions. At the same time, the soil must be installed in such a way that it corresponds to natural conditions as closely as possible. The representation of rain events can be realised sufficiently well by utilising sprinklers. In contrast, the production of snow is a major challenge. In most cases, natural snow deposits can probably not be brought into an experimental laboratory without significantly altering the snow properties. Alternatively, snow guns could be used to produce artificial snow directly in the laboratory. Although a sufficient amount of snow can be produced in a selected manner, the round and spherical artificial snow grains lack the natural properties of fluffy natural snow. Parallel field measurements could provide complementary data from natural conditions.

Measuring infiltration rates, preferential pathways, surface runoff, interlayer runoff, or baseflow in the vertical snow-soil profile require sophisticated measurement techniques, whether in laboratory experiments or field measurements. For instance, the stratification, as well as the local and temporal variations of temperature, moisture, and density must be determined in both the snow and the soil. In addition, quantitative and qualitative measurements of rain intensities, preferential pathways, as well as changes in mass and volume are necessary. Distinguishing the runoff’s proportional composition origins either from rain or from melting processes of the snow will be a particular challenge.

4.3. Numerical Challenges

There is a variety of numerical simulation tools available to model freezing and thawing in porous media. Such tools include the USGS SUTRA model [97], the COUP model [98], the SHAW model [99], FeFlow with the extension piFreeze [100,101], and the library Pflotran-ICE [102]. Those tools focus on infiltration and groundwater flow scenarios on a catchment scale [101,102] rather than on natural hazards or a microscopic perspective. Codes used to study freezing and thawing at a small scale are usually related to specific studies and applications, e.g., [55,76]. For snow, the most relevant software package is SNOWPACK [103] and the more comprehensive alpine surface model ALPINE3D [104]. SNOWPACK can calculate snow layering and snow properties undergoing seasonal change based on provided weather data and was originally designed for avalanche protection. Water infiltration into the snowpack and interaction with the soil are not focus points of those computer models. Most experiments dealing with water infiltration into frozen soil or snow, or providing information for a microscale perspective on the freezing/thawing process, can often be simplified to a one-dimensional problem. Therefore, computer codes are also often one-dimensional in space to compare the simulation results to the column experiments. However, one-dimensional geometries can not represent soil heterogeneity or processes along an inclined hill slope.

A complex mathematical model will increase the computational load of a numerical approximation. Simply by denying the assumption of a local thermal equilibrium, the calculations become cumbersome as each phase has its own heat equation. The separation of the phases increases memory demands and runtime, especially as the use of explicit heat transfer decreases the allowed time step due to stability and accuracy concerns [105]. In true multi-phase heat transfer models, the sequential or simultaneous solution of the heat equations and heat transfer terms will influence accuracy and possible time stepping. During melting or freezing, phases can be newly generated or vanish completely—from the system in general or locally. This requires dynamic positioning of boundary conditions of phases, and locally isolated patches of phases might exist. This might also occur for snow as the porous matrix might vanish, and moving boundary conditions, mesh deformation, or re-meshing might be necessary. Additional numerical issues arise due to the handling of possibly very small volume fractions of liquid water and ice in snow and soil. Defining numerical limits on possible volume fractions touch on the physical assumption of ice nucleation and when ice grains are so small that they can be transported through the porous network.

Increasing spatial dimensions and also the spatial scale covered will naturally further increase the computational load. To transfer concepts from a microscopic scale to field scale might require upscaling techniques and possibly a depth-integrated mathematical model to improve computational performance at a reasonable loss of information. However, considering state-of-the-art slope stability simulations in full 3D solving for pore pressure diffusion, surface runoff, and poro-elasto-plastic deformation on a complex terrain, the coupling of such a model with an advanced thermo-hydraulic model for frozen soil seems feasible. Especially in surface flow and slope stability calculations, it is known that a geometrical reduction might falsify simulation results [106]. With irregular freezing and thawing patterns in soil and snow, those effects would become even more significant. From the coupling of different physical processes, possibilities for numerical parallelisation arise by splitting physical processes across available resources considering varying demands on temporal resolution and computational costs.

5. Discussion

Summarising the above discussion on microscale effects in freezing and thawing processes in rain–snow–soil systems, several key aspects have been elaborated:

• The coincidence of melting snow on a (partly) frozen soil and rainfall has caused severe natural hazards in the past in the European Alps. Climate change predictions indicate an increased frequency of such events.
• The type of triggered gravitational mass flow, its size, and the evolved phases depend on numerous variations of properties and the history of the associated variables.
• Physical processes at porescale control the thermo-hydraulic state of the system with a strong coupling between separate phases, as well as between the hydraulic flow conditions, and the heat transport.
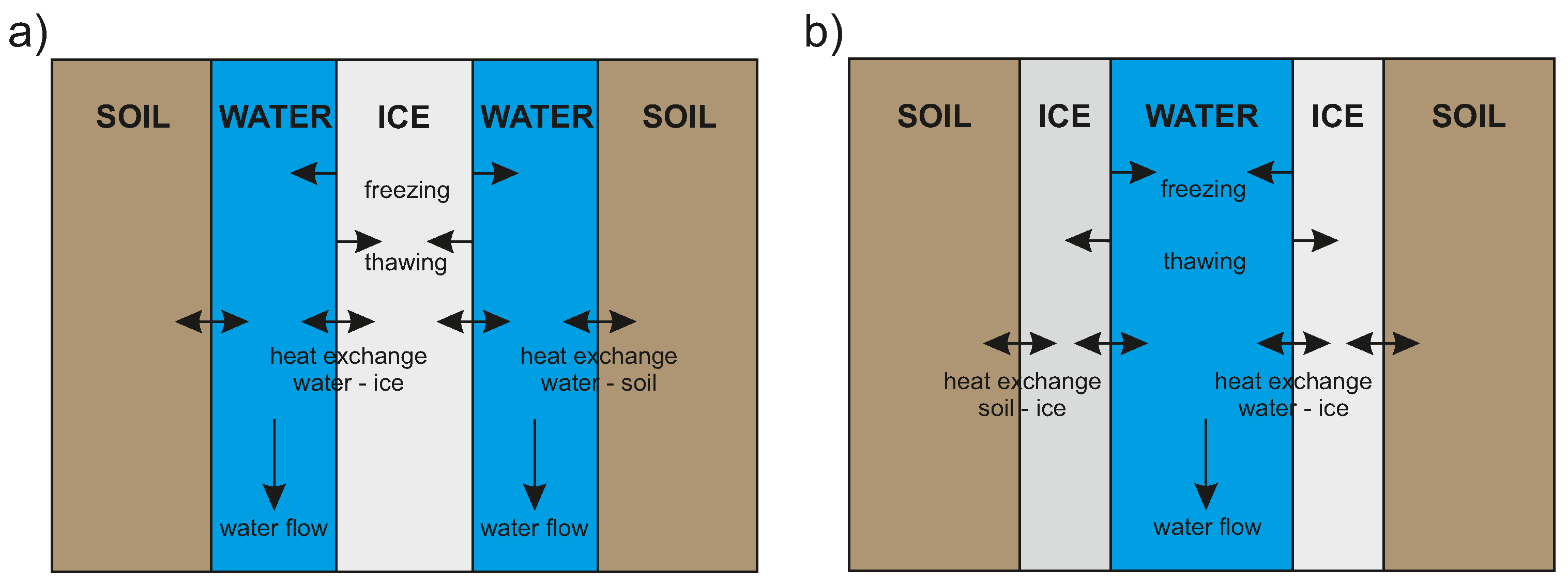
• Water infiltration into a snowpack or frozen soil possesses a local thermal non-equilibrium (LTNE) situation through the initially strongly diverging phase temperatures. An accurate description of heat transfer processes increases the complexity of mathematical models and currently lacks sufficient parameters.
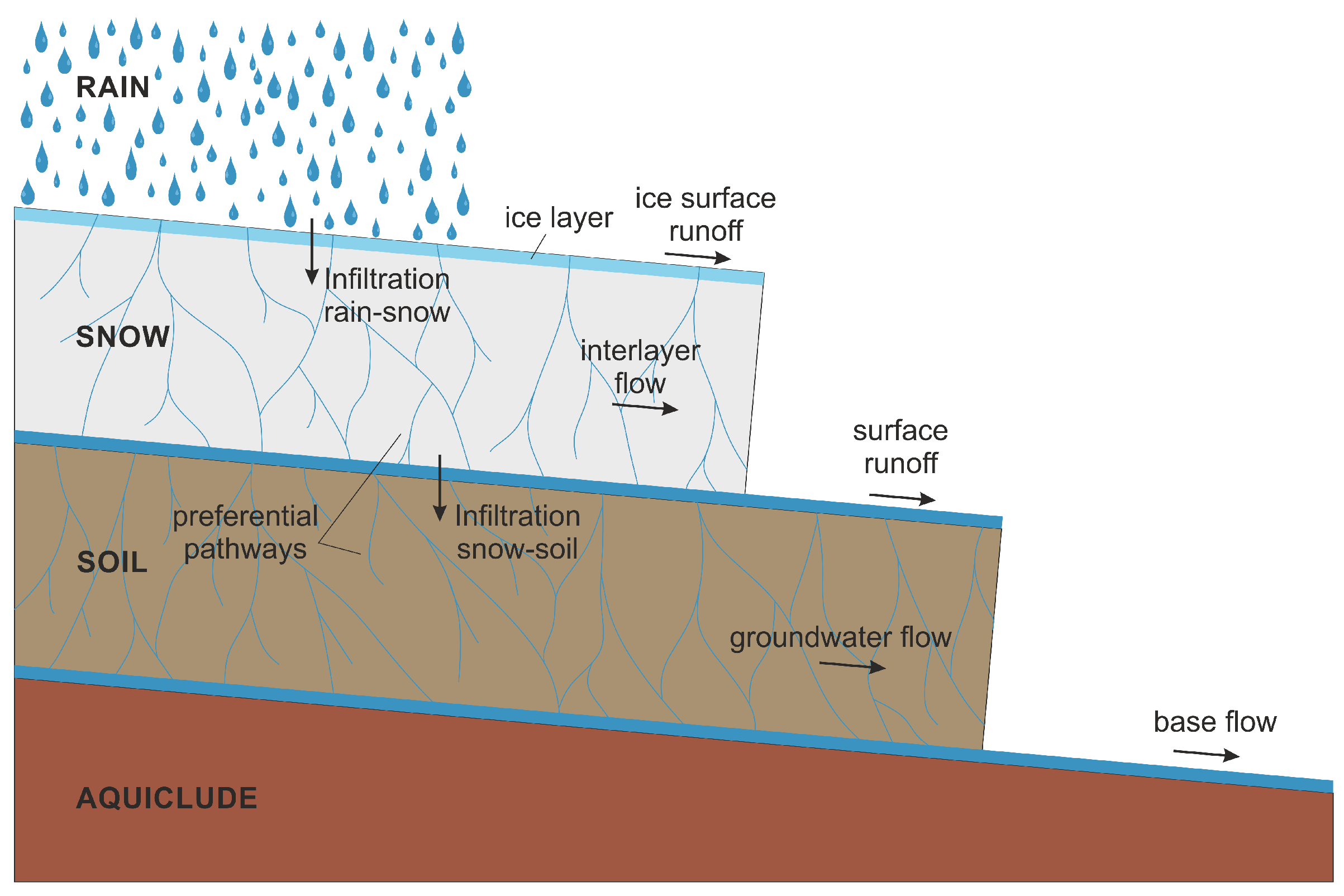
• The hydraulic systems of soil and snow are strongly heterogeneous. Preferential pathways are key to water infiltration as macropores experience a substantially different freezing behaviour than micropores.
• Former laboratory studies mostly focused on single processes at idealised geometries. Studies of more complex scenarios and in more complex geometries are needed to better understand the coupling between processes and phases. Field investigations might provide required complementary data from natural conditions.
• Obtaining required system variables and parameters from field or laboratory investigations demands sophisticated measurement techniques and a thorough control or logging of environmental conditions.
• Current theoretical and numerical models provide various possibilities for improvement, such as the incorporation of preferential pathways, macroscopic heterogeneity, and anisotropy, heat transfer between phases, or coupling to surface flow and slope stability.

An increased research effort in the multi-phase system of solid rock or soil, liquid water, ice and snow from a theoretical, experimental, and numerical perspective is demanded facing the anticipated fundamental climatic changes in high mountain areas—in Europe and worldwide. Findings will also influence research in other fields, such as regarding permafrost regions and glaciers, as well as facilitate the understanding of the hydrology of areas of substantial local groundwater resources.