Mechanical Analysis and Prototype Testing of Prestressed Rock Anchors
Abstract
1. Introduction
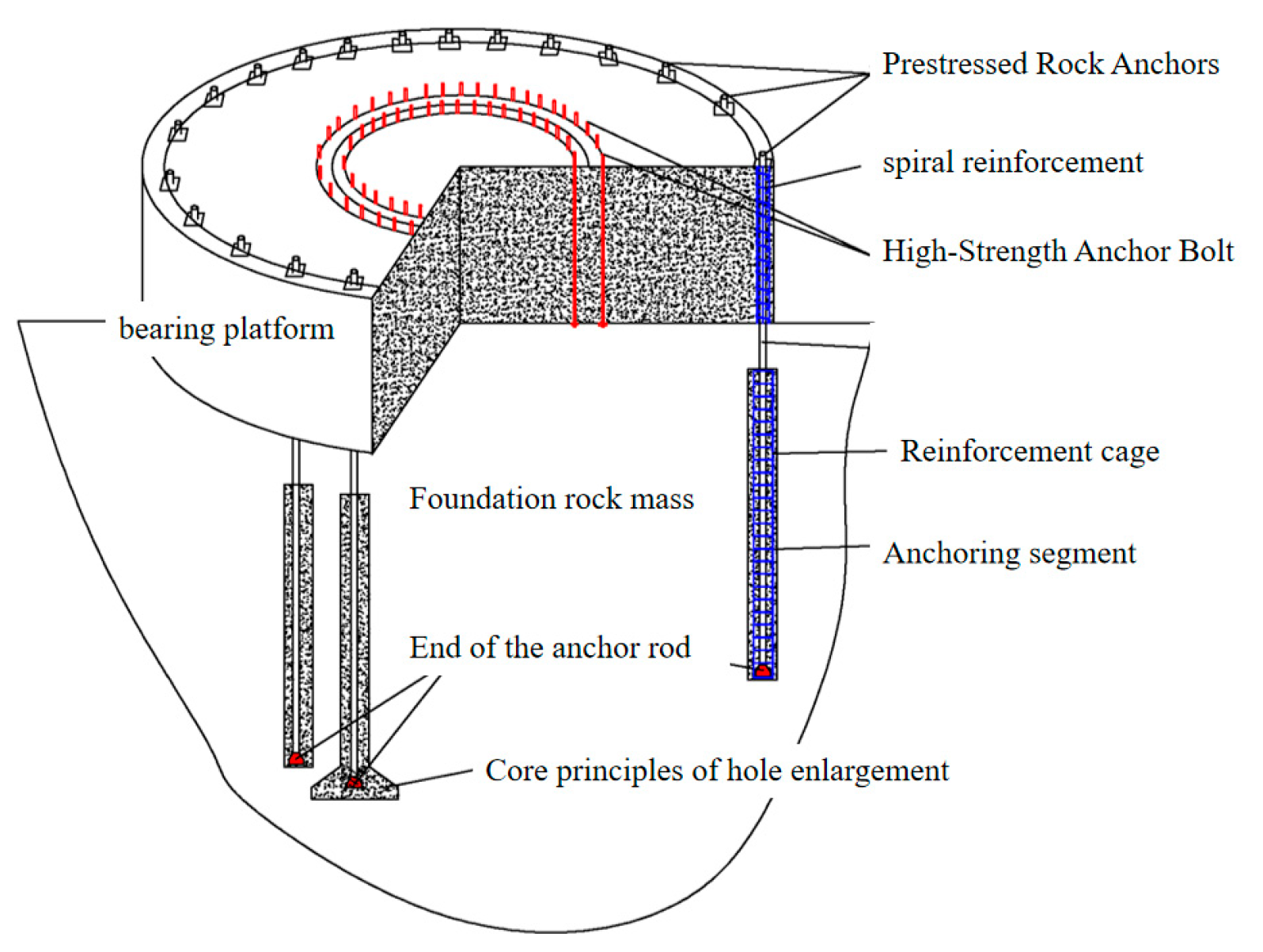
2. Analysis of Mechanical Behavior of Prestressed Rock Anchors
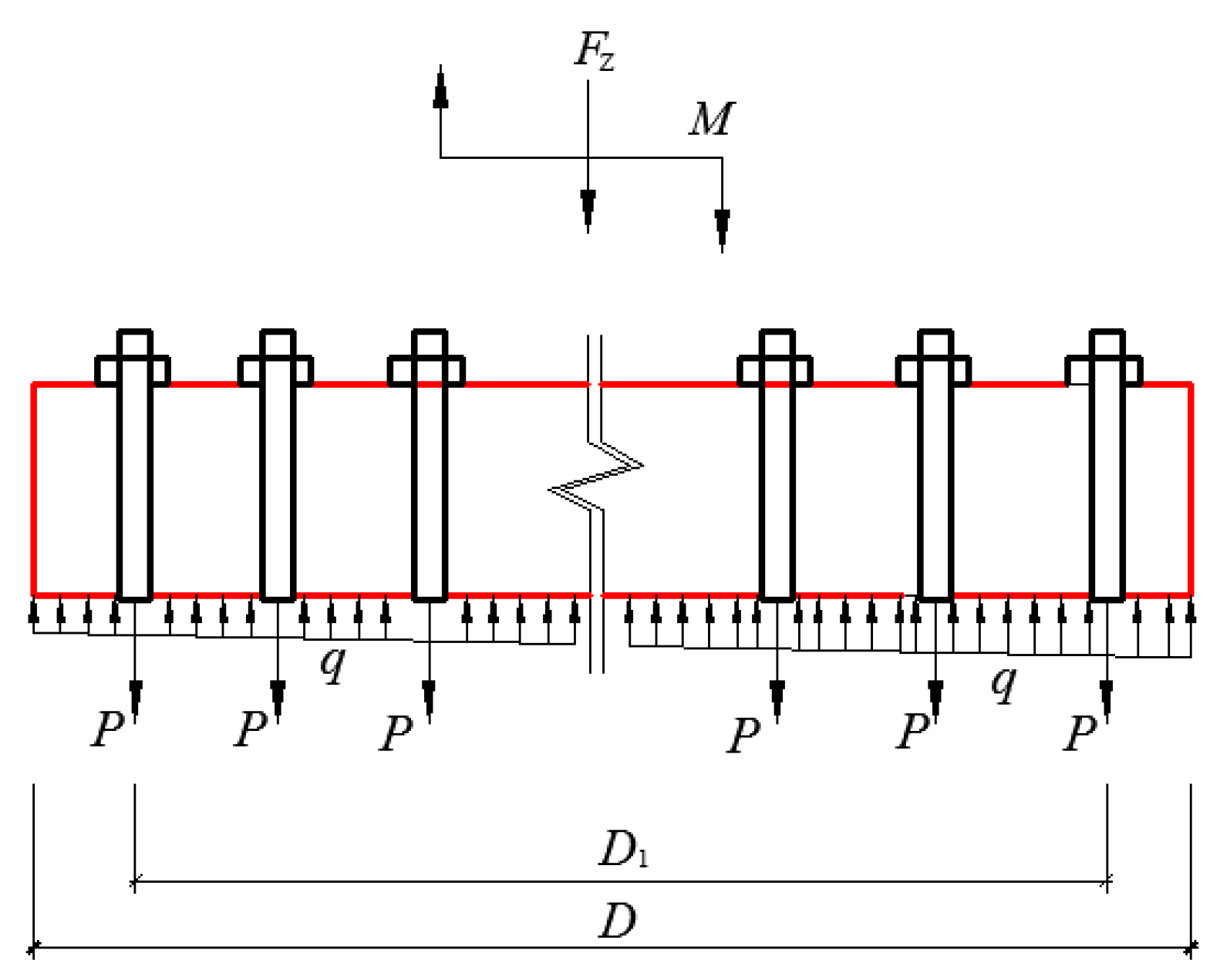
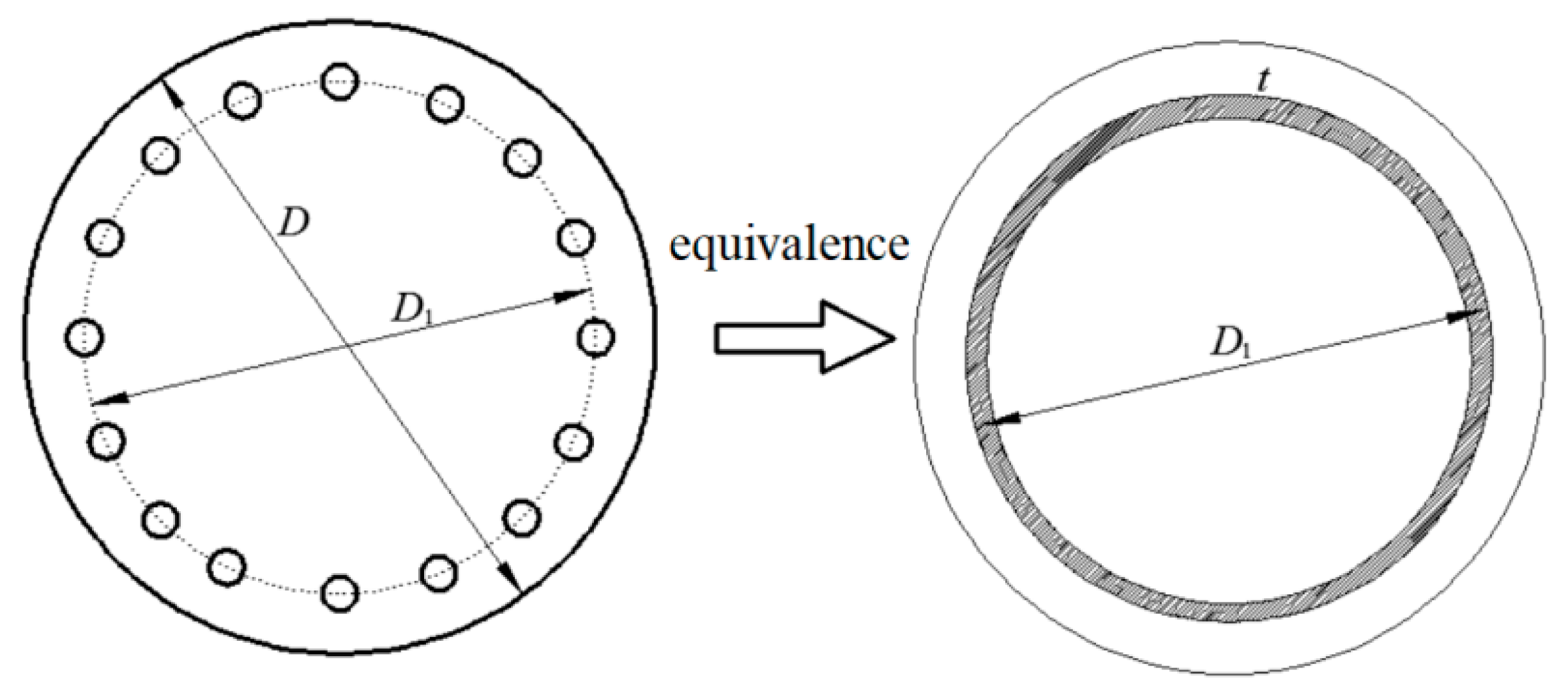
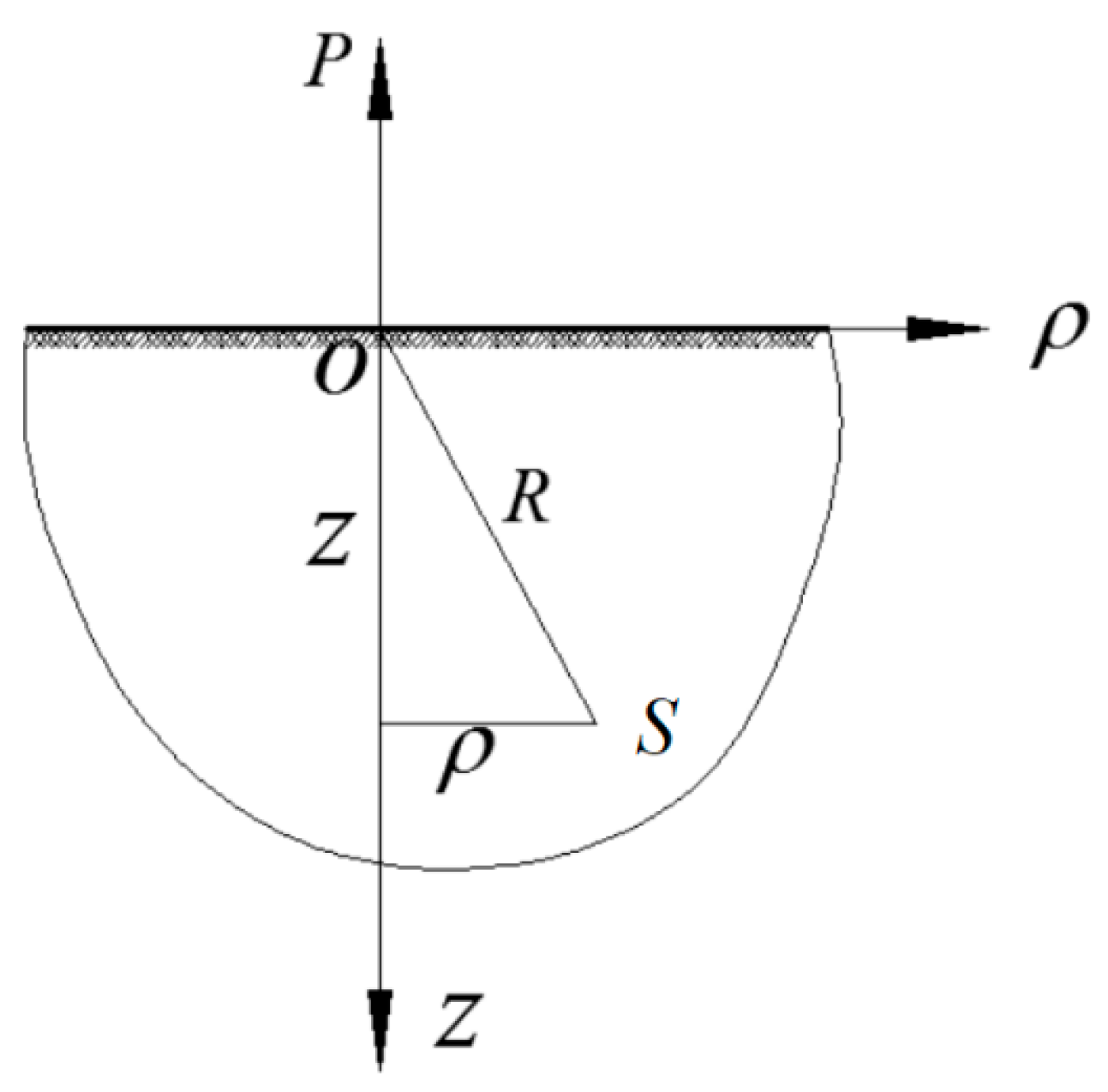
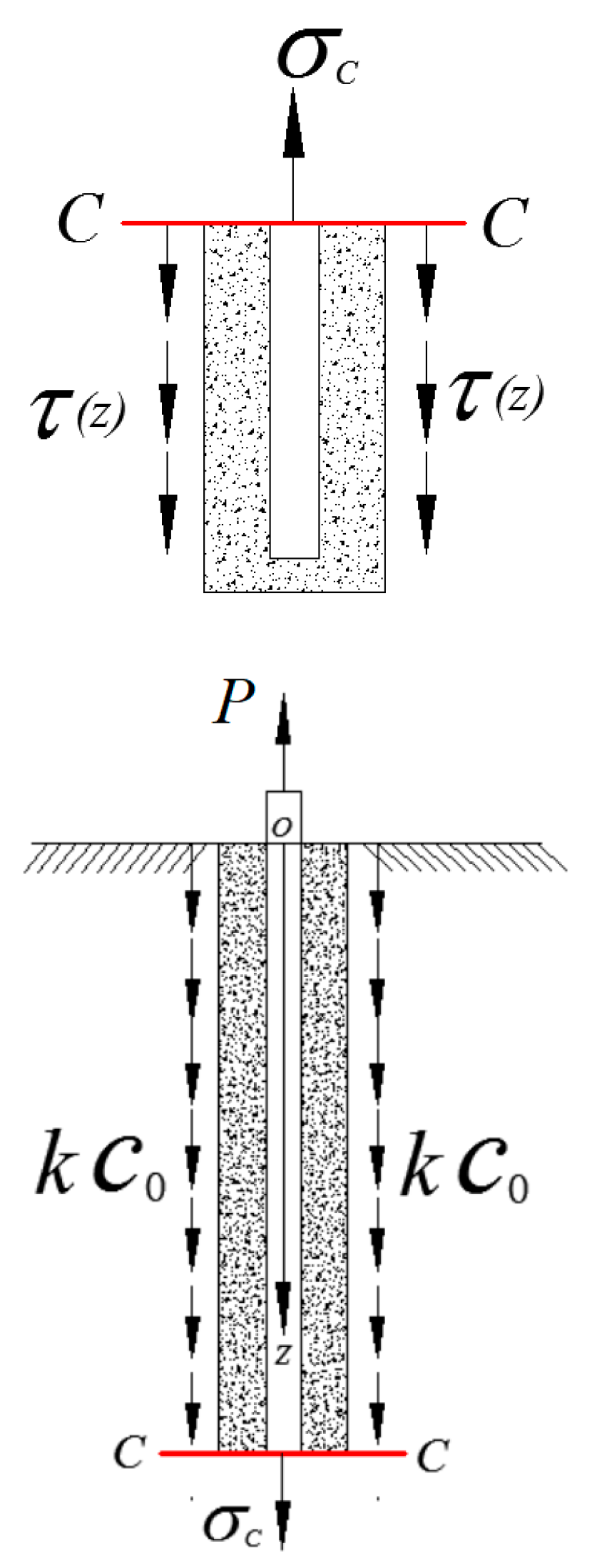
2.1. Elastic Analytical Solution of Prestressed Rock Anchors Under Uplift Force
2.2. Design of Prestressed Rock Anchors Based on Elastic Analysis
- (1)
- Rare Earthquake Condition
- (2)
- Rare Earthquake Condition
3. Establishment of the Mechanical Model for Anchor Pullout and Its Engineering Applications
3.1. Distribution Characteristics of Bond Strength at the Anchorage-Rock Interface and Definition of Effective Anchorage Length
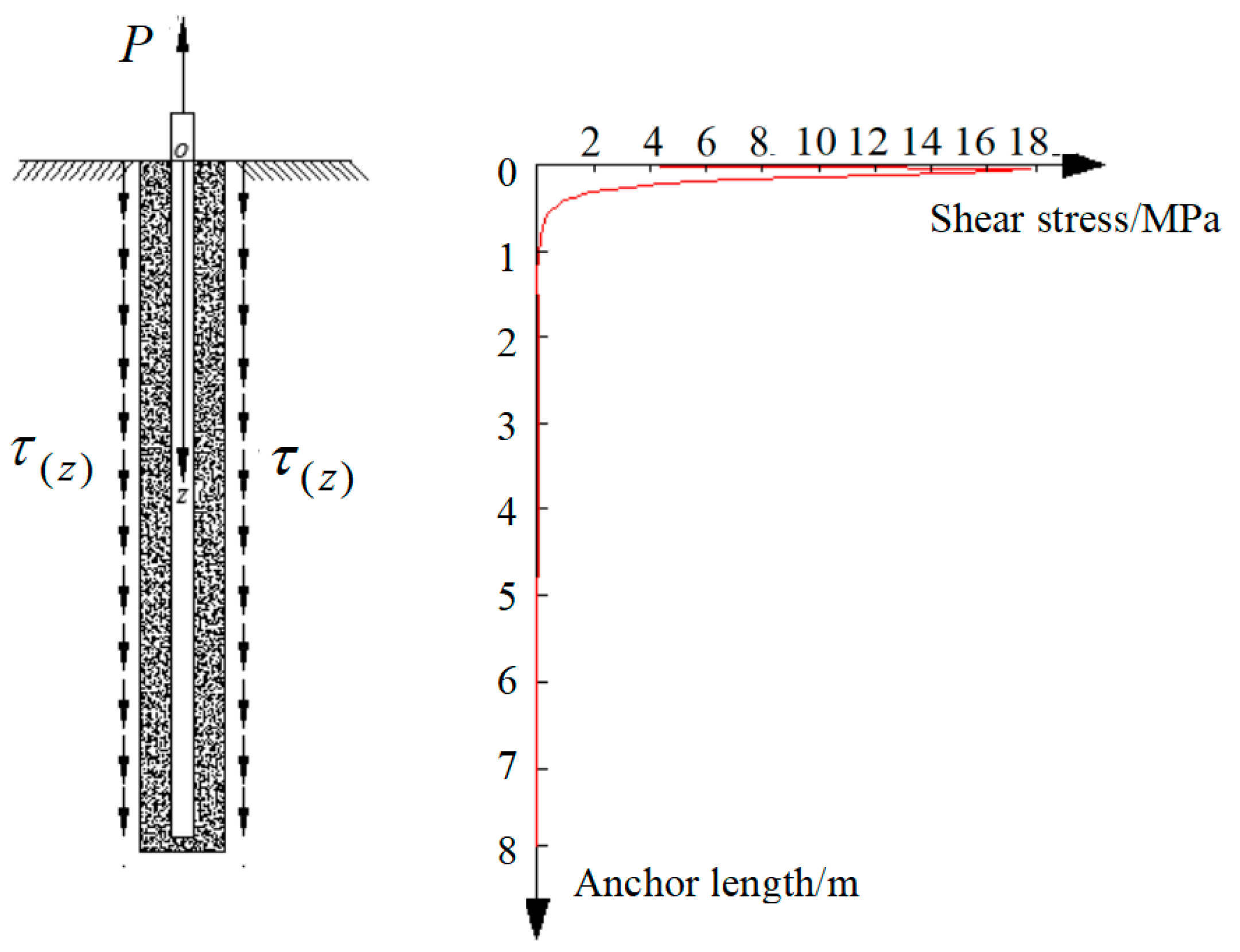
3.1.1. Non-Uniformity of Bond Strength Distribution at the Anchorage-Rock Interface
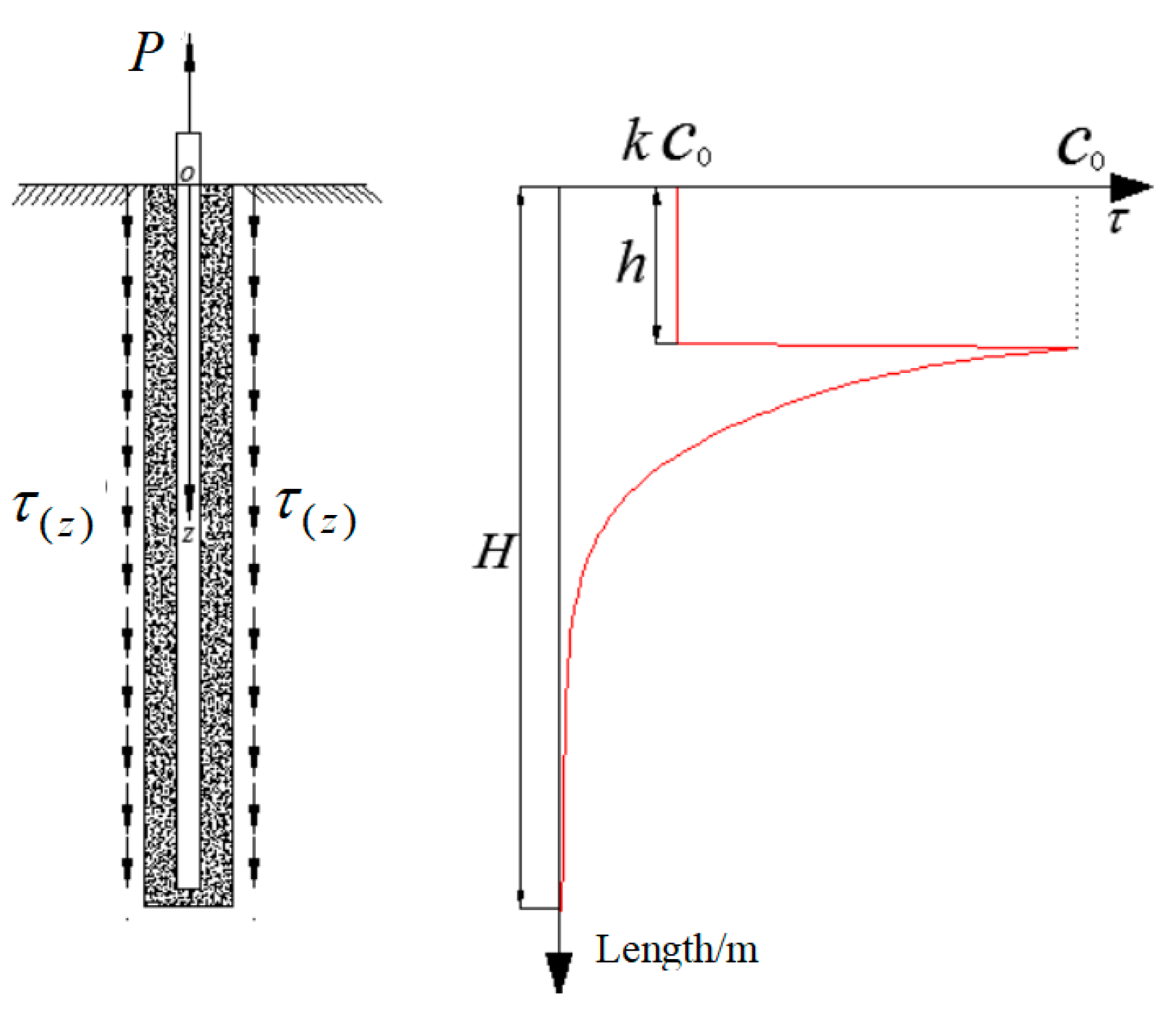
3.1.2. Definition of Effective Anchorage Length
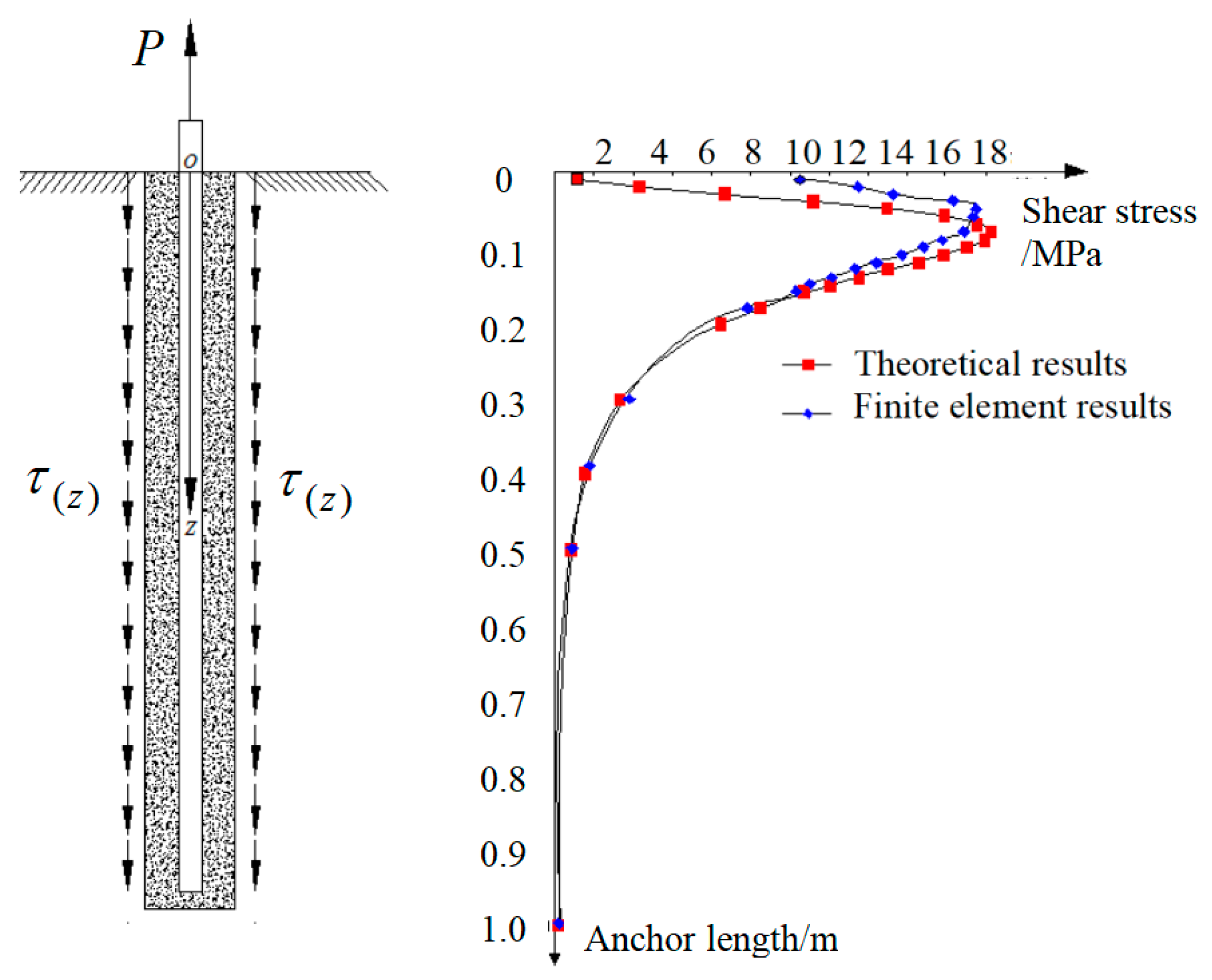
3.1.3. Numerical Verification of the Applicability of Theoretical Solutions for Concentrated Forces on Half-Space Bodies
3.2. Proposal and Establishment of the Mechanical Model for Anchor Pullout
3.2.1. Analysis of the Failure Mechanism at the Anchorage-Rock Interface During Anchor Pullout
3.2.2. Critical State of the Anchorage-Rock Interface During Anchor Pullout
3.2.3. Establishment and Solution of the Mechanical Model During Anchor Pullout
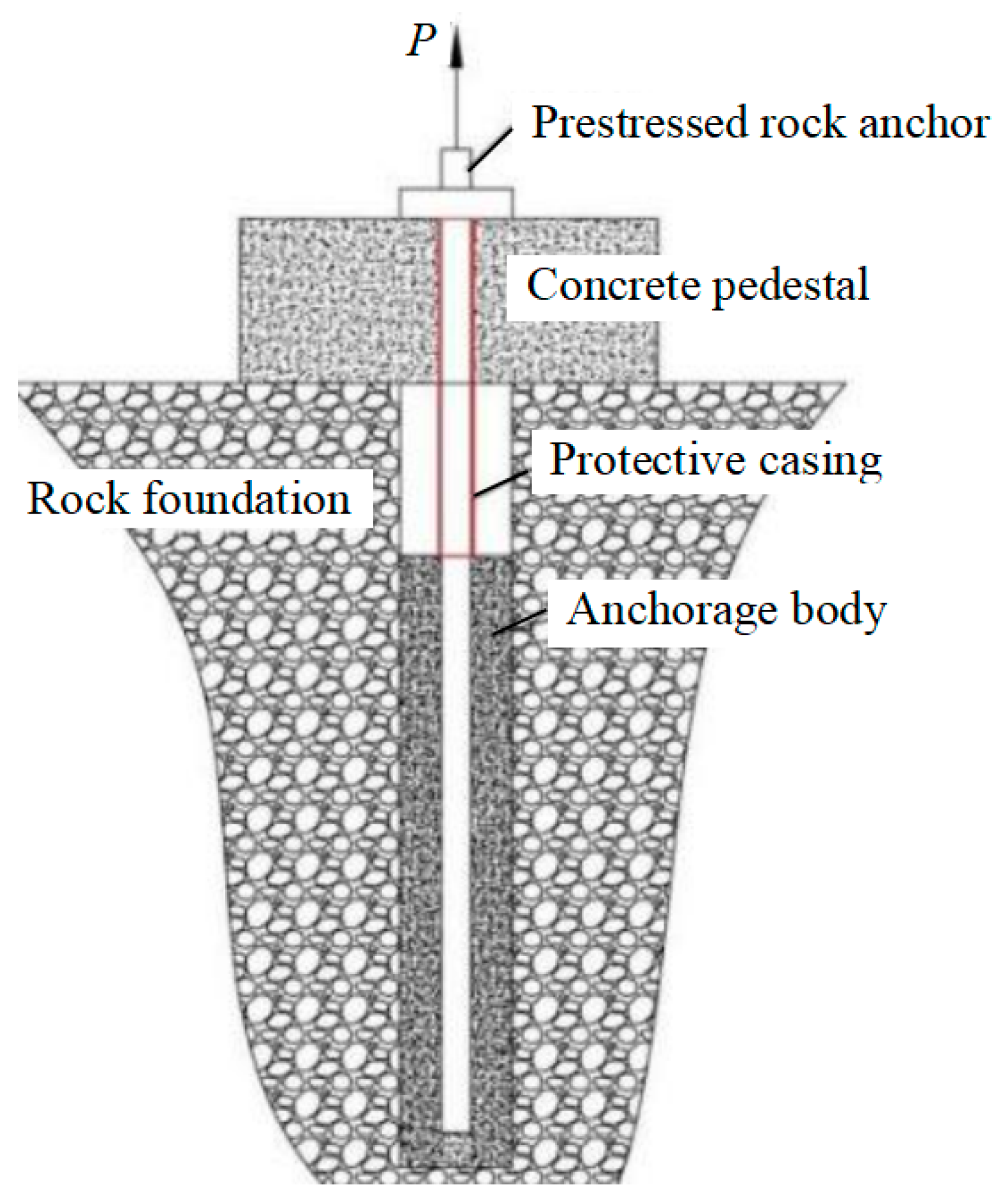
4. Full-Scale Testing Plan for the Uplift Bearing Capacity of Prestressed Rock Anchor Foundations
4.1. Test Loading Method and Load
4.2. Test Content and Procedure
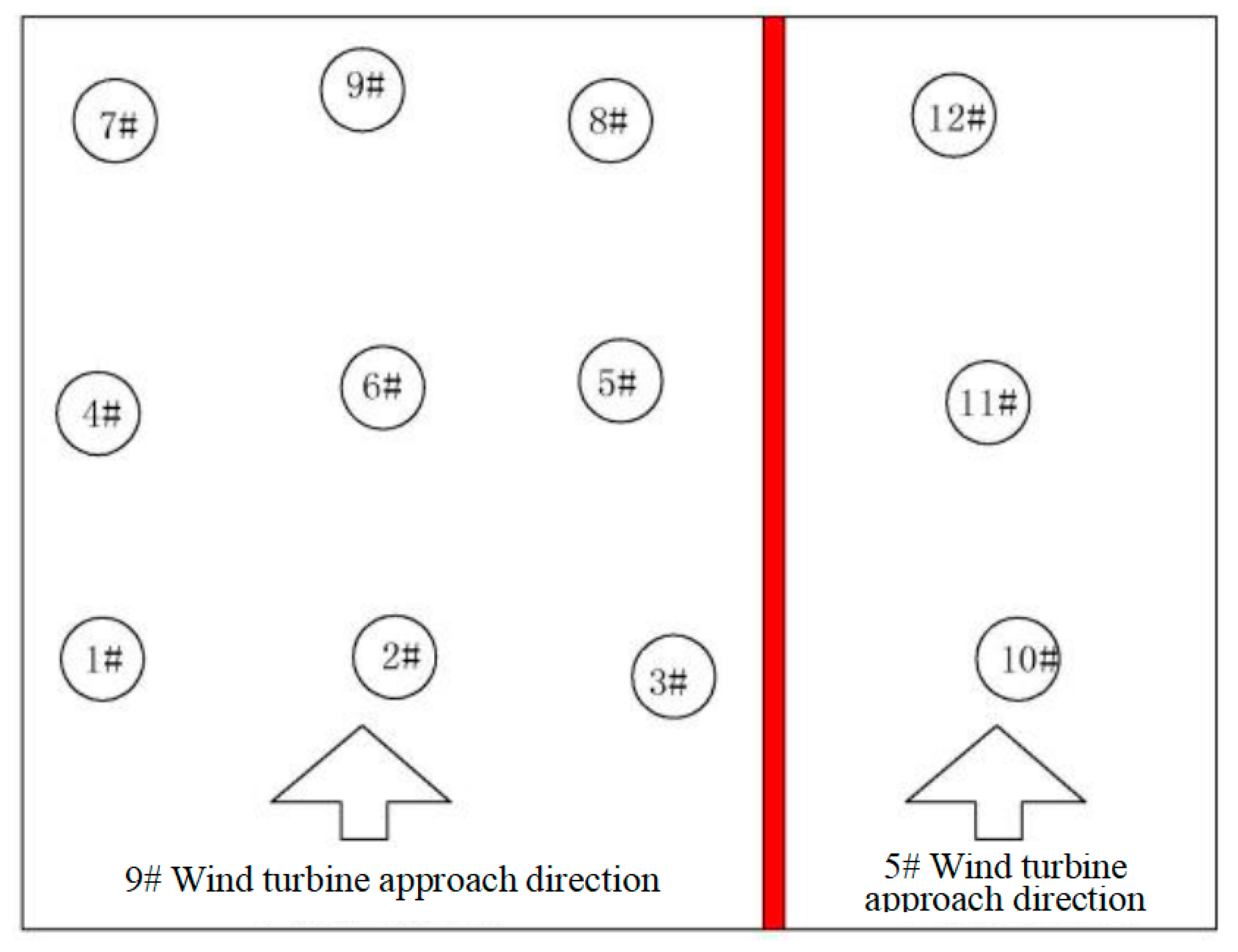
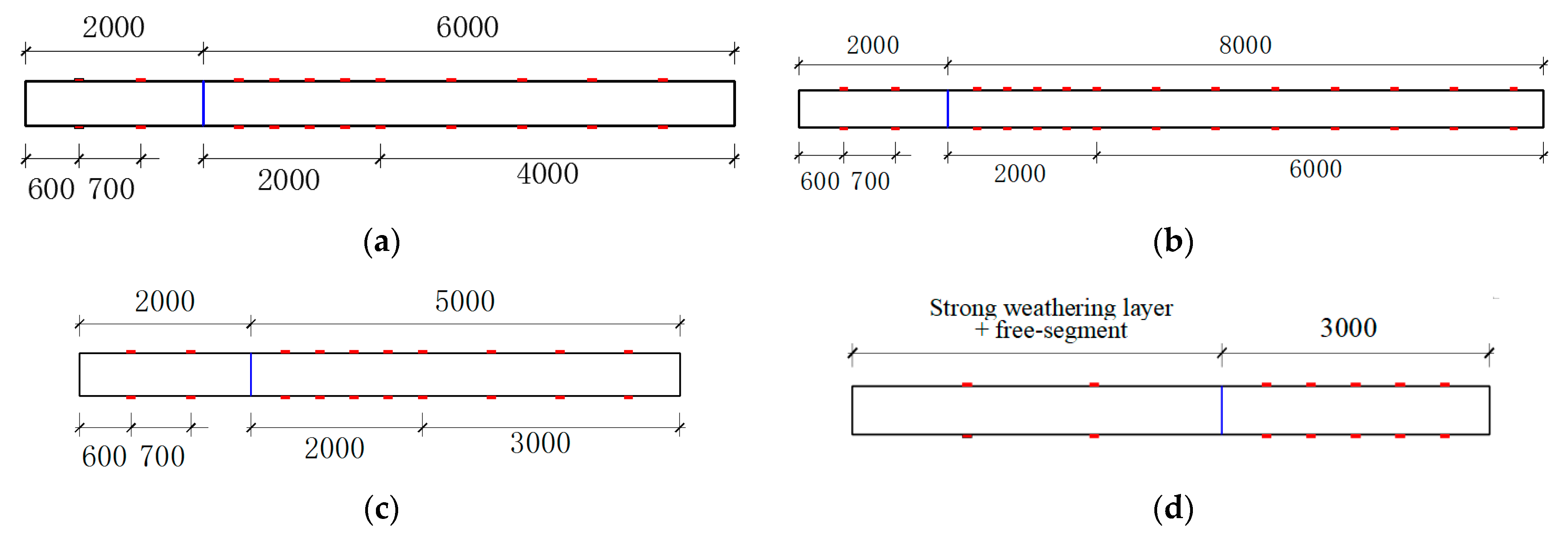
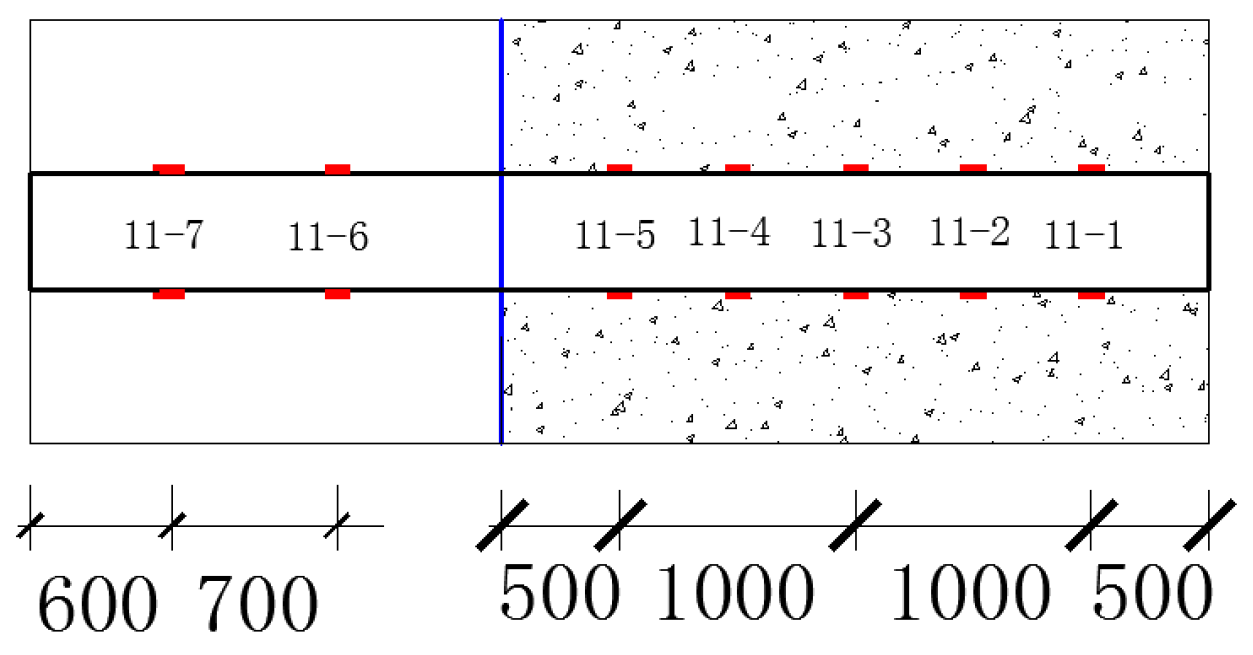
4.2.1. Sample Identification and Description
4.2.2. Test Measurement Content
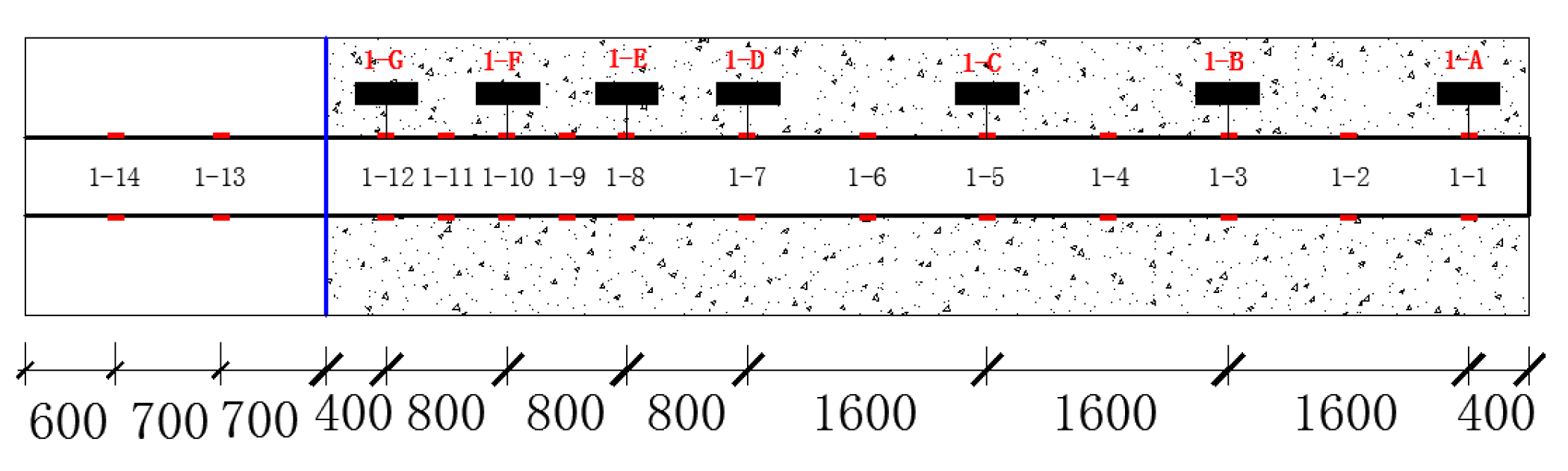
4.2.3. Overview of Strain Gauge Layout
4.2.4. Test Steps and Key Points
5. Processing and Analysis of Full-Scale Test Data for Rock Anchors
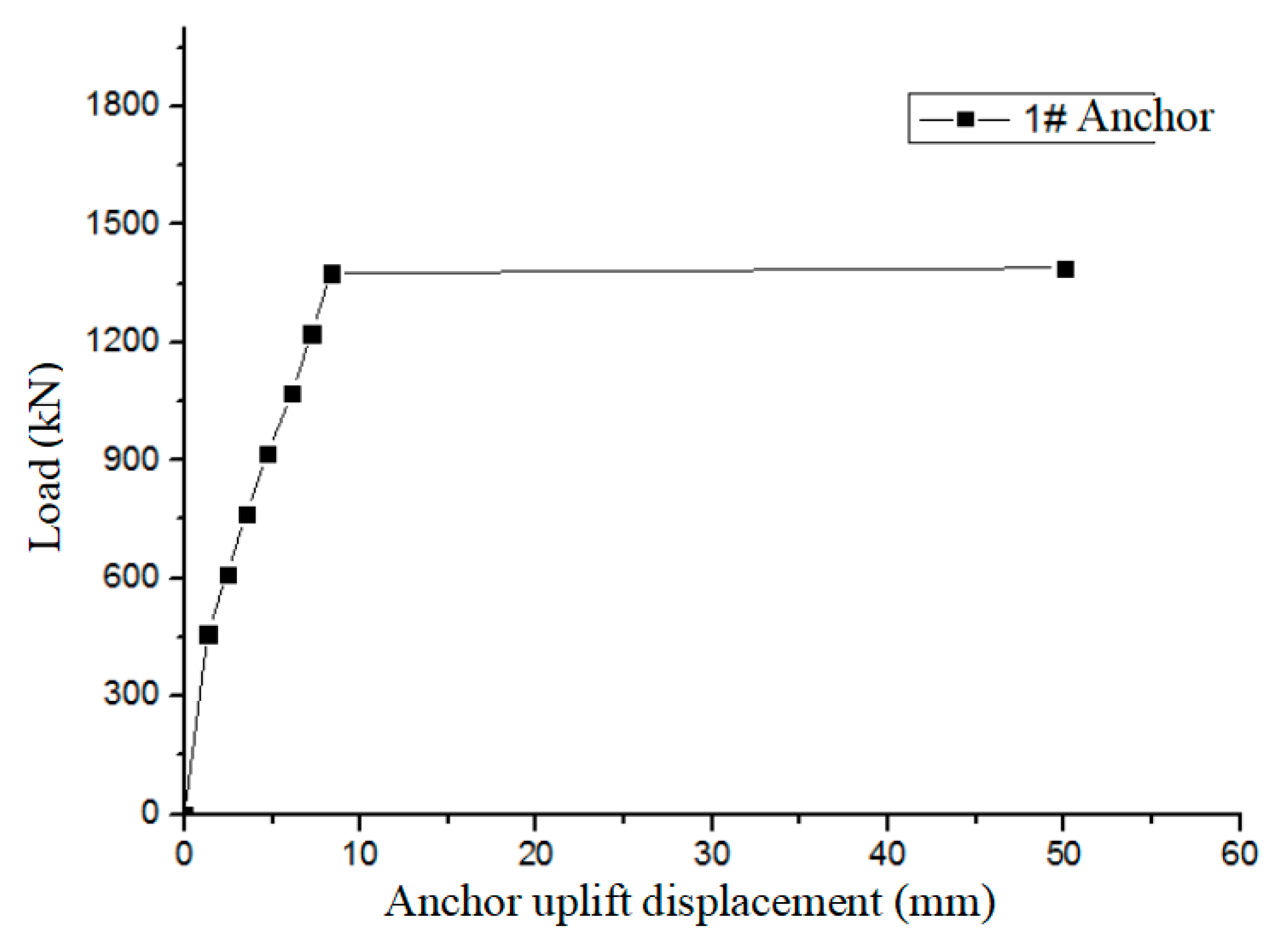
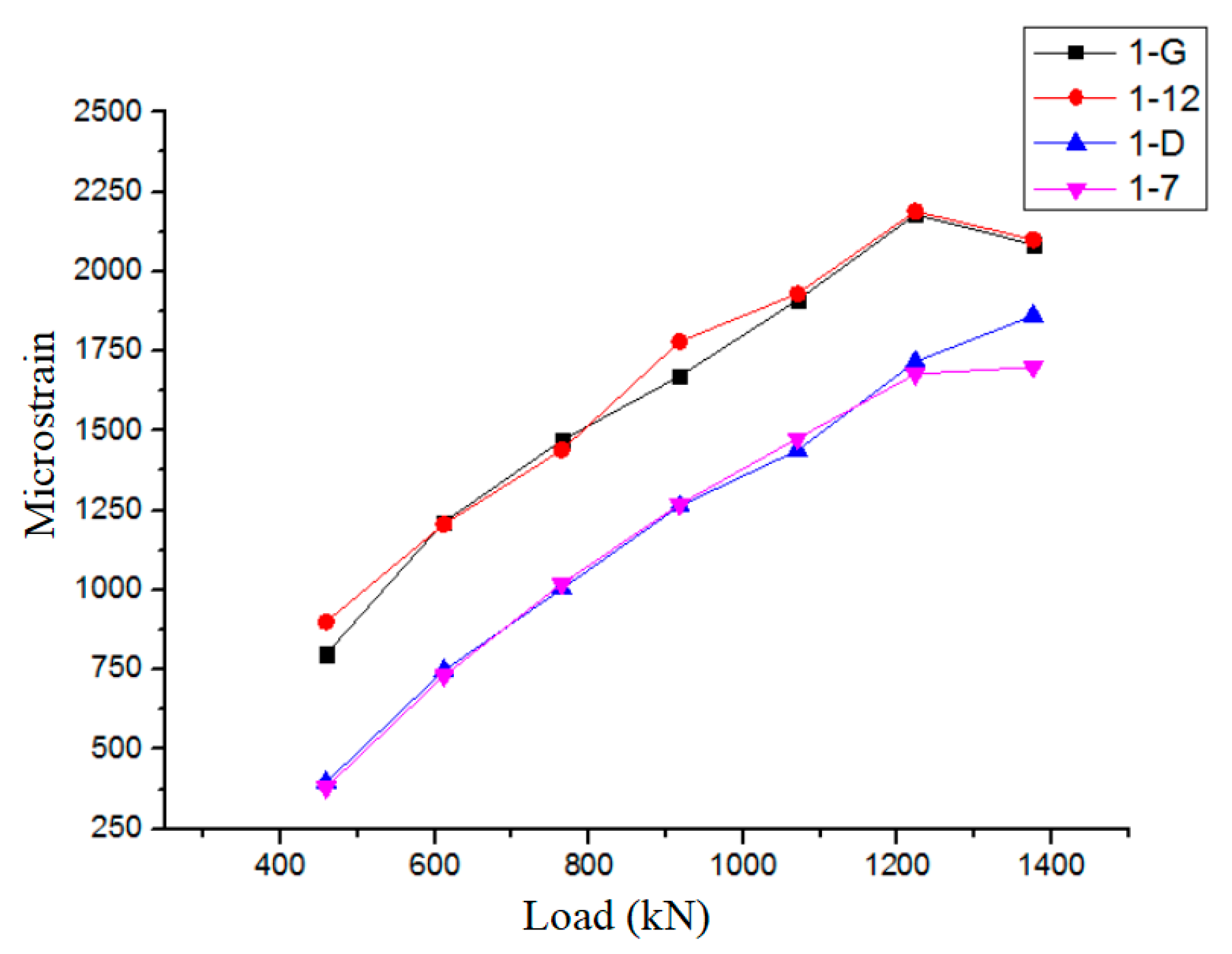
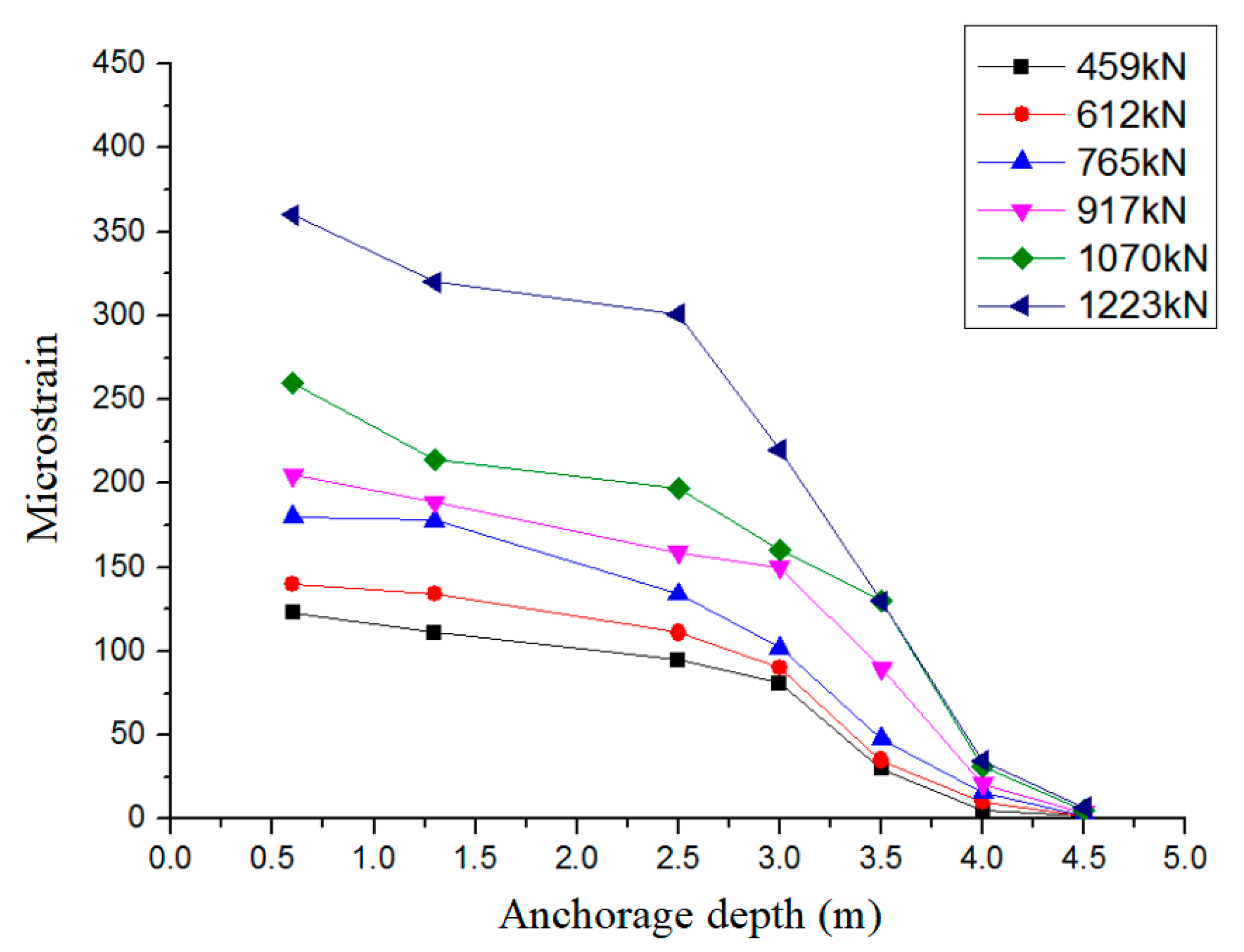
5.1. Data Processing for Each Anchor Test
5.2. Characteristic Values of Bond Strength at the Anchorage-Rock Interface
5.3. Calculation of Reasonable Anchorage Lengths to Meet Design Strength Requirement
- (1)
- Calculation of reasonable anchorage length under rare load conditions
- (2)
- Calculation of reasonable anchorage length under extreme load conditions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Krishta David, T.; Mansor, H.; Guan, J. Managing inverted arch heaving in Sanlian Tunnel: Analysis of inverted arch structure utilizing prestressed anchor rods. Geotech. Geol. Eng. 2024, 42, 4477–4507. [Google Scholar] [CrossRef]
- Yu, W.; Wang, B.; Zi, X.; Dong, J. Elastoplastic coupling analysis of surrounding rock-prestressed yielding anchor bolts/cables based on unified strength theory. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2024, 143, 105491. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, Z.; He, C.; Jiang, C.; Li, T. A solution method for tunnel supporting structure system incorporating the active control of surrounding rock deformation. Int. J. Geomech. 2024, 24, 04023243. [Google Scholar] [CrossRef]
- Li, P.; Chen, Y.; Huang, J.; Wang, X.; Liu, J.; Wu, J. Design principles of prestressed anchors for tunnels considering bearing arch effect. Comput. Geotech. 2023, 15, 105307. [Google Scholar] [CrossRef]
- Pi, J.; Zhao, Y.F.; Cao, R.L.; Jia, Z.X. Anchor spacing design of pre-stressed tunnel concrete lining with un-bonded annular anchors for Songhua River water supply project. Key Eng. Mater. 2017, 737, 505–510. [Google Scholar] [CrossRef]
- Wu, Y.; Fu, Y.; Hao, D.; Guo, G. Experimental research on the mechanical performance of the bolted rock under lateral impact load: Effect of prestress, body material, and anchorage style. Shock Vib. 2020, 2020, 8851364. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, L. Optimizing the design of rock anchors based on field tests. J. Geotech. Geoenviron. Eng. 2022, 148, 04021123. [Google Scholar]
- Li, G.; Hu, Y.; Tian, S.M.; Ma, W.; Huang, H.L. Analysis of deformation control mechanism of prestressed anchor on jointed soft rock in large cross-section tunnel. Bull. Eng. Geol. Environ. 2021, 80, 9089–9103. [Google Scholar] [CrossRef]
- Guo, X.; Zheng, X.; Li, P.; Lian, R.; Liu, C.; Shahani, N.M.; Wang, C.; Li, B.; Xu, W.; Lai, G. Full-stress anchoring technology and application of bolts in the coal roadway. Energies 2021, 14, 7475. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, L.; Liu, C.; Li, Y. Mechanism and application of new prestressed yield bolt for controlling deep high-stress rock mass. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2022, 119, 104254. [Google Scholar]
- Wang, Z.; Zhang, Z.; Dai, G.; Zhou, Y.; Su, T.; Ma, T. Seismic displacement analysis of slope reinforced by frame prestressed anchor rod structure. Soil Dyn. Earthq. Eng. 2024, 181, 108666. [Google Scholar] [CrossRef]
- Zeng, H.; Ye, S.; Zhang, J. Seismic stability analysis of slope reinforced by frame anchors considering prestress. KSCE J. Civ. Eng. 2024, 28, 1238–1252. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhu, Y.; Hou, H.; Li, L. Stability analysis of loess fill slope supported by frame prestressed anchors considering tensile strength cut-off. Sci. Rep. 2024, 14, 3007. [Google Scholar] [CrossRef]
- Ye, S.; Fang, G.; Zhu, Y. Model establishment and response analysis of slope reinforced by frame with prestressed anchors under seismic considering the prestress. Soil Dyn. Earthq. Eng. 2019, 122, 228–234. [Google Scholar] [CrossRef]
- Nakamoto, S.; Seki, S.; Iwasa, N.; Takemura, J. A centrifuge model study on a slope reinforced by rock bolts with prestressed facing plate. Jpn. Geotech. Soc. Spec. Publ. 2016, 2, 948–952. [Google Scholar] [CrossRef]
- Wang, H.; Cheng, J.-h.; Guo, Y.-c.; Gao, X.-j. Failure mechanism of soil nail—Prestressed anchor composite retaining structure. Geotech. Geol. Eng. 2016, 34, 1889–1898. [Google Scholar] [CrossRef]
- Fu, K.Y.; Wu, Z.Y.; Hao, Y.D. Experimental study on lateral impact resistance of the prestressed anchored rock mass. Arab. J. Geosci. 2023, 16, 569. [Google Scholar] [CrossRef]
- Kang, Y.; Hou, C.; Xu, C.; Liu, B.; Xiao, J. Investigation on mechanical behavior of pre-tensioned bolt in fractured rock mass using continuum discontinuum element method (CDEM). Eng. Anal. Bound. Elem. 2023, 151, 30–40. [Google Scholar] [CrossRef]
- Jiang, M.; Bo, Y.; Wang, H.; Che, N. Study on the reinforcement mechanism of grouted bolts with or without prestress via the hybrid DEM-FDM method. Transp. Geotech. 2023, 40, 100967. [Google Scholar] [CrossRef]
- Bui, T.Q. Finite element analysis of rock anchors in various geological conditions. Comput. Geotech. 2020, 120, 103426. [Google Scholar]
- Yang, X.; Zhang, T. The role of anchorage length in the performance of rock anchors. Int. J. Geomech. 2021, 21, 04020106. [Google Scholar]
- Zhao, T.; Wang, X.; Liu, G.; Zhu, J.; Yin, S. The thermal conductivity of graphite composite insulation boards: A theoretical and experimental study. Compos. Sci. Technol. 2024, 256, 11076. [Google Scholar] [CrossRef]
- Kumar, A. Assessment of the bond strength of rock anchors: A case study. Geotech. Test. J. 2020, 43, 546–558. [Google Scholar]
- Alavi, A.; Ranjbar, A. Laboratory investigation of the bond strength of rock anchors. Soils Found. 2018, 58, 675–689. [Google Scholar]
- Teng, T.; Chen, Y.; Wang, Y.; Qiao, X. In Situ Nuclear Magnetic Resonance Observation of Pore Fractures and Permeability Evolution in Rock and Coal under Triaxial Compression. J. Energy Eng. 2025, 151, 04025036. [Google Scholar] [CrossRef]
- Ranjbarnia, M.; Rashedi, M.M.; Dias, D. Analytical and numerical simulations to investigate effective parameters on pre-tensioned rockbolt behavior in rock slopes. Bull. Eng. Geol. Environ. 2022, 81, 74. [Google Scholar] [CrossRef]
- Xu, R.; Zhou, H. Experimental investigation of the anchoring effect of two different types of rock bolts on fractured rock. Adv. Mater. Sci. Eng. 2019, 2019, 9290318. [Google Scholar] [CrossRef]
- Zhao, T.; Wang, X.; Yin, S. Comprehensive average model for determining the effective thermal conductivity of graphite composite insulation boards: Experimental validation and numerical simulation verification. J. Build. Eng. 2024, 95, 110217. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, Y.; Huang, D. Prestress loss mechanism and constitutive model of an anchored joint rock mass under low-frequency fatigue loading. Rock Mech. Rock Eng. 2022, 56, 1517–1535. [Google Scholar] [CrossRef]
- Xu, Z.L. Elementary Course on Elastic Mechanics, 5th ed.; Higher Education Publisher: Beijing, China, 2018; pp. 181–182. [Google Scholar]
- GB 50007-2011; Code for Design of Building Foundation. China Architecture & Building Press: Beijing, China, 2011.
- JGJ 106-2014; Technical Code for Testing of Building Foundation Piles. China Architecture & Building Press: Beijing, China, 2014.







| Load Condition | (kN) | (kN) | (kN) | (kN·m) |
|---|---|---|---|---|
| Normal Operating Load | 430.2 | 0 | 2948.1 | 31,616 |
| Extreme Load Condition | 836 | 0 | 3000.6 | 60,785 |
| Rare Earthquake Condition | 1267.008 | 0 | 2468.166 | 91,927.91 |
| Anchor Circle Radius | Number of Anchors | Uplift Force (kN) | Prestress P (kN) | Maximum Compressive Stress in Pedestal (MPa) | Maximum Tensile Stress in Pedestal (MPa) |
|---|---|---|---|---|---|
| 5.5 | 36 | 1506 | 1500 | 1.08 | −0.009 |
| 5.5 | 24 | 1506 | 1500 | 0.93 | 0.151 |
| 5.5 | 24 | 1206 | 1200 | 0.864 | 0.215 |
| 5.5 | 20 | 1206 | 1200 | 0.822 | 0.258 |
| 5.5 | 16 | 1206 | 1200 | 0.78 | 0.301 |
| Anchor Circle Radius | Number of Anchors | Uplift Force (kN) | Prestress P (kN) | Maximum Compressive Stress in Pedestal (MPa) | Maximum Tensile Stress in Pedestal (MPa) |
|---|---|---|---|---|---|
| 5.5 | 24 | 1404 | 1400 | 0.728 | −0.015 |
| 5.5 | 20 | 1404 | 1400 | 0.679 | 0.035 |
| 5.5 | 20 | 1204 | 1200 | 0.644 | 0.07 |
| 5.5 | 16 | 1204 | 1200 | 0.601 | 0.113 |
| 5.5 | 12 | 1204 | 1200 | 0.559 | 0.155 |
| Test Group and ID | Anchorage Depth (m) | Free-Segment Depth (m) | Total Bore Depth | Smooth/Rough |
|---|---|---|---|---|
| Group 1: 1,2,3 | 6 (Strongly Weathered) + 0 (Moderately Weathered) | +2 | 8 m | Rough |
| Group 2: 4,5,6 | 8 (Strongly Weathered) + 0 (Moderately Weathered) | +2 | 10 m | |
| Group 3: 7,8,9 | 5 (Strongly Weathered) + 0 (Moderately Weathered) | +2 | 7 m | |
| Group 4: 10,11,12 | (Through Strongly Weathered) + 3 (Moderately Weathered) | >+2 | >5 m |
| No. | 1–13 | 1–14 | ||||
|---|---|---|---|---|---|---|
| Measured Values ) | Theoretical Value ) | Error Percentage (%) | Measured Values ) | Theoretical Value ) | Error Percentage (%) | |
| 6 MPa | 1106 | 1168.7 | 5.4 | 1094 | 1168.7 | 6.4 |
| 8 MPa | 1530 | 1558.3 | 1.8 | 1498 | 1558.3 | 3.9 |
| 10 MPa | 1930 | 1947.8 | 0.9 | 1896. | 1947.8 | 2.7 |
| 12 MPa | 2309 | 2337.4 | 1.2 | 2215 | 2337.4 | 5.2 |
| 14 MPa | 2598.0 | 2726.9 | 4.7 | 2556.0 | 2726.9 | 6.3 |
| 16 MPa | 2987.0 | 3116.5 | 4.2 | 3076.0 | 3116.5 | 1.3 |
| 18 MPa | 3417.0 | 3506.1 | 2.5 | 3408.0 | 3506.1 | 2.8 |
| No. | Anchorage Depth (m) | Free Length (m) | Loading Method | Load Capacity (kN) |
|---|---|---|---|---|
| 1 | 8 | 2 | Conventional Pullout | 1376 |
| 2 | 8 | 2 | Conventional Pullout | 765 |
| 3 | 8 | 2 | Conventional Pullout | 612 |
| 4 | 6 | 2 | Conventional Pullout | 1300 |
| 5 | 6 | 2 | Free Length Grouted + Steel Tube | 1070 |
| 6 | 6 | 2 | Free Length Grouted | 917 |
| 7 | 5 | 2 | Conventional Pullout | 1223 |
| 8 | 5 | 2 | Grouted + Steel Tube + Steel Beam | <500 |
| 9 | 5 | 2 | Conventional Pullout | 720 |
| 10 | 4.5 | 0 | Free Length Grouted + Steel Ring | 2003 |
| 11 | 3 | 2 | Conventional Pullout | 1223 |
| 12 | 5 | 0 | Free Length Grouted + Steel Ring | 1529 |
| Site | Anchor No. | Measured Bond Strength (MPa) | Characteristic Bond Strength (MPa) |
|---|---|---|---|
| 9# | 1 | 0.873 | 0.436 |
| 2 | 0.485 | 0.243 | |
| 3 | 0.387 | 0.194 | |
| 4 | 1.102 | 0.551 | |
| 5 | 0.907 | 0.453 | |
| 6 | 0.778 | 0.389 | |
| 7 | 1.246 | 0.623 | |
| 8 | - | - | |
| 9 | 0.734 | 0.367 | |
| 5# | 10 | 1.283 | 0.642 |
| 11 | 1.213 | 0.607 | |
| 12 | 0.876 | 0.438 |
| Site | Anchor No. | Test Anchorage Length (m) | Reasonable Anchorage Length Under Rare Load (m) | Reasonable Anchorage Length Under Extreme Load (m) |
|---|---|---|---|---|
| 9# | 1 | 8 | 17.46 | 16.30 |
| 2 | 8 | 31.42 | 29.30 | |
| 3 | 8 | 39.34 | 36.68 | |
| 4 | 6 | 13.85 | 12.90 | |
| 5 | 6 | 16.83 | 15.69 | |
| 6 | 6 | 19.62 | 18.29 | |
| 7 | 5 | 12.26 | 11.43 | |
| 8 | 5 | - | - | |
| 9 | 5 | 20.79 | 19.38 | |
| 5# | 10 | 4.5 | 6.64 | 6.21 |
| 11 | 3 | 7.01 | 6.55 | |
| 12 | 5 | 9.61 | 8.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, X.; Zhu, R.; Huang, Z.; Xiao, F.; Yin, H.; Zhao, T.; Huang, M. Mechanical Analysis and Prototype Testing of Prestressed Rock Anchors. Buildings 2025, 15, 3952. https://doi.org/10.3390/buildings15213952
Xiao X, Zhu R, Huang Z, Xiao F, Yin H, Zhao T, Huang M. Mechanical Analysis and Prototype Testing of Prestressed Rock Anchors. Buildings. 2025; 15(21):3952. https://doi.org/10.3390/buildings15213952
Chicago/Turabian StyleXiao, Xianzhi, Risheng Zhu, Zhi Huang, Fengying Xiao, Huajie Yin, Tengfei Zhao, and Mojia Huang. 2025. "Mechanical Analysis and Prototype Testing of Prestressed Rock Anchors" Buildings 15, no. 21: 3952. https://doi.org/10.3390/buildings15213952
APA StyleXiao, X., Zhu, R., Huang, Z., Xiao, F., Yin, H., Zhao, T., & Huang, M. (2025). Mechanical Analysis and Prototype Testing of Prestressed Rock Anchors. Buildings, 15(21), 3952. https://doi.org/10.3390/buildings15213952






