Abstract
It is a well-known fact that the value of the Bond work index (wi) for a given ore varies along with the grinding size. In this study, a variability bysis is carried out with the Bond standard grindability tests on different critical metal ores (W, Ta), ranging from coarse grinding (rod mills) to fine grinding (ball mills). The relationship between wi and grinding size did not show a clear correlation, while the grindability index (gpr) and the grinding size showed a robust correlation, fitting in all cases to a quadratic curve with a very high regression coefficient. This result suggests that, when performing correlation studies among ore grindability and rock mechanics parameters, it is advised to use the grindability index instead of the Bond work index.
1. Introduction
Comminution is an essential operation for the mining and mineral processing industry. It also plays a central role in the cement production, ceramics and chemical industries. In the mineral industry, the liberation of valuable minerals from the gangue is a fundamental requirement for all subsequent separation or extraction operations, and this is achieved through several stages of rock fragmentation, that is, by comminution of the ore [1].
Schönert [2] estimated that minerals comminution consumes 3% of all the energy produced by industrialized countries, in line with former studies [3]. More recent evaluations estimate that comminution operations are responsible for 3–5% of energy consumption at a global scale [4]. Moreover, in terms of OPEX in mineral processing plants, comminution operations amount to 40–50% of the energy consumption.
Considering the above, any gain in efficiency can significantly impact the plant operating costs and the consequent conservation of resources [5]. In this sense, an improvement in knowledge of ore grinding behavior can allow modification of the operation and control strategies of the grinding operations, resulting in significant energy savings. This would increase the competitiveness of operations and reduce emissions.
It is common to process multicomponent ores, made up of at least two mineralogical components with differences in their physical and physicomechanical properties. Some authors [6,7] show that disregarding the variability of the feed mineralogical composition produces large deviations in the planned metallurgical efficiency, along with problems in the treatment of the ores with such characteristics. On the other hand, between the initial exploration work for the design of any mineral beneficiation plant and the reaching of its full operating regime, and even after reaching it, there will be variations in the plant feed composition, implying substantial changes in mineral properties. Therefore, it would be advisable to adjust the operating and control conditions of the treatment plant in general and the size reduction section in particular.
The energy–size relationships in comminution processes have been an object of research since the first industrial revolution [8]. Rittinger [9] proposed the first law of comminution, supposing that the amount of created surface is proportional to the specific energy consumption in grinding operations, as expressed in Equation (1):
where E is the specific energy consumption [kWh/t], KR is the proportionality coefficient and P and F are the particle sizes of the product and feed, respectively [µm].
Kick [10], in the second law of comminution, argued that according to his calculations, the specific energy consumption would be proportional to the volume reduction, as expressed in Equation (2), where KK is a different proportionality coefficient.
The differences between the Rittinger and Kick models lasted for years, until the proposal of the third theory of comminution by F. Bond [11,12,13], which is summarized in Equation (3),
where KB = 10·wi, and wi is expressed in kWh/t.
Subsequent studies [14] explained that the three laws derive from a generalized comminution differential equation, each one best applied to a different size range (Rittinger’s law for fine grinding; Bond’s law for coarse grinding and secondary/tertiary crushing; and Kick’s law for primary crushing). The novelty in the third law’s proposal was the procedure for determining wi in the case of crushing, rod milling and ball milling [13,15]. The practical interest of wi is unquestionable. From a technical perspective, it constitutes the most reliable method of characterizing ore grindability when designing the necessary tumbling mills to process that ore. Bearman et al. (1997) showed that other mechanical characterization tests are insufficient when predicting the grinding ore behavior.
A logical reasoning process should suggest finding some correlation among mechanical parameters (hardness, Young’s modulus, uniaxial compression strength (UCS), etc.) and the ore grinding behavior. Several researchers [4,16,17,18] followed that inspiration, but no generalizable results have been obtained since grindability behavior is usually evaluated under closed-circuit conditions, which means that not only breakage but breakage plus classification operations are involved. Moreover, we can easily find ores with high hardness and high grindability values, but among the highest grindability values, we can find quite soft ores (graphite or mica group minerals). On the other hand, diamond mineral shows modest grindability values. Thus, it is worth emphasizing that the Bond work index tries to characterize the ore grinding behavior in a closed circuit, encompassing the ore mechanical behavior before the mill action (i.e., whatever the type of the mill and its characteristics of action), but also the screening or classification stage involved in the closed circuit, which is greatly influenced by product size and shape.
Due to the fact that Bond’s proposal was undoubtedly linked to a market-dominant firm, i.e., Allis Chalmers, which even owned the patent of the standard mill, several proposals soon emerged to define alternative test approaches, which can be grouped in the following types:
- Indirect work index determination in other lab mills [19,20,21,22,23,24].
- Specific energy determination from correlations in different devices [25,26,27].
- Work index calculation through lab tests and simulation [28,29,30,31].
It is essential to notice that despite the almost unanimous consideration of the wi as the characteristic parameter of ore grinding behavior, it is not fully understood at the industrial level, even being handled as a constant value. Bond himself usually reported in his papers separately the grindability values for the Bond rod mill test (BRM) and the Bond ball mill test (BBM), but no study could be found analyzing the information from BRM and BBM test values and deepening them to explain the variability obtained.
In this work, the analysis of grindability results obtained in a broad particle size range and several critical metal ores (W, Ta) is carried out. The variability of the work indices in BRM and BBM tests is studied to propose a methodology to model said variability.
2. Materials and Methods
2.1. Materials
This study was carried out on three ores from W mines and two ores from a Ta mine. Two of the W ore samples were Scheelite ores, received from Barruecopardo (Spain) and Mittersill (Austria). A detailed description of Barruecopardo ore can be found in recent publications [32,33]. In the case of Mittersill, an ore description can be found in [34]. The third W ore was Wolframite from the Panasqueira Mine (Portugal), and a detailed description of this ore can be found in [35]. In the case of Ta ores, two different samples were received from Penouta Mine (Spain), one from the open pit and the other one from the tailings pond of the former Tin mining activities in that mine. Characterization studies of those samples have been previously published [36,37]. It must be pointed out that, in the particular case of Barruecopardo mine, two different samples were taken from different heaps. The sample size in each case, considering the largest particle size, was enough to perform the series of Bond ball mill grindability tests separately (see Section 2.2), but not enough to perform the series of Bond rod mill grindability tests separately for each sample (see Section 2.3). Accordingly, it was decided to blend and homogenize the Barruecopardo samples and perform the rod mill test on the samples blend.
2.2. Bond Ball Mill (BBM) Standard Test
The procedures to carry out the Bond grindability tests in ball mills and rod mills are outlined in Section 2.2 and Section 2.3. They are usually referred to as the standard tests, but it must be highlighted that the procedures haven’t been defined by ISO or ASTM standards. The closest attempt to a standard definition was the initiative of the Global Mining Standard Group [38].
The Bond work index most commonly referred to is the BBM work index. This value is obtained in a 12” × 12” laboratory mill running at 70 rpm, with rounded inner edges and without lifters. The grinding charge is comprised of a distribution of steel balls with several diameters. Table 1 shows the original Bond proposal [13], while the last Bond recommendation can be found in Table 2 [39].

Table 1.
Ball grinding charge distribution proposed by Bond.

Table 2.
Ball charge distribution used in this research.
The mill feed must be prepared by controlled crushing until 100% passes through a 6 Tyler mesh (3.35 mm). The first grinding cycle feed must be 700 cm3, and this volume’s weight is fixed as the mill charge in all subsequent cycles. Additionally, fresh feed particle size distribution (PSD) is obtained to calculate the 80% passing size (F80) and undersize weight already present in the feed.
The test procedure consists of performing several dry grinding cycles to simulate a continuous closed-circuit operation with 250% circulating load (Figure 1). The circuit is closed by a sieve (P100) selected according to the industrial grinding size target, always between 28 and 325 Tyler mesh (40–600 microns).
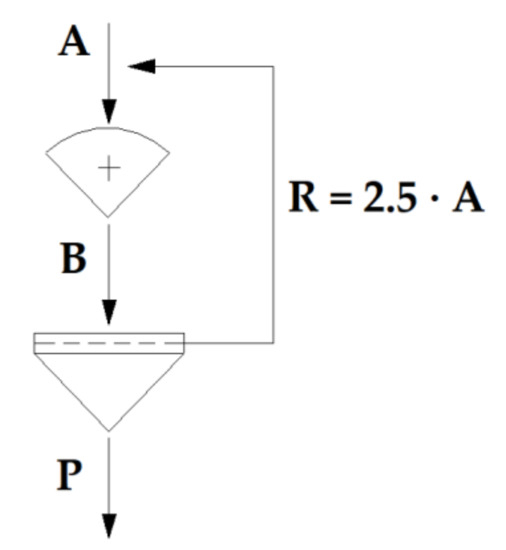
Figure 1.
Closed-circuit BBM test objective layout.
The first cycle starts with an arbitrary number of mill revolutions, usually 100 revolutions with hard-to-grind ores and 50 revolutions with soft ores. The first run product is sieved, the undersize is weighed, and the net grams produced (gpr) of the first run is calculated, considering the undersize already present in the feed.
The second cycle feed is constituted by the former cycle’s oversize product plus enough fresh feed to complete the initial 700 cm3 weight. The second cycle number of revolutions is calculated considering the predefined circulating load value (250%), according to Equation (4),
where ni is the number of mill revolutions at run i; PS is the expected product weight once it reaches the steady state (g), calculated by dividing the initial 700 cm3 weight by 3.5; Ff,i is the weight of fines already in the feed (g), which can be calculated from the feed PSD and the total fresh feed weight added in the run i (which equals the total undersize product in the run i−1) and gpri−1 is the net grams produced in the previous run, i−1.
Subsequent grinding cycles are carried out (at least five) until gpr reaches equilibrium. The final value of gpr is calculated as the average of the last three cycles. The final cycle product PSD is calculated to obtain P80, and the BBM work index can be calculated using Equation (5),
where the BBM work index, wi, is expressed in kWh/sht; P100, F80 and P80 are expressed in microns and gpr is expressed in g/rev. Bond named gpr as the grindability index.
According to Bond [13], wi should conform with the motor output power to an average overflow ball mill of 8 ft inner diameter grinding wet in a closed circuit. This value should be multiplied by correcting factors to conform with other situations, such as dry grinding (at least 1.30) or different inner mill diameters. A complete and updated description of correction factors was written by Rowland [40].
2.3. Bond Rod Mill (BRM) Standard Test
In this case, the procedure is very similar to BBM test, and only some differences are commented on [13]. The feed must be prepared until 100% passes ½” (1, 27 mm), with a feed volume of 1250 cm3. Dry grinding cycles are performed with 100% circulating load in a laboratory rod mill 12” × 24” with a wave-type lining, running at 46 rpm. The grinding charge consists of six 1.25” diameter and two 1.75” diameter steel rods 21” long, weighing 33.380 kg. In this case, P100 values can range from 4 to 65 Tyler mesh (4.7 mm to 200 microns).
In order to equalize segregation at the mill ends, it is rotated level for eight revolutions, then tilted up 5° for one revolution, down 5° for another revolution and returned to level for eight revolutions continuously through each grinding cycle. At the end of each cycle, the mill is discharged by tilting downward at 45° for 30 revolutions. Once equilibrium is reached, gpr and P80 are calculated, and the BRM work index is calculated from Equation (6).
Again, wi should conform with the motor output power to an average overflow rod mill of 8 ft inner diameter grinding wet in an open circuit.
2.4. Grindability Tests
A series of tests was defined to analyze the variation of grindability properties in the selected ores. Depending on sample availability, a minimum of three BBM tests and a minimum of 2 BRM tests were performed, each test at a different P100 for every ore. Then, the values of gbp and wi were obtained for each ore, and an attempt to model their variation with P100 was performed in each case. Full details of the performed tests and results are available in the supplementary material.
It is generally accepted that, provided samples are representative, BBM and BRM grindability test repetitions are unnecessary. This is justified by the iterative nature of the grindability tests procedures, and both rod and ball mill tests’ repeatability were proven to be less than ±4% at two standard deviations [41].
3. Results and Discussion
In the case of Penouta tailings pond ore, the variation of wi versus P100 is plotted in Figure 2, for both BBM and BRM tests. The obtained values show a lack of continuity, and a clear trend function could hardly be defined. Nonetheless, when observing Figure 3, which depicts the variation of gpr versus P100 in both BBM and BRM tests, a fairly clear trend can be seen; according to this, Figure 3 also shows the quadratic fit of gpr consolidated values versus P100, with a determination coefficient of 99.76%.
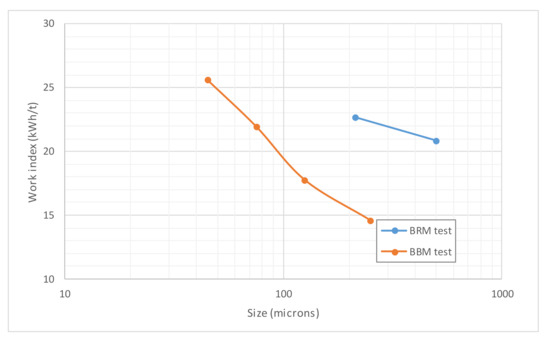
Figure 2.
Variation of BBM and BRM wi values with P100, Penouta tailings pond ore.
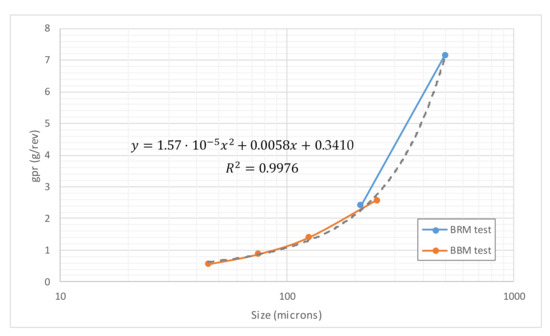
Figure 3.
Variation of BBM and BRM gpr values with P100, Penouta tailings pond ore.
A similar analysis was performed in the case of Penouta mine ore (see Figure 4 and Figure 5). In this case, despite wi versus P100 plot revealing a lack of continuity again (Figure 4), plotting gpr versus P100 (Figure 5) showed a similar trend to the previous ore. Moreover, the quadratic fit was almost perfect in this case, with a coefficient of determination of 100.00%.
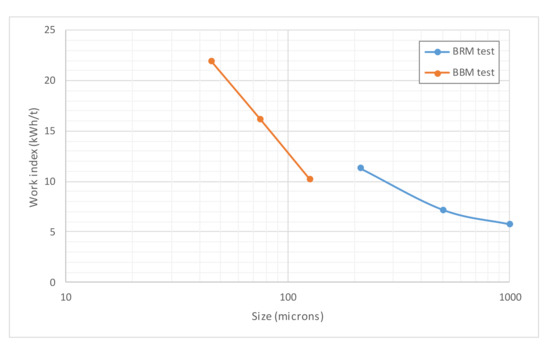
Figure 4.
Variation of BBM and BRM wi values with P100, Penouta mine ore.
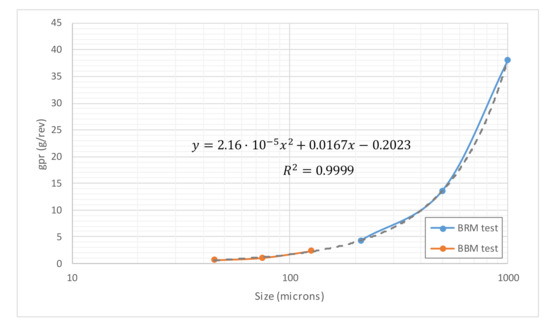
Figure 5.
Variation of BBM and BRM gpr values with P100, Penouta mine ore.
In the case of Mittersill ore (Figure 6 and Figure 7), the transition between BBM and BRM wi values with P100 shows a better continuity than in previous cases (Figure 7), so the determination coefficient reached again a very high value, 99.89%.
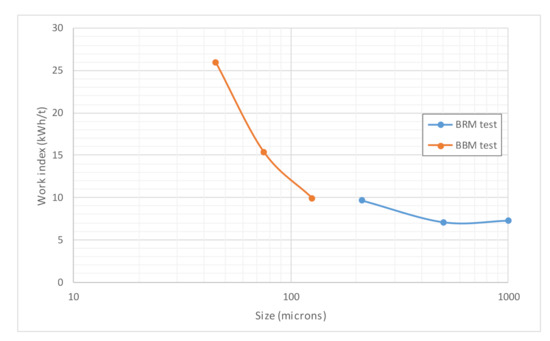
Figure 6.
Variation of BBM and BRM wi values with P100, Mittersill ore.
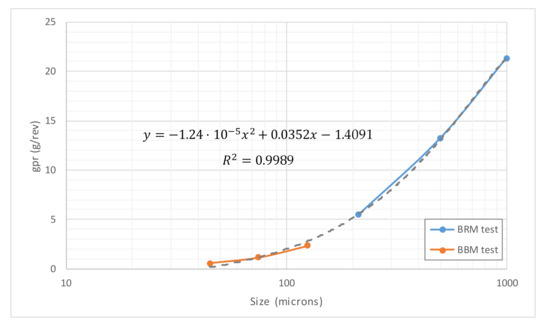
Figure 7.
Variation of BBM and BRM gpr values with P100, Mittersill ore.
Plotting BBM and BRM wi values versus P100 in the case of Panasqueira ore yeilded a clear trend in the case of BBM wi values, but a with a roller-coaster type shape in the case of BRM wi values (Figure 8). Unexpectedly, when plotting gpr values versus P100 (Figure 9), again a quadratic fit yielded a very high value of the determination coefficient, 99.10%.
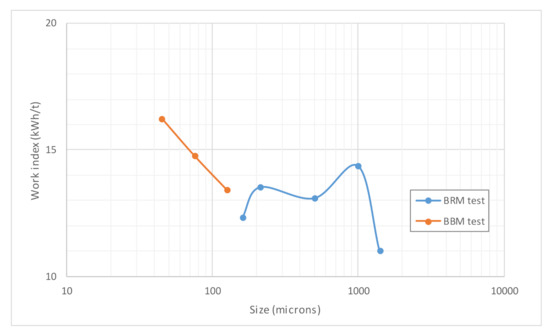
Figure 8.
Variation of BBM and BRM wi values with P100, Panasqueira ore.
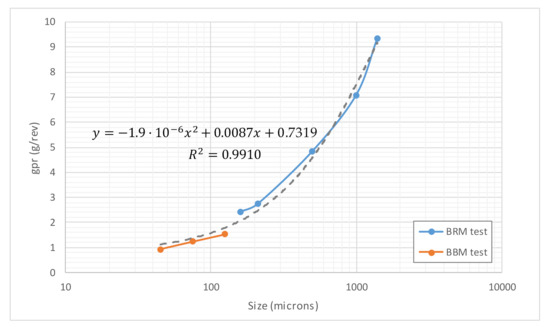
Figure 9.
Variation of BBM and BRM gpr values with P100, Panasqueira ore.
Finally, Barruecopardo ore samples results are depicted in Figure 10 and Figure 11. As mentioned above, BBM tests were performed on the same ore samples but with different origins, while BRM tests were performed on the composite obtained after blending both samples. Once more, with an evident lack of continuity in the wi versus P100 plot (Figure 10), a clear quadratic trend was obtained when plotting gpr values versus P100 (Figure 11), with a very high value of the determination coefficient, 99.95%.
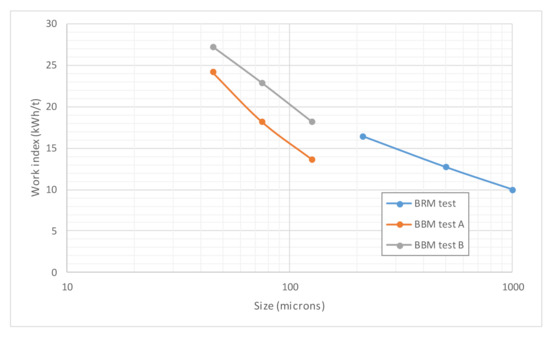
Figure 10.
Variation of BBM and BRM wi values with P100, Barruecopardo ore.
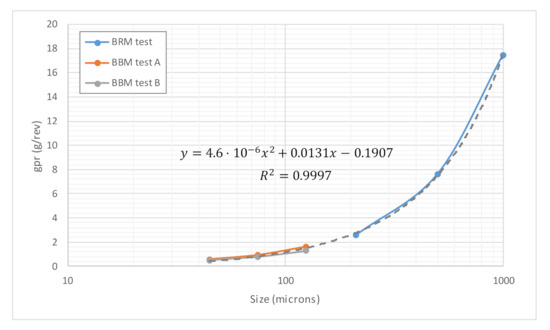
Figure 11.
Variation of BBM and BRM gpr values with P100, Barruecopardo ore.
Given the results obtained, it is evident that there is significant variability of wi values with grinding size, both in BBM and BRM grindability tests. While wi versus P100 plots show no continuity in general (being erratic in the case of Panasqueira ore, BRM wi values) when plotting gpr versus P100, a parabolic shape is clearly depicted with all ores. Furthermore, the quadratic fitting determination coefficients overcame 99.7% in all cases.
A recommendation can be made in the light of these results: any energy consumption model based on correlating wi with mechanical parameters (geotechnical) or operational parameters (drilling, blasting) should be revised considering gpr values instead of wi values, which probably would yield a better determination coefficient.
These results also invited us to perform a conceptual review of the Fred Bond literature to seek relevant considerations about the significance of gpr. Thus, it gains additional value that gpr was already named “grindability” since the paper led by Walter Maxson [42], in which Fred Bond was also a co-author. Fred Bond, in his subsequent papers, also utilized this definition. Considering that wi is worldwide known as the Bond index, and without the intention of subtracting an iota of importance from the broad contribution of Fred Bond (wi is the most practical tool in rod and ball mill calculation), it seems fair to propose the naming of gpr as the Maxson index. This so-called Maxson index should be meaningful, not only for being the critical parameter to obtain the Bond work index but also for characterizing the ore breakage behavior.
4. Conclusions
The following conclusions summarize the results obtained in this research:
- According to the obtained results, BBM and BRM grindability tests showed no continuity or clear correlation when considering wi values versus P100, but a clear tendency was obtained in all cases when plotting gpr versus P100.
- It is advised that energy consumption modelling based on correlations involving wi and other mechanical or operational parameters would yield a better determination coefficient using gpr values instead.
- The re-signifying of gpr evidenced to characterize the ore breakage behavior and its origin justify the proposal of naming gpr as the Maxson grindability index.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/met11060970/s1, Table S1. PENOUTA (tailings pond) BRM, Table S2. PENOUTA (tailings pond) BBM, Table S3. PENOUTA (mine) BRM, Table S4. PENOUTA (mine) BBM, Table S5. MITTERSILL BRM, Table S6. MITTERSILL BBM, Table S7. PANASQUEIRA BRM, Table S8. PANASQUEIRA BBM, Table S9. BARRUECOPARDO BRM, Table S10. BARRUECOPARDO BBM (test A), Table S11. BARRUECOPARDO BBM (test B).
Author Contributions
Conceptualization, A.L.C.-V. and J.M.M.-A.; methodology, G.G.G. and J.M.M.-A.; validation, G.G.G. and J.M.M.-A.; formal analysis, G.G.G., E.G. and H.A.; investigation, G.G.G., E.G. and H.A.; resources, J.O. and J.M.M.-A.; writing—original draft preparation, G.G.G. and J.M.M.-A.; writing—review and editing, A.L.C.-V., J.O. and J.M.M.-A.; visualization, G.G.G. and J.M.M.-A.; supervision, A.L.C.-V.; project administration, J.O. and J.M.M.-A.; funding acquisition, J.O. and J.M.M.-A. All authors have read and agreed to the published version of the manuscript.
Funding
This work is part of the OptimOre project funded by the European Union Horizon 2020 Research and Innovation Programme under grant agreement No 642201.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fuerstenau, D.W.; Phatak, P.B.; Kapur, P.C.; Abouzeid, A.-Z.M. Simulation of the grinding of coarse/fine (heterogeneous) systems in a ball mill. Int. J. Miner. Process. 2011, 99, 32–38. [Google Scholar] [CrossRef]
- Schönert, K. Aspects of the physics of breakage relevant to comminution. In Proceedings of the 4th Tewksbury Symposium Fracture, February, Melbourne, Australia, 12–14 February 1979; University of Melbourne: Melbourne, Australia, 1979; p. 3. [Google Scholar]
- Austin, L.G.; Klimpel, R.R. The Theory of Grinding Operations. Ind. Eng. Chem. 1964, 56, 18–29. [Google Scholar] [CrossRef]
- Deniz, V.; Ozdag, H. A new approach to bond grindability and work index: Dynamic elastic parameters. Miner. Eng. 2003, 16, 211–217. [Google Scholar] [CrossRef]
- Fuerstenau, D.W.; Abouzeid, A.-Z.M. Effect of fine particles on the kinetics and energetics of grinding coarse particles. Int. J. Miner. Process. 1991, 31, 151–162. [Google Scholar] [CrossRef]
- Menéndez-Aguado, J.M.; Coello-Velázquez, A.L.; Dzioba, B.R.; Diaz, M.A.R. Process models for simulation of Bond tests. Transactions of the Institutions of Mining and Metallurgy, Section C. Miner. Process. Extr. Met. 2006, 115, 85–90. [Google Scholar] [CrossRef]
- Coello Velázquez, A.L.; Menéndez-Aguado, J.M.; Brown, R.L. Grindability of lateritic nickel ores in Cuba. Powder Technol. 2008, 182, 113–115. [Google Scholar] [CrossRef]
- Nikolić, V.; Trumić, M. A new approach to the calculation of Bond work index for finer samples. Miner. Eng. 2021, 165, 106858. [Google Scholar] [CrossRef]
- Rittinger von, P.R. Lehrbuch der Aufbereitungskunde; Ernst und Korn: Berlin, Germany, 1867. [Google Scholar]
- Kick, F. Das Gesetz der Proportionalen Widerstände und Seine Anwendungen; Arthur Felix: Leipzig, Germany, 1885. [Google Scholar]
- Bond, F.C.; Maxson, W.L. Standard grindability tests and calculations. Trans. AIME Min. Eng. 1943, 153, 362–372. [Google Scholar]
- Bond, F.C. Third theory of comminution. Trans. AIME Min. Eng. 1952, 193, 484–494. [Google Scholar]
- Bond, F.C. Crushing and grinding calculations. Br. Chem. Eng. 1961, 6, 378–385. [Google Scholar]
- Hukki, R.T. Proposal for a solomonic settlement between the theories of von Rittinger, Kick, and Bond. Trans. AIME 1961, 220, 403–408. [Google Scholar]
- Deister, R.J. How to determine the Bond Work Index using lab ball mill grindability tests. Eng. Min. J. 1987, 188, 42–45. [Google Scholar]
- Bearman, R.A.; Briggs, C.A.; Kojovic, T. The Application of Rock Mechanics Parameters to the Prediction of Comminution Behaviour. Miner. Eng. 1997, 10, 255–264. [Google Scholar] [CrossRef]
- Ram Chandar, K.; Deo, S.N.; Baliga, A.J. Prediction of Bond’s work index from field measurable rock properties. Int. J. Miner. Process. 2016, 157, 134–144. [Google Scholar] [CrossRef]
- Aras, A.; Özsen, H.; Dursun, A.E. Using Artificial Neural Networks for the Prediction of Bond Work Index from Rock Mechanics Properties. Miner. Process. Extr. Metall. Rev. 2020, 41, 145–152. [Google Scholar] [CrossRef]
- Berry, T.F.; Bruce, R.W. A simple method of determining the grindability of ores. Can. Min. J. 1966, 87, 63–65. [Google Scholar]
- Yap, R.F.; Sepulveda, J.L.; Jauregui, R. Determination of the Bond Work Index Using Ordinary Laboratory Batch Ball Mill. In Design and Installations of Comminution Circuits; Mular, A.L., Jergensen, G.V., Eds.; AIME: New York, NY, USA, 1982; p. 176. [Google Scholar]
- Bonoli, A.; Ciancabilla, F. The Ore Grindability Definition as an Energy Saving Tool in the Mineral Grinding Processes. In Proceedings of the 2nd International Congress “Energy, Environment and Technological Innovation”, Rome, Italy, 12–16 October 1992. [Google Scholar]
- Chakrabarti, D.M. Simple approach to estimation of the work index. Transactions of the Institutions of Mining and Metallurgy, Section C. Miner. Process. Extr. Metall. 2000, 109, 83–89. [Google Scholar] [CrossRef]
- Menéndez-Aguado, J.M.; Dzioba, B.R.; Coello-Velázquez, A.L. Determination of work index in a common laboratory mill. Miner. Metall. Process. 2005, 22, 173–176. [Google Scholar] [CrossRef]
- Nikolic, V.; Trumic, M.; Menéndez-Aguado, J.M. Determination of Bond work index in non-standard mills. In Proceedings of the XIV International Mineral Processing and Recycling Conference (2021 IMPRO), Belgrade, Serbia, 12–14 May 2021. [Google Scholar]
- Napier-Munn, T.J.; Morrell, S.; Morrison, R.D.; Kojovic, T. Mineral Comminution Circuits: Their Operation and Optimisation University of Queensland; Julius Kruttschnitt Mineral Research Centre: Indooroopilly, Australia, 1996. [Google Scholar]
- Mwanga, A.; Rosenkranz, J.; Lamberg, P. Development and experimental validation of the Geometallurgical Comminution Test (GCT). Miner. Eng. 2017, 108, 109–114. [Google Scholar] [CrossRef]
- Faramarzi, F.; Napier-Munn, T.; Morrison, R.; Kanchibotla, S.S. The extended drop weight testing approach—What it reveals. Miner. Eng. 2020, 157, 106550. [Google Scholar] [CrossRef]
- Karra, V.K. Simulation of the Bond grindability test. CIM Bull. 1981, 74, 195–199. [Google Scholar]
- Lewis, K.A.; Pearl, M.; Tucker, P. Computer Simulation of the Bond Grindability Test”. Miner. Eng. 1990, 3, 199–206. [Google Scholar] [CrossRef]
- Aksani, B.; Sönmez, B. Simulation of Bond grindability test by using Cumulative Based Kinetic Model. Miner. Eng. 2000, 13, 673–677. [Google Scholar] [CrossRef]
- Ciribeni, V.; Bertero, R.; Tello, A.; Puerta, M.; Avellá, E.; Paez, M.; Menéndez-Aguado, J.M. Application of the Cumulative Kinetic Model in the Comminution of Critical Metal Ores. Metals 2020, 10, 925. [Google Scholar] [CrossRef]
- Alfonso, P.; Hamid, S.A.; Anticoi, H.; Garcia-Valles, M.; Oliva, J.; Tomasa, O.; López-Moro, F.J.; Bascompta, M.; Llorens, T.; Castro, D.; et al. Liberation characteristics of Ta-Sn ores from Penouta, NW Spain. Minerals 2020, 10, 509. [Google Scholar] [CrossRef]
- Nava, J.V.; Llorens, T.; Menéndez-Aguado, J.M. Kinetics of dry-batch grinding in a laboratory-scale ball mill of Sn-Ta-Nb minerals from the Penouta Mine (Spain). Metals 2020, 10, 1687. [Google Scholar] [CrossRef]
- Hamid, S.A.; Alfonso, P.; Oliva, J.; Anticoi, H.; Guasch, E.; Sampaio, C.H.; Garcia-Vallès, M.; Escobet, T. Modeling the liberation of comminuted scheelite using mineralogical properties. Minerals 2019, 9, 536. [Google Scholar] [CrossRef]
- Mateus, A.; Figueiras, J.; Martins, I.; Rodrigues, P.C.; Pinto, F. Relative abundance and compositional variation of silicates, oxides and phosphates in the W-Sn-rich lodes of the Panasqueira mine (Portugal): Implications for the ore-forming process. Minerals 2020, 10, 551. [Google Scholar] [CrossRef]
- Alfonso, P.; Tomasa, O.; Garcia-Valles, M.; Tarragó, M.; Martínez, S.; Esteves, H. Potential of tungsten tailings as glass raw materials. Mater. Lett. 2018, 228, 456–458. [Google Scholar] [CrossRef]
- Nava, J.V.; Coello-Velázquez, A.L.; Menéndez-Aguado, J.M. Grinding kinetics study of tungsten ore. Metals 2021, 11, 71. [Google Scholar] [CrossRef]
- GMG -Global Mining Guidelines Group. Determining the Bond Efficiency of Industrial Grinding Circuits. 2016. Available online: https://gmggroup.org/wp-content/uploads/2016/02/Guidelines_Bond-Efficiency-REV-2018.pdf (accessed on 14 May 2021).
- Braun International Co. Standard Bond Ball Mill Operating Handbook; Braun International Co.: Chengdu, China, 1999. [Google Scholar]
- Rowland, C.A. Using the Bond work index to measure operating comminution efficiency. Miner. Metall. Process. 1998, 15, 32–36. [Google Scholar] [CrossRef]
- Mosher, J.B.; Tague, C.B. Precision and Repeatability of Bond Grindability Testing. Miner. Eng. 2001, 14, 1187–1197. [Google Scholar] [CrossRef]
- Maxson, W.L.; Cadena, F.; Bond, F.C. Grindability of various ores. Trans. AIME 1933, 112, 130–145. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).