Abstract
Štore Steel Ltd. is one of the major flat spring steel producers in Europe. Until 2016 the company used a three-strand continuous casting machine with 6 m radius, when it was replaced by a completely new two-strand continuous caster with 9 m radius. For the comparison of the tensile strength of 41 hypoeutectoid steel grades, we conducted 1847 tensile strength tests during the first period of testing using the old continuous caster, and 713 tensile strength tests during the second period of testing using the new continuous caster. It was found that for 11 steel grades the tensile strength of the rolled material was statistically significantly lower (t-test method) in the period of using the new continuous caster, whereas all other steel grades remained the same. To improve the new continuous casting process, we decided to study the process in more detail using the Multiple Linear Regression method and the Genetic Programming approach based on 713 items of empirical data obtained on the new continuous casting machine. Based on the obtained models of the new continuous casting process, we determined the most influential parameters on the tensile strength of a product. According to the model’s analysis, the secondary cooling at the new continuous caster was improved with the installation of a self-cleaning filter in 2019. After implementing this modification, we performed an additional 794 tensile tests during the third period of testing. It was found out that, after installation of the self-cleaning filter, in 6 steel grades out of 19, the tensile strength in rolled condition improved statistically significantly, whereas all the other steel grades remained the same.
1. Introduction
Tensile strength, as a genuine material property, is defined as the maximal stress achieved during stretching of a material before breaking [1,2,3]. For determination of the tensile strength of steel and steel products representative test pieces are needed. Accordingly, orientation (relative to the principle direction of working), location (related to segregations originating from the solidification process) and preparation (cutting, machining and heat treatment) of these test pieces are essential. On the other hand, the basis for typical steel tensile strength prediction is its chemical composition [4,5,6,7], but contemporary models also involve solidification influences, including grain size and morphology [8,9,10], microstructure [8,9,10,11,12,13,14,15,16,17], macrostructure [8,10,12,15,18,19], chemical non-homogeneities segregations [6,7,19,20,21,22,23] and casting defects [24,25]. The tensile strength researches are related mostly with individual steel grades, but also more general prediction models were developed [5,14,26]. Below, few studies are presented where, besides the chemical composition, the influence of solidification on the mechanical properties of steel was also elaborated, including continuous casting.
Hardenability related to the cracking of high alloyed steel 0.4C1.5Mn2Cr0.35Mo1.5Ni steel was analyzed in paper [20]. The influence of segregations of carbon, sulfur, chromium and molybdenum were also studied, besides the time-temperature influence on martensite formation. The authors concluded that segregations also influence martensite formation and, consequently, hardenability and crack susceptibility.
Fourlakidis and Diószegib [14] analyzed the influence of chemical composition variations and cooling rates on microstructure during solidification. The geometry of the castings was also considered. The tensile strength could be estimated based on the measured distance between the formed pearlite grains.
Nolan et al. [26] used an Artificial Neural Network for predicting the impact toughness of quenched and tempered steel grades for pressure vessels which were exposed to a heat treatment process after welding, the hardness of the heat affected zone in pipeline and tap fitting steels, and the hot tensile strength and ductility of microalloyed steel grades at temperatures occurring during strand straightening during the continuous casting process. For hot tensile strength prediction of microalloyed steel, the cooling rate (°C/min) and chemical composition (content of C, Mn, S, Cr, B, Si, Cu, Ni, Mo, V, P, Ti, Al, Nb and N) were used as input parameters. The higher deviation between predicted and experimental data can also be attributed to difficult test design related to the solidification process (e.g., probe location, segregations).
Hangyu et al. [21] observed the remelting of the crack vicinity of continuously cast low carbon boron steel. A high temperature confocal laser scanning microscope was used for remelting. It was found out that the boron segregated, even at low concentrations (0.0013%) at the crack regions. It is also concentrated at grain boundaries and, as such, increases brittleness and lowers material ductility.
Jingling et al. [22] studied the influence of segregations on the mechanical properties of bainitic steel. The segregations caused changes in the microstructure. The lath bainite in the segregated region changed to martensite, and, as such, reduced the strain accommodation and crack deflection drastically. Consequently, the toughness decreased in the segregated regions.
Similarly, the co-authors of the previously mentioned paper [15], analyzed the influence of segregations of continuously cast billets on segregated bands‘ formation during hot rolling. It was found out that segregations are influenced by superheating and the intensity of the secondary cooling. Both influence columnar crystal growth, which increases with the increase of superheating and secondary cooling intensity. With the increased ratio of columnar crystals, the segregations and banding of rolled products are decreased and, consequently, elongation and fracture toughness is improved.
The surface roughness and yield strength of a QSn6.5-0.1 slab was optimized in [10]. Columnar-grained slabs were continuously cast horizontally. The casting and heating-mold temperature, cooling water flow rate and casting speed were varied, to obtain proper surface quality mechanical properties without the presence of segregations. It was found out that all requirements are related to columnar grains, which are influenced mostly by the heating-mold temperature.
Katsuo et al. [23] studied crack sensitivities of continuously cast high-alloy and stainless steels related to segregations of sulfur and phosphorus. They conducted hot tensile tests and examined the fracture surface microscopically. It was found out that segregations and precipitations of both chemical elements at grain boundaries increase crack sensitivity in the studied steel grades. Accordingly, it was suggested to decrease the sulfur and phosphorus content, and also to decrease slab reheating after exiting the mold and secondary cooling. Consequently, surface and subsurface cracks’ occurrence improved.
The microstructure, tensile strength, impact toughness and ballistic properties of high strength low alloy steel were studied in the paper [9]. Different thickness plates were used, rolled from continuous cast steel, and a conventional ingot. The continuous cast steel displayed better ballistic performance.
The main motive of the research was to acquire good insight into the mechanism of continuous casting of steel, and, consequently, to improve the tensile strength of rolled bars after installation of the new two-strand continuous caster. To achieve the goal, we used experimental data of the tensile strength from the three different time periods and two different continuous casters, namely: (1) On the old three-strand continuous casting machine, (2) On the new two-strand continuous caster and (3) On the new two-strand continuous caster after implementing changes of the casting process (parameters). Analysis of the data obtained from the third period showed that the tensile strength had improved. A wide range of influencing parameters, not only chemical composition, but also casting parameters, were used for the prediction of tensile strength for several hypoeutectoid steel grades. Multiple Linear Regression and Genetic Programming were used for modeling. The problem related to replacing the old 6 m radius continuous caster with the new 9 m radius continuous caster and achieving of tensile strength is presented in the beginning of the paper. In addition, presented are the average values of the collected parameters and tensile strength. Afterwards, the tensile strength prediction is given, using Multiple Linear Regression and Genetic Programming. The results of the steelmaking process optimization are outlined, followed by details of the main findings.
2. Materials and Methods
Production in the Štore Steel Ltd. (Štore, Slovenia) steel plant consists of melting of the scrap using an electric arc furnace, tapping, ladle treatment (i.e., secondary metallurgy) and continuous casting of the billets. After cooling the billets down they are reheated and rolled in the rolling plant. The rolled bars can, additionally, be straightened, examined, cut, sawn, chamfered, drilled and peeled in the cold finishing plant.
2.1. Process Data
The samples for the tensile test were taken after rolling from the middle of the rolled billet. The tensile test specimens were taken and prepared from rough specimens according to ISO 377:2017. The tensile tests were conducted according to ISO 6892-1:2019. Please bear in mind that the tensile test is conducted only in the case of customer requirement.
Until March 2016 the company used a three-strand continuous casting machine with a 6 m radius, when it was replaced by a completely new two-strand continuous caster with a 9 m radius. The comparison of tensile strength of 41 hypoeutectoid steel grades was conducted within the period of using the old (from January 2013 to April 2016, 1847 tensile tests) and new continuous caster (from April 2016 to March 2019, 713 tensile tests). In March 2019 it was found out that in 11 steel grades (out of 41 hypoeutectoid steel grades) the tensile strength of the rolled material was statistically significantly (t-test) lower in the period of using the new continuous caster, whereas all the other steel grades remained the same. Consequently, the following influencing parameters were gathered in the period from April 2016 to March 2019:
- −
- Chemical composition: Content of carbon, silicon, manganese, sulfur, chromium, molybdenum, nickel, aluminum, vanadium. Chemical composition influences the microstructure and, consequently, the mechanical properties.
- −
- Casting parameters:
- ∘
- Average casting temperature [°C]. Casting temperature influences the thermal field in the mold, which influences the heat removal and solidification. Due to the thermo-mechanical behavior of melt in the mold, the melt solidifies gradually, forming a layered non-homogeneous structure. This structure influences the mechanical properties.
- ∘
- Average difference between input and output cooling water temperature for each mold [°C] (i.e., for each of the two strands). This temperature difference is a measure of the efficiency of heat removal from the mold (i.e., primary cooling). The mold is cooled with water. The heating up of the cooling water flowing through the mold indicates the efficiency of the heat removal, which influences the melt solidification.
- ∘
- The average cooling water pressure in the first (directly below the mold), second and third zones of secondary cooling for each of the two strands. The melt solidifies primarily in the mold. After exiting the mold (the mold is a 1 m long copper tube), the strand is cooled by water sprays, where water flux can be set automatically varying the water pressure. Consequently, water pressure is a measure of water spray nozzle clogging. In the event of water spray nozzle clogging, the pressure should be increased to achieve the same water flux, which enables cooling of the cast billets. Secondary cooling influences the billets’ macrostructure directly, including chemical composition, segregations (i.e., chemical non-homogeneity) or material defects’ formation, which all influence the mechanical properties.
- −
- Reduction rate (i.e., the ratio between the billet and rolled bar cross-section): Location and preparation of samples for tensile testing was conducted according to ISO 377:2017. The location of the tensile test samples depends on the rolled bar dimensions. Consequently, due to the layered, segregated, solidified macrostructure, the mechanical properties (e.g., tensile strength) varied across the cross-section of the rolled bar.
- −
- Tensile strength.
The minimal and maximal values of the gathered parameters are presented in Table 1.

Table 1.
Minimal and maximal values of the gathered parameters.
2.2. Modeling of Tensile Strength
In this paper, we used a Multiple Linear Regression method and Genetic Programming to model the continuous steel casting process.
In general, linear regression is a very powerful statistical method, and is intended to determine the relationship between the independent input variables (i.e., explanatory variables) of the system and the dependent output variable (i.e., response of a system) [27].
Genetic Programming is one of the methods of Evolutionary Computation [28]. The method is similar to the Genetic Algorithm, which is a widely used approach in various engineering fields (see for example [29,30,31,32]). However, Genetic Programming usually involves much more complex structures (i.e., individuals or organisms) that are manipulated during evolution [27]. In Genetic Programming, the structures undergoing simulated evolution are computer programs the content of which depends on the problem we are solving. For example, if the goal of research is modeling based on experimental/numerical data, the individual computer program (organism) has the form of a prediction model which consists of function genes and terminal genes [33,34,35,36]. Function genes are most often the basic analytical operations, such as the operation of addition, subtraction, multiplication, division. Terminal genes are usually independent variables of the system under study. The goal of the Genetic Programming is to find the individual computer program (i.e., the mathematical model in the narrow sense) that best solves the problem we are dealing with. In Genetic Programming, the shapes of the evolutionary manipulated models are not prescribed in advance, but are left to simulated evolution. In general, the Genetic Programming process can usually discover more complex relationships (patterns) in the given data set compared with the Multiple Linear Regression method, but usually the obtained models are more complex.
Based on the data gathered in Table 1, the prediction of tensile strength was conducted using the Multiple Linear Regression method and the Genetic Programming approach. We used the average percentage deviation as a fitness function for the purpose of this study. The average percentage deviation is defined as:
where n is the number of fitness cases (i.e., the number of the experiments executed), and and are the measured and the predicted tensile strengths, respectively.
2.2.1. Modeling of Tensile Strength Using Multiple Linear Regression
On the basis of the Multiple Linear Regression results, it is possible to conclude that the model predicts the tensile strength significantly (p < 0.05, ANOVA, accessed on 28 May 2021), and that 93.5% of total variances can be explained by independent variables’ variances (R-square). Significantly influential parameters (p > 0.05) are the casting temperature (T_TUNDISH), average difference between input and output cooling water temperature for the mold of the first strand (DELTA_T_S1), the average cooling water pressure in the third zone of secondary cooling of the first strand (P_S1_Z3), the average cooling water pressure in the first, second and the third zones of secondary cooling of the second strand (P_S2_Z1, P_S2_Z2, P_S2_Z1) and the content of carbon (C), manganese (Mn), sulfur (S), chromium (Cr), molybdenum (Mo), nickel (Ni) and aluminum (Al).
The linear regression model is:
The corresponding ANOVA results are given in Table 2. The average deviation of the predictions obtained using Equation (2) from the experimental data is 4.17%.

Table 2.
ANOVA results.
2.2.2. Modeling of Tensile Strength Using Genetic Programming
In this paper, we used the arithmetical operations of addition (+), subtraction (–), multiplication (*) and division (/) as the function genes, and the list of independent input variables (parameters) as the terminal genes (see Table 1 for the list of input parameters). In the initial generation, random computer programs (i.e., individuals and/or organisms) for the tensile strength (Rm) are generated using the prescribed function and terminal genes. In this research, we used the genetic operations of reproduction, crossover and mutation. Each organism in each generation is evaluated for all fitness cases (i.e., for all combinations of input variables), and compared with the corresponding experimental values of dependent output variable according to Equation (1). The processes of genetic alteration and evaluation of organisms are repeated until the successful solution is obtained.
We developed the Genetic Programming System (University of Maribor, Faculty of Mechanical Engineering, Slovenia; Štore Steel Ltd., Štore, Slovenia) in the AutoLISP computer language inside the AutoCAD CAD/CAM systems [34,35,36]. The following evolutionary settings were used; population size: 1000; maximum number of generations: 1000; probability of reproduction: 0.4, probability of crossover: 0.6; maximum depth of organisms in the initial generation: 30; maximum permissible depth of offspring after the performing of crossover: 30; smallest permissible depth of organisms in the initial generation: 2; tournament size for selection operation: 7; number of independent runs: 100.
Each run lasted approximately 50 min on an Intel® Core™ i7 Processor and 16 GB of RAM. The best mathematical model for prediction of tensile strength (Rm) was the following evolutionary obtained organisms:
The average deviation of the predictions obtained using Equation (3) from the experimental data was 8.72%.
3. Results and Discussion: Improving of Tensile Strength Using the Developed Models
Figure 1 and Figure 2 show the calculated influences of individual parameters on tensile strength using the Multiple Linear Regression model and the Genetic Programming model, respectively, while changing individual parameters separately within the individual parameter range.
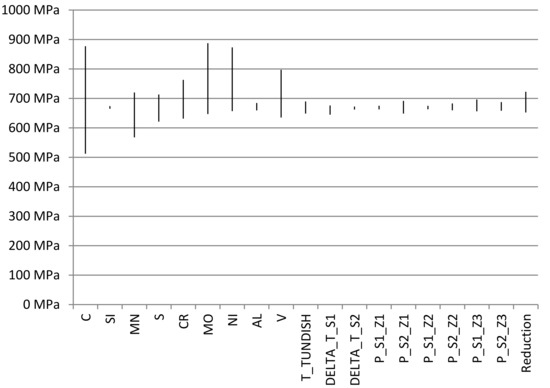
Figure 1.
Calculated influences of individual parameters on tensile strength using the Multiple Linear Regression model.
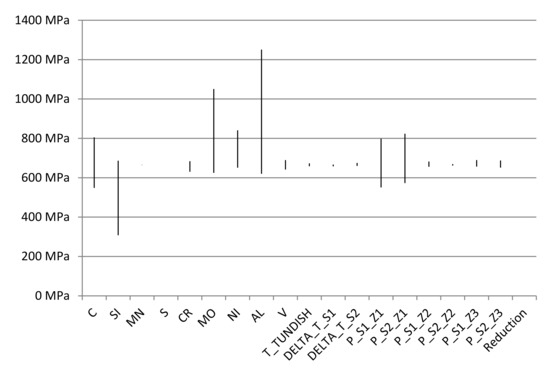
Figure 2.
Calculated influences of individual parameters on tensile strength using the Genetic Programming model.
Based on the Multiple Linear Regression results (Figure 1), besides chemical composition, the significantly influential parameters (p > 0.05) were the casting temperature (T_TUNDISH), the average difference between input and output water temperature for the mold of the first strand (DELTA_T_S1), the average cooling water pressure in the third zone of secondary cooling of the first strand (P_S1_Z3), the average cooling water pressure in the first, second and the third zones of secondary cooling of the second strand (P_S2_Z1, P_S2_Z2, P_S2_Z3).
Please bear in mind that, based on the technical delivery conditions, the chemical composition variations are allowed only within the required limits. The casting temperature depends on the ladle treatment time, number of sequences (i.e., ordered quantity) and production pace, dependent on peak electricity hours. Accordingly, practical changes related to the casting temperature (T_TUNDISH) are not possible. It is similar with the mold and its heat removal, which is related to the average difference between the input and output cooling water temperatures (DELTA_T_S1). The only possibility is to change the already worn-out molds on time. The measurements of the molds’ internal profile with an accurate mold profile measurement tool are conducted on a weekly basis. Originally installed spray nozzles at secondary cooling are prone to clogging, which is influenced by nozzle geometry and water quality. It is important to emphasize that the pressure of the secondary cooling system is regulated automatically during casting according to the preset water flux. Accordingly, in the case of nozzle clogging, the water pressure increases automatically to enable sufficient cooling water flux. Furthermore, the reduction rate (the ratio between the billet and the rolled bar cross-section) depends only on the ordered rolled bar dimensions—the billet cross-section is always 180 mm × 180 mm.
While observing the calculated influences of individual parameters using the Genetic Programming model (Figure 2), besides chemical composition, the most influential is the average cooling water pressure in the first zone of secondary cooling of both strands (P_S1_Z1, P_S2_Z1).
Based on Figure 1 and Figure 2 and the fact that the chemical composition and rolled bar dimension are required by the customer, it is possible to conclude that the only possibility is to influence the secondary cooling of a continuous caster. It has already been mentioned that the originally installed spray nozzles at secondary cooling are prone to clogging, which is influenced by the nozzle geometry and water quality.
Accordingly, the installation of the self-cleaning filter in April 2019 was conducted based on both models. In the period from April 2019 to November 2020, 794 tensile tests of rolled material were conducted. It was found out that in 6 steel grades out of 19 the tensile strength in rolled condition improved statistically significantly (t-test), whereas all other steel grades remained the same (Table 3). Please bear in mind that only the steel grades are presented in Table 3, where at least 4 tensile test results were available for each period—without the installed self-cleaning filter or with the installed self-cleaning filter.

Table 3.
Tensile test results for 19 steel grades for each period—without the installed self-cleaning filter or with the installed self-cleaning filter.
For the same period, the relative deviations from experimental data for the Multiple Linear Regression model and the Genetic Programming model were 4.33% and 8.91%, respectively. The average cooling water pressure in all zones of secondary cooling decreased statistically significantly, while the other observed parameters remained the same (Table 4).

Table 4.
The parameters’ comparison between the period without the self-cleaning filter (713 cases) and with the self-cleaning filter installed for the cooling water of the secondary cooling of the continuous caster (794 cases).
Comparison of the accuracy of the model obtained by the linear regression and the model developed by the Genetic Programming showed that both methods were suitable for modeling the continuous steel casting and for determining the influencing parameters on the tensile strength. In this specific case, the linear regression model even had a slightly better predictive performance than the evolutionarily derived model. The reason for this can be attributed to the problem specific characteristic of the collected data (i.e., the ranges of values of the input variables and the output variable), which led to the better predictive performance of the model obtained by the linear regression. Therefore, it is very difficult to define clearly which method is better, as the success of the modeling method depends mostly on the characteristics of the measured experimental data. In general, however, in the case of very demanding data sets, the Genetic Programming can capture the regularities hidden in the experimental data much more effectively, as the shape of the model is the consequence of the simulated evolution (i.e., the shape of the model is not prespecified by the user). Contrarily, in the case of Multiple Linear Regression, the shape of the model is given in advance by the user.
4. Conclusions
The new continuous caster was installed in the steel plant in 2016. From April 2016 to March 2019, 713 tensile test results for rolled material (41 different hypoeutectoid steel grades) were available. In March 2019 it was found out that, in 11 steel grades (out of 41 hypoeutectoid steel grades), the tensile strength of the rolled material was statistically significantly (t-test) lower in the period of using the new continuous caster, whereas all the other steel grades remained the same.
Accordingly, data were collected on the chemical composition (content of C, Si, Mn, S, Cr, Mo, Ni, Al and V), casting parameters and reduction rate (the ratio between the cast billet cross-section and final rolled bar cross-section).
Based on the collected data, a Multiple Linear Regression model and the Genetic Programming model were developed. The Multiple Linear Regression results showed that, besides chemical composition, significantly influential parameters (p > 0.05) were the casting temperature, the average difference between the input and output water temperature for the mold of the first strand, the average cooling water pressure in the third zone of secondary cooling of the first strand, the average cooling water pressure in the first, second and the third zones of secondary cooling of the second strand. Similarly, according to the genetically developed model, the most influential were the average cooling water pressure in the first zone of secondary cooling of both strands. The influence of the average cooling water pressure at secondary cooling can be attributed to clogging of the originally installed spray nozzles, which is influenced by nozzle geometry and water quality.
According to the technical delivery conditions, the chemical composition requirements and dimensions (i.e., reduction rate) should be followed. The average difference between input and output water temperature for a mold is related to heat removal during solidification. It is influenced mostly by the mold wear-out, which is checked regularly using an accurate mold profile measurement tool on a weekly basis. Consequently, changes could only be conducted related to the cooling water pressure of secondary cooling. Accordingly, the installation of the self-cleaning filter was conducted in April 2019.
After installation of the self-cleaning filter, 794 tensile tests of rolled material were conducted (in the period from April 2019 to November 2020. It was found out that, in 6 steel grades out of 19, the tensile strength in rolled condition improved statistically significantly (t-test), whereas all the other steel grades remained the same. The average cooling water pressure in all zones of secondary cooling decreased statistically significantly, while the other observed parameters remained the same.
In our further research, we will examine in more detail how the quality of the steel is affected by the allowable variations of the chemical components. Namely, the required customer limits of the chemical composition allow a certain variation of the chemical composition, which, in turn, can affect the mechanical properties. For this purpose, we plan to use an even more extensive set of experimental data than we have used so far. Usually, the more extensive data set can cover the hidden relationships between the independent input variables and the dependent output variable(s) better.
From the modeling perspective, we will refine the existing Genetic Programming system by limiting the number of functional and terminal genes that can be included in a genetically evolving model. This will ensure that the genetically developed models will be significantly less complex and, thus, more suitable for practical use.
Author Contributions
Conceptualization, M.B.; methodology, M.B.; software, M.B.; validation, M.B. and U.Ž.; formal analysis, M.B. and U.Ž.; investigation, M.B.; writing—original draft preparation, M.B.; writing—review and editing, M.B. and U.Ž.; project administration, U.Ž.; All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Slovenian Research Agency (Programme title and code: Technological systems for smart manufacturing, P2-0157), and the Štore Steel Ltd., Štore, Slovenia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The authors confirm that the data supporting the findings of this study are available within the paper.
Conflicts of Interest
The authors declare that there is no conflict of interest.
References
- ISO 6892-1:2019 Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature; International Organization for Standardization: Geneva, Switzerland, 2019; p. 87.
- ASTM E8/E8M-16ae1 Standard Test Methods for Tension Testing of Metallic Materials; ASTM International: West Conshohocken, PA, USA, 2016.
- Horvath, C.D. Advanced steels for lightweight automotive structures. In Materials, Design and Manufacturing for Lightweight Vehicles; Elsevier: Amsterdam, The Netherlands, 2021; pp. 39–95. [Google Scholar]
- Ruiz, E.; Ferreño, D.; Cuartas, M.; López, A.; Arroyo, V.; Gutiérrez-Solana, F. Machine learning algorithms for the prediction of the strength of steel rods: An example of data-driven manufacturing in steelmaking. Int. J. Comput. Integr. Manuf. 2020, 33, 880–894. [Google Scholar] [CrossRef]
- Iza-Mendia, A.; Gutiérrez, I. Generalization of the existing relations between microstructure and yield stress from ferrite–pearlite to high strength steels. Mater. Sci. Eng. A 2013, 561, 40–51. [Google Scholar] [CrossRef]
- Thomas, B.G. Continuous Casting: Complex Models. In Encyclopedia of Materials: Science and Technology; Elsevier: Oxford, UK, 2001; pp. 1599–1609. [Google Scholar]
- García Nieto, P.J.; García-Gonzalo, E.; Álvarez Antón, J.C.; González Suárez, V.M.; Mayo Bayón, R.; Mateos Martín, F. A comparison of several machine learning techniques for the centerline segregation prediction in continuous cast steel slabs and evaluation of its performance. J. Comput. Appl. Math. 2018, 330, 877–895. [Google Scholar] [CrossRef]
- Mapelli, C.; Baragiola, S. Development of solidification microstructures in continuously cast billets of boron and resulphurised steel grades. Ironmak. Steelmak. 2008, 35, 441–451. [Google Scholar] [CrossRef]
- Jena, P.K.; Singh, B.B.; SivaKumar, K.; ShingWeker, A.; Amte, N.; Singh, A.K.; Madhu, V. Microstructure, mechanical and ballistic property evaluation of a high strength low alloy steel produced through continuous casting route. Adv. Mater. Process. Technol. 2020, 2020, 1–17. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Fu, H.; Lou, M.; Xie, J. Effects of process parameters on surface quality, composition segregation, microstructure and properties of QSn6. 5-0. 1 alloy slabs fabricated by HCCM horizontal continuous casting. J. Iron Steel Res. Int. 2017, 24, 273–281. [Google Scholar] [CrossRef]
- Combeau, H.; Založnik, M.; Bedel, M. Predictive Capabilities of Multiphysics and Multiscale Models in Modeling Solidification of Steel Ingots and DC Casting of Aluminum. JOM 2016, 68, 2198–2206. [Google Scholar] [CrossRef]
- Zavalishchin, A.N.; Kozhevnikova, E.V. Effect of Continuous Casting Technology on Low-Alloy Steel Structure in Different Production Stages. Metallurgist 2018, 61, 1048–1054. [Google Scholar] [CrossRef]
- Jiang, D.; Wang, R.; Zhang, Q.; Zhang, Z.; Tu, T.; Wang, J.; Ren, Z. Effect of final electromagnetic stirring on solidification microstructure of GCr15 bearing steel in simulated continuous casting. J. Iron Steel Res. Int. 2020, 27, 141–147. [Google Scholar] [CrossRef]
- Fourlakidis, V.; Diószegi, A. A generic model to predict the ultimate tensile strength in pearlitic lamellar graphite iron. Mater. Sci. Eng. A 2014, 618, 161–167. [Google Scholar] [CrossRef]
- Guo, F.; Wang, X.; Wang, J.; Misra, R.D.K.; Shang, C. The Significance of Central Segregation of Continuously Cast Billet on Banded Microstructure and Mechanical Properties of Section Steel. Metals 2020, 10, 76. [Google Scholar] [CrossRef]
- Rasouli, D.; Khameneh Asl, S.; Akbarzadeh, A.; Daneshi, G.H. Effect of cooling rate on the microstructure and mechanical properties of microalloyed forging steel. J. Mater. Process. Technol. 2008, 206, 92–98. [Google Scholar] [CrossRef]
- Forouzanfar, M.; Doustmohammadi, A.; Menhaj, M.B.; Hasanzadeh, S. Modeling and estimation of the natural gas consumption for residential and commercial sectors in Iran. Appl. Energy 2010, 87, 268–274. [Google Scholar] [CrossRef]
- Wang, W.; Hou, Z.; Chang, Y.; Cao, J. Effect of superheat on quality of central equiaxed grain zone of continuously cast bearing steel billet based on two-dimensional segregation ratio. J. Iron Steel Res. Int. 2018, 25, 9–18. [Google Scholar] [CrossRef]
- Choudhary, S.K.; Ganguly, S.; Sengupta, A.; Sharma, V. Solidification morphology and segregation in continuously cast steel slab. J. Mater. Process. Technol. 2017, 243, 312–321. [Google Scholar] [CrossRef]
- Chu, R.; Li, Z.; Fan, Y.; Liu, J.; Ma, C.; Wang, X. Cracking and segregation in high-alloy steel 0.4C1.5Mn2Cr0.35Mo1.5Ni produced by thick continuous casting. Heliyon 2019, 5, e01329. [Google Scholar] [CrossRef]
- Zhu, H.; Sun, J.; Wang, W.; Wang, W.; Lei, J.; Xue, Z. Experimental investigation on segregation and remelting behaviors of boron-containing steel with low carbon. Results Phys. 2019, 12, 67–72. [Google Scholar] [CrossRef]
- Wang, J.; Guo, F.; Wang, Z.; Xie, Z.; Shang, C.; Wang, X. Influence of centerline segregation on the crystallographic features and mechanical properties of a high-strength low-alloy steel. Mater. Lett. 2020, 267, 127512. [Google Scholar] [CrossRef]
- Kinoshita, K.; Yoshii, Y.; Kitaoka, H.; Kawaharada, A.; Nishikawa, H.; Tanigawa, O. Continuous Casting of High-Alloy Steels. JOM 1984, 36, 38–43. [Google Scholar] [CrossRef]
- Jayet-Gendrot, S.; Gilles, P.; Migné, C. Behavior of duplex stainless steel casting defects under mechanical loadings. Nucl. Eng. Des. 2000, 197, 141–153. [Google Scholar] [CrossRef]
- Kulkarni, M.S.; Subash Babu, A. Managing quality in continuous casting process using product quality model and simulated annealing. J. Mater. Process. Technol. 2005, 166, 294–306. [Google Scholar] [CrossRef]
- Sterjovski, Z.; Nolan, D.; Carpenter, K.R.; Dunne, D.P.; Norrish, J. Artificial neural networks for modelling the mechanical properties of steels in various applications. J. Mater. Process. Technol. 2005, 170, 536–544. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2003. [Google Scholar]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Gračnar, A.; Kovačič, M.; Brezocnik, M. Decreasing of guides changing with pass design optimization on continuous rolling mill using a genetic algorithm. Mater. Manuf. Process. 2020, 35, 663–667. [Google Scholar] [CrossRef]
- Ojstersek, R.; Tang, M.; Buchmeister, B. Due date optimization in multi-objective scheduling of flexible job shop production. Adv. Produc. Engineer. Manag. 2020, 15, 481–492. [Google Scholar] [CrossRef]
- Amjad, M.K.; Butt, S.I.; Anjum, N.; Chaudhry, I.A.; Faping, Z.; Khan, M. A layered genetic algorithm with iterative diversification for optimization of flexible job shop scheduling problems. Adv. Produc. Engineer. Manag. 2020, 15, 377–389. [Google Scholar] [CrossRef]
- Jurković, Z.; Cukor, G.; Brezocnik, M.; Brajkovic, T. A comparison of machine learning methods for cutting parameters prediction in high speed turning process. J. Intell. Manuf. 2018, 29, 1683–1693. [Google Scholar] [CrossRef]
- Brezocnik, M.; Kovačič, M.; Ficko, M. Prediction of surface roughness with genetic programming. J. Mater. Process. Technol. 2004, 157–158, 28–36. [Google Scholar] [CrossRef]
- Kovačič, M.; Župerl, U. Genetic programming in the steelmaking industry. Genet. Program. Evolvable Mach. 2020, 21, 99–128. [Google Scholar] [CrossRef]
- Kovačič, M.; Šarler, B. Genetic programming prediction of the natural gas consumption in a steel plant. Energy 2014, 66, 273–284. [Google Scholar] [CrossRef]
- Kovačič, M.; Dolenc, F. Prediction of the natural gas consumption in chemical processing facilities with genetic programming. Genet. Program. Evolvable Mach. 2016, 17, 231–249. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).