Effects of the 12 May 2021 Geomagnetic Storm on Georeferencing Precision
Abstract
:1. Introduction
2. Materials and Methods
2.1. Estimation of the Ionospheric Total Electron Content
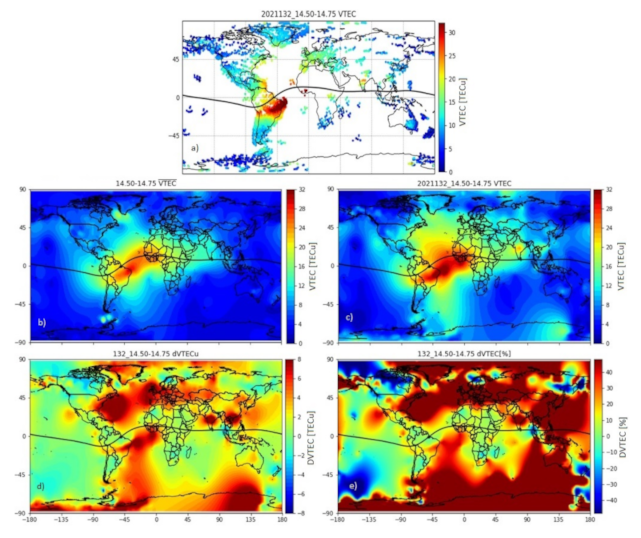
Ionospheric TEC Maps
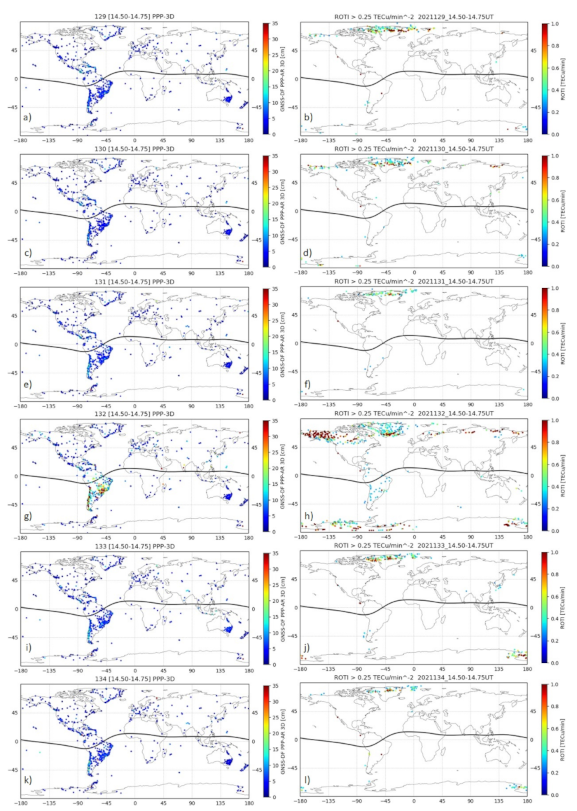
2.2. ROT and ROTI
2.3. Apparent Position Variation Using Precise Point Positioning
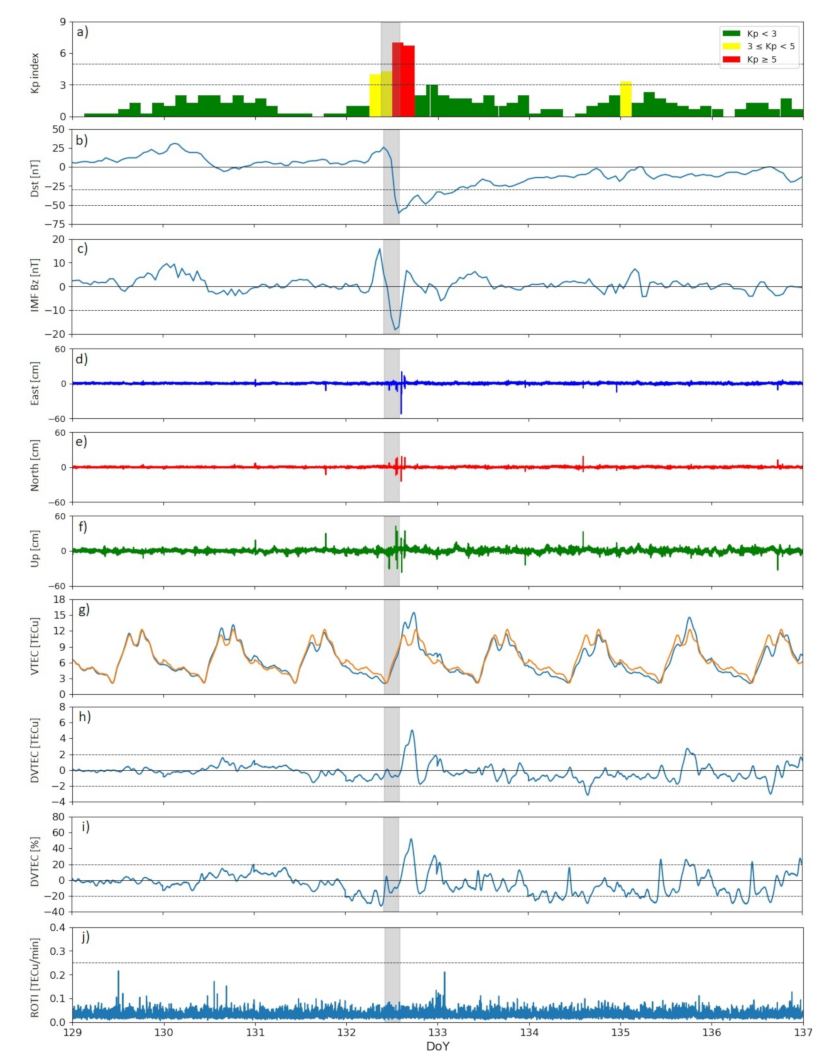
2.4. Geophysical and Geomagnetic Conditions
2.5. Possible Earthquakes Perturbations
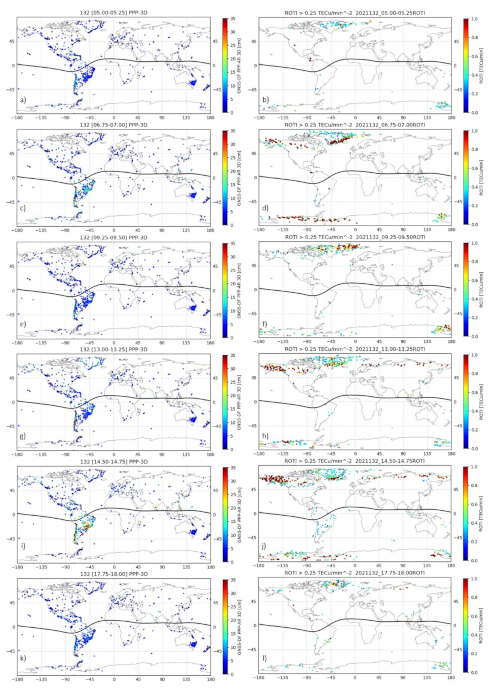
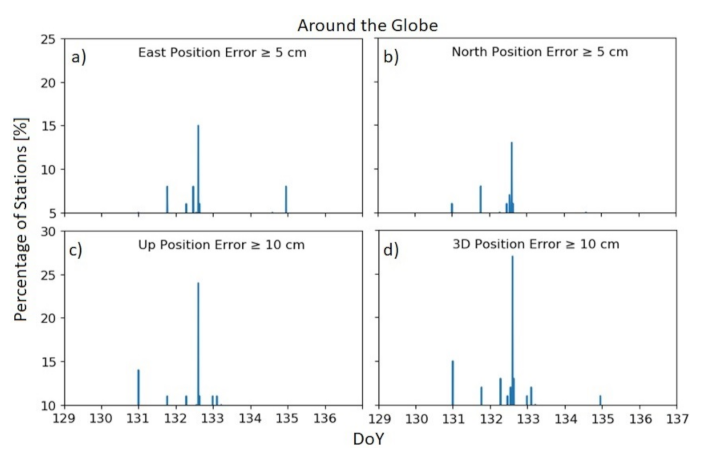
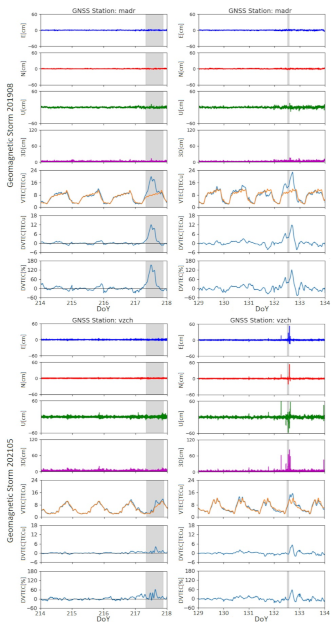
3. Results
4. Discussion and Main Conclusions
4.1. 12 May 2021 Geomagnetic Storm
4.2. The 27 March 2017 and 5 August 2019 Geomagnetic Storms
4.3. Ionospheric Effects
4.4. Positioning Errors
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Adebiyi, S.; Ikubanni, S.; Adebesin, B.; Joshua, B.; Adekoya, B. Variations of GPS-TEC at an African Low Latitude Station during Geomagnetic Disturbances. Phys. Mem.-J. Theor. Appl. Phys. 2019, 1, 113–125. [Google Scholar]
- Gonzalez, W.D.; Tsurutani, B.T.; De Gonzalez, A.L.C. Interplanetary origin of geomagnetic storms. Space Sci. Rev. 1999, 88, 529–562. [Google Scholar] [CrossRef]
- Tsidu, G.M.; Abraha, G. Moderate geomagnetic storms of 22–25 January 2012 and their influences on the wave components in ionosphere and upper stratosphere-mesosphere regions. Adv. Space Res. 2014, 54, 1793–1812. [Google Scholar] [CrossRef]
- Gonzalez, W.; Joselyn, J.A.; Kamide, Y.; Kroehl, H.W.; Rostoker, G.; Tsurutani, B.; Vasyliunas, V. What is a geomagnetic storm? J. Geophys. Res. Space Phys. 1994, 99, 5771–5792. [Google Scholar] [CrossRef]
- Joshua, B.; Adeniyi, J.; Adimula, I.; Oladipo, O.; Olawepo, O.; Adebiyi, S. Ionospheric response to the storm-time disturbance of 29 May, 2010. Adv. Space Res. 2014, 53, 219–225. [Google Scholar] [CrossRef]
- Joshua, B.; Adeniyi, J.; Reinisch, B.; Adimula, I.; Olawepo, A.; Oladipo, O.; Adebiyi, S. The response of the ionosphere over Ilorin to some geomagnetic storms. Adv. Space Res. 2014, 54, 2224–2235. [Google Scholar] [CrossRef]
- Davis, T.N.; Sugiura, M. Auroral electrojet activity index AE and its universal time variations. J. Geophys. Res. 1966, 71, 785–801. [Google Scholar] [CrossRef] [Green Version]
- Boroyev, R.; Vasiliev, M. Relationship of the ASY-H index with interplanetary medium parameters and auroral activity in magnetic storm main phases during CIR and ICME events. Sol.-Terr. Phys. 2020, 6, 35–40. [Google Scholar] [CrossRef]
- Adebesin, B.; Ikubanni, S.; Kayode, J.; Adekoya, B. Variability of solar wind dynamic pressure with solar wind parameters during intense and severe storms. Afr. Rev. Phys. 2013, 8, 119–128. [Google Scholar]
- Borovsky, J.E.; Shprits, Y.Y. Is the Dst index sufficient to define all geospace storms? J. Geophys. Res. Space Phys. 2017, 122, 11–543. [Google Scholar] [CrossRef] [Green Version]
- Matzka, J.; Stolle, C.; Yamazaki, Y.; Bronkalla, O.; Morschhauser, A. The Geomagnetic Kp Index and Derived Indices of Geomagnetic Activity. Space Weather 2021, 19, e2020SW002641. [Google Scholar] [CrossRef]
- Ferreira, A.A.; Borges, R.A. Performance Analysis of Distinct Feed-forward Neural Networks Structures on the AE Index Prediction. In Proceedings of the 2021 IEEE Aerospace Conference (50100), Big Sky, MT, USA, 6–13 June 2021; pp. 1–7. [Google Scholar]
- Desai, M.V.; Shah, S.N. Impacts of intense geomagnetic storms on NavIC/IRNSS system. Ann. Geophys. 2018, 61, 557. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez, W.; Echer, E. A study on the peak Dst and peak negative Bz relationship during intense geomagnetic storms. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
- Mendillo, M. Storms in the ionosphere: Patterns and processes for total electron content. Rev. Geophys. 2006, 44. [Google Scholar] [CrossRef]
- Joshua, B.; Adeniyi, J.; Oladipo, O.; Doherty, P.; Adimula, I.; Olawepo, A.; Adebiyi, S. Simultaneous response of NmF2 and GPS-TEC to storm events at Ilorin. Adv. Space Res. 2018, 61, 2904–2913. [Google Scholar] [CrossRef]
- Cai, X.; Burns, A.G.; Wang, W.; Qian, L.; Solomon, S.C.; Eastes, R.W.; McClintock, W.E.; Laskar, F. Investigation of a neutral “tongue” observed by GOLD during the geomagnetic storm on May 11, 2019. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028817. [Google Scholar] [CrossRef]
- Yu, T.; Wang, W.; Ren, Z.; Yue, J.; Yue, X.; He, M. Middle-Low Latitude Neutral Composition and Temperature Responses to the 20 and 21 November 2003 Superstorm From GUVI Dayside Limb Measurements. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028427. [Google Scholar] [CrossRef]
- Verkhoglyadova, O.P.; Tsurutani, B.T.; Mannucci, A.J.; Saito, A.; Araki, T.; Anderson, D.; Abdu, M.; Sobral, J. Simulation of PPEF effects in dayside low-latitude ionosphere for the 30 October 2003, superstorm. Wash. DC Am. Geophys. Union Geophys. Monogr. Ser. 2008, 181, 169–177. [Google Scholar]
- Inyurt, S. Investigation of Ionospheric Variations During Magnetic Storm Over Turkey. Geomagn. Aeron. 2020, 60, 131–135. [Google Scholar] [CrossRef]
- Liu, L.; Wan, W.; Zhang, M.L.; Zhao, B.; Ning, B. Prestorm enhancements in NmF2 and total electron content at low latitudes. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef]
- Gao, Q.; Liu, L.B.; Zhao, B.Q.; Wan, W.X.; Zhang, M.L.; Ning, B.Q. Statistical Study of the Storm Effects in Middle and Low Latitude Ionosphere in the East-Asian Sector. Chin. J. Geophys. 2008, 51, 435–443. [Google Scholar] [CrossRef]
- Stankov, S.; Stegen, K.; Warnant, R. Seasonal variations of storm-time TEC at European middle latitudes. Adv. Space Res. 2010, 46, 1318–1325. [Google Scholar] [CrossRef]
- Sharma, S.; Galav, P.; Dashora, N.; Dabas, R.; Pandey, R. Study of ionospheric TEC during space weather event of 24 August 2005 at two different longitudes. J. Atmos. Sol.-Terr. Phys. 2012, 75, 133–140. [Google Scholar] [CrossRef]
- Blagoveshchenskii, D. Effect of geomagnetic storms (substorms) on the ionosphere: 1. A review. Geomagn. Aeron. 2013, 53, 275–290. [Google Scholar] [CrossRef]
- Cherniak, I.; Zakharenkova, I.; Redmon, R.J. Dynamics of the high-latitude ionospheric irregularities during the 17 March 2015St. Patrick’s Day storm: Ground-based GPS measurements. Space Weather 2015, 13, 585–597. [Google Scholar] [CrossRef]
- Fagundes, P.R.; Cardoso, F.; Fejer, B.; Venkatesh, K.; Ribeiro, B.; Pillat, V. Positive and negative GPS-TEC ionospheric storm effects during the extreme space weather event of March 2015 over the Brazilian sector. J. Geophys. Res. Space Phys. 2016, 121, 5613–5625. [Google Scholar] [CrossRef] [Green Version]
- Tsurutani, B.; Mannucci, A.; Iijima, B.; Abdu, M.A.; Sobral, J.H.A.; Gonzalez, W.; Guarnieri, F.; Tsuda, T.; Saito, A.; Yumoto, K.; et al. Global dayside ionospheric uplift and enhancement associated with interplanetary electric fields. J. Geophys. Res. Space Phys. 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Mannucci, A.; Tsurutani, B.; Iijima, B.; Komjathy, A.; Saito, A.; Gonzalez, W.; Guarnieri, F.; Kozyra, J.; Skoug, R. Dayside global ionospheric response to the major interplanetary events of 29–30 October 2003 “Halloween Storms”. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
- Lastovicka, J. Monitoring and forecasting of ionospheric space weather—effects of geomagnetic storms. J. Atmos. Sol.-Terr. Phys. 2002, 64, 697–705. [Google Scholar] [CrossRef]
- Fuller-Rowell, T.; Codrescu, M.; Rishbeth, H.; Moffett, R.; Quegan, S. On the seasonal response of the thermosphere and ionosphere to geomagnetic storms. J. Geophys. Res. 1996, 101, 2343–2353. [Google Scholar] [CrossRef]
- Kleimenova, N.; Gromova, L.; Gromov, S.; Malysheva, L. Strong Magnetic Storm on 25–26 August 2018 with Reference to the Solar Cycle 24 Declining. Sol. Influ. Magnetos. Ionos. Atmos. 2019, 107–112. [Google Scholar] [CrossRef] [Green Version]
- Kleimenova, N.; Gromova, L.; Gromov, S.; Malysheva, L. The Magnetic Storm of August 25–26, 2018: Dayside High Latitude Geomagnetic Variations and Pulsations. Geomagn. Aeron. 2019, 59, 660–667. [Google Scholar] [CrossRef]
- Redmon, R.; Seaton, D.; Steenburgh, R.; He, J.; Rodriguez, J. September 2017’s geoeffective space weather and impacts to Caribbean radio communications during hurricane response. Space Weather 2018, 16, 1190–1201. [Google Scholar] [CrossRef] [Green Version]
- Aa, E.; Huang, W.; Liu, S.; Ridley, A.; Zou, S.; Shi, L.; Chen, Y.; Shen, H.; Yuan, T.; Li, J.; et al. Midlatitude plasma bubbles over China and adjacent areas during a magnetic storm on 8 September 2017. Space Weather 2018, 16, 321–331. [Google Scholar] [CrossRef]
- SAĞIR, S.; ATICI, R.; DÖLEK, İ. Investigation of the Severe Geomagnetic Storm Effects on Ionosphere at Nighttime through ROTI. Muş Alparslan Üniv. Fen Bilim. Derg. 2018, 6, 603–609. [Google Scholar]
- Teh, W.L.; Chen, W.S. Dependency of the Ionospheric Storm on the Local Time of Storm Onset in the Southeast Asia Sector. In Proceedings of the 2019 6th International Conference on Space Science and Communication (IconSpace), Johor Bahru, Malaysia, 28–30 July 2019; pp. 9–13. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Mei, J.; Zhang, C.; Wang, J. A Study on the Characteristics of the Ionospheric Gradient under Geomagnetic Perturbations. Sensors 2020, 20, 1805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wen, D.; Mei, D. Ionospheric TEC disturbances over China during the strong geomagnetic storm in September 2017. Adv. Space Res. 2020, 65, 2529–2539. [Google Scholar] [CrossRef]
- Fedrizzi, M.; de Paula, E.R.; Kantor, I.J.; Langley, R.B.; Santos, M.C.; Komjathy, A. Mapping the low-latitude ionosphere with GPS. GPS World 2002, 13, 41–47. [Google Scholar]
- Batista, I.S.; Abdu, M.; Souza, J.; Bertoni, F.; Matsuoka, M.; Camargo, P.; Bailey, G. Unusual early morning development of the equatorial anomaly in the Brazilian sector during the Halloween magnetic storm. J. Geophys. Res. Space Phys. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- de Abreu, A.; Sahai, Y.; Fagundes, P.R.; Becker-Guedes, F.; de Jesus, R.; Guarnieri, F.; Pillat, V.G. Response of the ionospheric F-region in the Brazilian sector during the super geomagnetic storm in April 2000 observed by GPS. Adv. Space Res. 2010, 45, 1322–1329. [Google Scholar] [CrossRef]
- Nogueira, P.; Abdu, M.; Batista, I.; De Siqueira, P. Equatorial ionization anomaly and thermospheric meridional winds during two major storms over Brazilian low latitudes. J. Atmos. Sol.-Terr. Phys. 2011, 73, 1535–1543. [Google Scholar] [CrossRef]
- De Siqueira, P.; De Paula, E.; Muella, M.; Rezende, L.; Abdu, M.; Gonzalez, W. Storm-time total electron content and its response to penetration electric fields over South America. Ann. Geophys. 2011, 29, 1765–1778. [Google Scholar] [CrossRef] [Green Version]
- De Abreu, A.; Sahai, Y.; Fagundes, P.; De Jesus, R.; Bittencourt, J.; Pillat, V. An investigation of ionospheric F region response in the Brazilian sector to the super geomagnetic storm of May 2005. Adv. Space Res. 2011, 48, 1211–1220. [Google Scholar] [CrossRef]
- Figueiredo, C.; Wrasse, C.; Takahashi, H.; Otsuka, Y.; Shiokawa, K.; Barros, D. Large-scale traveling ionospheric disturbances observed by GPS dTEC maps over North and South America on Saint Patrick’s Day storm in 2015. J. Geophys. Res. Space Phys. 2017, 122, 4755–4763. [Google Scholar] [CrossRef]
- Bravo, M.; Villalobos, C.; Leiva, R.; Tamblay, L.; Vega-Jorquera, P.; Ovalle, E.; Foppiano, A. Ionospheric Response to the Space Weather Events of 4–10 September 2017: First Chilean Observations. Open Atmos. Sci. J. 2019, 13. [Google Scholar] [CrossRef] [Green Version]
- Macho, E.P.; Correia, E.; Paulo, C.M.; Angulo, L.; Vieira, J.A.G. Ionospheric response to the June 2015 geomagnetic storm in the South American region. Adv. Space Res. 2020, 65, 2172–2183. [Google Scholar] [CrossRef]
- Kuai, J.; Liu, L.; Lei, J.; Liu, J.; Zhao, B.; Chen, Y.; Le, H.; Wang, Y.; Hu, L. Regional differences of the ionospheric response to the July 2012 geomagnetic storm. J. Geophys. Res. Space Phys. 2017, 122, 4654–4668. [Google Scholar] [CrossRef]
- Gao, Y. Precise Point Positioning (PPP). In Encyclopedia of Geodesy; Springer International Publishing: Cham, Switzerland, 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Jacobsen, K.S.; Andalsvik, Y.L. Overview of the 2015 St. Patrick’s day storm and its consequences for RTK and PPP positioning in Norway. J. Space Weather Space Clim. 2016, 6, A9. [Google Scholar] [CrossRef]
- Yang, L.; Gao, J.; Li, Z.; Li, F.; Chen, C.; Wang, Y. New Satellite Selection Approach for GPS/BDS/GLONASS Kinematic Precise Point Positioning. Appl. Sci. 2019, 9, 5280. [Google Scholar] [CrossRef] [Green Version]
- Abdallah, A.; Saifeldin, A.; Abomariam, A.; Ali, R. Efficiency of using GNSS-PPP for digital elevation model (DEM) production. Artif. Satell. 2020, 55, 17–28. [Google Scholar] [CrossRef]
- Yigit, C.O. Experimental assessment of post-processed kinematic Precise Point Positioning method for structural health monitoring. Geomat. Nat. Hazards Risk 2016, 7, 360–383. [Google Scholar] [CrossRef] [Green Version]
- Mendez Astudillo, J.; Lau, L.; Tang, Y.T.; Moore, T. Analysing the Zenith Tropospheric Delay Estimates in On-line Precise Point Positioning (PPP) Services and PPP Software Packages. Sensors 2018, 18, 580. [Google Scholar] [CrossRef] [Green Version]
- Shagimuratov, I.; Chernouss, S.; Despirak, I.; Filatov, M.; Efishov, I.; Tepenitsyna, N.Y. Occurrence of TEC fluctuations and GPS positioning errors at different longitudes during auroral disturbances. Sun Geosph. 2018, 13, 89–94. [Google Scholar] [CrossRef]
- Luo, X.; Gu, S.; Lou, Y.; Xiong, C.; Chen, B.; Jin, X. Assessing the performance of GPS precise point positioning under different geomagnetic storm conditions during solar cycle 24. Sensors 2018, 18, 1784. [Google Scholar] [CrossRef] [Green Version]
- Poniatowski, M.; Nykiel, G. Degradation of Kinematic PPP of GNSS Stations in Central Europe Caused by Medium-Scale Traveling Ionospheric Disturbances During the St. Patrick’s Day 2015 Geomagnetic Storm. Remote Sens. 2020, 12, 3582. [Google Scholar] [CrossRef]
- Yasyukevich, Y.; Vasilyev, R.; Ratovsky, K.; Setov, A.; Globa, M.; Syrovatskii, S.; Yasyukevich, A.; Kiselev, A.; Vesnin, A. Small-Scale Ionospheric Irregularities of Auroral Origin at Mid-Latitudes during the 22 June 2015 Magnetic Storm and Their Effect on GPS Positioning. Remote Sens. 2020, 12, 1579. [Google Scholar] [CrossRef]
- Yang, Z.; Mrak, S.; Morton, Y.J. Geomagnetic Storm Induced Mid-latitude Ionospheric Plasma Irregularities and Their Implications for GPS Positioning over North America: A Case Study. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS). IEEE, Portland, OR, USA, 20–23 April 2020; pp. 234–238. [Google Scholar] [CrossRef]
- Rajesh, P.; Lin, C.; Lin, C.; Chen, C.H.; Liu, J.; Matsuo, T.; Chen, S.P.; Yeh, W.; Huang, C. Extreme Positive Ionosphere Storm Triggered by a Minor Magnetic Storm in Deep Solar Minimum Revealed by FORMOSAT-7/COSMIC-2 and GNSS Observations. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028261. [Google Scholar] [CrossRef]
- Seemala, G.; Valladares, C. Statistics of total electron content depletions observed over the South American continent for the year 2008. Radio Sci. 2011, 46. [Google Scholar] [CrossRef]
- Piñón, D.A.; Gómez, D.D.; Smalley, R.; Cimbaro, S.R.; Lauría, E.A.; Bevis, M.G. The history, state, and future of the Argentine continuous satellite monitoring network and its contributions to geodesy in Latin America. Seismol. Res. Lett. 2018, 89, 475–482. [Google Scholar] [CrossRef] [Green Version]
- Orus, R.; Hernandez-Pajares, M.; Juan, J.; Sanz, J. Improvement of global ionospheric VTEC maps by using kriging interpolation technique. J. Atmos. Sol.-Terr. Phys. 2005, 67, 1598–1609. [Google Scholar] [CrossRef]
- Monte Moreno, E.; García Rigo, A.; Hernández-Pajares, M.; Yang, H. TEC Forecasting Based on Manifold Trajectories. Remote Sens. 2018, 10, 988. [Google Scholar] [CrossRef] [Green Version]
- Monte-Moreno, E.; Hernandez-Pajares, M.; Lyu, H.; Yang, H.; Aragon-Angel, A. Estimation of Polar Depletion Regions by VTEC Contrast and Watershed Enhancing. IEEE Trans. Geosci. Remote. Sens. 2021, 1–20. [Google Scholar] [CrossRef]
- Yang, H.; Monte-Moreno, E.; Hernandez-Pajares, M.; Roma-Dollase, D. Real-time interpolation of global ionospheric maps by means of sparse representation. J. Geod. 2021, 95, 1–20. [Google Scholar] [CrossRef]
- Basu, S.; Groves, K.; Quinn, J.; Doherty, P. A comparison of TEC fluctuations and scintillations at Ascension Island. J. Atmos. Sol.-Terr. Phys. 1999, 61, 1219–1226. [Google Scholar] [CrossRef]
- Ma, G.; Maruyama, T. A super bubble detected by dense GPS network at east Asian longitudes. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Ke, F.; Qi, X.; Wang, Y.; Liu, X. Statistics of ionospheric responses to Southeast Asia’s typhoons during 2006–2018 using the rate of change in the TEC index. Adv. Space Res. 2020, 66, 1724–1742. [Google Scholar] [CrossRef]
- Harsha, P.B.S.; Ratnam, D.V.; Nagasri, M.L.; Sridhar, M.; Raju, K.P. Kriging-based ionospheric TEC, ROTI and amplitude scintillation index (S 4) maps for India. IET Radar Sonar Navig. 2020, 14, 1827–1836. [Google Scholar] [CrossRef]
- Zhou, W.; Gu, S.; Ge, M.; Wang, J. Analysis of the Effect of the 06-09-2017 Solar Flare on GNSS Signal and Positioning Performance. In China Satellite Navigation Conference; Springer: Berlin/Heidelberg, Germany, 2018; pp. 555–569. [Google Scholar]
- Liu, X.; Yuan, Y.; Tan, B.; Li, M. Observational Analysis of Variation Characteristics of GPS-Based TEC Fluctuation over China. ISPRS Int. J. Geo-Inf. 2016, 5, 237. [Google Scholar] [CrossRef] [Green Version]
- Alkan, R.M.; Erol, S.; Ozulu, I.M.; Ilci, V. Accuracy comparison of post-processed PPP and real-time absolute positioning techniques. Geomat. Nat. Hazards Risk 2020, 11, 178–190. [Google Scholar] [CrossRef]
- Nose, M.; Iyemori, T.; Sugiura, M.; Kamei, T. Geomagnetic Dst index. World Data Cent. Geomagn. Kyoto 2015, 10, 15–31. [Google Scholar] [CrossRef]
- Matzka, J.; Bronkalla, O.; Tornow, K.; Elger, K.; Stolle, C. Geomagnetic Kp index. V. 1.0, GFZ Data Services. 2021. Available online: https://dataservices.gfz-potsdam.de/panmetaworks/showshort.php?id=escidoc:5216888 (accessed on 3 December 2021).
- Kotulak, K.; Krankowski, A.; Froń, A.; Flisek, P.; Wang, N.; Li, Z.; Błaszkiewicz, L. Sub-Auroral and Mid-Latitude GNSS ROTI Performance during Solar Cycle 24 Geomagnetic Disturbed Periods: Towards Storm’s Early Sensing. Sensors 2021, 21, 4325. [Google Scholar] [CrossRef] [PubMed]
- Kotulak, K.; Zakharenkova, I.; Krankowski, A.; Cherniak, I.; Wang, N.; Fron, A. Climatology Characteristics of Ionospheric Irregularities Described with GNSS ROTI. Remote Sens. 2020, 12, 2634. [Google Scholar] [CrossRef]
- Katsigianni, G.; Loyer, S.; Perosanz, F. PPP and PPP-AR Kinematic Post-Processed Performance of GPS-Only, Galileo-Only and Multi-GNSS. Remote Sens. 2019, 11, 2477. [Google Scholar] [CrossRef] [Green Version]
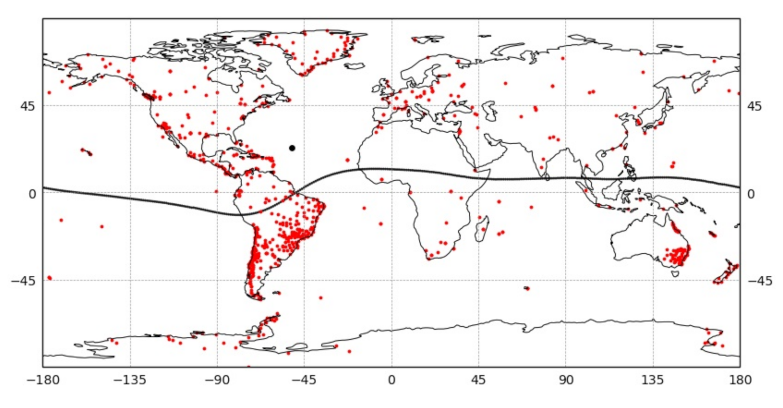
| Geomagnetic Storm | Dst [nT] | Kp | AE [nT] | Stations N | Kinematic PPP | Method |
|---|---|---|---|---|---|---|
| 7 January 2015 [56] | −99 | 6 | 2031 | 3 | GIPSY-OASIS | ROTI |
| 17 March 2015 [57] | −223 | 8 | 2298 | ∼500 | GPS PPP Model | ROTI |
| 17 March 2015 [58] | −223 | 8 | 2298 | 15 | gLAB software | DVTEC, TIDs |
| 22, 23 June 2015 [59] | −204 | 8 | 2698 | 5172 | GAMP software | Spread-F, S4 |
| 20 December 2015 [57] | −155 | 7 | 1946 | ∼500 | GPS PPP Model | ROTI |
| 27 March 2017 [57] | −74 | 6 | 1505 | ∼500 | GPS PPP Model | ROTI |
| 8 September 2017 [60] | −124 | 8 | 2677 | ∼700 | RTKLIB package | ROTI |
| Error Intervals [cm] | East [%] | East gs [%] | North [%] | North gs [%] | Up [%] | Up gs [%] | 3D [%] | 3D gs [%] |
|---|---|---|---|---|---|---|---|---|
| <5 | 98 | 85 | 99 | 87 | 73 | 52 | 71 | 48 |
| 5–10 | 2 | 8 | 1 | 8 | 24 | 23 | 26 | 25 |
| 10–20 | 0 | 5 | 0 | 2 | 3 | 16 | 3 | 17 |
| 20–40 | 0 | 1 | 0 | 2 | 0 | 6 | 0 | 7 |
| 40–60 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 60–100 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| >100 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| Error Intervals [cm] | East [%] | East gs [%] | North [%] | North gs [%] | Up [%] | Up gs [%] | 3D [%] | 3D gs [%] |
|---|---|---|---|---|---|---|---|---|
| <5 | 98 | 70 | 98 | 72 | 55 | 13 | 50 | 9 |
| 5–10 | 2 | 16 | 2 | 19 | 39 | 33 | 43 | 32 |
| 10–20 | 0 | 11 | 0 | 6 | 5 | 35 | 6 | 38 |
| 20–40 | 0 | 2 | 0 | 2 | 1 | 15 | 1 | 15 |
| 40–60 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 2 |
| 60–100 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 2 |
| >100 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 2 |
| Station | DoYs | RMS [cm] | MAX [cm] | DVTEC | %DVTEC | ROTI | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [Season] | E | N | U | 3D | E | N | U | 3D | [TECu] | [%] | [] | |
| madr | QD2017 | 0.4 | 0.5 | 1.0 | 1.1 | 1.6 | 2.0 | 5.5 | 5.7 | |||
| DoY 86 | 0.6 | 0.5 | 1.2 | 1.4 | 2.2 | 1.5 | 4.4 | 4.5 | 9.9 | 110 | 0.1 | |
| [Spring] | ||||||||||||
| QD2019 | 0.6 | 0.5 | 1.5 | 1.7 | 2.7 | 2.2 | 6.2 | 6.3 | ||||
| DoY 217 | 1.0 | 0.9 | 2.8 | 2.8 | 3.1 | 2.6 | 11.6 | 11.7 | 12.0 | 153 | 0.52 | |
| [Summer] | ||||||||||||
| QD2021 | 0.7 | 0.6 | 1.7 | 1.9 | 2.4 | 2.7 | 8.7 | 8.8 | ||||
| DoY 132 | 1.2 | 1.1 | 3.5 | 3.7 | 3.9 | 4.1 | 15.4 | 17.0 | 11.9 | 120 | 0.3 | |
| [Spring] | ||||||||||||
| vzch | QD2017 | |||||||||||
| DoY 86 | ||||||||||||
| [Fall] | ||||||||||||
| QD2019 | 0.6 | 0.5 | 1.5 | 1.7 | 5.2 | 3.7 | 15.4 | 15.4 | ||||
| DoY 217 | 0.9 | 0.7 | 2.2 | 2.5 | 6.0 | 3.5 | 15.0 | 15.1 | 4.1 | 62 | 0.11 | |
| [Winter] | ||||||||||||
| QD2021 | 0.6 | 0.5 | 1.6 | 1.8 | 7.0 | 6.8 | 18.7 | 18.9 | ||||
| DoY 132 | 1.5 | 1.4 | 3.8 | 4.4 | 52.4 | 52.9 | 58.8 | 82.5 | 5.3 | 56 | 0.08 | |
| [Fall] | ||||||||||||
| vita | QD2017 | 0.6 | 0.6 | 1.8 | 2.0 | 2.9 | 3.1 | 8.4 | 8.4 | |||
| DoY 86 | 1.0 | 1.1 | 2.8 | 3.2 | 3.5 | 3.0 | 10.0 | 10.0 | 23.5 | 150 | 0.09 | |
| [Fall] | ||||||||||||
| QD2019 | ||||||||||||
| DoY 217 | ||||||||||||
| [Winter] | ||||||||||||
| QD2021 | 0.6 | 0.6 | 1.7 | 1.9 | 11.1 | 11.6 | 26.8 | 30.3 | ||||
| DoY 132 | 1.7 | 1.2 | 4.3 | 4.8 | 52.5 | 25.0 | 41.9 | 61.2 | 5.1 | 51 | 0.13 | |
| [Fall] | ||||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valdés-Abreu, J.C.; Díaz, M.A.; Báez, J.C.; Stable-Sánchez, Y. Effects of the 12 May 2021 Geomagnetic Storm on Georeferencing Precision. Remote Sens. 2022, 14, 38. https://doi.org/10.3390/rs14010038
Valdés-Abreu JC, Díaz MA, Báez JC, Stable-Sánchez Y. Effects of the 12 May 2021 Geomagnetic Storm on Georeferencing Precision. Remote Sensing. 2022; 14(1):38. https://doi.org/10.3390/rs14010038
Chicago/Turabian StyleValdés-Abreu, Juan Carlos, Marcos A. Díaz, Juan Carlos Báez, and Yohadne Stable-Sánchez. 2022. "Effects of the 12 May 2021 Geomagnetic Storm on Georeferencing Precision" Remote Sensing 14, no. 1: 38. https://doi.org/10.3390/rs14010038
APA StyleValdés-Abreu, J. C., Díaz, M. A., Báez, J. C., & Stable-Sánchez, Y. (2022). Effects of the 12 May 2021 Geomagnetic Storm on Georeferencing Precision. Remote Sensing, 14(1), 38. https://doi.org/10.3390/rs14010038






