Abstract
Integration of renewable energy sources (RESs) into power systems is growing due to eco-friendly concerns and ever-increasing electricity demand. Voltage source converters (VSCs) are the main interface between RESs and power grids, which have neither rotational inertia nor damping characteristics. Lack of these metrics make the power grid sensitive to frequency disturbances and thereby under frequency, to load shedding activation or even large-scale collapse. In this regard, the contribution of this paper is to develop a new control technique for VSCs that can provide virtual inertia and damping properties with the DC-link capacitors inhered in the DC-side of grid-tied VSCs. The applied VSC is controlled in the current controlled model, with the capability of injecting extra active power with the aim of frequency support during perturbations. The dynamics assessment of the proposed platform is derived in detail. It is revealed that the control scheme performs in a stable region even under weak-grid conditions. Finally, simulations are conducted in MATLAB to depict the efficacy and feasibility of the proposed method. The results show that frequency deviation is mitigated under step up/down changes in the demand, and the rate of change of frequency is improved by 47.37% compared to the case in which the synthetic inertia loop is canceled out.
1. Introduction
In conventional power grids, the major portion of electricity demand is generated by synchronous generators (SGs), which have inherent rotational inertia and damping properties. During major disturbances (typically loss of generating unit or stochastic demand fluctuation), primary and secondary controls are triggered to maintain stable system frequency and restore power balance [1]. The kinetic energy preserved in the rotational mass of the SGs is highly important in the primary control, which imposes a limit on the frequency oscillations and slows down frequency dynamics [2,3]. Lack of this energy in low-inertia grids might lead to undesirable situations such as pole slipping and catastrophic failure of SGs under frequency load shedding activation or even cascading failure after perturbation. The power system can be more vulnerable to these problems under high levels of renewable energy sources (RESs) penetration [4,5]. In other words, the power electronics-based generators have no rotational inertia and damping characteristics. The frequency regulation adequacy is assessed by two more cited metrics: (1) frequency nadir or the minimum frequency reached following a disturbance and (2) rate of change of frequency [3]. The overall grid inertia is the main factor affecting the aforesaid indices, i.e., the more inertia, the better primary frequency regulation [6]. On the other hand, the diminution of grid inertia limits further increase in RESs integration. To address this issue, grid-connected converters, such as the interface between RESs and power systems, must be equipped with grid supportive functionalities defined by new grid codes [7,8].
Intensive research has been conducted on the control of grid-tied converters with respect to the aforementioned concerns [9,10,11,12,13,14,15,16,17,18,19,20,21,22]. Changing the requirements of rate of change of frequency (RoCoF) withstand capabilities of SGs is a straightforward solution that has been accepted as an efficient approach by system operators in Ireland [9]. However, the inertia concern is not solved in this method and the cost increment with regard to generator testing might bind its applications. Employing backup SGs with partial loading (i.e., spinning reserve) or synchronous condensers to provide more rotating masses is another possible solution for inertia augmentation [10]. Nevertheless, these approaches yield high capital and operating cost. Motivated by conventional SG dynamics, the concept of providing synthetic inertia using virtual synchronous generators (VSGs) VSGs was introduced in 2007 [11]. This method emulates the inertial response of real SGs by the grid-connected voltage source converters (VSCs) through a control technique, resulting in fast frequency support during contingencies. Since then, similar concepts, named synchronverter and inducverter, have been developed, on which detailed information can be found in [12,13]. Additionally, [14] improved the power quality and grid stability of distributed generation using VISMA. This technique aims to set up static and dynamic characteristics of SGs on the three-phase hysteresis controlled inverters. Similar to conventional generators, wind turbines enjoy a considerable amount of kinetic energy preserved in their blades. However, a variable speed wind turbine generator (e.g., doubly-fed induction generator or permanent magnet synchronous generator) does not naturally contribute to the grid inertia due to the converter interface [15]. Various control mechanisms have been introduced to enable wind turbines to provide inertia support. For example, an enhanced control technique is proposed in [16] that adjusts the turbine torque set point as a function of the frequency deviation Δf and the RoCoF, enabling wind generator to emulate inertia. Employing energy storage systems (ESS) ESSs such as supercapacitors and battery banks on the DC-side of VSCs and proportional linking their active power references with the frequency oscillations is another emerging method of enhancing inertial response in power systems [17,18]. These approaches can provide sufficient inertia and damping properties for fast restoring power balance in the grid. The research work in [19] designed a high-performance battery converter system for providing virtual inertia at the distributed network level in which the grid frequency is measured to derive design criteria for the control system. The frequency derivative-based (df/dt) method is the other technique of inertia emulation by VSCs. Nonetheless, the research conducted in [20] shows that df/dt-based synthetic inertia emulation can induce instability into two modes of the system, one associated with the output filter and the other one with the inner current control loop. In [21], the authors developed a new technique of emulating virtual inertia through the DC-link capacitors adhered to the DC-side of grid-tied converters. The concerns with respect to this approach are instability problems due to applying df/dt based inertia emulation and the limitation of its responsiveness [20,22].
The main contribution of this work to the research field is summarized as follows: we develop a new control technique for the provision of synthetic inertia support through grid-tied voltage source converters employed in the power grids dominated by RESs. The proposed platform comprises two main control loops, i.e., an inner current loop and outer voltage loop equipped with a new synthetic inertia control. The synchronous reference frame transformation introduced by the phase-locked loop (PLL) dynamics is also included in the control system for the required compensation. It is noteworthy that the DC-link capacitance is applied as the energy buffer for grid inertia augmentation. With the proposed control scheme, (1) the system stability margin and (2) the inertial response of the converter are improved compared to the method in [21].
The rest of this paper is organized as follows. Following Section 1, a brief analysis of inertial response in the real SGs is presented in Section 2. Then, a detailed model of the proposed VSC controller is derived in Section 3. The stable operation of the system is revealed in Section 4 by deriving closed-loop transfer functions of the system and bode analyses. Furthermore, Section 4 includes the comparison of the proposed method with [21] in terms of system stability margin. Section 5 provides simulations to depict the efficacy of the system under step up/down changes in the demand. The results demonstrate that the proposed controller enhances the RoCoF metric by 47.37% and 23.1% compared to the conventional VSC system and [21], respectively. The paper ends with the conclusion presented in Section 6.
2. Inertial Response of Synchronous Machines
It is known that the stability of a power system can be analyzed by the swing equation [1] describing the power imbalance between input mechanical power and electromagnetic power following a contingency. Thereby, the equation of motion is represented by:
Note that in (1), it is assumed that the pole pairs of SG is one. During steady state operation, (1) can be rewritten as:
in which m = 1/D is synonymous with the droop coefficient. It is clear that the primary motion equation-based control is the developed version of simple droop control [23]. After a disturbance, the small-signal model of (1) in terms of inertia constant (H = Jωr2/2VAbase) is represented by [24]:
The frequency control diagram of a real SG is illustrated in Figure 1, and the corresponding parameters are defined in Table 1. Since only the primary frequency regulation and inertial response are of interest in this work, the automatic generation control signal (ΔPAGCpu) is neglected. To analyze the effect of rotational inertia on the system frequency response, the transfer function of frequency deviation (Δω) over the load disturbance (ΔPe) is derived as (4).
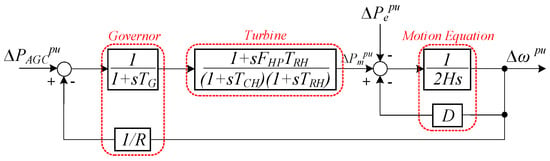
Figure 1.
The frequency response control of a synchronous generator (SG).

Table 1.
A typical set of the synchronous generator parameters.
The grid frequency response under a 5% step-up change in the demand (ΔPe = 5%) is depicted in Figure 2 for different values of H. It is clear that increasing H results in a lower RoCoF level and frequency nadir and, thereby, better primary frequency regulation during the transient time.
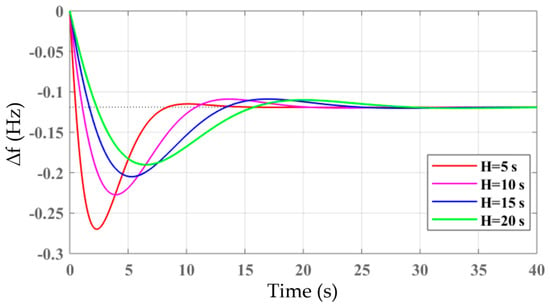
Figure 2.
Grid frequency variations for different inertia constants.
3. The Proposed Converter Control Scheme
Figure 3 demonstrates the single-line diagram of a grid-tied VSC, comprised of a RES generator, a DC-link capacitor connected to a conventional three-phase full-bridge inverter, a resistance-inductance filter (Rc, Lc), and a balanced power grid (ug) with the impedance of Rg and Lg. Generally, supercapacitors or battery energy storages can be applied as the DC-side energy buffer for frequency support. Herein, the DC-link capacitor acts as the energy buffer that does not impose any extra cost on the VSC hardware. This is because the DC-link capacitors are essential for voltage support and harmonics filtering in power conversion systems. The variables up, ec, and i in Figure 3 stand for point of common coupling (PCC) voltage, converter terminal voltage, and injected current to the PCC in the natural abc reference frame, respectively.
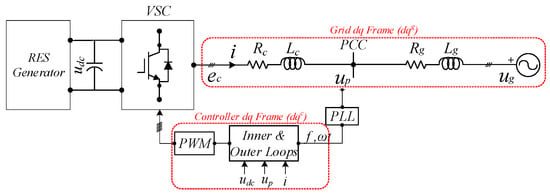
Figure 3.
Schematic of the grid-tied voltage source converter (VSC).
3.1. Analysis of the Interfaced Converter Under Dynamic Operating Condition
The AC-side of the converter can be described mathematically as:
where p denotes the differential operator, L = Lc + Lg, and r = Rc + Rg. Transforming (5) into the grid synchronous reference frame (dqg) using Park Transformation (Tabc/dq) results in:
where Gplant(s) is expressed as:
The subscripts d and q stand for the d-axis and q-axis components of the corresponding variables. It is clear that the d and q axes are coupled through the terms ωrLid and ωrLiq, which gives rise to the control complexity. Nonetheless, the cross-coupling terms can be eliminated by applying appropriate current feedforward control. The inner current loops (7) are controlled via two separate proportional integral (PI) PI controllers (Gi(s) = kcp + kci/s) since the dq variables are constant in the synchronous reference frame.
Ignoring power losses in the converter, the output current of the VSC can be translated into the DC-link capacitor voltage (udc) by:
The voltage udc reaches its reference by controlling the d-axis current through a PI controller (Gu(s) = −kup − kui/s), which forms the outer control loop. The time-delay introduced by the pulse-width modulation (PWM) PWM updates and reference computations can be approximately modeled using a first-order function Gd(s) in which fs denotes the sampling frequency [25].
3.2. Dynamic Analysis of the Phase-Locked Loop
The synchronization of the VSC with the network is obtained using a PLL. Due to the operation of the PLL, the system shown in Figure 3 comprises two separate dq frames: dqg frame corresponding to the grid and dqc frame corresponding to the VSC controller. In steady state operating conditions, the controller dq frame is aligned with the grid dq frame. When a small contingency occurs in the system, the two frames are no longer aligned due to the dynamics of the PLL. It means that the dqc frame lags Δθ as demonstrated in Figure 4a.
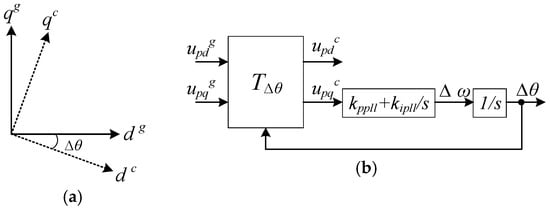
Figure 4.
(a) The grid and controller SRFs, (b) SRF-PLL model.
The averaged model of the synchronous reference frame PLL (SRF-PLL) is shown in Figure 4b, in which the PCC voltage vector in the dqg frame is rotated to the dqc frame using matrix TΔθ for feedback control purpose [26]. During steady state operation, we can conclude (12):
where the vectors upg and upc denote the PCC voltage in the grid frame and the controller frame, respectively. Equation (12) points out that the angle difference (Δθ) between PCC voltage vectors in the two frames is zero. Using matrix TΔθ, (12) can be rewritten as:
A disturbance in the grid leads to small signal deviations in the PCC voltage vector. Then, (13) can be rewritten as:
By simplifying trigonometric functions and ignoring the steady state values, the connection between PCC voltage vectors in the dqc and dqg frames can be expressed as:
Substituting (16) into (15) results in the relationship between Δθ and ugpq as:
Because in the synchronous reference frame Ugpq = 0 and assuming the VSC is operating in the unity power factor, (15) can be further simplified to (18) as follows:
From (18), we can conclude that the dynamics introduced by the operation of the PLL during perturbations add −Ugpd·Δθ and + Id·Δθ terms in the q-axis control loop, as depicted in Figure 5. On the other hand, due to the coupling between two axes, any variations in Δθ leads to the changes in id (this correlation is elaborated in Section 4).
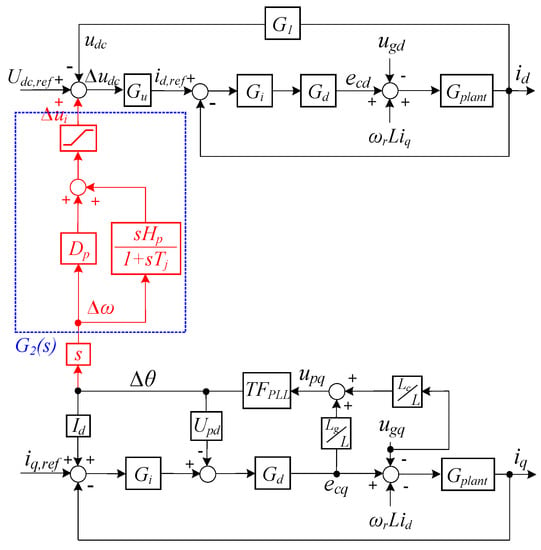
Figure 5.
The d-q control loops augmented with the frequency support controller.
3.3. Fast Grid Frequency Support
The imbalance between generation and demand following a contingency would cause the frequency to fall/rise at a rate determined by the total grid inertia. The less inertia, the faster and higher frequency deviations. Various methodologies for providing synthetic inertia have been reported, which further information can be found in [27]. A promising technique recommended in [21], in which the frequency support is conducted by means of regulating the DC-link capacitor voltage. This method is based on a basic proportional controller that bounds its responsiveness [22]. Herein, this problem is fixed using a supplementary controller composed of a frequency-time derivative (df/dt) term (aimed at mitigation of the RoCoF) with a scheduled active power injection and delivery time Tj. The time delay Tj in discharging the DC-link capacitor is analogous to gradually releasing the kinetic energy of rotational SGs. The controller is added to the outer voltage loop during the initial support period. The proposed technique is described mathematically as:
where Hp and Dp emulate the inertia and damping characteristics of the real SGs, respectively. A disturbance in the power system results in a small deviation in the variables around their steady state values. Thus, the corresponding small-signal model of the synthetic inertia loop can be derived by canceling the steady state values of (19) as:
It is noteworthy that Δui = 0 during steady state operation of the system. Indeed, the frequency support level is limited by the maximum acceptable DC-link voltage deviations in the foregoing method. This is because udc must be kept in an acceptable range for linear modulation of the converter and limiting current flow through components of the conversion system. Thereby, the d-q control loops augmented with the frequency support controller are formed as Figure 5.
4. Dynamics Assessment of the Proposed Control Technique
To validate the effectiveness of the proposed control system, it is necessary to analyze the stability of the control loops. According to Figure 5, the closed-loop transfer functions of inner current loops corresponding to the d-q axes can be obtained as (21) and (22).
Because of the coupling between the d-q axes, there is a correlation between Δθ and id, which produces an effect on the outer voltage controller by the synthetic inertia loop. This relationship is visible in Figure 5. Hence, the transfer function between Δθ and id is derived as (23).
In addition, the frequency support can be provided by incorporating the angular frequency deviations (Δω) into the DC-link voltage regulator. Mathematically, Δω is equivalent to the time-derivative of Δθ, as illustrated in Figure 4b. Thereby, the transfer function between Δui and id is derived as:
According to Figure 5, the transfer function between Δui and id can be considered in parallel with G1. This is because the two corresponding paths start with id and reach the identical summer. It means that the dynamics caused by the PLL in the q-axis are reflected in the d-axis by means of the virtual inertia loop. Then, the function that appeared in the feedback path is formed as follows:
Finally, the open-loop and closed-loop transfer functions of the proposed control system are derived as follows, respectively:
The stability of the system is investigated by bode diagram and zero-pole map analyses. Figure 6 depicts the bode-plot of the frequency response of the open-loop model, with the parameters listed in Table 2. As can be seen from this figure, the gain and phase margins are 45 dB and 27.2 deg, respectively, which validate the stable operation of the model described by (26). Moreover, the zero-pole diagram of the closed-loop transfer function (27) is demonstrated in Figure 7. The zeros and poles are represented by circles and crosses, respectively. It is clear that all the poles are located in the left-hand side of the complex plane, which signifies the stability of the whole system. Therefore, the proposed controller is mathematically proved to operate stably.
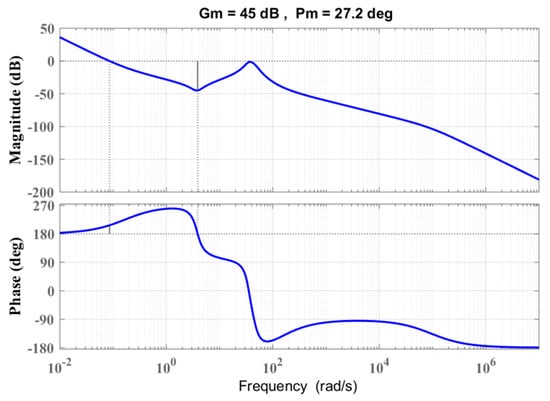
Figure 6.
Bode diagram of the proposed control system.

Table 2.
The specifications of the implemented system.
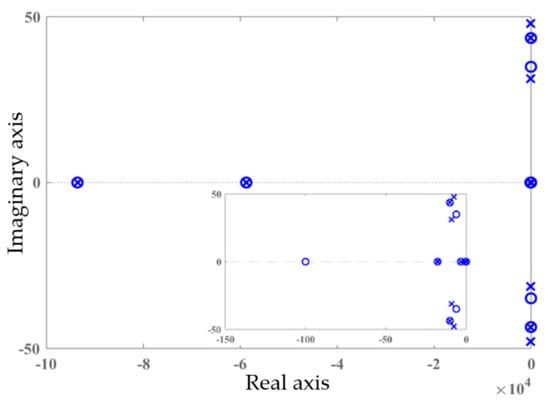
Figure 7.
Zero-pole diagram of the proposed control system.
To demonstrate the advantage of the proposed controller compared to [21] in terms of stability margin, the same bode analysis has been carried out for [21], and the result is illustrated in Figure 8. As observed from this figure, the gain margin and phase margin of the VSC system controlled by the method in [21] drop to 4.33 dB and 20.4 deg, respectively. This deterioration in the stability metrics arises from only applying the df/dt term and its corresponding gain in [21], in which this problem is solved in the proposed control scheme using transfer function G2(s) (Figure 5). Thus, the proposed controller has better performance in comparison to [21] regarding the system stability margin.
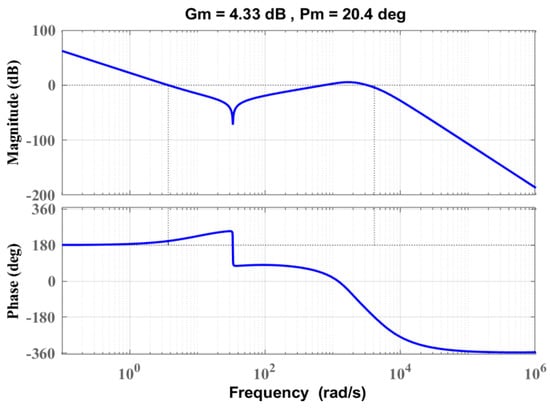
Figure 8.
Bode diagram of the method in [21].
5. Simulation Results and Discussions
Simulations have been conducted in MATLAB to demonstrate the validity of the proposed technique for control of the grid-tied VSCs. The main parameters of the implemented system are tabulated in Table 2. A 100 kW synchronous generator models the power grid with the internal impedance of 0.001 + j0.94 Ω. The grid-tied VSC operates under the following conditions. The rated power is 15 kW. The maximum acceptable DC-link voltage deviation is ±60 V, and the modulation index is considered ma = 0.86. Two scenarios are considered for simulations, step-up and step-down changes in the demand. Then, in each scenario, the proposed controller is compared with the method in [21] and the conventional VSC system in terms of frequency stability metrics (i.e., frequency nadir and RoCoF).
5.1. Scenario 1
In this scenario, a 5% step-up change in the demand occurs at t = 20 s. Figure 9 depicts frequency variations when the grid-interactive converter is controlled by the (1) proposed controller, (2) method in [21], and (3) conventional control system without virtual inertia functionality. As observed from this figure, without providing synthetic inertia, the frequency nadir and RoCoF peaks at 49.82 Hz and 0.19 Hz/s, respectively, and the grid frequency is stabilized after 6 s. The VSC system augmented with the proposed virtual inertia loop can improve the RoCoF level by 47.37% and 23.1% compared to the conventional controller and [21], respectively. Moreover, the proposed technique yields lower maximum frequency oscillations (i.e., 49.85 Hz) in comparison to the other ones. It should be mentioned that further providing inertia support by the method in [21] leads to the instability of the whole system, which is in agreement with the stability analysis presented in Figure 8. Thus, better primary frequency regulation during transient time is achieved with the proposed supplementary controller. The DC-link capacitor voltage oscillation is illustrated in Figure 10. The voltage drops to 690 V right after the step change in the load and returns to the nominal value (750 V). It means that the discharged energy by the DC-link capacitor supports the frequency, which is analogous to the released kinetic energy of SGs during perturbation.
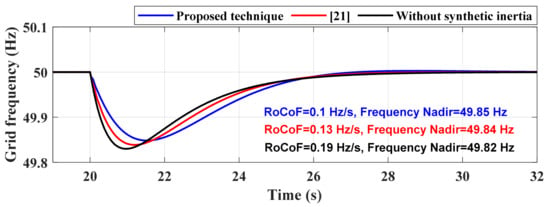
Figure 9.
Frequency nadir and rate of change of frequency (RoCoF) metrics under a 5% step-up change in the demand.
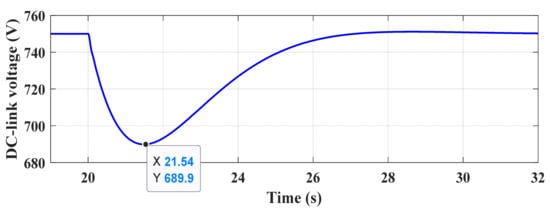
Figure 10.
DC-link voltage oscillation under a step-up change in the demand.
As stated earlier, the DC-link voltage deviations must be limited, which means to a finite frequency support level. When the DC-link voltage is reduced with the aim of frequency support, the modulation index (ma) must increase in order to (1) increase the difference angle between converter voltage and PCC voltage (Δ) and (2) prevent reactive power exchange with the grid (i.e., the equation ed = ma × udc × cosΔ = upd holds true). This can be observed in Figure 11. The modulation index peaks at around 0.93 in the time interval at which the capacitor is discharged. Then, it rebounds to the value of pre-perturbation. The supportive power supplied by the VSC is shown in Figure 12. It is clear that the power reaches approximately 15 kW and then drops to the steady state value when the frequency returns to 50 Hz.
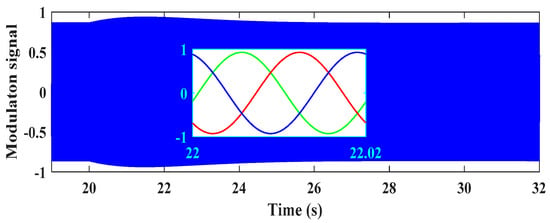
Figure 11.
Modulation signal waveform in the first scenario.
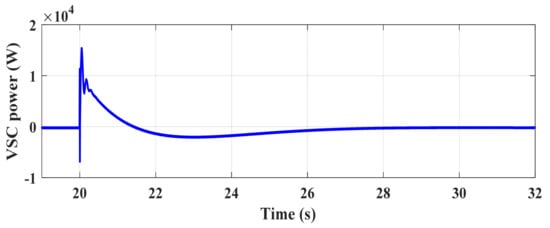
Figure 12.
Active power exchange with the grid in the first scenario.
5.2. Scenario 2
In this case study, the demand drops by 5% at t = 20 s. Figure 13 illustrates frequency deviations of the system with (1) the proposed control scheme, (2) the method in [21], and without providing synthetic inertia. It is clear that the frequency nadir peaks at 50.17 Hz when the synthetic inertia loop is canceled out. The RoCoF level is also 0.19 Hz/s. Taking the proposed supplementary controller into account can effectively improve the grid frequency stability and bring the frequency back to the reference (50 Hz). In this case, the rate of change of frequency is enhanced by 47.37% and 23.1% compared to the conventional controller and [21], respectively. Thus, the obtained results validate the effectiveness of the proposed control technique in enhancing frequency stability following a disturbance. The DC-link capacitor voltage deviation of this scenario is also illustrated in Figure 14. Clearly, the voltage rises to 810 V right after the loss of demand and reaches the steady state value after around 6 s.
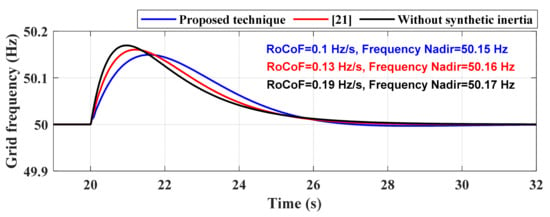
Figure 13.
Frequency nadir and RoCoF metrics under a 5% step-down change in the demand.
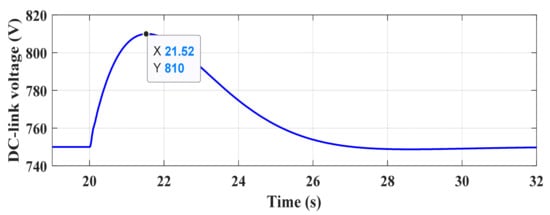
Figure 14.
DC-link voltage oscillation under a step-down change in the demand.
The same analysis can be carried out for the decrease in modulation index when the DC-link voltage starts to rise. This is because the difference angle Δ must increase while the reactive power exchange remains zero during contingency (again, the equation ed = ma × udc × cosΔ = upd holds true). Then, the modulation index decreases as the DC-link capacitor voltage increases. The modulation signal in this scenario is observed in Figure 15. The power absorbed by the VSC with the aim of frequency support is also brought in Figure 16. The power reaches approximately −15 kW after the loss of demand and becomes zero when the grid frequency returns to 50 Hz.
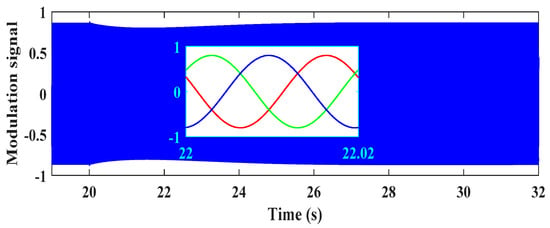
Figure 15.
Modulation signal waveform in the second scenario.
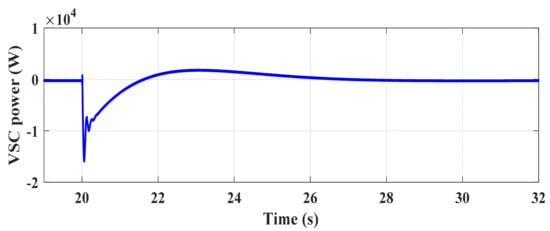
Figure 16.
Active power exchange with the grid in the second scenario.
6. Conclusions
This paper proposed a new control scheme for grid-tied voltage source converters, which is composed of a conventional inner current loop, outer voltage loop, and a new synthetic inertia function. The virtual inertia loop provides primary frequency support through discharging/charging the DC-link capacitors of converters employed in the power electronics-based generators, e.g., solar and wind farms. The synchronous reference frame transformation introduced by the PLL dynamics has also been included in the control system for the required compensation. The dynamics model of the proposed scheme has been built and the bode-plot and zero-pole map analyses have confirmed that the proposed controller can perform in a stable operating condition. The stability analyses depicted that the proposed controller has a better performance compared to [21] in terms of the system stability margin. Moreover, the simulations illustrated that the rate of change of frequency is improved by 47.37% and 23.1% compared to the conventional controller and the method in [21], respectively.
Author Contributions
All authors worked on this manuscript together and all authors have read and approved the final manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Abbreviations: | |
| dqg, dqc | Synchronous reference frames corresponding to the grid and the controller |
| ESS | Energy storage system |
| PLL | Phase-locked loop |
| PCC | Point of common coupling |
| RESs | Renewable energy sources |
| RoCoF | Rate of change of frequency |
| SGs | Synchronous generators |
| VSC | Voltage source converter |
| VSG | Virtual synchronous generator |
| Variables: | |
| i | Current flowing into the grid |
| ma | Modulation Index |
| Pm | Input mechanical power of SG |
| Pe | Electromagnetic power of SG |
| udc, ec, up, ug | DC-link capacitor voltage, converter voltage, PCC voltage, grid voltage |
| upg, upc | PCC voltage vectors in the grid frame and the controller frame |
| ω | Angular velocity/frequency of the rotor/grid |
| Δ | The difference angle between the converter voltage and the PCC voltage |
| Parameters: | |
| C | DC-link capacitance |
| D, Dp | Damping coefficient, virtual damping coefficient |
| FHP | Turbine coefficient |
| fs | Sampling frequency |
| H, Hp | Inertia constant, virtual inertia constant |
| Id | Rated value of the current i in the d-axis |
| J | Moment of inertia of the turbine and the generator |
| kcp, kci | Proportional and integral gains of the current controller |
| kup, kui | Proportional and integral gains of the voltage controller |
| kppll, kipll | Proportional and integral gains of the PLL |
| Lc, Lg | Inductance of the filter and the grid |
| Rc, Rg | Resistance of the filter and the grid |
| R | Droop coefficient |
| TG | Governor time constant |
| TCH | Inlet volume time constant |
| TRH | Re-heater time constant |
| Udc,ref | DC-link voltage reference |
| Upd | Nominal PCC voltage in the d-axis |
| ωr | Reference angular velocity/frequency of the rotor/grid |
References
- Kundur, P. Power System Stability and Control, 1st ed.; McGraw-Hill Education: New York, NY, USA, 1994. [Google Scholar]
- Alipoor, J.; Miura, Y.; Ise, T. Power System Stabilization Using Virtual Synchronous Generator with Alternating Moment of Inertia. J. Emerg. Sel.Top. Power Electron. 2015, 3, 451–458. [Google Scholar] [CrossRef]
- Saeedian, M.; Eskandari, B.; Taheri, S.; Hinkkanen, M.; Pouresmaeil, E. A Control Technique Based on Distributed Virtual Inertia for High Penetration of Renewable Energies Under Weak Grid Conditions. IEEE Syst. J. 2020. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. On the Inertia of Future More-Electronics Power Systems. J. Emerg. Sel.Top. Power Electron. 2018, 7, 2130–2146. [Google Scholar] [CrossRef]
- Dreidy, M.; Mokhlis, H.; Mekhilef, S. Inertia Response and Frequency Control Techniques for Renewable Energy Sources: A Review. Renew. Sustain. Energy Rev. 2017, 69, 144–155. [Google Scholar] [CrossRef]
- Vorobev, P.; Greenwood, D.M.; Bell, J.H.; Bialek, J.; Taylor, P.; Turitsyn, K. Deadbands, Droop, and Inertia Impact on Power System Frequency Distribution. IEEE Trans. Power Syst. 2019, 34, 3098–3108. [Google Scholar] [CrossRef]
- Mehrasa, M.; Pouresmaeil, E.; Sepehr, A.; Pournazarian, B.; Catalão, J.P.S. Control of Power Electronics-Based Synchronous Generator for the Integration of Renewable Energies into the Power Grid. Int. J. Electr. Power Energy Syst. 2019, 111, 300–314. [Google Scholar] [CrossRef]
- Golpîra, H.; Messina, A.R.; Bevrani, H. Emulation of Virtual Inertia to Accommodate Higher Penetration Levels of Distributed Generation in Power Grids. IEEE Trans. Power Syst. 2019, 34, 3384–3394. [Google Scholar] [CrossRef]
- EirGrid/SONI. RoCoF Modification Proposal—TSOs’ Recommendations; EirGrid/SONI: Dublin, Ireland, 2012. [Google Scholar]
- Nguyen, H.T.; Yang, G.; Nielsen, A.H.; Højgaard Jensen, P. Combination of Synchronous Condenser and Synthetic Inertia for Frequency Stability Enhancement in Low-Inertia Systems. IEEE Trans. Sustain. Energy 2019, 10, 997–1005. [Google Scholar] [CrossRef]
- Beck, H.-P.; Hesse, R. Virtual Synchronous Machine. In Proceedings of the 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9–11 October 2007; pp. 1–6. [Google Scholar]
- Zhong, Q.; Weiss, G. Synchronverters: Inverters That Mimic Synchronous Generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Ashabani, M.; Freijedo, F.D.; Golestan, S.; Guerrero, J.M. Inducverters: PLL-Less Converters with Auto-Synchronization and Emulated Inertia Capability. IEEE Trans. Smart Grid 2016, 7, 1660–1674. [Google Scholar] [CrossRef]
- Chen, Y.; Hesse, R.; Turschner, D.; Beck, H.-P. Improving the Grid Power Quality Using Virtual Synchronous Machines. In Proceedings of the International Conference on Power Engineering, Energy and Electrical Drives, Malaga, Spain, 11–13 May 2011; pp. 1–6. [Google Scholar]
- Wang, S.; Tomsovic, K. Fast Frequency Support From Wind Turbine Generators With Auxiliary Dynamic Demand Control. IEEE Trans. Power Syst. 2019, 34, 3340–3348. [Google Scholar] [CrossRef]
- Morren, J.; de Haan, S.W.H.; Kling, W.L.; Ferreira, J.A. Wind Turbines Emulating Inertia and Supporting Primary Frequency Control. IEEE Trans. Power Syst. 2006, 21, 433–434. [Google Scholar] [CrossRef]
- Kim, J.; Gevorgian, V.; Luo, Y.; Mohanpurkar, M.; Koritarov, V.; Hovsapian, R.O.; Muljadi, E. Supercapacitor to Provide Ancillary Services with Control Coordination. IEEE Trans. Ind. Appl. 2019, 55, 5119–5127. [Google Scholar] [CrossRef]
- Namor, E.; Sossan, F.; Cherkaoui, R.; Paolone, M. Control of Battery Storage Systems for the Simultaneous Provision of Multiple Services. IEEE Trans. Smart Grid 2019, 10, 2799–2808. [Google Scholar] [CrossRef]
- Gollenstede, J.; Beushausen, L.; Benger, R.; Beck, H.-P.; Schael, M.; Kruschel, W.; Ulbrich, T.; Schmies, S. Design of a High-Performance Battery Converter System for Providing Synthetic Inertia at Distribution Network Level. In Proceedings of the 20th European Conference on Power Electronics and Applications, Riga, Latvia, 17–21 September 2018; pp. 1–10. [Google Scholar]
- Duckwitz, D.; Fischer, B. Modeling and Design of df/dt-Based Inertia Control for Power Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1553–1564. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. Distributed Power System Virtual Inertia Implemented by Grid-Connected Power Converters. IEEE Trans. Power Electron. 2018, 33, 8488–8499. [Google Scholar] [CrossRef]
- Marković, U.; Früh, N.; Aristidou, P.; Hug, G. Interval-Based Adaptive Inertia and Damping Control of a Virtual Synchronous Machine. In Proceedings of the 2019 IEEE PowerTech conference IEEE, Milano, Italy, 23–27 June 2019. [Google Scholar]
- Wu, W.; Chen, Y.; Luo, A.; Zhou, L.; Zhou, X.; Yang, L.; Dong, Y.; Guerrero, J.M. A Virtual Inertia Control Strategy for DC Microgrids Analogized With Virtual Synchronous Machines. IEEE Trans. Ind. Electron. 2017, 64, 6005–6016. [Google Scholar] [CrossRef]
- Pournazarian, B.; Pouresmaeil, E.; Saeedian, M.; Lehtonen, M.; Chan, R.; Taheri, S. Microgrid Frequency & Voltage Adjustment Applying Virtual Synchronous Generator. In Proceedings of the International Conference on Smart Energy Systems and Technologies (SEST), Porto, Portugal, 9–11 September 2019; pp. 1–6. [Google Scholar]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Analysis of D-Q Small-Signal Impedance of Grid-Tied Inverters. IEEE Trans. Power Electron. 2016, 31, 675–687. [Google Scholar] [CrossRef]
- Rodriguez, P.; Pou, J.; Bergas, J.; Candela, J.I.; Burgos, R.; Boroyevich, D. Decoupled Double Synchronous Reference Frame PLL for Power Converters Control. IEEE Trans. Power Electron. 2007, 22, 584–592. [Google Scholar] [CrossRef]
- Tamrakar, U.; Shrestha, D.; Maharjan, M.; Bhattarai, B.; Hansen, T.; Tonkoski, R. Virtual Inertia: Current Trends and Future Directions. J. Appl. Sci. 2017, 7, 654. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).