Cyclic Plasticity and Low Cycle Fatigue of an AISI 316L Stainless Steel: Experimental Evaluation of Material Parameters for Durability Design
Abstract
:1. Introduction
2. Plasticity Models: Theoretical Background
3. Experimental Tests
3.1. Material and Testing Setup
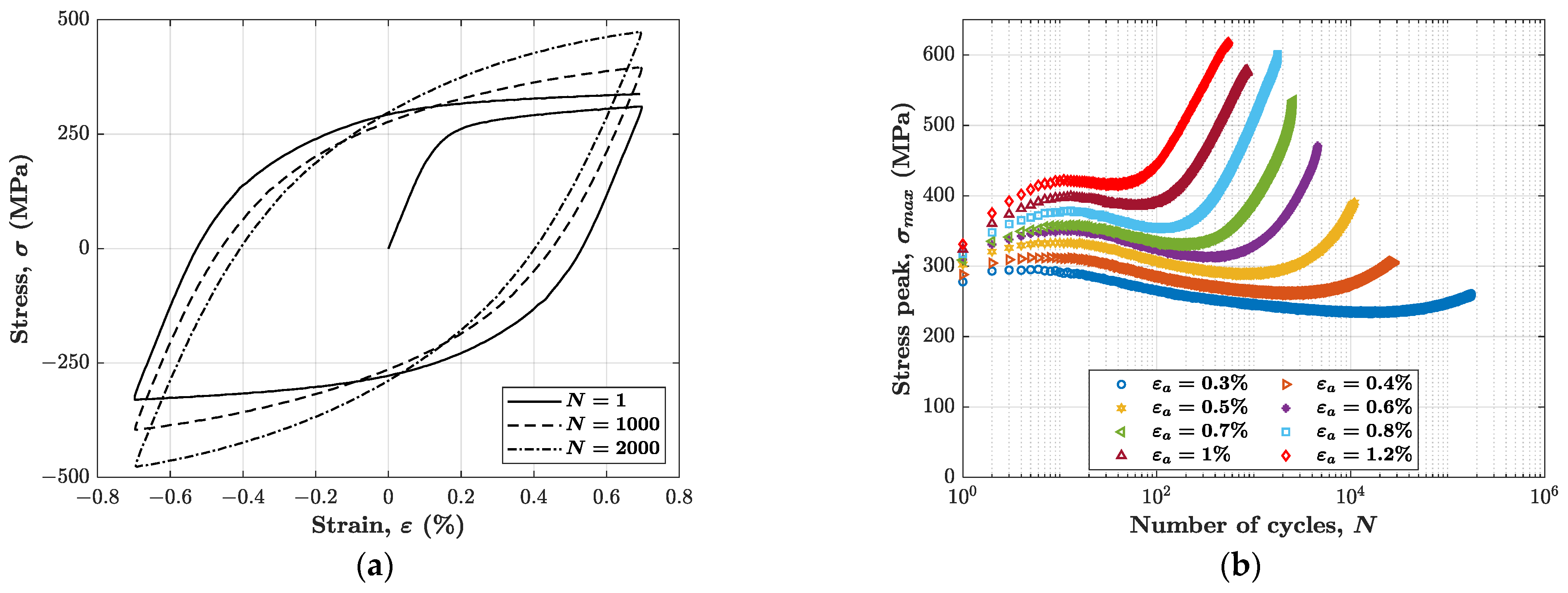
3.2. Brief Analysis of the Experimental Material Behaviour
4. Plasticity Models: Identification of Material Parameters
4.1. Young’s Modulus and Yield Stress
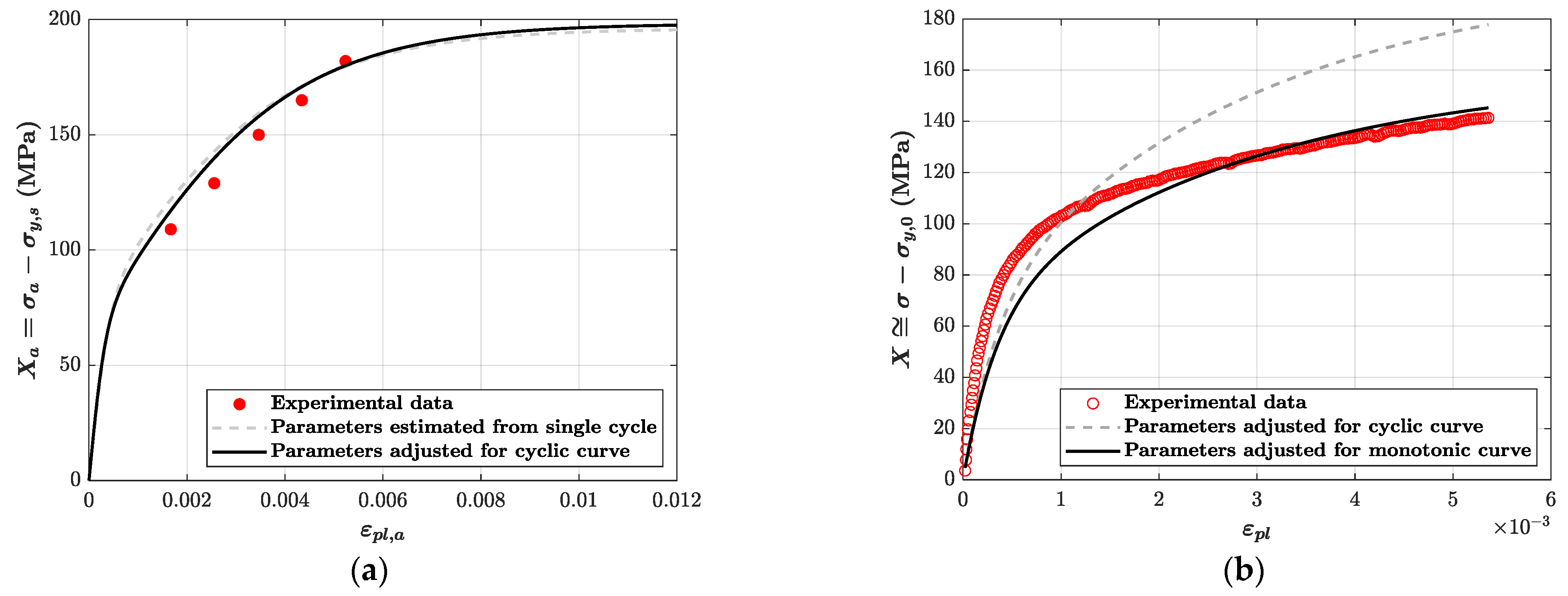
4.2. Kinematic Hardening Model
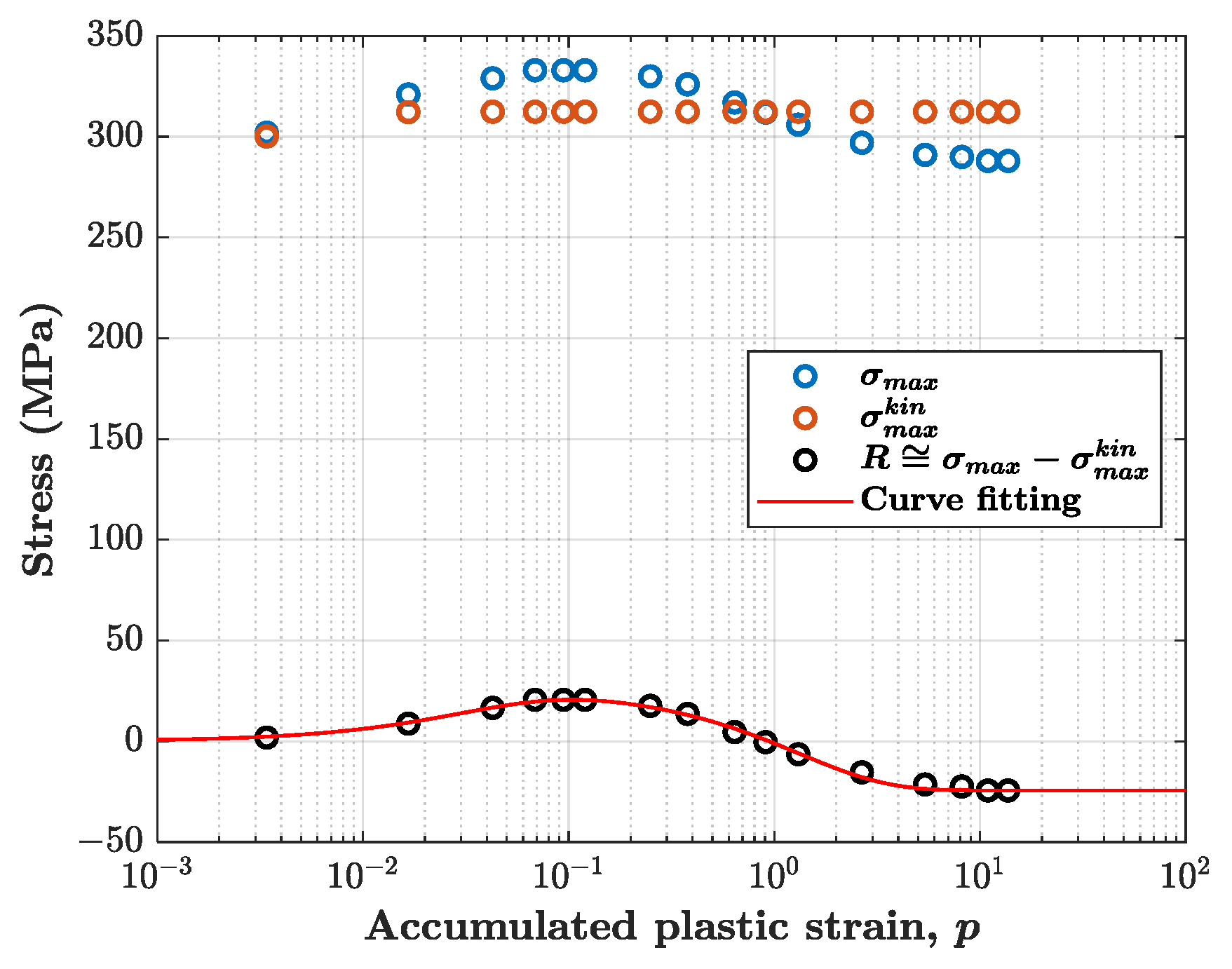
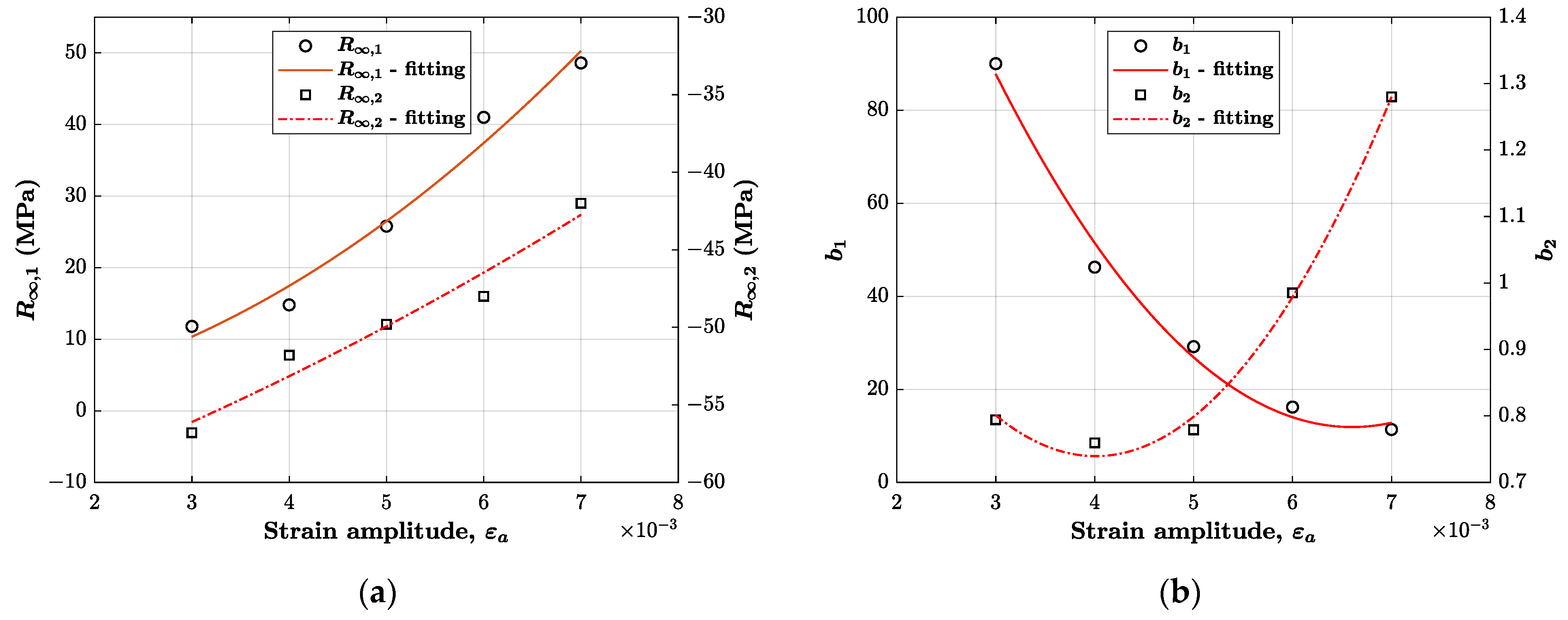
4.3. Isotropic Hardening Model
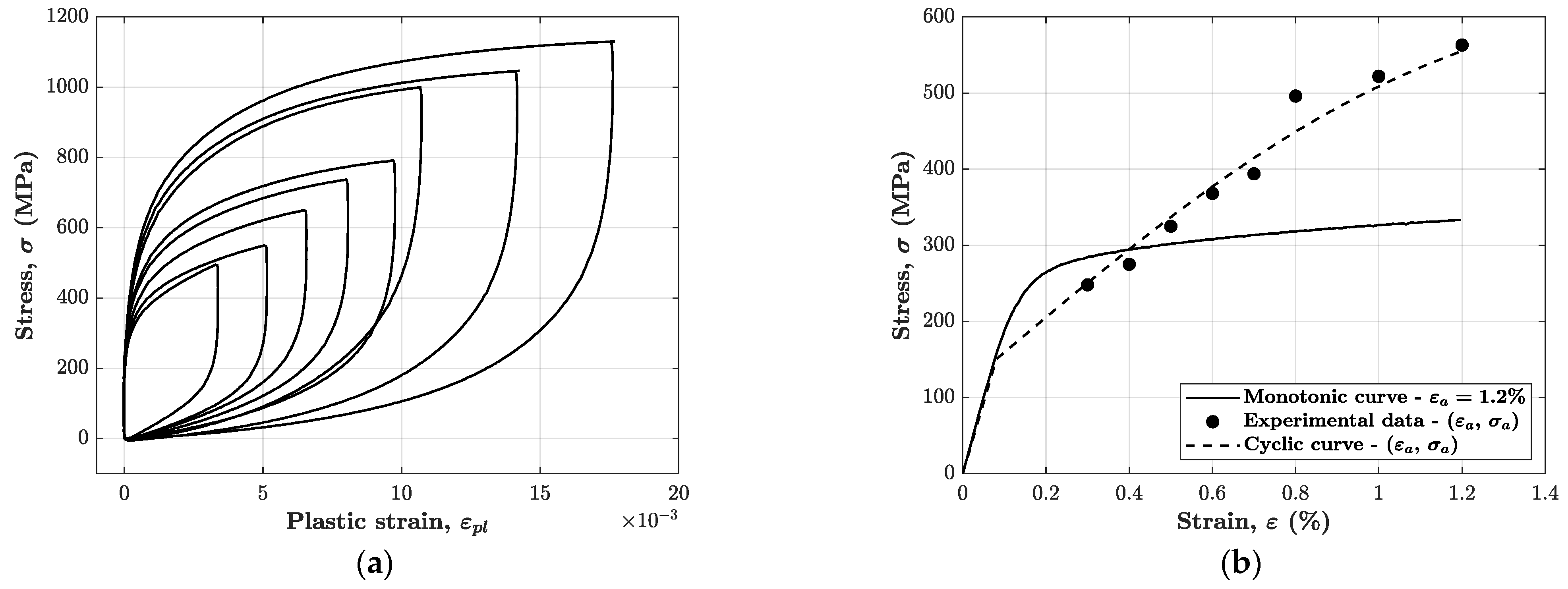
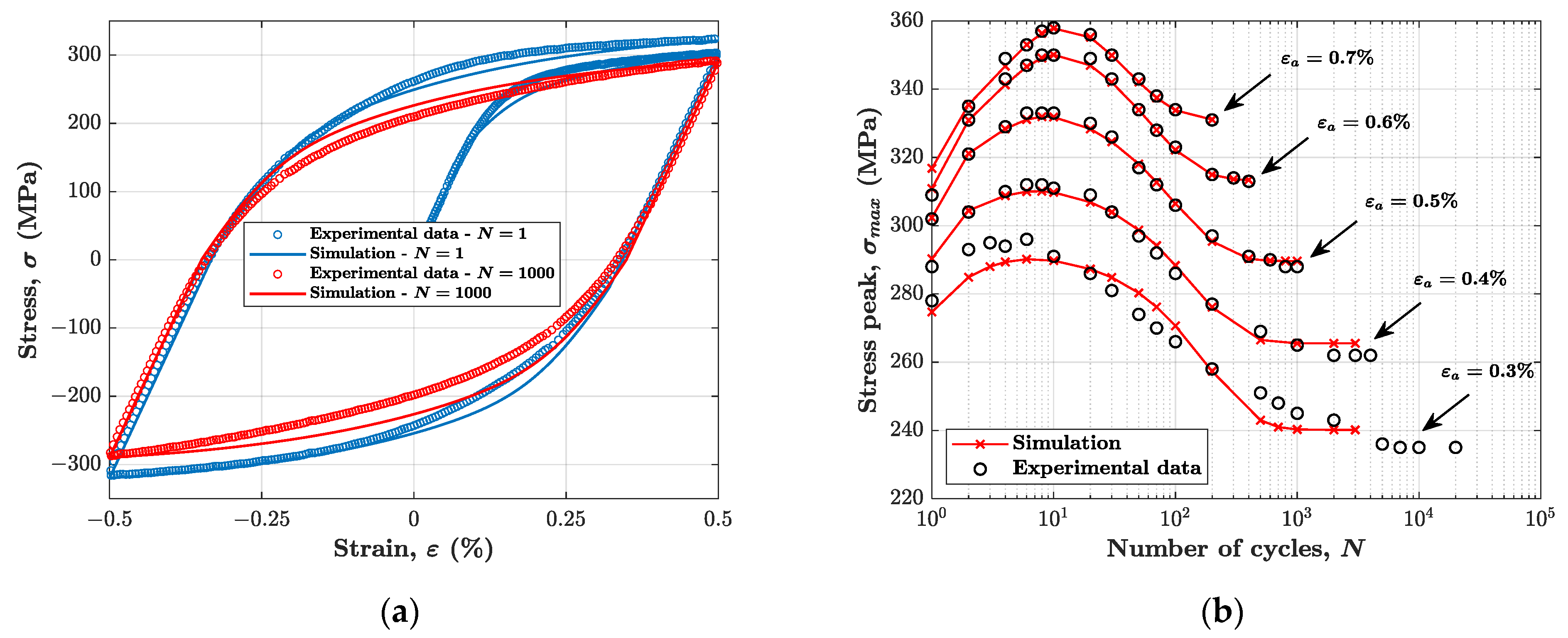
4.4. Model vs. Experiment Comparison
5. Low-Cycle Fatigue Curves
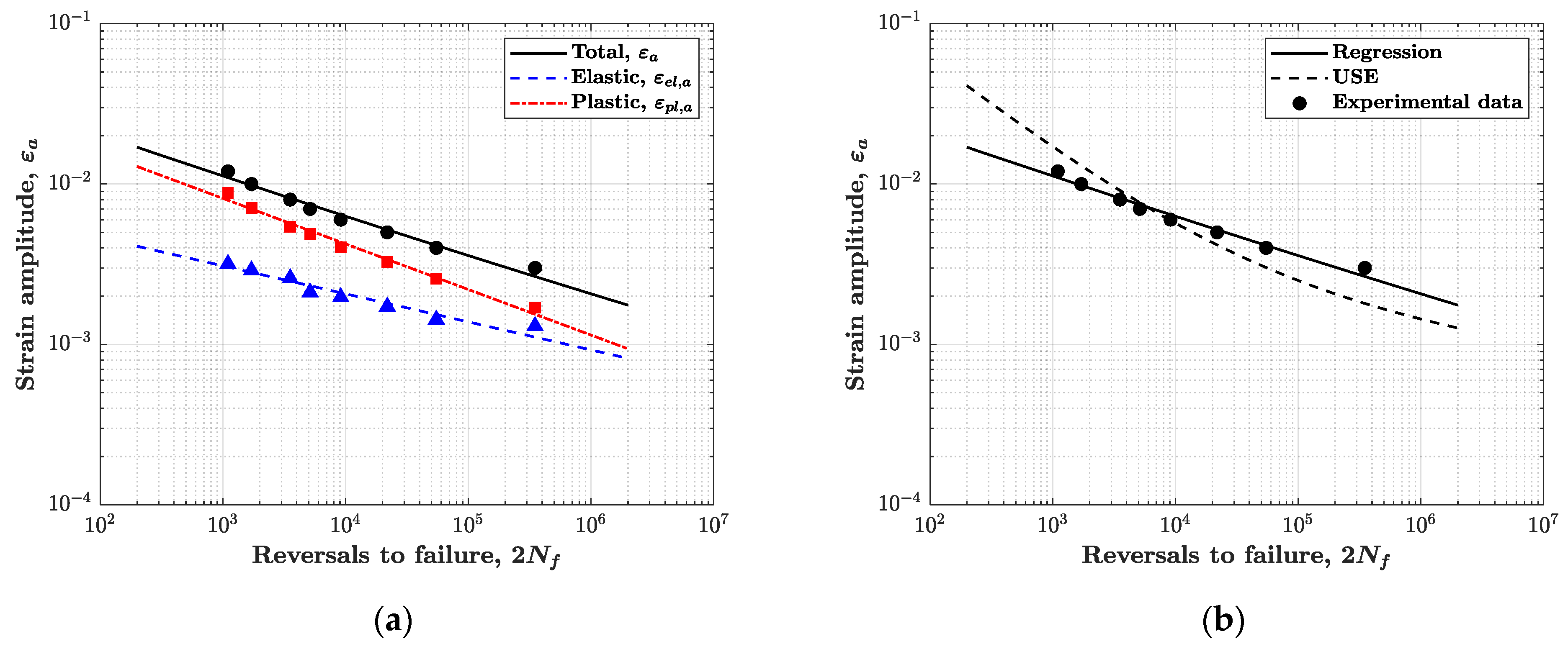
5.1. Approximate Strain–Life Curves from Monotonic Tensile Properties
5.2. Statistical Methods and Strain–Life Design Curves
5.2.1. Deterministic Method (“2 sigma” or “3 sigma”)
5.2.2. One-Side Tolerance Interval Method
5.2.3. Prediction Interval Method
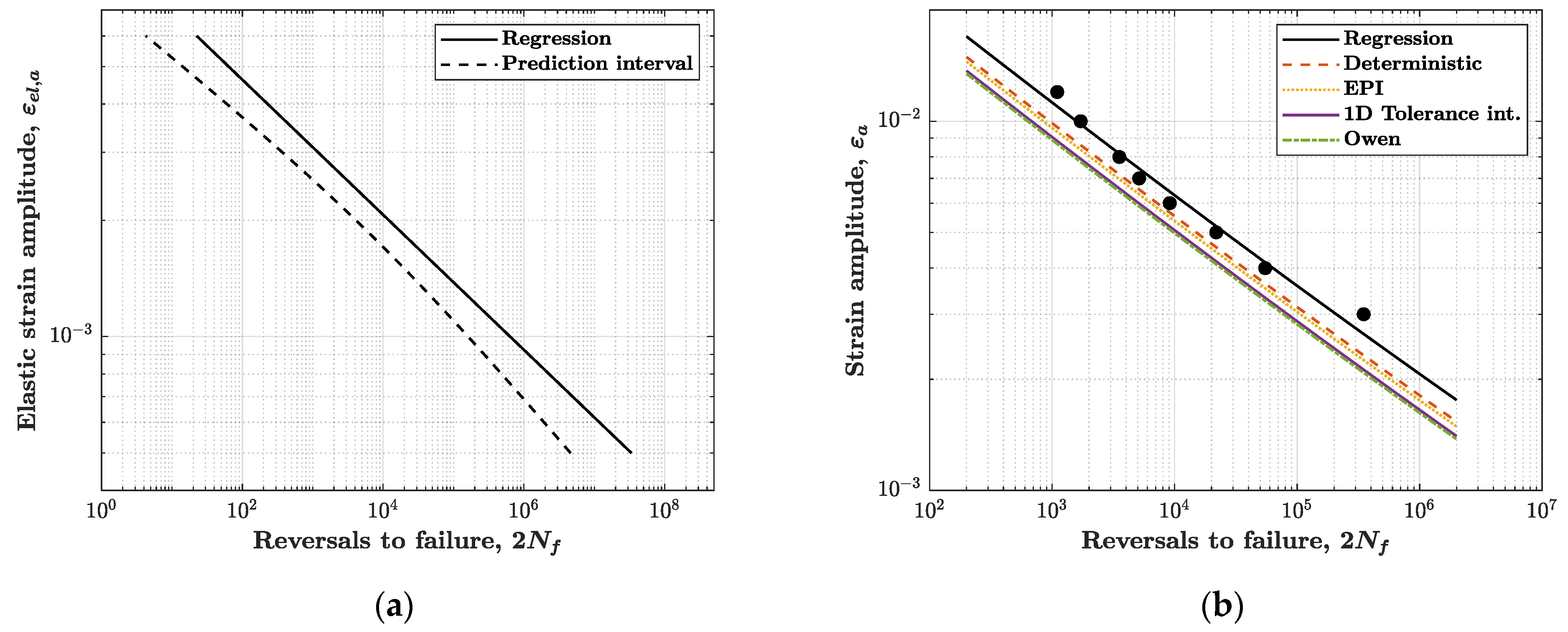
5.2.4. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
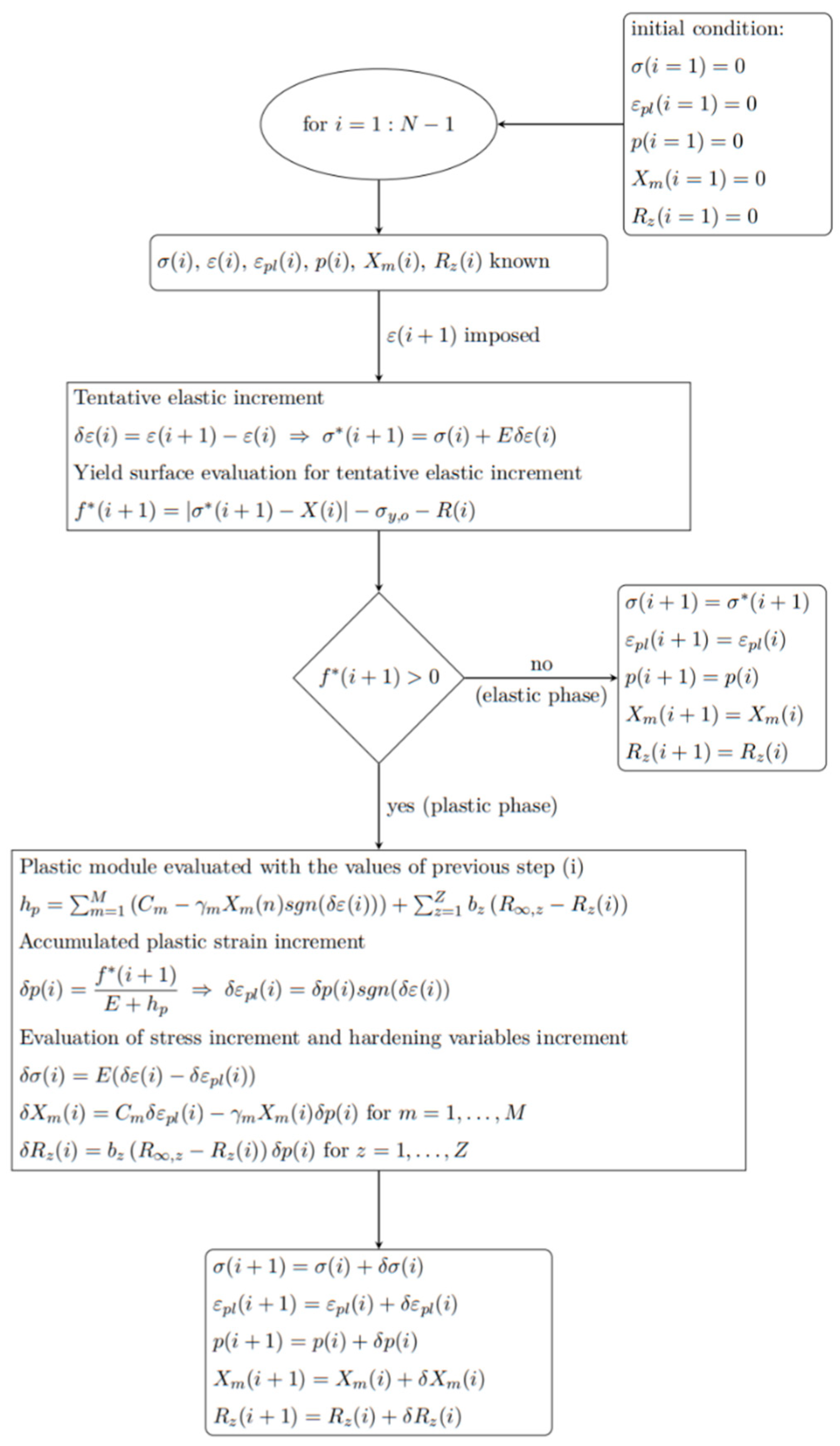
References
- Polák, J.; Obrtlík, K.; Hájek, M. Cyclic Plasticity in type 316L austenitic stainless steel. Fatigue Fract. Eng. Mater. Struct. 1994, 17, 773–782. [Google Scholar] [CrossRef]
- Mayama, T.; Sasaki, K.; Kuroda, M. Quantitative evaluations for strain amplitude dependent organization of dislocation structures due to cyclic plasticity in austenitic stainless steel 316L. Acta Mater. 2008, 56, 2735–2743. [Google Scholar] [CrossRef]
- Pham, M.S.; Solenthaler, C.; Janssens, K.G.F.; Holdsworth, S.R. Dislocation structure evolution and its effects on cyclic deformation response of AISI 316L stainless steel. Mater. Sci. Eng. A 2011, 528, 3261–3269. [Google Scholar] [CrossRef]
- Pham, M.S.; Holdsworth, S.R.; Janssens, K.G.F.; Mazza, E. Cyclic deformation response of AISI 316L at room temperature: Mechanical behaviour, microstructural evolution, physically-based evolutionary constitutive modelling. Int. J. Plast. 2013, 47, 143–164. [Google Scholar] [CrossRef]
- Zhou, J.; Sun, Z.; Kanouté, P.; Retraint, D. Experimental analysis and constitutive modelling of cyclic behaviour of 316L steels including hardening/softening and strain range memory effect in LCF regime. Int. J. Plast. 2018, 107, 54–78. [Google Scholar] [CrossRef]
- Xie, X.-F.; Jiang, W.; Chen, J.; Zhang, X.; Tu, S.-T. Cyclic hardening/softening behavior of 316L stainless steel at elevated temperature including strain-rate and strain-range dependence: Experimental and damage-coupled constitutive modeling. Int. J. Plast. 2019, 114, 196–214. [Google Scholar] [CrossRef]
- Baudry, G.; Pineau, A. Influence of strain-induced martensitic transformation on the low-cycle fatigue behavior of a stainless steel. Mater. Sci. Eng. 1977, 28, 229–242. [Google Scholar] [CrossRef]
- Pegues, J.W.; Shao, S.; Shamsaei, N.; Schneider, J.A.; Moser, R.D. Cyclic strain rate effect on martensitic transformation and fatigue behaviour of an austenitic stainless steel. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 2080–2091. [Google Scholar] [CrossRef]
- Alain, R.; Violan, P.; Mendez, J. Low cycle fatigue behavior in vacuum of a 316L type austenitic stainless steel between 20 and 600 °C part I: Fatigue resistance and cyclic behavior. Mater. Sci. Eng. A 1997, 229, 87–94. [Google Scholar] [CrossRef]
- Gerland, M.; Alain, R.; Ait Saadi, B.; Mendez, J. Low cycle fatigue behaviour in vacuum of a 316L-type austenitic stainless steel between 20 and 600 °C-Part II: Dislocation structure evolution and correlation with cyclic behaviour. Mater. Sci. Eng. A 1997, 229, 68–86. [Google Scholar] [CrossRef]
- Runciman, A.; Xu, D.; Pelton, A.R.; Ritchie, R.O. An equivalent strain/Coffin–Manson approach to multiaxial fatigue and life prediction in superelastic Nitinol medical devices. Biomaterials 2011, 32, 4987–4993. [Google Scholar] [CrossRef]
- Livieri, P.; Salvati, E.; Tovo, R. A non-linear model for the fatigue assessment of notched components under fatigue loadings. Int. J. Fatigue 2016, 82, 624–633. [Google Scholar] [CrossRef]
- Srnec Novak, J.; De Bona, F.; Benasciutti, D. Benchmarks for Accelerated Cyclic Plasticity Models with Finite Elements. Metals 2020, 10, 781. [Google Scholar] [CrossRef]
- Lemaitre, J.; Chaboche, J.-L. Mechanics of Solid Materials; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Chaboche, J.L. Time-independent constitutive theories for cyclic plasticity. Int. J. Plast. 1986, 2, 149–188. [Google Scholar] [CrossRef]
- Chaboche, J.L. A review of some plasticity and viscoplasticity constitutive theories. Int. J. Plast. 2008, 24, 1642–1693. [Google Scholar] [CrossRef]
- Voce, E. The relationship between stress and strain for homogeneous deformations. J. Inst. Met. 1948, 74, 537–562. [Google Scholar]
- Chaboche, J.L.; Van, K.D.; Cordier, G. Modelization of the Strain Memory Effect on the Cyclic Hardening Of 316 Stainless Steel. In Proceedings of the International Association for Structural Mechanics in Reactor Technology, Berlin, Germany, 9–21 August 1979; p. 12. [Google Scholar]
- ASTM E606/E606M-12, Standard Test. Method for Strain-Controlled Fatigue Testing; ASTM International: West Conshohocken, PA, USA, 2012; Available online: www.astm.org (accessed on 11 September 2020).
- Jiang, Y.; Zhang, J. Benchmark experiments and characteristic cyclic plasticity deformation. Int. J. Plast. 2008, 24, 1481–1515. [Google Scholar] [CrossRef]
- Benasciutti, D.; Srnec Novak, J.; Moro, L.; De Bona, F.; Stanojević, A. Experimental characterisation of a CuAg alloy for thermo-mechanical applications. Part 1: Identifying parameters of non-linear plasticity models. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 1364–1377. [Google Scholar] [CrossRef]
- Bari, S.; Hassan, T. Anatomy of coupled constitutive models for ratcheting simulation. Int. J. Plast. 2000, 16, 381–409. [Google Scholar] [CrossRef]
- ASTM E739-10(2015), Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (S-N) and Strain-Life (ε-N.) Fatigue Data; ASTM International: West Conshohocken, PA, USA, 2015; Available online: www.astm.org (accessed on 11 September 2020).
- Marohnić, T.; Basan, R.; Franulović, M. Evaluation of methods for estimation of cyclic stress-strain parameters from monotonic properties of steels. Metals 2017, 7, 17. [Google Scholar] [CrossRef] [Green Version]
- Roessle, M.L.; Fatemi, A. Strain-controlled fatigue properties of steels and some simple approximations. Int. J. Fatigue 2000, 22, 495–511. [Google Scholar] [CrossRef]
- Manson, S.S. Fatigue: A complex subject-Some simple approximations-Both ends of the fatigue spectrum are covered in this lecture. On the one hand, the present state of understanding of the mechanism is reviewed and the complexity of the process observed. On the other hand, some approximations useful in design are outlined and their application illustrated. Exp. Mech. 1965, 5, 193–226. [Google Scholar] [CrossRef]
- Manson, S.S.; Halford, G.R. Fatigue and Durability of Structural Materials; ASM International: Materials Park, OH, USA, 2006. [Google Scholar]
- Novak, J.S.; Benasciutti, D.; De Bona, F.; Stanojević, A.; De Luca, A.; Raffaglio, Y. Estimation of material parameters in nonlinear hardening plasticity models and strain life curves for CuAg alloy. IOP Conf. Ser.: Mater. Sci. Eng. 2016, 119, 012020. [Google Scholar] [CrossRef]
- Williams, C.R.; Lee, Y.L.; Rilly, J.T. A practical method for statistical analysis of strain-life fatigue data. Int. J. Fatigue 2003, 25, 427–436. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers. Eur. J. Eng. Educ. 1994, 19, 383. [Google Scholar] [CrossRef]
- Ralph, I.S.; Fatemi, A.; Stephens, R.R.; Fuchs, H.O. Metal. Fatigue in Engineering, 2nd ed.; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Lee, Y.-L.; Hathaway, R.; Pan, J.; Barkey, M.E. Fatigue Testing and Analysis: Theory and Practice; Butterworth-Heinemann: Oxford, UK, 2004. [Google Scholar]
- Shen, C.L.; Wirsching, P.H.; Cashman, G.T. Design curve to characterize fatigue strength. J. Eng. Mater. Technol. Trans. ASME 1996, 118, 535–541. [Google Scholar] [CrossRef]
- Owen, D.B. Survey of Properties and Applications of the Noncentral t-Distribution. Technometrics 1968, 10, 445–478. [Google Scholar] [CrossRef]
- Wirsching, P.H.; Hsieh, S. Linear model in probabilistic fatigue design. ASCE J. Eng. Mech. Div. 1980, 106, 1265–1278. [Google Scholar] [CrossRef]
- Simo, J.C.; Hughes, T.J.R. Computational Inelasticity; Springer: New York, NY, USA, 1998. [Google Scholar]

| %C | %Si | %Mn | %P | %S | %N | %Cr | %Mo | %Ni | %Cu | %Co |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.019 | 0.37 | 1.75 | 0.024 | 0.026 | 0.079 | 16.60 | 2.07 | 10.16 | 0.47 | 0.13 |
| Isotropic Model | Kinematic Model | ||||
|---|---|---|---|---|---|
| (MPa) | (MPa) | ||||
| 0.3% | 13.7 | −58.9 | 90.00 | 0.8841 | = 189500 MPa = 2950 = 33500 MPa = 350 |
| 0.4% | 14.8 | −51.8 | 46.26 | 0.7596 | |
| 0.5% | 25.8 | −49.8 | 29.18 | 0.7792 | |
| 0.6% | 41.0 | −48.0 | 16.19 | 0.9851 | |
| 0.7% | 48.6 | −42 | 11.37 | 1.280 | |
| Parameter | |||
|---|---|---|---|
| (MPa) | 0.5143106 | 408.5609 | 957143.9 |
| 266.8643 | −77254.43 | 5852143 | |
| (MPa) | −63.42285 | 2054.282 | 128571.8 |
| 1.710213 | −484.2335 | 60392.39 |
| Error, MAPE | Error, APE (Last Stress Peak) | |
|---|---|---|
| 0.3% | 1.81% | 2.19% |
| 0.4% | 0.551% | 1.34% |
| 0.5% | 0.298% | 0.569% |
| 0.6% | 0.233% | 0.126% |
| 0.7% | 0.359% | 0.0282% |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| - | 0.01034 | −0.1748 | 0.05799 | −0.2842 | 0.3031 | - | |
| - | 0.00636 | −0.12 | 0.90604 | −0.6 | 0.2068 | 31.8% | |
| 1.645 | 0.00890 | −0.1748 | 0.05138 | −0.2842 | 0.2654 | 12.4% | |
| 2.0187 | 0.00860 | −0.1748 | 0.04999 | −0.2842 | 0.2575 | 15.1% | |
| 1D tolerance interval | 2.755 | 0.00804 | −0.1748 | 0.04735 | −0.2842 | 0.2427 | 19.9% |
| 1D tolerance interval Owen | 2.9864 | 0.00787 | −0.1748 | 0.04655 | −0.2842 | 0.2382 | 21.4% |
| , std. deviation from regression analysis of experimental data | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pelegatti, M.; Lanzutti, A.; Salvati, E.; Srnec Novak, J.; De Bona, F.; Benasciutti, D. Cyclic Plasticity and Low Cycle Fatigue of an AISI 316L Stainless Steel: Experimental Evaluation of Material Parameters for Durability Design. Materials 2021, 14, 3588. https://doi.org/10.3390/ma14133588
Pelegatti M, Lanzutti A, Salvati E, Srnec Novak J, De Bona F, Benasciutti D. Cyclic Plasticity and Low Cycle Fatigue of an AISI 316L Stainless Steel: Experimental Evaluation of Material Parameters for Durability Design. Materials. 2021; 14(13):3588. https://doi.org/10.3390/ma14133588
Chicago/Turabian StylePelegatti, Marco, Alex Lanzutti, Enrico Salvati, Jelena Srnec Novak, Francesco De Bona, and Denis Benasciutti. 2021. "Cyclic Plasticity and Low Cycle Fatigue of an AISI 316L Stainless Steel: Experimental Evaluation of Material Parameters for Durability Design" Materials 14, no. 13: 3588. https://doi.org/10.3390/ma14133588
APA StylePelegatti, M., Lanzutti, A., Salvati, E., Srnec Novak, J., De Bona, F., & Benasciutti, D. (2021). Cyclic Plasticity and Low Cycle Fatigue of an AISI 316L Stainless Steel: Experimental Evaluation of Material Parameters for Durability Design. Materials, 14(13), 3588. https://doi.org/10.3390/ma14133588









