Abstract
This article aimed to assess the accuracy of the COPERT model in predicting CO2 emissions and energy consumption in real operating conditions, represented by the WLTP homologation tests. Experimental data obtained for a Euro 6 vehicle were compared with the values estimated by the COPERT model, assuming identical speed conditions. MLP and SANN artificial neural networks were also used to create a model describing the complex relationships between emissions, speed, and energy consumption. The results indicate an apparent overestimation of CO2 and energy consumption values by the COPERT model, especially in the low-speed range typical of urban traffic. The minimum energy consumption values were observed at speeds of 50–70 km/h, indicating the existence of an optimal drive system operation zone. The neural models showed high efficiency in predicting the tested parameters—the best results were obtained for the MLP 6-10-1 architecture, whose correlation coefficient exceeded 0.98 in the validation set. The paper highlights the need to calibrate the COPERT model using local experimental data and integrate artificial intelligence methods in modern emission inventories.
1. Introduction
In the face of the ongoing climate crisis and increasing regulatory pressure from international institutions, a thorough assessment of greenhouse gas (GHG) emissions and energy consumption in the road transport sector is becoming a key tool for effective environmental policy. Road transport remains one of the largest final energy consumers and a significant source of CO2 emissions in Europe [1].
In the European Union, the basis for the inventory of road transport emissions is computational models, the most widespread of which is COPERT (Computer Program to calculate Emissions from Road Transport). Developed by the European Environment Agency, this model is used to estimate emissions based on data on vehicle type, fuel type, fleet age, average driving speed, and driving cycles [2,3].
Despite its wide application, numerous studies have highlighted significant limitations of COPERT, especially in the context of the realistic representation of operating conditions. This model uses an average-speed approach, ignoring traffic variability, dynamic accelerations, stops, or the influence of driver driving style [4,5]. As a result, the estimates may significantly deviate from the actual values, which has significant implications for the credibility of national emission reports.
The uncertainty of COPERT emission estimates is significant. For example, [6] showed that imprecision in input data, such as fleet composition or annual mileage, can lead to errors of up to several dozen percent. According to [3], the uncertainty range in emission estimates can span from −58% to +76%, depending on driving conditions and driving style. In another study, [2] found that neglecting the actual speed distribution leads to an underestimation of fuel consumption by 25% and NOx emissions by 36%.
Due to these limitations, increasing attention is being paid to the use of high-resolution data from ITS (Intelligent Transport Systems), GPS, or Internet-of-Vehicles (IoV) systems [7,8,9]. Such sources enable more realistic emission modeling and identification of local emission hotspots in urban agglomerations. Moreover, real-world road surface conditions influence vehicle dynamics, emissions, and energy consumption [10]. This study demonstrated that using accelerometer data and neural networks enables effective pavement classification, providing valuable inputs for enhancing emission models with dynamic road condition factors. Comparable implementations of neural networks have also been applied in industrial measurement optimizations, such as the modeling of optimal probe measurement times on CNC machine tools [11], the prediction of emissions from hydrogen-fueled engines [12] in real driving emission diagnostics [13], and vehicle condition classification under biodiesel operation scenarios [14].
Validation of the COPERT model using empirical data remains an indispensable step. The research uses two main methods: laboratory tests on chassis dynamometers and measurements in real conditions using PEMS systems (Portable Emissions Measurement Systems). The results of these studies confirm that the COPERT model tends to underestimate emissions in dynamic situations [15] and Kousoulidou et al. [16] showed that NOx emissions measured using PEMS can be up to 1.6 times higher than model estimates. Similar conclusions were also confirmed in our own studies, where significant discrepancies were shown between emissions recorded in cold-start conditions and values estimated by static models, especially in urban conditions and for alternative fuels [17]. Additional laboratory studies involving dual-fuel diesel–CNG engines also highlighted the trade-off between NOx reduction and the increase in unburned hydrocarbon and carbon monoxide emissions due to fuel substitution strategies [18].
Additionally, energy consumption analyses in electric and hybrid vehicles indicate the significant impact of driving style and operating conditions on energy efficiency, with a visible optimal range of driving speeds [17,19]. Similar effects have been confirmed in internal combustion vehicles during chassis dynamometer studies, where energy efficiency was shown to depend strongly on vehicle load and velocity patterns [20]. Observations in the context of small-scale biomass machinery additionally demonstrated that CO2 emissions can reach nearly 2 kg/h, depending on operating conditions and machine type [21]. Complementary work on dust and heavy metal emissions from friction systems, omitted in most models, confirms the need for a comprehensive approach to emission inventory [22]. The importance of synergy between experimental data and computational methods using AI in a local approach has also been emphasized in studies comparing ICE and BEV vehicles [23]. Similar findings were reported by [24], who emphasized that emissions from tribological systems, such as brakes and tires, contribute significantly to total particulate matter and heavy metal emissions and are mainly overlooked in standard emission models such as COPERT.
Discrepancies also apply to CO2 emissions and energy consumption, and [25] observed that for LPG-fueled vehicles, CO2 emissions predicted by COPERT were significantly overestimated compared with the results obtained on the chassis dynamometer. PM emissions differed by up to 90%; [26] indicated that PN emissions can be up to eight times higher than the catalogue values adopted in COPERT and HBEFA.
In the context of alternative fuels, the impact of their properties on the efficiency of drive systems was also confirmed in research by Mikielewicz et al. [27], who showed that using biofuels in gas turbines leads to changes in the efficiency of energy cycles. This indicates the need to take into account the fuel characteristics in emission and energy consumption models, especially for vehicles and installations using unconventional fuels.
The importance of driving speed as an emission variable is well documented. Farzaneh et al. [28] showed that for spark-ignition-engined vehicles, CO2 emissions increase rapidly at speeds above 65 km/h, with a maximum at 90–105 km/h. In the city, where speeds below 30 km/h predominate, emissions increase due to frequent changes in driving dynamics and limited engine thermal efficiency.
Driver behavior, such as driving style, also directly impacts emissions. Alessandrini et al. [29] proved that applying eco-driving principles can reduce CO2 emissions by up to 30%. Suarez et al. [30] confirmed that acceleration and speed variability translate directly into fuel consumption and emissions, further exposing the shortcomings of models based on average values. Additionally, technical factors such as tire conditions may influence driving dynamics and energy consumption. Orynycz et al. [31] demonstrated that deteriorated or improperly maintained tires significantly impair braking efficiency, potentially altering driving behavior and affecting fuel use.
Considering the results cited, it is becoming increasingly important to develop and apply next-generation predictive models that can take into account nonlinear dependencies and the local variability of road traffic conditions. Integrating data from measurement systems and using artificial intelligence methods—such as artificial neural networks—offer new perspectives on increasing the accuracy of emission forecasts. Recent developments include XAI-enhanced deep learning for CO2 prediction in vehicles [32], two-stream neural architectures for COPERT corrections of NOx [33], ensemble NNs handling uncertainty in energy efficiency prediction [34], PEMS-based COPERT validations refined by NN engine maps [35], and lightweight surrogate emission models such as NeuralMOVES covering CO2 estimation under variable traffic [36]. Other promising approaches include real driving emission prediction via Elman neural networks [37], DNN-based instantaneous emission forecasting [38], systematic literature surveys on ML for carbon emission estimation [39], hybrid DNN/LSTM models for soot prediction in transient cycles [40], and fine-grained street-level CO2 emission mapping using ML [41]. Real-world applications of intelligent transportation systems, where driving speeds are optimized based on real-time data, have already demonstrated significant reductions in CO2 emissions and energy consumption [42]. Recent studies by Kozłowski et al. [43] have demonstrated that instantaneous energy consumption and recuperation events significantly impact the overall energy balance during real-world driving, emphasizing the inadequacy of models relying solely on average-speed approaches.
This work aims to provide a detailed analysis of the discrepancies between the CO2 emission and energy consumption values estimated by the COPERT model and the data measured during vehicle tests in laboratory conditions (WLTP). Additionally, the effectiveness of using artificial neural networks (MLP, SANN) to model the relationship between speed, emissions, and energy consumption was assessed. The results will be used to determine the usefulness of the COPERT model in the local context and formulate recommendations for further calibration. The study not only evaluates the accuracy of the COPERT model but also explores the potential of integrating machine learning methods such as MLP and SANNs into emission modeling. These techniques offer an opportunity to improve the model’s adaptability by enabling local calibration based on empirical data and real-world traffic dynamics.
Global climate policies have significantly tightened vehicle emission regulations, encouraging the development of advanced modeling tools that accurately reflect real driving emissions (RDE). Conventional inventory models such as COPERT, while widely used, rely on averaged driving cycles, which may not capture dynamic driving behaviors. This study introduces artificial neural networks (ANNs) as a flexible alternative for emission prediction, capable of modeling complex nonlinear relationships between speed, acceleration, load, and emissions. Comparable implementations of ANNs have been successfully applied in diverse transport-related contexts, including fuel-saving driver behavior systems [44], pavement condition classification [45,46], and real-time vehicle parameter estimation [47]. This research fills a gap in integrating laboratory WLTP data with ANN architectures to improve emission estimations and support life-cycle assessment methodologies.
2. Materials and Methods
The tests were carried out on a chassis dynamometer using a vehicle meeting the Euro 6 emission standard and equipped with a spark-ignition engine. The tests were carried out in accordance with the WLTP procedure, but for comparison purposes only those cycle stages were selected that correspond to urban and suburban driving conditions at a maximum speed of up to 80 km/h. This selection allowed for a focus on the conditions of real traffic, which are most important from the point of view of emissions in urban environments. The technical parameters of the tested vehicle are listed in Table 1.

Table 1.
Data of the tested vehicle.
For the purposes of comparative analysis, the emission and energy consumption values obtained from measurements on the chassis dynamometer were compared with the results of the COPERT model. For this purpose, a vehicle configuration corresponding to the class and technology of the tested car was selected in the COPERT calculation environment, assuming identical average-speed values for the analyzed urban and suburban phases. On this basis, model data on CO2 emissions and fuel consumption were obtained, which were subjected to direct comparison with the experimental results.
In addition, a set of input variables including vehicle speed, instantaneous energy consumption, and selected emission components were used to build predictive models. On this basis, artificial neural networks of the MLP (Multi-Layer Perceptron) and SANN (Self-Associative Neural Networks) types were used, the aim of which was to predict energy consumption and map the relationship between emissions and driving parameters.
The dependent variable in the classical analysis is CO2 emission [g/km], and in the energy analysis it is energy consumption [MJ/km]. In the case of modeling using neural networks, the instantaneous speed value and emissions were also predicted based on input data representing typical operating profiles (Figure 1 and Figure 2).
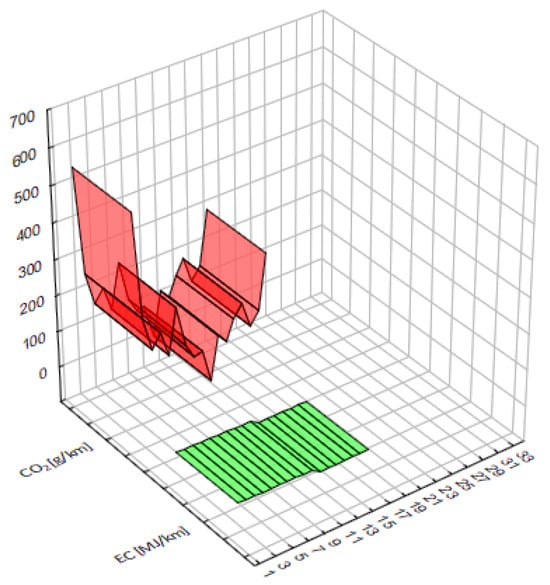
Figure 1.
Dependence of CO2 emissions on vehicle speed and energy consumption—data from the chassis dynamometer test in the WLTP homologation test (urban and suburban phases).
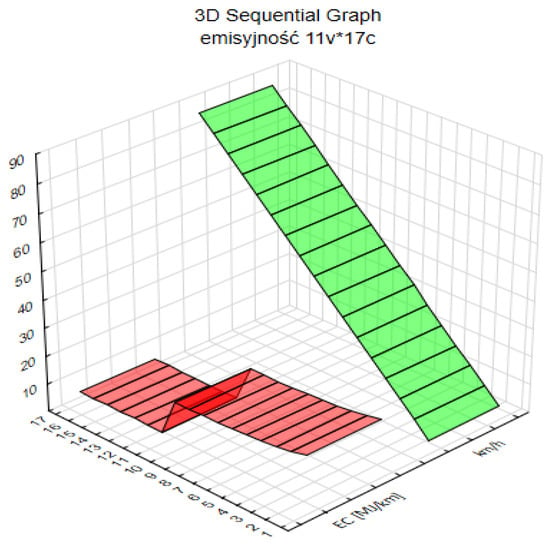
Figure 2.
Specific energy consumption (EC) as a function of speed—data from the WLTP homologation test (MJ/km).
The next part of this paper presents the results of the emission and energy studies and their comparison with the COPERT model estimates.
The next step was to determine the energy consumed [MJ/km]; Figure 3 presents a comparison of travel speed and energy consumed.
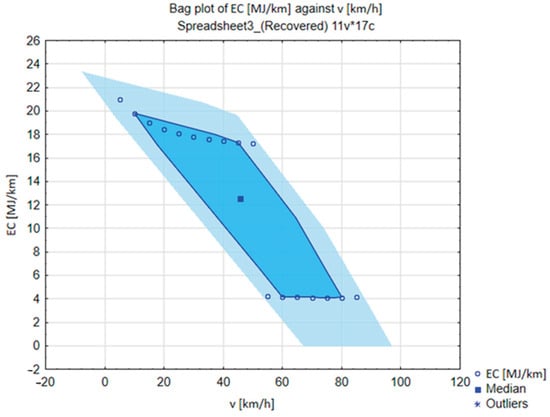
Figure 3.
Distribution of energy consumption (EC) as a function of speed—bag plot based on data from the WLTP test.
The bag plot graph shown in Figure 3 shows the dependence of energy consumption (EC) on speed (v). The blue points in this plot (o) represent the actual EC values [MJ/km] for different speeds. The square (■) indicates the median or central value of energy consumption for the analyzed data. The inner darker area (“bag”) contains the central 50% of the observations, meaning that values in this range are most typical. The outer lighter area (“fence”) indicates the area where most of the observations are, but points outside it may be potential outliers, marked with an asterisk.
The EC [MJ/km] values decrease with increasing speed, reaching a minimum in the range of about 50–70 km/h. For higher speeds (75–85 km/h), energy consumption increases again. However, for low speeds (5–10 km/h) energy consumption is much higher and goes beyond the “fence” area. This shows that moving at very low speeds generates disproportionately high energy consumption. The graph does not show any significant outliers for high speeds, which suggests more stable energy consumption in this range. Furthermore, based on Figure 3, it can be concluded that the most efficient speed range is 50–70 km/h, where the EC [MJ/km] is the lowest. On the other hand, very low and high (80–85 km/h) speeds lead to high energy consumption.
The variations in energy consumption (EC [MJ/km]) with speed observed in Figure 3 can be explained by the processes occurring in the combustion chamber of the spark- ignition engine. The key factors are combustion efficiency, thermal losses, internal resistance, and torque characteristics.
Figure 4 shows the relationship between vehicle speed (X-axis) and specific energy consumption (EC [TJ/km], Y-axis) for the training and validation samples used in the MLP model. A clear decrease in energy consumption is visible with increasing speed, ranging from 10 to about 45 km/h, which corresponds to typical urban and suburban conditions.
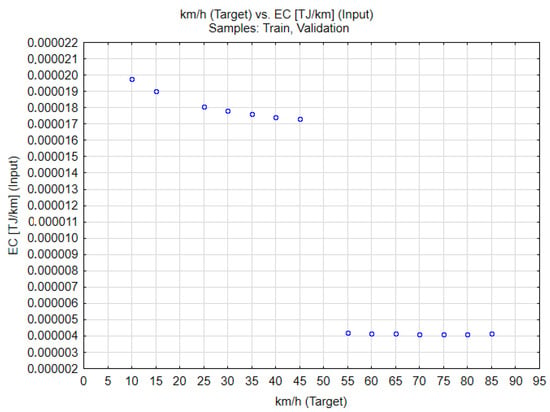
Figure 4.
Dependence of energy consumption (EC) on vehicle speed—input data to the prediction model (training and validation set).
In the higher speed range (above 55 km/h), the EC values stabilize at a lower level, which suggests that a more efficient operating point of the drive system has been achieved. This may indicate the optimization of combustion processes and reduction of mechanical losses during stabilized driving in extraurban conditions. The lack of values in the speed range > 85 km/h results from the limitation of the study to city and suburban cycles, consistent with the WLTP test range (without the motorway phase). The distribution of the data confirms the accuracy of their selection for training neural models that are to predict energy consumption in the range of real operating conditions.
Figure 5 shows the relationship between specific energy consumption (EC) and carbon dioxide (CO2) emissions based on measurement data from chassis dynamometer tests and linear regression results. A positive correlation between these variables is visible, but the linear correlation coefficient (r = 0.21757) indicates a weak linear relationship. The determined linear regression equation has the form:
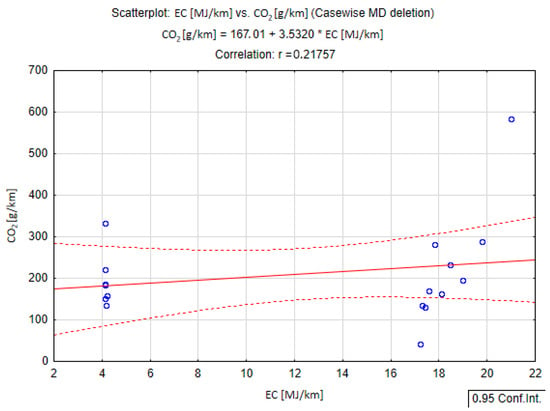
Figure 5.
Dependence of CO2 emissions [g/km] on energy consumption EC [MJ/km]—linear regression analysis for chassis dynamometer data.
Despite the clearly positive regression trend, the large scatter of points and wide confidence intervals (95%) indicate the significant variability of results, especially in the low and high energy consumption ranges. This variability may result from differences in engine operating conditions (e.g., warm-up phase, load) and driving dynamics, which strongly affect the instantaneous CO2 emission values.
Due to the detected positive relationship, the analysis indicates the need to use more advanced models capable of capturing nonlinearities and local anomalies.
The need to model nonlinear, complex relationships between many engines’ operating parameters, emissions, speed, and energy consumption prompted the authors to develop a matrix model.
Exhaust gas emission Ei for each substance i ∈ {CO2, CO, THC, CH4} depends on the fuel combustion characteristics and the engine load. We can write it as a function:
where
Ei = αi EC + βi v + γi
αi—coefficient related to the intensity of fuel combustion,
βi—dependence of emissions on speed,
γi—constant component (dependent on engine technology and emission standard).
EC = f(v, v2, dv/dt)—in the matrix equation it appears in the feedback.
The matrix coefficients are determined based on the vehicle physical parameters and empirical emission factors.
The experimental research should be conducted under real-world traffic conditions, covering routes with diverse characteristics, including urban, suburban, and highway segments. Measurements should be carried out using a Portable Emissions Measurement System (PEMS), which enables the direct recording of instantaneous emissions of major pollutants such as carbon dioxide (CO2), carbon monoxide (CO), total hydrocarbons (THC), and methane (CH4). Simultaneously, vehicle speed, acceleration, and instantaneous fuel consumption should be recorded. Traffic data should be obtained using a GPS system integrated with an inertial measurement unit (IMU), while instantaneous fuel consumption should be recorded using a mass flowmeter system.
The collected data should be synchronized in time and then processed to obtain structured input and output vectors. The input data should include values of vehicle speed, its square, acceleration, and instantaneous fuel consumption, whereas the output data would consist of the recorded emission values of the respective pollutants. To describe the relationship between emissions and driving parameters, a linear model of the form:
is applied, where Y(t) is the emission vector, X(t) is the input variable vector including driving and combustion parameters, while matrix A and vector B contain the coefficients estimated during the analysis. The coefficients should be estimated using the least squares method, extending the input data matrix with an additional column of ones to account for the constant terms, following the approach used in the PHEM model [33,34] and COPERT [35,36]. The developed model allows for a quantitative assessment of the impact of driving parameters on pollutant emission levels under real-world vehicle operation conditions.
Y(t) = A⋅X(t) + BY(t)
Given the limitations in performing large-scale on-road measurements under real-world driving conditions, the present study is based on chassis dynamometer data. Consequently, the experimental analysis was conducted using an alternative methodology, specifically selected to correspond to the characteristics and constraints of the available measurement dataset.
In the initial phase of the WLTP test, covering speeds in the range of 5–20 km/h, increased fuel consumption and CO2 emissions were observed. This phenomenon results primarily from the unstable operation of the drive system after a cold start and frequent speed changes characteristic of city driving. In this range, thermal and mechanical losses dominate, and the engine operates in conditions of reduced efficiency, which results in increased energy consumption per unit of distance.
The lowest energy consumption was recorded in the range of 50–70 km/h, which indicates the existence of optimal operating conditions. In this range, a favorable balance is achieved between aerodynamic drag, mechanical losses, and combustion efficiency. The engine runs stably, and the power demand is low enough to achieve the highest energy efficiency and minimize CO2 emissions.
The increase in energy consumption observed in the upper range of test speeds (up to 80 km/h) can be attributed to increasing aerodynamic drag and increased demand for engine power. Although the operating conditions of the drive system are more stable than at low speeds, increasing motion resistance requires more intensive engine work, which translates into increased fuel consumption and carbon dioxide emissions.
The conclusion is that both in the lower and upper speed ranges, energy consumption increases due to the decrease in the energy efficiency of the drive system. The 50–70 km/h range is the most energy-efficient operating point, which is confirmed by the minimum EC values observed in the tested cycle.
To better understand the complex relationships between operating parameters and emissions, artificial intelligence models were also used, namely MLP and SANN artificial neural networks.
Artificial neural networks were used to model the relationship between exhaust emission parameters and speed and energy consumption. Particular attention was paid to SANNs (Self-Associative Neural Networks), which are used in time series analysis. Their advantage is the ability to capture nonlinear dependencies and time delays, which makes them a more flexible tool compared with classical statistical methods such as linear regression or ARIMA models.
SANNs use self-association, meaning that they learn to map input data based on their own previous states, preserving the temporal context of the phenomenon being analyzed. In practice, this allows them to effectively predict emissions or vehicle speed from training data. By fully connecting the layers, SANNs can effectively model time-dependent variables such as exhaust emissions in dynamic driving conditions.
To ensure proper generalization of the neural network model to unseen data, cross-validation and regularization techniques were systematically applied. During hyperparameter optimization, a k-fold cross-validation procedure (with k = 5) was utilized to partition the dataset into multiple train-validation subsets, allowing the assessment of model stability across varying data splits. This approach minimized the risk of overfitting and provided a reliable estimate of model performance under real-world variability, including differences in driving cycles, traffic intensity, road gradients, and transient engine states.
Additionally, dropout regularization was implemented with a dropout rate of 15% after each hidden layer. This technique randomly deactivates a fraction of neurons during training, forcing the model to avoid excessive reliance on any single subset of features and thus improving its ability to generalize across different operational conditions. The combination of k-fold cross-validation and dropout regularization contributed to stable validation loss curves and consistently small gaps between training and validation errors, indicating robust model learning and limited overfitting.
When applying SANNs to time series regression, the goal is to minimize the prediction error. This can be expressed using a loss function (e.g., mean square error—MSE) [28,30]:
where N is the number of samples in the test set; yi is the actual value on the i-th sample; is the predicted value by the model; and θ are the model parameters (e.g., weights in the neural network).
In SANNs, the learning process consists of adjusting the weights in the neural network to minimize the difference between the model predictions and the actual results. This is performed using the classical backpropagation algorithm, which calculates the gradient of the loss function with respect to the network parameters and updates them in the direction of reducing the error.
In order to predict time series values, a neural network is trained on a set of training data, which are treated as inputs. In the case of regression, the model’s task is to predict future values based on past data.
The prediction algorithm using SANNs is as follows:
- Data preparation: Temporal data is typically transformed into inputs and outputs in the form of pairs (xi, yi), where xi is the input in the form of lagged time series values and yi is the value to be predicted.
- Model Training: The SANN neural network is trained to minimize the loss function, based on the training data.
- Forecasting: Once the network is trained, the model is used to predict future values based on available data.
The advantage of using SANNs in time series analysis is the ability of neural networks, including SANNs, to capture complex, nonlinear dependencies in time series data that may be difficult to model using classical statistical methods. Moreover, another advantage is adaptability. Neural networks can adapt to changing patterns in time series data, which is useful in the case of nonstationary time series. Additionally, performance in long-term forecasting is observed. Thanks to their auto-association mechanism, SANNs can exploit long-term dependencies in the data.
3. Results
This section presents the results of emission-based vehicle speed prediction using various MLP neural network architectures. Neural networks, especially Self-Associative Neural Networks (SANNs), are a powerful tool for modeling and forecasting time series in the context of regression. SANNs are particularly suitable for modeling nonlinear and nonstationary time series, as they can capture complex dependencies and adapt to evolving data patterns. We applied both Multi-Layer Perceptron (MLP) and Static Artificial Neural Network (SANN) models. Input variables were normalized using Min-Max scaling. Training utilized 70% data for learning, 15% for validation, and 15% for testing. Early stopping and L2 regularization were implemented to prevent overfitting. Hyperparameters were as follows (Table 3):—Layers: 3 (input-hidden-output)—Neurons: 5-10-1—Learning rate: 0.001—Optimizer: Adam—Epochs: 300.
1: network for predicting v [km/h]
First, a model was created using artificial neural networks of the speed of harmful components emitted in exhaust gases (CO2, CO, THC, CH4, NMHC) and energy consumption. Table 2 presents the input data, and the goal divided into three sets.

Table 2.
Input data and velocity prediction set (MLP).
The validation data covers a wide speed range, which allows for the assessment of the model’s prediction quality in a variety of driving conditions, both urban and suburban.
The analysis of the CO2 emission values in Table 2 indicates higher emission levels at low speeds (10–20 km/h). This phenomenon may be related to the intense variability of the engine load and frequent changes in driving speed in urban conditions. With increasing speed, CO2 emissions are reduced, reaching lower values in the range of 50–70 km/h, which suggests that in this range the driving conditions are more conducive to the vehicle’s energy stability.
A similar trend is observed for energy consumption (EC [MJ/km]), which reaches its highest values at the lowest speeds and then decreases with increasing speed. In the range of 50–70 km/h, the minimum EC values were recorded, which indicates the existence of an optimal driving range in terms of energy efficiency. Above this range, a new increase in EC is observed, which may be due to the increase in power demand at higher driving speeds.

Table 3.
Correlation coefficients for MLP models.
Table 3.
Correlation coefficients for MLP models.
| Train [km/h] | Test [km/h] | Validation [km/h] | |
|---|---|---|---|
| 1.MLP 6-6-1 | 0.958644 | 0.832050 | 0.987982 |
| 2.MLP 6-4-1 | 0.956190 | 0.832050 | 0.993118 |
| 3.MLP 6-4-1 | 0.963044 | 0.832050 | 0.997390 |
| 4.MLP 6-11-1 | 0.959227 | 0.832050 | 0.984440 |
| 5.MLP 6-10-1 | 0.961213 | 0.832050 | 0.998323 |
Table 4 shows the correlation coefficients for different MLP (Multi-Layer Perceptron) models used to predict vehicle speed (km/h). The train column shows the correlation values on the training set for individual network models (rows). Test shows correlation on the test set. Validation shows correlation on the validation set. The correlation coefficient (R) measures the strength of the relationship between the actual and predicted values. Values close to 1 indicate a strong relationship (the model predicts well). Values close to 0 indicate no relationship, and close to −1 indicate an inverse relationship (which is not the case in our case). Interpreting the values of the correlation coefficients obtained in Table 4, it can be seen that the values for Train 0.958—0.961 are very high, which indicates that the models learn the relationships in the training set well. The values for Test (0.832) are constant for all models, which means that the model achieves moderate quality on new data. The values for Validation 0.984—0.998 are very high, hence the models generalize well on the validation set. Furthermore, the MLP 6-10-1 model has the highest validation correlation 0.998323, suggesting the best agreement with the actual values.

Table 4.
Prediction error statistics for MLP models.
From the above analysis of Table 4, it can be concluded that all models are well trained R>0.95 for Train. The model performs worse on the test set R = 0.832, which may indicate insufficient generalization or differences in the test data. As mentioned above, the best model is MLP 6-10-1 because it has the highest correlation coefficient on the validation set 0.998.
Table 4 shows the prediction statistics for different MLP (Multi-Layer Perceptron) models for the vehicle speed target (km/h) in three sets: train—the training set on which the model was trained; test—the test set used to assess the quality of the model; and validation—the validation set, checking the generalization of the model and any gaps (which do not occur in our data). The stability and precision of the MLP 6-10-1 model indicates its potential for applications in predictive emission inventories, especially in urban environments.
Prediction ranges (minimum and maximum predicted values), residuals (differences between actual and predicted values), and standardized residuals (residuals divided by the standard deviation) were analyzed.
Examining the data in Table 4, it is clear that the models predict values in different ranges. Train: All models learn well, but they differ in the range of values. MLP 6-11-1 has the narrowest range (8.94–68.88 km/h), which may indicate limited model flexibility. MLP 6-6-1 and MLP 6-10-1 have wider ranges, which may be more realistic. Test and Validation: MLP 6-10-1 and MLP 6-6-1 predict values close to the actual validation data; MLP 6-4-1 has the widest range on validation (72.18 km/h), which may indicate greater variability [28].
The most stable models in terms of prediction range are MLP 6-6-1 and MLP 6-10-1.
Minimum and Maximum Residuals show how wrong the model is. In Train, the best training model is MLP 6-10-1 because it has the smallest residual spread (–13.43 to 16.83), which means that it represents the training data well. In Test, the largest errors are in MLP 6-6-1 and MLP 6-4-1 because they have the largest deviations (–19.11 to 18.27 km/h). The best test model is MLP 6-10-1 (–16.83 to 16.83 km/h), due to its more stable predictions. In Validation, the smallest validation residuals are in MLP 6-11-1 and MLP 6-10-1 because they have the smallest errors, which indicates good generalization [48,49].
This table also shows that the best model, this time in terms of residuals on validation, is the 6-10-1 model.
Again, the MLP 6-10-1 model is the best of the analyzed models generated during training on the dataset available from the experiment analyzed in this article. It is characterized by a good fit to the training set, stable residuals in validation and test, and the best prediction range. In addition, it generalizes well to new data.
Figure 6 shows the spatial visualization of the speed estimation error by the MLP 6-10-1 model as a function of the target value (Target), the predicted value (Output), and the energy consumption (EC). The analysis shows that the lowest values of the prediction error (green and blue) occur in the range of medium speeds, especially between 30 and 60 km/h, which confirms the effectiveness of the model in this operating range. An increase in the error (yellow–red colors) is observed at extremely low and high speeds, which may be the result of both greater data variability in these areas and a smaller number of observations in the training set. Despite local extremes, the overall course of the error surface remains relatively regular, which indicates good model stability and its ability to generalize in the analyzed data range [48,49].
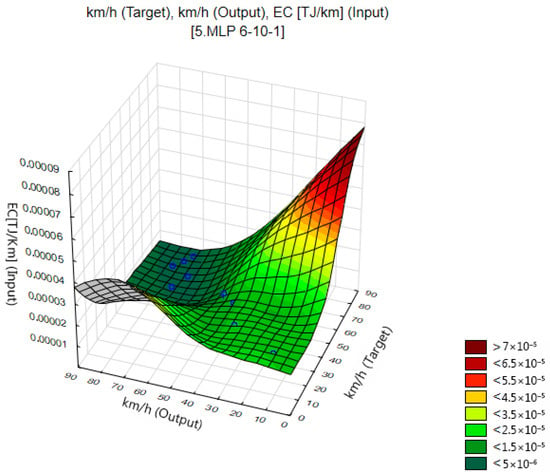
Figure 6.
Speed estimation error [km/h] as a function of the set and predicted value by the MLP 6-10-1 model depending on the energy consumption [TJ/km].
Figure 7 shows the three-dimensional speed estimation error surface generated by the MLP 6-10-1 model, where the input variable is CO2 emission. A curvilinear relationship is clearly visible; the lowest CO2 values (dark green) occur in the medium speed range (approx. 30–60 km/h), both on the target and predicted side. On the other hand, in the low (<20 km/h) and high speed (above 70 km/h) areas, a sharp increase in CO2 emission is observed (yellow, orange, and red areas), which corresponds to the increased energy demand of the vehicle in these conditions [48,49].
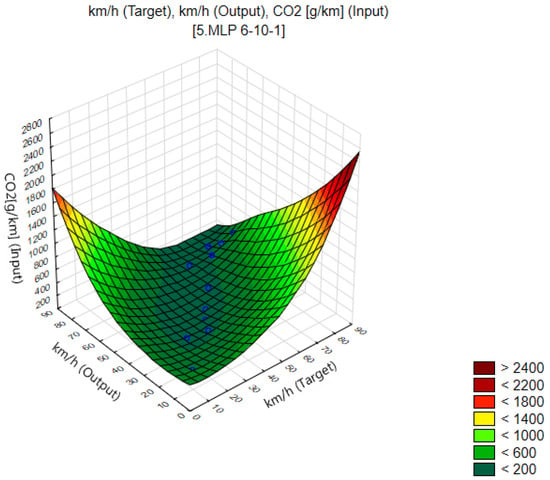
Figure 7.
Vehicle speed estimation by the MLP 6-10-1 model as a function of actual and predicted value [km/h] based on CO2 emissions [g/km].
This model shows good prediction agreement in the range of average speeds, which confirms the precision of the representation for typical operating conditions. At the same time, the surface structure indicates the increasing difficulty of estimation in the areas of extreme CO2 values, which are characteristic of dynamic phases of city driving or accelerations on suburban sections. The whole confirms the effectiveness of the MLP 6-10-1 model in representing complex nonlinear dependencies of emissions on variable road traffic [27].
Figure 8 shows a comparison of vehicle speed prediction results obtained using five MLP (Multi-Layer Perceptron) neural network models with different architectures (marked as MLP 6-6-1, 6-4-1, 6-11-1, 6-10-1) with respect to the actual values (blue line). The values are presented as ordered measurement cases for training and validation sets.
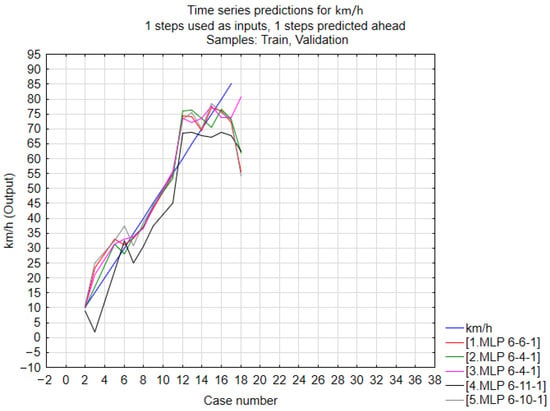
Figure 8.
Comparison of speed predictions by different MLP models against reference values [km/h]—training and validation data.
The apparent agreement of the prediction course with the reference curve in the range of 10–75 km/h confirms the good performance of all architectures in reproducing the general trend of speed changes. The MLP 6-10-1 model stands out in particular, which most faithfully reproduces the speed variability in the entire range of cases, with minimal scatter and without visible over- or underestimation in the speed range of 30–55 km/h.
Noticeable deviations of predictions from reference values in some cases—especially for MLP 6-4-1—may indicate insufficient network depth to capture complex nonlinear dependencies between emission and velocity. Differences between architectures highlight the importance of selecting the number of hidden neurons in the context of estimation accuracy. These conclusions support the selection of the MLP 6-10-1 model for further prediction analyses.
Analysis of experimental data obtained on a chassis dynamometer under WLTP test conditions showed a clear variability of pollutant emissions and energy consumption depending on vehicle speed. As shown in Figure 1, CO2, CO, THC, and CH4 emissions take the highest values in the low-speed range (below 20 km/h), which is characteristic of urban operating conditions. In this range, incomplete combustion and high thermal and mechanical losses dominate.
Figure 2 integrates emission data with operating parameters, confirming observed trends and indicating correlations between dynamic speed changes and emission spikes. Energy consumption values (Figure 3 and Figure 4) show a clear “U” shape; EC [MJ/km] is highest at very low (5–20 km/h) and high speeds (above 75 km/h), and the minimum occurs in the range of 50–70 km/h.
Further analysis of the linear regression of CO2 emissions on energy consumption (Figure 5) showed a moderate positive correlation, but with considerable variability, suggesting the need to use more advanced nonlinear models.
In this context, artificial neural networks of the MLP and SANN type were used, which allowed for mapping the relationship between exhaust emissions, speed, and energy consumption. Table 4 presents the correlation coefficients of speed prediction, reaching values above 0.98 in the validation set, with the MLP 6-10-1 model showing the best generalization properties.
Figure 6, Figure 7 and Figure 8 show spatial visualizations of prediction errors and mapping of curvilinear dependencies of CO2 emissions and energy consumption with respect to actual values. The MLP 6-10-1 model maintains high prediction accuracy in the speed range of 30–60 km/h, while the largest errors are observed in the range of extreme speeds, which may result from greater variability of operating conditions and smaller representation of these data in the training set.
Neural models outperformed COPERT matrix models in RMSE, MAE, and R2 metrics across all datasets. Cross-validation confirmed minimal overfitting. U-shaped relationships were observed due to low thermal efficiency at low speeds, rising aerodynamic drag at high speeds, and optimal efficiency zones at mid-range velocities.
4. Discussion
The experimental results obtained confirm the limitations of the COPERT model known from the literature in terms of the realistic representation of emissions and energy consumption in dynamic conditions. The overestimation of CO2 emissions and energy consumption observed in the study is consistent with the findings of Bellin et al. [25], who showed that COPERT can significantly overestimate emissions, especially for vehicles powered by alternative fuels (e.g., LPG), where the differences from the chassis dynamometer test data exceeded 50–90% for CO2 and PM. Keuken et al. [26] also indicated that particulate matter (PN) emissions can actually be up to eight times higher than those estimated by COPERT and HBEFA, which emphasizes the need to verify these models in operating conditions.
One of the key factors of estimation error is the use of average speeds by COPERT, which does not take into account the variability of the microcycle driving. As shown by Lejri et al. [2], the failure to take into account the full speed distribution results in the underestimation of fuel consumption by 25% and NOx emissions by up to 36%. Our results are consistent with these findings; CO, THC and CH4 emissions increase significantly in the low-speed range (5–20 km/h), typical for the urban environment, which indicates the dominance of suboptimal combustion conditions (cold engine, intermittent driving, and rich mixture). The results obtained using MLP and SANN models suggest that these approaches can be used to supplement the COPERT model by capturing nonlinear patterns and local anomalies that are not reflected in average-speed-based estimations. This hybrid approach—combining deterministic models with AI-based corrections—could enhance the accuracy and relevance of national emission inventories, especially in urban environments. Similar findings were reported by Gemma et al. [50], who demonstrated that motorway traffic emissions are significantly affected by stochastic fluctuations in traffic dynamics, and that using average-speed approaches underestimates the variability and magnitude of real-world emissions.
In turn, Dey et al. [3] drew attention to the enormous sensitivity of the emission model to input data; their analysis showed uncertainty ranging from −58% to +76%. In the context of our research, this confirms the need for local calibration of the COPERT model, especially in conditions deviating from the assumptions of test cycles (e.g., WLTP), as well as the adjustment of model parameters to the realities of the domestic fleet. Analogous conclusions regarding the influence of the choice of operational technologies on energy consumption and emissions were also confirmed in the agricultural sector. Orynycz [30] showed that using no-tillage technologies in rapeseed cultivation significantly improves the energy balance, which emphasizes the need to consider the characteristics of technological processes when estimating emissions in various sectors of the economy.
The need for local verification is also confirmed by Notter et al. [6], who emphasize that errors in emission inventories result not only from inaccuracies in input data, but also from not taking into account seasonality and driver behavior variability. In practice, this means that emission models should be supported by real data, both from stationary and mobile PEMS systems. Moreover, the energy balance and emissions associated with fuel production processes should also be considered. Orynycz and Wasiak [51] demonstrated that the embodied energy of biodiesel production significantly affects its overall energetic effectiveness, highlighting the importance of holistic assessments in emission modeling.
Our results also show that energy consumption increases at both low and high speeds, with a minimum in the 50–70 km/h range. Such characteristics have already been demonstrated in the literature, e.g., by Wen et al. [4] and Ren et al. [5], who argue that the actual energy balance of a vehicle strongly depends on dynamic overloads, instantaneous power, and rolling and aerodynamic resistance.
The use of artificial neural networks, such as MLP 6-10-1, allowed for accurate representation of nonlinear relationships between energy consumption, CO2 emissions, and driving speed. The achieved correlation coefficients (>0.98) in the validation set indicate that machine learning models are a reliable alternative to classical methods based on average values. According to the literature, the use of machine learning in vehicle emission prediction (e.g., SANN, MLP) allows for significantly improving the temporal and spatial resolution of the model and adapting it to specific local conditions [5]. Similar advantages of machine learning in improving the accuracy of complex data analysis tasks have been demonstrated in other fields, such as reflective ultrasound tomography [52], suggesting the broader potential of AI-based models over traditional deterministic approaches.
The applied artificial neural network (ANN) models effectively capture transient driving dynamics that are often neglected in average-speed approaches such as COPERT. Incorporating real-world transient operating data substantially improves the predictive accuracy of emission estimates, particularly for urban driving conditions and detailed emission inventories. However, certain limitations of the current study include the restricted size of the test vehicle fleet and the absence of Portable Emissions Measurement System (PEMS) data, which could further enhance model calibration and validation.
5. Conclusions
The conducted studies confirm that the COPERT model, although commonly used in emission inventories, does not fully reflect the actual operating conditions of vehicles, especially in urban and suburban environments. The results of chassis dynamometer tests showed a systematic overestimation of CO2 emissions and energy consumption by the COPERT model, which may lead to erroneous conclusions in national emission reports and environmental policies.
CO, THC, and CH4 emissions, as well as energy consumption, were highest at low speeds (5–20 km/h), which indicates the dominance of suboptimal combustion conditions characteristic of urban driving. In turn, the lowest energy consumption occurred in the speed range of 50–70 km/h, which confirms the existence of the zone of the highest energy efficiency of the analyzed vehicle.
The use of artificial neural networks (MLP, SANN) has proven to be an effective method for predicting both CO2 emissions and energy consumption. These models capture nonlinear relationships and demonstrate high predictive accuracy (r > 0.98), making them a valuable tool for supplementing or calibrating classical computational models.
In light of the results obtained, it is recommended to supplement standard emission models with empirical data and consider implementing models based on machine learning in local emission inventories. Such an approach increases the precision of forecasts and allows for better adjustment of modeling tools to diverse road and technological conditions.
Author Contributions
Conceptualization, O.O., M.Z.-L. and E.K.; methodology O.O., M.Z.-L. and E.K.; software, O.O., M.Z.-L. and E.K.; validation, O.O., M.Z.-L. and E.K.; formal analysis, O.O., M.Z.-L. and E.K.; resources, O.O., M.Z.-L. and E.K.; writing—original draft preparation, O.O., M.Z.-L. and E.K.; writing—review and editing, O.O., M.Z.-L. and E.K.; visualization, O.O., M.Z.-L. and E.K.; supervision O.O., M.Z.-L. and E.K.; funding acquisition, O.O. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financed in part by the Faculty of Engineering Management (WIZ) of Bialystok University of Technology, No. WZ/WIZ-INZ/2/2025.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ANN | Artificial Neural Network |
| CO2 | Carbon Dioxide |
| COPERT | Computer Program to calculate Emissions from Road Transport |
| EC | Energy Consumption |
| IQR | Interquartile Range |
| MLP | Multi-Layer Perceptron |
| PEMS | Portable Emissions Measurement System |
| RMSE | Root Mean Square Error |
| SANN | Simple Artificial Neural Network |
| WLTP | Worldwide Harmonized Light Vehicles Test Procedure |
References
- Zschausch, F.; Rosenberger, S. Energy Consumption and Greenhouse Gas Emissions Arising from Logistical Activities within the Field of Road Transportation—A Review of Annual Balances and Mitigation Measures, 9th ed.; Die Bundesvereinigung Logistik (BVL) e.V.: Bremen, Germany, 2023. [Google Scholar]
- Lejri, D.; Can, A.; Schiper, N.; Leclercq, L. Accounting for traffic speed dynamics when calculating COPERT and PHEM pollutant emissions at the urban scale. Transp. Res. Part D Transp. Environ. 2018, 63, 588–603. [Google Scholar] [CrossRef]
- Dey, S.; Caulfield, B.; Ghosh, B. Modelling uncertainty of vehicular emissions inventory: A case study of Ireland. J. Clean. Prod. 2019, 213, 1115–1126. [Google Scholar] [CrossRef]
- Wen, Y.; Zhang, S.; Zhang, J.; Bao, S.; Wu, X.; Yang, D.; Wu, Y. Mapping dynamic road emissions for a megacity by using open-access traffic congestion index data. Appl. Energy 2020, 260, 114357. [Google Scholar] [CrossRef]
- Ren, L.; Guo, X.; Wu, J.; Singh, A.K. Data mining and spatio-temporal characteristics of urban road traffic emissions: A case study in Shijiazhuang, China. PLoS ONE 2023, 18, e0295664. [Google Scholar] [CrossRef]
- La Notte, A.; Tonin, S.; Lucaroni, G. Assessing direct and indirect emissions of greenhouse gases in road transportation, taking into account the role of uncertainty in the emissions inventory. Environ. Impact Assess. Rev. 2018, 69, 82–93. [Google Scholar] [CrossRef]
- Jing, B.; Wu, L.; Mao, H.; Gong, S.; He, J.; Zou, C.; Song, G.; Li, X.; Wu, Z. Development of a vehicle emission inventory with high temporal–spatial resolution based on NRT traffic data and its impact on air pollution in Beijing—Part 1: Development and evaluation of vehicle emission inventory. Atmos Chem. Phys. 2016, 16, 3161–3170. [Google Scholar] [CrossRef]
- Park, J.; Park, S. Estimating regional CO2 and NOx emissions from road transport using real-world data-based emission factors in Korea. Environ. Pollut. 2024, 352, 124140. [Google Scholar] [CrossRef]
- Sulekha Devi, A.; Mary John Britto, M.; Fang, Z.; Gopan, R.; Singh Jassal, P.; Qazzaz, M.M.H.; Rajbhandari, S.; Al-Sallami, F.M. Internet-of-Vehicles Network for CO2 Emission Estimation and Reinforcement Learning-Based Emission Reduction. IEEE Access 2024, 12, 110681–110690. [Google Scholar] [CrossRef]
- Surblys, V.; Kozłowski, E.; Matijošius, J.; Gołda, P.; Laskowska, A.; Kilikevičius, A. Accelerometer-Based Pavement Classification for Vehicle Dynamics Analysis Using Neural Networks. Appl. Sci. 2024, 14, 10027. [Google Scholar] [CrossRef]
- Tomiło, P.; Pytka, J.; Józwik, J.; Gnapowski, E.; Muszyński, T.; Łukaszewicz, A. Latent Neural Network For Recognition of Annomalies in 3D-Print of a Scale Model for Wind Tunnel Measurements. In Proceedings of the 2023 IEEE 10th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Milan, Italy, 19–21 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 688–692. [Google Scholar] [CrossRef]
- Kamela, W.; Wojs, M.K.; Orliński, P. Calculation Method for Assessing the Storage Capacity of Nitrogen Compounds in LNT Reactors. Energies 2022, 15, 7819. [Google Scholar] [CrossRef]
- Andrych-Zalewska, M.; Chłopek, Z.; Merkisz, J.; Pielecha, J. Analysis of the operation states of internal combustion engine in the Real Driving Emissions test. Arch. Transp. 2022, 61, 71–88. [Google Scholar] [CrossRef]
- Bednarski, M.; Orliński, P.; Wojs, M.; Gis, M. Evaluation of the heat release rate during the combustion process in the diesel engine chamber powered with fuel from renewable energy sources. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 1333–1339. [Google Scholar] [CrossRef]
- O’Driscoll, R.; ApSimon, H.M.; Oxley, T.; Molden, N.; Stettler, M.E.J.; Thiyagarajah, A. A Portable Emissions Measurement System (PEMS) study of NOx and primary NO2 emissions from Euro 6 diesel passenger cars and comparison with COPERT emission factors. Atmos. Environ. 2016, 145, 81–91. [Google Scholar] [CrossRef]
- Kousoulidou, M.; Fontaras, G.; Ntziachristos, L.; Bonnel, P.; Samaras, Z.; Dilara, P. Use of portable emissions measurement system (PEMS) for the development and validation of passenger car emission factors. Atmos. Environ. 2013, 64, 329–338. [Google Scholar] [CrossRef]
- Laskowski, P.; Zimakowska-Laskowska, M.; Jan, M.; Wiśniowski, P. The problem of cold start emissions from vehicles. Combust. Engines 2024, 199, 43–51. [Google Scholar] [CrossRef]
- Smigins, R.; Skrzek, T.; Górska, M.; Pawlak, G. Investigation of Harmful Chemical Compounds from Dual-Fuelled Diesel Engine. Adv. Sci. Technol. Res. J. 2020, 14, 21–29. [Google Scholar] [CrossRef]
- Kozłowski, E.; Wiśniowski, P.; Gis, M.; Zimakowska-Laskowska, M.; Borucka, A. Vehicle Acceleration and Speed as Factors Determining Energy Consumption in Electric Vehicles. Energies 2024, 17, 4051. [Google Scholar] [CrossRef]
- Gonera, J.; Janulin, M.; Vrublevskyi, O. Effect of vehicle operating parameters on fuel consumption and the overall energy efficiency of the drive system. Arch. Transp. 2024, 72, 109–128. [Google Scholar] [CrossRef]
- Warguła, Ł.; Nati, C.; Wieczorek, B.; Bembenek, M. The carbon dioxide emission balance and ability to chip wood by 10 kW machines used in urban areas in terms of increasing interest in using wood biomass resources for personal use. Adv. Sci. Technol. Res. J. 2025, 19, 402–416. [Google Scholar] [CrossRef]
- Zimakowska-Laskowska, M.; Kozłowski, E.; Laskowski, P.; Wiśniowski, P.; Świderski, A.; Orynycz, O. Vehicle exhaust emissions in the light of modern research tools: Synergy of chassis dynamometers and computational models. Combust. Engines 2025, 200, 145–154. [Google Scholar] [CrossRef]
- Zimakowska-Laskowska, M.; Laskowski, P. Emission from Internal Combustion Engines and Battery Electric Vehicles: Case Study for Poland. Atmosphere 2022, 13, 401. [Google Scholar] [CrossRef]
- Laskowski, P.P.; Zimakowska-Laskowska, M. The problem of emission of total particulate matter and heavy metals from tribological systems in vehicles. Combust. Engines 2024, 198, 13–19. [Google Scholar] [CrossRef]
- Bellin, T.; Casadei, S.; Rossi, T.; Bernetti, A.; De Lauretis, R.; Lonati, G. Determination of Euro 6 LPG passenger car emission factors through laboratory and on-road tests: Effect on nation-wide emissions assessment for Italy. Atmos. Environ. X 2022, 15, 100186. [Google Scholar] [CrossRef]
- Keuken, M.P.; Moerman, M.; Voogt, M.; Zandveld, P.; Verhagen, H.; Stelwagen, U.; de, D.J. Particle number concentration near road traffic in Amsterdam (the Netherlands): Comparison of standard and real-world emission factors. Atmos. Environ. 2016, 132, 345–355. [Google Scholar] [CrossRef]
- Mikielewicz, D.; Kosowski, K.; Tucki, K.; Piwowarski, M.; Stępień, R.; Orynycz, O.; Włodarski, W. Influence of Different Biofuels on the Efficiency of Gas Turbine Cycles for Prosumer and Distributed Energy Power Plants. Energies 2019, 12, 3173. [Google Scholar] [CrossRef]
- Farzaneh, M.; Schneider, W.H.; Zietsman, J. Field Evaluation of Carbon Dioxide Emissions at High Speeds. Transp. Res. Rec. J. Transp. Res. Board 2010, 2191, 152–157. [Google Scholar] [CrossRef]
- Alessandrini, A.; Cattivera, A.; Filippi, F.; Ortenzi, F. Driving style influence on car CO2 emissions. In 2012 international emission inventory conference. Transp. Res. Part D Transp. Environ. 2012, 17, 524–528. [Google Scholar]
- Suarez, J.; Makridis, M.; Anesiadou, A.; Komnos, D.; Ciuffo, B.; Fontaras, G. Benchmarking the driver acceleration impact on vehicle energy consumption and CO2 emissions. Transp. Res. Part D Transp. Environ. 2022, 107, 103282. [Google Scholar] [CrossRef] [PubMed]
- Orynycz, O.; Tucki, K.; Wasiak, A.; Sobótka, R.; Gola, A. Evaluation of the Brake’s Performance Dependence Upon Technical Condition of Car Tires as a Factor of Road Safety Management. Energies 2019, 13, 9. [Google Scholar] [CrossRef]
- Alam, G.M.I.; Arfin Tanim, S.; Sarker, S.K.; Watanobe, Y.; Islam, R.; Mridha, M.F.; Nur, K. Deep learning model based prediction of vehicle CO2 emissions with eXplainable AI integration for sustainable environment. Sci. Rep. 2025, 15, 3655. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, R.; Pan, K.; Li, J.; Wu, Q. Two-Stream Networks for COPERT Correction Model with Time-Frequency Features Fusion. Atmosphere 2023, 14, 1766. [Google Scholar] [CrossRef]
- Khiari, J.; Olaverri-Monreal, C. Uncertainty-Aware Vehicle Energy Efficiency Prediction Using an Ensemble of Neural Networks. IEEE Intell. Transport. Syst. Mag. 2023, 15, 109–119. [Google Scholar] [CrossRef]
- Kousoulidou, M.; Ntziachristos, L.; Gkeivanidis, S.; Samaras, Z. Validation of the COPERT road emission inventory model with real-use data n.d. COPERT road emission inventory model with real-use data. In Proceedings of the 19th International Emission Inventory Conference, San Antonio, TX, USA, 27–30 September 2010. [Google Scholar]
- Xu, Z.; Kang, Y.; Cao, Y.; Li, Z. Deep amended COPERT model for regional vehicle emission prediction. Sci. China Inf. Sci. 2021, 64, 139202. [Google Scholar] [CrossRef]
- Miranda, M.H.R.; Silva, F.L.; Frutuoso, F.S.; Eckert, J.J.; Oliveira, M.L.M.; Silva, L.C.A. Novel prediction approach for exhaust gases using Elman neural network combined with particle swarm optimization. Energy 2025, 331, 136769. [Google Scholar] [CrossRef]
- Howlader, A.M.; Patel, D.; Gammariello, R. Data-driven approach for instantaneous vehicle emission predicting using integrated deep neural network. Transp. Res. Part D Transp. Environ. 2023, 116, 103654. [Google Scholar] [CrossRef]
- Al Nuaimi, H.S.; Acquaye, A.; Mayyas, A. Machine learning applications for carbon emission estimation. Resour. Conserv. Recycl. Adv. 2025, 27, 200263. [Google Scholar] [CrossRef]
- Shin, S.; Won, J.-U.; Kim, M. Comparative research on DNN and LSTM algorithms for soot emission prediction under transient conditions in a diesel engine. J. Mech. Sci. Technol. 2023, 37, 3141–3150. [Google Scholar] [CrossRef]
- Anjos, M.; Meier, F. Zooming into Berlin: Tracking street-scale CO2 emissions based on high-resolution traffic modeling using machine learning. Front. Environ. Sci. 2025, 12, 1461656. [Google Scholar] [CrossRef]
- Yang, Z.; Peng, J.; Wu, L.; Ma, C.; Zou, C.; Wei, N.; Zhang, Y.; Liu, Y.; Andre, M.; Li, D.; et al. Speed-guided intelligent transportation system helps achieve low-carbon and green traffic: Evidence from real-world measurements. J. Clean. Prod. 2020, 268, 122230. [Google Scholar] [CrossRef]
- Kozłowski, E.; Zimakowska-Laskowska, M.; Dudziak, A.; Wiśniowski, P.; Laskowski, P.; Stankiewicz, M.; Šnauko, B.; Lech, N.; Gis, M.; Matijošius, J. Analysis of Instantaneous Energy Consumption and Recuperation Based on Measurements from SORT Runs. Appl. Sci. 2025, 15, 1681. [Google Scholar] [CrossRef]
- Munahar, S.; Triwiyatno, A.; Munadi, M.; Setiawan, J.D. Fuel Saving Indeks Assessment on Driving Behavior Control System Prototype Model Using Neural Network. Arch. Transp. 2022, 63, 123–141. [Google Scholar] [CrossRef]
- Tomiło, P. Classification of the Condition of Pavement with the Use of Machine Learning Methods. Transp. Telecommun. J. 2023, 24, 158–166. [Google Scholar] [CrossRef]
- Chodakowska, E.; Nazarko, J.; Nazarko, Ł. Arima Models in Electrical Load Forecasting and Their Robustness to Noise. Energies 2021, 14, 7952. [Google Scholar] [CrossRef]
- Michałowska, J.; Tomiło, P. Measurement systems of electromagnetic field for aircraft with the use of a machine learning model. Metrol. Meas. Syst. 2024, 31, 577–594. [Google Scholar] [CrossRef]
- Kordos, M.; Duch, W. On Some Factors Influencing MLP Error Surface. In Artificial Intelligence and Soft Computing—ICAISC 2004, Proceedings of the 7th International Conference, Zakopane, Poland, 7–11 June 2004; Rutkowski, L., Siekmann, J.H., Tadeusiewicz, R., Zadeh, L.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3070, pp. 217–222. [Google Scholar] [CrossRef]
- Kordos, M.; Duch, W. A survey of factors influencing MLP error Surface, Control and Cybernetics. Surv. Factors Influ. MLP Error Surf. 2024, 33, 611–631. [Google Scholar]
- Gemma, A.; Giannattasio, O.; Mannini, L. Motorway Traffic Emissions Estimation through Stochastic Fundamental Diagram. Sustainability 2023, 15, 9871. [Google Scholar] [CrossRef]
- Orynycz, O.; Wasiak, A. Computer modelling of the effect of embodied energy on energetic effectiveness of biodiesel production. MATEC Web. Conf. 2019, 252, 06013. [Google Scholar] [CrossRef]
- Majerek, D.; Rymarczyk, T.; Wójcik, D.; Kozłowski, E.; Rzemieniak, M.; Gudowski, J.; Gauda, K. Machine Learning and Deterministic Approach to the Reflective Ultrasound Tomography. Energies 2021, 14, 7549. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).