Co-Optimized Design of Islanded Hybrid Microgrids Using Synergistic AI Techniques: A Case Study for Remote Electrification

Abstract

Off-grid and isolated rural communities in developing countries with limited resources require energy supplies for daily residential use and social, economic, and commercial activities. The use of data from space assets and space-based solar power is a feasible solution for addressing ground-based energy insecurity when harnessed in a hybrid manner. Advances in space solar power systems are recognized to be feasible sources of renewable energy. Their usefulness arises due to advances in satellite and space technology, making valuable space data available for smart grid design in these remote areas. In this case study, an isolated village in Namibia, characterized by high levels of solar irradiation and limited wind availability, is identified. Using NASA data, an autonomous hybrid system incorporating a solar photovoltaic array, a wind turbine, storage batteries, and a backup generator is designed. The local load profile, solar irradiation, and wind speed data were employed to ensure an accurate system model. Using HOMER Pro software V 3.14.2 for system simulation, a more advanced AI optimization was performed utilizing Grey Wolf Optimization and Harris Hawks Optimization, which are two metaheuristic algorithms. The results obtained show that the best performance was obtained with the Grey Wolf Optimization algorithm. This method achieved a minimum energy cost of USD 0.268/kWh. This paper presents the results obtained and demonstrates that advanced optimization techniques can enhance both the hybrid system’s financial cost and energy production efficiency, contributing to a sustainable electricity supply regime in this isolated rural community.

1. Background

Energy systems worldwide are undergoing a major transformation to reduce greenhouse gas emissions and improve power supply security. The combination of diverse renewable energy systems in hybrid notation (HRES), such as solar–PV, hydro, and wind power sources, represents a viable means of providing reliable and sustainable power. Southern Africa continues to experience challenges with energy supply, especially in rural areas. In Namibia, for example, electrification is hampered by the scattered nature of human settlements and the huge size of its territory. Although the national access rate is approximately 55%, the rural communities remain inadequately supplied. As a result, the country is highly reliant on electricity imports, hence its vulnerability. For solar and wind power, Namibia has considerable renewable energy potential, which can be used to develop hybrid renewable energy systems (HRESs) to increase electricity access and decrease dependence on electricity imports and reliance on conventional fossil sources [1].

A hybrid renewable energy system integrates one or more power production alternatives to satisfy a specific demand [2,3]. There is growing global interest in hybrid systems using renewables, with photovoltaic (PV) and wind power providing an option for supplying electricity to unserved communities [4,5]. The seasonal variability of both solar and wind sources enables them to complement each other; hence, their combination provides a reliable and continuous power supply [6,7]. Emergency power generally provides energy in periods of low insolation and low wind power. While diesel generators are considered environmentally unfriendly, they supplement intermittent renewable energy sources, as their electricity supply is not seasonal [8]. Since most renewable energy sources are intermittent, incorporating these DGs in the main electricity grid negatively affects the grid stability and power quality [5,9].

Stand-alone renewable energy source (RES)-based microgrid systems represent potentially the most feasible and the most cost-effective way to electrify remote off-grid communities [10,11]. Consequently, the optimal planning and design of such a system is economically and technically complex due to several factors. Among them is the incoherence and dependence of RES on meteorological data. Microgrid systems are frequently designed to be over- or undersized to satisfy load demand. Oversized microgrids will have higher operating costs and produce energy in excess. On the other hand, undersized microgrids cannot serve the required loads. Maximizing the benefits of a microgrid based on RES requires optimal microgrid sizing; hence, an energy management system (EMS) strategy is required [11,12].

The HRES, which combines solar–PV, a diesel generator (DG), storage batteries, and a wind turbine (WT), has proven to be a viable and cost-effective solution to the problem of rural electricity supply for sub-Saharan Africa, especially in areas of limited availability such as Namibia. Many studies have concentrated on these systems’ optimum sizing and performance, combining simulation tools such as HOMER and enhanced optimization algorithms, such as Harris Hawks Optimization (HHO) and Grey Wolf Optimizer (GWO).

In [13], an optimized configuration of a hybrid system for a remote Nigerian rural village based on HOMER is studied to reduce both the COE and the NPC. The authors in [14] applied a Grey Wolf Optimizer (GWO) in a multi-objective environment, enhancing the efficiency and the reliability. The authors in [15] used the Harris Hawks Optimization (HHO) algorithm to analyze hybrid systems under arid conditions, resulting in a higher rate of system convergence and a lower level of power losses. Furthermore, [16] uses the particle swarm optimization (PSO) algorithm for the optimization of PV–wind–battery systems in off-grid applications, while [17] shows that PSO is better than the genetic algorithm (GA) and artificial bee colony algorithm (ABC) for the speed of convergence and solution.

This underlines the increasing focus on combining conventional simulation techniques and AI-derived optimization to solve rural off-grid energy access problems. While HOMER offers a comprehensive technical–economic framework, GWO and HHO provide improved research capacities on complex, high-dimensional optimization issues. Although these methods have proven effective, there is a limited amount of literature comparing and applying the GWO and HHO optimization approaches to real hybrid systems from Namibia. This study contributes to this area of research by presenting the optimization results of a hybrid energy system in a rural location of Namibia, using the HOMER software V 3.14.2 in conjunction with the HHO and GWO techniques. The aim is to minimize the global cost of the system while optimizing energy reliability, utilizing renewable resources, and sizing the hybrid system. A summary of the related work is presented in

Table 1. Summary of related studies on PV–WT–DG–battery system optimization.

Reference	Location	Objective Function	Methods
[18]	Nigeria	NPC, COE	HOMER
[19]	Jordan	Cost, reliability, renewable fraction	GWO
[20]	Egypt	LPSP, NPC, COE	HHO
[21]	Indonesia	Economic and environmental optimization	Multi-objective BAT
[22]	China	Cost minimization and reliability improvement	GA
[23]	Saudi Arabia	System sizing, COE, LPSP	Hybrid Optimization

. This study provides a comparison and a robust approach, using both conventional and artificial intelligence tools, to evaluate a renewable energy system for remote communities. This approach involves the following components:

• Energy model of a hybrid energy system with technical–economic model equations.
• Optimization based on HOMER Pro as a benchmark reference tool.
• Optimization with the GWO and HHO algorithms, derived from biological models and applied in MATLAB software to analyze solutions.
• A comparative analysis of the optimal sizing, the cost of energy (COE), the probability of loss of power supply (LPSP), and the reliability of the system is carried out to identify the best solution required for rural electricity supply.

Several studies have been carried out to optimize PV–wind–diesel–battery hybrid systems in different places. In Nigeria, [18] applied HOMER to minimize NPC and COE. In Jordan, [19] used Grey Wolf Optimizer (GWO) to maximize the cost, reliability, and the renewable energy contribution. Harris Hawks Optimization (HHO) was applied in Egypt in [20] to minimize the LPSP, NPC, and COE. A multi-objective BAT approach was used in Indonesia [21] to measure both emissions and costs. In China, [22] employed genetic algorithms (GAs) to enhance costs and reliability, while [23] suggested a hybrid approach in Saudi Arabia to improve the sizing, COE, and LPSP.

Over the past decade, several advanced metaheuristic approaches have been applied to optimization for hybrid energy system studies. Mathaba [24] used adaptive optimization methods to develop diesel–wind–solar–battery power systems in off-grid conditions. Hassanin and Hassan [25] investigated various optimization algorithms, such as Salp swarm optimization, for stand-alone PV–wind–diesel power systems in Egypt. Ukoima [26] conducted a study on a hybrid renewable energy system, and Alzahrani [27] for a standalone renewable energy system. However, the combined implementation of Grey Wolf Optimization (GWO) and Harris Hawks Optimization (HHO) is not well studied, especially in remote rural electricity supply. This study aims to address this issue by applying GWO and HHO to the optimum design of an adapted hybrid energy system for a remote village in Namibia.

2. Materials and Methods

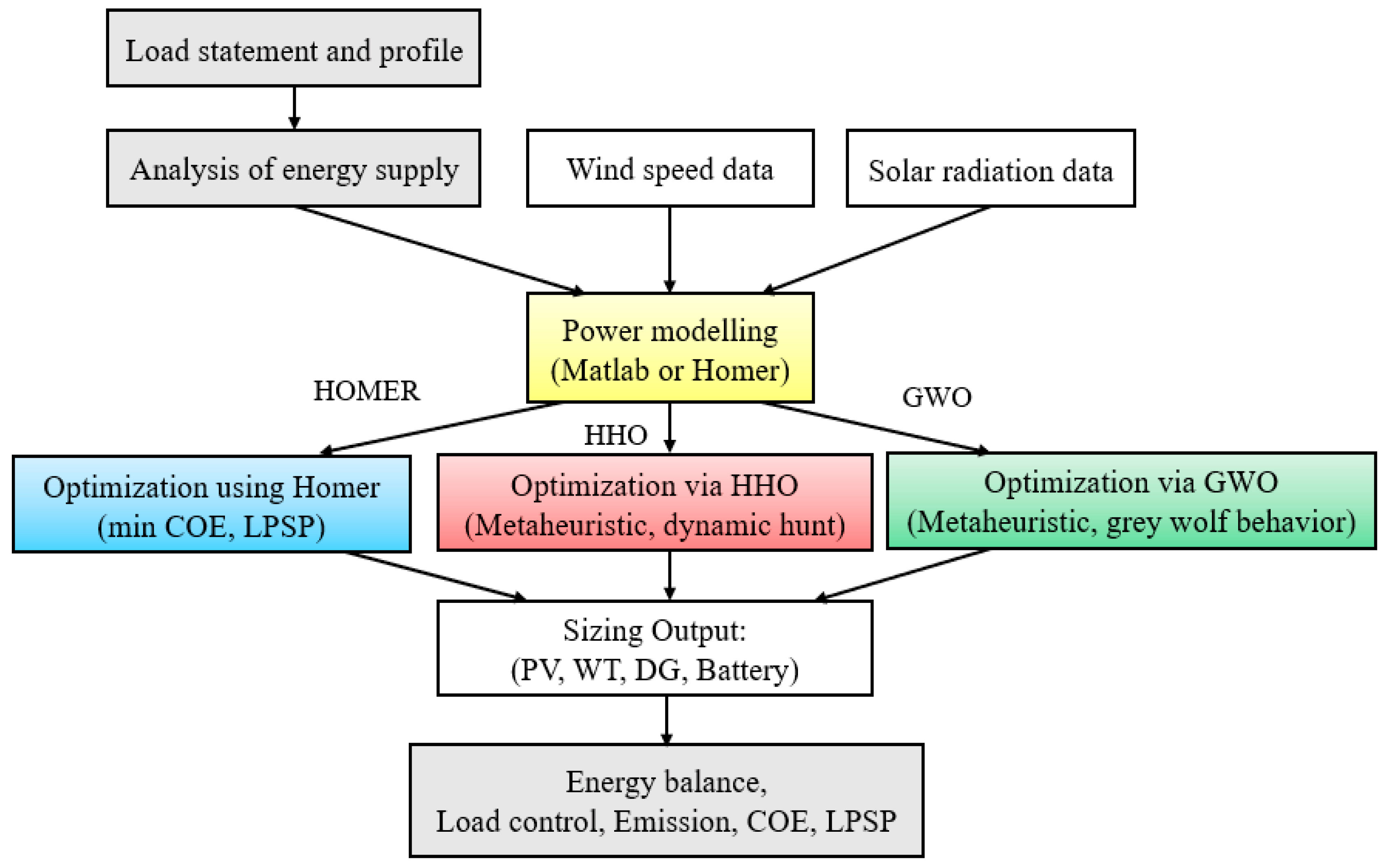
This study adopted the basic two-stage method for optimal hybrid system design at a rural site in Namibia. In the first step, HOMER V 3.14.2 software was used to carry out a technical–economic assessment and determine a feasible system configuration based on resource availability and basic constraints. This stage provided a baseline in terms of the component sizes and system cost. Advanced optimization methods were then applied using MATLAB to improve the system’s dimensioning and performance. The HHO and GWO methods were employed to identify the optimum number of solar–PV panels, DG capacity, storage batteries, and WTs. These methods aimed to minimize the key indicators of performance, such as NPC, COE, and LPSP.

The optimum configurations achieved by GWO and HHO were compared with the HOMER reference results. In addition, the optimal configurations have been tested in various weather conditions to evaluate the robustness and adaptability of the system design. Figure 1 shows the general framework of the research study.

2.1. Description of Namibia

Namibia, situated in the southwest of Africa, is extensively arid and semi-arid, which makes the country among the world’s sunniest. This plentiful supply of solar energy, coupled with wind power potential in some coastal and interior areas, provides exciting prospects for hybrid energy systems (HESs), especially in non-urban and remote rural villages with limited access to grid energy. This study selected a rural site in Namibia, which has a typical off-grid load demand profile, with an average base load of approximately 16.16 kW. 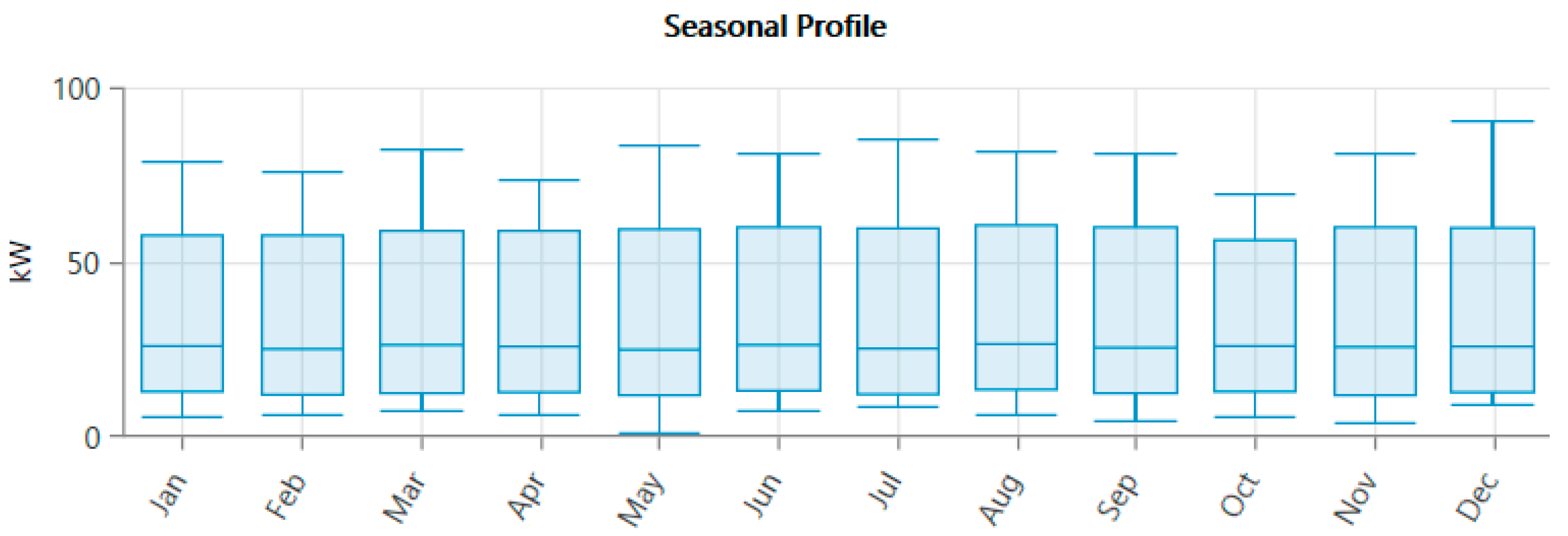Figure 2 presents the average daily load profile, characterized by three main consumption peaks: a morning peak from 7:00 to 8:00 am reaching 54.00 kW, a midday peak between 1:00 and 2:00 pm at 41.00 kW, and an evening peak between 7:00 and 8:00 pm. The overall daily peak load recorded for the area is 91.00 kW daily, and consumption is approximately 615 kWh/day.

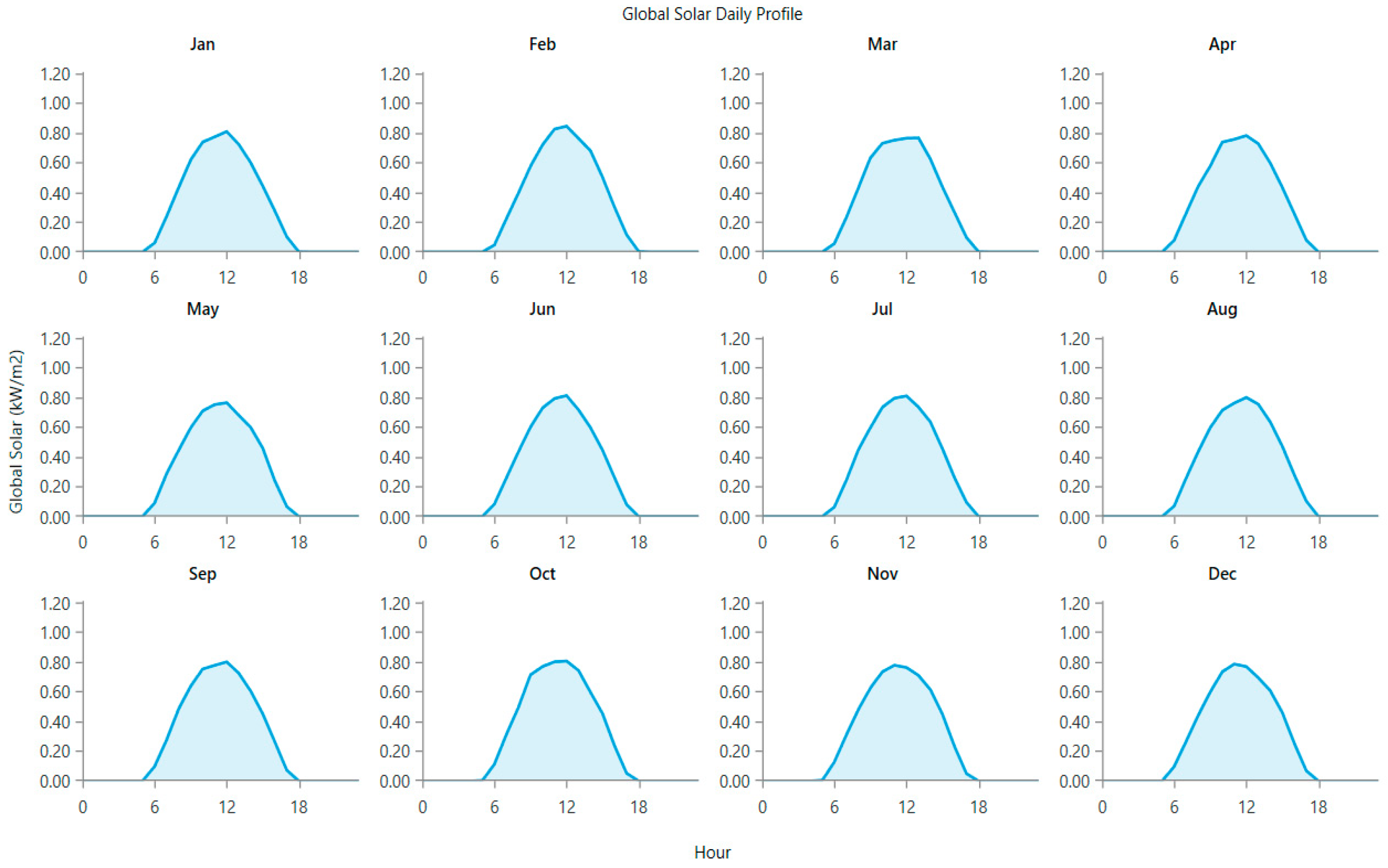
These characteristics make the location ideally placed for a hybrid energy system configuration, which is optimized to provide a cost-effective and reliable energy supply while exploiting the region’s renewable resources. Figure 3 shows the monthly profile of solar radiation over the study zone for one year. This profile is based on mean monthly data on solar radiation in the study site supplied by NASA [28]. The solar intensity is between 3.66 kWh/m²/day and 6.43 kWh/m²/day. 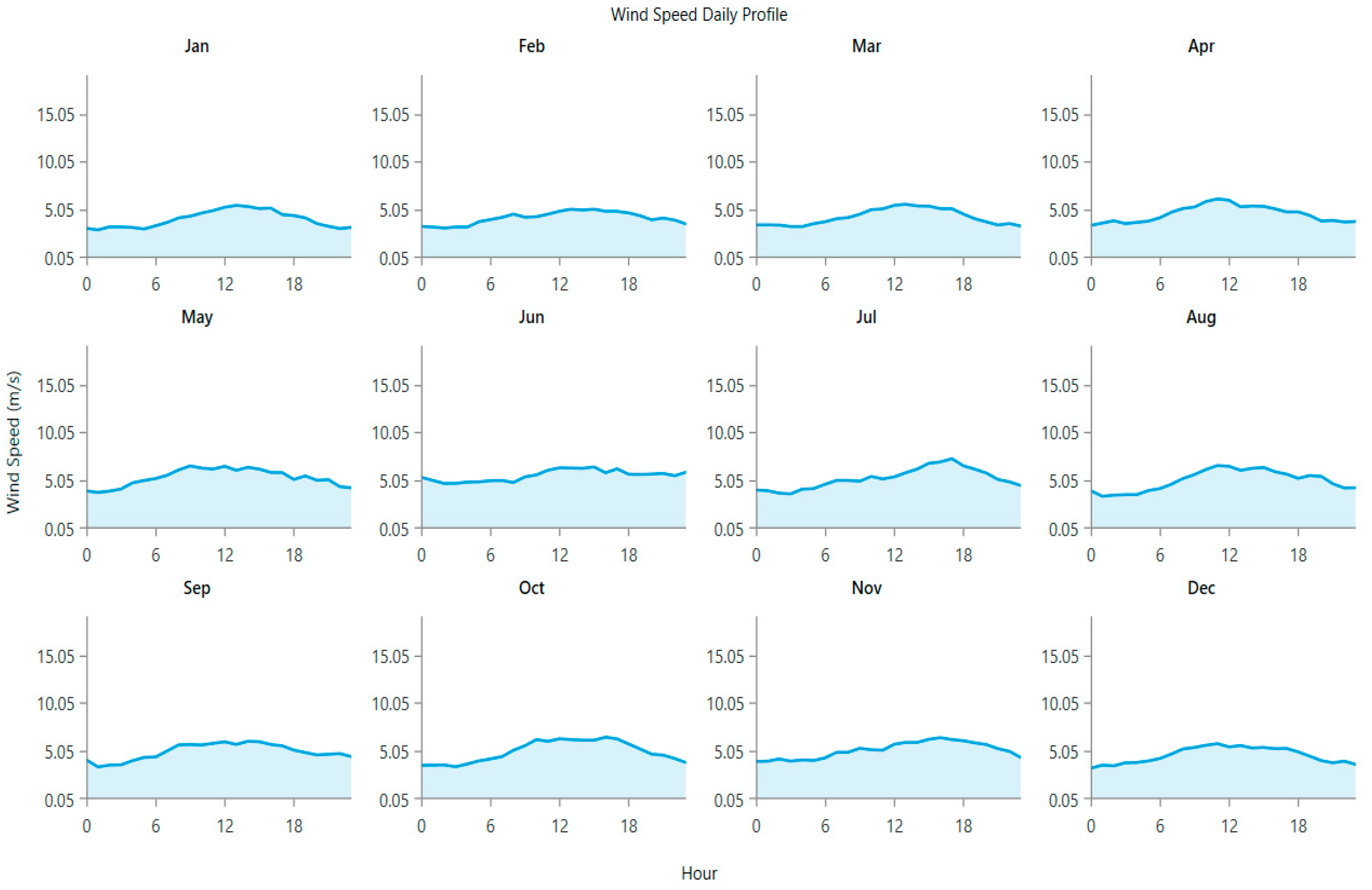Annual solar insolation is 5.13 kWh/m²/day. It is lowest in the winter season and highest in the summer season. The wind profile of the area under study over one year is shown in Figure 4. The average yearly wind speed recorded is approximately 3.5 m/s.

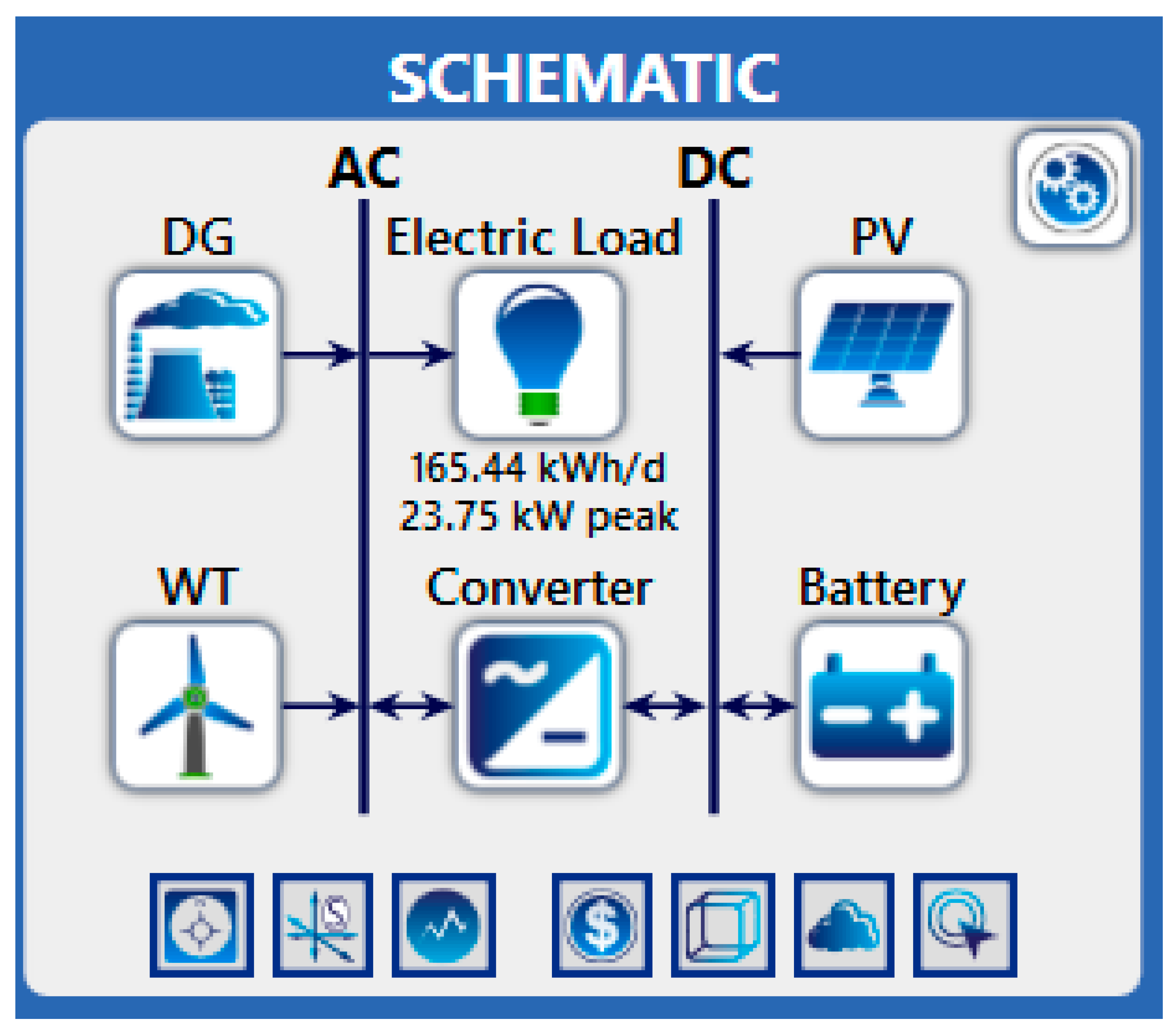
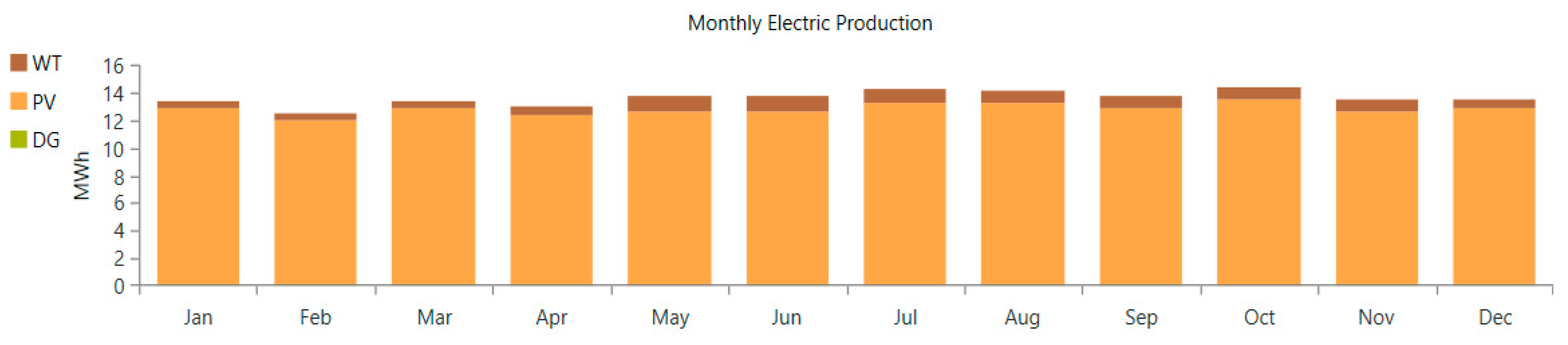
The energy supply system and the hybrid system at the Namibian site in southern Africa are shown in Figure 5. It consists of a solar–PV plant and a WT, which are used as a sustainable energy source. Back-up power supply is provided by a diesel generator in the event of insufficient power supply, while a battery farm provides compensation for production and converters.

2.2. System Modeling

Modeling of the hybrid energy system is designed to illustrate the dynamic performance of a photovoltaic–wind–diesel–battery microgrid designed to meet the requirements of a rural location in Namibia. The performance of the system can be evaluated with various weather parameters and with different charging profiles, using advanced optimization techniques. The data and costs for each source and formulation used for all hybrid system technical parameters, conversion models, and operational characteristics (PV, wind, diesel generator, and battery) are available in [25,26,27]. It was selected for its coherence with remote location conditions and the exhaustiveness of the data available covering the energy, economic, and dynamics data of each source.

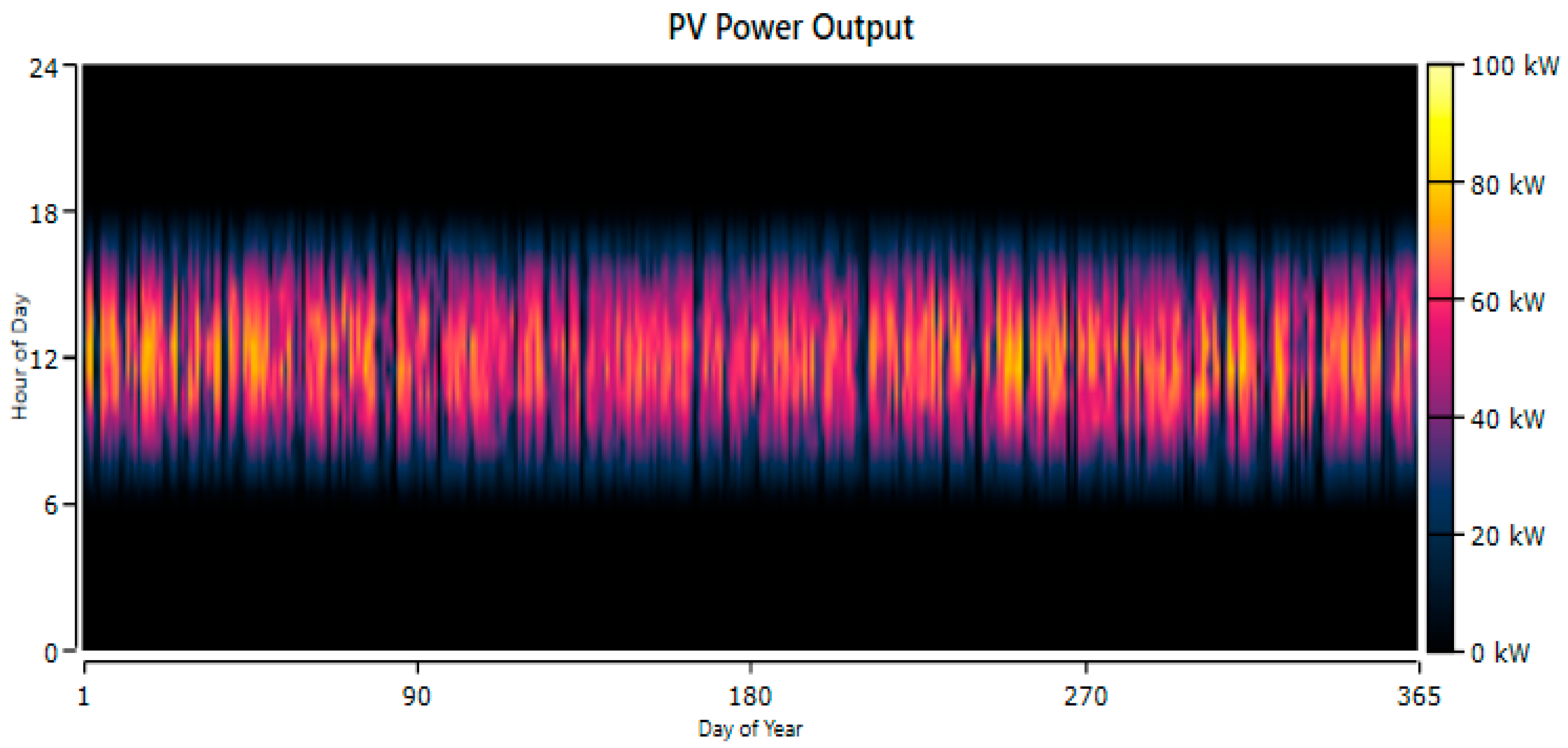
2.2.1. Models of Photovoltaic (PV) Panels

The power output from a solar–PV unit is dependent on the solar insolation and the temperature of the cells [29]:

$${\mathrm{P}}_{\mathrm{P}\mathrm{V}}\left(\mathrm{t}\right)={\mathrm{N}}_{\mathrm{P}\mathrm{V}}·{\mathrm{P}}_{\mathrm{P}\mathrm{V},\mathrm{r}\mathrm{e}\mathrm{f}}·\left({\displaystyle \frac{\mathrm{G}\left(\mathrm{t}\right)}{{\mathrm{G}}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}\right)·\left[1-{\mathrm{\alpha }}_{\mathrm{T}}·\left({\mathrm{T}}_{\mathrm{c}}\left(\mathrm{t}\right)-{\mathrm{T}}_{\mathrm{r}\mathrm{e}\mathrm{f}}\right)\right]$$

(1)

where N_PV indicates the number in the photovoltaic array, P_{PV, ref} is the rated power output of the array assuming G_ref = 1000 W/m², G (t) indicates the current radiation (W/m²), T_c (t) represents the temperature of the cells (°C), and α_T indicates the temperature coefficient of performance (%/°C).

2.2.2. Wind Turbine (WT) Model

The WT power output is represented by [29]:

$${\mathrm{P}}_{\mathrm{W}\mathrm{T}}\left(\mathrm{v}\right)=\left\{\begin{array}{c}0\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{if} \mathrm{v}<{\mathrm{v}}_{\mathrm{c}\mathrm{u}\mathrm{t}-\mathrm{i}\mathrm{n}}\\ {\mathrm{P}}_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}}·\left({\displaystyle \frac{{\mathrm{v}}^3-{\mathrm{v}}_{\mathrm{c}\mathrm{u}\mathrm{t}-\mathrm{i}\mathrm{n}}^3}{{\mathrm{v}}_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}}^3-{\mathrm{v}}_{\mathrm{c}\mathrm{u}\mathrm{t}-\mathrm{i}\mathrm{n}}^3}}\right)\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{if} {\mathrm{v}}_{\mathrm{c}\mathrm{u}\mathrm{t}-\mathrm{i}\mathrm{n}}\le \mathrm{v}<{\mathrm{v}}_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}}\\ \begin{array}{c}{\mathrm{P}}_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{if} {\mathrm{v}}_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}}\le \mathrm{v}<{\mathrm{v}}_{\mathrm{c}\mathrm{u}\mathrm{t}-\mathrm{o}\mathrm{u}\mathrm{t}}\\ 0\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{if} \mathrm{v}\ge {\mathrm{v}}_{\mathrm{c}\mathrm{u}\mathrm{t}-\mathrm{o}\mathrm{u}\mathrm{t}}\end{array} \end{array}\right.$$

(2)

where

v is the wind speed (m/s),

v_cut-in, v_rated, and v_cut-out are the characteristic speeds (m/s),

v_rated is the rated power of the WT.

2.2.3. Diesel Generator (DG) Model

The DG consumption of fuel depends on the loading [29]:

$$\begin{gathered} {\mathrm{F}}_{\mathrm{D}\mathrm{G}}\left(\mathrm{t}\right)=\mathrm{a}·{\mathrm{P}}_{\mathrm{D}\mathrm{G}}\left(\mathrm{t}\right)+\mathrm{b}·{\mathrm{P}}_{\mathrm{D}\mathrm{G},\mathrm{n}\mathrm{o}\mathrm{m}} \\ {\mathrm{P}}_{\mathrm{D}\mathrm{G}}\left(\mathrm{t}\right)=\left\{\begin{array}{c}0\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{if} \mathrm{SOC}>{\mathrm{S}\mathrm{O}\mathrm{C}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\\ {\mathrm{P}}_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}\left(\mathrm{t}\right)-{\mathrm{P}}_{\mathrm{R}\mathrm{E}\mathrm{S}}\left(\mathrm{t}\right)\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{if} {\mathrm{P}}_{\mathrm{R}\mathrm{E}\mathrm{S}}<{\mathrm{P}}_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}\end{array}\right. \end{gathered}$$

(3)

where

F_DG represents the fuel consumption per hour (L/h),

A and b represent specific coefficients of the generator,

P_DG,nom represents the rated power of the generator,

P_RES represents the combined solar photovoltaic and wind power generation,

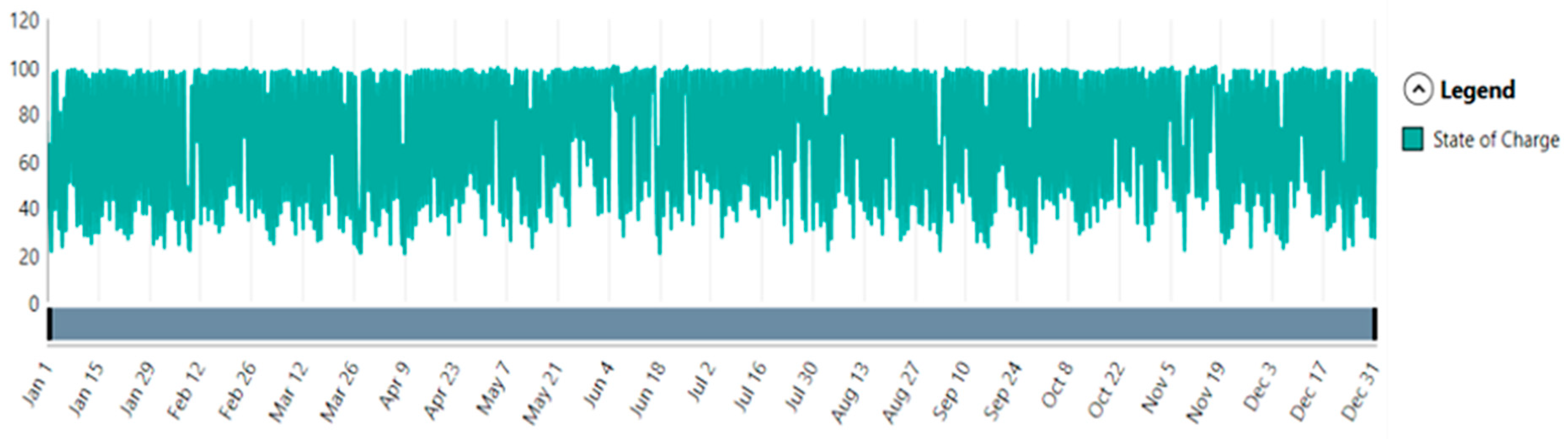
SOC is the battery state of charge.

2.2.4. Model of Battery Energy Storage System (BESS)

The SOC is modeled as in [29]:

$$\mathrm{S}\mathrm{O}\mathrm{C}\left(\mathrm{t}+1\right)=\mathrm{S}\mathrm{O}\mathrm{C}\left(\mathrm{t}\right)+{\displaystyle \frac{{\mathrm{\eta }}_{\mathrm{c}}·{\mathrm{P}}_{\mathrm{c}\mathrm{h}}\left(\mathrm{t}\right)-\frac{{\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{s}}\left(\mathrm{t}\right)}{{\mathrm{\eta }}_{\mathrm{d}}}}{{\mathrm{C}}_{\mathrm{b}\mathrm{a}\mathrm{t}}}}$$

(4)

where

P_ch (t) and P_dis (t) represent the charging and discharging output (kW),

η_c and η_d are the charging and discharging efficiency,

C_bat represents the nominal battery capacity (kWh).

2.3. Optimization Problem Formulation

The optimum system configuration for a hybrid solar–PV, DG, WT, and battery energy storage system (BAT) should provide an optimal solution for the power requirements of a rural, isolated zone. To meet these requirements, a multi-objective approach to optimize the system has been implemented, incorporating technical, economic, reliability, and environmental factors. It considers three different objective functions at the same time:

• Minimize the average COE (LCOE).
• Minimize LPSP.
• Maximize the renewable energy fraction (RF).

The problem’s mathematical formulation is shown in Equation (5):

$${\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathrm{x}}\left\{\begin{array}{c}{\mathrm{f}}_1\left(\mathrm{x}\right)=\mathrm{COE}\left(\mathrm{x}\right)\\ {\mathrm{f}}_2\left(\mathrm{x}\right)=\mathrm{LPSP}\left(\mathrm{x}\right)\\ {\mathrm{f}}_3\left(\mathrm{x}\right)=\mathrm{RF}\left(\mathrm{x}\right)\end{array}\right.$$

(5)

where

X = [P_PV, P_WT, P_DG, E_bat, P_inv] is the vector of the decision parameters, representing the power output of the PV, WT, DG, BAT, and the inverter, respectively.

The objective function can be defined as the discounted cost of energy (COE, and is obtained as [25,26,27]):

$$\mathrm{C}\mathrm{O}\mathrm{E}={\displaystyle \frac{{\mathrm{C}}_{\mathrm{t}\mathrm{o}\mathrm{t}}}{{\mathrm{E}}_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d},\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{d}}}}$$

(6)

where

C_tot represents the discounted total cost for the system during the project lifespan,

E_load,served represents the electrical energy supplied to the load.

The LPSP probability [25,26,27] is given by:

$$\mathrm{L}\mathrm{P}\mathrm{S}\mathrm{P}={\displaystyle \frac{{\sum }_{\mathrm{t}=1}^{\mathrm{T}}{\mathrm{E}}_{\mathrm{d}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{t}}\left(\mathrm{t}\right)}{{\sum }_{\mathrm{t}=1}^{\mathrm{T}}{\mathrm{E}}_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}\left(\mathrm{t}\right)}}$$

(7)

where

E_deficit (t) corresponds to the energy unmet at time t,

E_load (t) corresponds to the demand for energy.

The renewable fraction (RF) corresponds to the proportion of renewable energy resources in the overall generation and is given as [25,26,27]:

$$\mathrm{R}\mathrm{F}={\displaystyle \frac{{\mathrm{E}}_{\mathrm{P}\mathrm{V}}+{\mathrm{E}}_{\mathrm{W}\mathrm{T}}}{{\mathrm{E}}_{\mathrm{P}\mathrm{V}}+{\mathrm{E}}_{\mathrm{W}\mathrm{T}}+{\mathrm{E}}_{\mathrm{D}\mathrm{G}}}}$$

(8)

The following technical constraints must be met (boundary conditions):

$$\begin{gathered} {\mathrm{S}\mathrm{O}\mathrm{C}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\le \mathrm{S}\mathrm{O}\mathrm{C}\left(\mathrm{t}\right)\le {\mathrm{S}\mathrm{O}\mathrm{C}}_{\mathrm{m}\mathrm{a}\mathrm{x}} \\ {\mathrm{P}}_{\mathrm{P}\mathrm{V}},{\mathrm{P}}_{\mathrm{W}\mathrm{T}},{\mathrm{P}}_{\mathrm{D}\mathrm{G}},{\mathrm{E}}_{\mathrm{b}\mathrm{a}\mathrm{t}},{\mathrm{P}}_{\mathrm{i}\mathrm{n}\mathrm{v}}\ge 0 \\ \mathrm{L}\mathrm{P}\mathrm{S}\mathrm{P}\le {\mathrm{L}\mathrm{P}\mathrm{S}\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}} \end{gathered}$$

(9)

Constraints

The total energy generated must satisfy or surpass the demand:

$${\mathrm{E}}_{\mathrm{P}\mathrm{V}}+{\mathrm{E}}_{\mathrm{W}\mathrm{T}}+{\mathrm{E}}_{\mathrm{D}\mathrm{G}}+{\mathrm{E}}_{\mathrm{B}\mathrm{a}\mathrm{t}}\ge {\mathrm{E}}_{\mathrm{L}\mathrm{o}\mathrm{a}\mathrm{d}}$$

(10)

The components of the system have been designed according to their relative capacity limitations to guarantee their operational viability.

$$\begin{gathered} 0\le {\mathrm{P}}_{\mathrm{P}\mathrm{V}}\le {\mathrm{P}}_{\mathrm{P}\mathrm{V}}^{\mathrm{m}\mathrm{a}\mathrm{x}} \\ 0\le {\mathrm{P}}_{\mathrm{W}\mathrm{T}}\le {\mathrm{P}}_{\mathrm{W}\mathrm{T}}^{\mathrm{m}\mathrm{a}\mathrm{x}} \\ 0\le {\mathrm{P}}_{\mathrm{D}\mathrm{G}}\le {\mathrm{P}}_{\mathrm{D}\mathrm{G}}^{\mathrm{m}\mathrm{a}\mathrm{x}} \\ 0\le {\mathrm{P}}_{\mathrm{B}\mathrm{a}\mathrm{t}}\le {\mathrm{P}}_{\mathrm{B}\mathrm{a}\mathrm{t}}^{\mathrm{m}\mathrm{a}\mathrm{x}} \end{gathered}$$

(11)

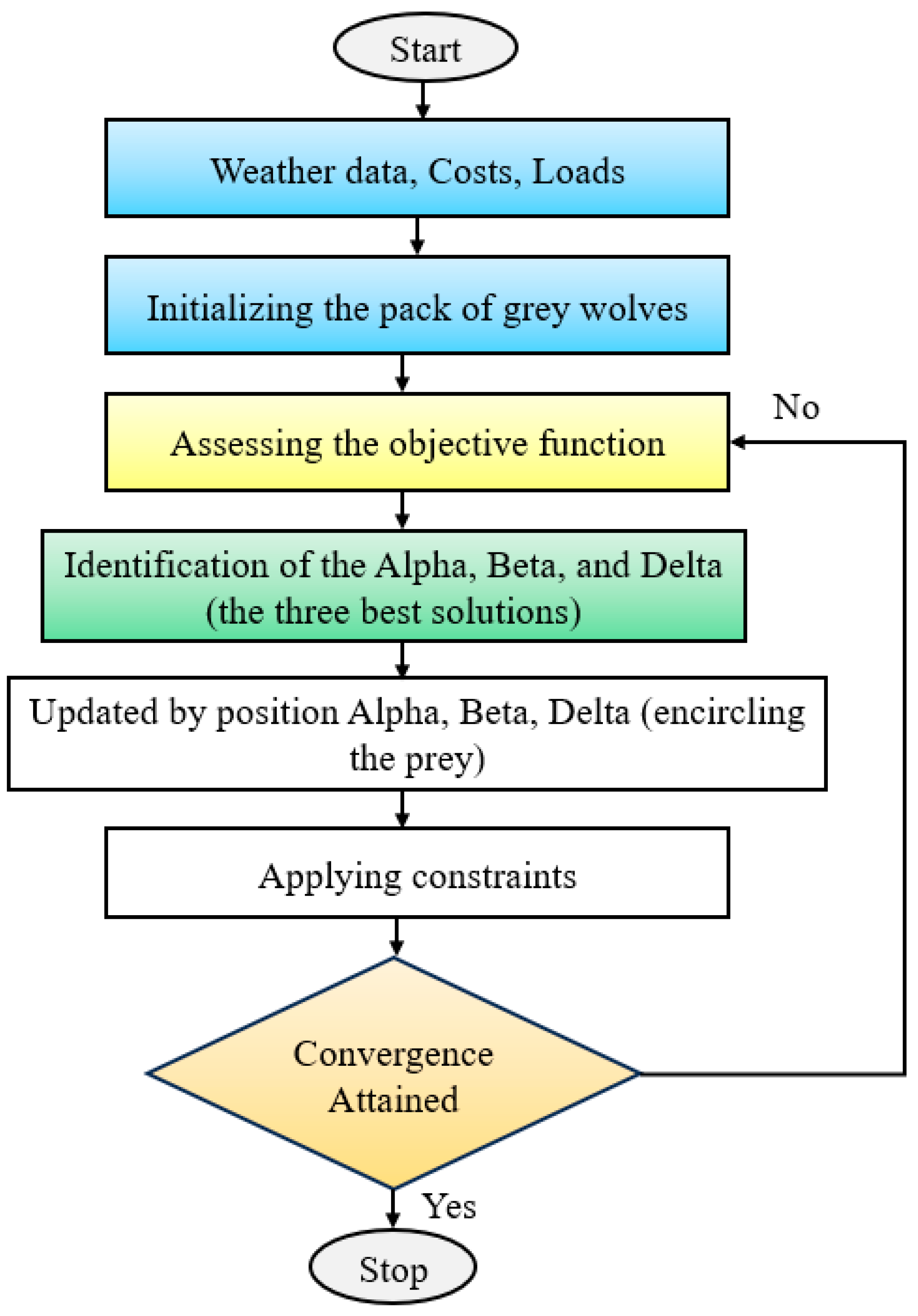
2.4. The Grey Wolf Optimizer Methods

GWO is a metaheuristic approach that is based on nature [30]. The GWO algorithm simulates the command hierarchy and behavior of natural grey wolves. This algorithm is noted for its robust simplicity, high global finding capacity, and effectiveness at resolving complicated optimization issues using minimum parameter settings.

In GWO, there are four hierarchical population levels, namely, alpha (α), beta (β), delta (δ), and omega (ω). The three most successful wolves (α, β, and δ) provide search guidance, while the remainder of the population (ω) discounts positions according to the leads. The process of hunting is modeled in mathematical terms by the mechanics of circling, attack, and prey search.

The position of each wolf symbolizes a feasible solution within the study area, and the target is the optimum of the objective function. During iterations, wolves approach the position of the prey to update their positions, under the guidance of the top three wolves. This balance of exploration and exploitation guarantees the convergence to the global optimum and prevents premature convergence.

The mechanism of position updating is ruled by [30,31] Equation (12):

$$\begin{gathered} \overrightarrow{\mathrm{D}}=\left|\overrightarrow{\mathrm{C}}·\overrightarrow{{\mathrm{X}}_{\mathrm{p}}}\left(\mathrm{t}\right)-\overrightarrow{\mathrm{X}}\left(\mathrm{t}\right)\right| \\ \overrightarrow{\mathrm{X}}\left(\mathrm{t}+1\right)=\overrightarrow{{\mathrm{X}}_{\mathrm{p}}}\left(\mathrm{t}\right)-\overrightarrow{\mathrm{A}}·\overrightarrow{\mathrm{D}} \end{gathered}$$

(12)

where

$\overrightarrow{{\mathrm{X}}_{\mathrm{p}}}$ is the position vector of the prey (best solution).

$\overrightarrow{\mathrm{X}}$ is the current position vector of the grey wolf.

$\overrightarrow{\mathrm{A}}$ and $\overrightarrow{\mathrm{C}}$ are both the coefficient vectors defined as follows [31]:

$$\begin{gathered} \overrightarrow{\mathrm{A}}=2\overrightarrow{\mathrm{a}}·\overrightarrow{{\mathrm{r}}_1}-\overrightarrow{\mathrm{a}} \\ \overrightarrow{\mathrm{C}}=2·\overrightarrow{{\mathrm{r}}_2} \end{gathered}$$

(13)

In this case, $\overrightarrow{\mathrm{a}}$ reduces linearly over iterations from 2 to 0, and $\overrightarrow{{\mathrm{r}}_1}$, $\overrightarrow{{\mathrm{r}}_2}$ ∈ [0,1] represents a random vector.

By iteratively adjusting the positions, GWO imitates the smart cooperative chasing strategies of grey wolves to efficiently achieve an optimum or near-optimum solution. Figure 6 shows the description of the GWO methods.

The main parameters of the GWO algorithm are population size and iterations. In order to ensure a fair comparison with HHO, the population sizes of 30 and 100 iterations have been implemented. They were determined from initial simulations and are consistent with [31,32]. In GWO, the control parameters ‘a’ were linearly reduced between 2 and 0, in line with the original wording, and no adjustment was required.

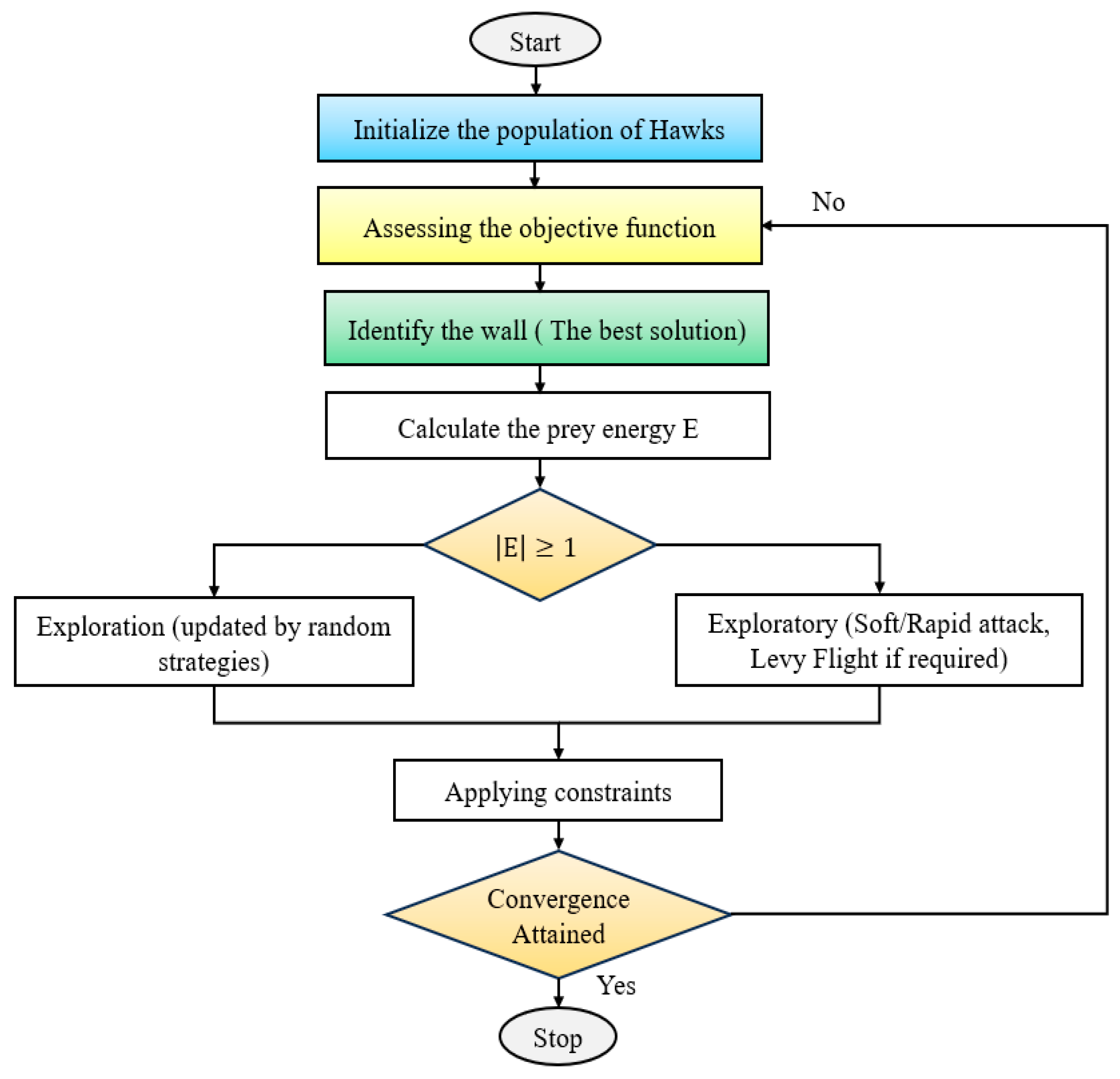
2.5. Harris Hawks Optimization Methods

The HHO algorithm is a population-based metaheuristic introduced by Heidari et al. [32] in 2019, based on the collaborative Harris’s hawk hunting strategy. These raptors display an intelligent and adaptable hunting behavior, often encircling and engaging their prey in a coordinated fashion. HHO mathematically models this dynamic behavior to solve complex optimization problems with high accuracy and robust convergence.

This algorithm provides a simulation of the exploratory and exploitative phases, depending on the prey’s energy and escape patterns. During the search phase, the falcons carry out a systematic random search for the prey in the solution space to keep the population diverse. When the target has been found, they enter the exploitation phase, where different strategies, such as gentle besieging, hard besieging, and fast diving, are used depending on the prey’s energy of escape. The phase transition is controlled by the prey’s escape energy (E), which can be described in [32]:

$$\mathrm{E}=2{\mathrm{E}}_0\left(1-{\displaystyle \frac{\mathrm{t}}{\mathrm{T}}}\right)$$

(14)

where

E₀ represents the prey’s starting energy (a random number within [−1,1]),

t represents the current iteration,

T represents the maximum iteration number.

The hawks are updating positions using a variety of different strategies according to both the value of E and a random probability r ∈ [0,1]:

• Soft seat (|E| ≥ 0.5 and r ≥ 0.5) [15]:

  $${\mathrm{X}}_{\mathrm{t}+1}=∆{\mathrm{X}}_{\mathrm{t}}-\mathrm{E}·\left[\mathrm{J}·{\mathrm{X}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{y}}-{\mathrm{X}}_{\mathrm{t}}\right]$$

  (15)
• Hard besiege (|E| < 0.5 and r ≥ 0.5) [15]:

  $${\mathrm{X}}_{\mathrm{t}+1}={\mathrm{X}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{y}}-\mathrm{E}·\left|∆{\mathrm{X}}_{\mathrm{t}}\right|$$

  (16)
• Soft seat with progressive fast dives (|E| ≥ 0.5 and r < 0.5) [15]:

  $${\mathrm{X}}_{\mathrm{t}+1}={\mathrm{X}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{y}}-\mathrm{E}·\left|\mathrm{J}·{\mathrm{X}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{y}}-{\mathrm{X}}_{\mathrm{t}}\right|+\mathrm{S}·\mathrm{L}\mathrm{F}\left(\mathrm{D}\right)$$

  (17)
• Hard seat with dips (|E| < 0.5 and r < 0.5) [15]:

$${\mathrm{X}}_{\mathrm{t}+1}={\mathrm{X}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{y}}-\mathrm{E}·\left|∆{\mathrm{X}}_{\mathrm{t}}\right|+\mathrm{S}·\mathrm{L}\mathrm{F}\left(\mathrm{D}\right)$$

(18)

where

X_t+1 represents the current position,

X_prey stands for the optimal solution found (prey),

ΔX_t is the difference between the prey and the falcon,

J is a random jump force,

LF(D) represents Lévy’s flight component.

Figure 7 shows a description of HHO.

The HHO algorithm’s main parameters comprise the size of a population and the number of iterations. For this study, the population values of 30 and 100 iterations were used. The values were selected according to the standard procedures detailed in [15] and after some tests, which demonstrated a reasonably good convergence performance at an attractive computation rate. The exhaust energy and the random coefficients in HHO are based on the definitions given in [32] and are unchanged.

3. Results

With HOMER Pro V 3.14.2 software and algorithms, GWO and HHO were used to perform simulations based on different scenarios of interconnected energy system sub-units. These methods were used to optimize the size of the various system components and determine the technical and economic performance of the proposed solutions. The cost of energy (COE) was used as the principal parameter for determining which option was the best in each case. The following subsections present the optimization results, including the economic and technical characteristics of the model studied.

3.1. Result by Homer Pro V 3.14.2 Software

Table 2. Electrical result for the hybrid system.

Electrical	Element	kWh/y	%
Production	PV	152,666	93.6
	Wind Turbine	9592	5.88
	DG	840	0.515
	Total	163,099	100
Consumption	AC Load	60,386	100
	Total	60,386
Quantity	Excess Electricity	93,074	57.1
	Capacity Shortage	33	0.0546

shows the results of the analysis of the energy system. The WT generates 60.8% of the electricity. The excess electricity, unserved load demand, and the capacity shortage are given as 393,722, 164, and 272 kWh/year, respectively.

Table 3. Energy system annual emissions report.

Quantity	Value	Units
Carbone Dioxide	847	kg/yr
Carbone Monoxide	6.41	kg/yr
Unburned Hydrocarbons	0.234	kg/yr
Particulate Matter	0.389	kg/yr
Sulfur Dioxide	2.08	kg/yr
Nitrogen Oxides	7.28	kg/yr

shows the yearly discharge of pollutants resulting from the system. Carbon dioxide (CO₂) is the main emission, with 847 kg/year, which indicates a substantial greenhouse gas emission impact. The other air pollutants comprise carbon monoxide (6.41 kg/year), nitrogen oxides (7.28 kg/year), and sulfur dioxide (2.08 kg/year), known for having an impact both on air safety and human health. The emissions of particulate pollutants (0.389 kg/year) and of unburnt hydrocarbons (0.234 kg/year) are relatively low. With these results, we can evaluate the system’s environmental performance measured by emissions of pollutants.

Figure 8 illustrates the economic flows of the system for 25 years. An initial investment cost of USD 85,000 is incurred. There are periodic fuel costs (approximately USD 30,000) at 4-year intervals, with a salvage cost of around USD 40,000 recorded at the system’s life. There are no significant operating or replacement costs. The overall system component cost is shown in

Table 4. Total cost of hybrid system components [29].

Component	Capital (USD)	Replacement (USD)	Fuel (USD)	Salvage (USD)	Total (USD)
PV	25,596.42	0	0	0	45,825.09
DG	3000.00	0	10,765.71	2788.10	12,139.34
Battery	45,600.00	240,681.37	0	20,441.96	299,474.27
WT	9000.00	0	0	0	28,915.38
System Converter	6085.27	5025.28	0	3592.88	12,006.21
System	89,281.69	245,706.66	10,765.71	26,822.94	398,360.30

($ is USD).

Based on the HOMER optimization result, the optimized sizing of the hybrid system components is selected based on optimal economics, as shown in

Table 5. Cost summary.

Cost	Base System	Optimal System
NPC (USD)	918,357	398,360
Initial Capital (USD)	20,622	89,282
LCOE (USD/kWh)	0.687	0.298

. As a stand-alone system, the penetration of renewable energy represents 100%, which can be observed from Figure 9.

Figure 10 shows the monthly electricity production estimated for the optimum configuration for each power source. Figure 11 shows the photovoltaic system’s hourly output over the year. The production peak occurs from 6 a.m. to 6 p.m., around midday, when the sun is most intense. Output is generally highest in summer (~180th day) but lowest during the winter, reflecting variations in sunshine levels over the year. The figure also illustrates the daily variations caused by changing meteorological factors. Figure 12 shows the inverter’s power and generation output profile over one year, with a 28.6% power factor in the inverter and a 0.140% power factor in the rectifier.

Figure 13 shows the yearly variation by state of charge and demonstrates stability, with an SoC usually ranging from 20% to 100%, reflecting the efficient management of storage. There are a few seasonal decreases, notably from March to June, but this does not affect the overall availability of the system.

3.2. Results by GWO and HHO Methods

Figure 14 shows a comparison based on the yearly energy source contribution of two optimization approaches, GWO and HHO. For both methods, solar power (PV) comes first, with a slightly larger contribution from GWO (58%) as compared than from HHO (54.1%). HHO makes greater demands on diesel generators (22.8% compared with 20.8%) and batteries (13.7% compared with 12.5%). Wind power (WT) accounts for a small proportion of both. GWO is favorable to solar power, while HHO has a more balanced distribution.

Table 6. Results based on economic and technical factors and optimum sizing using the proposed algorithm.

Proposed HERS	Method	COE (USD/kWh)	LPSP (%)	RF (%)	Nad	Ppv (kW)	NWT	Nbat
Hybrid system	GWO	0.268	0.234	87.79	5	161.54	8	9
	HHO	0.276	0.715	82.85	4	156.58	9	8
	Homer	0.298	--	98.6	--	91.4	3	152

compares the performances of the different hybrid systems (HERSs), which were analyzed by three methods: GWO, HHO, and HOMER. The results show that the GWO-based system provided the most cost-effective technical solution, offering a COE value of USD 0.268/kWh, with an LPSP of 0.234% and a relatively high reliability factor (RF) of 87.79%. The HHO-based system shows a higher COE (USD 0.276/kWh) and a lower reliability (82.85%). However, the system generated by HOMER, although very reliable (RF = 98.6%), has a significantly higher COE (USD 0.98/kWh), which makes it less economical.

4. Conclusions

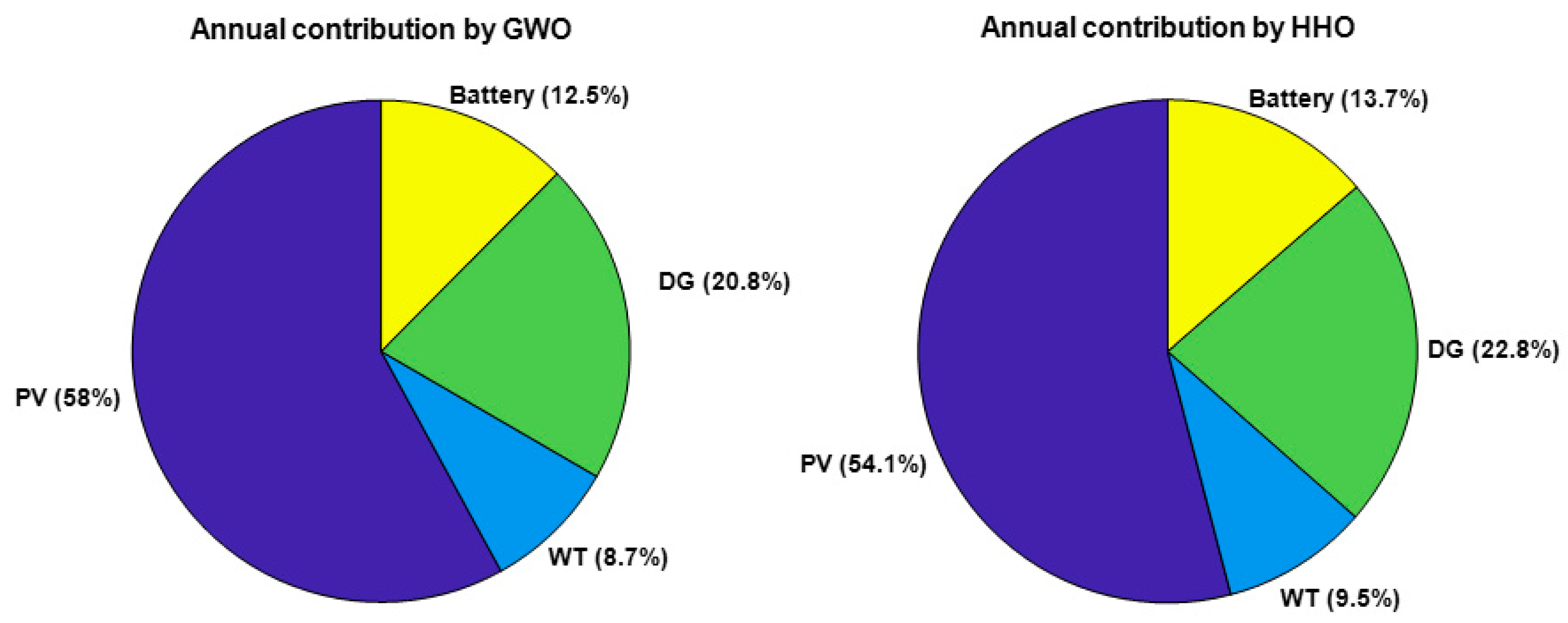
This study concentrated on the optimum sizing of a hybrid energy system that combined solar–PV, WT, DG, and storage batteries to supply an isolated rural community. Three approaches were used: HOMER Pro V 3.14.2 and two bio-inspired artificial intelligence approaches, namely, Grey Wolf Optimizer (GWO) and Harris Hawks Optimization (HHO). The main results of this study are as follows:

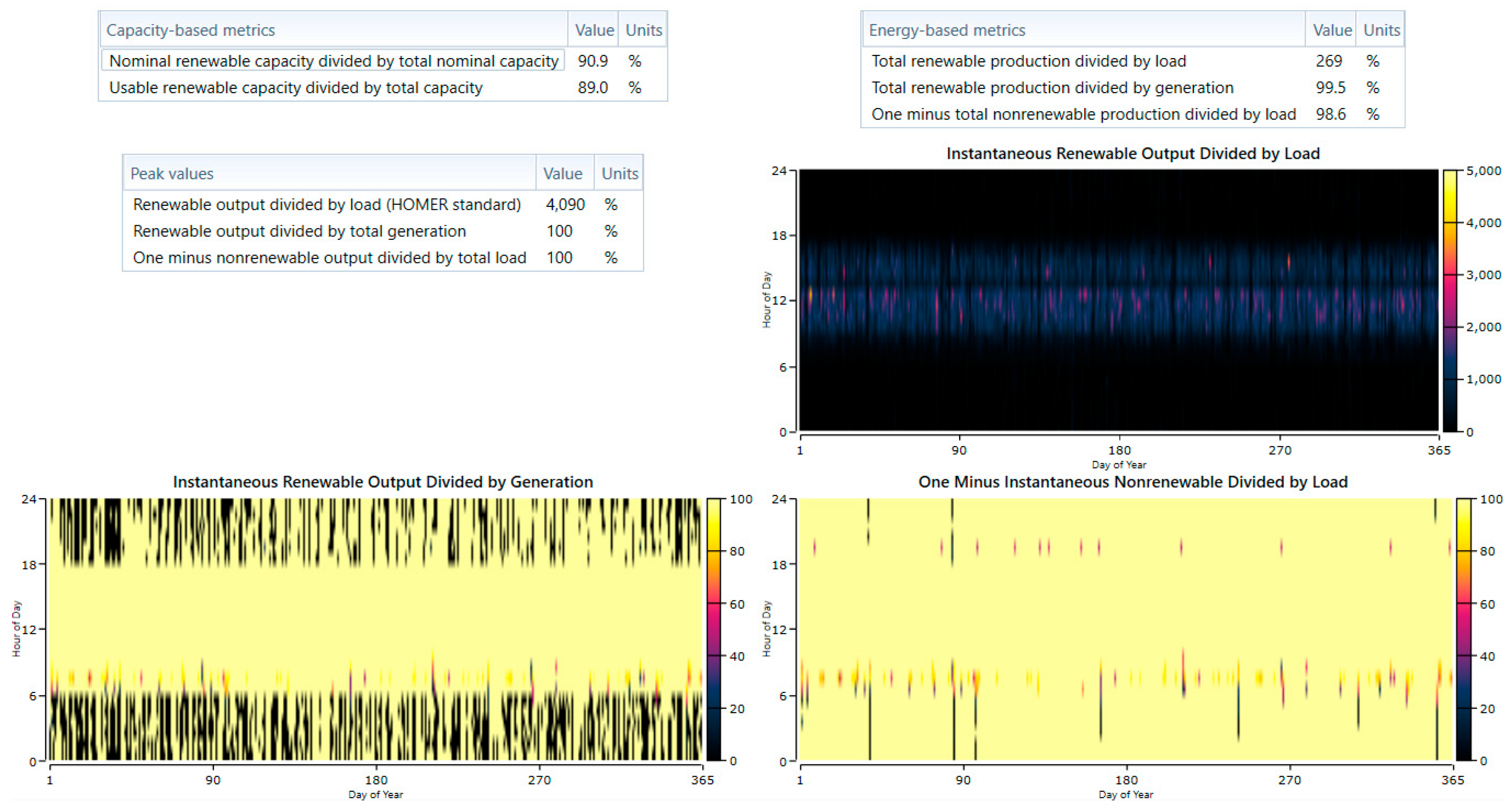
• The GWO and HHO approaches both achieved optimum systems configurations with a cost of energy (COE) of between USD 0.268 and USD 0.276/kWh.
• The loss of power supply probability (LPSP) was less than 1%, providing a reliable power system.
• Based on the solution, the smart methods resulted in a more cost-effective system, while the HOMER configuration achieved a COE of USD 0.298/kWh under more conservative battery capacity.
• Computational intelligence strategies are efficient for hybrid system design in remote regions.

Further research may consider the incorporation of alternative renewables and advanced energy management strategies to improve the system’s overall performance and flexibility in various environments.

This study concentrated on the optimum dimensioning of a hybrid energy system that combined solar–PV, WT, DG, and storage batteries to supply an isolated rural site. Three approaches were used: simulation with HOMER Pro V 3.14.2 and two bio-inspired artificial intelligence approaches, specifically Grey Wolf Optimizer (GWO) and Harris Hawks Optimization (HHO).

The results indicated that both the GWO and HHO approaches resulted in optimal system configurations that achieved a COE in the range of USD 0.268 to USD 0.276/kWh and an LPSP below 1%, ensuring high system availability and reliability. In comparison, with the HOMER method, a more conservative battery capacity configuration resulted in a COE of USD 0.298/kWh.

Our results demonstrate the value of computational intelligence approaches for designing suitable hybrid systems for remote sites. In the future, incorporating based on dynamic loading patterns, real-time optimization, and the cross-utilization between algorithms is a promising avenue for continuously improving the energy and financial efficiency of stand-alone systems.