Coordinated Control of a Hybrid Energy Storage System for Improving the Capability of Frequency Regulation and State-of-Charge Management
Abstract
1. Introduction
- An HESS control method with SOC management for FR application.
- Power allocation of an SC and battery in the HESS based on the coverage of the frequency band.
- Guideline for HESS sizing based on the proposed method.
- Investigation of battery lifetime extension in the HESS using SOH calculation.
2. Frequency Regulation Using a Hybrid Energy Storage System
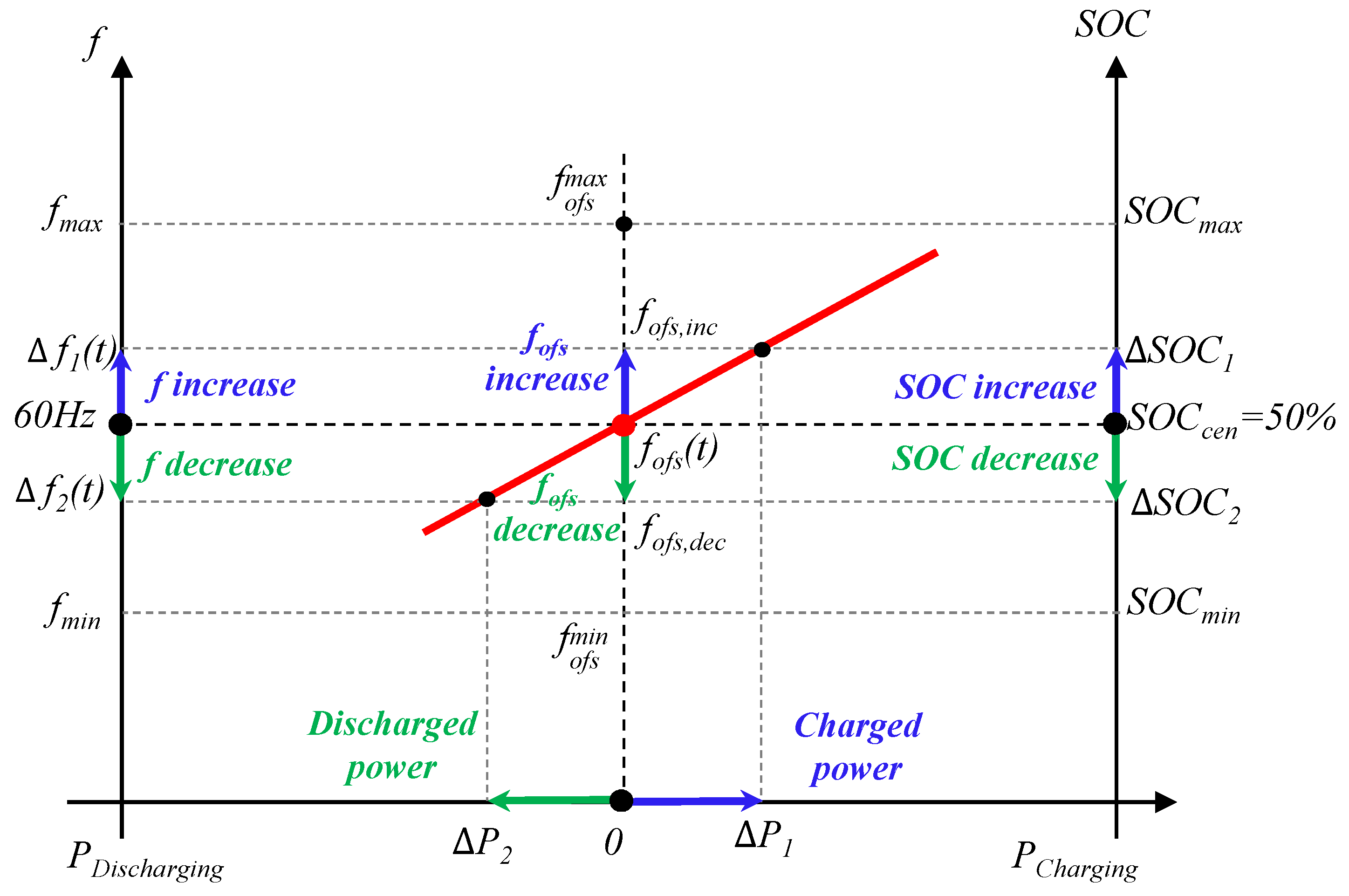
2.1. Droop Control with SOC Feedback: Review
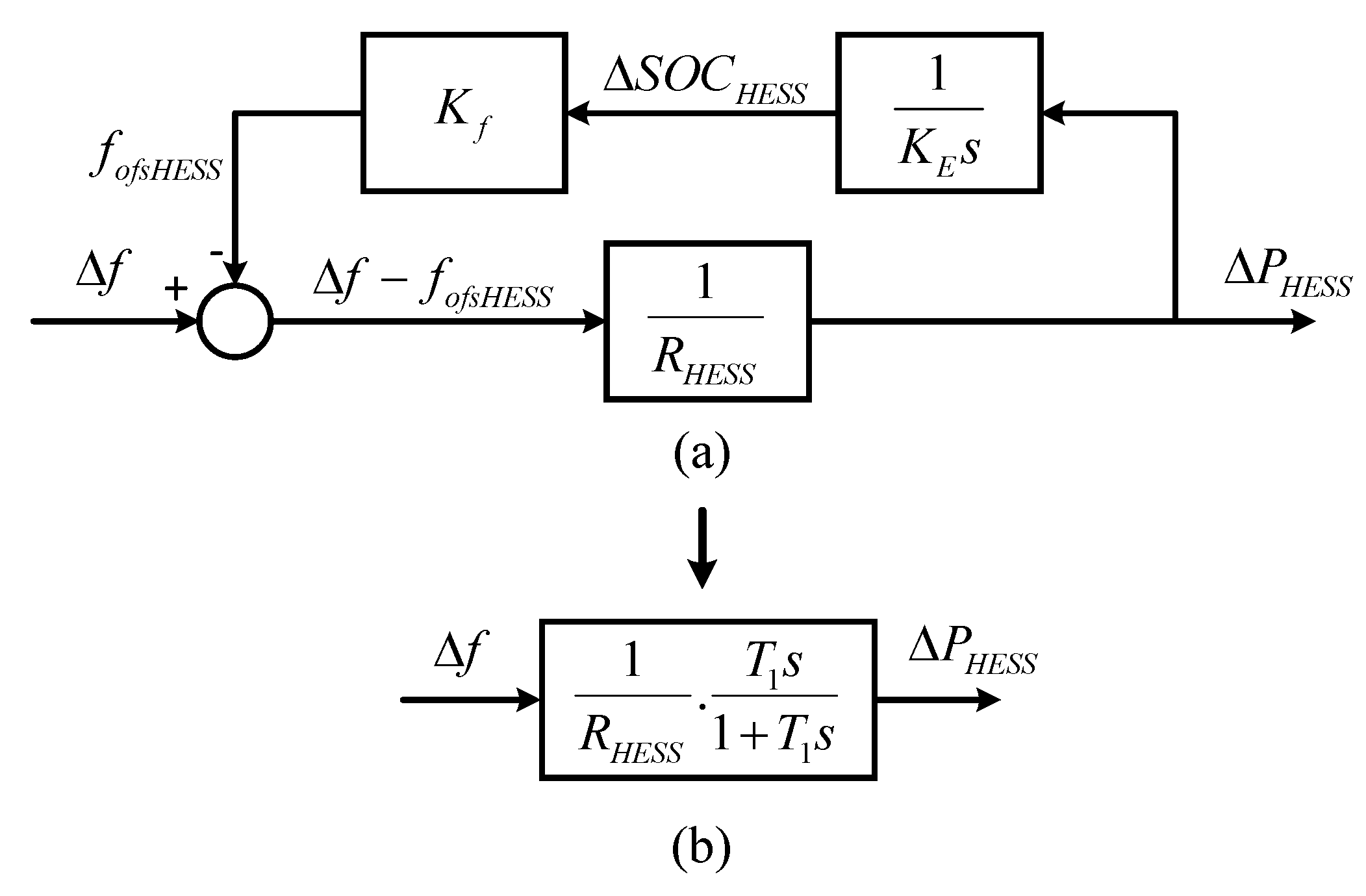
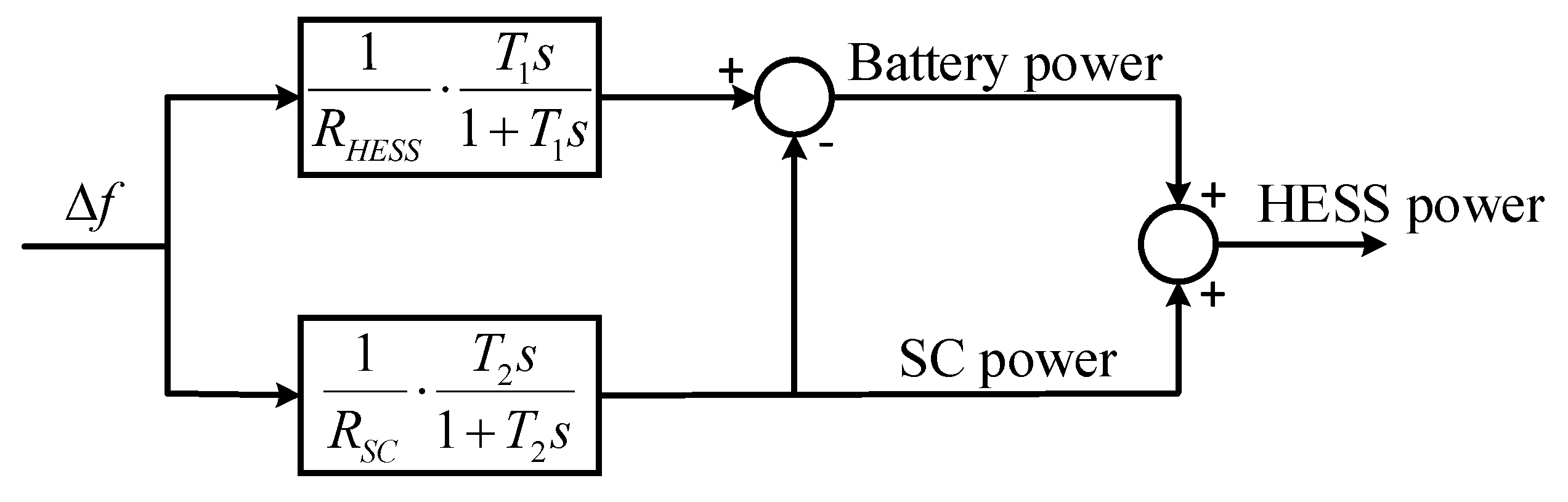
2.2. Proposed HESS Operation for FR
2.2.1. Proposed Hybrid ESS Operation Method
2.2.2. Proposed Supercapacitor Operation Method
2.2.3. Battery Operation
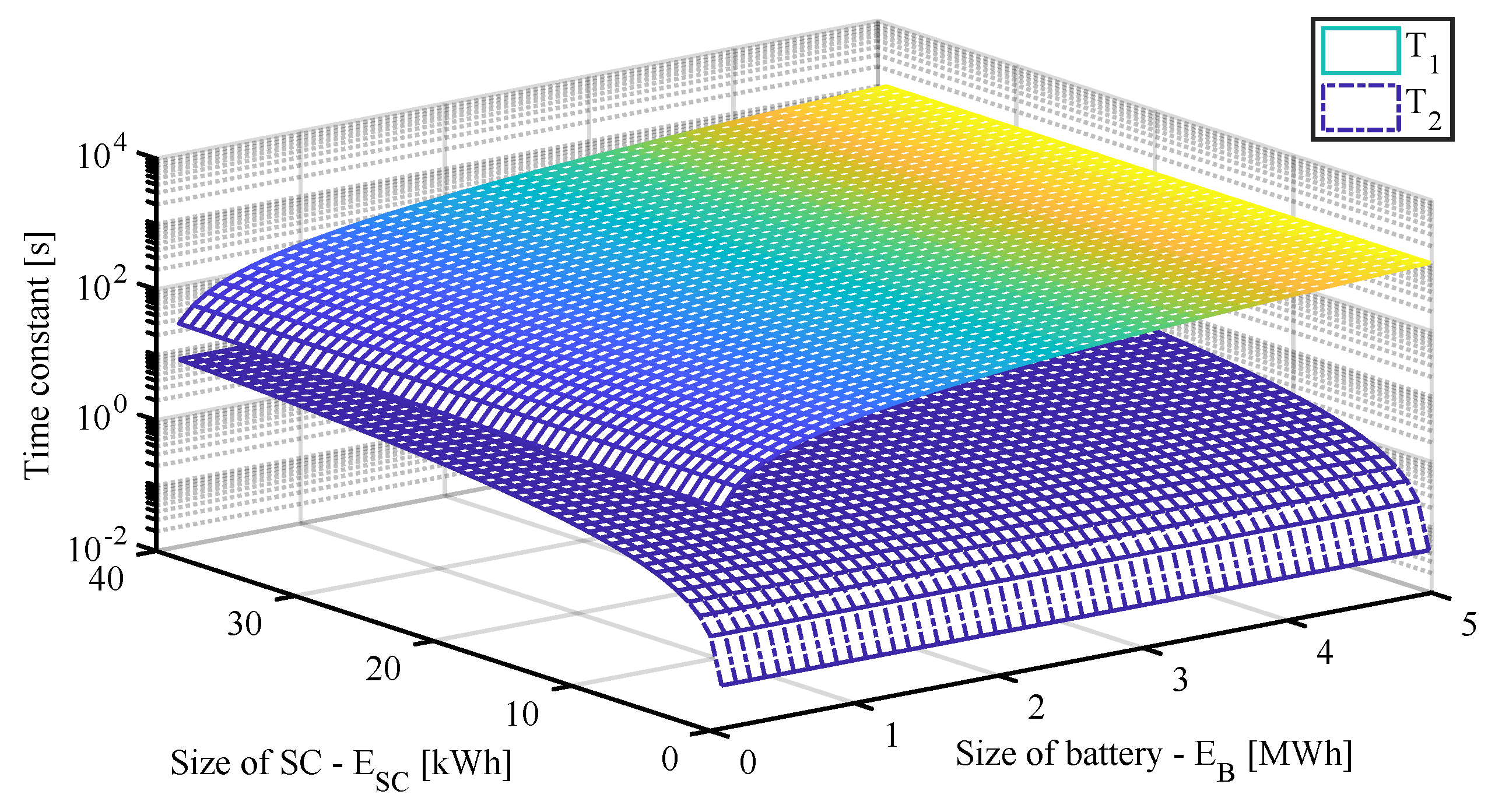
2.3. Sizing of the Battery and Supercapacitor
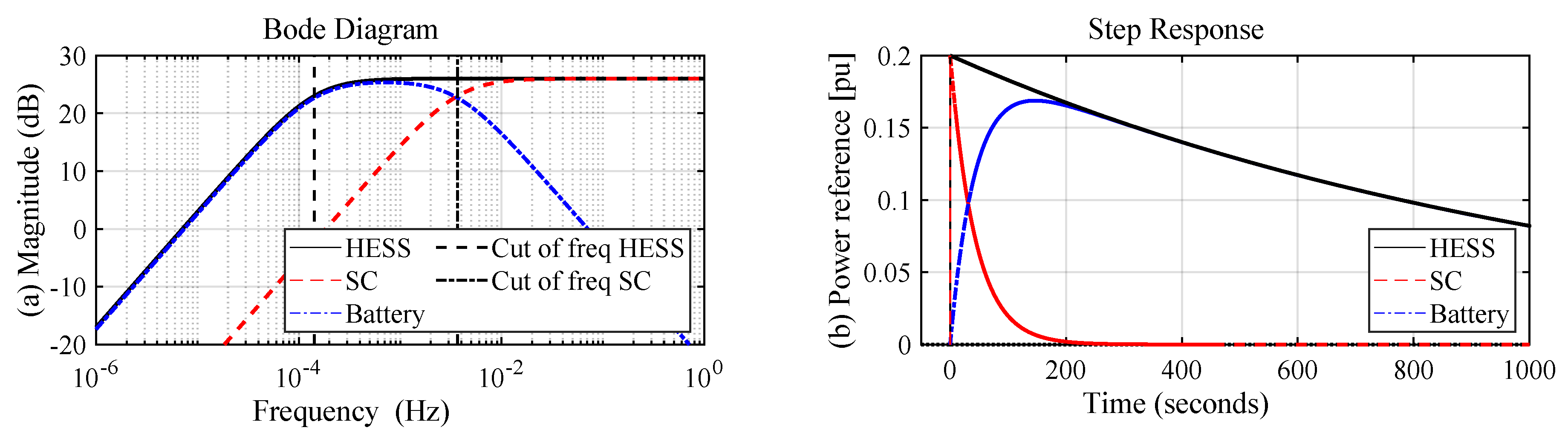
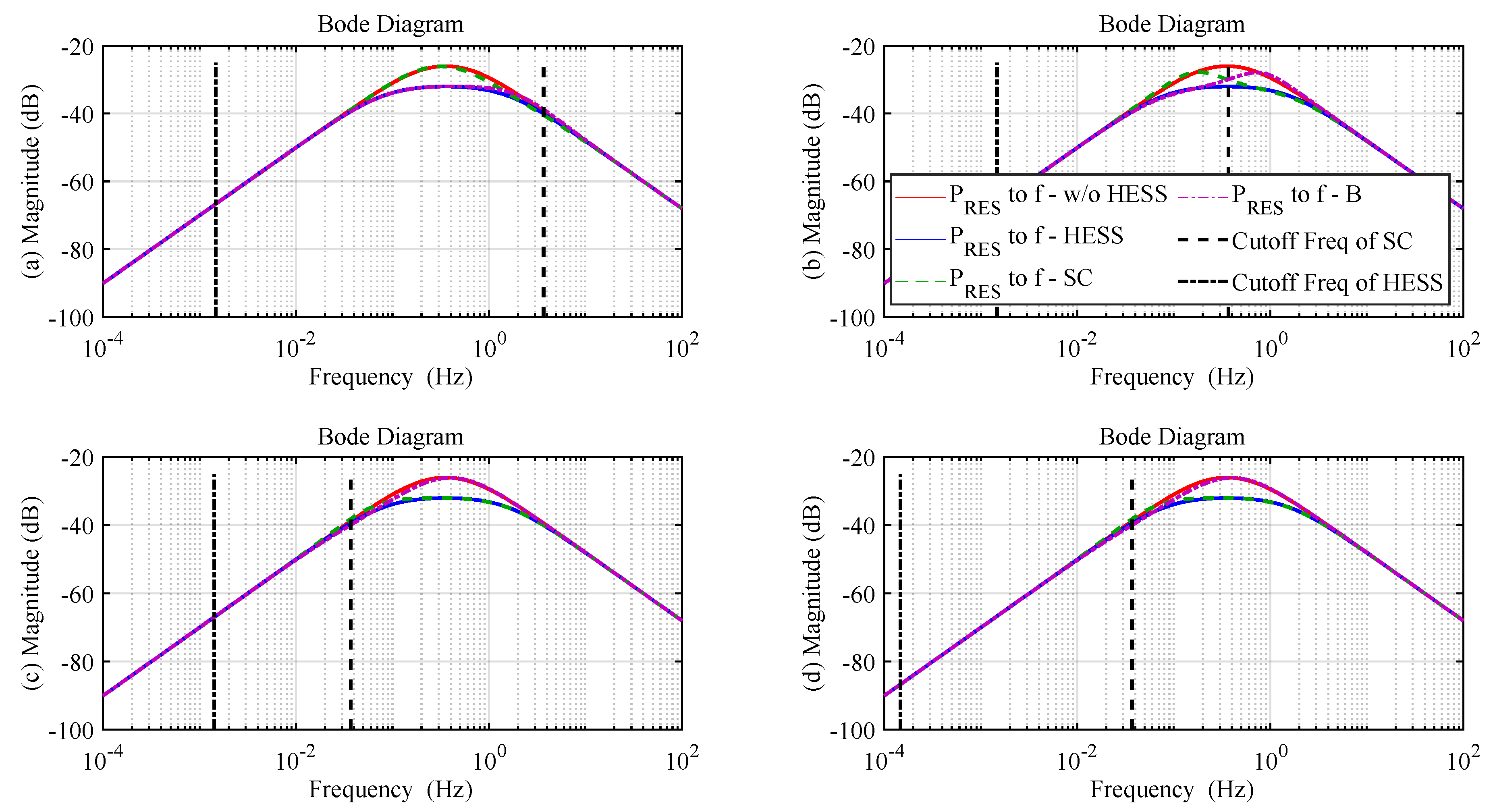
2.4. Frequency- and Time-Domain Analysis
3. Integration of the HESS in a Power Grid
3.1. Test System Configuration
3.2. Influence of the Capacity of the SC and Battery
3.3. Time-Domain Analysis for the Frequency Regulation and SOC Management
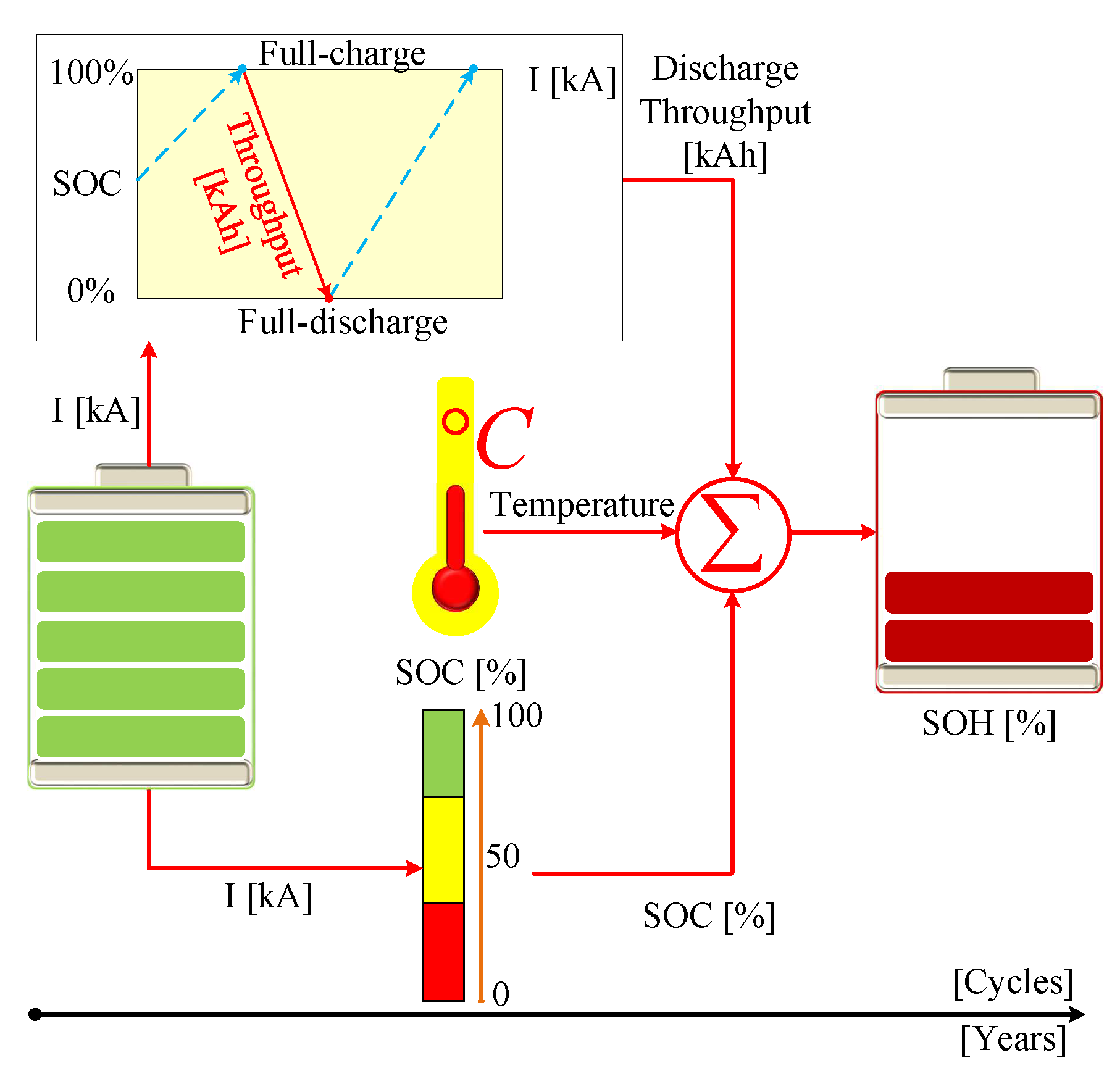
4. The Battery SOH Extension in a Hybrid Energy Storage System
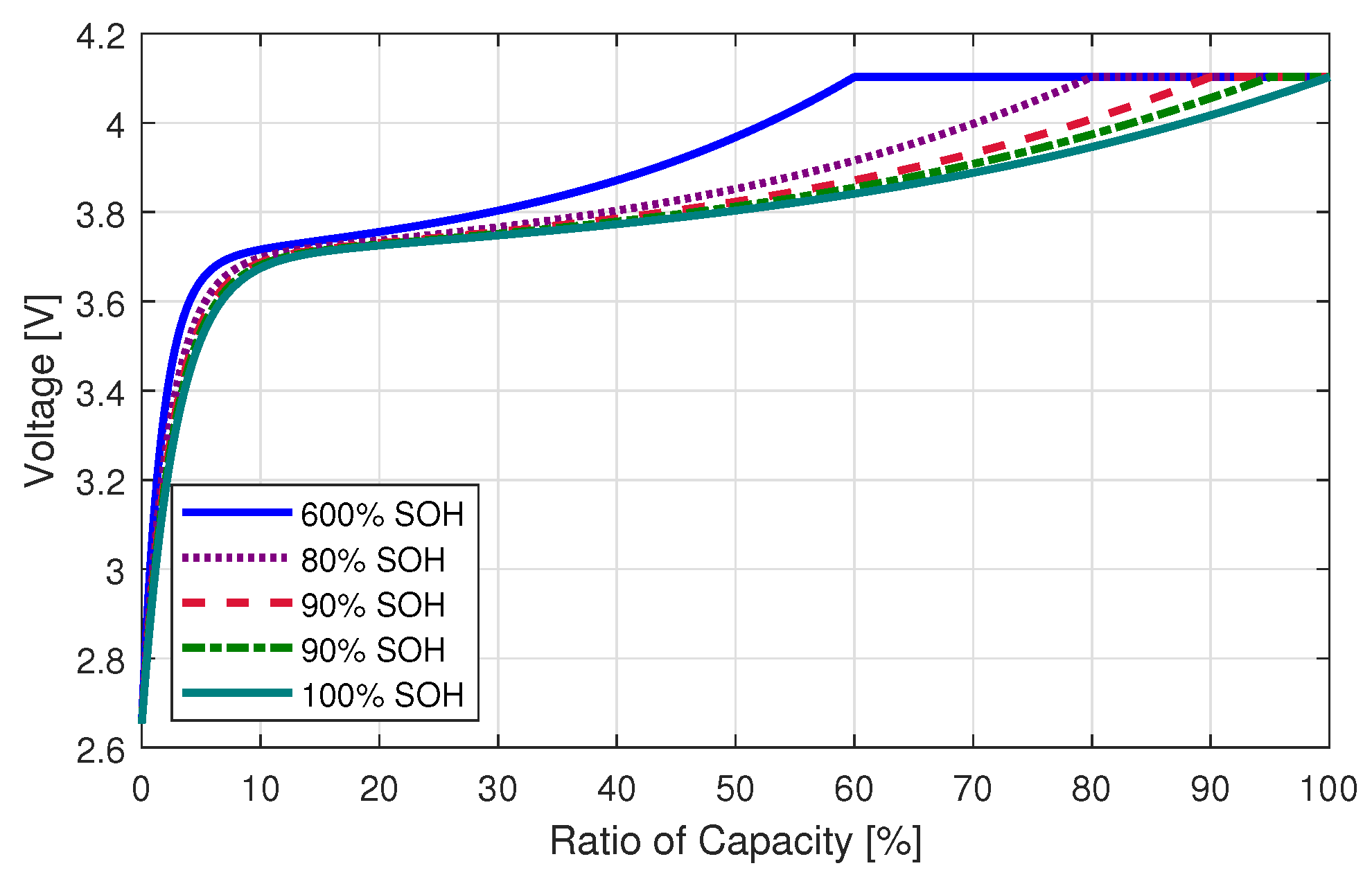
4.1. Definition of the SOH
4.2. Degradation Factors for SOH Assessment
4.2.1. Throughput Factor of Degradation
4.2.2. Degradation Factor from the SOC Change
4.2.3. Degradation Factor from the Temperature
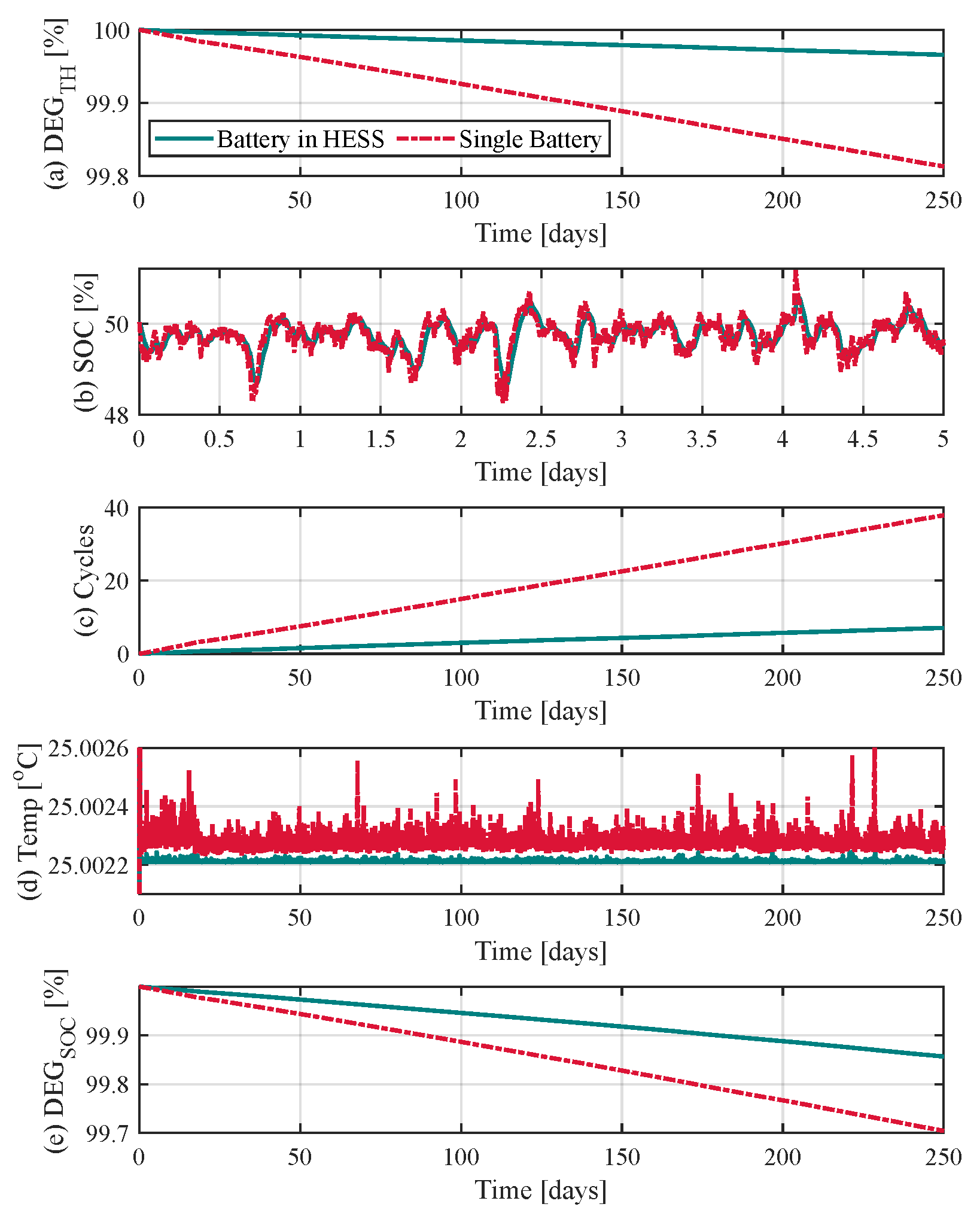
4.3. The Battery Lifetime Expansion in the Hybrid ESS Structure
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| ESS | Energy storage system |
| HESS | Hybrid energy storage system |
| SC | Supercapacitor |
| SMES | Superconducting magnetic energy storages |
| SOC | State-of-charge |
| SOH | State-of-health |
| FR | Frequency regulation |
| RES | Renewable energy resource |
| AGC | Automatic generation control |
| DSOF | Droop control with SOC feedback |
| , , and | Compensation power of the battery, SC, and HESS |
| and | SOC of the SC and HESS |
| , , and | Droop rate of the battery, SC, and HESS |
| and | Frequency offset of the HESS and SC |
| Maximum frequency compensation of the ESS | |
| Minimum frequency compensation of the ESS | |
| Frequency deviation from nominal frequency | |
| Central value of the SOC | |
| and | SOC deviation from of the SC and HESS |
| , , and | Operating coefficient of the battery, SC, and HESS |
| , , and | Energy of the battery, SC, and HESS |
| , , and | Capacity of the battery, SC, and HESS |
| and | Smoothing time constant of the SC and HESS |
| and | Cut-off frequency of the SC and HESS |
| H | Inertia constant (MWs/MVA) |
| Droop rate of the generator | |
| Maximal releasable capacity of the battery | |
| Rated capacity of the battery | |
| Open-circuit voltage | |
| Depth of discharge | |
| Estimated SOH after degrading | |
| Initial value of the SOH | |
| SOH degradation factor related to the SOC distribution of the battery | |
| SOH degradation factor related to the temperature of the battery | |
| SOH degradation factor related to the throughput of the battery | |
| Throughput of the battery | |
| Amount of decreased temperature per second | |
| Amount of increased temperature per second | |
| Function of the cell temperature | |
| Ambient temperature of the cell | |
| SOH of the battery |
Appendix A
References
- Bevrani, H.; Ghosh, A.; Ledwich, G. Renewable energy sources and frequency regulation: Survey and new perspectives. IET Renew. Power Gener. 2010, 4, 438–457. [Google Scholar] [CrossRef]
- Li, J.; Xiong, R.; Yang, Q.; Liang, F.; Zhang, M.; Yuan, W. Design/test of a hybrid energy storage system for primary frequency control using a dynamic droop method in an isolated microgrid power system. Appl. Energy 2016. [Google Scholar] [CrossRef]
- Li, J.; Yang, Q.; Robinson, F.; Liang, F.; Zhang, M.; Yuan, W. Design and test of a new droop control algorithm for a SMES/battery hybrid energy storage system. Energy 2016, 118. [Google Scholar] [CrossRef]
- Shim, J.W.; Verbič, G.; Zhang, N.; Hur, K. Harmonious Integration of Faster-Acting Energy Storage Systems Into Frequency Control Reserves in Power Grid with High Renewable Generation. IEEE Trans. Power Syst. 2018, 33, 6193–6205. [Google Scholar] [CrossRef]
- Shim, J.W.; Verbič, G.; Kim, H.; Hur, K. On Droop Control of Energy-Constrained Battery Energy Storage Systems for Grid Frequency Regulation. IEEE Access 2019, 7, 166353–166364. [Google Scholar] [CrossRef]
- Conover, D.R.; Crawford, A.J.; Viswanathan, V.V.; Ferreira, S.; Schoenwald, D. Protocol for Uniformly Measuring and Expressing the Performance Of Energy Storage Systems; Technical Report; Pacific Northwest National Lab. (PNNL): Richland, WA, USA, 2014.
- Greenwood, D.; Lim, K.Y.; Patsios, C.; Lyons, P.; Lim, Y.S.; Taylor, P. Frequency response services designed for energy storage. Appl. Energy 2017, 203, 115–127. [Google Scholar] [CrossRef]
- Rosewater, D.; Ferreira, S. Development of a frequency regulation duty-cycle for standardized energy storage performance testing. J. Energy Storage 2016, 7, 286–294. [Google Scholar] [CrossRef]
- Zhang, F.; Tokombayev, M.; Song, Y.; Gross, G. Effective flywheel energy storage (FES) offer strategies for frequency regulation service provision. In Proceedings of the 2014 Power Systems Computation Conference, Wroclaw, Poland, 18–22 August 2014; pp. 1–7. [Google Scholar]
- Indu, P.; Jayan, M. Frequency regulation of an isolated hybrid power system with superconducting magnetic energy storage. In Proceedings of the 2015 International Conference on Power, Instrumentation, Control and Computing (PICC), Thrissur, India, 9–11 December 2015; pp. 1–6. [Google Scholar]
- Stroe, D.I.; Knap, V.; Swierczynski, M.; Stroe, A.I.; Teodorescu, R. Suggested operation of grid-connected lithium-ion battery energy storage system for primary frequency regulation: Lifetime perspective. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 1105–1111. [Google Scholar]
- Świerczyński, M.; Stroe, D.I.; Stan, A.I.; Teodorescu, R. Primary frequency regulation with Li-ion battery energy storage system: A case study for Denmark. In Proceedings of the 2013 IEEE ECCE Asia Downunder, Melbourne, Australia, 3–6 June 2013; pp. 487–492. [Google Scholar]
- Mongkoltanatas, J.; Riu, D.; LePivert, X. Energy storage design for primary frequency control for islanding micro grid. In Proceedings of the IECON 2012 38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 5643–5649. [Google Scholar]
- Cho, Y.; Shim, J.W.; Kim, S.J.; Min, S.W.; Hur, K. Enhanced frequency regulation service using hybrid energy storage system against increasing power-load variability. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Yue, M.; Wang, X. Grid Inertial Response-Based Probabilistic Determination of Energy Storage System Capacity Under High Solar Penetration. IEEE Trans. Sustain. Energy 2015, 6, 1039–1049. [Google Scholar] [CrossRef]
- Wickramasinghe Abeywardana, D.B.; Hredzak, B.; Agelidis, V.G. A Fixed-Frequency Sliding Mode Controller for a Boost-Inverter-Based Battery-Supercapacitor Hybrid Energy Storage System. IEEE Trans. Power Electron. 2017, 32, 668–680. [Google Scholar] [CrossRef]
- Akram, U.; Khalid, M. A Coordinated Frequency Regulation Framework Based on Hybrid Battery-Ultracapacitor Energy Storage Technologies. IEEE Access 2018, 6, 7310–7320. [Google Scholar] [CrossRef]
- Cao, J.; Du, W.; Wang, H.; McCulloch, M. Optimal Sizing and Control Strategies for Hybrid Storage System as Limited by Grid Frequency Deviations. IEEE Trans. Power Syst. 2018, 33, 5486–5495. [Google Scholar] [CrossRef]
- Akram, U.; Shah, R.; Mithulananthan, N. Hybrid energy stoarage system for frequency regulation in microgrids with source and load uncertainties. IET Gener. Transm. Distrib. 2019, 13, 5048–5057. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; The EPRI Power System Engineering Series; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Xiao, J.; Wang, P.; Setyawan, L. Hierarchical control of hybrid energy storage system in DC microgrids. IEEE Trans. Ind. Electron. 2015, 62, 4915–4924. [Google Scholar] [CrossRef]
- Pahasa, J.; Ngamroo, I. PHEVs bidirectional charging/discharging and SoC control for microgrid frequency stabilization using multiple MPC. IEEE Trans. Smart Grid 2014, 6, 526–533. [Google Scholar] [CrossRef]
- Liu, H.; Hu, Z.; Song, Y.; Wang, J.; Xie, X. Vehicle-to-grid control for supplementary frequency regulation considering charging demands. IEEE Trans. Power Syst. 2014, 30, 3110–3119. [Google Scholar] [CrossRef]
- Tan, J.; Zhang, Y. Coordinated control strategy of a battery energy storage system to support a wind power plant providing multi-timescale frequency ancillary services. IEEE Trans. Sustain. Energy 2017, 8, 1140–1153. [Google Scholar] [CrossRef]
- Gundogdu, B.M.; Nejad, S.; Gladwin, D.T.; Foster, M.P.; Stone, D.A. A battery energy management strategy for UK enhanced frequency response and triad avoidance. IEEE Trans. Ind. Electron. 2018, 65, 9509–9517. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Shim, J.W. Virtual Capacity of Hybrid Energy Storage Systems Using Adaptive State of Charge Range Control for Smoothing Renewable Intermittency. IEEE Access 2020, 8, 126951–126964. [Google Scholar] [CrossRef]
- Soon Ng, K.; Moo, C.S.; Chen, Y.P.; Hsieh, Y.C. Enhanced Coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Huang, S.C.; Tseng, K.H.; Liang, J.W.; Chang, C.L.; Pecht, M. An online SOC and SOH estimation model for lithium-ion batteries. Energies 2017, 10, 512. [Google Scholar] [CrossRef]
- Chen, M.; Rincon-Mora, G.A. Accurate electrical battery model capable of predicting runtime and I-V performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Kim, W. Real Time SOH Estimation Method for Lithium Ion Batteries By Accumulation of Faded Capacity. Master’s Thesis, Yonsei University, Seoul, Korea, 2016. [Google Scholar]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO 4 cells. Lancet 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- González-Longatt, F.M. Circuit based battery models: A review. Congreso Iberoamericano de Estudiantes de Ingenieria Electrica. Cibelec. 2006. Available online: https://www.semanticscholar.org/paper/Circuit-Based-Battery-Models3A-A-Review-Gonzalez-Longatt/5a79ca86eaea1de96f7c3ea1248ea4b28f55c2f1?p2df (accessed on 28 November 2020).



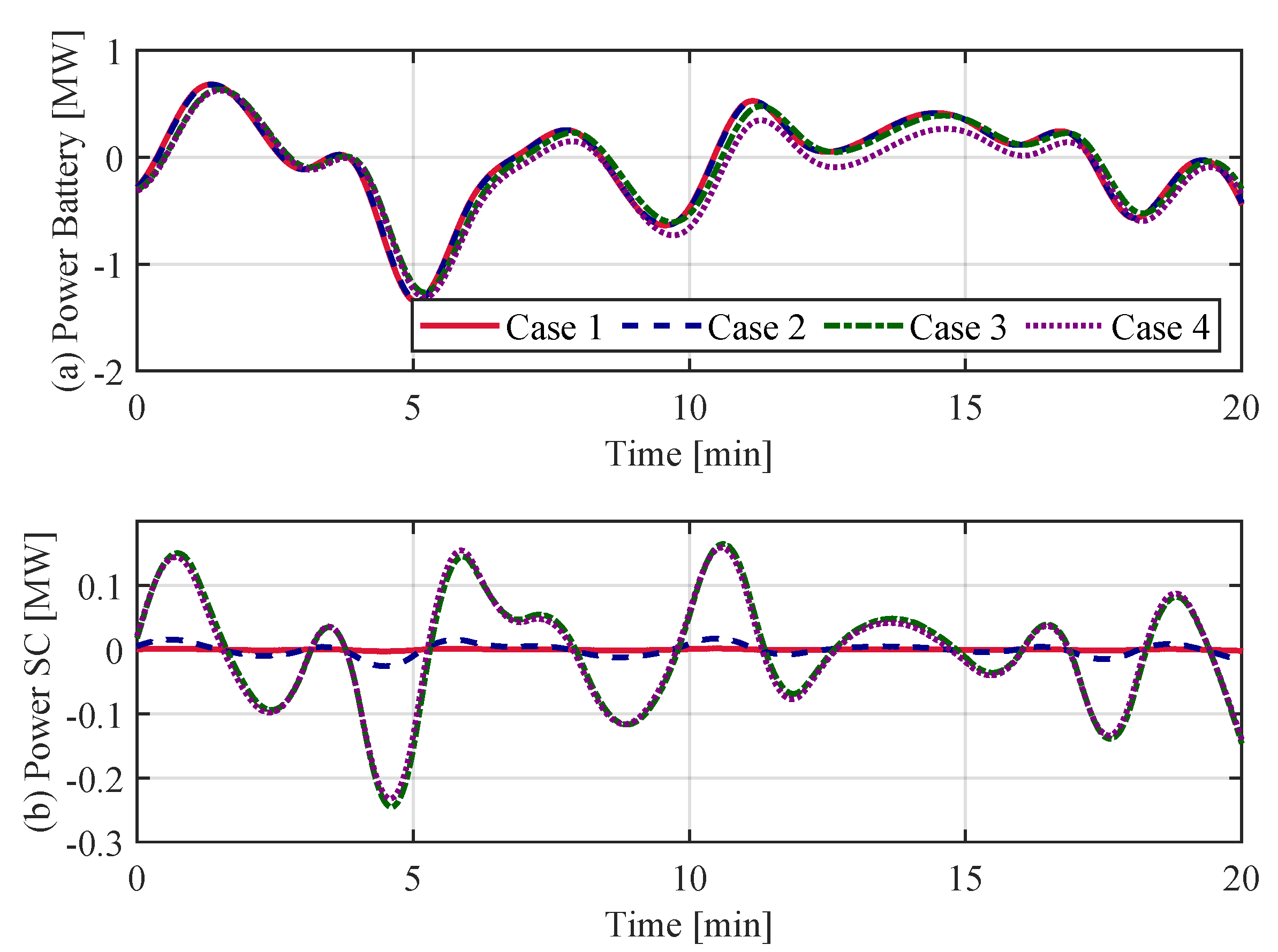


| Case | SC (kWh) | Battery (MWh) |
|---|---|---|
| 1. Small SC, small battery | 0.2 | 0.5 |
| 2. Medium SC, small battery | 2 | 0.5 |
| 3. Large SC, small battery | 20 | 0.5 |
| 4. Large SC, large battery | 20 | 5 |
| Symbols | Parameters | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|---|
| Time Constant | 678.85 s | 684.2 s | 705.72 s | 6812.3 s | |
| Time Constant | 0.2714 s | 2.7144 s | 27.1739 s | 27.1739 s | |
| Cut-off frequency | 1.473 mHz | 1.467 mHz | 1.416 mHz | 0.1467 mHz | |
| Cut-off frequency | 3.6841 Hz | 0.3684 Hz | 0.0368 Hz | 0.0368 Hz |
| Type of Battery | SC (kWh) | Battery (MWh) |
|---|---|---|
| 1. Battery in the HESS | 20 | 5 |
| 2. Single Battery | 0 | 5 |
| Temp | Base 60 C | Temperature Degradation () |
|---|---|---|
| 25 | 35 | 2 + 0.0703 |
| 33 | 27 | 3 + 0.1195 |
| 40 | 20 | 4 + 0.2476 |
| 50 | 10 | 3 + 0.7643 |
| 60 | 0 | 1 |
| Type of ESS | Cycles | ||||
|---|---|---|---|---|---|
| Independent battery | 40 | 58.5% | 0.24% | 99.81% | 99.67% |
| Battery in the HESS | 40 | 58.7% | 0.22% | 99.97% | 99.84% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen-Huu, T.-A.; Nguyen, V.T.; Hur, K.; Shim, J.W. Coordinated Control of a Hybrid Energy Storage System for Improving the Capability of Frequency Regulation and State-of-Charge Management. Energies 2020, 13, 6304. https://doi.org/10.3390/en13236304
Nguyen-Huu T-A, Nguyen VT, Hur K, Shim JW. Coordinated Control of a Hybrid Energy Storage System for Improving the Capability of Frequency Regulation and State-of-Charge Management. Energies. 2020; 13(23):6304. https://doi.org/10.3390/en13236304
Chicago/Turabian StyleNguyen-Huu, Thien-An, Van Thang Nguyen, Kyeon Hur, and Jae Woong Shim. 2020. "Coordinated Control of a Hybrid Energy Storage System for Improving the Capability of Frequency Regulation and State-of-Charge Management" Energies 13, no. 23: 6304. https://doi.org/10.3390/en13236304
APA StyleNguyen-Huu, T.-A., Nguyen, V. T., Hur, K., & Shim, J. W. (2020). Coordinated Control of a Hybrid Energy Storage System for Improving the Capability of Frequency Regulation and State-of-Charge Management. Energies, 13(23), 6304. https://doi.org/10.3390/en13236304







