Study on Date–Jimbo–Kashiwara–Miwa Equation with Conformable Derivative Dependent on Time Parameter to Find the Exact Dynamic Wave Solutions
Abstract
:1. Introduction
2. Explanation of the Two-Variable (G’/G, 1/G)-Expansion Method
3. Regular Traveling Wave Solutions of the CDJKM Equation
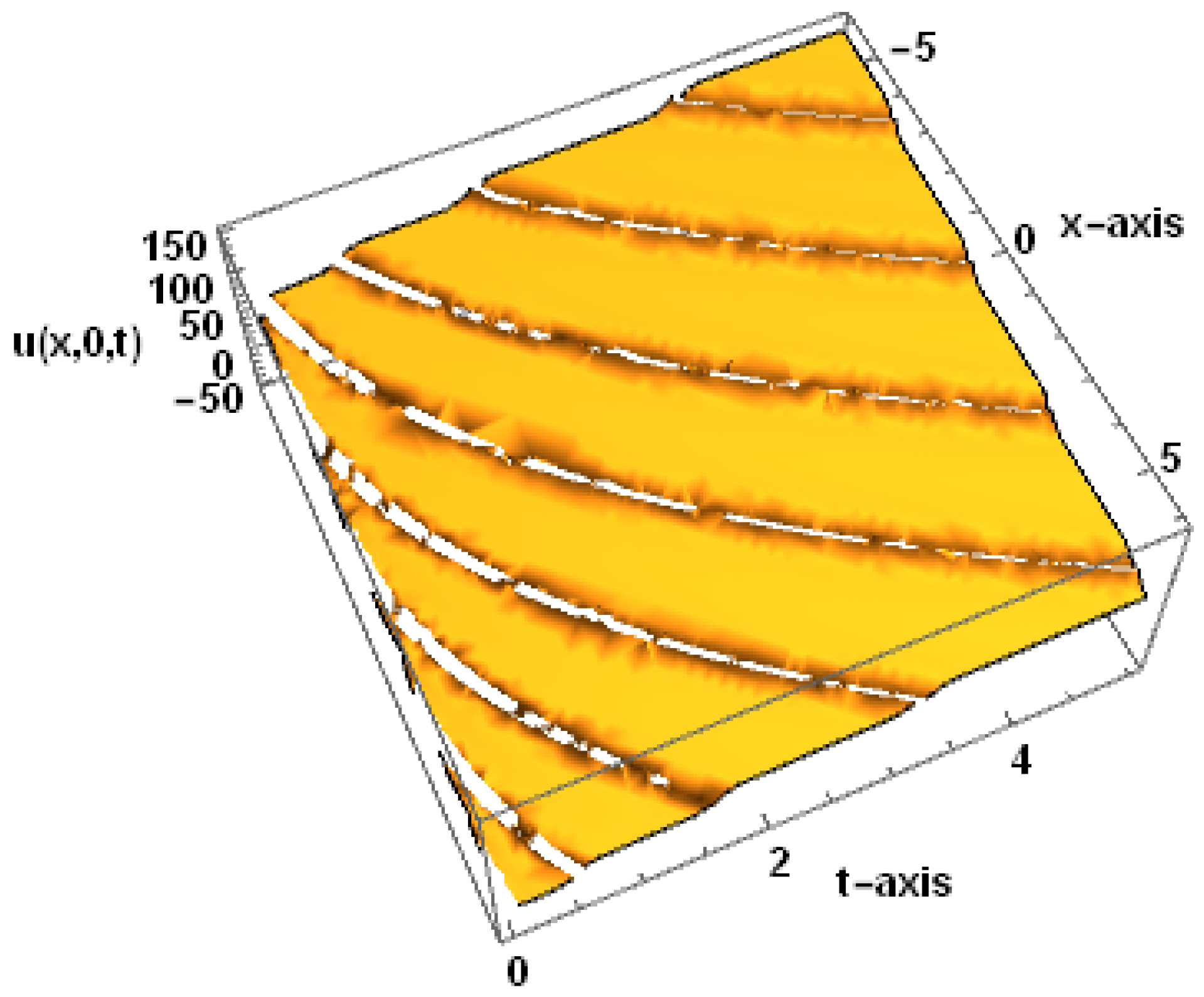
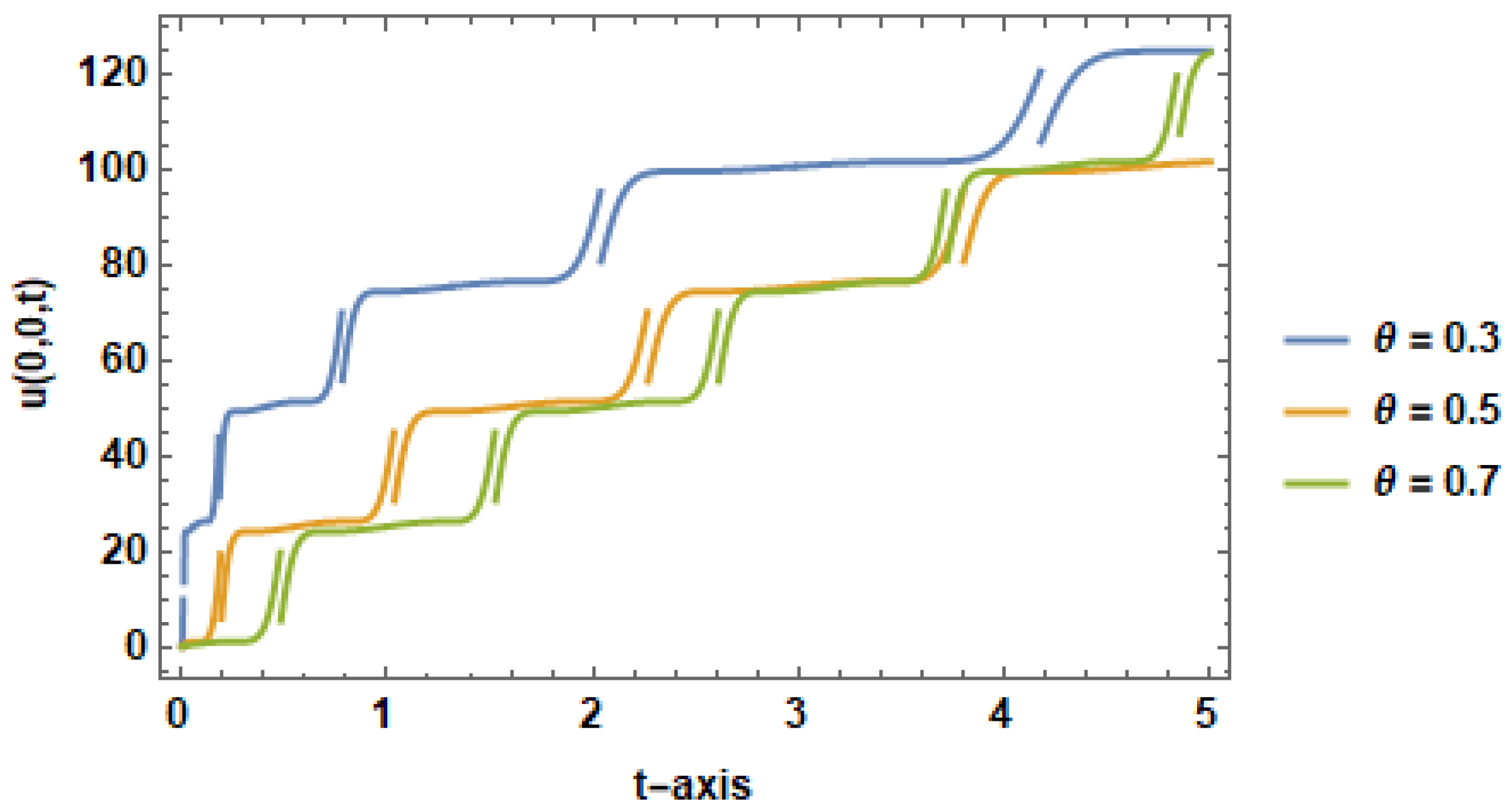
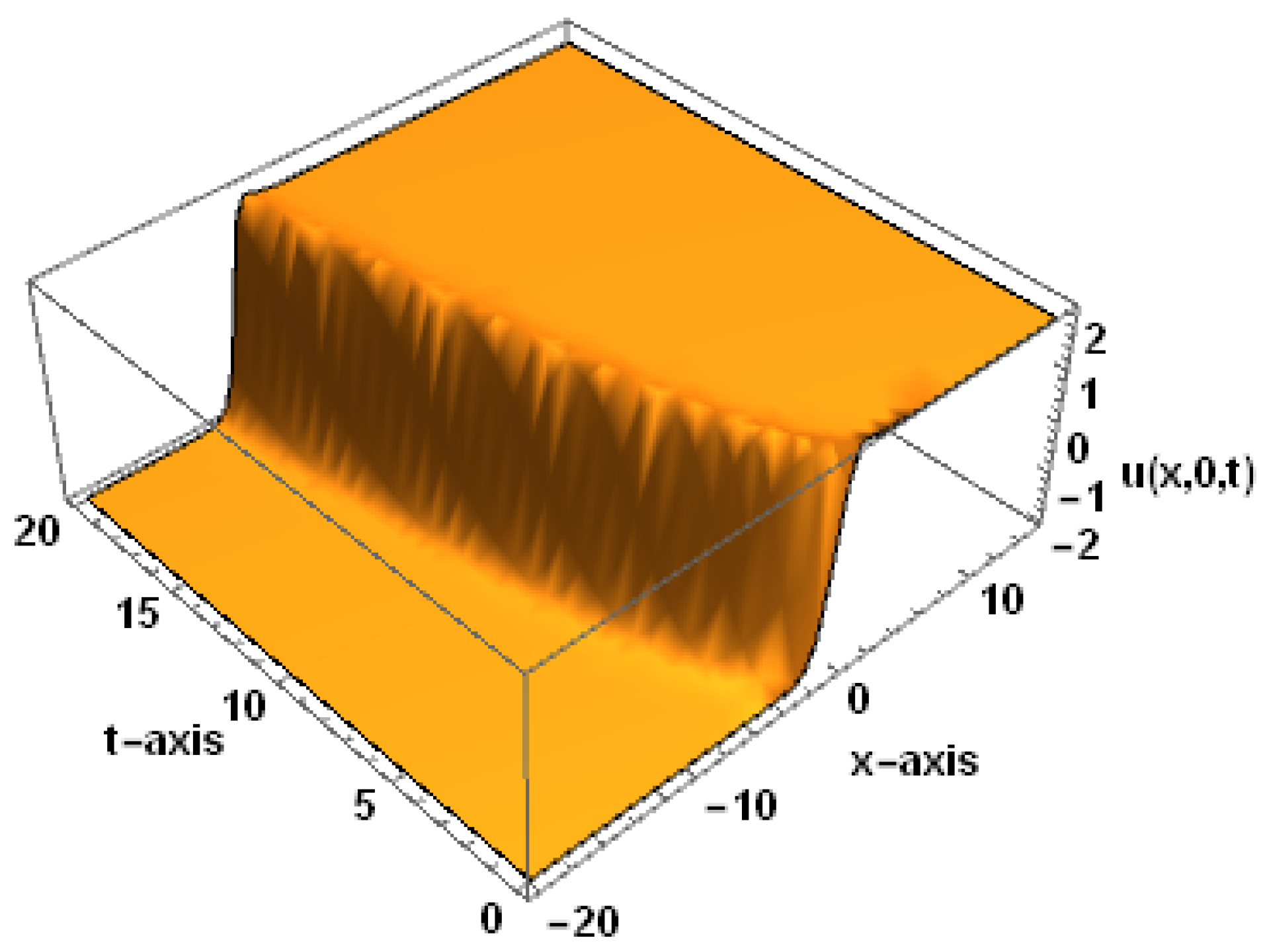
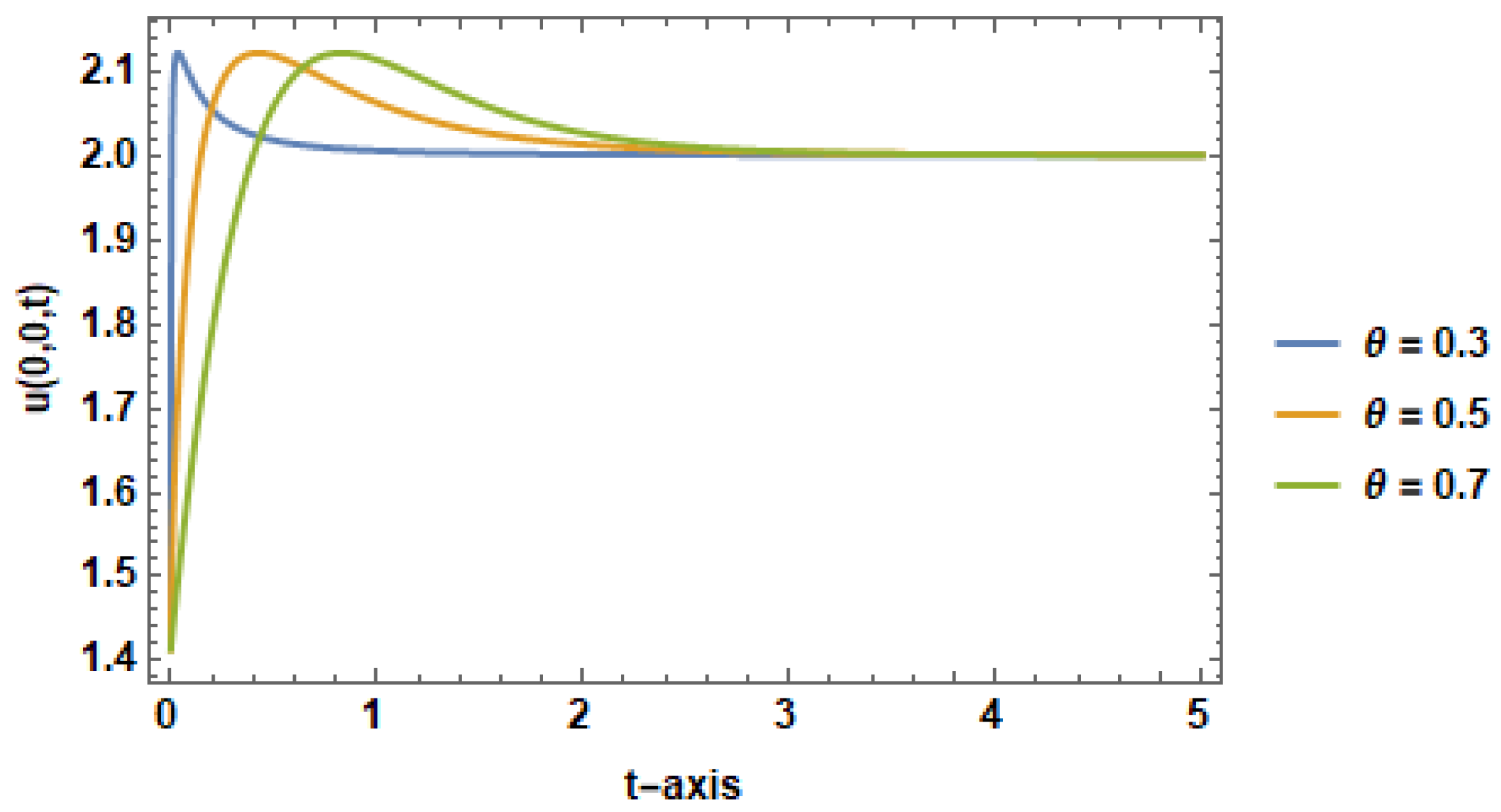
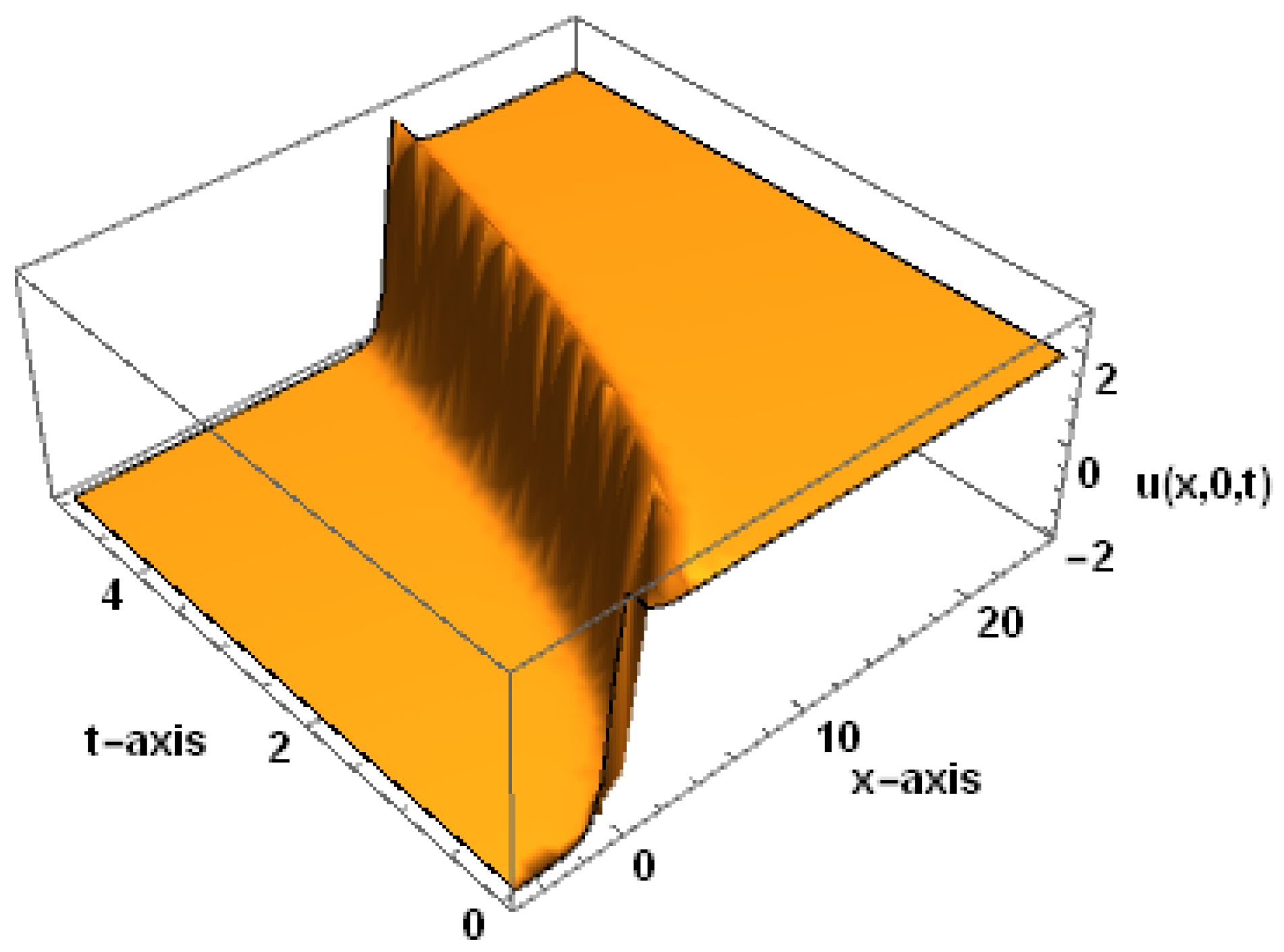
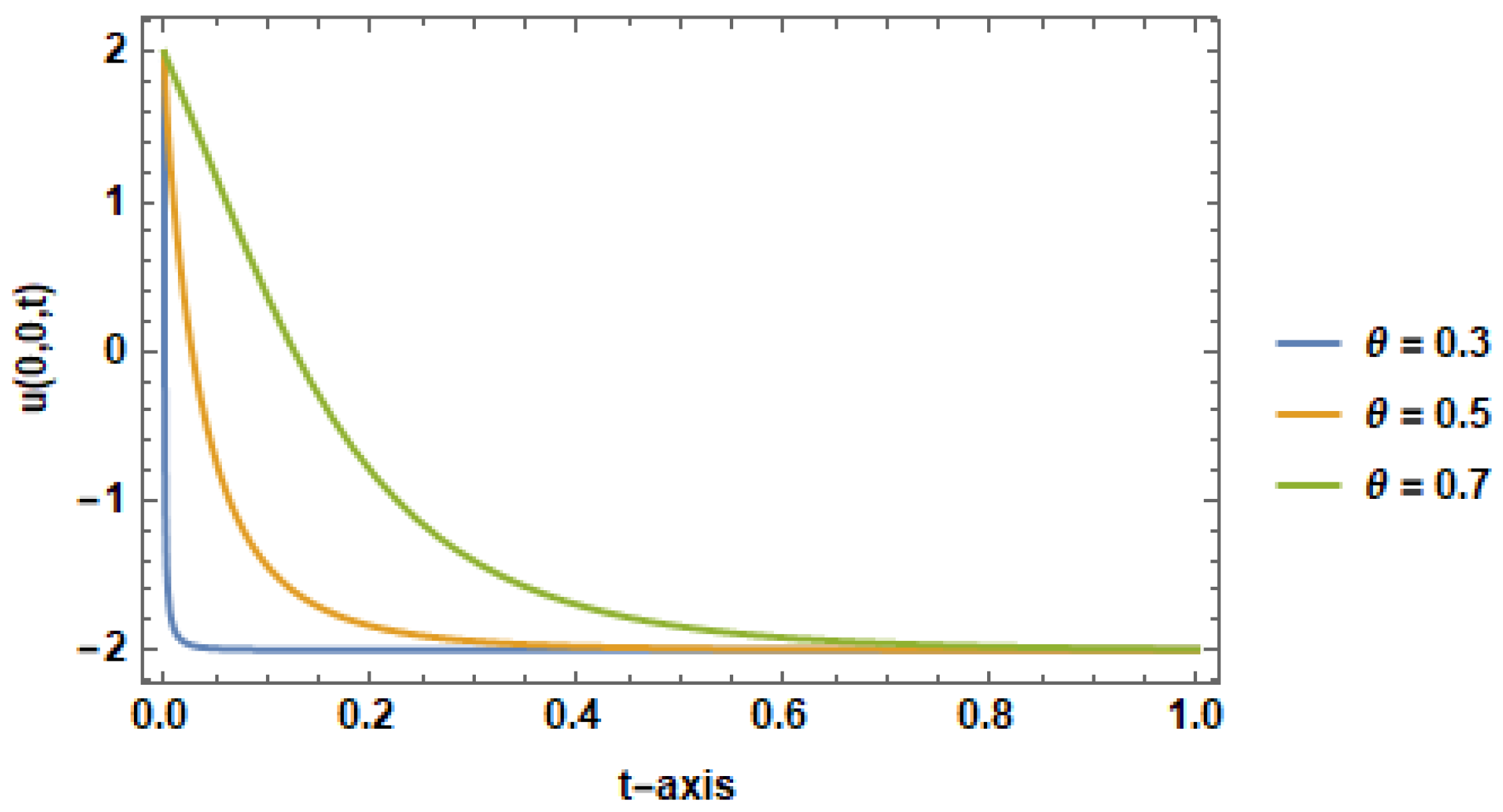
4. Figures and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Wang, M.L.; Zhou, Y.B.; Li, Z.B. Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics. Phys. Lett. A 1996, 216, 67–75. [Google Scholar] [CrossRef]
- Fan, E.; Zhang, H. A note on the homogeneous balance method. Phys. Lett. A 1998, 246, 403–406. [Google Scholar] [CrossRef]
- Mahak, N.; Akram, G. Exact solitary wave solutions of the (1+1)-dimensional Fokas-Lenells equation. Optik 2020, 208, 1–9. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Manafian, J.; Khodadad, F.S.; Nazari, F. Traveling wave solutions for density dependent conformable fractional diffusion-reaction equation by the first integral method and the improved tan ( )-expansion method. Opt. Quantum Electron. 2018, 50, 1–15. [Google Scholar]
- Lü, D. Jacobi elliptic function solutions for two variant Boussinesq equations. Chaos Soliton Fractals 2005, 24, 1373–1385. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Q. Extended Jacobi elliptic function rational expansion method and abundant families of Jacobi elliptic function solutions to (1+1)-dimensional dispersive long wave equation. Chaos Soliton Fractals 2005, 24, 745–757. [Google Scholar] [CrossRef]
- Bekir, A. Application of the exp-function method for nonlinear differential-difference equations. Appl. Math. Comput. 2010, 215, 4049–4053. [Google Scholar] [CrossRef]
- He, J.-H.; Wu, X.-H. Exp-function method for nonlinear wave equations. Chaos, Solitons Fractals 2006, 30, 700–708. [Google Scholar] [CrossRef]
- Fan, E. Extended tanh-function method and its applications to nonlinear equations. Phys. Lett. A 2000, 277, 212–218. [Google Scholar] [CrossRef]
- Parkes, E.; Duffy, B. An automated tanh-function method for finding solitary wave solutions to non-linear evolution equations. Comput. Phys. Commun. 1996, 98, 288–300. [Google Scholar] [CrossRef]
- Zhang, Z.Y. Exact traveling wave solutions of the perturbed Klein-Gordon equation with quadratic nonlinearity in (1+1)-dimension. Part I: Without local inductance and dissipation effect. Turk. J. Phys. 2013, 37, 259–267. [Google Scholar] [CrossRef]
- Domairry, G.; Mohsenzadeh, A.; Famouri, M. The application of homotopy analysis method to solve nonlinear differential equation governing Jeffery–Hamel flow. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 85–95. [Google Scholar] [CrossRef]
- Kumar, A.; Pankaj, R.D. Tanh–coth scheme for traveling wave solutions for Nonlinear Wave Interaction model. J. Egypt. Math. Soc. 2015, 23, 282–285. [Google Scholar] [CrossRef] [Green Version]
- Ali, K.K.; Osman, M.; Abdel-Aty, M. New optical solitary wave solutions of Fokas-Lenells equation in optical fiber via Sine-Gordon expansion method. Alex. Eng. J. 2020, 59, 1191–1196. [Google Scholar] [CrossRef]
- Ali, M.N.; Osman, M.S.; Husnine, S.M. On the analytical solutions of conformable time-fractional extended Zakharov-Kuznetsov equation through ( / )-expansion method and the modified Kudryashov method. SeMA J. 2019, 76, 15–25. [Google Scholar]
- Abdel-Gawad, H.I.; Osman, M. On shallow water waves in a medium with time-dependent dispersion and nonlinearity coefficients. J. Adv. Res. 2014, 6, 593–599. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abdel-Gawad, H.I.; Osman, M.S. On the Variational Approach for Analyzing the Stability of Solutions of Evolution Equations. Kyungpook Math. J. 2013, 53, 661–680. [Google Scholar] [CrossRef] [Green Version]
- Gao, W.; Rezazadeh, H.; Pinar, Z.; Baskonus, H.M.; Sarwar, S.; Yel, G. Novel explicit solutions for the nonlinear Zoomeron equation by using newly extended direct algebraic technique. Opt. Quantum Electron. 2020, 52, 1–13. [Google Scholar] [CrossRef]
- Raza, N.; Aslam, M.R.; Rezazadeh, H. Analytical study of resonant optical solitons with variable coefficients in Kerr and non-Kerr law media. Opt. Quantum Electron. 2019, 51, 59. [Google Scholar] [CrossRef]
- Raza, N.; Afzal, U.; Butt, A.R.; Rezazadeh, H. Optical solitons in nematic liquid crystals with Kerr and parabolic law nonlinearities. Opt. Quantum Electron. 2019, 51, 107. [Google Scholar] [CrossRef]
- Jafari, H.; Kadkhoda, N.; Baleanu, D. Fractional Lie group method of the time-fractional Boussinesq equation. Nonlinear Dyn. 2015, 81, 1569–1574. [Google Scholar] [CrossRef]
- Liu, J.-G.; Eslami, M.; Rezazadeh, H.; Mirzazadeh, M. Rational solutions and lump solutions to a non-isospectral and generalized variable-coefficient Kadomtsev–Petviashvili equation. Nonlinear Dyn. 2018, 95, 1027–1033. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The Hirota’s bilinear method and the tanh-coth method for multiple-soliton solutions of the Sawada-Kotera-Kadomstsev-Petviashvili equation. Appl. Math. Comput. 2008, 200, 160–166. [Google Scholar]
- Ali, K.K.; Osman, M.S.; Baskonus, H.M.; Elazabb, N.S.; Ilhan, E. Analytical and numerical study of the HIV-1 infection of CD4 + T-cells conformable fractional mathematical model that causes acquired immunodeficiency syndrome with the effect of antiviral drug therapy. Math. Methods Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Habib, M.A.; Ali, H.M.S.; Miah, M.M.; Akbar, M.A. The generalized Kudryshov method for new closed form traveling wave solutions to some NLEEs. AIMS Math. 2019, 4, 896–909. [Google Scholar] [CrossRef]
- Rahman, M.M.; Habib, M.A.; Ali, H.M.S.; Miah, M.M. The generalized Kudryshov method: A renewed mechanism for performing exact solitary wave solutions of some NLEEs. J. Mech. Cont. Math Sci. 2019, 14, 323–339. [Google Scholar]
- Jianming, L.; Jie, D.; Wenjun, Y. Bäcklund Transformation and New Exact Solutions of the Sharma-Tasso-Olver Equation. Abstr. Appl. Anal. 2011, 2011, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Sales, A.H.; Gomez, C.A. Application of the Cole-Hopf transformation for finding exact solutions to several forms of the seventh-order KDV equation. Math. Probl. Eng. 2010. [Google Scholar] [CrossRef]
- Malwe, B.H.; Betchewe, G.; Doka, S.Y.; Kofane, C.T. Travelling wave solutions and soliton solutions for the nonlinear transmission line using the generalized Riccati equation mapping method. Nonlinear Dyn. 2015, 84, 171–177. [Google Scholar] [CrossRef]
- Wang, M.L.; Li, X.Z.; Zang, J.L. The G’⁄G-expansion method and traveling wave solutions of nonlinear evolution equation in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Hossain, D.; Alam, K.; Akbar, M.A. Abundant wave solutions of the Boussinesq equation and the (2+1)-dimensional extended shallow water wave equation. Ocean Eng. 2018, 165, 69–76. [Google Scholar] [CrossRef]
- Rani, A.; Hssan, Q.; Ayub, K.; Ahmad, J.; Zulfiqar, A. Soliton solutions of Nonlinear Evolution Equations by Basic (G’/G)-Expansion Method. Math. Model. Eng. Probl. 2020, 7, 242–250. [Google Scholar] [CrossRef]
- Naher, H.; Abdullah, F.A. The improved -expansion method to the (2+1)-dimensional breaking soliton equation. J. Comput. Anal. Appl. 2014, 16, 220–235. [Google Scholar]
- Naher, H.; Abdullah, F.A. New generalized and improved -expansion method for nonlinear evolution equations in mathematical physics. Egypt. Math. Soc. 2014, 22, 390–395. [Google Scholar]
- Inc, M.; Miah, M.; Akher, C.; Ali, S.; Rezazadeh, H.; Akinlar, M.A.; Chu, Y.-M. New exact solutions for the Kaup-Kupershmidt equation. AIMS Math. 2020, 5, 6726–6738. [Google Scholar] [CrossRef]
- Li, L.X.; Li, E.Q.; Wang, M.L. The ( / , 1/ )-expansion method and its application to traveling wave solutions of the Zakharov equations. Appl. Math.-A J. Chin. Univ. 2010, 25, 454–462. [Google Scholar]
- Zayed, E.M.E.; Alurrfi, K.A.E. The ( / , 1/ )-expansion method and its applications to two nonlinear Schr dinger equations describing the propagation of femtosecond pulses in nonlinear optical fibers. Optik 2016, 127, 1581–1589. [Google Scholar]
- Chowdhury, M.A.; Miah, M.M.; Ali, H.S.; Chu, Y.-M.; Osman, M. An investigation to the nonlinear (2 + 1)-dimensional soliton equation for discovering explicit and periodic wave solutions. Results Phys. 2021, 23, 104013. [Google Scholar] [CrossRef]
- Yuan, Y.Q.; Tian, B.; Sun, W.R.; Chai, J.; Liu, L. Wronskian and Grammian solutions for a (2+1)-dimensional Date-Jimbo-Kashiwara-Miwa equation. Comput. Math. Appl. 2017, 74, 873–879. [Google Scholar] [CrossRef]
- Singh, M.; Gupta, R.K. On Painleve’ analysis, symmetry group and conservation laws of Date-Jimbo-Kashiwara-Miwa equation. Int. J. Appl. Comput. Math. 2018, 4, 88. [Google Scholar] [CrossRef]
- Wang, S.N.; Hu, J. Grammian solutions for a (2+1)-dimensional integrable coupled modified Date-Jimbo-Kashiwara-Miwa equation. Mod. Phys. Lett. B 2019, 33, 1950119. [Google Scholar] [CrossRef]
- Ali, K.K.; Mehanna, M.S.; Wazwaz, A.-M. Analytical and numerical treatment to the (2+1)-dimensional Date-Jimbo-Kashiwara-Miwa equation. Nonlinear Eng. 2021, 10, 187–200. [Google Scholar] [CrossRef]
- Ismael, H.F.; Seadawy, A.; Bulut, H. Rational solutions, and the interaction solutions to the (2 + 1)-dimensional time-dependent Date–Jimbo–Kashiwara–Miwa equation. Int. J. Comput. Math. 2021, 98, 2369–2377. [Google Scholar] [CrossRef]
- Guo, F.; Lin, J. Interaction solutions between lump and stripe soliton to the (2+1)-dimensional Date-Jimbo-Kashiwara-Miwa equation. Nonlinear Dyn. 2019, 96, 1233–1274. [Google Scholar] [CrossRef]
- Kumar, A.; Ilhan, E.; Ciancio, A.; Yel, G.; Baskonus, H.M. Extractions of some new travelling wave solutions to the conformable Date-Jimbo-Kashiwara-Miwa equation. AIMS Math. 2021, 6, 4238–4264. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, R.; Osman, M.S.; Samet, B. A wavelet based numerical scheme for fractional order SEIR epidemic of measles by using Genocchi polynomials. Numer. Methods Partial. Differ. Equ. 2020, 37, 1250–1268. [Google Scholar] [CrossRef]
- Osman, M.S.; Abdel-Gawad, H.I. Multi-wave solutions of the (2+1)-dimensional Nizhnik-Novikov-Veselov equations with variable coefficients. Eur. Phys. J. Plus 2015, 130. [Google Scholar] [CrossRef]
- Abdel-Gawad, H.I.; Tantawy, M.; Osman, M.S. Dynamic of DNA’s possible impact on its damage. Math. Methods Appl. Sci. 2016, 39, 168–176. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iqbal, M.A.; Wang, Y.; Miah, M.M.; Osman, M.S. Study on Date–Jimbo–Kashiwara–Miwa Equation with Conformable Derivative Dependent on Time Parameter to Find the Exact Dynamic Wave Solutions. Fractal Fract. 2022, 6, 4. https://doi.org/10.3390/fractalfract6010004
Iqbal MA, Wang Y, Miah MM, Osman MS. Study on Date–Jimbo–Kashiwara–Miwa Equation with Conformable Derivative Dependent on Time Parameter to Find the Exact Dynamic Wave Solutions. Fractal and Fractional. 2022; 6(1):4. https://doi.org/10.3390/fractalfract6010004
Chicago/Turabian StyleIqbal, Md Ashik, Ye Wang, Md Mamun Miah, and Mohamed S. Osman. 2022. "Study on Date–Jimbo–Kashiwara–Miwa Equation with Conformable Derivative Dependent on Time Parameter to Find the Exact Dynamic Wave Solutions" Fractal and Fractional 6, no. 1: 4. https://doi.org/10.3390/fractalfract6010004





