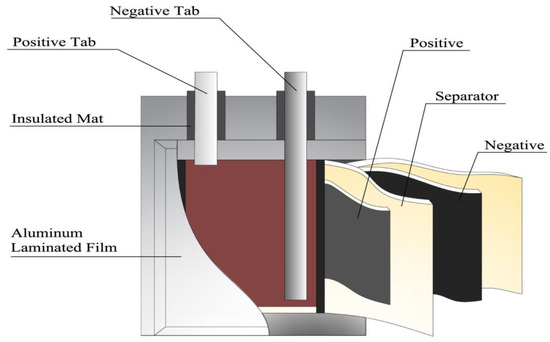
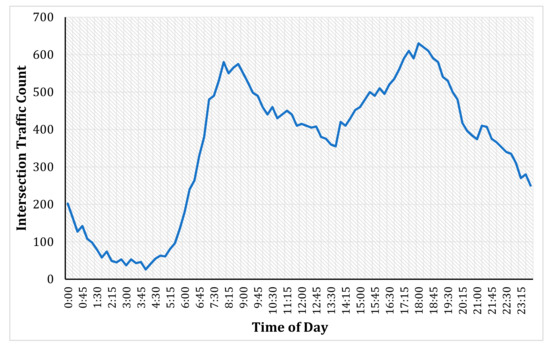
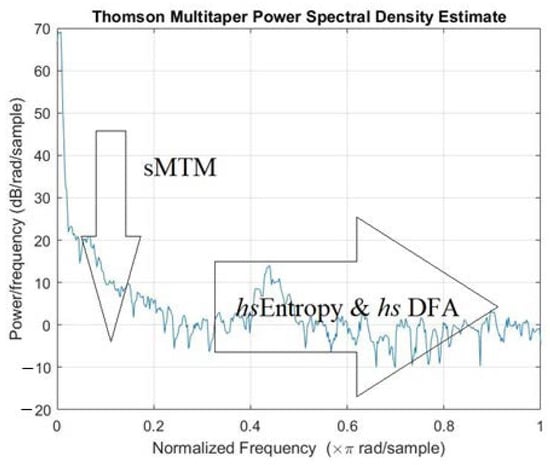
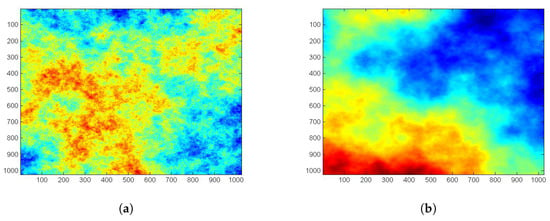
Wavelets, Fractals and Information Theory
A topical collection in Entropy (ISSN 1099-4300). This collection belongs to the section "Multidisciplinary Applications".
Viewed by 72174Editor
Interests: computational methods; mathematical physics; nonlinear systems
Special Issues, Collections and Topics in MDPI journals
Topical Collection Information
Dear Colleagues,
Wavelet analysis and fractals are playing fundamental roles in science, engineering applications, and information theory. Wavelets and fractals are the most suitable methods for the analysis of complex systems, localized phenomena, singular solutions, non-differentiable functions, and, in general, nonlinear problems. Nonlinearity and non-regularity usually characterize the complexity of a problem; they are thus the most-studied features in order to approach a solution to complex problems. Wavelets, fractals, and fractional calculus might also help to improve the analysis of the entropy and complexity of a system.
In information theory, entropy encoding might be considered a sort of compression in a quantization process, and this can be further investigated using wavelet compression. There are many types of definition of entropy that are very useful in the engineering and applied sciences, such as Shannon–Fano entropy, Kolmogorov entropy, etc. However, only entropy encoding is optimal for the complexity of large data analysis, such as in data storage. In fact, the principal advantage of modelling a complex system via wavelet analysis is the minimization of the memory space for storage or transmission. Moreover, this kind of approach reveals some new aspects and promising perspectives for many other kinds of applied and theoretical problems. For instance, in engineering applications, the best way to model traffic in wireless communications is based on fractal geometry, whereas the data are efficiently studied on a wavelet basis.
This Topical Collection will also be an opportunity to extend the research fields of image processing, differential/integral equations, number theory and special functions, image segmentation, the sparse component analysis approach, generalized multiresolution analysis, and entropy as a measure of all aspects of the theoretical and practical studies of mathematics, physics, and engineering.
The main topics of this Topical Collection include (but are not limited to):
- Entropy encoding, wavelet compression, and information theory
- Fractals, non-differentiable functions; Theoretical and applied analytical problems of fractal type, fractional equations
- Fractals, entropy and complexity
- Fractals, wavelets, fractional methods in the stochastic process, stochastic equations
- Fractal and wavelet solutions of fractional differential equations
- Wavelet analysis, integral transforms and applications
- Wavelets, fractals and fractional methods in fault diagnosis, in signal analysis, in nonlinear time series
- Wavelet-fractal entropy encoding and computational mathematics in data analysis and time series, including in image analysis
- Wavelet–fractal approach
- Fractional nonlinear equations
- Chaotic dynamics
- Artifical neural networks.
Prof. Dr. Carlo Cattani
Collection Editor
Manuscript Submission Information
Manuscripts should be submitted online at www.mdpi.com by registering and logging in to this website. Once you are registered, click here to go to the submission form. Manuscripts can be submitted until the deadline. All submissions that pass pre-check are peer-reviewed. Accepted papers will be published continuously in the journal (as soon as accepted) and will be listed together on the collection website. Research articles, review articles as well as short communications are invited. For planned papers, a title and short abstract (about 250 words) can be sent to the Editorial Office for assessment.
Submitted manuscripts should not have been published previously, nor be under consideration for publication elsewhere (except conference proceedings papers). All manuscripts are thoroughly refereed through a single-blind peer-review process. A guide for authors and other relevant information for submission of manuscripts is available on the Instructions for Authors page. Entropy is an international peer-reviewed open access monthly journal published by MDPI.
Please visit the Instructions for Authors page before submitting a manuscript. The Article Processing Charge (APC) for publication in this open access journal is 2600 CHF (Swiss Francs). Submitted papers should be well formatted and use good English. Authors may use MDPI's English editing service prior to publication or during author revisions.
Keywords
- Fractal
- Fractional
- Wavelet
- Entropy
- Nonlinear time series
- Data analysis
- Image Analysis
- Dynamical System
- Chaos
- Differential Operators
Related Special Issues
- Wavelets, Fractals and Information Theory III in Entropy (21 articles)
- Wavelets, Fractals and Information Theory II in Entropy (21 articles)
- Wavelets, Fractals and Information Theory I in Entropy (18 articles)