Local Complexity Estimation Based Filtering Method in Wavelet Domain for Magnetic Resonance Imaging Denoising
Abstract
:1. Introduction
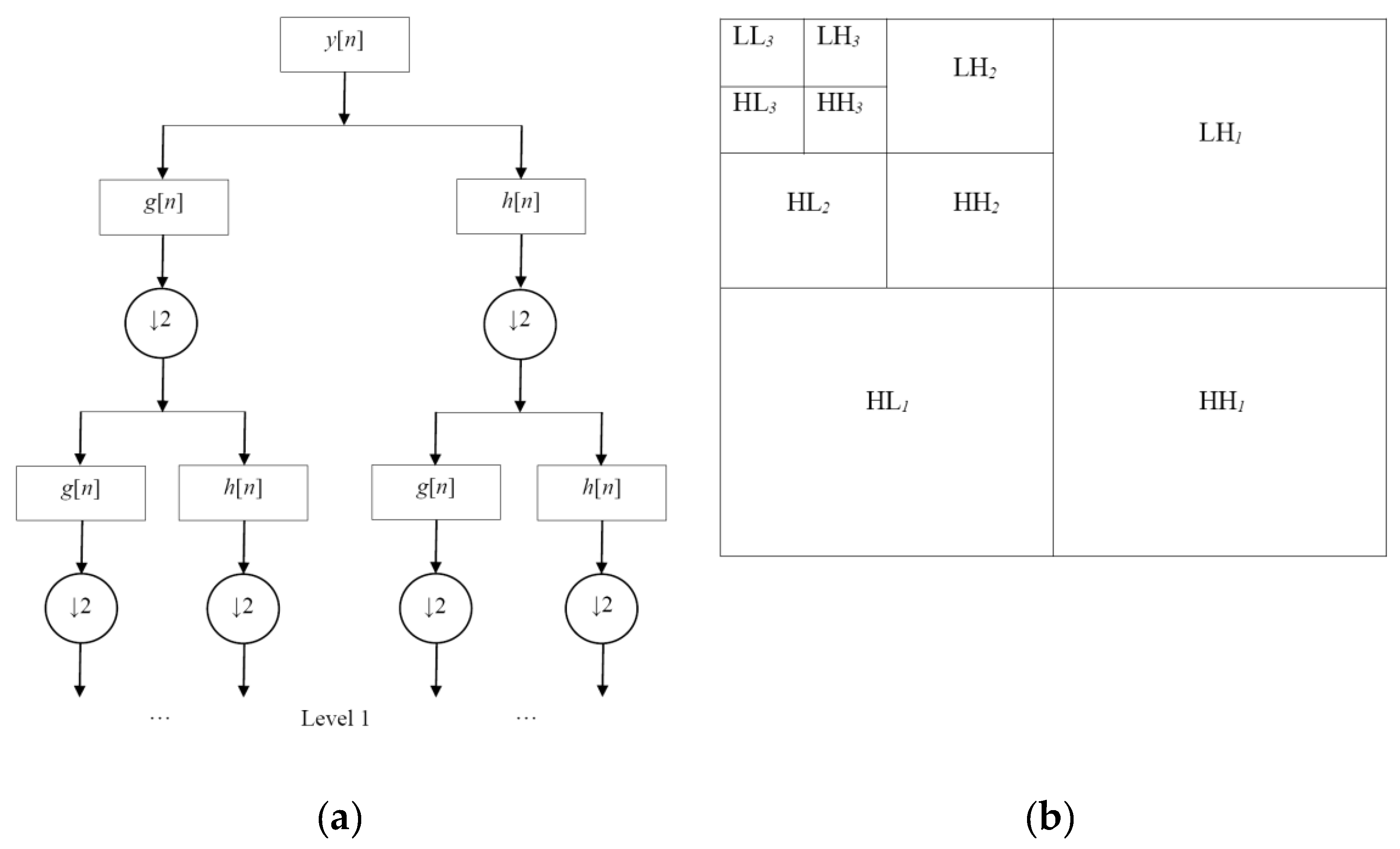
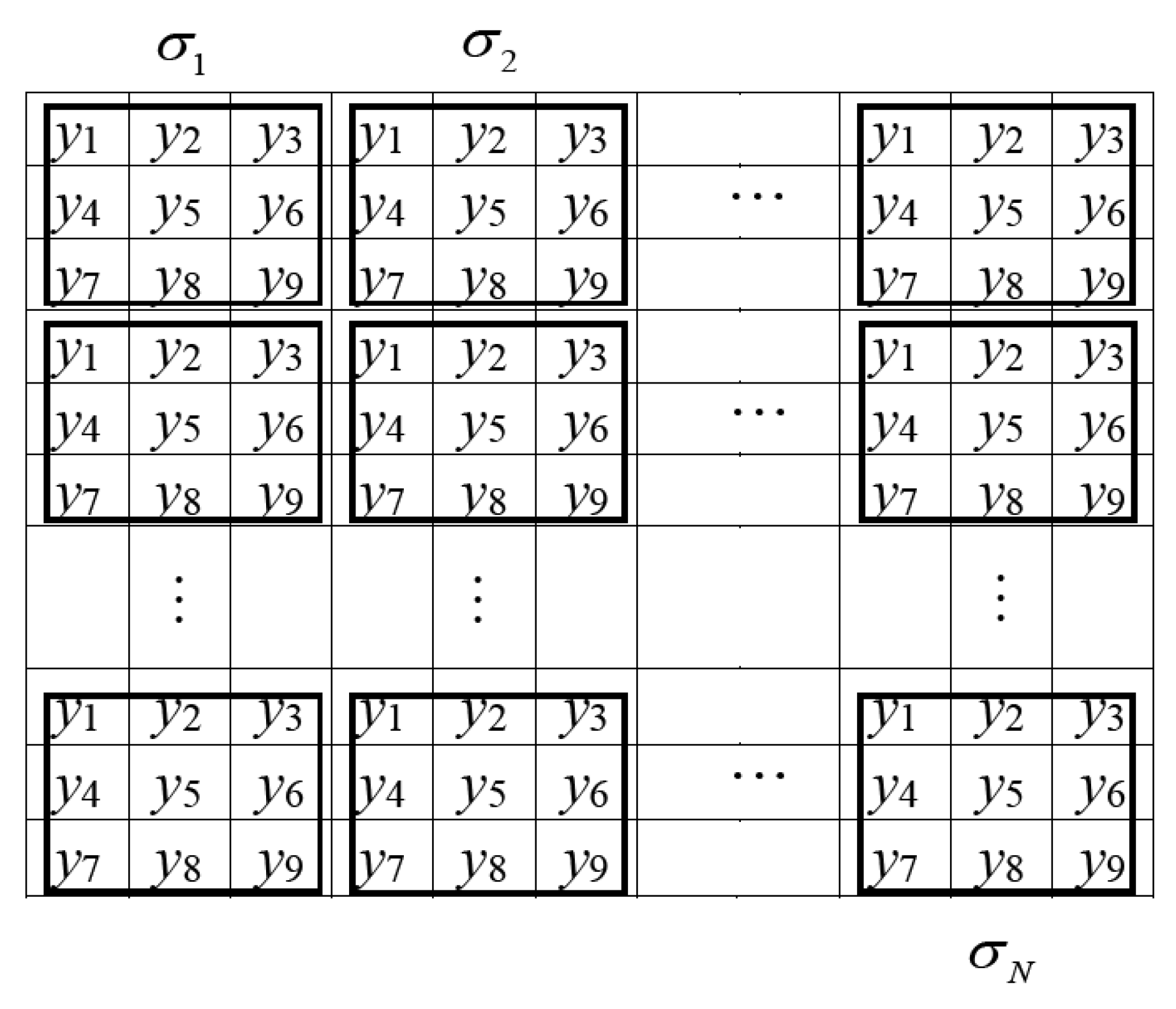
2. Proposed Method
3. Simulation Results
3.1. Comparative Performance of Different Wavelets
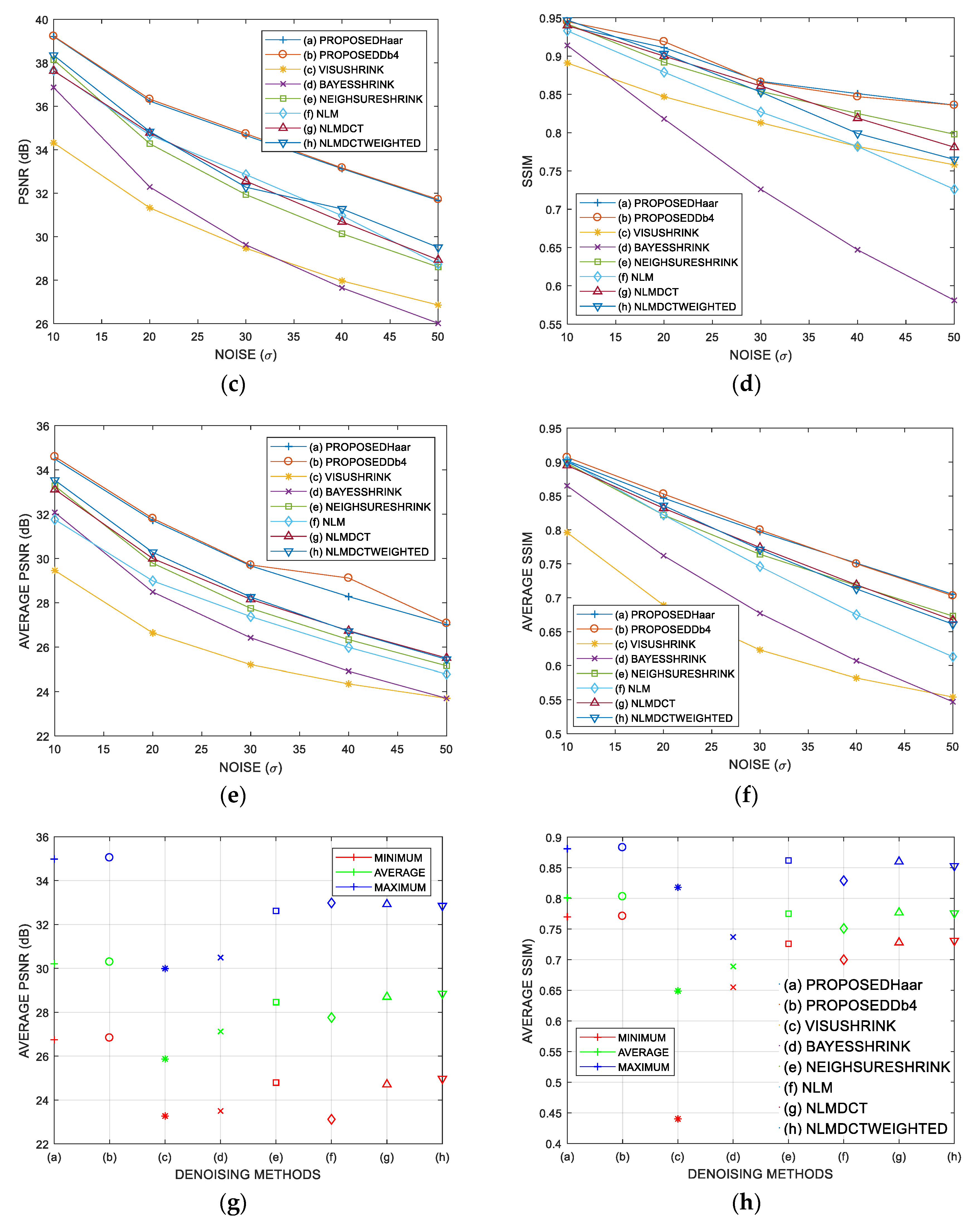
3.2. Comparative Performance in Standard Images
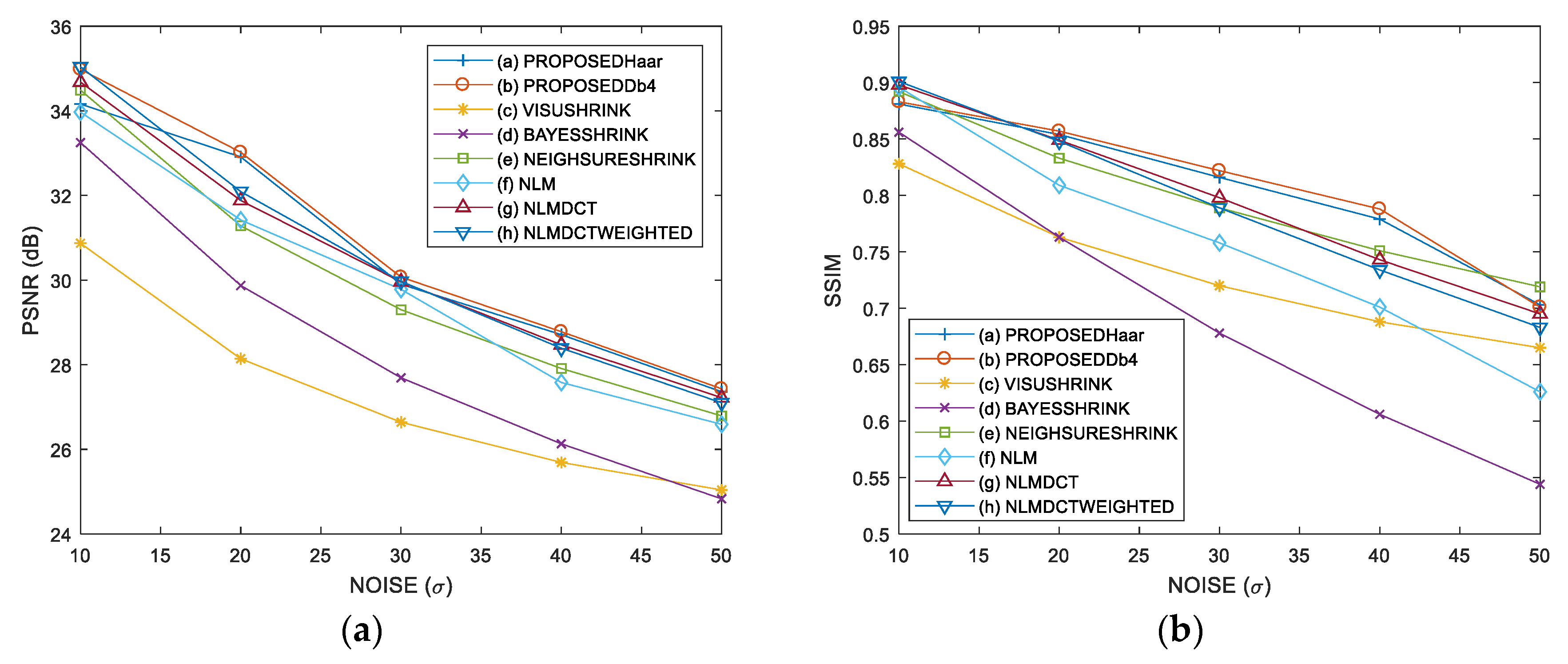
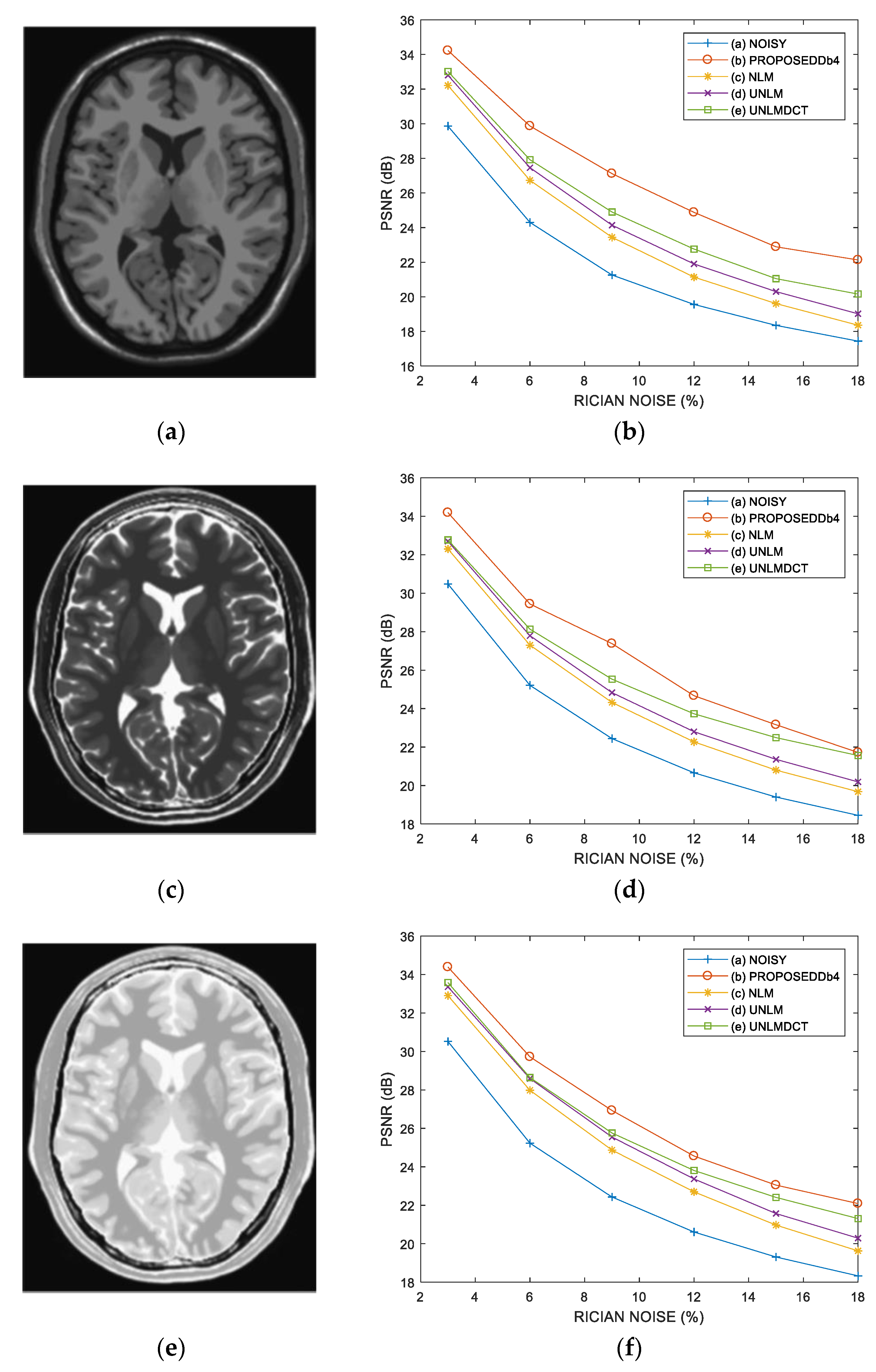
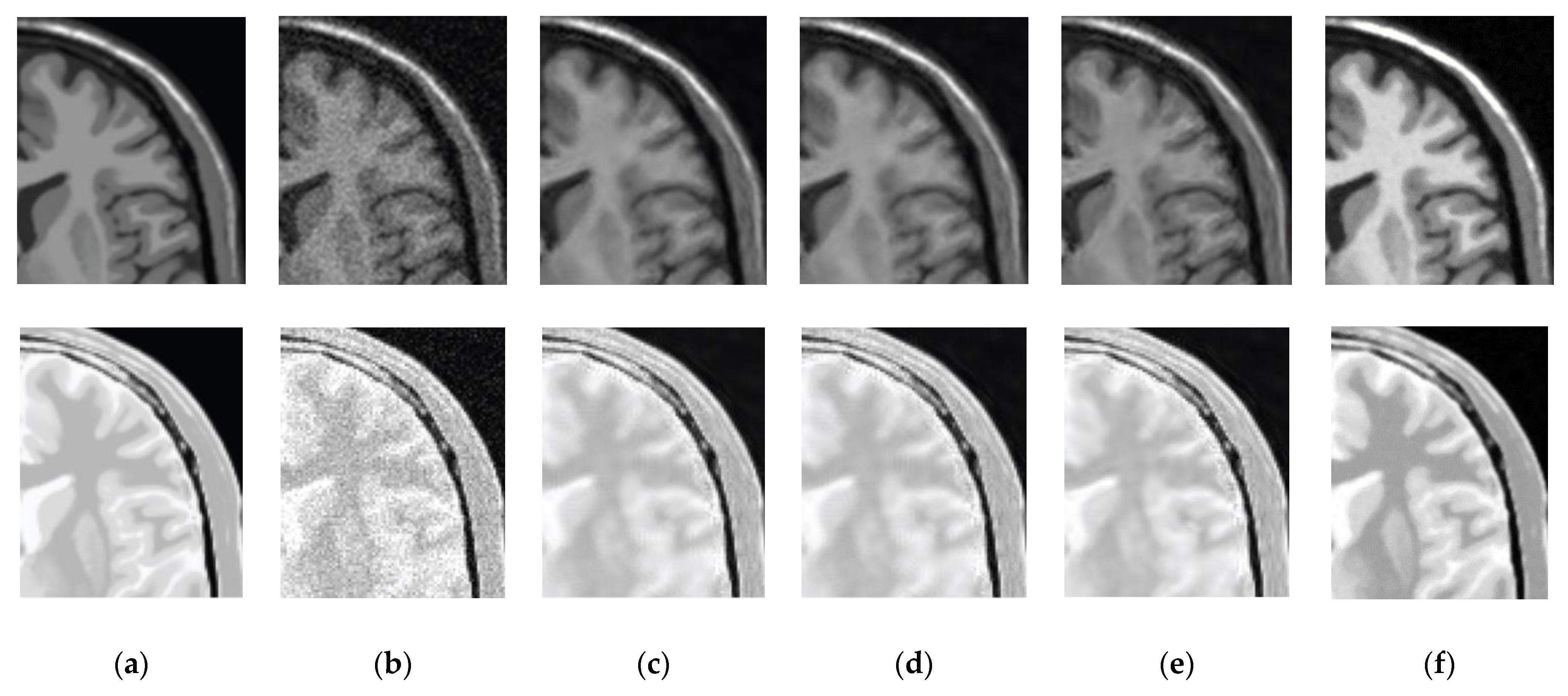
3.3. Comparative Performance in Simulated MRI
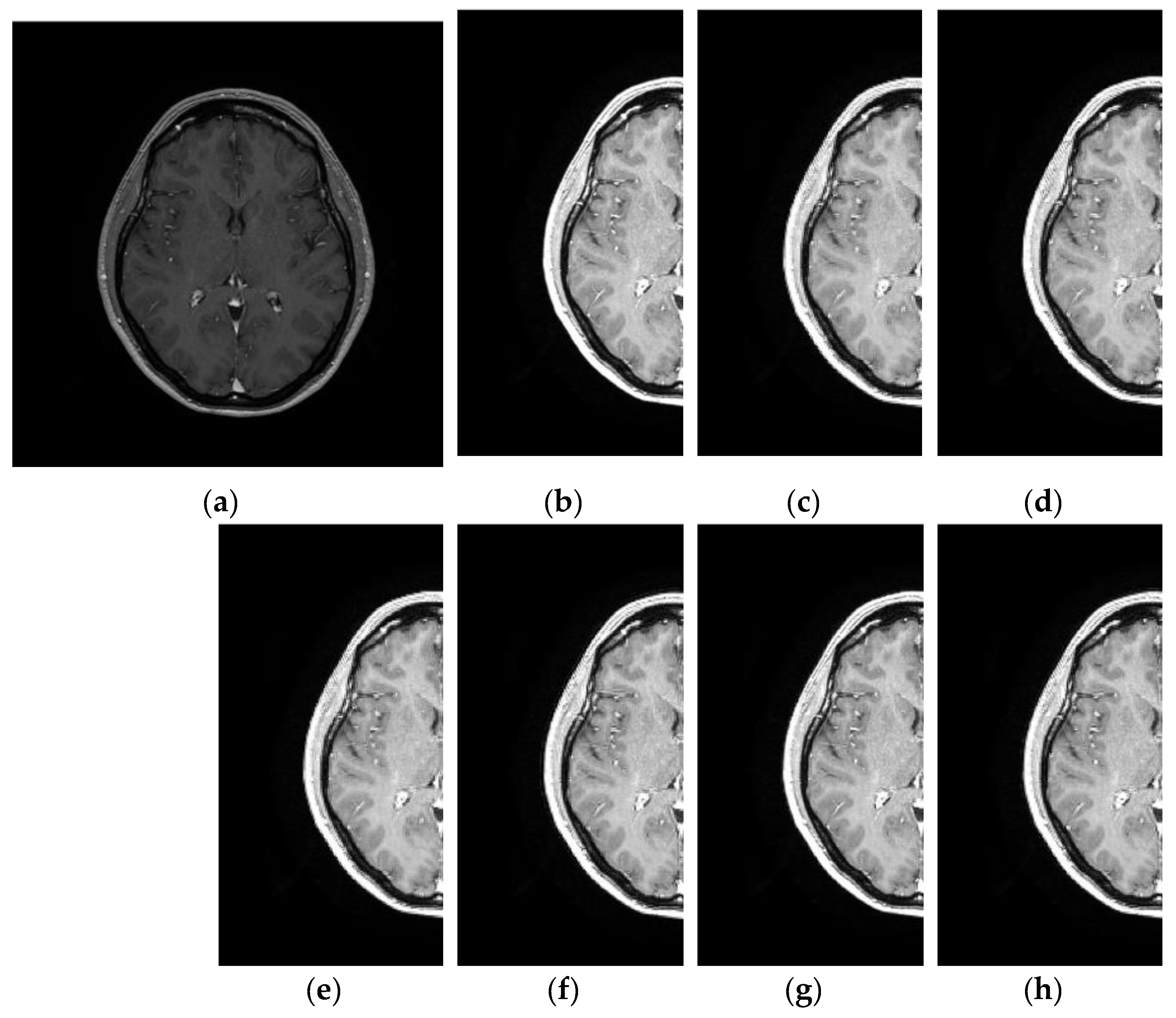
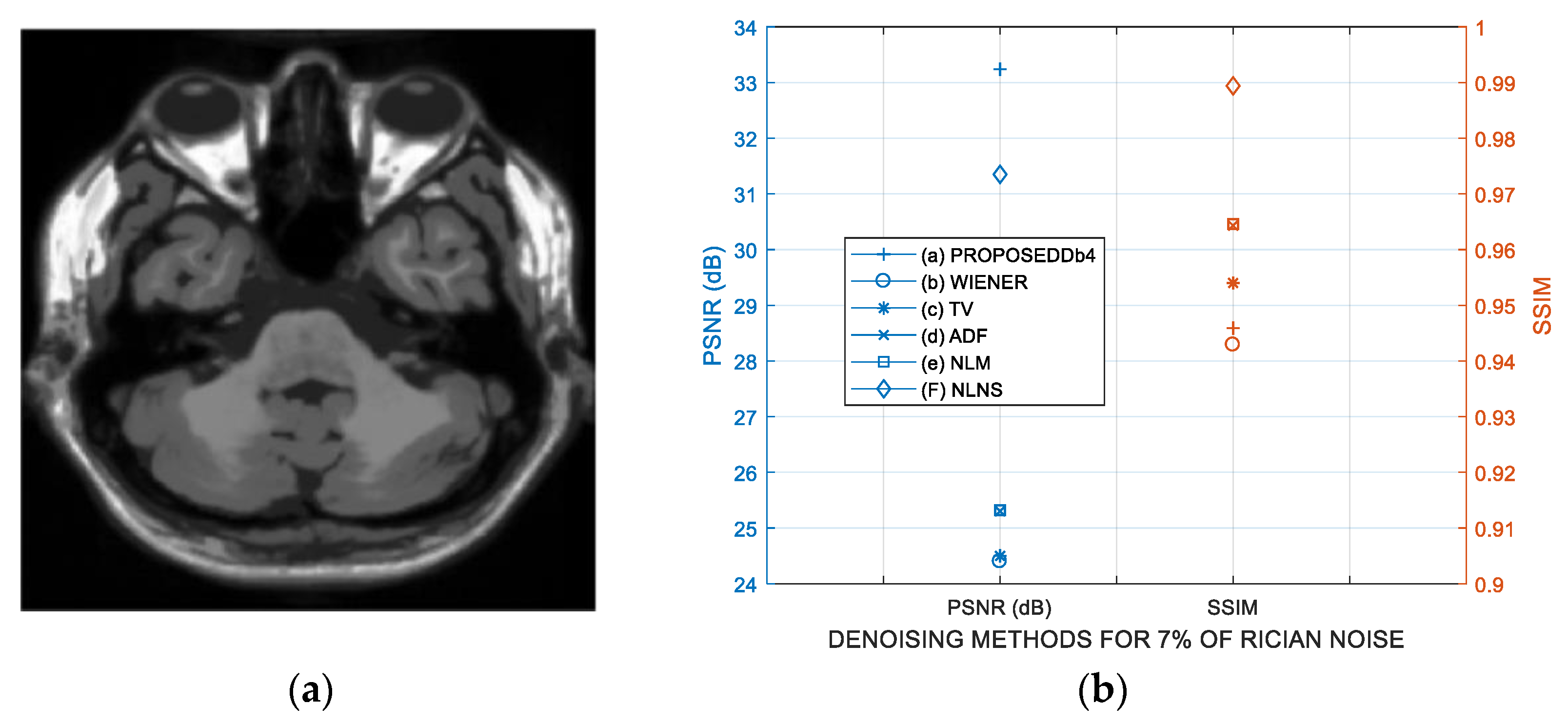
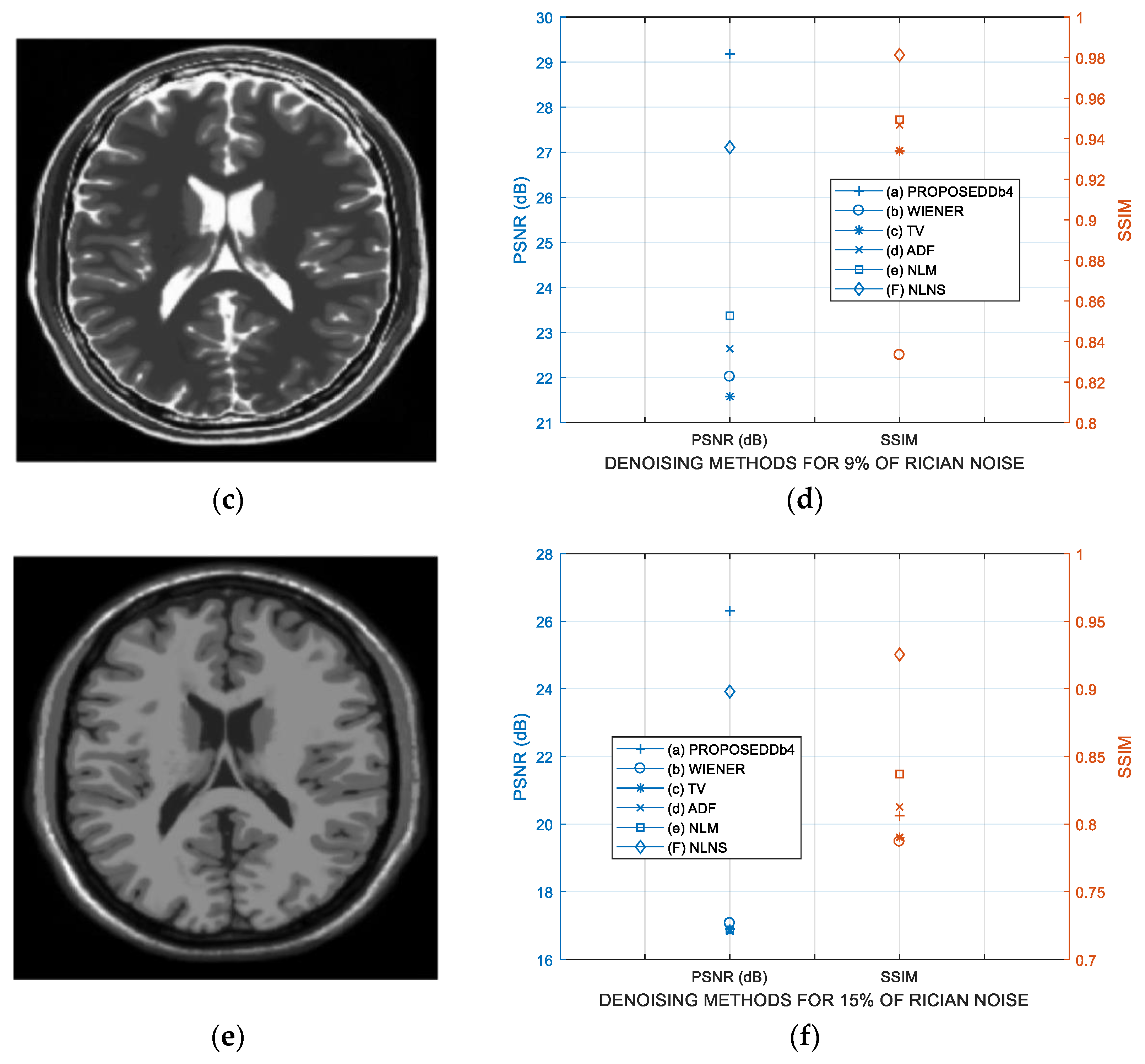
3.4. Comparative Performance in Real MRI
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Makropoulos, A.; Counsell, S.J.; Rueckert, D. A review on automatic fetal and neonatal brain MRI segmentation. NeuroImage 2018, 170, 231–248. [Google Scholar] [CrossRef] [PubMed]
- El Hassani, A.; Majda, A. Efficient image denoising method based on mathematical morphology reconstruction and the Non-Local Means filter for the MRI of the head. In Proceedings of the 4th IEEE International Colloquium on Information Science and Technology (CiSt), Tangier, Morocco, 24–26 October 2016; pp. 422–427. [Google Scholar]
- Dora, L.; Agrawal, S.; Panda, R.; Abraham, A. State-of-the-Art Methods for Brain Tissue Segmentation: A Review. IEEE Rev. Biomed. Eng. 2017, 10, 235–249. [Google Scholar] [CrossRef]
- Gordillo, N.; Montseny, E.; Sobrevilla, P. State of the art survey on MRI brain tumor segmentation. Magn. Reson. Imaging 2013, 31, 1426–1438. [Google Scholar] [CrossRef]
- El-Dahshan, E.A.; Mohsen, H.M.; Revett, K.; Salem, A.M. Computer-aided diagnosis of human brain tumor through MRI: A survey and a new algorithm. Expert Syst. Appl. 2014, 41, 5526–5545. [Google Scholar] [CrossRef]
- Malka, D.; Vegerhof, A.; Cohen, E.; Rayhshtat, M.; Libenson, A.; Shalev, M.A.; Zalevsky, Z. Improved Diagnostic Process of Multiple Sclerosis Using Automated Detection and Selection Process in Magnetic Resonance Imaging. Appl. Sci. 2017, 7, 831. [Google Scholar] [CrossRef]
- Anand, C.S.; Sahambi, J.S. Wavelet domain non-linear filtering for MRI denoising. Magn. Reson. Imaging 2010, 28, 842–861. [Google Scholar] [CrossRef]
- Xu, R.; Wunsch, D.C. Clustering Algorithms in Biomedical Research: A Review. IEEE Rev. Biomed. Eng. 2010, 3, 120–154. [Google Scholar] [CrossRef]
- Shabairou, N.; Cohen, E.; Wagner, O.; Malka, D.; Zalevsky, Z. Color image identification and reconstruction using artificial neural networks on multimode fiber images: Towards an all-optical design. Opt. Lett. 2018, 43, 5603–5606. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Li, M.; Wang, J.; Wu, F.; Liu, T.; Pan, Y. A survey of MRI-based brain tumor segmentation methods. Tsinghua Sci. Technol. 2014, 19, 578–595. [Google Scholar]
- Mohan, J.; Krishnaveni, V.; Guo, Y. A survey on the magnetic resonance image denoising methods. Biomed. Signal Process. Control 2014, 9, 56–69. [Google Scholar] [CrossRef]
- Singh, K.; Ranade, S.K.; Singh, C. Comparative performance analysis of various wavelet and nonlocal means based approaches for image denoising. Optik 2017, 131, 423–437. [Google Scholar] [CrossRef]
- Foi, A.; Boracchi, G. Foveated Nonlocal Self-Similarity. Int. J. Comput. Vis. 2016, 120, 78–110. [Google Scholar] [CrossRef]
- Hyder, S.A.; Sukanesh, R. An efficient algorithm for denoising MR and CT images using digital curvelet transform. Adv. Exp. Med. Biol. 2011, 696, 471–480. [Google Scholar]
- Anila, S.; Sivaraju, S.S.; Devarajan, N. A new contourlet based multiresolution approximation for MRI image noise removal. Natl. Acad. Sci. Lett. 2017, 40, 39–41. [Google Scholar] [CrossRef]
- Nowak, R.D. Wavelet-Based Rician Noise Removal for Magnetic Resonance Imaging. IEEE Trans. Image Process. 1999, 8, 1408–1419. [Google Scholar] [CrossRef]
- He, L.; Greenshields, I.R. A Nonlocal Maximum Likelihood Estimation Method for Rician Noise Reduction in MR Images. IEEE Trans. Med. Imaging 2009, 28, 165–172. [Google Scholar] [PubMed]
- Baselice, F.; Ferraioli, G.; Pascazio, V.; Sorriso, A. Bayesian MRI Denoising in complex domain. Magn. Reson. Imaging 2017, 38, 112–122. [Google Scholar] [CrossRef]
- Jiang, D.; Dou, W.; Vosters, L.; Xu, X.; Sun, Y.; Tan, T. Denoising of 3D magnetic resonance images with multichannel residual learning of convolutional neural network. Jpn. J. Radiol. 2018, 39, 566–574. [Google Scholar] [CrossRef]
- Rajan, J.; den Dekker, A.J.; Sijbers, J. A new non-local maximum likelihood estimation method for Rician noise reduction in magnetic resonance images using the Kolmogorov–Smirnov. Signal Process. 2014, 103, 16–23. [Google Scholar] [CrossRef]
- Baselice, F.; Ferraioli, G.; Pascazio, V.; Sorriso, A. Denoising of MR images using Kolmogorov-Smirnov distance in a Non Local Framework. Magn. Reson. Imaging 2019, 57, 176–193. [Google Scholar] [CrossRef] [PubMed]
- Unser, M.; Aldroubi, A. A review of wavelets in biomedical applications. Proc. IEEE 1996, 84, 626–638. [Google Scholar] [CrossRef]
- Lo, S.C.; Li, H.; Freedman, M.T. Optimization of Wavelet Decomposition for Image Compression and Feature Preservation. IEEE Trans. Med. Imaging 2003, 22, 1141–1151. [Google Scholar] [CrossRef]
- Maheswaran, R.; Khosa, R. Comparative study of different wavelets for hydrologic forecasting. Comput. Geosci. 2012, 46, 284–295. [Google Scholar] [CrossRef]
- Arora, M.; Bashani, S.; Gupta, K.K.; Mohammed, A.M. Wavelet denoising: Comparative analysis and optimization using machine learning. In Proceedings of the 2014 9th International Conference on Industrial and Information Systems (ICIIS), Gwalior, India, 15–17 December 2014; pp. 1–6. [Google Scholar]
- Mitra, S.K. Digital Signal Processing: A Computer Based Approach, 2nd ed.; McGraw-Hill International: Columbus, OH, USA, 2003. [Google Scholar]
- Carvajal-Gamez, B.E.; Gallegos-Funes, F.J.; Rosales-Silva, A.J. Color local complexity estimation based steganographic (CLCES) method. Expert Syst. Appl. 2013, 40, 1132–1142. [Google Scholar] [CrossRef]
- Gallegos-Funes, F.J.; Rosales-Silva, A.J.; Toledo-Lopez, A. Multichannel image processing by using the Rank M-type L-filter. J. Vis. Commun. Image Represent. 2012, 23, 323–330. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C. A Universal Image Quality Index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Arellano-Reynoso, A. Instituto Nacional de Neurología y Neurocirugía. Available online: http://www.innn.salud.gob.mx/ (accessed on 25 February 2019).
- Donoho, D.L.; Johnstone, I.M. Ideal spatial adaptation via wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Chang, S.G.; Yu, B.; Vetterli, M. Adaptive wavelet thresholding for image denoising and compression. IEEE Trans. Image Process. 2000, 9, 1532–1546. [Google Scholar] [CrossRef]
- Zhou, D.; Cheng, W. Image denoising with an optimal threshold and neighboring window. Pattern Recognit. Lett. 2008, 29, 1694–1697. [Google Scholar]
- Buades, A.; Coll, B.; Morel, J. A nonlocal algorithm for image denoising. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; pp. 60–65. [Google Scholar]
- Hu, J.; Pu, Y.; Zhang, Y.; Liu, Y.; Zhou, J. A novel nonlocal means denoising method using the DCT. In Proceedings of the International Conference on Image Processing, Computer Vision, and Pattern Recognition IPCV’11, Las Vegas, NV, USA, 18–21 July 2011; pp. 1–5. [Google Scholar]
- BrianWeb. Available online: http://www.bic.mni.mcgill.ca/brainweb/ (accessed on 25 February 2019).
- Hu, J.; Pu, Y.; Wu, X.; Zhang, Y.; Zhou, J. Improved DCT-based non local means filter for MR images denoising. Comput. Math. Methods Med. 2012, 2012, 1–14. [Google Scholar] [CrossRef]
- Manjón, J.V.; Carbonell-Caballero, J.; Lull, J.J.; García-Martí, G.; Martí-Bonmatí, L.; Robles, M. MRI denoising using nonlocal means. Med Image Anal. 2008, 12, 514–523. [Google Scholar] [CrossRef]
- Mohan, J.; Krishnaveni, V.; Guo, Y. MRI denoising using nonlocal neutrosophic set approach of Wiener filtering. Biomed. Signal Process. Control 2013, 8, 779–791. [Google Scholar] [CrossRef]
- Perona, P.; Malik, J. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 629–639. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 4th ed.; Pearson: Upper Saddle River, NJ, USA, 2017. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Aja-Fernandez, S.; Niethammer, M.; Kubicki, M.; Shenton, M.; Westin, C.-F. Restoration of DWI data using a Rician LMMSE estimator. IEEE Trans. Med. Imaging 2008, 27, 1389–1403. [Google Scholar] [CrossRef]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef]
- Gerig, G.; Kubler, O.; Kikinis, R.; Jolesz, F. Nonlinear anisotropic filtering of MRI data. IEEE Trans. Med Imaging 1992, 11, 221–232. [Google Scholar] [CrossRef]


| Wavelet | PSNR | SSIM |
|---|---|---|
| Haar | 31.60 | 0.941 |
| DB2 | 33.50 | 0.928 |
| DB4 | 35.80 | 0.936 |
| SYM2 | 34.50 | 0.889 |
| SYM4 | 32.65 | 0.891 |
| COIF1 | 31.55 | 0.878 |
| COIF2 | 34.10 | 0.870 |
| Image | Noise(σ) | Proposed Denoising Method | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HAAR | DB2 | DB4 | SYM2 | SYM4 | COIF2 | COIF4 | |||||||||
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | ||
| Lena | 10 | 34.16 | 0.881 | 34.22 | 0.883 | 34.98 | 0.883 | 34.14 | 0.878 | 33.92 | 0.874 | 34.15 | 0.880 | 34.08 | 0.878 |
| 20 | 32.91 | 0.854 | 32.46 | 0.854 | 33.02 | 0.857 | 32.19 | 0.850 | 32.08 | 0.848 | 32.38 | 0.851 | 32.36 | 0.852 | |
| 30 | 29.90 | 0.816 | 30.00 | 0.819 | 30.07 | 0.822 | 29.91 | 0.812 | 29.86 | 0.812 | 29.89 | 0.814 | 29.88 | 0.813 | |
| 40 | 28.71 | 0.779 | 28.70 | 0.779 | 28.78 | 0.788 | 28.66 | 0.772 | 28.39 | 0.764 | 28.45 | 0.768 | 28.42 | 0.766 | |
| 50 | 27.36 | 0.703 | 27.40 | 0.699 | 27.43 | 0.701 | 27.34 | 0.689 | 27.29 | 0.686 | 27.31 | 0.686 | 27.33 | 0.684 | |
| Jetplane | 10 | 35.05 | 0.919 | 35.14 | 0.922 | 35.17 | 0.922 | 35.01 | 0.906 | 34.89 | 0.902 | 34.92 | 0.910 | 34.99 | 0.904 |
| 20 | 31.86 | 0.871 | 31.87 | 0.873 | 31.92 | 0.874 | 31.82 | 0.865 | 31.80 | 0.862 | 31.84 | 0.864 | 31.84 | 0.863 | |
| 30 | 29.92 | 0.819 | 29.92 | 0.821 | 29.96 | 0.827 | 29.90 | 0.816 | 29.87 | 0.815 | 29.91 | 0.817 | 29.90 | 0.815 | |
| 40 | 28.24 | 0.788 | 28.25 | 0.782 | 28.25 | 0.784 | 28.20 | 0.762 | 20.18 | 0.761 | 28.18 | 0.763 | 28.18 | 0.763 | |
| 50 | 27.09 | 0.745 | 27.08 | 0.744 | 27.11 | 0.744 | 27.03 | 0.726 | 26.98 | 0.724 | 27.00 | 0.724 | 27.01 | 0.726 | |
| Mandrill | 10 | 34.39 | 0.922 | 34.44 | 0.922 | 34.46 | 0.924 | 34.36 | 0.913 | 34.35 | 0.905 | 34.37 | 0.917 | 34.36 | 0.909 |
| 20 | 31.67 | 0.837 | 31.71 | 0.844 | 31.75 | 0.847 | 31.63 | 0.832 | 31.61 | 0.826 | 31.63 | 0.834 | 31.62 | 0.829 | |
| 30 | 29.56 | 0.779 | 29.57 | 0.786 | 29.61 | 0.791 | 29.54 | 0.763 | 29.53 | 0.763 | 29.54 | 0.771 | 29.56 | 0.773 | |
| 40 | 27.89 | 0.705 | 27.93 | 0.701 | 27.94 | 0.704 | 27.86 | 0.692 | 27.85 | 0.688 | 27.88 | 0.691 | 27.87 | 0.687 | |
| 50 | 27.08 | 0.661 | 27.11 | 0.661 | 27.15 | 0.660 | 27.05 | 0.650 | 27.01 | 0.639 | 27.03 | 0.654 | 27.03 | 0.638 | |
| House | 10 | 39.21 | 0.939 | 39.23 | 0.944 | 39.23 | 0.945 | 39.16 | 0.936 | 39.15 | 0.921 | 39.17 | 0.937 | 39.18 | 0.924 |
| 20 | 36.24 | 0.911 | 36.30 | 0.914 | 36.33 | 0.919 | 36.22 | 0.904 | 36.19 | 0.901 | 36.22 | 0.903 | 36.19 | 0.902 | |
| 30 | 34.66 | 0.867 | 34.67 | 0.863 | 34.74 | 0.866 | 34.55 | 0.869 | 34.52 | 0.865 | 34.59 | 0.867 | 34.58 | 0.866 | |
| 40 | 33.13 | 0.851 | 33.12 | 0.842 | 33.17 | 0.847 | 33.03 | 0.840 | 32.98 | 0.827 | 32.99 | 0.832 | 33.03 | 0.828 | |
| 50 | 31.67 | 0.836 | 31.70 | 0.834 | 31.72 | 0.836 | 31.64 | 0.819 | 31.64 | 0.814 | 31.65 | 0.818 | 31.67 | 0.818 | |
| Boat | 10 | 34.00 | 0.891 | 34.17 | 0.883 | 34.19 | 0.889 | 33.94 | 0.869 | 33.91 | 0.864 | 33.93 | 0.871 | 33.94 | 0.866 |
| 20 | 31.83 | 0.821 | 31.85 | 0.825 | 31.88 | 0.829 | 31.79 | 0.812 | 31.71 | 0.804 | 31.77 | 0.816 | 31.77 | 0.806 | |
| 30 | 29.67 | 0.766 | 29.69 | 0.769 | 29.69 | 0.767 | 29.49 | 0.758 | 29.48 | 0.755 | 29.53 | 0.759 | 29.58 | 0.759 | |
| 40 | 28.00 | 0.723 | 28.04 | 0.721 | 28.07 | 0.723 | 27.92 | 0.709 | 27.90 | 0.700 | 27.97 | 0.707 | 27.96 | 0.704 | |
| 50 | 26.77 | 0.651 | 26.77 | 0.647 | 26.79 | 0.648 | 26.70 | 0.638 | 26.69 | 0.629 | 26.72 | 0.636 | 26.76 | 0.633 | |
| Lake | 10 | 33.07 | 0.888 | 33.07 | 0.897 | 33.08 | 0.897 | 32.96 | 0.876 | 32.95 | 0870 | 32.98 | 0.875 | 32.99 | 0.867 |
| 20 | 30.29 | 0.823 | 30.33 | 0.829 | 30.37 | 0.826 | 30.26 | 0.819 | 30.26 | 0.809 | 30.26 | 0.817 | 30.28 | 0.811 | |
| 30 | 28.78 | 0.780 | 28.79 | 0.783 | 28.81 | 0.784 | 28.73 | 0.766 | 28.72 | 0.766 | 28.76 | 0.774 | 28.75 | 0.769 | |
| 40 | 27.34 | 0.739 | 27.39 | 0.737 | 27.44 | 0.739 | 27.30 | 0.724 | 27.28 | 0.723 | 27.31 | 0.720 | 27.33 | 0.721 | |
| 50 | 26.76 | 0.701 | 26.84 | 0.696 | 26.88 | 0.699 | 26.77 | 0.689 | 26.72 | 0.689 | 26.74 | 0.691 | 26.74 | 0.692 | |
| Peppers | 10 | 34.79 | 0.879 | 34.84 | 0.888 | 34.85 | 0.882 | 34.77 | 0.868 | 34.76 | 0.856 | 34.77 | 0.863 | 34.78 | 0.863 |
| 20 | 33.45 | 0.821 | 33.46 | 0.826 | 33.49 | 0.827 | 33.44 | 0.817 | 33.39 | 0.811 | 33.42 | 0.808 | 33.42 | 0.809 | |
| 30 | 31.37 | 0.781 | 31.36 | 0.781 | 31.40 | 0.783 | 31.33 | 0.779 | 31.28 | 0.769 | 31.34 | 0.772 | 31.33 | 0.770 | |
| 40 | 30.09 | 0.746 | 30.10 | 0.742 | 30.10 | 0.746 | 29.91 | 0.733 | 29.87 | 0.732 | 29.88 | 0.734 | 26.87 | 0.732 | |
| 50 | 28.87 | 0.716 | 28.90 | 0.713 | 28.94 | 0.715 | 28.85 | 0.698 | 28.82 | 0.681 | 28.83 | 0.697 | 28.81 | 0.694 | |
| Barbara | 10 | 33.39 | 0.886 | 33.39 | 0.886 | 33.41 | 0.888 | 33.34 | 0.877 | 33.30 | 0.875 | 33.35 | 0.876 | 33.31 | 0.879 |
| 20 | 29.02 | 0.829 | 29.07 | 0.829 | 29.17 | 0.831 | 29.00 | 0.817 | 28.97 | 0.812 | 28.98 | 0.813 | 29.01 | 0.815 | |
| 30 | 27.00 | 0.761 | 27.02 | 0.760 | 27.02 | 0.763 | 26.89 | 0.750 | 26.76 | 0.744 | 26.72 | 0.747 | 26.74 | 0.749 | |
| 40 | 25.61 | 0.726 | 25.61 | 0.724 | 25.65 | 0.725 | 25.54 | 0.719 | 25.52 | 0.712 | 25.52 | 0.714 | 25.50 | 0.714 | |
| 50 | 24.98 | 0.678 | 25.02 | 0.672 | 25.02 | 0.674 | 24.97 | 0.656 | 24.92 | 0.655 | 24.95 | 0.658 | 24.94 | 0.661 | |
| Pirate | 10 | 34.10 | 0.887 | 34.12 | 0.890 | 34.17 | 0.890 | 34.06 | 0.876 | 34.00 | 0.876 | 34.05 | 0.879 | 34.06 | 0.875 |
| 20 | 31.94 | 0.827 | 32.01 | 0.833 | 32.01 | 0.835 | 31.86 | 0.820 | 31.83 | 0.814 | 31.88 | 0.808 | 31.89 | 0.813 | |
| 30 | 29.46 | 0.779 | 29.51 | 0.781 | 29.52 | 0.780 | 29.44 | 0.755 | 29.41 | 0.752 | 29.44 | 0.756 | 29.42 | 0.752 | |
| 40 | 28.64 | 0.722 | 28.69 | 0.720 | 28.72 | 0.720 | 28.61 | 0.711 | 28.59 | 0.710 | 28.61 | 0.712 | 28.60 | 0.708 | |
| 50 | 26.78 | 0.686 | 26.79 | 0.677 | 26.79 | 0.682 | 26.73 | 0.659 | 26.71 | 0.662 | 26.73 | 0.663 | 26.72 | 0.664 | |
| Texture | 10 | 32.35 | 0.936 | 32.48 | 0.943 | 32.49 | 0.944 | 32.36 | 0.928 | 32.35 | 0.924 | 32.33 | 0.928 | 32.34 | 0.928 |
| 20 | 28.07 | 0.885 | 28.11 | 0.889 | 28.14 | 0.893 | 28.04 | 0.877 | 28.04 | 0.869 | 28.06 | 0.875 | 28.04 | 0.873 | |
| 30 | 26.28 | 0.823 | 26.33 | 0.822 | 26.36 | 0.824 | 26.27 | 0.807 | 26.25 | 0.800 | 26.27 | 0.803 | 26.26 | 0.807 | |
| 40 | 24.11 | 0.737 | 24.15 | 0.731 | 24.15 | 0.733 | 24.05 | 0.722 | 24.02 | 0.722 | 24.04 | 0.719 | 24.05 | 0.721 | |
| 50 | 22.88 | 0.681 | 22.97 | 0.674 | 23.03 | 0.676 | 22.88 | 0.663 | 22.83 | 0.660 | 22.87 | 0.664 | 22.86 | 0.661 | |
| Average | 10 | 34.49 | 0.902 | 34.51 | 0.905 | 34.60 | 0.907 | 34.41 | 0.892 | 34.35 | 0.886 | 34.40 | 0.893 | 34.38 | 0.889 |
| 20 | 31.72 | 0.847 | 31.71 | 0.851 | 31.81 | 0.853 | 31.62 | 0.841 | 31.58 | 0.835 | 31.64 | 0.838 | 31.64 | 0.837 | |
| 30 | 29.67 | 0.797 | 29.68 | 0.798 | 29.71 | 0.800 | 26.66 | 0.786 | 29.56 | 0.784 | 29.59 | 0.788 | 29.60 | 0.783 | |
| 40 | 28.28 | 0.751 | 29.09 | 0.749 | 29.12 | 0.750 | 28.10 | 0.738 | 27.25 | 0.733 | 28.08 | 0.736 | 27.78 | 0.734 | |
| 50 | 27.02 | 0.705 | 27.05 | 0.701 | 27.08 | 0.703 | 26.99 | 0.688 | 26.96 | 0.683 | 26.98 | 0.689 | 26.96 | 0.687 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orea-Flores, I.Y.; Gallegos-Funes, F.J.; Arellano-Reynoso, A. Local Complexity Estimation Based Filtering Method in Wavelet Domain for Magnetic Resonance Imaging Denoising. Entropy 2019, 21, 401. https://doi.org/10.3390/e21040401
Orea-Flores IY, Gallegos-Funes FJ, Arellano-Reynoso A. Local Complexity Estimation Based Filtering Method in Wavelet Domain for Magnetic Resonance Imaging Denoising. Entropy. 2019; 21(4):401. https://doi.org/10.3390/e21040401
Chicago/Turabian StyleOrea-Flores, Izlian Y., Francisco J. Gallegos-Funes, and Alfonso Arellano-Reynoso. 2019. "Local Complexity Estimation Based Filtering Method in Wavelet Domain for Magnetic Resonance Imaging Denoising" Entropy 21, no. 4: 401. https://doi.org/10.3390/e21040401
APA StyleOrea-Flores, I. Y., Gallegos-Funes, F. J., & Arellano-Reynoso, A. (2019). Local Complexity Estimation Based Filtering Method in Wavelet Domain for Magnetic Resonance Imaging Denoising. Entropy, 21(4), 401. https://doi.org/10.3390/e21040401





