Abstract
A new -emitting 214U has been recently observed experimentally. This opens the window to theoretically investigate the ground-state properties of the lightest known even–even neutron deficient 214,216,218U isotopes and to examine -particle clustering around the shell closure. The decay half-lives are calculated within the preformed cluster-decay model (PCM). To obtain the -daughter interaction potential, the RMF densities are folded with the newly developed R3Y and the well-known M3Y NN potentials for comparison. The alpha preformation probability is calculated from the analytic formula of Deng and Zhang. The WKB approximation is employed for the calculation of the transmission probability. The individual binding energies (BE) for the participating nuclei are estimated from the relativistic mean-field (RMF) formalism and those from the finite range droplet model (FRDM) as well as WS3 mass tables. In addition to , the so-called abnormal enhancement region, i.e., and , is normalised by an appropriately fitted neck-parameter . On the other hand, the discrepancy sets in due to the shell effect at (and around) the proton magic number and 84, and thus a higher scaling factor ranging from – is required. Additionally, in contrast with the experimental binding energy data, large deviations of about 5–10 MeV are evident in the RMF formalism despite the use of different parameter sets. An accurate prediction of -decay half-lives requires a Q-value that is in proximity with the experimental data. In addition, other microscopic frameworks besides RMF could be more reliable for the mass region under study. -particle clustering is largely influenced by the shell effect.
1. Introduction
Instability is highly prevalent in heavy nuclei due to the Coulomb repulsion of several protons involved. To gain stability, heavy nuclei naturally dispose of the excess positive charges via alpha ()-decay. An -particle itself is characterised by high stability and a tightly bound structure. The discovery of -decay dates back to 1896 when it was observed as natural radioactivity and later confirmed in Rutherford’s experiment in 1908. This was given credence in the theoretical interpretation of -decay explained as a quantum tunnelling effect. Thereafter, the relationship between the decay energy of -particles and half-lives was empirically deduced by Geiger and Nuttal [1,2]. Alpha decay has been proven to be a powerful tool that incorporates nuclear structure information [3,4], such as ground-state half-life and energy [5,6], stellar nucleosynthesis [7,8], cluster decay [9], exotic nuclei in the superheavy mass region [8], closed-shell region [10,11], proton-neutron drip line region [12,13], and the shell structure [11,14].
The development of radioactive beams across the globe since they were first used a few decades ago has extended the frontiers of the knowledge of the nuclear shell structure, especially in light nuclei. Yet, from the experimental front, little is presently known of the structure evolution in the heavy nuclei around and below the neutron shell closure at [12,15,16]. Particularly, some neutron-deficient nuclei around the region in the heavy-ion reaction are often excluded in the in-beam -ray experiments [17]. On the other hand, all theoretical probes on this shell closure emanate from either the nuclear fission [18,19,20] or Gamow theory of -decay [21,22,23,24,25]. The former relegates the idea of preformation; i.e., it is assumed that clusters are formed during the separation/deformation process of the parent nucleus while penetrating the confining interaction barrier. In Gamow’s prescription [26], the -particle decay is considered as a quantum tunnelling process of a preformed -particle penetrating the potential barrier. This presupposes that -preformation probability could be incorporated into -decay theories as -cluster preformation. One of the models that embraces this theory is the preformed cluster-decay model (PCM), which stems from the well-known quantum mechanical fragmentation theory (QMFT). In the PCM, an -particle is assumed to be preborn within the parent nucleus and thereafter tunnels through the potential barrier generated by the superposition of the nuclear and Coulomb potentials [26,27,28]. Obtaining the Coulomb potential is straightforward, whereas the nuclear potential can be deduced via phenomenological [29,30] and microscopic approaches [31,32]. Thus, to gain insight into the decay phenomena, the choice of nuclear potential is crucial [30]. In addition to the fundamental approaches [33,34], the newly developed R3Y nucleon-nucleon (NN) potential [35,36], which is analogous to the phenomenological M3Y [37], is derived from the relativistic mean-field (RMF) Lagrangian and is applied in the present work for the study of emission using the NL parameter set, which has been successfully employed in the study of various ground- and excited-state properties [38,39,40].
Recently, a new neutron-deficient -emitting isotope produced by the fusion- evaporation reaction has been observed [15]. Its -decay energy and half-life were measured to be KeV and ms, respectively. Hence, is the lightest known even-A uranium isotope until now. This necessitates a detailed investigation of the ground-state properties of . The authors [15] also reported that an abnormal enhancement was observed in the reduced width of other re-measured light even-even isotopes around the proton closed-shell and neutron closed-shell . This constitutes our motivation to theoretically examine this phenomenon in the -decay chain of these lighter uranium isotopes using the PCM within the RMF framework [41,42,43], which is cognate with the energy density functional formalism and gives an accurate description of both ground and excited-state properties across the entire nuclear landscape [44]. However, previous theoretical studies [28,45] hold that a constant scaling factor (CSF) of is required for the calculation of the -decay half-lives of nuclei in the superheavy region within the PCM framework at the ground state (at temperature, ). Thus, the present study is also aimed at answering two pertinent questions: (1) Does the -decay of lighter uranium follow a similar trend as those from other superheavy nuclei? More precisely, does the constant scaling factor that appears in PCM calculations for the superheavy region apply to other regions in the nuclear chart? (2) If yes, what will be the course (of the CSF) for the lightest isotopes (around and shell closures) where an abnormal enhancement has just been observed?
The only variable parameter in the PCM is the neck-length parameter , which assimilates the neck formation effect between two nuclei and determines the first turning point of the barrier penetration. In this context, is always fitted to the experimental data within the proximity potential limit of up to 2 fm [28,46]. The inputs of PCM include the preformation probability (), calculated from the analytic formula of Deng and Zhang [47,48], and penetration probability (P), using the WKB approximation [49,50,51]. The binding energy (BE) estimated from the microscopic RMF formalism and those from the FRDM [52] and WS3 [53] are utilised to calculate the Q-values of the -decay. Thus, the dynamics of -decay are analysed in detail.
The paper is organised as follows: In Section 2, the relativistic mean-field formalism and the nucleus–nucleus potential obtained from the double-folding procedure for R3Y and M3Y NN-potential using the densities of the daughter and cluster. This section concludes with a brief overview of the PCM. Section 3 is assigned to the discussion of the results obtained from our calculation. The summary of our findings and a brief conclusion is given in Section 4.
2. Theoretical Framework
The isotopes of uranium, namely U, are studied here microscopically within the relativistic mean-field formalism in which the interaction between the many-body system of nucleons and mesons is expressed via the non-linear effective Lagrangian [41,42,43,54,55,56,57,58],
The scalar meson and vector meson account for the medium-range attraction and the short-range repulsion between the nucleons, respectively. The isovector-vector meson describes the isospin-dependent effects in the nuclei. Their respective masses are , and with the coupling constants , and . The Dirac Spinor, isospin and its third component are denoted as , and , respectively. Parameters , and are the coupling constants of the non-linear terms. M is the mass of nucleon and stands for the electromagnetic field. The -meson is not considered since its contribution is negligible owing to its pseudoscalar nature [42,57]. From Equation (1), the classical variation principle is employed to deduce the Dirac equation,
to obtain the nuclear spinors and the Klein–Gordon equations
A numerical solution is then carried out self-consistently using an iterative approach with NL3* parameter set [59]. Taking the limit of a single-meson exchange for static baryonic medium, the scalar, - and vector -fields are expressed in terms of the nucleon–nucleon potentials as
The contribution of -meson is subsumed in the -field [57] and, hence, is negligible. The sum of the expressed NN interactions in Equations (4) gives the RMF-based-R3Y NN effective interactions plus a single-nucleon exchange effect [60]
where MeV fm. represents the mass of the -particle and symbolises the energy measured in the centre of mass of the decay fragments (-daughter) system whose magnitude is equal to energy released for the decay process (-value). Unlike the energies required in high-energy -scattering, could be independent of the -value and is often used in its approximated form, as seen in Ref. [61].
The M3Y (Michigan-3-Yukawa) is composed of a 0.25 fm medium-range attractive part, 0.4 fm short-range repulsive part and 1.414 fm long-range tail of one-pion exchange potential (OPEP), which proceeds from the fitting of G-matrix elements predicated on Reid-Elliott soft-core NN interaction [37] on an oscillator basis. The M3Y plus exchange term takes the form
where the unit of the ranges are in fm and the strength is in MeV. The nuclear interaction potential is calculated here within the double-folding approach [37] and is given as
Here, and are the nuclear matter density distributions of the alpha particle () and the daughter nucleus (d), respectively. To obtain the alpha–daughter interaction potential, the nuclear potential is added to the Coulomb potential and is given as
This potential is used in the calculation of the WKB penetration probability in the PCM.
Preformed Cluster-Decay Model (PCM)
The alpha-decay half-life in the preformed cluster-decay model (PCM) can be estimated as [62,63]
The decay constant denotes the probability per unit time for each nucleus to decay. It is assumed that clusters are preborn within the parent nucleus with certain preformation and hits the potential barrier with an assault frequency , given as
and thereafter tunnels with a probability P. represents the radius of the parent nucleus. A necessary condition for the energetically favoured spontaneous emission of the -particle is a positive Q-value. This is the total energy available for the decay process. The Q-values are obtained from the ground-state binding energies from the expression
where , and are the binding energies of the parent and daughter nuclei and the emitted -particle, respectively. The Q values are rationed between both fragments such that -particle and the recoil energy of the daughter since .
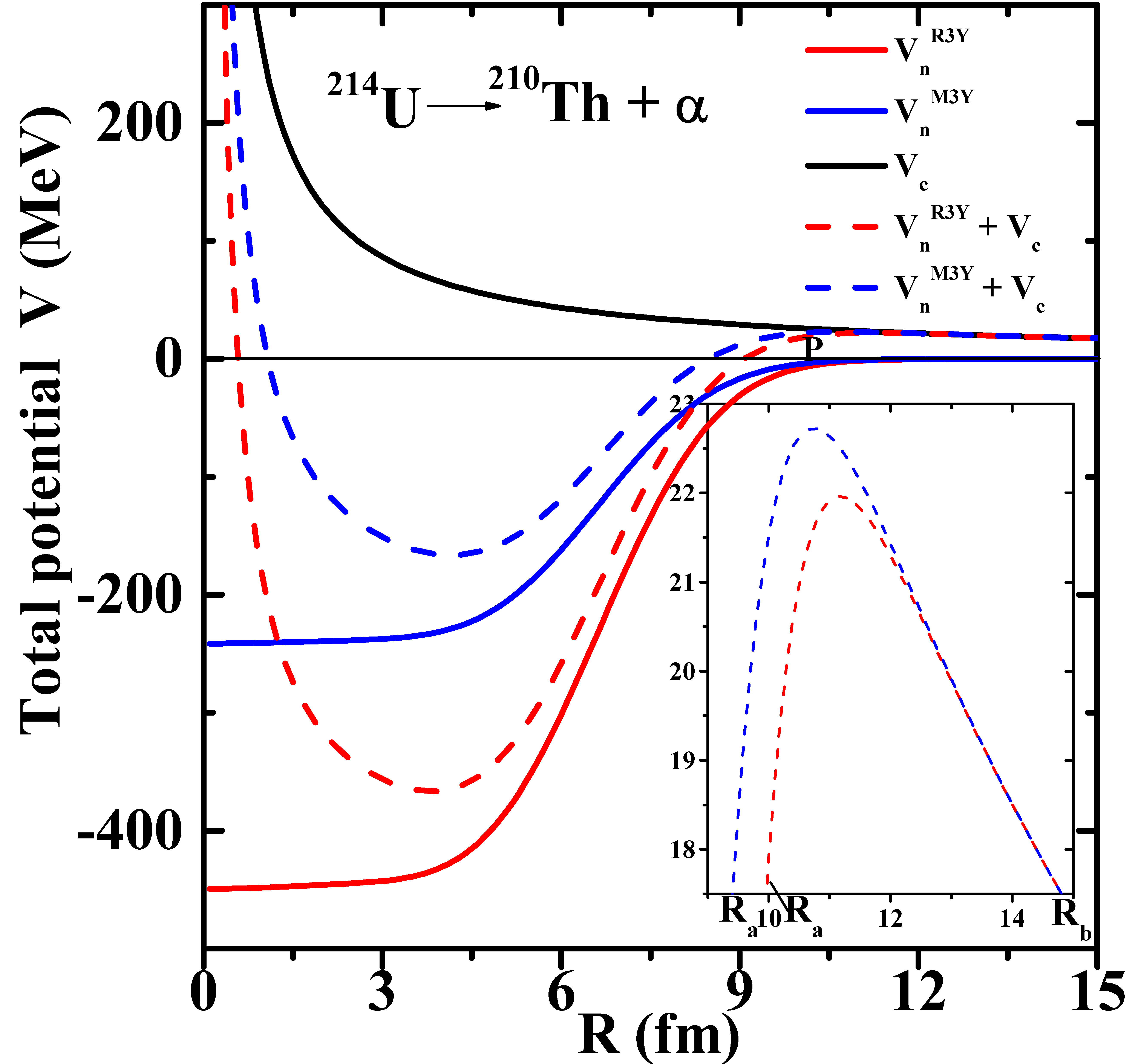
The first turning point shown in Figure 1, which illustrates the penetration path of the decaying compound nucleus , is given as
Here, is the relative separation distance between two outcoming nuclei, which incorporates the neck formation effects between them and hence is referred to as the neck-length parameter. is introduced similarly as those of the scission point [64] and saddle point [65,66] in statistical fission models. In the present context, the neck parameter is fitted to predict the experimentally measured half-lives. It is pertinent to note that the Q-value of the reaction influences the choice of the neck length. As such, it is required that the potential at the first turning point should be higher than the Q-value.
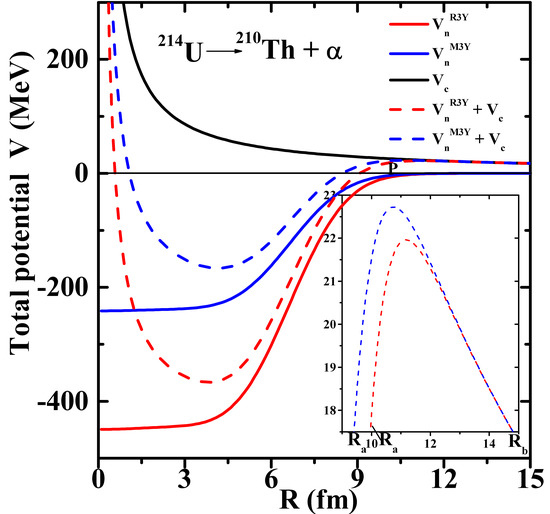
Figure 1.
The total nucleus-nucleus interaction potential V (MeV) and its components, namely, nuclear and Coulomb potentials as a function of radial separation R (fm) for R3Y (NL) and M3Y NN potentials as a representative case of U →Th + . The inset shows a magnified view of the barrier height and position.
Figure 1.
The total nucleus-nucleus interaction potential V (MeV) and its components, namely, nuclear and Coulomb potentials as a function of radial separation R (fm) for R3Y (NL) and M3Y NN potentials as a representative case of U →Th + . The inset shows a magnified view of the barrier height and position.
In the PCM framework, the preformation probability (otherwise called the spectroscopic factor) encapsulates the structural information of the decaying parent nucleus. From a microscopic perspective, it is difficult to obtain the exact value of due to the complexities associated with the nuclear many-body problem. Nonetheless, could be several orders of magnitude below unity [22,62]. Here, the -particle preformation is calculated from the analytic formula of Deng and Zhang [47,48], who successfully employed it in the investigation of some neutron-deficient nuclei. The authors also reported that this formula gives an accurate prediction of -decay half-lives for known and unsynthesised superheavy nuclei and sheds light on some microscopic nuclear structure information such as odd-even staggering and the shell effect. It takes the expression
where
The mass and proton numbers of the decaying parent nucleus are denoted as , respectively. l is the angular momentum carried by the -particle. In this study, since all nuclei are considered to be in the ground state. The adjustable parameters and k have been fitted with the experimental data as given in Ref. [47] and their respective values are the same for the region, as mentioned in Ref. [48]. It is worth noting that this analytical formula from Deng et al. is based on the GLDM with an elliptic lemniscatoid geometry. The family of the elliptic lemniscatoid geometries are obtained by the inversion of spheroids [67], in which the daughter nucleus is assumed to be almost spherical. Moreover, it has been established [68] that the shape evolves continuously from one spherical nucleus to two touching spherical nuclei and naturally results in the formation of a conspicuous neck. This geometry may not be the best compromise in -emission since its touching-point configuration is characterised by the existence of cusp, leading to an abrupt reversal in motion of the relative distance (see Ref. [69] for elaborate details). However, our goal in the present work is to investigate the behaviour of the RMF formalism. A more suitable preformation formula is being developed and will be communicated shortly.
The -particle tunnels through the interaction potential , starting from the first turning point , and terminates at the second turning point , whose corresponding potential for ground-state decays (illustrated in the inset of Figure 1). On the other hand, , where (as adopted by Malik et al. [62]) is the energy with which the -particle or daughter nucleus decays into an excited state. At the radius of the parent nucleus , the potential of the system is equal to its Q value. The shape of the parent nucleus changes as instability sets in, leading to the separation of the -particle and neck formation. To deduce the barrier penetration probability P, using the WKB approximation, three basic steps are involved [62]: (a) the penetrability from to , (b) the (inner) de-excitation probability at , taken as one [70], and (c) the penetrability from to , which leads to the penetration probability
where and are the integrals in the WKB approximation and are given as:
where is the reduced mass given by . The above integrals in Equations (15) and (16) are solved numerically to obtain the penetration probability.
3. Calculations and Discussions
The present work aims to theoretically investigate the -decay properties of the newly measured as well as the even-even isotopes within the PCM framework. The nuclear interaction potential (shown in Figure 1) is deduced from the RMF approach using the recently developed R3Y (with NL parameter set) and the well-known phenomenological M3Y NN interactions. Three different sets of Q-values calculated from the binding energy data FRDM [52], WS3 [53] and those from the RMF formalism (NL) were employed.
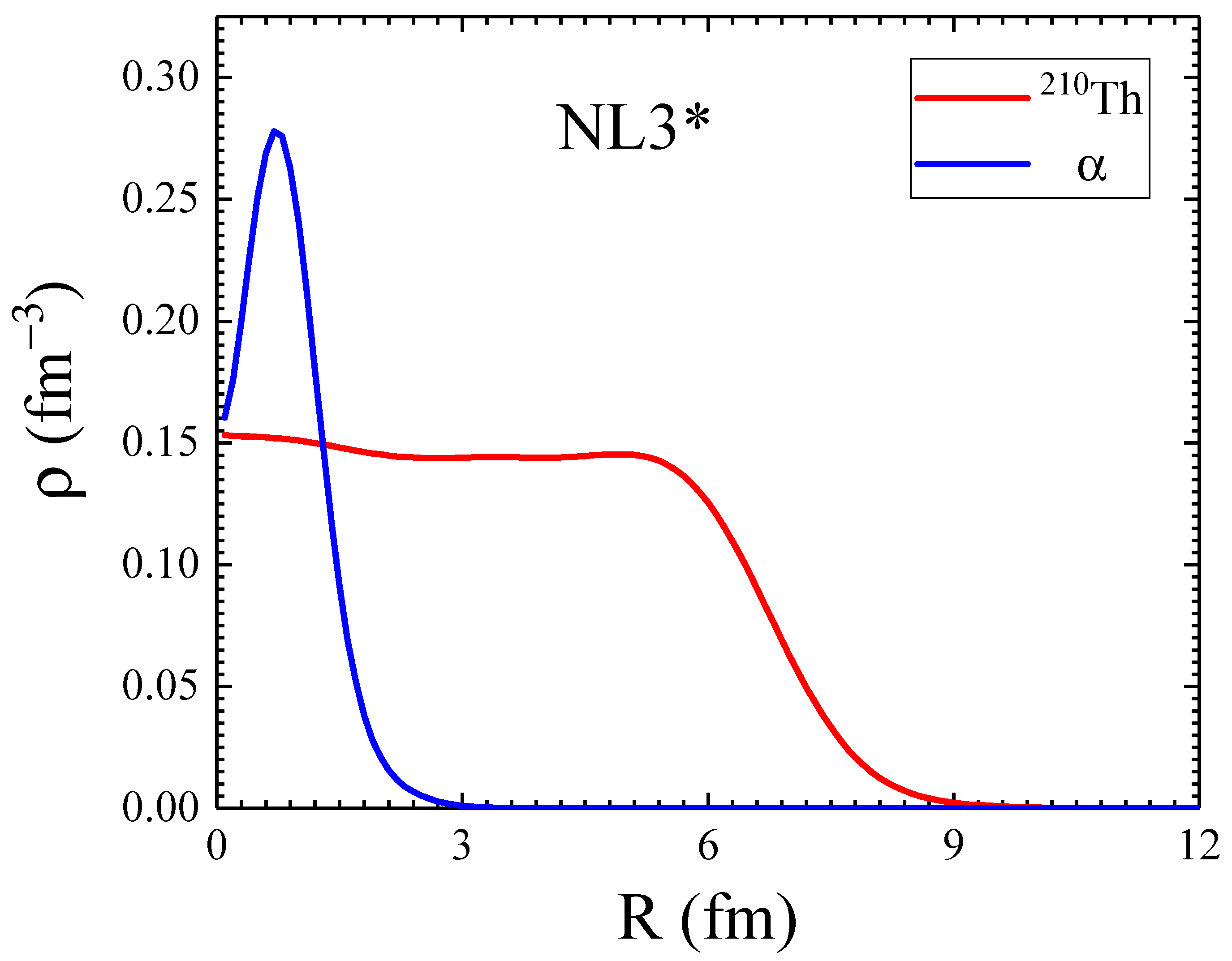
As a representative case, the total radial density distribution of the fragments (daughter nucleus Th (red line) and -particle (blue line)) in Figure 1 is conspicuously shown in Figure 2 as a function of the radius. A similar figure can be obtained for all the participating nuclei under study (but not shown here for the sake of clarity). From the figure, the density of Th displays a lower magnitude around the central position and increases towards the surface region while the reverse is observed for the -particle due to Coulomb repulsion and the difference in their respective mass. It is imperative to note that in Ref. [71], the density-dependent M3Y (DDM3Y) NN interactions were introduced to reproduce the saturation properties of nuclear matter. The inclusion of the DDM3Y NN interaction in the double-folding approach leads to the modification of nuclear potential, especially at small separation distances where the density overlap is larger and hence the density dependence of NN interaction becomes important. However, the present study aims to compare the results of widely adopted M3Y and recently proposed relativistic R3Y NN interactions. Therefore, to avoid complexities, we have only considered the simple density-independent M3Y NN interaction. A more comprehensive study involving the density dependence of both M3Y and R3Y is under process and will be communicated shortly. The respective neck parameter is optimised for each reaction system about the experimental half-life for both the cases of M3Y and R3Y NN interactions.
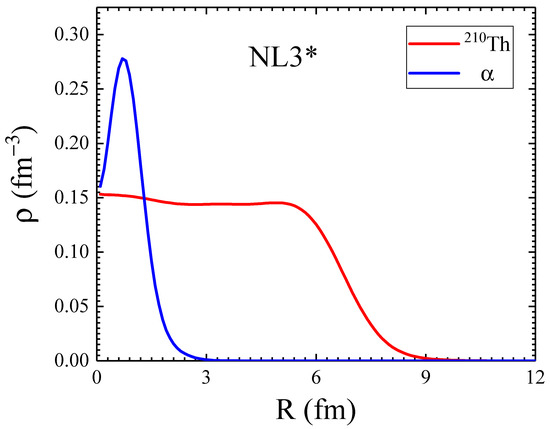
Figure 2.
The total radial density distribution of obtained from the RMF (NL) parameter set and those of -particle, deduced from the experimental data [72] (following the illustration in Figure 1). See text for details.
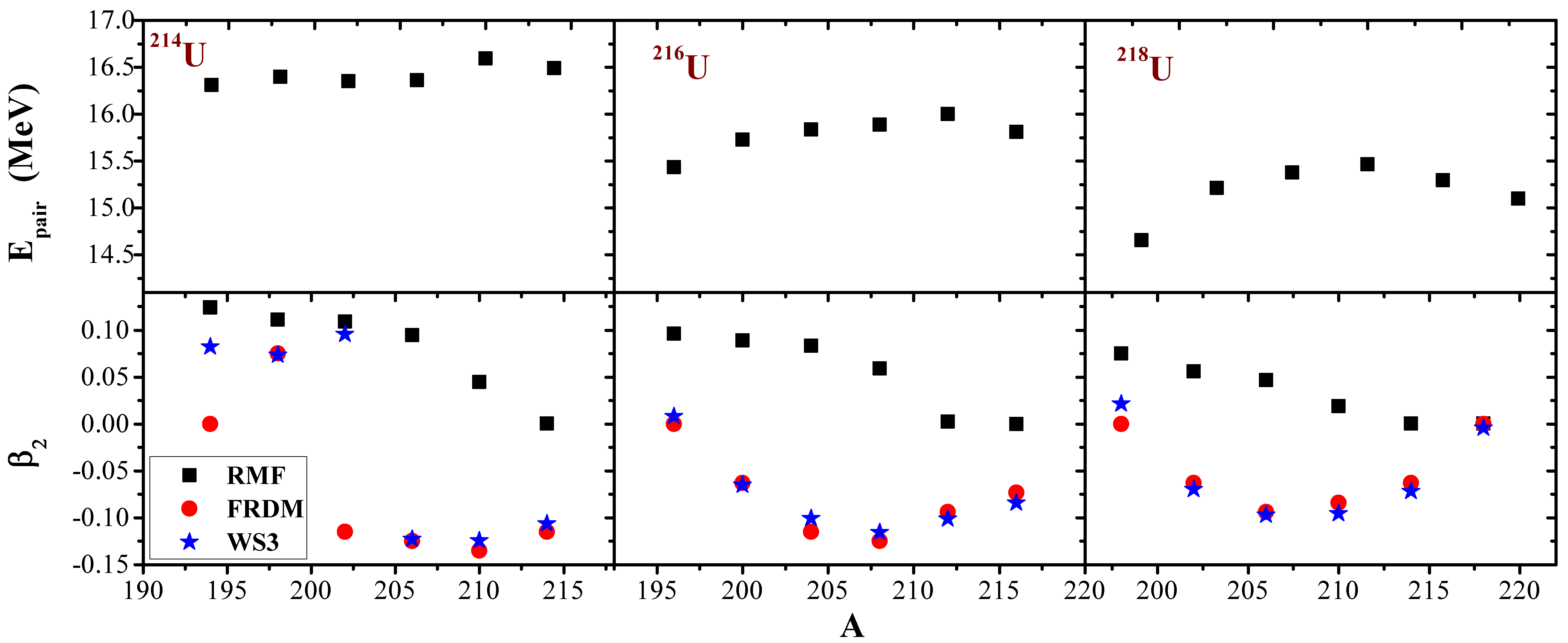
Several parameters are involved in estimating the ground-state properties of nuclei using the relativistic mean-field Lagrangian. Examples of such parameters which include the binding energy (BE), charge radius , quadrupole deformation parameter , pairing energies and other bulk properties, are replete in the literature [40,73,74]. These mentioned parameters are obtained from RMF predictions for all the participating nuclei in the first decay chain (), second decay chain () and the third decay chain () and are compared with those of the FRDM ones given in the Table 1. As such, with an appropriate choice of parameter set, the predicted results are nearly force independent [6]. Note that, in Table 1, the RMF (NL) results are displayed in columns 2–10 and their respective FRDM and WS3 predictions are given in columns 11–13 and 14–16, respectively.

Table 1.
The RMF (NL) predictions for the binding energy (BE), pairing energy , deformation , root-mean-square radii (rms), charge radii , proton radii and neutron radii in comparison with their results from FRDM [52] and WS3 [53]. The energy is in MeV and radii in fm.
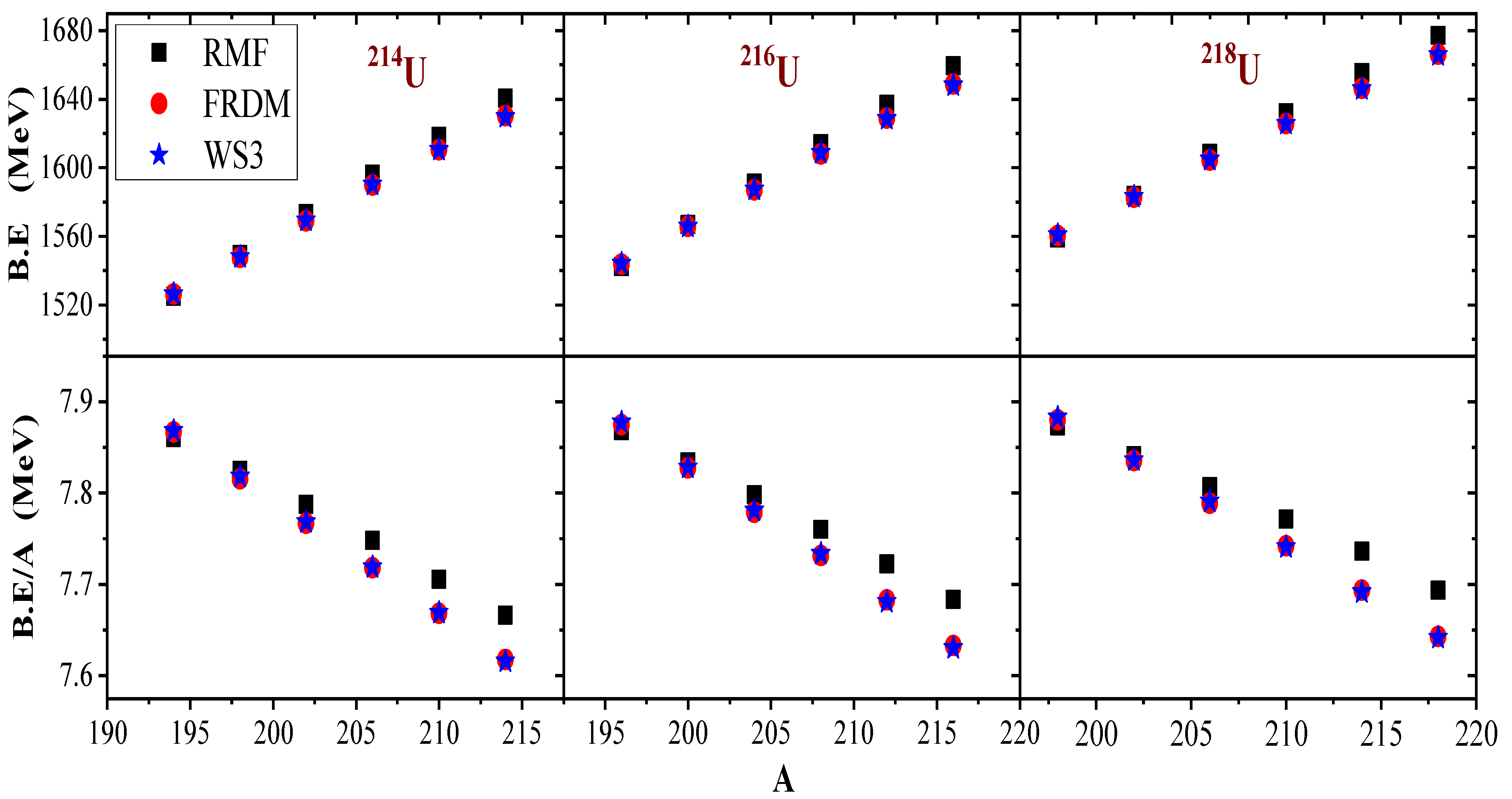
The newly measured -emitting isotope [15], produced via a fusion evaporation reaction and the re-measured even-even , furnishes us with helpful data with which the RMF (NL) is tested. In addition to the calculation of the -decay energies, binding energies can be employed to probe the stability of nuclei as well as test the reliability of the model adopted if it can quantitatively replicate the experimental binding energies. Figure 3 displays the variation of the binding energy (B.E) and the binding energy per particle (B.E/A) with the mass number of their respective parent nuclei. In each case, the values of the binding energies increase proportionately with the increasing mass of the parent nuclei until notable peaks are formed at and 218 (near and) at magic numbers and 126, respectively. Unlike the former, the B.E/A values decrease, leading to a higher mass until a minimum is observed around the same closed shell. In both varied parameters, similar trends are observed. It is seen that the FRDM and WS3 predicted binding energies agree closely, while the RMF (NL) predictions display a considerable deviation, gradually decreasing from uranium to radon isotopes with about 5–10 MeV (comparing the corresponding values in columns 4, 11 and 14 of Table 1). As a necessary input for the calculation of the -decay energies, this deviation would lead to an inaccurate estimation of the decay properties.
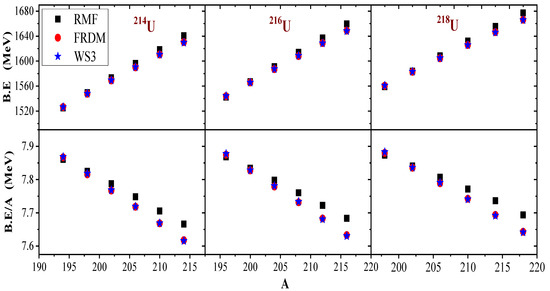
Figure 3.
The binding energy B.E (upper panel) and the binding energy per particle B.E/A (lower panel) for the decay chains of even-even isotopes, estimated from the RMF (NL) in comparison with the results from FRDM [52] and WS3 [53].
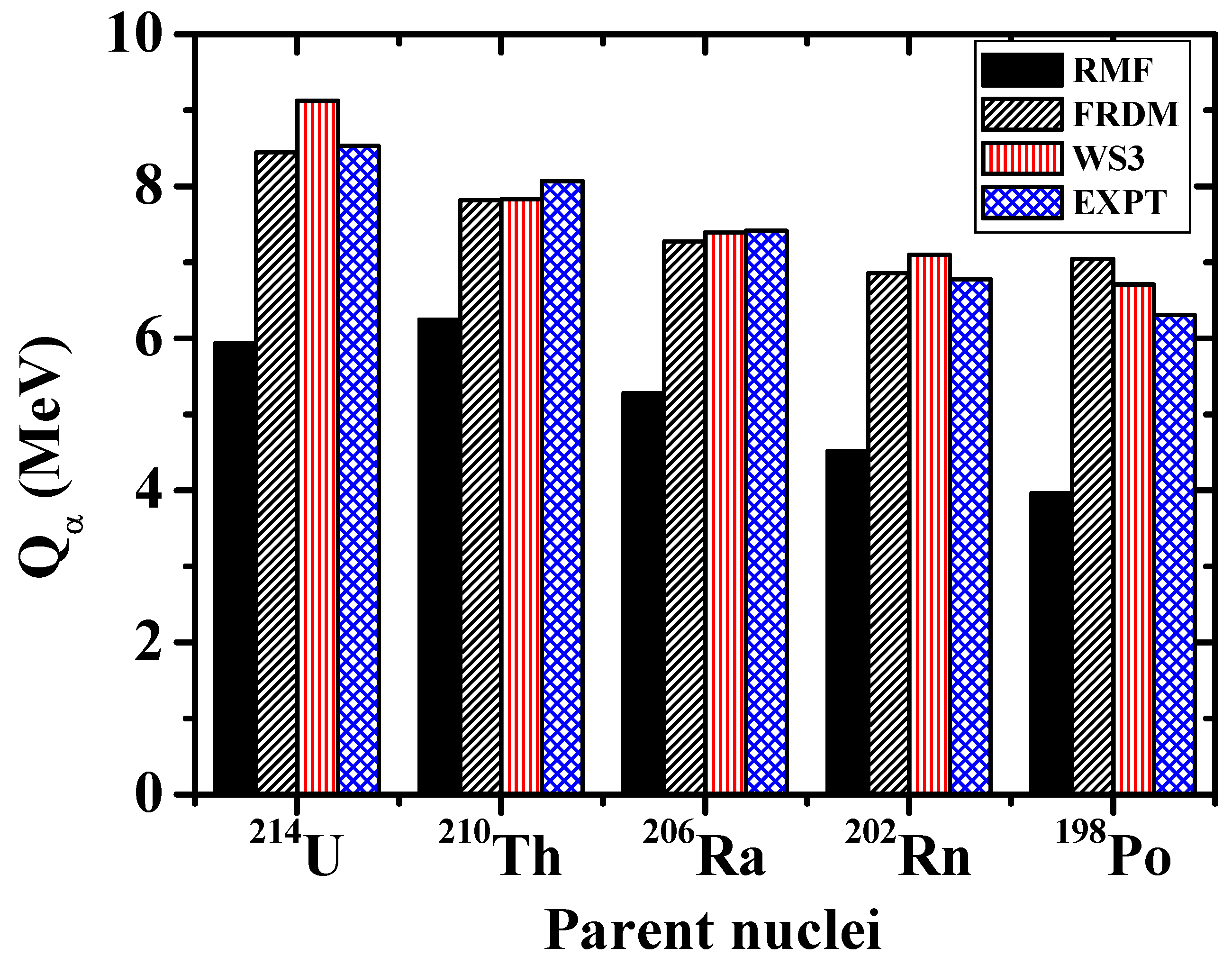
The decay energy (Q-value) plays an indispensable role in the calculation of the half-lives of nuclei [75]. From Figure 4 and Table 2 (columns 5–7), it is observed that the estimated alpha-decay energies from FRDM and WS3 are in good agreement with the experimental data and notably, the FRDM gives a perfect fit. Meanwhile, the RMF predictions are found to be at least 2 MeV less as compared with the recent experimental measurement, although it accurately reproduces a similar trend of with the neutron number [17]. We have also compared the RMF Q-values using NL3, NL3 and DD-ME2 parameter sets with the experimental Q-values and those of WS3 (not shown in the present analysis for the sake of brevity), yet, a discrepancy of about 2 MeV is still present. This underestimated RMF prediction of the -decay energies is obvious in all the comparisons made in this study. It is well known that little deviation in the Q values alters the resulting half-lives by a few orders of magnitude [5]. This suggests that the RMF formalism is not the best compromise to accurately estimate the values (for the region under study) and hence certain improvements in the interaction term of the Lagrangian density are needed to ensure its reliability in the prediction of the -decay half-lives. The parameters of the macroscopic–microscopic FRDM have been fitted to the ground-state masses of about 1654 nuclei (Z, N ≥ 8), while the RMF approach is predicated on a Lagrangian describing the interactions of nucleons through the exchange of mesons and photons [76].
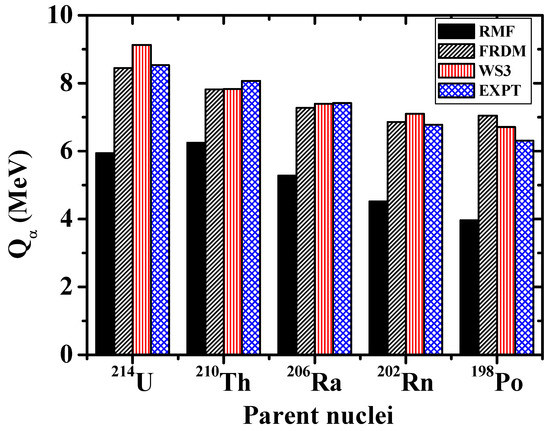
Figure 4.
The energies for the -decay chain of isotopes obtained from the RMF formalism (NL) in comparison with those from the FRDM [52], WS3 [53] and the recent experimental measurement of Zhang et al. [15].

Table 2.
The R3Y and M3Y predictions of the -decay half-lives within the PCM () and the calculation details for the decay chains of the neutron-deficient even–even isotopes from RMF (NL) in comparison with the experimental data [15,77,78]. The Q-values also are calculated using the binding energies from FRDM [52] and WS3 [53] for comparison.
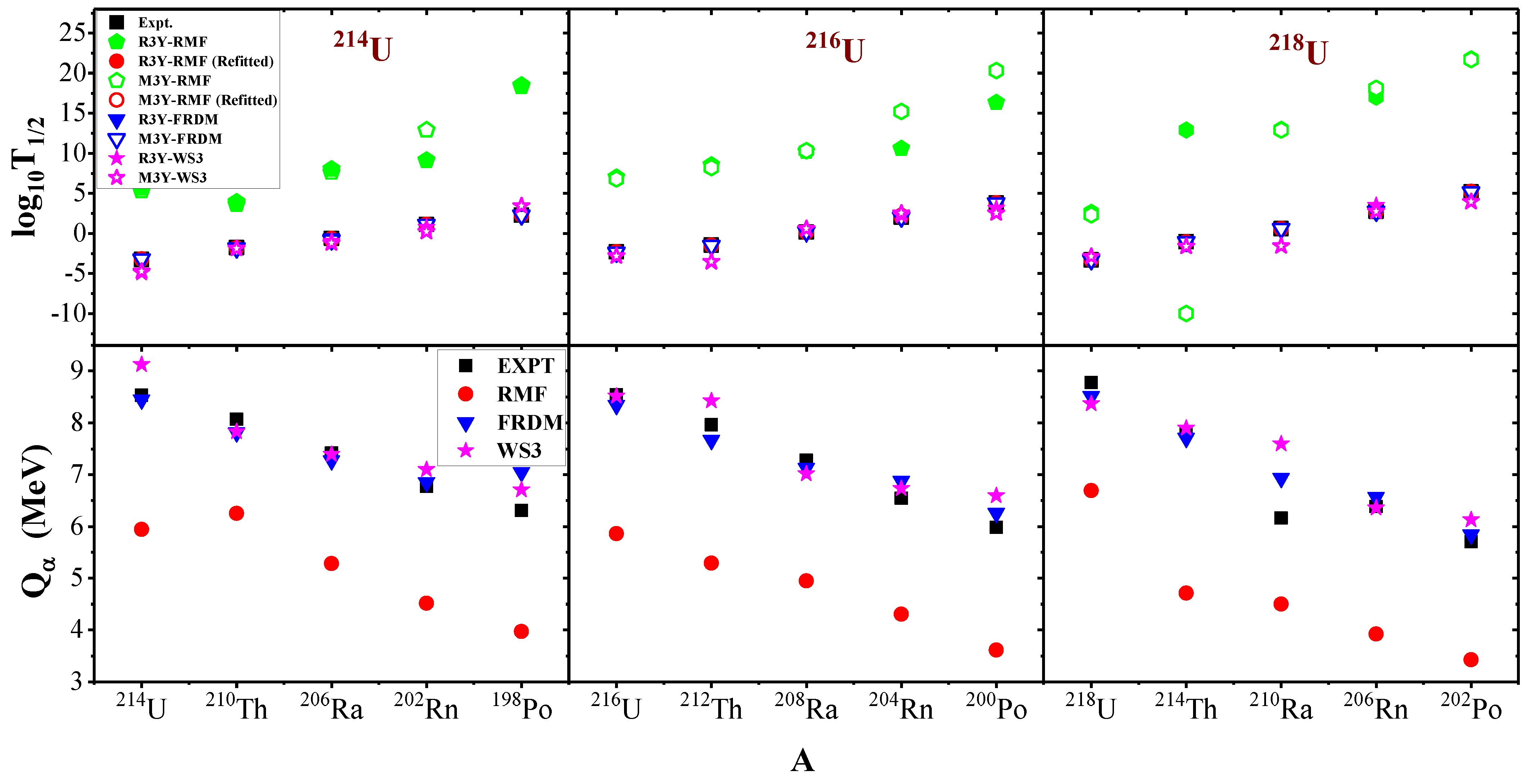
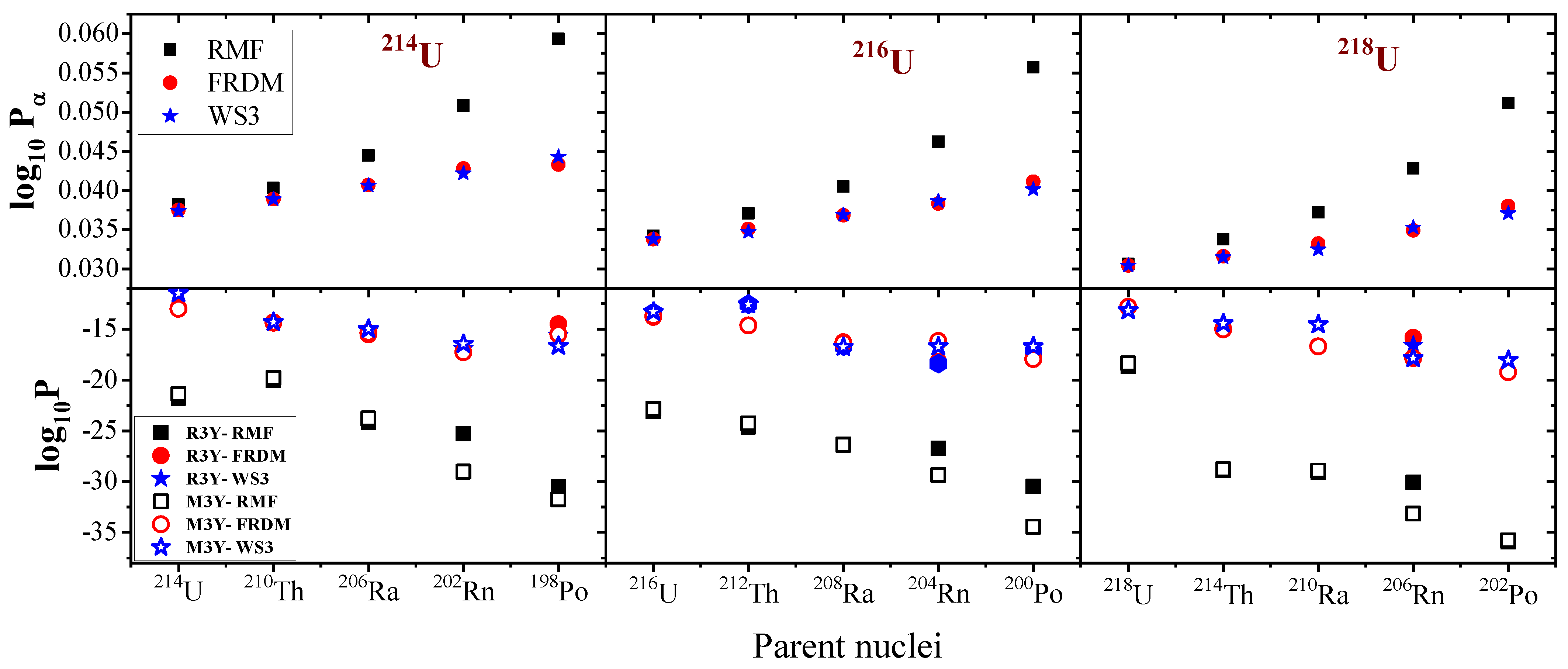
In summary, the difference in the Q-values estimated from the considered mass tables can be attributed to their respective parameterisations [76] and the mass correlation distance between surrounding nuclei, which is usually r ≤ 3, but ranges up to r ∼ 10 for RMF, being characterised with a larger rms deviation [79]. The -decay half-life is a viable tool used in nuclear structure physics to reveal the shell effect of both parent and daughter nuclei. Figure 5 shows the profile of the logarithmic half-lives as a function of different -emitting parent nuclei for the three decay chains, starting from the lightest uranium isotope . Again, the FRDM predictions appear to be the most consistent with the measured data [77,80]. Likewise, the WS3 is in fair agreement with the experimental data with a tolerable difference. On the other hand, the RMF half-life predictions were all-time higher with a wide difference, traceable to its relatively low alpha-decay energy. These discrepancies in the RMF predictions are reconciled by a random fitting (not following the systematic trend of FRDM and WS3) of the scaling factor, as well as the neck-length parameter R, as shown in Table 3. From the table, it is clear that an appropriate scaling and fitting can compensate for the divergent RMF values. Nonetheless, the refitting process appears to play a small effect on the penetration probability P. This is because the decay energy directly imparts and determines the magnitude of cluster penetration in the decay process. As reported by Kumar and collaborators [81,82,83], parent nuclei with stabilised shells are marked with high half-life values and such a situation in the daughter nuclei results in relatively lower values of the half-life. The shell structure effect is prominent in all cases for the -emitting parent having higher values. On the other hand, from Figure 5, the decay energy of Polonium isotopes, whose daughter Pb has a proton number at (or near) the magic shell closure , which assumes the deepest minima as a result of its stability. This stability can be linked to the magicity of protons at (or near) or of the neutrons magic numbers . This phenomenon was also reported by Phookan [22] and Manjunatha and Sowmya [84]. Interestingly, in Figure 5, the variation in seems to be the inverse of those of the logarithmic half-lives . Yet, a similar profile with the experimental data is maintained from the calculated values of RMF, FRDM and WS3. It is also noticed that increases to the size of the (neutron number of) the parent nuclei.
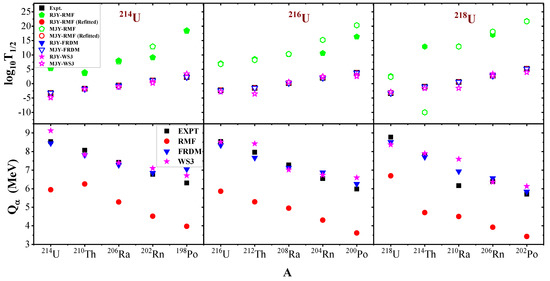
Figure 5.
The logarithmic half-lives (upper panel) and the for the -decay chain of U, U and U, obtained of from the RMF formalism (NL) in contrast with those from the FRDM [52], WS3 [53] and the recent experimental measurement of Zhang et al. [15].

Table 3.
Details of the random fitting of the neck-length R and scaling factor due to the deviations found in RMF (only).
In the PCM framework, it is assumed that the penetration probability will be less than unity and manifests an abrupt reduction with an increasing mass number A of the parent nuclei. Here, our calculated values are in tune with the shell model, with notable minima around the magic numbers. This conforms with the recent findings of [24,25], in which it was demonstrated that can be influenced by the isospin asymmetry of the parents, the deformation of the daughter nuclei, and pairing and shell effects and that the minima of can be ascribed to the presence of proton, neutron shells and sub-shell closures. A careful evaluation of Figure 6, which portrays the relationship between the preformation probability and the penetrability P, where both parameters are shown as a function of the mass number, reveals that lower values correspond to a higher P and vice versa, such that their products are near to the same order for all the decay chains under study.
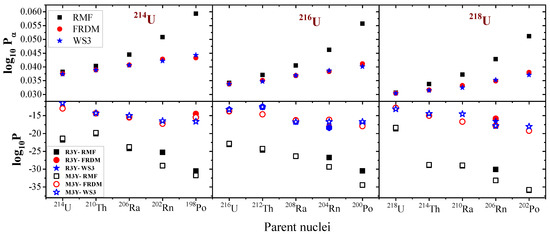
Figure 6.
Preformation probability (calculated from Equation (13)) and the penetration probability P using the Q-values estimated from RMF (NL), FRDM [52] and WS3 [53] for U, U and U decay chains.
Pairing is a vital quantity used in determining the nuclear properties of open-shell nuclei. Here, the pairing correlation is taken into account using the BCS approach. There exists a marginal relationship between the pairing energy and the deformation parameter [6]. In other words, the variation of yield a meagre change in . Figure 7 (upper panel) outlines the variation of the pairing energy with the mass number A of the parent nuclei. In our context, the pairing is found to increase until a peak is reached at Th, Th and Ra, corresponding to , respectively, just before the neutron magic shell closure. However, in the first decay chain, the sudden surge at indicates the presence of shape coexistence [14,85,86,87]. Shape coexistence is a habitual hallmark of neutron-deficient nuclei [14,87,88]. The RMF formulation has been successfully employed in the investigation of the quadrupole moment and found to be in harmony with the experimental data [86,89]. Figure 7 (lower panel) shows the changes in the quadrupole deformation parameter obtained from the RMF (NL), FRDM and WS3 results as a function of the mass number A. The RMF predicts far from the others. In the first chain, shape changes are observed with increasing mass numbers. Except for from the FRDM results, a shape change is noticed, from prolate to oblate, at and thereafter descends steeply to a highly deformed oblate at . Most of these isotopes are nearly spherical in their ground-state configurations [90]. Additionally, a closer examination of the FRDM predictions (which is the most consistent with the experimental data in our study) of values in Table 1 shows that the deformation at (and near) the shell closures and are approximately zero, indicating a state of stability.
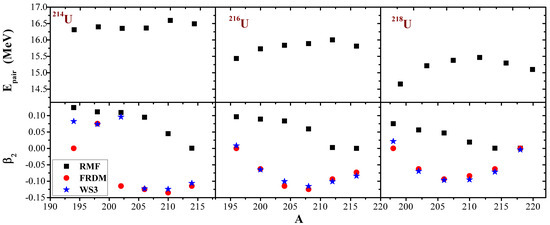
Figure 7.
Pairing energies from RMF prediction and the quadrupole deformation parameter obtained from the RMF (NL), FRDM [52] and WS3 [53] for the three decay chains.
In the present study, we have also extended the theoretical investigation of Sawhney et al. [28] to neutron-deficient nuclei using the preformed cluster-decay model (PCM) within the RMF framework at temperature for generalisation. The details of our calculations are shown in Table 2, highlighting the -transitions (Columns 1 and 2), the experimental and calculated Q values (Columns 3 to 7), and details of R3Y calculations (Columns 8 to 12), as well as those of the M3Y (Columns 13 to 17) of the alpha-decay chains. The large deviation of the RMF-calculated Q values seen in their corresponding logarithmic half-life predictions have been extensively discussed. Columns 8 and 13 of Table 2 show the trend in the fitted neck-length parameter participating in the three decay chains for R3Y and M3Y, respectively. A close difference can be observed in the values, except in the case of Polonium (, in which a smaller is required for its fitting. One very clear observation is that, in addition to the Po, almost all the values in M3Y were smaller than those of R3Y. This alludes to the fact that the R3Y and M3Y NN interactions have different barrier characteristics [91].
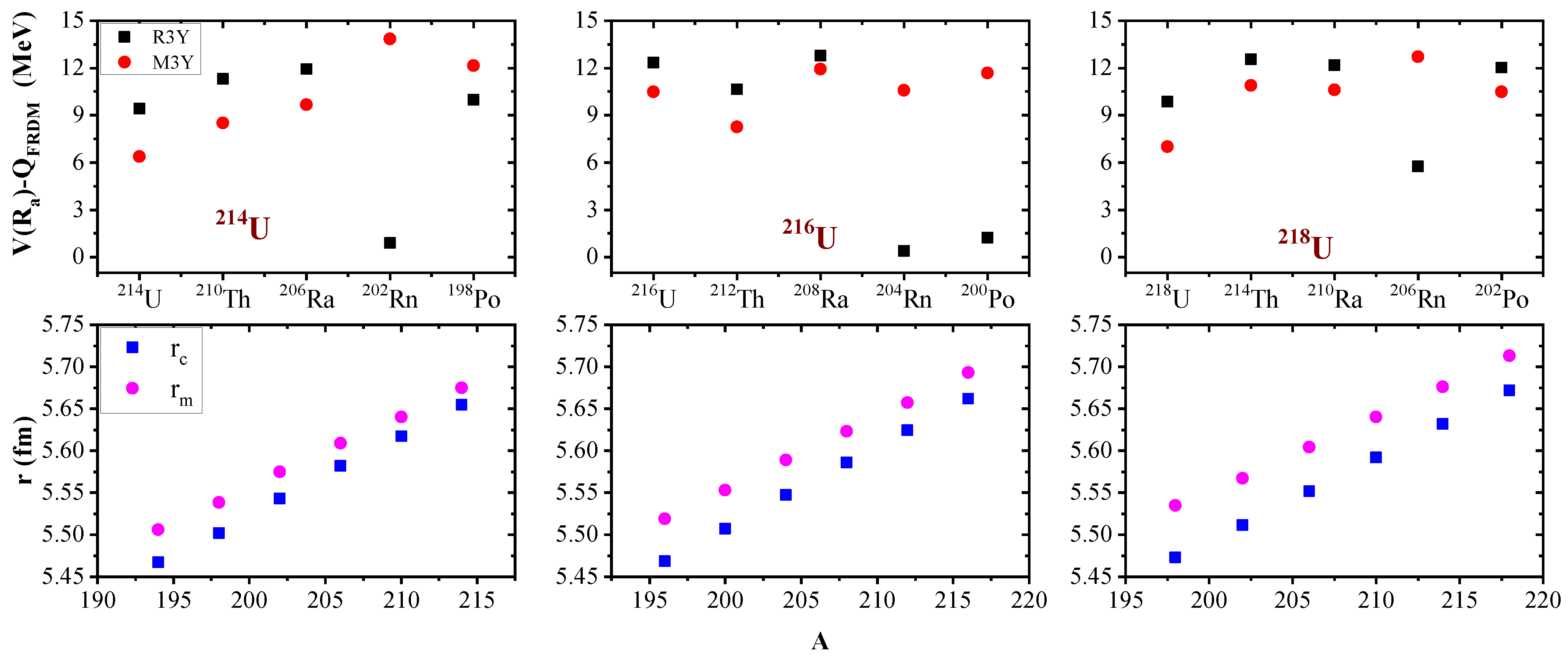
The difference in the effective R3Y and M3Y interactions is conspicuously shown in the driving potential (). Figure 8 displays the driving potential as a function of the mass number of the parent nuclei for R3Y (in black squares) and M3Y (in red circles) NN interactions for the three decay chains. The FRDM-calculated Q-values were chosen for this comparison. Despite the well-fitted neck-parameter , the influence of the different barrier characteristics of the R3Y and M3Y NN potential is visible. Mostly, the R3Y driving potential was found to be higher than M3Y, except for Rn and (in the second decay chain) Po isotopes. This anomaly occurs because these nuclei are found in the vicinity of the proton shell closure . Indeed, -decay studies of neutron-deficient isotopes provide information on nuclei near the proton drip line [92].
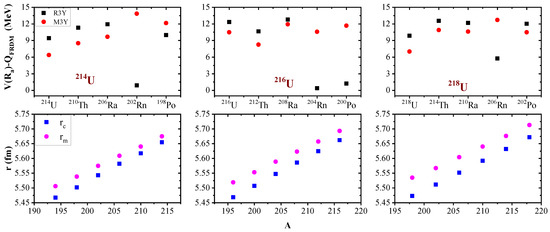
Figure 8.
Upper panel: The driving potential () for the decay chains of isotopes for R3Y (in black squares) and M3Y (in red circles) NN potentials as a function of the parent nuclei A. The lower panel illustrates the rms radii for matter distribution and charge distribution for the isotopes using the relativistic mean-field formalism RMF (NL).
The scaling factors for the decay chains of the considered Uranium isotopes are given in columns 9 and 14 of Table 2. The previous findings [28,45] at PCM (), indicating ground-state -decays, are confirmed for the first three -transitions in each of the chains. However, higher scaling factors in the range – are required to normalise the penetrability P of the decay channels around the proton shell closure . This is obvious for and 84, whose scaling factors are given in the footnote “a”. The deviation in the RMF Q-values necessitates the use of random scaling to attain the measured experimental half-lives, as shown in Table 3. Despite this fact, the need for higher scaling factors around the proton magic number is confirmed, as highlighted with the footnote “b”. Thus, the previous knowledge is now broadened around the proton magic number 82. The root mean square (rms) and the charge radii are deduced from the RMF formalism with the NL force parameter set and the corresponding values are given in the lower panel of Figure 8 as well as Columns 6 and 9 of Table 1, respectively. A similar behaviour and trend are noticed in the variation of both and . Specifically, both rms and charge radii increase monotonously with the increase in the mass of the parent nuclei. A close examination of the three decay chains reveals that the difference between and becomes larger with the increase in the neutron number. Currently, there are no available data for comparison.
4. Summary and Conclusions
The RMF framework is employed for the calculation of the ground-state properties (binding energies, quadrupole deformation, rms charge and matter radii and Q-values) of the newly measured and remeasured together with the decay product in their respective -decay chains and compared with those from the FRDM and WS3 mass tables. The -decay process was treated as a quantum tunnelling effect across a potential barrier using the WKB approximation and the half-lives are deduced within the PCM framework. The phenomenological M3Y and the recently developed R3Y NN potentials are used to obtain the nuclear interaction potential following the double-folding technique. In all cases, the FRDM data with the new R3Y NN potential are found to be in close agreement with the experimental half-lives. Moreover, from our calculations, we observed that in the so-called region of abnormal enhancement, the scaling factor is maintained and normalised with the optimised neck-parameter . Nonetheless, a discrepancy is noticed around the proton shell closure with and 84, and this is consistently found in all three decay chains. As such, the required scaling factor to estimate the experimental half-lives may range from – at Z = 82, 84. However, it has been lately demonstrated in another study that the need for scaling factor is not necessary when the temperature effect is considered. This assertion will be subsequently verified around the magic number . Moreover, a number of studies have demonstrated that the quantisation, deformation and orientation degrees of freedom can influence the alpha-decay half-lives quantitatively. These effects will also be incorporated in our future study. In contrast with the FRDM- and WS3-estimated binding energies for the considered neutron-deficient nuclei, an unusually large difference (gradually decreasing from uranium to radon isotopes with about 10.288 MeV up to 4.219 MeV) is also observed in the those of RMF despite various parameter sets employed. This contrast can be attributed to the difference in their respective parameterisations as well as the mass correlation distance between surrounding nuclei, which has a larger rms deviation for RMF. This indicates that certain improvements are needed in the RMF framework in this mass region.
Author Contributions
Conceptualisation, T.M.J., M.B. and R.K.; methodology, T.M.J.; software, T.M.J. and R.K.; validation, T.M.J., M.B. and R.K.; formal analysis, T.M.J.; investigation, T.M.J.; resources, K.A and N.A.; data curation, T.M.J., M.B. and R.K.; writing—original draft preparation, T.M.J. and N.J.; writing—review and editing, T.M.J. and N.J.; visualisation, T.M.J. and N.J.; supervision, M.B., R.K., K.A. and N.A.; project administration, T.M.J., M.B. and R.K.; funding acquisition, K.A. and N.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Education Malaysia (under the Grant No: FRGS/1/2019/STG02/UNIMAP/02/2). This work was supported by DAE-BRNS Project Sanction No. 58/14/12/2019-BRNS, FOSTECT Project Code: FOSTECT.2019B.04, and FAPESP Project Nos. 2017/05660-0.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are contained within the article.
Acknowledgments
One of the authors (TMJ) take this opportunity to convey special thanks to Shilpa Rana for fruitful discussions and suggestions towards the improvement of this manuscript. TMJ is also thankful to the Institute of Engineering Mathematics (IMK), UniMAP for providing computer facilities during the work.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CSF | Common Scaling Factor |
| PCM | Preformed Cluster-decay Model |
| WKB | Wentzel–Kramers–Brillouin |
| FRDM | Finite-Range-Droplet Model |
| RMF | Relativistic Mean-Field |
| M3Y | Michigan-3-Yukawa |
| R3Y | Relativistic (Mean-Field)-3-Yukawa |
| OPEP | One-Pion Exchange Potential |
| NN | Nucleon–Nucleon |
References
- Geiger, H.; Nuttall, J.M. The ranges of the α particles from various radioactive substances and a relation between range and period of transformation. Philos. Mag. 1911, 22, 613. [Google Scholar] [CrossRef]
- Geiger, H. Reichweitemessungen an α-Strahlen. Z. Phys. 1922, 8, 45. [Google Scholar] [CrossRef]
- Van Duppen, P.; Andreyev, A.N. Alpha decay and beta-delayed fission: Tools for nuclear physics studies. In The Euroschool on Exotic Beams; Scheidenberger, C., Pfutzner, M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 5, pp. 65–116. [Google Scholar]
- Qi, C.; Liotta, R.; Wyss, R. The single-particle unit for alpha decay. Prog. Part. Nucl. Phys. 2019, 105, 214. [Google Scholar] [CrossRef]
- Gupta, M.; Heinz, S.; Munzenberg, G. Half lives and Q values of nuclei appearing in the α-decay chains of recently reported new isotopes. Rom. J. Phys. 2018, 63, 304. [Google Scholar]
- Bhuyan, M.; Patra, S.K.; Gupta, R.K. Relativistic mean-field study of the properties of Z = 117 nuclei and the decay chains of the 293,294117 isotopes. Phys. Rev. C 2011, 84, 014317. [Google Scholar] [CrossRef]
- Fynbo, H.O.; Diget, C.A.; Bergmann, U.C.; Borge, M.J.; Cederkäll, J.; Dendooven, P.; Fraile, L.M.; Franchoo, S.; Fedosseev, V.N.; Fulton, B.R.; et al. Revised rates for the stellar triple-α process from measurement of 12C nuclear resonances. Nat. Lond. 2005, 433, 136. [Google Scholar] [CrossRef]
- Delion, D.S.; Sandulescu, A.; Greiner, W. Evidence for α clustering in heavy and superheavy nuclei. Phys. Rev. C 2004, 69, 044318. [Google Scholar] [CrossRef]
- Lovas, R.G.; Liotta, R.J.; Insolia, A.; Varga, K.; Delion, D.S. Microscopic theory of cluster radioactivity. Phys. Rep. 1998, 294, 265. [Google Scholar] [CrossRef]
- Seweryniak, D.; Starosta, K.; Davids, C.N.; Gros, S.; Hecht, A.A.; Hoteling, N.; Khoo, T.L.; Lagergren, K.; Lotay, G.; Peterson, D.; et al. α decay of 105Te. Phys. Rev. C 2006, 73, 061301(R). [Google Scholar] [CrossRef]
- Andreyev, A.N.; Huyse, M.; Van Duppen, P.; Weissman, L.; Ackermann, D.; Gerl, J.; Hessberger, F.P.; Hofmann, S.; Kleinböhl, A.; Münzenberg, G.; et al. A triplet of differently shaped spin-zero states in the atomic nucleus 186Pb. Nat. Lond. 2000, 405, 430. [Google Scholar] [CrossRef]
- Andreyev, A.N.; Huyse, M.; Van Duppen, P.; Qi, C.; Liotta, R.J.; Antalic, S.; Ackermann, D.; Franchoo, S.; Hessberger, F.P.; Hofmann, S.; et al. Signatures of the Z = 82 shell closure in α-decay process. Phys. Rev. Lett. 2013, 110, 242502. [Google Scholar] [CrossRef]
- Auranen, K.; Seweryniak, D.; Albers, M.; Ayangeakaa, A.D.; Bottoni, S.; Carpenter, M.P.; Chiara, C.J.; Copp, P.; David, H.M.; Doherty, D.T.; et al. Superallowed α Decay to Doubly Magic 100Sn. Phys. Rev. Lett. 2018, 121, 182501. [Google Scholar] [CrossRef]
- Wauters, J.; Bijnens, N.; Dendooven, P.; Huyse, M.; Hwang, H.Y.; Reusen, G.; von Schwarzenberg, J.; Van Duppen, P.; Kirchner, R.; Roeckl, E. Fine structure in the alpha decay of even-even nuclei as an experimental proof for the stability of the Z = 82 magic shell at the very neutron-deficient side. Phys. Rev. Lett. 1994, 72, 1329. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Yang, H.B.; Huang, M.H.; Gan, Z.G.; Yuan, C.X.; Qi, C.; Andreyev, A.N.; Liu, M.L.; Ma, L.; Zhang, M.M.; et al. New α-Emitting Isotope 214U and Abnormal Enhancement of α-Particle Clustering in Lightest Uranium Isotopes. Phys. Rev. Lett. 2021, 126, 152502. [Google Scholar] [CrossRef]
- Sorlin, O.; Porquet, M.G. Nuclear magic numbers: New features far from stability. Prog. Part. Nucl. Phys. 2008, 61, 602. [Google Scholar] [CrossRef]
- Zong-Qiang, S.; Jian-You, G. Study of the Alpha-Decay Chain for 194Rn with Relativistic Mean-Field Theory. Commun. Theor. Phys. 2008, 49, 1583. [Google Scholar] [CrossRef]
- Santhosh, K.P.; Sukumaran, I. Alpha decay studies on Po isotopes using different versions of nuclear potentials. Eur. Phys. J. A 2017, 53, 1. [Google Scholar] [CrossRef]
- Poenaru, D.N.; Ivascu, M.; Greiner, W. Half lives for spontaneous emission of heavy ions from atomic nuclei. International Journal of Radiation Applications and Instrumentation. Part D Nucl. Tracks Radiat. Meas. 1986, 12, 313. [Google Scholar] [CrossRef]
- Cui, J.P.; Xiao, Y.; Gao, Y.H.; Wang, Y.Z. α-decay half-lives of neutron-deficient nuclei. Nucl. Phys. A 2019, 987, 99–111. [Google Scholar] [CrossRef]
- Adel, A.; Abdulghany, A.R. Proton radioactivity and α-decay of neutron-deficient nuclei. Phys. Scr. 2021, 96, 125314. [Google Scholar] [CrossRef]
- Phookan, C.K. α-particle preformation of heavy nuclei using proximity potential. Chin. J. Phys. 2017, 55, 176. [Google Scholar] [CrossRef]
- He, Y.; Yu, X.; Zhang, H.F. Improved empirical formula for α particle preformation factor. Chin. Phys. C 2021, 45, 014110. [Google Scholar] [CrossRef]
- Seif, W.M. The α decay spectroscopic factor of heavy and superheavy nuclei. J. Phys. G Nucl. Part. Phys. 2013, 40, 105102. [Google Scholar] [CrossRef]
- Seif, W.M.; Botros, M.M.; Refaie, A.I. Preformation probability inside α emitters having different ground state spin-parity than their daughters. Phys. Rev. C 2015, 92, 044302. [Google Scholar] [CrossRef]
- Gamow, G. Zur quantentheorie des atomkernes. Z. Phys. 1928, 51, 204. [Google Scholar] [CrossRef]
- Gurney, R.W.; Condon, E.U. Wave mechanics and radioactive disintegration. Nature 1928, 122, 439. [Google Scholar] [CrossRef]
- Niyti, G.; Sawhney, M.K.; Sharma, R.K. Gupta, α-decay chains of recoiled superheavy nuclei: A theoretical study. Phys. Rev. C 2015, 91, 054606. [Google Scholar] [CrossRef]
- Quentin, P.; Flocard, H. Self-consistent calculations of nuclear properties with phenomenological effective forces. Annu. Rev. Nucl. Part. Sci. 1978, 28, 523. [Google Scholar] [CrossRef]
- Hornyak, W. Nuclear Structure; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Schunck, N.; Robledo, L.M. Microscopic theory of nuclear fission: A review. Rep. Prog. Phys. 2016, 79, 116301. [Google Scholar] [CrossRef]
- Vautherin, D.; Brink, D.T. Hartree-Fock calculations with Skyrme’s interaction. I. Spherical nuclei. Phys. Rev. C 1972, 5, 626. [Google Scholar] [CrossRef]
- Epelbaum, E.; Hammer, H.W.; Meiner, U.G. Modern theory of nuclear forces. Rev. Mod. Phys. 2009, 81, 1773. [Google Scholar] [CrossRef]
- Ekström, A.; Baardsen, G.; Forssén, C.; Hagen, G.; Hjorth-Jensen, M.; Jansen, G.R.; Machleidt, R.; Nazarewicz, W.; Papenbrock, T.; Sarich, J.; et al. Optimized chiral nucleon-nucleon interaction at next-to-next-to-leading order. Phys. Rev. Lett. 2013, 110, 192502. [Google Scholar] [CrossRef]
- Singh, B.; Bhuyan, M.; Patra, S.K.; Gupta, R.K. Optical potential obtained from relativistic-mean-field theory-based microscopic nucleon–nucleon interaction: Applied to cluster radioactive decays. J. Phys. G Nucl. Part. Phys. 2012, 39, 069501. [Google Scholar] [CrossRef]
- Singh, B.; Bhuyan, M.; Patra, S.K.; Gupta, R.K. A new microscopic nucleon-nucleon interaction derived from relativistic mean field theory. arXiv 2010, arXiv:1011.5732. [Google Scholar]
- Satchler, G.R.; Love, W.G. Folding model potentials from realistic interactions for heavy-ion scattering. Phys. Rep. 1979, 55, 183. [Google Scholar] [CrossRef]
- Biswal, S.K.; El Sheikh, M.A.; Biswal, N.; Yusof, N.; Kassim, H.A.; Patra, S.K.; Bhuyan, M. Nuclear matter properties of finite nuclei using relativistic mean field formalism. Nucl. Phys. A 2020, 1004, 122042. [Google Scholar] [CrossRef]
- Itagaki, N.; Afanasjev, A.V.; Ray, D. Possibility of 14C cluster as a building block of medium-mass nuclei. Phys. Rev. C 2020, 101, 034304. [Google Scholar] [CrossRef]
- Taninah, A.; Agbemava, S.E.; Afanasjev, A.V. Covariant density functional theory: An estimation of systematic uncertainties. Bull. Am. Phys. Soc. 2020, 65, 19. [Google Scholar]
- Horowitz, C.J.; Serot, B.D. Self-consistent hartree description of finite nuclei in a relativistic quantum field theory. Nucl. Phys. A 1981, 368, 503. [Google Scholar] [CrossRef]
- Serot, B.D.; Walecka, J.D. Relativistic nuclear many-body theory. Recent Prog. Many-Body Theor. 1992, 49, 49–92. [Google Scholar]
- Reinhard, P.G. The relativistic mean-field description of nuclei and nuclear dynamics. Rep. Prog. Phys. 1989, 52, 439. [Google Scholar] [CrossRef]
- Ebran, J.P.; Khan, E.; Lasseri, R.; Marevic, P.; Niksic, T.; Sandulescu, N.; Vretenar, D. Investigation of nuclear cluster phenomenology with the relativistic EDF approach. II Nuovo C. C-Colloq. Phys. 2019, 42, 2–3. [Google Scholar]
- Kumar, R.; Sandhu, K.; Sharma, M.K.; Gupta, R.K. Fusion-evaporation residues and α-decay chains of the superheavy element Z = 115 formed in the 243Am+ 48Ca reaction using the dynamical cluster-decay model. Phys. Rev. C 2013, 87, 054610. [Google Scholar] [CrossRef]
- Sharma, K.; Sawhney, G.; Sharma, M.K.; Gupta, R.K. Decay of Plutonium isotopes via spontaneous and heavy-ion induced fission paths. Nucl. Phys. A 2018, 972, 1. [Google Scholar] [CrossRef]
- Deng, J.G.; Zhang, H.F. Analytic formula for estimating the α-particle preformation factor. Phys. Rev. C 2020, 102, 044314. [Google Scholar] [CrossRef]
- Deng, J.G.; Zhang, H.F. Systematic study of α decay half-lives within the Generalized Liquid Drop Model with various versions of proximity energies. Chin. Phys. C 2021, 45, 024104. [Google Scholar] [CrossRef]
- Wentzel, G. Eine verallgemeinerung der quantenbedingungen für die zwecke der wellenmechanik. Z. Physik 1926, 38, 518. [Google Scholar] [CrossRef]
- Kramers, H.A. Wellenmechanik und halbzahlige Quantisierung. Z. Physik 1926, 39, 828. [Google Scholar] [CrossRef]
- Brillouin, L. Schr "o dinger’s undulatory method; a general method of r ’e solution by successive approximations. C. R. Acad. Sci. 1926, 183, 24. [Google Scholar]
- Möller, P.; Sierk, A.J.; Ichikawa, T.; Sagawa, H. Nuclear ground-state masses and deformations: FRDM. At. Data Nucl. Data Tables 2016, 109, 1. [Google Scholar] [CrossRef]
- Liu, M.; Wang, N.; Deng, Y.; Wu, X. Further improvements on a global nuclear mass model. Phys. Rev. C 2011, 84, 014333. [Google Scholar] [CrossRef]
- Singh, B.; Patra, S.K.; Gupta, R.K. Cluster radioactive decay within the preformed cluster model using relativistic mean-field theory densities. Phys. Rev. C 2010, 82, 014607. [Google Scholar] [CrossRef]
- Sahu, B.B.; Singh, S.K.; Bhuyan, M.; Biswal, S.K.; Patra, S.K. Importance of nonlinearity in the NN potential. Phys. Rev. C 2014, 89, 034614. [Google Scholar] [CrossRef]
- Bhuyan, M.; Patra, S.K.; Arumugam, P.; Gupta, R.K. Nuclear sub-structure in 112–122Ba nuclei within relativistic mean field theory. Int. J. Mod. Phys. E 2011, 20, 1227. [Google Scholar] [CrossRef]
- Ring, P. Relativistic mean field theory in finite nuclei. Prog. Part. Nucl. Phys. 1996, 37, 193. [Google Scholar] [CrossRef]
- Bhuyan, M. Structural evolution in transitional nuclei of mass 82 ≤ A ≤ 132. Phys. Rev. C 2015, 92, 034323. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Karatzikos, S.; Fossion, R.; Arteaga, D.P.; Afanasjev, A.V.; Ring, P. The effective force NL3 revisited. Phys. Lett. B 2009, 671, 36. [Google Scholar] [CrossRef]
- Gupta, R.K. Collective clusterization in nuclei and excited compound systems: The dynamical cluster-decay model. In Clusters in Nuclei; Springer: Berlin/Heidelberg, Germany, 2010; pp. 223–265. [Google Scholar]
- Basu, D.N. Folding model analysis of alpha radioactivity. J. Phys. G Nucl. Part. Phys. 2003, 29, 2079. [Google Scholar] [CrossRef][Green Version]
- Malik, S.S.; Gupta, R.K. Theory of cluster radioactive decay and of cluster formation in nuclei. Phys. Rev. C 1989, 39, 1992. [Google Scholar] [CrossRef]
- Gupta, R.K.; Greiner, W. Cluster radioactivity. Int. J. Mod. Phys. E 1994, 3, 335. [Google Scholar] [CrossRef]
- Matsuse, T.; Beck, C.; Nouicer, R.; Mahboub, D. Extended Hauser-Feshbach method for statistical binary decay of light-mass systems. Phys. Rev. C 1997, 55, 1380. [Google Scholar] [CrossRef]
- Sanders, S.J.; Kovar, D.G.; Back, B.B.; Beck, C.; Henderson, D.J.; Janssens, R.V.F.; Wang, T.F.; Wilkins, B.D. Binary decay of 56Ni formed in the 32+24Mg reaction. Phys. Rev. C 1989, 40, 2091. [Google Scholar] [CrossRef]
- Sanders, S.J. Fusion-fission in nuclear systems with 40 ≤ ACN ≤ 80. Phys. Rev. C 1991, 44, 2676. [Google Scholar] [CrossRef]
- Royer, G.; Normand, C.; Druet, E. Analytic description of the fusion and fission processes through compact quasi-molecular shapes. Nucl. Phys. A 1998, 634, 267. [Google Scholar] [CrossRef]
- Gao, J.; Bao, X.; Zhang, H.; Li, J.; Zhang, H. New numerical method for fission half-lives of heavy and superheavy nuclei at ground and excited states. Nucl. Phys. A 2014, 929, 246. [Google Scholar] [CrossRef]
- Poenaru, D.N. Particle Emission From Nuclei: Volume I: Nuclear Deformation Energy; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Greiner, M.; Scheid, W. Radioactive decay into excited states via heavy ion emission. J. Phys. G Nucl. Part. Phys. 1986, 12, L229. [Google Scholar] [CrossRef]
- Khoa, D.T.; Von Oertzen, W. Refractive alpha-nucleus scattering: A probe for the incompressibility of cold nuclear matter. Phys. Lett. B 1995, 342, 6. [Google Scholar] [CrossRef]
- De Vries, H.; De Jager, C.W.; De Vries, C. Nuclear charge-density-distribution parameters from elastic electron scattering. At. Data Nucl. Data Tables 1987, 36, 495. [Google Scholar] [CrossRef]
- Sahoo, T.; Patra, S.K. Search for the stable isotopes for Z = 119 and 121 superheavy elements using relativistic mean field model. Phys. Scr. 2020, 95, 085302. [Google Scholar] [CrossRef]
- Pattnaik, J.A.; Panda, R.N.; Bhuyan, M.; Patra, S.K. Isotopic shift and search of magic number in the superheavy region. Phys. Scr. 2021, 96, 125319. [Google Scholar]
- Hong-Fei, Z.; Jun-Qing, L.; Wei, Z.; Xiao-Hong, Z.; Zai-Guo, G. Systematic study on alpha decay half-lives of superheavy nuclei. Commun. Theor. Phys. 2007, 48, 545. [Google Scholar] [CrossRef]
- Patyk, Z.; Baran, A.; Berger, J.F.; Dechargé, J.; Dobaczewski, J.; Ring, P.; Sobiczewski, A. Masses and radii of spherical nuclei calculated in various microscopic approaches. Phys. Rev. C 1999, 59, 704. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, Z.Y.; Gan, Z.G.; Yang, H.B.; Yu, L.; Jiang, J.; Wang, J.G.; Tian, Y.L.; Wang, Y.S.; Guo, S.; et al. α-decay properties of the new isotope 216U. Phys. Rev. C 2015, 91, 051302. [Google Scholar] [CrossRef]
- NNDC. National Nuclear Data Center, Chart of Nuclides; Brookhaven National Lab. (BNL): Upton, NY, USA, 2020.
- Niu, Z.M.; Zhu, Z.L.; Niu, Y.F.; Sun, B.H.; Heng, T.H.; Guo, J.Y. Radial basis function approach in nuclear mass predictions. Phys. Rev. C 2013, 88, 024325. [Google Scholar] [CrossRef]
- Leppänen, A.P.; Uusitalo, J.; Leino, M.; Eeckhaudt, S.; Grahn, T.; Greenlees, P.T.; Jones, P.; Julin, R.; Juutinen, S.; Kettunen, H.; et al. α decay studies of the nuclides 218U and 219U. Phys. Rev. C 2007, 75, 054307. [Google Scholar]
- Kumar, S.; Balasubramaniam, M.; Gupta, R.K.; Münzenberg, G.; Scheid, W. The formation and decay of superheavy nuclei produced in 48Ca-induced reactions. J. Phys. G Nucl. Part. Phys. 2003, 29, 625. [Google Scholar] [CrossRef]
- Kumar, S.; Thakur, S.; Kumar, R. Decay studies of 288-287115 alpha-decay chains. J. Phys. G Nucl. Part. Phys. 2009, 36, 105104. [Google Scholar] [CrossRef][Green Version]
- Kumar, S. α decay chains study for the recently observed superheavy element Z = 117 within the isospin cluster model. Phys. Rev. C 2012, 85, 024320. [Google Scholar] [CrossRef]
- Manjunatha, H.C.; Sowmya, N. Competition between spontaneous fission ternary fission cluster decay and alpha decay in the super heavy nuclei of Z = 126. Nucl. Phys. A 2018, 969, 68. [Google Scholar] [CrossRef]
- Van de Vel, K. Shape Coexistence in Neutron-Deficient Polonium and Lead Nuclei. Ph.D. Thesis, Katholieke Universiteit Leuven, Leuven, Belgium, 2003. [Google Scholar]
- Bender, M.; Cornelius, T.; Lalazissis, G.A.; Maruhn, J.A.; Nazarewicz, W.; Reinhard, P.G. The Z = 82 shell closure in neutron-deficient Pb isotopes. Eur. Phys. J. A-Hadron. Nucl. 2002, 14, 23. [Google Scholar] [CrossRef][Green Version]
- Sun, X.D.; Zhang, H.F. α decay preformation probabilities across the N = 126 shell closure based on the single particle energy spectra. J. Phys. G Nucl. Part. Phys. 2018, 45, 075106. [Google Scholar] [CrossRef]
- Van Duppen, P.; Huyse, M. Shape coexistence around the Z = 82 closed shell probed by α-decay. Hyperfine Interact. 2000, 129, 149. [Google Scholar] [CrossRef]
- Swain, R.; Patra, S.K.; Sahu, B.B. Nuclear structure and decay modes of Ra isotopes within an axially deformed relativistic mean field model. Chin. Phys. C 2018, 42, 084102. [Google Scholar] [CrossRef]
- Julin, R.; Helariutta, K.; Muikku, M. Intruder states in very neutron-deficient Hg, Pb and Po nuclei. J. Phys. G Nucl. Part. Phys. 2001, 27, R109. [Google Scholar] [CrossRef]
- Sahu, B.; Agarwalla, S.K.; Patra, S.K. Half-lives of proton emitters using relativistic mean field theory. Phys. Rev. C 2011, 84, 054604. [Google Scholar] [CrossRef]
- Leino, M.; Uusitalo, J.; Allatt, R.G.; Armbruster, P.; Enqvist, T.; Eskola, K.; Hofmann, S.; Hurskanen, S.; Jokinen, A.; Ninov, V.; et al. Alpha decay studies of neutron-deficient radium isotopes. Phys. A Hadron. Nucl. 1996, 355, 157. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).