Relativistic Effects for a Hydrogen Rydberg Atom in a High-Frequency Laser Field: Analytical Results

Abstract

Previously published analytical results for the effects of a high-frequency laser field on hydrogen Rydberg atoms demonstrated that the unperturbed elliptical orbit of the Rydberg electron, generally is engaged simultaneously in the precession of the orbital plane about the direction of the laser field and in the precession within the orbital plane. These results were obtained while disregarding relativistic effects. In the present paper, we analyze the relativistic effect for hydrogenic Rydberg atoms or ions in a high-frequency linearly- or circularly-polarized laser field, the effect being an additional precession of the electron orbit in its own plane. For the linearly-polarized laser field, the general case, where the electron orbit is not perpendicular to the direction of the laser field, we showed that the precession of the electron orbit within its plane can vanish at some critical polar angle θ_c of the orbital plane. We calculated analytically the dependence of the critical angle on the angular momentum of the electron and on the parameters of the laser field. Finally, for the particular situation, where the electron orbit is perpendicular to the direction of the laser field, we demonstrated that the relativistic precession and the precession due to the laser field occur in the opposite directions. As a result, the combined effect of these two kinds of the precession is smaller than the absolute value of each of them. We showed that by varying the ratio of the laser field strength F to the square of the laser field frequency ω, one can control the precession frequency of the electron orbit and even make the precession vanish, so that the elliptical orbit of the electron would become stationary. This is a counterintuitive result.

1. Introduction

Analytical studies of effects of a high-frequency laser field on various Rydberg atoms and ions—the studies using the method of separating rapid and slow subsystems—have been presented in the literature: see, e.g., book [1] and references therein. In particular, analytical results for hydrogen Rydberg atoms were presented in paper [2] for the case of the linear polarization of the high-frequency laser field and in paper [3] for the cases of the elliptical or circular polarization of the high-frequency laser field.

Specifically, in paper [2] it was shown that the unperturbed elliptical orbit of the Rydberg electron, generally is engaged simultaneously in the precession of the orbital plane about the direction of the laser field and in the precession within the orbital plane, the corresponding precession frequencies being calculated analytically. In paper [2] it was also pointed out that the situation has a celestial analogy: it is mathematically equivalent to the motion of a satellite around an oblate planet (such as, e.g., the Earth), the results for the latter system being presented, e.g., in book [4]. Later in paper [5] it was demonstrated that there is also another celestial analogy: it is mathematically equivalent also to the motion of a planet around a circular binary star.

As for paper [3], their authors showed that the case of the circular polarization of the high-frequency laser field is mathematically equivalent to the motion of a satellite around a (fictitious) prolate planet, the results for the latter system being presented, e.g., in book [6]. The orbit of the electron in this case is also engaged simultaneously in the precession of the orbital plane about the direction of the laser field and in the precession within the orbital plane, the corresponding precession frequencies being calculated analytically [3].

The authors of paper [3] also obtained analytical results for the situation where the high-frequency laser field is elliptically-polarized in the plane of the electron orbit. They demonstrated that this situation is mathematically equivalent to a problem of celestial mechanics, where a satellite moves in an equatorial orbit about a slightly non-spherical planet. For this case the plane of the orbit does not change its orientation over the course of time: the only precession that is the precession of the periapsis (and apoapsis) of the ellipse in the orbital plane.

All of the above analytical results were obtained while disregarding relativistic effects. In the present paper we study the role of the relativistic effect for hydrogenic Rydberg atoms or ions in a high-frequency linearly- or circularly-polarized laser field, the effect being an additional (relativistic) precession of the electron orbit in its own plane. For the linearly-polarized laser field, in the general case, where the electron orbit is not perpendicular to the direction of the laser field, there can exist a critical polar angle θ_c of the orbital plane, for which the precession within the plane vanishes and only the precession of the orbital plane remains. We study the dependence of the critical angle both on the angular momentum of the electron and on the laser field parameters.

For the particular situation, where the electron orbit is perpendicular to the direction of the linearly-polarized laser field, we show that the relativistic precession and the precession due to the laser field occur in the opposite directions, so that their combined effect is smaller than the absolute value of each of them. Moreover, we show the existence and calculate the specific value of the laser field parameters, for which the two precessions cancel each other out, so that the elliptical orbit of the electron becomes stationary. This is a counterintuitive result.

2. Analytical Calculations for the Linearly-Polarized Laser Field in the General Case

We study a hydrogen atom or a hydrogen-like ion of charge Z which is subjected to a high-frequency linearly-polarized laser field of amplitude F, directed along the z-axis, and frequency ω. The interaction of the laser field with Rydberg states can be described classically. Relativistic effects are taken into account. The Hamiltonian of the system is therefore

$$H=H_0+zF\cos \mathsf{\omega }t,H_0=\sqrt{p^2{c}^2+m^2{c}^4}-m{c}^2-\frac{Z{e}^2}{r}$$

(1)

where m is the electron mass, e is the elementary charge, p is the momentum of the electron, r is the distance from the nucleus to the electron, and c is the speed of light. Atomic units (m = e = ħ = 1) are used throughout this study.

In the absence of the laser field, we approximate the time-independent part of the Hamiltonian for the case p << mc:

$$H_0=c^2\sqrt{1+\frac{p^2}{c^2}}-c^2-\frac{Z}{r}\approx \frac{p^2}{2}-\frac{p^4}{8c^2}-\frac{Z}{r}$$

(2)

From the non-relativistic Hamiltonian,

$$H_{NR}=\frac{p_0^2}{2}-\frac{Z}{r}=E_0$$

(3)

where p₀ is the non-relativistic momentum of the electron and E₀ is its energy, we express p₀

$$p_0^2=2\left(E_0+\frac{Z}{r}\right)$$

(4)

and substitute it in the second term in Equation (2), thus obtaining the further approximation:

$$H_0\approx \frac{p^2}{2}-\frac{Z}{r}\left(1+\frac{E_0}{c^2}\right)-\frac{Z^2}{2c^2{r}^2}-\frac{E_0}{2c^2}\equiv H_1-\frac{Z^2}{2c^2{r}^2}-\frac{E_0}{2c^2}$$

(5)

where H₁ is the Hamiltonian of the system without the relativistic correction. Therefore, the penultimate term in Equation (5) is the perturbing term due to the relativistic effects. (The last term in Equation (5) is constant and thus does not affect the motion.) In book [7], a relativistic treatment of the Kepler problem is presented. The effect of the relativistic correction on the orbit dynamics is the precession of the orbit in its plane with the frequency (scaled by the Kepler frequency ω_K)

$$\frac{{\mathsf{\Omega }}_c}{{\mathsf{\omega }}_K}=\frac{1}{\sqrt{1-\frac{Z^2}{L^2{c}^2}}}-1\approx \frac{Z^2}{2L^2{c}^2}$$

(6)

where L is the angular momentum of the electron (this result follows from Equation (10) in book [7]); we refer to the quantity (6) as the scaled relativistic precession. The precession is positive, i.e., its angular velocity has the same sign as the angular velocity of the Kepler motion.

Now we consider the above-mentioned system without the relativistic correction subjected to a linearly-polarized laser field of amplitude F and frequency ω which is much greater than the highest frequency of the unperturbed system. For such systems, it is appropriate to use the formalism of effective potentials [1,8,9,10]. As a result, the Hamiltonian H₁ in Equation (5) acquires a time-independent term. The zeroth-order effective potential,

$$U_0=\frac{1}{4{\mathsf{\omega }}^2}\left[V,\right[V,H_1]]=\frac{F^2}{4{\mathsf{\omega }}^2}$$

(7)

where V = zF and [P, Q] are the Poisson brackets, is a coordinate-independent energy shift, so it does not affect the dynamics of the system. The first-order effective potential gives the first non-vanishing effect on the system:

$$U_1\left(r,\mathsf{\theta }\right)=\frac{1}{4{\mathsf{\omega }}^4}\left[\left[V,H_1],[\right[V,H_1\right],H_1]]=-\frac{a\left(1+\frac{E_0}{c^2}\right)\left(3{\cos }^2\mathsf{\theta }-1\right)}{r^3}\approx -\frac{a\left(3{\cos }^2\mathsf{\theta }-1\right)}{r^3}$$

(8)

where a = ZF²/(4ω⁴); as E₀ << c², we can neglect the term E₀/c² in (8). The first term of U₁ is a perturbation of the Coulomb potential which makes the system mathematically equivalent to a satellite rotating around the oblate Earth [4], whose motion has the following property: the unperturbed elliptic orbit undergoes simultaneously two precessions, one of them being the precession of the orbit in its plane, and the other being the precession of the orbital plane about the vector F. Both precession frequencies are of the same order of magnitude and are much smaller than the Kepler frequency.

Without the relativistic correction, the first-order effective potential given in Equation (8) gives rise to two simultaneous effects on the Kepler orbit, as mentioned above. By using Equations (1.7.10) and (1.7.11) from book [4], we obtain the scaled frequencies of the precession of the orbit in its plane (“pip” stands for “precession in plane”) and the precession of the plane about the direction of the laser field (“pop” stands for “precession of plane”):

$$\frac{{\mathsf{\Omega }}_{pip}}{{\mathsf{\omega }}_K}=\frac{3aZ}{2L^4}\left(1-5{\sin }^2\mathsf{\theta }\right)$$

(9)

$$\frac{{\mathsf{\Omega }}_{pop}}{{\mathsf{\omega }}_K}=\frac{3aZ}{L^4}\sin \mathsf{\theta }$$

(10)

where θ is the angle between the orbital plane and the laser field. The precession of the orbital plane is realized by the plane’s rotation around the vector F, while its angle with the vector stays the same. For the case considered in the previous section, θ = π/2, the orbit plane precesses parallel to itself, therefore, the angular velocities from Equations (9) and (10) are both parallel to the laser field.

When the relativistic precession is taken into account, it creates an additional term for the precession in the plane. Thus, the plane of the orbit of the electron in this case undergoes the precession given by (10), while the orbit precesses in its own plane with the scaled frequency

$$\frac{{\mathsf{\Omega }}_{pip}}{{\mathsf{\omega }}_K}+\frac{{\mathsf{\Omega }}_c}{{\mathsf{\omega }}_K}=\frac{3aZ}{2L^4}\left(1-5{\sin }^2\mathsf{\theta }\right)+\frac{Z^2}{2L^2{c}^2}$$

(11)

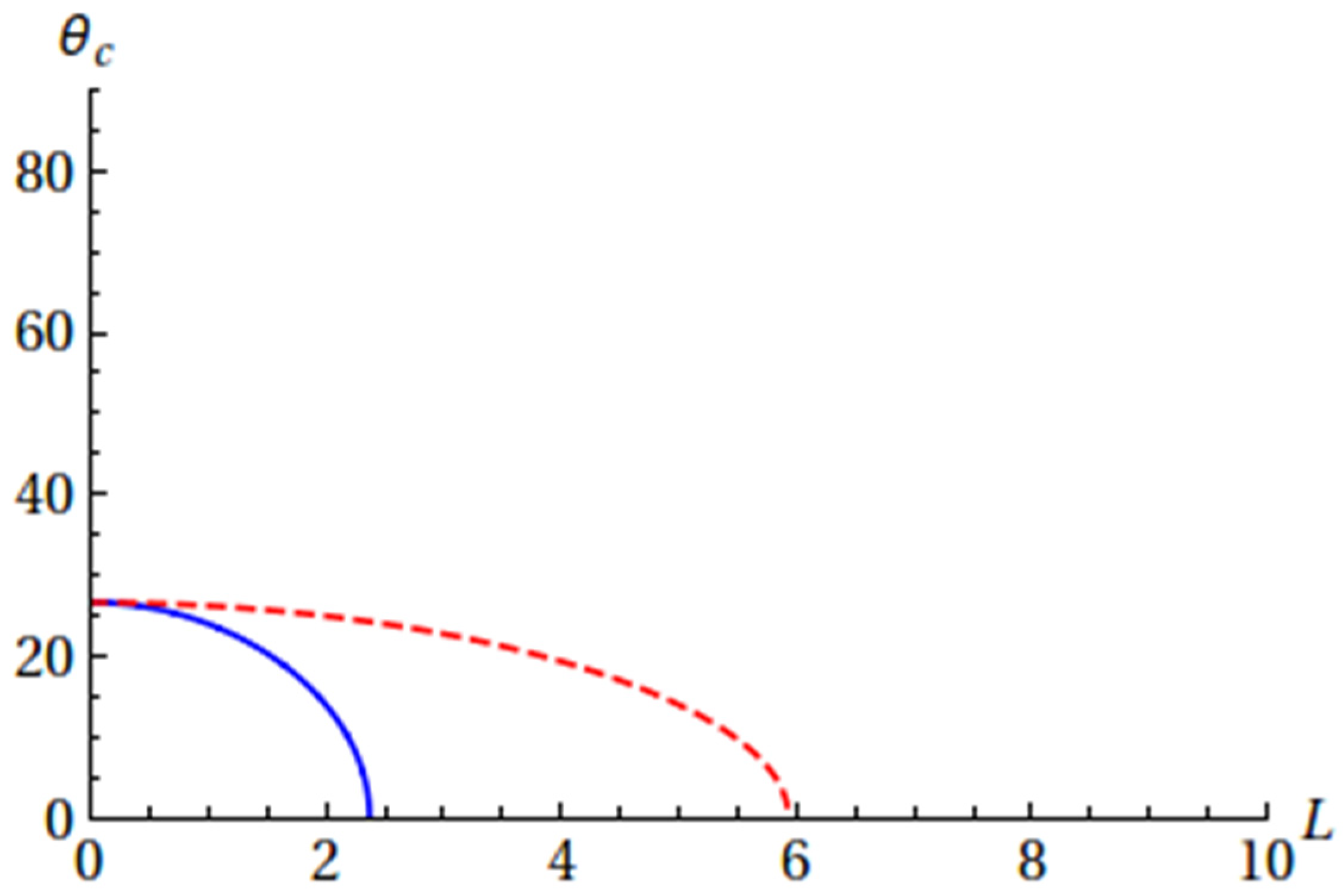
Without the relativistic effects, the critical angle θ_c at which there is no precession in the plane is given by arcsin (1/5^1/2) ≈ 26.6°. The relativistic effects increase the value of this critical angle: its value is given by

$${\mathsf{\theta }}_c=\arcsin \sqrt{\frac{1}{5}+\frac{4{\mathsf{\omega }}^4{L}^2}{15F^2{c}^2}}$$

(12)

Figure 1 shows the value of the critical angle in degrees depending on the angular momentum of the electron, for selected values of the laser field strength and frequency.

From Equation (12), we see that the situation when the precession in the orbital plane vanishes is possible when

$$L<\frac{F}{{\mathsf{\omega }}^2}c\sqrt{3}$$

(13)

i.e., the relativistic correction puts an upper limit on the value of the angular momentum of the electron when the vanishing of the precession in the orbital plane is possible, for the given values of the laser field strength and frequency. For example, when

$$\mathsf{\omega }>\sqrt{Fc\sqrt{3}}$$

(14)

the precession in the orbital plane never vanishes for any L ≥ 1; for example, if F = 2, then for the laser field frequency ω > 21.8 the precession in the plane never vanishes for any L ≥ 1.

3. The Case of the Electron Angular Momentum Collinear with the Linearly-Polarized Laser Field

Now we consider the situation when the angular momentum of the electron is collinear to the laser field, i.e., θ = π/2. In this case, the perturbation takes the following form:

$$U_1\left(r\right)=\frac{a}{r^3}$$

(15)

The calculation of the 1/rⁿ-perturbation for the Kepler orbit can be found in work [11] (the treatment for the cases n = 2 and n = 3 can be found also in the textbook [12]). For the Coulomb potential −α/r perturbed by the potential β/r^k, the orbit undergoes a precession with the perihelion advance

$$\mathsf{\delta }\mathsf{\Phi }=2m\mathsf{\beta }\frac{\partial }{\partial L}\left(\frac{1}{L}{p}^{2-k}\underset{0}{\overset{\mathsf{\pi }}{{\displaystyle \int }}}{\left(1+\mathsf{\epsilon }\cos \mathsf{\phi }\right)}^{k-2}d\mathsf{\phi }\right)$$

(16)

with the substituted quantities

$$p=\frac{L^2}{m\mathsf{\alpha }},\mathsf{\epsilon }=\sqrt{1+\frac{2E_0{L}^2}{m{\mathsf{\alpha }}^2}}$$

(17)

the first of which is the semi-latus rectum of the unperturbed elliptical orbit and the second is its eccentricity. The ratio of the precession frequency due to the perturbation to the Kepler frequency given by Equation (16) is therefore

$$\frac{{\mathsf{\Omega }}_1}{{\mathsf{\omega }}_K}=-\frac{3aZ}{L^4}=-\frac{3Z^2{F}^2}{4L^4{\mathsf{\omega }}^4}$$

(18)

to which we refer as scaled high-frequency precession. The precession caused by the high-frequency laser field is negative (its angular velocity is of the opposite sign to that of the Kepler motion). The ratio of the magnitudes of the precessions is

$$\frac{{\mathsf{\Omega }}_c}{{\mathsf{\Omega }}_1}=\frac{2L^2{\mathsf{\omega }}^4}{3c^2{F}^2}$$

(19)

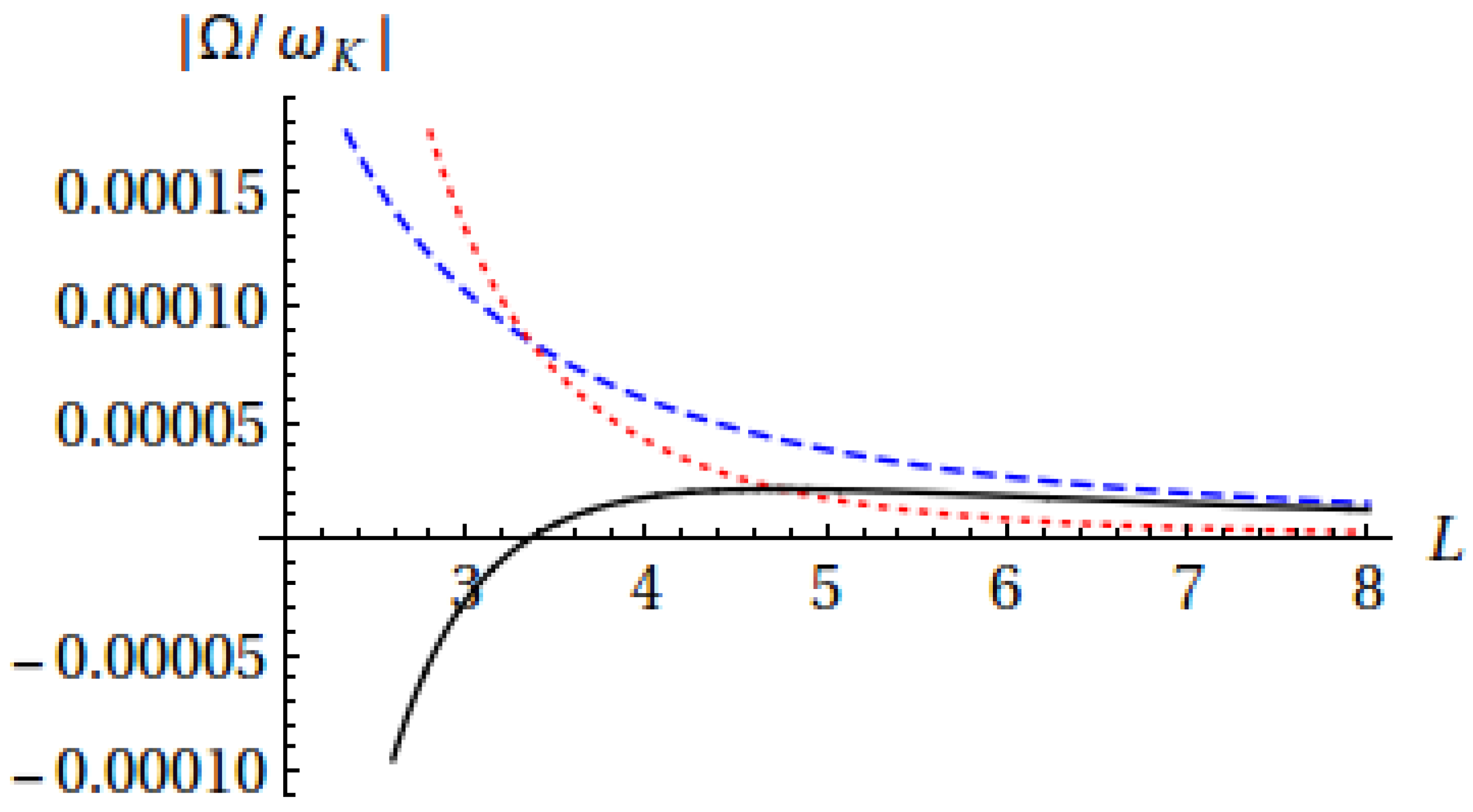
For example, for the values of the laser field amplitude F = 2 and frequency ω = 10, the ratio in Equation (19) is of the order of unity for L being in the approximate range between 3 and 6. Due to their opposite directions, the combined effect of the relativistic and high-frequency precessions is always less by absolute value than the greater precession by absolute value, and the two effects may cancel each other.

We note that the ratio of the frequencies in Equation (19) does not depend on the nuclear charge Z. However, if in the expansion in Equation (6) we would add higher order terms, then the ratio in Equation (19) would become weakly dependent on Z.

Figure 2 shows the dependence of the value of both corrections and of the combined effect of the two on the value of the angular momentum L of the electron for the nuclear charge Z = 6, the laser field amplitude F = 2 and frequency ω = 10.

The high-frequency laser field cancels the relativistic effect when

$$\frac{F}{{\mathsf{\omega }}^2}=\sqrt{\frac{2}{3}}\frac{L}{c}$$

(20)

For example, for L = 3, the laser field with F = 2 and ω = 10.5778 will make the orbit’s precession vanish. Figure 3 shows the critical value of the frequency of the laser field of selected amplitudes at which the precession of the electron orbit vanishes, depending on the angular momentum of the electron. As we see, the critical value of the laser field frequency stays much greater than the Kepler frequency of the electron 1/L³ and is therefore within the validity range of the method of effective potentials.

Thus, by varying the ratio of the laser field strength F to the square of the laser field frequency ω, one can control the precession frequency of the electron orbit and even make the precession vanish (according to Equation (20)), so that the elliptical orbit of the electron would become stationary. This is a counterintuitive result.

In general, any precession at some frequency Ω manifests in the radiation spectrum of a hydrogenic atom/ion as satellites separated from the unperturbed frequency of the spectral line by multiples of the precession frequency. Thus, the above situation where the elliptical orbit of the electron becomes stationary would manifest in the radiation spectrum as the disappearance of the satellites.

4. Analytical Calculations for the Circularly-Polarized Laser Field

In this section, we consider the case of circular polarization of the laser field. In this case, the field of amplitude F and frequency ω is perpendicular to the z-axis and varies as

$$F=F\left({\mathbf{e}}_{\mathbf{x}}\cos \mathsf{\omega }t+{\mathbf{e}}_{\mathbf{y}}\sin \mathsf{\omega }t\right)$$

(21)

where e_x and e_y are the Cartesian unit vectors. For our system, the relativistic correction stays the same as described in Section 2, while the effective potential due to the laser field is different. In this case, the Hamiltonian without the relativistic correction is

$$H_0=H_1+xF\cos \mathsf{\omega }t+yF\sin \mathsf{\omega }t$$

(22)

where H₁ is the Hamiltonian of the system without the relativistic correction. We denote

$$V=xF=Fr\sin \mathsf{\theta }\cos \mathsf{\phi },W=yF=Fr\sin \mathsf{\theta }\sin \mathsf{\phi }$$

(23)

where (r, θ, φ) are the spherical coordinates. We apply the method of effective potentials [8,9,10] and obtain the zeroth-order effective potential

$$U_0=\frac{1}{4{\mathsf{\omega }}^2}\left(\left[V,\right[V,H_1\left]]+[W,\right[W,H_1\right]])=\frac{F^2}{2{\mathsf{\omega }}^2}$$

(24)

which, as in the linear-polarization case, is a coordinate-independent energy shift, so it does not affect the dynamics of the system, and the first-order effective potential

$$\begin{array}{c}{U}_1=\frac{1}{4{\mathsf{\omega }}^4}\left(\left[\left[V,H_0],[\right[V,H_0\right],H_0\left]]+[\right[W,H_0],[\left[W,H_0\right],H_0\right]])+\\ +\frac{-1}{2{\mathsf{\omega }}^3}\left[\left[V,H_0],[W,H_0\right]\right]=\frac{a\left(3{\cos }^2\mathsf{\theta }-1\right)}{r^3}\end{array}$$

(25)

which is the opposite of that in the linear-polarization case. Thus, the results for the circular-polarization case can be obtained by effectively replacing a with −a in the linear-polarization case. In particular, in the case of the angular momentum collinear with the laser field, the precession due to the circularly-polarized laser field is positive, the same as the precession due to the relativistic correction, so these two effects cannot cancel each other. The ratio of the magnitudes of these two precessions is the same as in Equation (13) for the linear-polarization case. In the general case of the orientation of the angular momentum with respect to the direction of the laser field, the precession of the orbit in its plane and the precession of the orbit plane both have the direction opposite to that in the linear-polarization case and are expressed by Equations (15) and (16) multiplied by −1.

The precession in the orbital plane vanishes when the critical angle is

$${\mathsf{\theta }}_c=\arcsin \sqrt{\frac{1}{5}-\frac{4{\mathsf{\omega }}^4{L}^2}{15F^2{c}^2}}$$

(26)

Figure 4 shows the dependence of the critical angle corresponding to zero precession on the angular momentum of the electron, for the cases of F = 2 and F = 5 and ω = 10.

We see that the range of possible angles is more narrow than in the linear-polarization case, being 0 ≤ θ ≤ arcsin(1/5^1/2), with the possibility of zero precession at polar orbits (θ = 0) when

$$L=\frac{F}{{\mathsf{\omega }}^2}c\frac{\sqrt{3}}{2}$$

(27)

So the upper limit of the angular momentum is twice as small as in the linear-polarization case (19).

5. Conclusions

We analyzed the relativistic effect for hydrogenic Rydberg atoms or ions in a high-frequency linearly- or circularly-polarized laser field. For the general case, where the electron orbit is not perpendicular to the direction of the laser field, we showed that the precession of the electron orbit within its plane can vanish at some critical polar angle θ_c of the orbital plane. We calculated analytically the dependence of the critical angle on the angular momentum of the electron and on the parameters of the laser field.

For the particular situation, where the electron angular momentum is collinear with the linearly-polarized laser field, we demonstrated that the relativistic precession and the precession due to the laser field occur in the opposite directions. As a result, the combined effect of these two kinds of the precession is smaller than the absolute value of each of them. We showed that, by varying the ratio of the laser field strength F to the square of the laser field frequency ω, one can control the precession frequency of the electron orbit and even make the precession vanish, so that the elliptical orbit of the electron would become stationary. This is a counterintuitive result.

In general, any precession at some frequency Ω manifests in the radiation spectrum of a hydrogenic atom/ion as satellites separated from the unperturbed frequency of the spectral line by multiples of the precession frequency. So, the above situation where the elliptical orbit of the electron becomes stationary would manifest in the radiation spectrum as the disappearance of the satellites.

We hope that the fundamental nature of our analytical results for the hydrogenic atoms/ions, i.e., for atomic systems serving as the test bench of our understanding of atomic physics, makes the results significant.