Early Results on GNSS Receiver Antenna Calibration System Development ^†

Abstract

Precise global navigation satellite system (GNSS) positioning is based on carrier phase observations, where the understanding of the receiver antenna’s phase center corrections (PCCs) is critical. With the main goal of determining the PCC models of GNSS receiver antennas, only a few antenna calibration systems are in operation or under development worldwide. In this paper, a new automated GNSS receiver antenna calibration system, recently developed at the Laboratory for Measurements and Measuring Technique (LMMT) of the Faculty of Geodesy of the University of Zagreb in Croatia, is briefly presented. The developed system is an absolute field calibration system based on the utilization of a Mitsubishi MELFA RV-4FML-Q 6-axis industrial robot. The antenna’s PCC modeling is based on triple-difference carrier phase observations and spherical harmonic (SH) expansion. Our early calibration results for the global positioning system (GPS) L1 frequency show sub-millimeter agreements with the IGS approved Geo++ GmbH values.

1. Introduction

For high-accuracy global positioning applications on the centimeter and millimeter level, global navigation satellite system (GNSS) receivers are essential sensors. To obtain the required accuracy level, all influential factors and error sources must be understood and, in an appropriate manner, accounted for. One such important influence is the phase center correction (PCC) of GNSS receiver antennas.

Because of the antenna’s design characteristics and electromagnetic properties [1], the geometric location of the GNSS signal reception, i.e., the antenna phase center (PC), changes with respect to the incoming signal’s direction and frequency [2,3,4]. Such variations cause advances and delays in carrier phase observations and corresponding range errors. Therefore, receiver antenna calibration is needed.

Today, absolute filed calibration is the state of the art when it comes to GNSS receiver antenna calibration. Only a few calibration systems utilizing a precise robot are operational or under development worldwide [5,6,7,8,9,10,11,12], and even fewer are accredited by the International GNSS Service (IGS) to provide antenna calibration results [13]. Since this topic is of high interest to the scientific antenna community, and a new calibration system is highly desirable, at the Laboratory for Measurements and Measuring Technique (LMMT) of the Faculty of Geodesy of the University of Zagreb in Croatia, a new antenna calibration system has been developed [14].

In this article, preliminary antenna calibration results for the Global Positioning System (GPS) L1 frequency (G01) are presented and elaborated. Furthermore, the results on LMMT calibration validation with Geo++ GmbH are presented and discussed.

2. Materials and Methods

2.1. The Receiver Antenna Phase Center Correction Model

To fulfill the requirements of high-accuracy positioning applications, the receiver antenna PCCs must be determined. In line with the IGS convention, and as depicted in Figure 1, PCC is divided into the phase center offset (PCO) vector and the azimuth- and elevation-dependent phase center variation (PCV) [4,6,10,11,12,14]:

$$PCC\left({\alpha }^i,z^i\right)=-\hspace{0.17em}{e}^{\mathrm{T}}\left({\alpha }^i,z^i\right)\cdot PCO+PCV\left({\alpha }^i,z^i\right)+r.$$

(1)

where $e\left({\alpha }^i,z^i\right)$ is the line-of-sight unit vector from the receiver to the satellite i, and $r$ is the constant part equal in all directions present due to the relative characteristics of GNSS measurements [4,6]. The PCO is a vector from the antenna reference point (ARP) to an arbitrarily defined mean phase center (MPC). The PCV is the direction-dependent range correction function, i.e., the difference between the real and ideal phase wavefront. The PCCs, and all corresponding antenna-related points, vectors, and scalars, are defined in a 3D antenna-fixed left-handed coordinate system (antenna frame–AF).

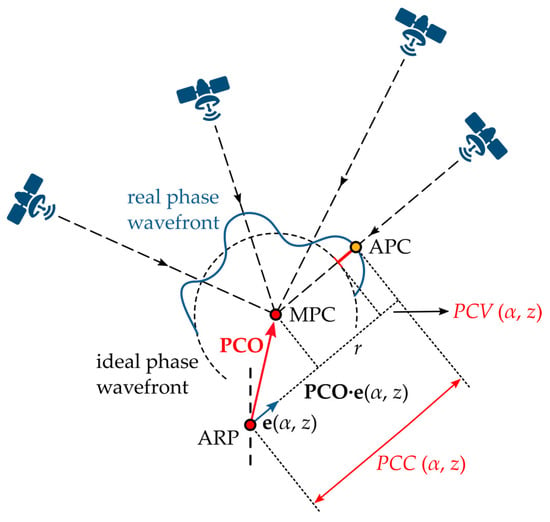
Figure 1. Definition and geometrical interpretation of the adopted GNSS receiver antenna phase center correction (PCC) model; ARP—antenna reference point; MPC—mean phase center; APC—actual phase center; PCO—phase center offset; PCV—phase center variation.

A set of PCCs of an antenna are transformed to PCO and PCVs using a least squares (LSQ) adjustment and by simultaneously fulfilling two conditions. Firstly, the PCV at the antenna zenith are constrained to zero, i.e., zero-zenith constraint, by $PCV\left({\alpha }^i,z^i=0°\right)=0$. Secondly, the PCO is determined such that the sum of the squared PCVs is minimal, i.e., ${\displaystyle \sum \left[PCV{\left({\alpha }^i,z^i\right)}^2\right]}\to \min$.

2.2. Antenna Calibration Method at LMMT

To efficiently sample the entire antenna-under-test (AUT) hemisphere during calibration, at LMMT, a 6-axis industrial robot Mitsubishi MELFA RV-4FLM-Q is utilized. The robot turns the AUT in 2088 different antenna orientations, with stationary 2.5 s at every single orientation. Therefore, depending on the calibration timing parameters, a full calibration at LMMT lasts approx. 2 h. During calibration, a reference station (REF) on a 5 m short baseline is used. On both stations (REF and AUT), simultaneous 10 Hz raw carrier phase observations are registered with equal receiver settings. Afterwards, prior to PCC LSQ estimation, the carrier phase measurements are preprocessed to eliminate the majority of the GNSS error sources.

Generally, the calibration system at LMMT is based on the triple-difference (TD) approach, i.e., time-differenced double-difference carrier phase observations [15]. A generic GNSS observation equation from receiver A to satellite i, in units of length is expressed as follows [16]:

$${\Phi }_{\mathrm{A}}^i={\rho }_{\mathrm{A}}^i+c\left(\delta t_{\mathrm{A}}-\delta t^i+d{t}^{\mathrm{rel}}\right)+{\xi }_{\mathrm{A}}^i+c\left(d{t}_{\mathrm{A}}-d{t}^i\right)+T_{\mathrm{A}}^i-I_{\mathrm{A}}^i+\lambda N_{\mathrm{A}}^i+\lambda {\omega }_{\mathrm{A}}^i+M{P}_{\mathrm{A}}^i+{\epsilon }_{\mathrm{A}}^i,$$

(2)

where ${\rho }_{\mathrm{A}}^i$ is the geometric distance, $c$ is the speed of light, $\delta t_{\mathrm{A}}$ and $\delta t^i$ are the receiver and satellite clock errors, $d{t}^{\mathrm{rel}}$ is the relativistic effects term, ${\xi }_{\mathrm{A}}^i$ is the combined satellite and receiver antennas’ PCC value, $d{t}_{\mathrm{A}}$ and $d{t}^i$ are the receiver and satellite hardware delays, $T_{\mathrm{A}}^i$ is the tropospheric delay, $I_{\mathrm{A}}^i$ is the ionospheric delay, $\lambda$ is the signal wavelength, $N_{\mathrm{A}}^i$ is the integer phase ambiguity, ${\omega }_{\mathrm{A}}^i$ is the carrier phase wind-up (PWU) effect, $M{P}_{\mathrm{A}}^i$ is the multipath term, and ${\epsilon }_{\mathrm{A}}^i$ is the phase observation noise term.

Forming the TD carrier phase observations needed for antenna calibration includes eight raw observations, from Equation (2), on the REF (R) and AUT (T) receivers for two satellites i and j, in two epochs $t_k$ and $t_{k+1}$:

$$\begin{array}{lll}T{D}_{\mathrm{T},\mathrm{R}}^{ij}\left(t_k,t_{k+1}\right)& =& {\Phi }_{\mathrm{R}}^j\left(t_{k+1}\right)-{\Phi }_{\mathrm{T}}^j\left(t_{k+1}\right)-{\Phi }_{\mathrm{R}}^i\left(t_{k+1}\right)+{\Phi }_{\mathrm{T}}^i\left(t_{k+1}\right)-{\Phi }_{\mathrm{R}}^j\left(t_k\right)+{\Phi }_{\mathrm{T}}^j\left(t_k\right)+{\Phi }_{\mathrm{R}}^i\left(t_k\right)-{\Phi }_{\mathrm{T}}^i\left(t_k\right)\\ & =& -PC{C}_{\mathrm{T}}^j\left(t_{k+1}\right)+PC{C}_{\mathrm{T}}^i\left(t_{k+1}\right)+PC{C}_{\mathrm{T}}^j\left(t_k\right)-PC{C}_{\mathrm{T}}^i\left(t_k\right)+\partial {\epsilon }_{\mathrm{T},\mathrm{R}}^{ij}.\end{array}$$

(3)

By exploiting the high spatial and temporal correlations of GNSS observations, and by forming TDs on a short baseline between two time-adjacent AUT orientations, the final TDs contain only the AUT PCCs and the differential phase noise $\partial {\epsilon }_{\mathrm{T},\mathrm{R}}^{ij}$. At LMMT, the PCCs are parametrized by spherical harmonic (SH) expansion with a degree and order resolution of $m=n=8$ as follows:

$$PCC\left({\alpha }^i,z^i\right)={\displaystyle \sum _{m=0}^{m_{\max }}{\displaystyle \sum _{n=0}^m{\tilde{P}}_{mn}\left[\cos \left(z^i\right)\right]}}\cdot \left[a_{mn}\cos \left(n{\alpha }^i\right)+b_{mn}\cos \left(n{\alpha }^i\right)\right].$$

(4)

where ${\tilde{P}}_{mn}$ is the fully normalized Legendre function, $a_{mn}$ and $b_{mn}$ are the SH coefficients, and ${\alpha }^i$ and $z^i$ are the azimuth and zenith angles in the AF.

The SH coefficients are determined by a constrained LSQ adjustment. Afterwards, the PCCs of the AUT are calculated for the entire antenna hemisphere according to Equation (4), transformed to PCO/PVC, and exported to the IGS ANTEX (ANTenna EXchange) format.

For an in-depth description of the antenna calibration methodology at LMMT, an interested reader is referred to Tupek et al. [14].

2.3. Antenna Calibration System at LMMT

The GNSS receiver antenna calibration system developed at LMMT consists of two major parts: hardware and software. Hardware-wise, the calibration system consists of a 6-axis industrial robot Mitsubishi MELFA RV-4FLM-Q with its corresponding controller Mitsubishi MELFA CR750, two GNSS receivers (Trimble NetR5) and antennas, and a personal computer. An on-site calibration set-up at LMMT is depicted in Figure 2. The in-house custom-made software components of the calibration system, all written in Python, are the antenna calibration module (ACM), time synchronization module (TISY), and the PCC estimation module. An in-depth description of the calibration system operation can be found in Tupek et al. [14].

Figure 2. GNSS antenna calibration system at the Laboratory for Measurements and Measuring Technique (LMMT) of the Faculty of Geodesy of the University of Zagreb in Croatia; REF—reference antenna (TRM57971.00 NONE); AUT—antenna-under-test (LEIAX1202GG NONE). The calibration field consists of two 5-m-spaced pillars, which are part of the Calibration Baseline of the Faculty of Geodesy of the University of Zagreb [17].

3. Results and Discussion

To test the antenna calibration system at LMMT and to validate the calibration results with Geo++ GmbH, an IGS approved calibration institution, from April to June of 2023, four calibration campaigns of the same GNSS antenna Trimble Zephyr 2 Geodetic (TRM57971.00 NONE, S/N: 30739001) for the GPS L1 frequency were conducted. Figure 3 visualizes the main benefit of using a robot for antenna calibration, i.e., a full coverage of the entire antenna hemisphere, even after only approx. 2 h of calibration.

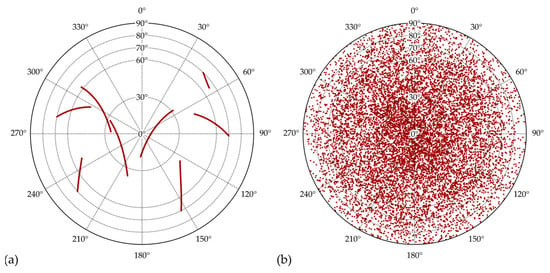
Figure 3. Satellite azimuth and zenith angle plot (sky-plot) during antenna calibration at LMMT: (a) topocentric frame (TF); (b) antenna frame (AF).

To validate the LMMT antenna calibration results, a comparison with an independent calibration was conducted. For that purpose, the investigated antenna was calibrated individually by Geo++ GmbH, an IGS approved institution, on 5 August 2022.

According to the new calibration method at LMMT, PCCs have been estimated for every conducted antenna calibration campaign. Lastly, to obtain a final solution, calibration results have been averaged, and the final PCO and PVC grids were exported to ANTEX. Table 1 summarizes the LMMT and Geo++ GmbH estimated PCOs. The PCO differences between the LMMT and Geo++ GmbH calibrations are on the sub-millimeter level. The PCVs of the investigated antenna for the GPS L1 frequency, per calibration institution, are depicted in Figure 4. Both individual calibration results show similar PCV behaviors over the entire antenna hemisphere, with noticeable larger values at the antenna horizon for the Geo++ calibrations. Also, for both calibration results (LMMT and Geo++ GmbH), small azimuthal variations are noticeable.

Table 1. PCO vector components of antenna TRM57971.00 NONE (S/N: 30739001) of GPS L1 (G01) frequency per calibration institution. All values are in millimeters (mm).

Calibration Institution	Phase Center Offset (PCO)
	North	East	Up
Geo++ GmbH	0.79	0.32	66.96
LMMT	1.24	0.11	67.24

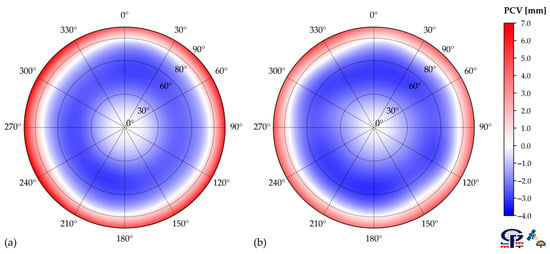
Figure 4. (a) Geo++ GmbH and (b) LMMT phase center variations (PCVs) of antenna TRM57971.00 NONE (S/N: 30739001) for GPS L1 (G01) frequency.

To estimate the accuracy of LMMT individual antenna calibration results, the Geo++ GmbH calibration results are taken as reference values. The PCC differences $\Delta PCC$ of antenna TRM57971.00 NONE (S/N: 30739001) for GPS L1 (G01) frequency, over the entire antenna hemisphere, are calculated, and they are depicted in Figure 5. By a simple visualization of the gained difference pattern, it is evident that values around zero prevail with larger values mainly located at low antenna elevations, e.g., for an azimuth of approx. 300°.

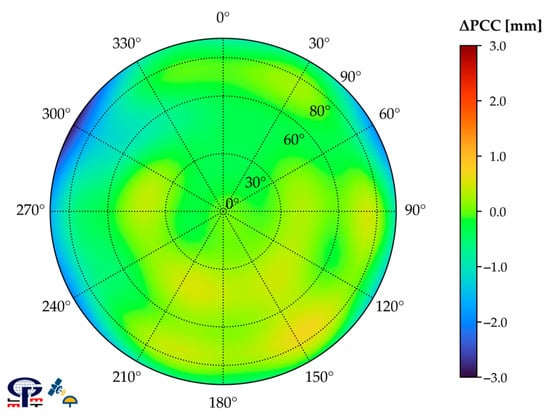
Figure 5. Geo++ GmbH and LMMT PCC differences ($\Delta PCC$) of antenna TRM57971.00 NONE (S/N: 30739001) for GPS L1 (G01) frequency after transformation to common PCO and datum.

To obtain a quantitative accuracy estimation of LMMT calibration results, the following scalar measures of the PCC difference pattern are calculated: minimum and maximum $\Delta PCC$, root-mean-square (RMS) deviation of $\Delta PCC$, range of the $\Delta PCC$, and the interquartile range (IQR) of the $\Delta PCC$. All calculated values are given in Table 2. Furthermore, because during the majority of GNSS applications, a standard elevation mask of a minimum of 10° is used, a 10° elevation-reduced antenna hemisphere analysis is justified. All accuracy measures were determined accordingly and are given in Table 2.

Table 2. Quantitative measures of the difference between Geo++ GmbH’s and LMMT’s individual absolute calibrations: minimum, maximum, root-mean-square (RMS) deviation, range, and interquartile range of $\Delta PCC$. All values are in millimeters (mm).

Full Antenna Hemisphere (0° Elevation Cut-Off)					Reduced Antenna Hemisphere (10° Elevation Cut-Off)
Min.	Max.	RMS	Range	IQR	Min.	Max.	RMS	Range	IQR
–2.92	0.72	0.52	3.64	0.44	–1.64	0.72	0.34	2.36	0.41

Considering the full antenna hemisphere, the LMMT and Geo++ GmbH PCC differences are in the interval from −2.92 to 0.72 mm, with the middle 50% of $\Delta PCC$ being within 0.44 mm. The RMS of the differences is 0.52 mm. However, if only the elevation-reduced antenna hemisphere is considered, accuracy measures significantly improve. The range of all $\Delta PCC$ is 2.36 mm with an RMS value of 0.34 mm whereby the middle 50% of the differences does not exceed 0.41 mm.

Therefore, to summarize, with the newly developed LMMT antenna calibration system, an estimated agreement with the accredited Geo++ GmbH calibrations, within 0.52 mm, was achieved.

4. Conclusions

The new GNSS receiver antenna calibration system developed at the Laboratory for Measurements and Measuring Technique (LMMT) of the Faculty of Geodesy of the University of Zagreb in Croatia can provide meaningful antenna calibration results for the GPS L1 frequency. According to the obtained experimental research results regarding the Trimble Zephyr 2 Geodetic antenna, an estimated agreement within 0.52 mm, in terms of RMS, with the accredited Geo++ GmbH results, was achieved. Therefore, our calibration results also confirm the compatibility of LMMT GPS L1 calibrations with the IGS accredited Geo++ GmbH calibrations.