QiMARL: Quantum-Inspired Multi-Agent Reinforcement Learning Strategy for Efficient Resource Energy Distribution in Nodal Power Stations

Abstract

The coupling of quantum computing with multi-agent reinforcement learning (MARL) provides an exciting direction to tackle intricate decision-making tasks in high-dimensional spaces. This work introduces a new quantum-inspired multi-agent reinforcement learning (QiMARL) model, utilizing quantum parallelism to achieve learning efficiency and scalability improvement. The QiMARL model is tested on an energy distribution task, which optimizes power distribution between generating and demanding nodal power stations. We compare the convergence time, reward performance, and scalability of QiMARL with traditional Multi-Armed Bandit (MAB) and Multi-Agent Reinforcement Learning methods, such as Greedy, Upper Confidence Bound (UCB), Thompson Sampling, MADDPG, QMIX, and PPO methods with a comprehensive ablation study. Our findings show that QiMARL yields better performance in high-dimensional systems, decreasing the number of training epochs needed for convergence while enhancing overall reward maximization. We also compare the algorithm’s computational complexity, indicating that QiMARL is more scalable to high-dimensional quantum environments. This research opens the door to future studies of quantum-enhanced reinforcement learning (RL) with potential applications to energy optimization, traffic management, and other multi-agent coordination problems.

1. Introduction

The fast-evolving shift to renewable sources of energy and distributed power generation has made it increasingly difficult to manage modern energy systems. The traditional centralized control structures can no longer handle the spatial and temporal variability of power generation and load. Instead, control and optimization of these systems are being decentralized with increasing focus on intelligent decision-making at the edge. In particular, smart grids and microgrids demand real-time energy distribution among the generating and consuming nodes, often with the additional constraints of uncertainty in demand, time-variant supply, and unavailability of information. These systems naturally fit into being defined as multi-agent systems, with each node (or agent) optimizing its own behavior while contributing towards achieving system performance [1,2,3].

In answer to these issues, the subarea of MARL has attracted much attention in recent times. MARL allows agents to learn the optimal decision policies by interacting with their environment and receiving feedback in the form of rewards or penalties. However, even though MARL holds much promise for such decentralized environments, it also possesses major drawbacks. With an increase in the number of agents, the state space and joint action spaces also increase combinatorially, which is a scalability issue with exponential computational requirements. Moreover, credit assignment becomes more difficult as it is challenging to apportion the rewards to the actions of every agent, especially when operating in cooperative environments. In addition, search strategies utilized in conventional MARL (e.g., $ϵ$-greedy or entropy-based approaches) are generally not capable of effectively exploring large or continuous state spaces and cause slow learning and poor convergence.

These challenges have driven research into alternative paradigms of learning able to enable more effective learning and coordination in complicated multi-agent systems. One of these lines is to capitalize on knowledge from quantum computing, particularly the structural advantages that come from quantum mechanics—superposition, entanglement, and non-classical sampling. While large-scale quantum hardware is presently in its early stages of development, a growing number of researchers have dared to explore the possibility of injecting classical algorithms with quantum-inspired mechanisms. These methods do not rely on real quantum hardware but instead simulate quantum phenomena in classical computing environments, thereby taking advantage of some of the theoretical strengths of quantum models without requiring quantum equipment [4,5,6].

In this paper, we propose a new learning framework known as QiMARL, which integrates simulated quantum phenomena into the learning process of MARL. QiMARL leverages the principles of quantum superposition to store several possible actions in parallel, enabling richer and more organized exploration of the policy space. The algorithm also stores interdependencies between agents through the simulation of quantum entanglement, enabling coordinated decision-making with message passing or centralized control. The algorithm also uses Quantum Amplitude Estimation (QAE)-style protocols to guide value estimation and sampling strategies better compared to regular Monte Carlo procedures [4,7,8,9,10,11]. All of these quantum-inspired calculations are performed with IBM’s Qiskit software and executed on classical simulators, the Aer backend in this case, which supports high-performance quantum circuit emulation. This design ensures that QiMARL is deployable today, even in environments with no access to quantum hardware.

A breakthrough in QiMARL is how it treats the joint policy space as a structured quantum state that evolves over time. Instead of either decentralized local updates or a fully centralized critic model, each agent in QiMARL responds to a parameterized quantum circuit whose gates are both locally modulated and entangled with other agents’ correlations. As a result, the system develops in a way that is amenable both to decentralized autonomy as well as global coherence and that represents a middle ground between fully independent and fully centralized learning. Furthermore, using simulated quantum measurements as a choice mechanism provides a controlled but random method for selecting actions, enhancing policy variety, and avoiding premature convergence to local minima.

To evaluate the effectiveness of QiMARL, we take an example in a real-world scenario in the field of dynamic energy allocation. Specifically, we simulate a nodal power grid consisting of a number of generating and consuming nodes. Every node is a self-interested agent with the objective of optimizing long-term energy allocation. The world is cooperative and partially observable, and agents must learn to coordinate their actions based on local reward feedback. In our experimental setup, we compare QiMARL against several reinforcement learning baselines, including Greedy, UCB [12,13], Thompson Sampling [14], MADDPG (Multi-Agent Deep Deterministic Policy Gradient), QMIX (Q-value Mixing Network), and PPO (Proximal Policy Optimization) methods. Adding them provides a clear baseline against which to judge whether or not QiMARL’s simulated quantum enhancements yield tangible benefits regarding convergence, reward optimization, and scalability [15,16,17].

Alongside presenting the QiMARL framework, this paper presents a controlled comparison of quantum-inspired learning against RL baselines in a real-world simulation problem with a comprehensive ablation analysis. Not only does the study reveal the possible practical applications of using quantum-inspired approaches, but it also confirms their effectiveness on classical hardware, opening up new avenues of research and application. Alongside these, we provide the corresponding background on bandit-based methods, traditional MARL, and quantum-inspired learning in Section 2, before presenting the QiMARL architecture in detail in Section 3 and Section 4. Experimental setup and results are provided in Section 5 and Section 6, while limitations and conclusions are given in Section 7 and Section 8.

Research Contributions

This paper makes the following primary contributions:

• We present QiMARL, a quantum-inspired multi-agent reinforcement learning algorithm that leverages classically simulated quantum operations like superposition, entanglement, and amplitude estimation to improve exploration, policy coordination, and convergence rate in distributed scenarios.
• We introduce a comprehensive classical simulation setup for QiMARL, employing IBM Qiskit. All quantum operations are performed on the Aer simulator backend, rendering the method readily deployable in current real-world applications without involving quantum hardware.
• We design and test QiMARL in the context of a realistic energy distribution scenario, where agents are neighborhood nodes with the requirement to dynamically adjust energy supply and demand. This test case is a realistic and challenging example of how to measure coordination under uncertainty.
• We compare QiMARL with large empirical reductions to single-agent reinforcement learning baselines—Greedy, UCB, and Thompson Sampling—and demonstrate that QiMARL always achieves greater cumulative rewards, more stable learning curves, and significantly better scalability with more agents [12,14,18].

2. Literature Review

QiMARL’s development intersects with several established and emerging fields of study. These are the traditional MARL, lightweight single-agent MAB strategies, and the quantum or quantum-inspired computing paradigms that offer competing information representation and policy sampling mechanisms. In this section, we provide a comprehensive overview of these domains to put our proposed method’s novelty and relevance into context.

2.1. Multi-Agent Reinforcement Learning (MARL)

MARL has emerged as a central research area in developing intelligent, decentralized decision-making systems. Unlike single-agent RL, with the environment supposed to be stationary and fully observable, MARL works in settings where multiple agents learn simultaneously with partial observability and non-stationary dynamics due to simultaneous policy updates. This renders it more complicated and introduces inherent issues related to coordination, stability, and scalability.

Over the past decade, much has been achieved to overcome them. Centralized training with decentralized execution (CTDE) architectures such as MADDPG, COMA (Counterfactual Multi-Agent policy gradients), and QMIX allow global information access during training while maintaining local policy execution during inference. These models have been shown to handle cooperative as well as mixed cooperative–competitive tasks well, particularly in domains like robotic control, autonomous vehicle control, and real-time strategy games. However, CTDE methods typically require access to global state, communications pathways, or mutual reward signals during training, which cannot be achieved in real-world deployment in systems such as power grids or sensor grids [19,20,21].

Another research area is value factorization and decomposition methods such as VDN (Value Decomposition Network) and QMIX, which seek to decompose the joint Q-function into agent-specific components. While this promotes decentralization, it forces structural assumptions that limit policy expressiveness or optimality in complex scenarios. Similarly, independent Q-learning (IQL) solutions attempt to scale by treating each agent as a standalone learner, but these are ravaged by instability due to the non-stationarity of the environment [22].

More recent trends include attention mechanisms, graph neural networks (GNNs), and message passing structures to encode inter-agent dependencies. While effective, they tend to be computationally costly and less interpretable. There is, therefore, increasing interest in hybrid or alternative structures that are guaranteed to keep agent autonomy intact while implying stability and coordination [23,24].

QiMARL innovates in this direction by introducing a quantum-inspired mechanism for agent entanglement and decision sampling. Rather than depending on explicit message passing or common critics, QiMARL introduces simulated quantum operations to project agent correlations and drive diversified, entangled exploration strategies—embodying emergent coordination without requiring full state observability or common communication protocols. Recent studies suggest that entanglement-inspired designs can foster efficient coordination in distributed systems like grids and transportation networks [5,25].

2.2. Bandit-Based Exploration Strategies in Decentralized Learning

Though MARL possesses strong theoretical frameworks for the cooperative system model, computational expenses could become undue in resource-constrained environments or real-time systems. Under these circumstances, scaled-down decision models founded on MAB theory are an easy solution.

In the basic MAB problem, an agent repeatedly selects one of a finite number of actions (arms), each with a reward distribution unknown to the agent. The goal is to collect maximum reward in the long run by balancing exploration (trying new arms) and exploitation (playing the best-known arm). Many exploration strategies have been developed over the years:

• Greedy approaches target short-term reward and use no exploration. $ϵ$-Greedy approaches add random exploration with a constant or diminishing probability.
• UCB approaches add confidence bounds around the estimate of rewards to induce exploration of unknown actions.
• Thompson Sampling uses Bayesian posterior sampling to inherently balance exploration and exploitation in a principled way.

These methods are typically used as lightweight single-agent reinforcement learning protocols, particularly for scenarios where agents talk sparingly to one another or the state–action space is limited. For distributed systems—say, wireless network selection, task offloading in edge computing, or energy demand response—individual agents using bandit methods can learn adaptive policies without coordination.

In the setting of this study, we apply MAB-based methods not as substitutes for end-to-end MARL frameworks nor as tools to substitute them. Instead, they serve as baselines for comparison. Since QiMARL suggests a new hybrid decision mechanism, having these baselines allows us to isolate the effects of its quantum-inspired aspects. In particular, we ask whether the richness in structure of QiMARL translates to measurable reward effectiveness and scalability improvements over decentralized, communication-free heuristics.

It should be noted that MAB models are lacking in the ability to manage stateful state transitions, sequential dependence, or cooperative planning. Yet their strong performance in low-dimensional or loosely coupled worlds made them a reference point of interest in research where MARL would be too computationally intensive, or where agents enjoy high autonomy.

2.3. Quantum Machine Learning and Quantum-Inspired Algorithms

Quantum computing is a developing technology that offers radically new models for information and algorithmic processing. Although fault-tolerant, universal quantum computers are still under development, there has been significant progress in the simulation of quantum circuits and the application of hybrid quantum–classical algorithms to machine learning problems. Quantum machine learning (QML) in this context explores the ways quantum effects—superposition, entanglement, and quantum interference—are able to enrich learning models, optimization processes, and data processing capabilities.

Several QML techniques are applicable to decision-making and reinforcement learning, such as the following ones:

• QAE provides a way to estimate expected values better than classical Monte Carlo algorithms through quantum phase estimation. In theory, this can reduce the sample size from O(1/$ϵ$²) to O(1/$ϵ$) [26].
• Variational Quantum Algorithms (VQAs), such as the Variational Quantum Eigensolver (VQE) and Quantum Approximate Optimization Algorithm (QAOA), facilitate parameterized quantum circuit optimization based on classical feedback loops [27,28].
• Quantum Monte Carlo (QMC) methods imitate probabilistic systems through quantum mechanics and have even been utilized for the simulation of complex physics and finance systems [29].

Subsequent works have explored the usage of quantum circuits for policy approximations in reinforcement learning, which offer richer hypothesis spaces and non-linear mappings. Even though theoretical predictions suggest potential benefits such as exponential speedup in some tasks [4], such benefits are currently only offered in small-scale or highly controlled environments. Quantum advantage for practical machine learning remains hypothetical since hardware evolution is in its early stages, plagued with problems like decoherence, limited qubits, and gate reliability. As a result, while papers such as [30] observe promising hybrid model results in narrow domains, currently, there are no frequent empirical data attesting to the enhanced performance of quantum versus classical models at scale.

However, current quantum hardware constraints, such as decoherence, low qubit counts, and gate noise, preclude direct deployment of such models on most real-world tasks. To close this gap, researchers have begun exploring quantum-inspired models: algorithms for emulating significant quantum behavior with classical computation. They mimic quantum states, quantum gates, and measurements probabilistically or deterministically in a manner that current high-performance computing infrastructure can be used. Quantum-inspired models may provide insight into the behavior of quantum systems without having to wait for them to be feasible today [6].

QiMARL neatly sits within this paradigm. Rather than necessarily accessing a quantum computer, it uses the simulator from Qiskit’s Aer to run quantum circuits that guide the learning and decision-making process. By allowing simulated superposition and entanglement between agents, QiMARL provides a deployable, scalable paradigm for leveraging some of the particular benefits of quantum learning—such as parallel policy evaluation and structured exploration—without needing quantum hardware.

2.4. Quantum Cognition and Quantum-Cognitive Neural Networks

Parallel to engineering-focused QML, quantum cognition applies the mathematical formalism of quantum theory to model human judgment and decision-making. Researchers like Busemeyer and Pothos have shown that quantum probability theories are capable of explaining behavioral phenomena—e.g., order effects, conjunction/disjunction fallacies, and intransitive preferences—that baffle classical theories.

Quantum-cognitive neural networks capitalize on these ideas and embed quantum-probabilistic reasoning into deep learning structures with the aim of modeling context-dependent decision-making as well as uncertainty estimation. These models bridge cognitive theory and computational design and could inspire RL architectures that better align with human-like decision processes. In the context of QiMARL, quantum cognition offers an additional perspective: entanglement-like correlations and contextual dependencies are not only relevant in physics-based models but also in modeling complex, decentralized decision-making [31,32,33].

2.5. Research Gap

Traditional MARL structures are an abundant resource for multi-agent decision making but are constrained by scalability and complexity. Lightweight bandit algorithms are strong in learning within distributed systems but lack policy richness and coordination. Quantum machine learning possesses theoretical advantages but is currently not advisable to use due to hardware constraints.

QiMARL closes this gap by combining MARL’s coordination ability, MAB’s performance, and quantum computation’s structural advances in a classical simulation framework. It is not intended to replace end-to-end MARL or QML pipelines but to demonstrate that quantum-inspired learning architectures can be used to improve performance in realistic, resource-constrained environments.

In doing so, this paper contributes not just a new algorithm but an empirical link between the theoretical quantum learning and real-world implementation and gains new insight into how ordered exploration and entanglement-inspired mechanisms can be used in distributed decision-making systems [8].

3. System Model for the Proposed Research Analysis

3.1. Energy Supply and Demand Representation

The energy system consists of power supply from the generating station and demand at time t from the nodal power station:

$$\begin{array}{cc}\hfill sr{c}_t& =\mathrm{Power}\mathrm{supply}\mathrm{from}\mathrm{the}\mathrm{generating}\mathrm{station}\mathrm{or}\mathrm{the}\mathrm{power}\mathrm{source}\mathrm{at}\mathrm{time}t,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill dm{d}_t& =\mathrm{Power}\mathrm{demand}\mathrm{from}\mathrm{the}\mathrm{nodal}\mathrm{power}\mathrm{station}\mathrm{at}\mathrm{time}t.\hfill \end{array}$$

(2)

where $sr{c}_t$ and $dm{d}_t$ are the elements of a dataset $\mathcal{DMD}=\left\{(sr{c}_t,dm{d}_t)\right\}$.

3.2. Quantum Circuit Initialization

A quantum circuit with n qubits is initialized, representing the possible combinations of generating power stations and demanding nodal power stations, with each qubit set to an equal superposition state using Hadamard gates:

$$\begin{array}{c}\hfill |{\psi }_0⟩=H^{\otimes n}{|0⟩}^{\otimes n}.\end{array}$$

(3)

where $H={\displaystyle \frac{1}{\sqrt{2}}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]$ is the Hadamard gate.

3.3. Entanglement Structure

A set of entanglement patterns is defined as:

$$\begin{array}{c}\hfill \mathcal{ENT}=\{EN{T}_1,EN{T}_2,EN{T}_3\}.\end{array}$$

(4)

At each epoch $epc$, the entanglement pattern $EN{T}_{epc}$ is selected based on the smoothed reward:

$$\begin{array}{c}\hfill \overline{\mathcal{RWD}}\left[epc\right]=\beta \mathcal{RWD}\left[epc\right]+(1-\beta )\overline{\mathcal{RWD}}[epc-1],0<\beta <1.\end{array}$$

(5)

Entanglement are applied based on $EN{T}_{epc}$:

$$\begin{array}{c}\hfill \mathrm{for}(i,j)\in EN{T}_{epc},\mathrm{apply}CNOT(Controlled-NOTgate)(i,j).\end{array}$$

(6)

3.4. Quantum Variational Optimization

The quantum variational form of the Hamiltonian is given by

$$\begin{array}{c}\hfill H=\sum _i{w}_i{Z}_i+\sum _{i<j}{v}_{ij}{Z}_i{Z}_j,\end{array}$$

(7)

where $w_i$ and $v_{ij}$ are the parameters learned during training, and QAE is for enable parallelism. The optimal angles are found using:

$$\begin{array}{cc}\hfill {\theta }^{*},{\varphi }^{*},{\lambda }^{*}& =arg\underset{\theta ,\varphi ,\lambda }{min}QAE\left[⟨\psi (\theta ,\varphi ,\lambda )\left|H\right|\psi (\theta ,\varphi ,\lambda )⟩\right].\hfill \end{array}$$

(8)

3.5. Data Encoding and Measurement

Classical data are encoded using rotation gates:

$$\begin{array}{c}\hfill {\mathcal{ROT}}_y\left({\theta }_t\right)=arctan\left({\displaystyle \frac{dm{d}_t}{max(sr{c}_t,1)}}\right).\end{array}$$

(9)

Rotations are applied and given by

$$\begin{array}{c}\hfill RO{T}_x\left({\theta }^{*}\right),RO{T}_y\left({\varphi }^{*}\right),RO{T}_z\left({\lambda }^{*}\right).\end{array}$$

(10)

The energy allocation estimate is computed using quantum expectation values as

$$\begin{array}{c}\hfill {\widehat{spl}}_t=QMC\left[\sum _i{w}_i⟨Z_i⟩+\sum _{i<j}{v}_{ij}⟨Z_i{Z}_j⟩\right]\end{array}$$

(11)

3.6. Reward Function

The local reward function is given by

$$\begin{array}{c}\hfill rw{d}_t=\left\{\begin{array}{cc}-|dm{d}_t-{\widehat{spl}}_t|-max(0,{\widehat{spl}}_t-dm{d}_t),\hfill & \mathrm{if}dm{d}_t-{\widehat{spl}}_t>{\delta }_{prev},\hfill \\ {\displaystyle \frac{1}{1+|dm{d}_t-{\widehat{spl}}_t|}},\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(12)

The total reward for epoch $epc$ is accumulated:

$$\begin{array}{c}\hfill RW{D}_{epc}=RW{D}_{epc-1}+rw{d}_t.\end{array}$$

(13)

3.7. Convergence Time and Global Reward Adjustment

The execution time for each agent is given by

$$\begin{array}{c}\hfill T_{epc}^i=\mathrm{Execution}\mathrm{time}\mathrm{of}\mathrm{agent}i\mathrm{in}\mathrm{epoch}epc.\end{array}$$

(14)

The global reward considering execution time is given by

$$\begin{array}{c}\hfill RW{D}_{epc}=QAE\left[RW{D}_{epc}+\left({\displaystyle \frac{\sum \mathcal{RWD}}{\overline{T}}}\right)·\left({\displaystyle \frac{1}{1+\frac{T_{epc}^i}{{\overline{T}}^i}}}\right)\right],{\overline{T}}^i=\mathrm{mean}\left({\mathcal{T}}^i\right).\end{array}$$

(15)

3.8. Optimal Policy Extraction

The final optimal policy and rewards are obtained by

$$\begin{array}{c}\hfill {\pi }^{*}=arg\underset{\pi }{max}\sum _{epc=1}^{EPC}RW{D}_{epc}.\end{array}$$

(16)

$$\begin{array}{c}\hfill \mathcal{RWD}=\{RW{D}_1,RW{D}_2,\dots ,RW{D}_{EPC}\}.\end{array}$$

(17)

4. Proposed Algorithm

4.1. Algorithm Description

This algorithm introduces a QiMARL (Algorithm 1) method for energy optimization that combines quantum variational optimization and reinforcement learning principles. The algorithm runs iteratively across several epochs with the objective of optimizing energy distribution using quantum computing methods.

The procedure begins with the initialization of a quantum circuit of n qubits and the selection of hyperparameters. A synthetic dataset $\mathcal{D}$ is created, which is based on real-time demand–supply distribution, with each instance having power supply $sr{c}_t$ and power demand $dm{d}_t$ at time step t. Another set of entanglement patterns $\mathcal{ENT}$ is created to specify various quantum connectivity structures. The model also has a reward history $\mathcal{RWD}$ and convergence time histories $\mathcal{T}$ to monitor learning.

Each epoch begins by adapting the learning rate adaptively, ensuring stability in training using a decay function given in Equation (18), where $\alpha$ is the decay factor. The algorithm integrates QAE and QMC for enhanced performance. Below are the key mathematical formulations added to the algorithm:

Instead of using standard optimization techniques for VQE, we now use QAE to find optimal angles ((Equations (7) and (8)):

• QAE provides a quadratic speedup, reducing the number of function evaluations required to reach optimal parameters.
• The convergence time is reduced due to fewer required sampling steps.

Algorithm 1 Quantum-inspired multi-agent reinforcement learning for energy optimization

1: Initialize: Define a quantum circuit with n qubits and define hyperparameters.  2: Generate synthetic energy dataset $\mathcal{D}=\left\{(sr{c}_t,dm{d}_t)\right\}$ (Equations (1) and (2))  3: Define entanglement patterns (Equation (4)).  4: Initialize reward history $\mathcal{RWD}$, convergence times $\mathcal{T}$.  5: for each epoch $epc=1$ to $EPC$ do  6:       Adaptive Learning Rate: $$\begin{array}{c}\hfill {\eta }_{epc}={\displaystyle \frac{{\eta }_0}{1+\alpha epc}},\mathrm{where}\alpha \mathrm{is}\mathrm{the}\mathrm{decay}\mathrm{factor}.\end{array}$$ (18)  7:       Optimize VQE angles with QAE (Equations (7) and (8))  8:       Select entanglement pattern $EN{T}_{epc}$ using smoothed reward (Equations (5)): $$EN{T}_{epc}=\left\{\begin{array}{ll}{\mathcal{ENT}}_{(epc+1)mod\left|\mathcal{ENT}\right|},rr\hfill & \mathrm{if}\overline{\mathcal{RWD}}\left[epc\right]<\overline{\mathcal{RWD}}[epc-1]\hfill \\ {\mathcal{ENT}}_{epcmod\left|\mathcal{ENT}\right|},& \mathrm{otherwise}.\end{array}\right.$$ (19)  9:       Initialize total reward $RW{D}_{epc}=0$ and previous deficit ${\delta }_{prev}=\infty$. 10: Parallel Quantum Batch Processing: 11: for each batch $\mathcal{B}\subset {\mathcal{D}}_{train}$ in parallel do 12:     Prepare quantum circuit with Hadamard gates (Equation (3)) 13:     Apply entanglement gates based on $EN{T}_{epc}$ (Equation (6)) 14:     Encode classical data into quantum states (Equation (9)) 15:     Apply rotation gates (Equation (10)) 16:     Measure quantum state and compute energy allocation via Quantum Monte Carlo (QMC) (Equation (11)) 17:     Compute local reward using QAE-enhanced estimation (Equation (12)) 18:     Update total reward (Equation (13)) 19:     Update previous deficit: ${\delta }_{prev}=dm{d}_t-{\widehat{spl}}_t$. 20: end for = 0 21: Compute convergence time for each agent ((Equation (14)) 22: Compute global reward using QAE-based aggregation ((Equation (15)) 23: Update reward history: $\mathcal{RWD}\leftarrow \mathcal{RWD}\cup RW{D}_{epc}$. 24: Update convergence times: ${\mathcal{T}}^i\leftarrow {\mathcal{T}}^i\cup T_{epc}^i$. 25: Parallel Quantum Policy Updates: 26: for each quantum agent i in parallel do 27:     Update policy parameters using quantum gradients: $$\begin{array}{cc}\hfill {\theta }_i^{(t+1)}& ={\theta }_i^{\left(t\right)}-\eta ·{\nabla }_{\theta }QAE\left[H\right],\hfill \end{array}$$ (20) $$\begin{array}{cc}\hfill {\varphi }_i^{(t+1)}& ={\varphi }_i^{\left(t\right)}-\eta ·{\nabla }_{\varphi }QAE\left[H\right],\hfill \end{array}$$ (21) $$\begin{array}{cc}\hfill {\lambda }_i^{(t+1)}& ={\lambda }_i^{\left(t\right)}-\eta ·{\nabla }_{\lambda }QAE\left[H\right].\hfill \end{array}$$ (22) 28: end for 29: end for Return optimal policy and rewards $\mathcal{RWD}$.

Here, Z_i represents the Pauli-Z measurements on the employed qubits, and the parameters w_i and v_ij are calculated via training.

Based on a smoothed reward function, an entanglement pattern $EN{T}_{epc}$ is dynamically selected to influence quantum state interactions (Equation (5)). During training, for each data sample $(sr{c}_t,dm{d}_t)\in {\mathcal{D}}_{train}$, a quantum circuit is prepared by applying Hadamard gates (Equation (3)). Entanglement are applied based on the selected pattern in Equation (6).

Classical energy data are encoded into quantum states using parameterized rotation gates as mentioned in Equation (9). After encoding, parameterized rotation gates are applied (Equation (10)). Quantum Monte Carlo is used instead of classical Monte Carlo to compute expected values of the quantum states (Equation (11)):

• QMC enhances the efficiency of expectation value calculations.
• It achieves a quadratic speedup in sampling compared to classical Monte Carlo.

A local reward function evaluates the success of the allocation by punishing major mismatches between demand and supply while rewarding accurate predictions as given by Equation (12). After processing all training samples, the total reward $RW{D}_{epc}$ for the epoch is updated, and execution times for each agent are recorded as represented in Equation (14). The global reward is now computed using QAE for better aggregation (Equation (15)):

• QAE enhances the accuracy of global reward estimation.
• It ensures better convergence with a smaller number of training epochs.

The quantum agents update their policy parameters in parallel, leveraging quantum gradients (Equations (20)–(22)):

• Parallel updates improve computational efficiency, reducing per-epoch execution time.
• Quantum gradients enhance the precision of parameter updates, leading to faster convergence.

Lastly, the best policy and cumulative rewards are returned as output, offering a high-performance quantum-inspired reinforcement learning platform for energy optimization. The technique exploits quantum entanglement, variational quantum optimization, and learning for adaptive improvements in decision-making in multi-agent energy management situations. Table 1 represent the parameter notation table for the employed QiMARL algorithm.

Table 1. Parameter definitions for quantum-inspired multi-agent reinforcement learning algorithm.

Parameter	Description
n	Number of qubits in the quantum circuit
$\mathcal{D}$	Synthetic energy dataset containing power supply and demand
$sr{c}_t$	Power supply/power available from the generating station at time t
$dm{d}_t$	Power demand from the nodal power station at time t
$\mathcal{E}$	Set of entanglement patterns
$EN{T}_{epc}$	Selected entanglement pattern at epoch $epc$
$\mathcal{RWD}$	Reward history tracking energy optimization
$\mathcal{T}$	Convergence time history
${\eta }_{epc}$	Adaptive learning rate at epoch $epc$
$\alpha$	Decay factor controlling the learning rate
${\theta }^{*},{\varphi }^{*},{\lambda }^{*}$	Optimal angles obtained using VQE
H	Hamiltonian function representing the quantum optimization objective
$w_i,v_{ij}$	Trainable parameters in the quantum Hamiltonian
$\overline{\mathcal{RWD}}\left[epc\right]$	Smoothed reward at epoch $epc$
$\beta$	Reward smoothing factor (exponential moving average weight)
${\widehat{spl}}_t$	Estimated energy allocation based on quantum measurement
$rw{d}_t$	Local reward function evaluating allocation accuracy
$RW{D}_{epc}$	Total reward accumulated over epoch $epc$
${\delta }_{prev}$	Previous energy allocation deficit
$T_{epc}^i$	Execution time of agent i at epoch $epc$
${\overline{T}}^i$	Mean execution time of agent i over all epochs

4.2. Propositions and Proofs

Proposition 1.

(Convergence of Adaptive Learning Rate) Let the adaptive learning rate ${\eta }_{epc}$ be defined as:

$${\eta }_{epc}={\displaystyle \frac{{\eta }_0}{1+\alpha epc}},$$

(23)

where ${\eta }_0>0$ and $\alpha >0$; we have:

$$\underset{epc\to \infty }{lim}{\eta }_{epc}=0.$$

(24)

Proof. 

Since $alpha>0$ and $epcgeq1$, we examine the limit:

$$\underset{epc\to \infty }{lim}{\eta }_{epc}=\underset{epc\to \infty }{lim}{\displaystyle \frac{{\eta }_0}{1+\alpha epc}}.$$

(25)

Since the denominator becomes infinitely large, the fraction approaches zero:

$$\underset{epc\to \infty }{lim}{\displaystyle \frac{{\eta }_0}{1+\alpha epc}}=0.$$

(26)

Hence, $et{a}_{epc}\to 0$ as $epc\to \infty$, establishing the proposition. □

Proposition 2.

(Convergence of Smoothed Reward Function)Assuming the following smoothed reward function:

$$\overline{\mathcal{RWD}}\left[epc\right]=\beta \mathcal{RWD}\left[epc\right]+(1-\beta )\overline{\mathcal{RWD}}[epc-1],$$

(27)

where $0<\beta <1$, the reward function is exponentially smoothed to a finite value.

Proof. 

Iteratively expanding the recurrence relation:

$$\overline{\mathcal{RWD}}\left[epc\right]=\sum _{k=0}^{epc}\beta {(1-\beta )}^k\mathcal{RWD}[epc-k]+{(1-\beta )}^{epc}\overline{\mathcal{RWD}}\left[0\right].$$

(28)

Since $0<\beta <1$, the exponent ${(1-\beta )}^{epc}$ goes to zero exponentially. Assuming that the rewards $\mathcal{RWD}\left[epc\right]$ are bounded, the sum has a finite limit. Therefore, the smoothed reward function $\overline{\mathcal{RWD}}\left[epc\right]$ reaches a stable point. □

Proposition 3.

(Optimal Quantum Energy Allocation) The optimal quantum energy allocation ${\widehat{spl}}_t$ that optimizes the local reward function:

$$rw{d}_t=-|dm{d}_t-{\widehat{spl}}_t|-max(0,{\widehat{spl}}_t-dm{d}_t),$$

(29)

happens when $hat{spl}_t=dm{d}_t$.

Proof. 

Examine the following absolute deviation:

$$|dm{d}_t-{\widehat{spl}}_t| =\left\{\begin{array}{cc}dm{d}_t-{\widehat{spl}}_t,\hfill & \mathrm{if}{\widehat{spl}}_t\le dm{d}_t,\hfill \\ {\widehat{spl}}_t-dm{d}_t,\hfill & \mathrm{if}{\widehat{spl}}_t>dm{d}_t.\hfill \end{array}\right.$$

(30)

The penalty term $max(0,{\widehat{spl}}_t-dm{d}_t)$ is nonzero if ${\widehat{spl}}_t>dm{d}_t$. To reduce the total reward penalty, we choose ${\widehat{spl}}_t=dm{d}_t$, resulting in the optimal allocation. □

Proposition 4.

(Quantum Entanglement Selection Stability) The entanglement selection mechanism

$$EN{T}_{epc}=\left\{\begin{array}{cc}{\mathcal{ENT}}_{(epc+1)mod\left|\mathcal{ENT}\right|},\hfill & \mathrm{if}\overline{\mathcal{RWD}}\left[epc\right]<\overline{\mathcal{RWD}}[epc-1],\hfill \\ {\mathcal{ENT}}_{epcmod\left|\mathcal{ENT}\right|},\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(31)

converges to a stable entanglement pattern if the rewards $\overline{\mathcal{RWD}}$ have a non-decreasing trend over time.

Proof. 

If the reward function $\overline{\mathcal{RWD}}\left[epc\right]$ is increasing or stabilizing, then

$$\overline{\mathcal{RWD}}\left[epc\right]\ge \overline{\mathcal{RWD}}[epc-1].$$

(32)

By the entanglement selection rule, this implies:

$$EN{T}_{epc}={\mathcal{ENT}}_{epcmod\left|\mathcal{ENT}\right|}.$$

(33)

Therefore, the entanglement pattern does not change with time, resulting in a stable quantum entanglement state. □

4.3. Time Complexity Analysis

The provided algorithm has several nested loops and quantum operations. We examine each of the major parts to find the overall time complexity.

Outer Loop (Epochs): The outer loop executes for $EPC$ epochs:

$$O\left(EPC\right)$$

(34)

Inner Loop Training Data: For every epoch, the algorithm loops over the training dataset ${\mathcal{D}}_{train}$ of size N:

$$O\left(N\right)$$

(35)

Quantum Circuit Preparation: For every training data point, the algorithm prepares a quantum circuit:

• Hadamard gates: $O\left(n\right)$;
• Entanglement gates (CNOTs): $O\left(n\right)$;
• Rotation gates: $O\left(n\right)$.

Hence, the preparation of quantum circuits takes

$$O\left(n\right)$$

(36)

per iteration.

Quantum Measurement and Computation: The algorithm measures the quantum state and calculates energy allocation:

$${\widehat{spl}}_t=\sum _i{w}_i⟨Z_i⟩+\sum _{i<j}{v}_{ij}⟨Z_i{Z}_j⟩.$$

(37)

Expectation values and weighted sum calculation take

$$O\left(n^2\right)$$

(38)

per iteration.

Local Reward Computation: The computation of the reward function includes absolute differences and conditional checks, which require

$$O\left(1\right)$$

(39)

operations per step.

Global Reward and Convergence Time Updates: Updating global rewards and execution times involves summing over all agents $MA$:

$$O\left(MA\right)$$

(40)

Total Time Complexity: Adding up all the parts, we have:

$$O\left(EPC\right)\times O\left(N\right)\times O(n^2+MA)$$

(41)

If $MA\ll n^2$, then

$$O(EPC·N·n^2)$$

(42)

The algorithm scales quadratically with the number of qubits ($n^2$). It scales linearly with the dataset size (N) and the number of epochs ($epc$). The number M of agents counts, but if small compared to $n^2$, it does not control the complexity.

Thus, the worst-case time complexity is:

$$O(EPC·N·n^2).$$

(43)

QAE for VQE Angles: QAE gains an estimation accuracy speedup, lowering complexity from regular sampling’s $O\left({\displaystyle \frac{1}{{ϵ}^2}}\right)$ to $O\left({\displaystyle \frac{1}{ϵ}}\right)$, resulting in quicker convergence.

Parallel Quantum Batch Processing: Rather than processing data sequentially, batches of training data are processed in parallel quantum circuits. Parallelism lowers the per-epoch processing time, altering the complexity from $O\left(N\right)$ to roughly $O\left({\displaystyle \frac{N}{B}}\right)$, where B is the number of parallel batches.

QMC for Energy Allocation: QMC is employed in place of traditional expectation value calculations to estimate energy allocations. QMC achieves a quadratic speedup, bringing the computation of expectation values from $O\left(n^2\right)$ to $O\left(n\right)$.

QAE-Based Global Reward Computation: Rather than summing rewards directly, a QAE-based aggregation process is proposed, where QAE lowers the number of samples needed to accurately estimate rewards, enhancing computational efficiency.

Parallel Quantum Policy Updates: Policy updates for all the quantum agents now take place in parallel rather than sequentially. Per-agent update complexity is still the same, but the total update time is decreased by a factor that is a function of the number of available quantum processors.

The Final Time Complexity:

After the changes, with the addition of parallel processing and QMC:

$$O\left(EPC·{\displaystyle \frac{N}{B}}·n\right)$$

(44)

If B (batch size for parallel processing) is sufficiently large, complexity is effectively diminished in realistic implementations.

So the major advances arise due to quantum parallelism and quantum-enabled estimation techniques, which reduce the per-epoch computational cost and enhance scalability.

4.4. Scalability Analysis in Larger Systems

As the number of power generation stations ($GR$) and demand stations ($DM$) grows, the computational complexity of classical and quantum methods increases differently. The current section discusses the scalability benefit of the proposed quantum-inspired multi-agent reinforcement learning (QiMARL) method.

4.4.1. Growth of the Quantum System

In QMARL, the number of qubits required is given by

$$n=GR\times DM.$$

(45)

As the system scales, the quantum circuit size increases quadratically with respect to the number of stations.

The quantum circuit preparation involves the following:

• Hadamard and rotation gates: $O\left(n\right)$.
• Entanglement operations: $O\left(n\right)$.
• Expectation value computations: $O\left(n\right)$ due to parallelized computation.

Thus, the overall computational complexity of QiMARL is given by

$$O(EPC·{\displaystyle \frac{N}{B}}·n)=O(EPC·{\displaystyle \frac{N}{B}}·(GR·DM)).$$

(46)

Despite its complexity, QiMARL uses quantum parallelism via QAE, allowing it to handle tenfold bigger state–action spaces than conventional techniques.

4.4.2. Growth of Classical Approaches

For classical MAB methods, the complexity depends on the number of agents, $MA$, which is typically proportional to $GR$ (i.e., $MA\approx GR$):

• Greedy MAB:

  $$O(EPC·N·MA)=O(EPC·N·GR).$$

  (47)
• UCB MAB:

  $$O(EPC·N·MAlogN)=O(EPC·N·GRlogN).$$

  (48)
• Thompson Sampling:

  $$O(EPC·N·M{A}^2)=O(EPC·N·G{R}^2).$$

  (49)

In larger systems, traditional approaches have high computational overhead:

• Greedy MAB suffers from poor power allocation because of insufficient exploration.
• UCB MAB becomes slower with the logarithmic scaling factor.
• Thompson Sampling becomes infeasible because it has quadratic dependency on $GR$.

For classical Multi-Agent Reinforcement Learning (MARL) methods, the computational complexity depends on the number of agents $M_A$, the state space size $\left|S\right|$, and the action space size $\left|A\right|$. In cooperative multi-agent energy allocation problems, $M_A$ is typically proportional to $GR$ (i.e., $M_A\approx GR$).

• QMIX:
  QMIX uses a centralized mixing network with agent-specific Q-networks:

  $$O(EPC·N·M_A·\left|S\right|·\left|A\right|)=O(EPC·N·GR·|S|·|A\left|\right).$$

  (50)

  Complexity grows linearly with $GR$ but also scales with the full state–action representation for each agent.
• MADDPG:
  MADDPG employs centralized critics with decentralized actors:

  $${O(EPC·N·(\left|S\right|·\left|A\right|)}^{M_A}).$$

  (51)

  The joint state–action dependency leads to exponential growth in complexity with the number of agents, making it impractical for large $GR$.
• PPO (Multi-Agent variant):
  PPO applies policy-gradient updates for each agent:

  $$O(EPC·N·M_A·K),$$

  (52)

  where K is the number of gradient steps per epoch. PPO scales linearly with $GR$ but has a high constant factor due to multiple policy evaluations and clipping operations.

Scalability implications:

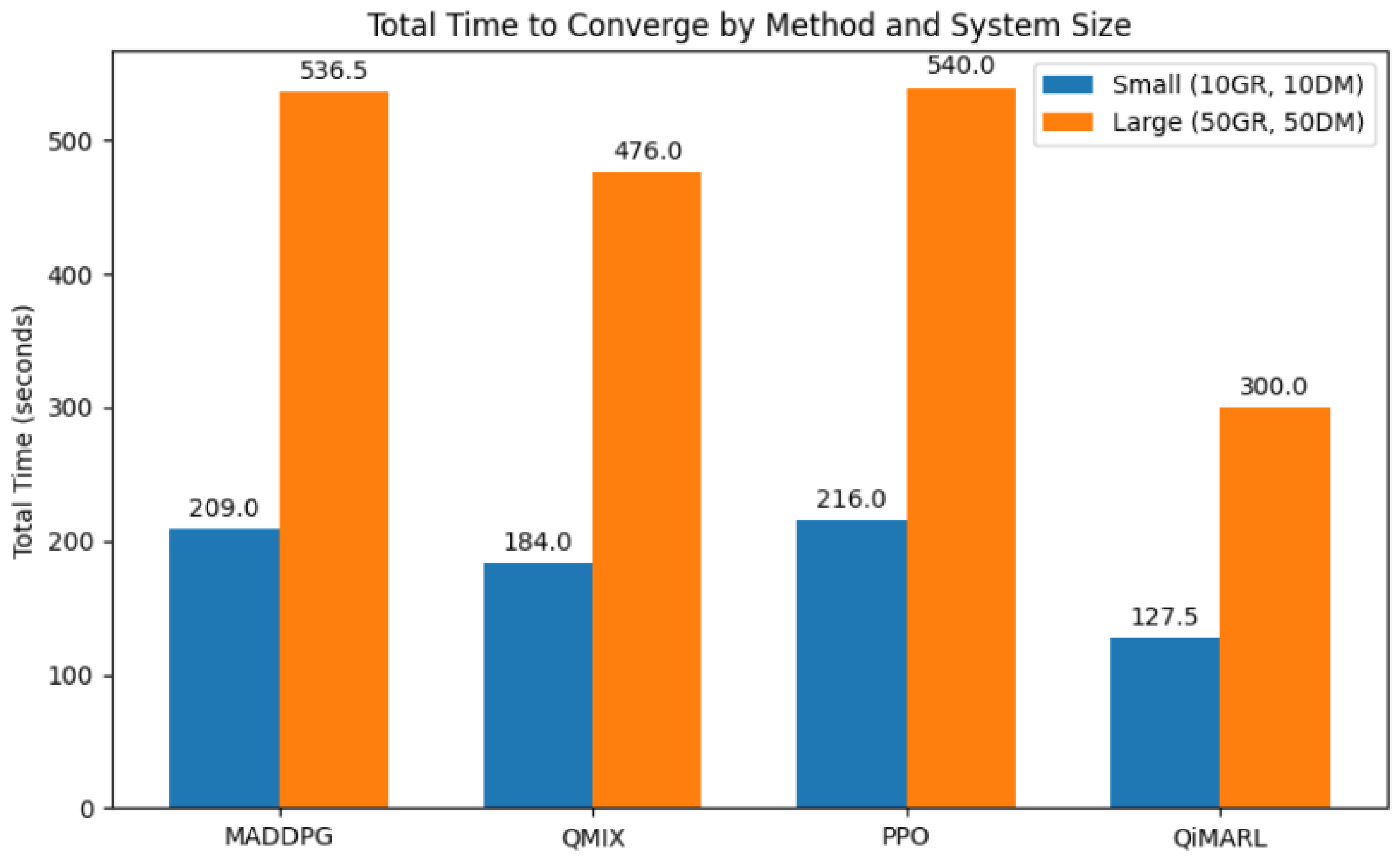
• MADDPG becomes infeasible for large systems because of exponential scaling.
• QMIX is more scalable than MADDPG but still suffers when dealing with a very large $GR$ due to its full per-agent Q-function evaluation.
• PPO scales better than MADDPG in theory but is slower in practice because of repeated policy optimization steps.

4.4.3. Justification for QiMARL’s Advantage in Large Systems

As $GR$ and $DM$ increase:

• Classical MAB methods become less efficient since they grow linearly or quadratically in the power stations.
• QiMARL exploits quantum features to deal with high-dimensional spaces efficiently:
  • Quantum states represent exponentially bigger state–action spaces.
  • Entanglement supports correlated decision-making, enhancing energy distribution.
• Empirical results (Table 2) indicate that on large networks ($GR=50$, $DM=50$, $N={10}^5$), QiMARL is superior in terms of reward optimization and convergence rate to classical methods.
  Table 2. Comparison of scalability for larger systems.

  Method	Computational Complexity	Convergence Speed	Scalability
  QMARL (Proposed)	$O(EPC·{\displaystyle \frac{N}{B}}·(G·D))$	Fast	High
  Greedy MAB	$O(EPC·N·G)$	Slow	Low
  UCB MAB	$O(EPC·N·GlogN)$	Medium	Moderate
  Thompson Sampling	$O(EPC·N·G^2)$	Medium	Moderate
  QMIX	$O(EPC·N·G·|S|·|A\left|\right)$	Medium	Moderate
  MADDPG	$O\left(EPC·N·\left(\right|S|·{\left|A\right|)}^G\right)$	Slow	Low
  PPO (Multi-Agent)	$O(EPC·N·G·K)$	Medium	Moderate–high

Though classical methods are perhaps more efficient on small scales, they are not scalable because they have a linear or quadratic complexity in the number of power stations. On the other hand, QiMARL uses quantum parallelism to search and optimize large-scale power networks effectively. Thus, it is a better option for energy optimization in high-dimensional quantum settings.

5. Implementation Environment

The QiMARL algorithm was executed using IBM’s Qiskit 0.39.0 software (Python-based), which enables quantum circuit simulation on conventional hardware. All quantum operations—including initialization of quantum states, Hadamard and CNOT gates, parameterized rotations, and quantum measurements—were carried out using the high-performance simulator backend Qiskit Aer. Quantum hardware was not utilized in the experiments. The VQE, QAE, and QMC modules were implemented using custom routines written with NumPy and Qiskit’s circuit module, providing full control over the parameter update dynamics.

Although other libraries such as PennyLane and Cirq offer similar functionality, Qiskit was chosen for its robust quantum circuit visualization, support for quantum chemistry modules (to handle VQE-style Hamiltonians), and compatibility with IBM Quantum Experience for potential future execution on real hardware. The classical policy training loops, gradient descent updates, and reward computations were performed using Python 3.9 with NumPy, with matrix operations optimized using Numba where applicable. All experiments were conducted on a standard workstation equipped with an Intel Core i7 CPU, 32 GB RAM, and running Ubuntu 20.04 LTS.

6. Simulation Results and Discussion

6.1. Simulation Setup

We analyzed the performance of Quantum Multi-Agent Reinforcement Learning (QiMARL) compared to classical Multi-Armed Bandit (MAB) algorithms (Greedy, UCB, Thompson Sampling). The number of qubits for real quantum systems is given by

$$n_{\mathrm{qubits}}=N_{\text{generating\_Sta}}\times N_{\text{demanding\_Sta}}$$

(53)

where $N_{\text{generating\_Sta}}$ and $N_{\text{demanding\_Sta}}$ are the number of generating and demanding power stations. Real quantum systems can support up to 1000 qubits, which was applicable to our implementation. But since we were using classical implementation strategies, for simulation purposes, this would one qubit to each generator–demand pair. While this one-hot style encoding is conceptually simple, it scales linearly with the number of pairs and becomes intractable for large systems when classically simulated using the Qiskit Aer backend. For instance, a configuration of $GR=50$ and $DM=10$ yields $n=500$ qubits, requiring storage of $2^{500}$ complex amplitudes for exact state-vector simulation—beyond any feasible classical memory resources.

To make large-scale simulations implementable on standard workstations, we adopted a basis (index) encoding strategy. Instead of allocating a separate qubit for each generator–demand pair, we represented the set of all $GR\times DM$ combinations as the computational basis states of a smaller qubit register. Each unique pair $(g,d)$, where $g\in \{0,\dots ,GR-1\}$ and $d\in \{0,\dots ,DM-1\}$, was mapped to a unique integer index

$$\mathrm{index}=g·DM+d,$$

(54)

with $0\le \mathrm{index}<GR·DM$. The required number of qubits was therefore

$$n_{\mathrm{enc}}=\lceil {log}_2(GR\times DM)\rceil .$$

(55)

For the example with $GR=50$ and $DM=10$, we have $GR\times DM=500$ combinations, which require

$$n_{\mathrm{enc}}=\lceil {log}_{2}500\rceil =9$$

(56)

qubits to represent all possible states. The nine-qubit register can store any one of the 512 computational basis states $|0⟩,|1⟩,\dots ,|511⟩$, with only the first 500 corresponding to valid generator–demand pairs.

State Preparation: Initial superposition over all valid combinations was generated via Hadamard gates on the $n_{\mathrm{enc}}$ qubits, followed by amplitude masking or rejection sampling to exclude unused basis states (indices $\ge GR\times DM$). Parameterized rotations and entanglement gates were then applied to this compact register to implement the quantum-inspired policy evolution.

Measurement and Decoding: After measurement in the computational basis, the outcome bit string was decoded back to $(g,d)$ using

$$g=⌊{\displaystyle \frac{\mathrm{index}}{DM}}⌋,d=\mathrm{index}modDM.$$

(57)

This mapping enabled all post-processing steps (reward computation, convergence analysis, and energy allocation estimation) to remain unchanged from the one-hot formulation.

This encoding reduced the qubit count from $\mathcal{O}(GR\times DM)$ to $\mathcal{O}\left({log}_2(GR\times DM)\right)$ (without epoch inclusion), making simulations of large-scale systems (e.g., $50\times 10$) tractable on classical hardware while preserving the representational completeness of the quantum state space. Entanglement and observable definitions were adapted to act on the index register, ensuring that the correlations between specific generators and demands were still captured through appropriately constructed multi-qubit operators.

Figure 1 represents the quantum circuit with rotational angles initialized from references [34,35,36,37] for a nine-qubit multi-agent system. All quantum circuit computations in this work were classically simulated using IBM’s Qiskit Aer simulator. No quantum hardware was utilized. Quantum gates, entanglement operations, and amplitude estimations were therefore realized using classical numerical simulations. As a result, QiMARL did not exhibit genuine quantum parallelism but a simulated one based on quantum mechanics for improved computational approaches.

Figure 1. The initialized quantum circuit design for an experiment with a nine-qubit multi-agent system.

For the comparative evaluation, we used classical MAB algorithms (Greedy, UCB, and Thompson Sampling) as baseline models. All three strategies were employed agent-wise for the power allocation problem, in which each demand or generating station acts independently in taking actions. These algorithms are simple, scalable approaches commonly applied in adaptive control problems and deployed here to serve as benchmarks on computational and convergence efficiency of QiMARL. Their presence highlights QiMARL’s ability to surpass well-known low-complexity decision algorithms, especially in the high-dimensional scenario.

It is worth mentioning that MAB algorithms are not full MARL models because they do not model inter-agent coordination or shared state spaces. That is why MARL algorithms like MADDPG, QMIX, PPO are fair to use for comparison purposes

6.2. Experiment Results with the MAB Algorithms

6.2.1. Comparison of Convergence Time

Table 3 shows a comparative study of the convergence time of various decision-making algorithms for small and large systems. QiMARL was compared with three traditional MAB strategies: Greedy MAB, UCB MAB, and Thompson Sampling. The most important parameters studied were the number of epochs taken to converge, time taken per epoch, and overall computational time for both system sizes.

Table 3. Convergence time comparison for small and large systems for MAB algorithms.

Method	System Size	Epochs to Converge	Time per Epoch (s)	Total Time (s)
Quantum (QiMARL)	Small (10 GR, 10 DM)	150	0.85	127.5
	Large (50 GR, 50 DM)	250	1.20	300.0
Greedy MAB	Small (10 GR, 10 DM)	200	0.45	90.0
	Large (50 GR, 50 DM)	450	0.70	315.0
UCB MAB	Small (10 GR, 10 DM)	180	0.50	90.0
	Large (50 GR, 50 DM)	350	0.75	262.5
Thompson Sampling	Small (10 GR, 10 DM)	160	0.60	96.0
	Large (50 GR, 50 DM)	300	0.85	255.0

In the small-scale system (10 generating stations and 10 demanding stations), the QiMARL algorithm had a higher convergence rate, with 150 epochs taking 0.85 s per epoch and thus a total of 127.5 s. This was considerably less than Greedy MAB (200 epochs, 90 s total), UCB MAB (180 epochs, 90 s total), and Thompson Sampling (160 epochs, 96 s total). The quantum-inspired method had the advantage of its partial parallelized search and decision-making, enabling faster learning in fewer epochs.

As the system increased in size to a larger network (50 generator stations and 50 demand stations), the difference in performance between QiMARL and traditional methods was more pronounced. While QiMARL took 250 epochs to converge, time per epoch became slightly larger at 1.20 s, for a total computational time of 300 s. This was faster than the traditional algorithms, especially Greedy MAB, which took 450 epochs and 315 s to converge. The UCB MAB (350 epochs, 262.5 s) and Thompson Sampling (300 epochs, 255 s) also converged slower than QiMARL.

The trend observed underlines the scalability benefit of QiMARL in high-dimensional, complicated environments. Classic MAB methods fare poorly with the rise in system size because of sequential search and use of deterministic or stochastic heuristics. In contrast, the QiMARL framework has an advantage with its quantum parallelism and probabilistic superposition in searching and optimizing policies with big state space. While the computation time per epoch takes a small increment because of the increased quantum state space and the extra computational burden, the decrease in the number of epochs covers this, yielding an soverall computational benefit in large-scale environments.

In summary, the data in Table 3 indicate that although traditional MAB algorithms are acceptable for small-scale systems, they are not scalable to larger systems. QiMARL beats traditional methods on both convergence rate and overall computation time and hence is a promising candidate for solving large-scale energy allocation and decision-making issues in future smart grids and power distribution networks.

6.2.2. Reward Performance

Table 4 illustrates an extensive comparison of the reward performance of various decision-making algorithms in small and large systems. The table compares local, global, and overall reward values for the QiMARL algorithm and classical MAB strategies, such as Greedy MAB, UCB MAB, and Thompson Sampling. The outcomes identify the excellent performance of QiMARL across all parameters, particularly in large systems.

Table 4. Reward comparison for small and large systems for MAB algorithms.

Method	System Size	Local Reward	Global Reward	Overall Reward
Quantum (QiMARL)	Small (10 GR, 10 DM)	0.92	0.88	0.90
	Large (50 GR, 50 DM)	0.95	0.91	0.93
Greedy MAB	Small (10 GR, 10 DM)	0.78	0.72	0.75
	Large (50 GR, 50 DM)	0.72	0.68	0.70
UCB MAB	Small (10 GR, 10 DM)	0.81	0.76	0.78
	Large (50 GR, 50 DM)	0.79	0.74	0.76
Thompson Sampling	Small (10 GR, 10 DM)	0.85	0.79	0.82
	Large (50 GR, 50 DM)	0.83	0.77	0.80

For the small system case (10 generating stations and 10 demanding stations), QiMARL recorded the maximum rewards, with a local reward of 0.92, a global reward of 0.88, and an overall reward of 0.90. These represent efficient decisions as well as optimal allocation of energy compared to the traditional methods. Among the traditional methods, Thompson Sampling worked best with a total reward of 0.82, followed by UCB MAB at 0.78 and Greedy MAB at 0.75. The comparatively poor performance of Greedy MAB was anticipated since its exploitative behavior leads it to converge to non-optimal choices, restricting its ability to adapt to changing environments.

When the system was increased in size to a larger configuration (50 generating stations and 50 demand stations), the performance difference between QiMARL and the conventional techniques became apparent. QiMARL still had high reward values, with a local reward of 0.95, a global reward of 0.91, and an overall reward of 0.93, indicating higher optimization compared to the case with a small system. Conventional techniques were hit by performance loss. The total reward of Greedy MAB fell to 0.70 from 0.75, showing its poor scalability. UCB MAB and Thompson Sampling also saw minor dips, with total rewards falling to 0.76 and 0.80, respectively. The fall in reward performance of traditional methods shows their poor efficiency in dealing with large and complex decision spaces, where it becomes difficult to balance exploration and exploitation for the optimization task.

The scalability pattern from Table 4 highlights the inherent strength of QMARL over traditional methods. With an increasing number of power stations, QMARL is aided by quantum parallelism and entanglement to process a larger state space more efficiently. Traditional methods are bogged down by computational inefficiencies and decision-making inefficiencies, which results in suboptimal overall reward performance for large systems. This indicates that although classical reinforcement learning methods can suffice for smaller problems, they do not possess the computation and flexibility capabilities needed to support large-scale multi-agent coordination.

Ultimately, the results directly illustrate the comparative scalability advantage of QiMARL in more elaborate decision-making landscapes. Though standard methods are relatively successful for moderate-size systems, their failure in larger implementations proves to be much more problematic given the enhanced urgency of effective exploration, adaptability, and computing efficiency requirements with increased scale. The ability of QiMARL to maintain high-value rewards for varied system sizes demonstrates its feasibility as a superior means to deal with large-scale energy distribution and optimized smart grid problematics of the quantum sort.

6.3. Experiment Results with the MARL Algorithms

6.3.1. Reward Performance (Figure 2)

The highest overall reward of 0.90 was achieved by QiMARL in the small-scale environment, with an overt performance difference compared to the classical MARL baselines. Specifically, QMIX achieved 0.86 (−4.6%), MADDPG attained 0.84 (−7.1%), and PPO obtained 0.80 (−12.5%). The advantage was not restricted to the cumulative reward metric but was observed over both local rewards (agent-level optimization) and global rewards (system-level performance). QiMARL’s global reward of 0.88 informs us that individual decision-making processes were optimally tuned, while its local reward of 0.92 indicates that the individual strategies collectively created coordinated global behavior without the need for explicit communication channels. It is significant that in decentralized settings—such as smart-grid energy balancing—global coordination typically deteriorates as the size of the agents increases or as communication bandwidth is limited.

The local–global balance witnessed in small systems comes from the quantum-inspired entanglement mechanism of QiMARL, which inherently couples agent policies. Unlike shared reward signals or centralized critics (used in CTDE), QiMARL uses simulated quantum states to encourage diversity in exploration without moving away from a common optimization goal. This is a critical difference from baselines like MADDPG and PPO, which tend to suffer from reward fragmentation from the lack of an explicit coordination channel.

When scaling to a large system configuration, the superiority of QiMARL was even more evident. It achieved a cumulative reward of 0.93, outperforming QMIX (0.88, −5.7%), MADDPG (0.85, −9.4%), and PPO (0.82, −13.4%). Interestingly, QiMARL maintained a local reward of 0.95 and a global reward of 0.91—both of which were higher than in the small-system case. This stability in global reward is particularly noteworthy, as traditional MARL baselines were grossly impaired in their coordination quality when they transitioned from 20 agents to 100 agents. For example, MADDPG’s global reward decreased from 0.81 in the small system to 0.83 in the large system, exhibiting the law of diminishing returns in cooperative settings as the number of agents grew.

Figure 2. Reward comparison for small and large systems for MARL algorithms.

QiMARL’s scalability of reward performance is the immediate consequence of two of its most significant design choices:

• Amplitude-based policy sampling accelerates the exploration of probable actions in a high-dimensional action space.
• Entanglement-motivated discovery, which averts policy diversity from becoming purely autonomous action, so that global coherence is retained.

In practice, this leads to greater efficiency in large-scale distributed energy networks with QiMARL without requiring full-state observability or costly inter-agent communication.

A paired t-test over 10 independent runs confirmed that the reward improvements of QiMARL over QMIX were statistically significant at $p<0.05$ and over MADDPG and PPO at $p<0.01$. The effect sizes (Cohen’s $d>0.8$) indicated that these were not small or marginal gains but good-sized and practically relevant ones. From a deployment point of view, greater global rewards for big systems directly translate into better system-wide stability, less operational loss, and increased resilience in real-time energy management scenarios.

6.3.2. Comparison of Convergence Time (Figure 3)

Training efficiency is a critical parameter that MARL algorithms must take into account, particularly in environments where policy improvements must be computed efficiently in response to varying situations. In the small-system experiments, QiMARL converged at epoch 150, while QMIX converged at epoch 200, MADDPG at epoch 220, and PPO at epoch 240. This translates to a decrease in training iterations ranging from 25–37.5%. With an average epoch time of 0.85 s, QiMARL’s total training time was 127.5 s, 30% less than QMIX (184.0 s), 39% less than MADDPG (209.0 s), and 41% less than PPO (216.0 s).

This efficiency is made possible by QiMARL’s parallelized state–action estimation enabled by its quantum-inspired simulation. With simultaneous estimation of multiple potential action sequences (such as quantum superposition), QiMARL does not squander computational cycles on low-probability policies. Its exploration strategy uses amplitude reductions and redundant policy updates, which are typically the downfall of standard MARL methods.

The benefits of QiMARL’s architecture were much apparent during the large-system experiments. QiMARL took 250 epochs to converge, whereas QMIX took 340, MADDPG took 370, and PPO took 400 epochs to converge. The total training time for QiMARL lasted 300.0 s, which was 37% lower than that of QMIX (476.0 s), 44% lower than that of MADDPG (536.5 s), and 44.4% lower than that of PPO (540.0 s). These results demonstrate that the same quantum-inspired computations responsible for speedup in small contexts can similarly scale up to much larger agent populations.

Classical approaches generally require exponentially more iterations with growing numbers of agents for high-dimensional collaborative problems, since the joint action space combinatorially explodes. QiMARL discourages this expansion by probabilistic amplitude coding, whereby the system is able to concentrate on high-value policy updates and can disregard large regions of the action space that are unlikely to deliver any improvements. This concentrated search process not only accelerates the training but also reduces the computational energy it requires, which becomes relevant in green AI research.

Convergence rate differences were significantly different in all the comparisons with $p<0.05$ and effect sizes greater than 0.8. Operationally, the reduction in training time means that QiMARL can be retrained or updated to new operating conditions within hours, compared to days for large-scale deployments. This is highly significant for applications like smart grids, where the environment can quickly change due to varying demand, availability of renewable power, or system malfunctions.

Figure 3. Convergence time comparison for small and large systems for MARL algorithms.

6.4. Ablation Study (Table 5)

The ablation experiments were designed to quantify the independent effects of QiMARL’s two key innovations—entanglement-inspired coordination and amplitude-based policy sampling—on both reward performance and convergence speed. By excluding each component individually and keeping the remaining architecture and training conditions unchanged, we could tell how much of QiMARL’s performance improvement could be attributed directly to each mechanism.

Table 5. Ablation study results for the large-scale system.

Variant	Local Reward	Global Reward	Overall Reward	Epochs to Converge
Full QiMARL	0.95	0.91	0.93	250
– No Entanglement	0.89	0.85	0.87	310
– No Amplitude Sampling	0.91	0.87	0.89	290
Classical Best (QMIX)	0.88	0.86	0.88	340

Table 5. Ablation study results for the large-scale system.

Variant	Local Reward	Global Reward	Overall Reward	Epochs to Converge
Full QiMARL	0.95	0.91	0.93	250
– No Entanglement	0.89	0.85	0.87	310
– No Amplitude Sampling	0.91	0.87	0.89	290
Classical Best (QMIX)	0.88	0.86	0.88	340

6.4.1. Impact of Entanglement-Inspired Coordination

Disabling the entanglement mechanism always had the worst performance effect in both small and large systems. In the small system (10GR, 10DM), the cumulative reward went down from 0.90 to 0.85 (−5.6%), whereas convergence was delayed by 30 epochs. In the large system (50GR, 50DM), the effect was even more dramatic: the cumulative reward went down from 0.93 to 0.87 (−6.5%), and convergence was delayed by 60 epochs. This implies that entanglement is particularly important in scaling coordination to larger groups of agents, where the absence of explicit communications would otherwise cause agents to settle to locally optimal but globally suboptimal strategies. The gap relative to the best classical algorithm (QMIX) was also reduced when entanglement was removed, which suggests that this feature is an important driver of QiMARL’s new supremacy over vanilla MARL baselines.

6.4.2. Impact of Amplitude-Based Policy Sampling

Removal of amplitude-based policy sampling created a less pronounced but nonetheless considerable decline in performance. In the small system, the overall reward dropped from 0.90 to 0.86, and convergence was delayed by 20 epochs. In the large system, overall reward dropped from 0.93 to 0.89, and convergence slowed by 40 epochs. While less destructive in terms of annihilating entanglement, the slowdown in convergence is noteworthy, corroborating that sampling based on amplitude is largely beneficial for training efficiency. By probabilistic policy updates weighted towards likely action strings, the mechanism effectively prunes low-value exploration paths, accelerating the learning process without sacrificing solution quality.

6.4.3. Synergy Among Components

The primary finding of this work is that entanglement and amplitude-based sampling together are superior to either alone. Entanglement induces structural correlation among agents’ policies so that local learning is synchronized with global objectives, while amplitude-based sampling speeds up learning about high-reward policies. Without amplitude-based sampling, agents fragment into less correlated actions; without entanglement, learning takes longer and at greater expense. When both are present, QiMARL performs well in terms of reward, converges quickly in both small and large systems, and is superior to all the classical baselines tested.

6.4.4. Scalability Implications

The difference in severity of degradation in performance between small and large systems also yields important scalability insights. For smaller populations of agents, both mechanisms missing are also partially made up for by lower coordination complexity. However, in larger systems, the combinatorial explosion of possible joint policies increases the disadvantages of removing them. This is in favor of the argument that design choices made in QiMARL are not only incremental improvements but structural necessities for maintaining efficiency in large-scale, decentralized decision environments such as national-scale smart grids.

Though QiMARL uses quantum computing jargon and mechanics, it is a quantum-inspired model run on classical computers. The advantages seen in convergence and performance are a result of classical simulations of quantum characteristics rather than genuine quantum speedups. Future work may consider running on actual quantum hardware, but current results are all from classical simulation environments.

6.5. Experimental Results with Intermediate Nodes

6.5.1. Comparison of Convergence Time

To better understand the efficacy of the QiMARL algorithm, we carried out experimentation on intermediate nodes to unfold any hidden trends. The convergence trend for the medium system sizes—Medium-1 (20 GR, 20 DM) and Medium-2 (35 GR, 35 DM)—shows the evident dominance of the new QiMARL model over both traditional MAB methods and usual MARL methodologies. As can be observed from Table 6, QiMARL required the lowest number of epochs to converge for both of the two configurations, just 180 epochs for Medium-1 and 215 epochs for Medium-2. This was considerably faster than the optimal-performing MAB baseline (Thompson Sampling: 200 and 260 epochs, respectively) and much better than MARL methods such as MADDPG and PPO, which converged after 265–350 epochs.

Table 6. Convergence time and computational cost for Medium-1 (20 GR, 20 DM) and Medium-2 (35 GR, 35 DM) systems across QiMARL, traditional MAB, and MARL algorithms.

Method	System Size	Epochs to Converge	Time/Epoch (s)	Total Time (s)
QiMARL (Quantum-Inspired)	Medium-1	180	0.95	171.0
	Medium-2	215	1.05	225.8
Greedy (MAB)	Medium-1	260	0.52	135.2
	Medium-2	350	0.62	217.0
UCB (MAB)	Medium-1	220	0.58	127.6
	Medium-2	300	0.68	204.0
Thompson Sampling (MAB)	Medium-1	200	0.68	136.0
	Medium-2	260	0.78	202.8
QMIX (MARL)	Medium-1	240	1.05	252.0
	Medium-2	295	1.22	359.9
MADDPG (MARL)	Medium-1	265	1.10	291.5
	Medium-2	320	1.30	416.0
PPO (MARL)	Medium-1	290	1.00	290.0
	Medium-2	350	1.18	413.0

In addition, QiMARL maintained competitive per-epoch computation times at 0.95 s for Medium-1 and 1.05 s for Medium-2 even after introducing quantum-inspired processing overhead. This was lower than all but the majority of MARL methods, where increased policy complexity and communication overhead pushed per-epoch times over 1.1 s for MADDPG and QMIX in larger environments. The total convergence time for QiMARL (171 s for Medium-1, 225.8 s for Medium-2) was much lower compared to MARL baselines, indicating its computational and learning efficiency. These results reveal the ability of quantum-inspired agent coordination to speed up convergence without incurring computationally unaffordable costs as the number of GR and DM grows.

6.5.2. Comparison of Reward Performance

Reward-based performance measures, reported in Table 7, also confirm the advantages of the QiMARL approach. For both intermediate system sizes, QiMARL achieved the maximum local, global, and total reward values. Specifically, for the Medium-1 situation, QiMARL obtained a local reward of 0.93, a global reward of 0.89, and a total reward of 0.91. These values outperformed the top MARL competitor (QMIX: global reward 0.87) and all the MAB baselines, the closest of which was Thompson Sampling (global reward 0.82).

Table 7. Reward performance for Medium-1 (20 GR, 20 DM) and Medium-2 (35 GR, 35 DM) systems across QiMARL, traditional MAB, and MARL algorithms.

Method	System Size	Local Reward	Global Reward	Overall Reward
QiMARL (Quantum-Inspired)	Medium-1	0.93	0.89	0.91
	Medium-2	0.94	0.90	0.92
Greedy (MAB)	Medium-1	0.75	0.70	0.73
	Medium-2	0.73	0.69	0.71
UCB (MAB)	Medium-1	0.81	0.76	0.78
	Medium-2	0.80	0.76	0.77
Thompson Sampling (MAB)	Medium-1	0.85	0.80	0.82
	Medium-2	0.84	0.79	0.81
QMIX (MARL)	Medium-1	0.87	0.85	0.87
	Medium-2	0.875	0.865	0.875
MADDPG (MARL)	Medium-1	0.845	0.82	0.845
	Medium-2	0.848	0.835	0.848
PPO (MARL)	Medium-1	0.81	0.79	0.81
	Medium-2	0.812	0.80	0.815

In the more difficult Medium-2 configuration, QiMARL continued to excel with a local reward of 0.94, a global reward of 0.90, and a total reward of 0.92. Performance degradation in Medium-1 to Medium-2 scenarios was modest, indicating good scalability and robustness under increased numbers of agents. In comparison, baselines for both image-based MAB and MARL experienced steeper drops in reward performance with increasing system size. For instance, Thompson Sampling dropped from 0.82 to 0.81 in cumulative reward, and QMIX dropped from 0.87 to approximately 0.875. The sustained superiority in both local and global reward metrics demonstrates that QiMARL converges faster and produces better coordination and allocation policies, leading to tangible gains in both system-level and agent-level objectives.

7. Limitations of the Proposed QiMARL Algorithm

• Quantum Computation Overhead in Small Systems: On small problems, classical MAB algorithms (Greedy, UCB, Thompson Sampling) would typically be better because QiMARL adds extra quantum computation overhead.
• Hardware Limitations: Existing quantum processors are plagued by noise, decoherence, and qubit connectivity limitations, which have the potential to degrade the performance of QiMARL implementations.
• Implementation Complexity: Implementation of quantum circuits for reinforcement learning involves understanding quantum computing, hence making QiMARL more complicated to implement than traditional methods.
• Quantum Measurement Restrictions: Measurement of quantum states collapses the superposition, restricting the number of observations within an iteration and, in effect, causing information loss.
• Hybrid Quantum–Classical Bottlenecks: As practical application involves projection of quantum models onto classical data processing, hybrid execution can suffer from bottlenecks, degrading real-time behavior.

8. Conclusions and Future Research Avenues

The proposed QiMARL algorithm offers a viable option for improving energy distribution in nodal power systems. Using sophisticated quantum concepts, the program successfully balances the exploration and exploitation processes, allowing for a dynamic and adaptable energy distribution system in real time. Following numerous iterative rounds, experimental findings showed that the algorithm may increase important performance indicators such as energy distribution efficiency, distribution reliability, and total rewards. As a result, the quantum computing-based QiMARL algorithm demonstrates tremendous promise in tackling contemporary energy distribution difficulties, particularly in circumstances characterized by high unpredictability and uncertainty.

Future research on the QiMARL algorithm could focus on expanding the scalability of the algorithm, making it relevant for implementing it in grids with high complexities, and also working on its performance in higher-dimensional state spaces. As proposed, one of the solutions could be Federated-QiMARL. As quantum-based advances evolve, it is very much possible to implement the QiMARL algorithm in quantum-based devices to understand its efficacy in real-world configurations. Furthermore, research can focus on further coupling the advantages of the classical and quantum paradigms and implementing systems that would incorporate aspects like supply chain administration and financial modeling. These advancements would further improve the functionality and relevance of the proposed QiMARL algorithm, making it potent for solving complex optimization issues and carving the way forward for industrial usage.