Neural Network-Based Weight Loss Prediction: Behavioral Integration of Stress and Sleep in AI Decision Support
Abstract
1. Introduction
Main Contributions of This Study
- Develops a neural network model for weight loss prediction, incorporating both traditional physiological indicators and behavioral variables such as stress level (SL) and sleep quality (SQ);
- Quantitatively evaluates the individual and combined impact of excluding SQ and SL on prediction accuracy;
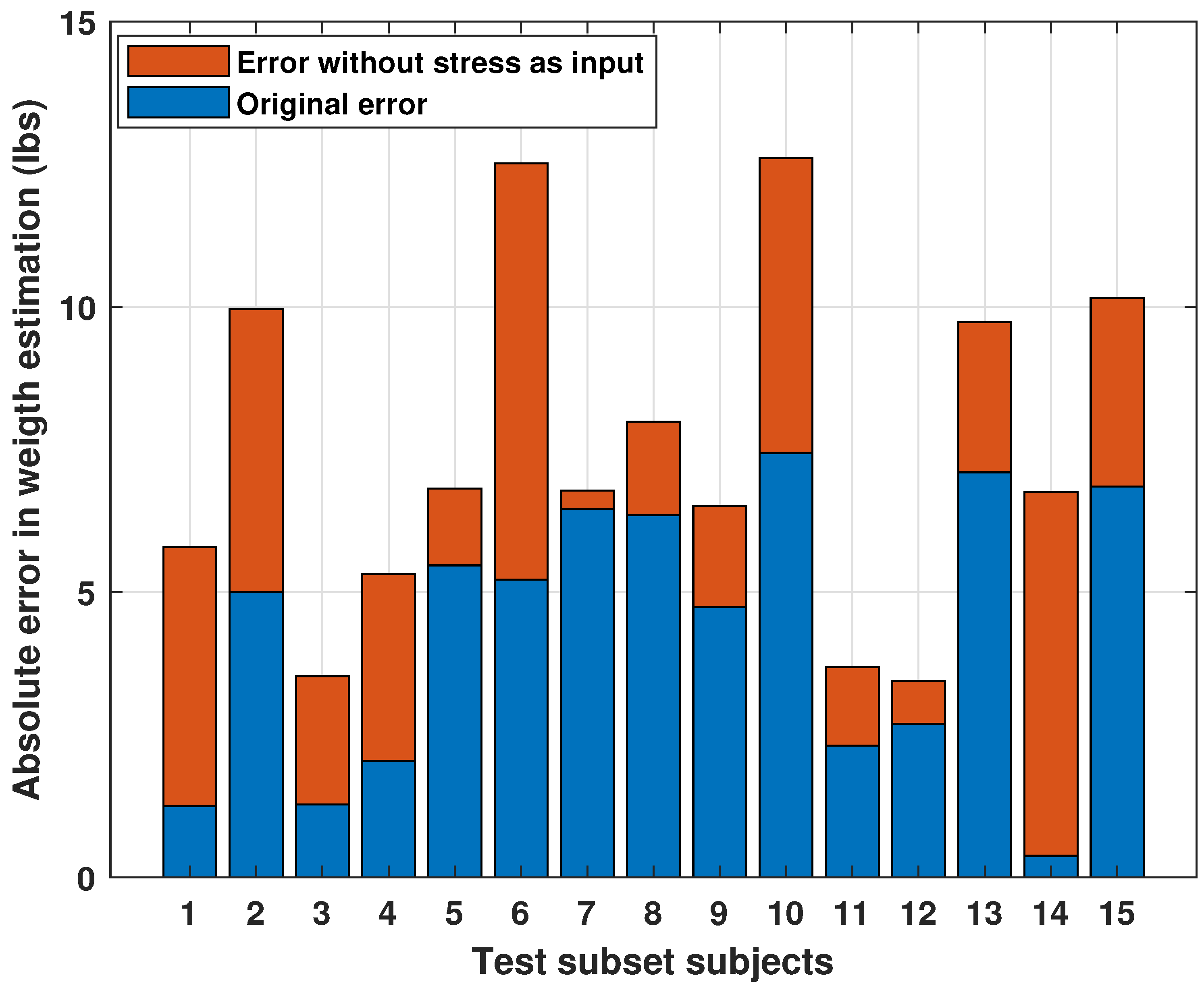
- Demonstrates that including these variables improves model performance by up to 30%, with RMSE dropping from 3.44% to 2.40%;
- Highlights the value of using low-cost, self-reported data for AI-based prediction in personalized health.
2. Materials and Methods
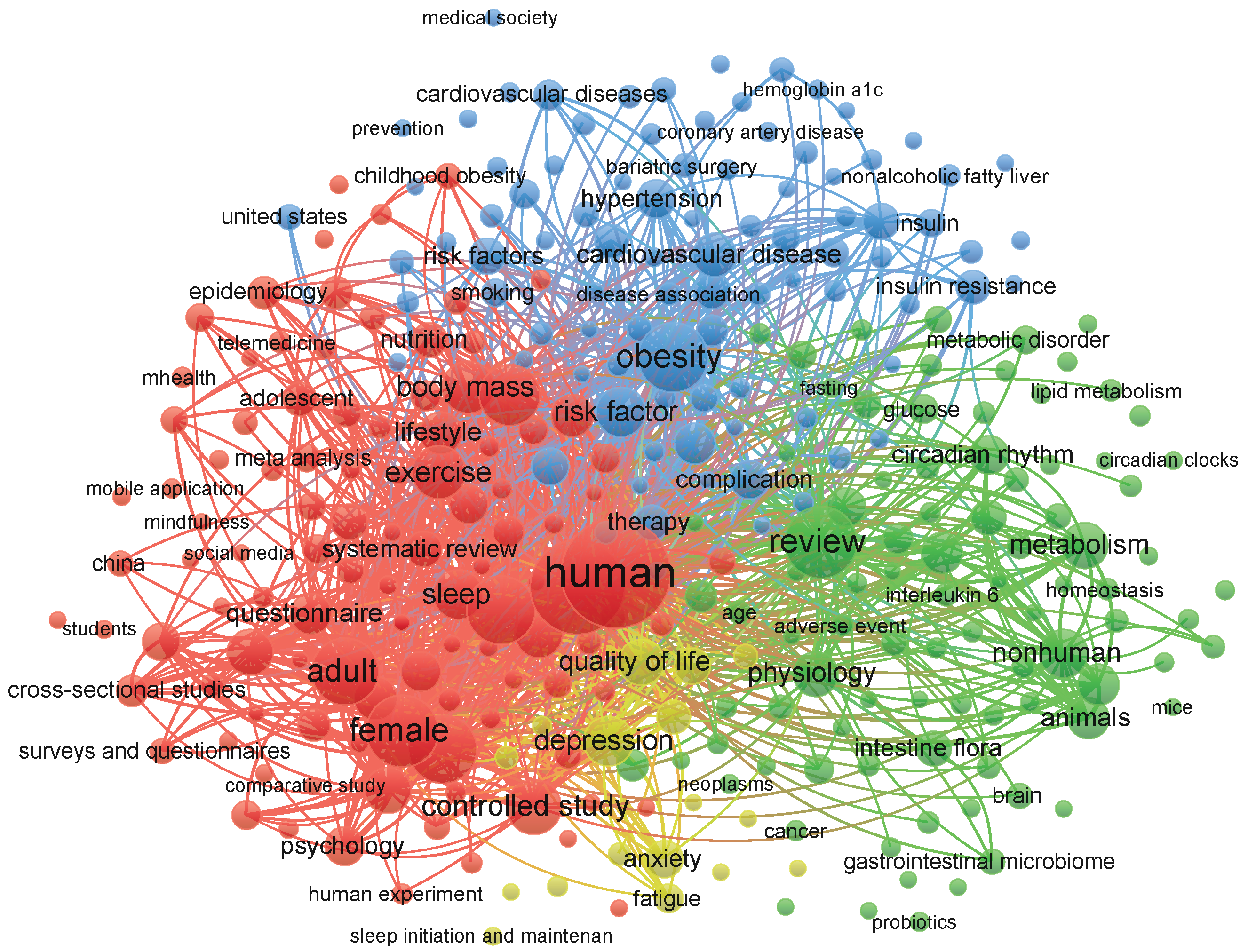
2.1. Bibliometric Mapping and Conceptual Association
2.2. Dataset
2.3. Artificial Neural Networks and Architecture Selection
- = actual value;
- = predicted value;
- n = number of observations.
- A = Age;
- S = Gender;
- = Current weight;
- = Daily caloric consumption;
- D = Duration of measurement (in weeks);
- = Physical activity level;
- = Sleep quality;
- = Stress sevel;
- = Basal metabolic rate.
3. Results and Discussion
3.1. Data Analysis and Justification for Behavioral Variable Integration
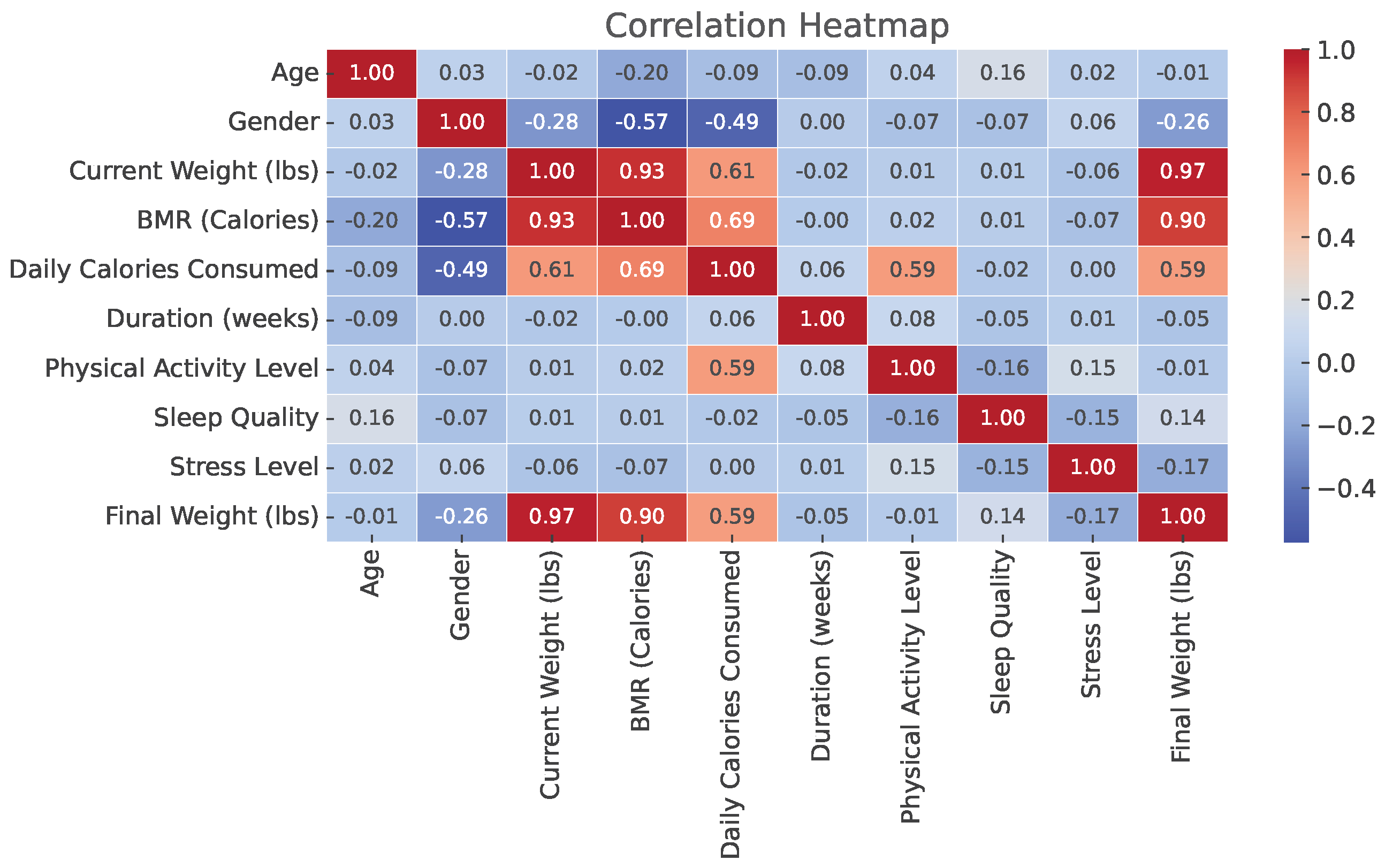
3.1.1. Correlation Matrix Analysis
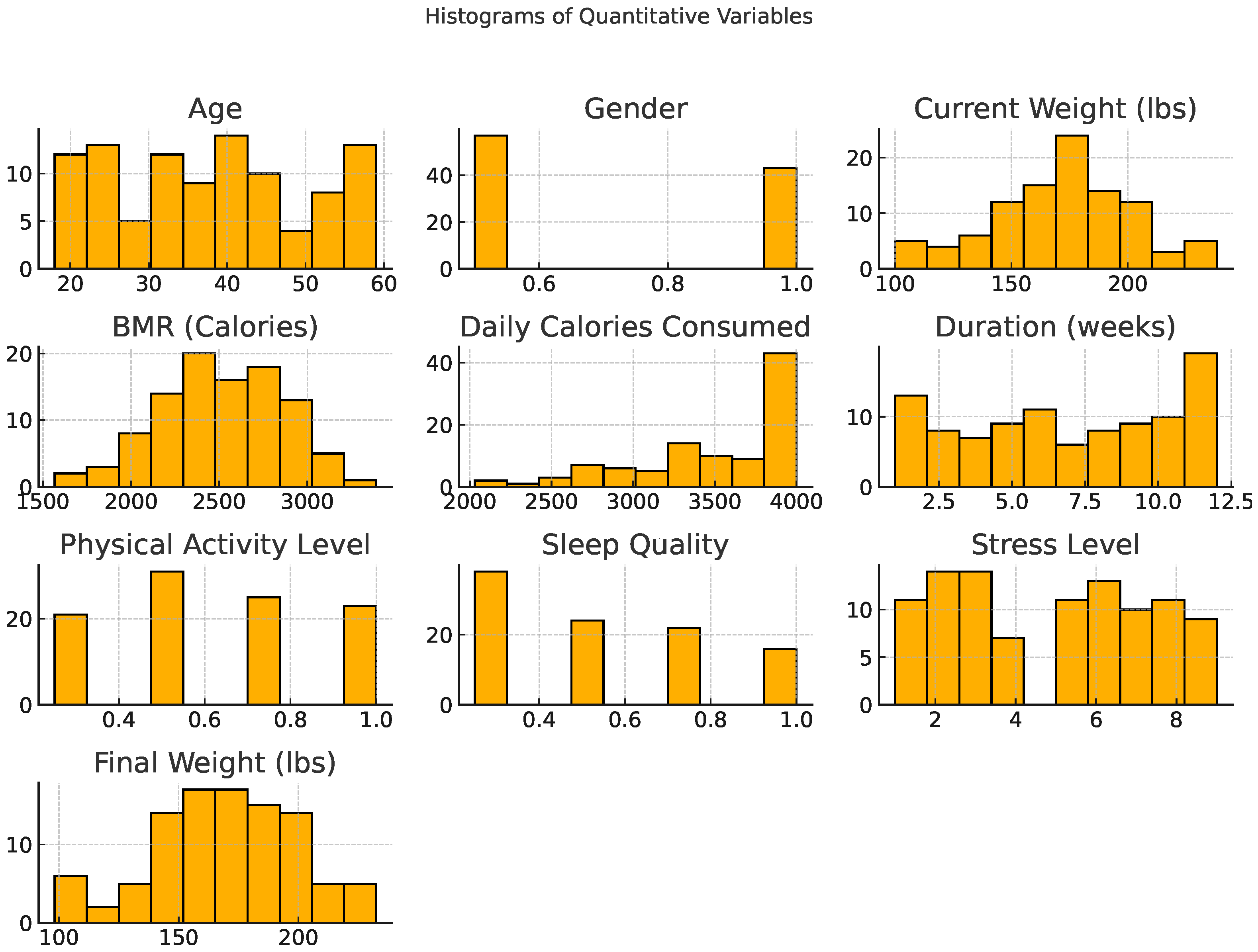
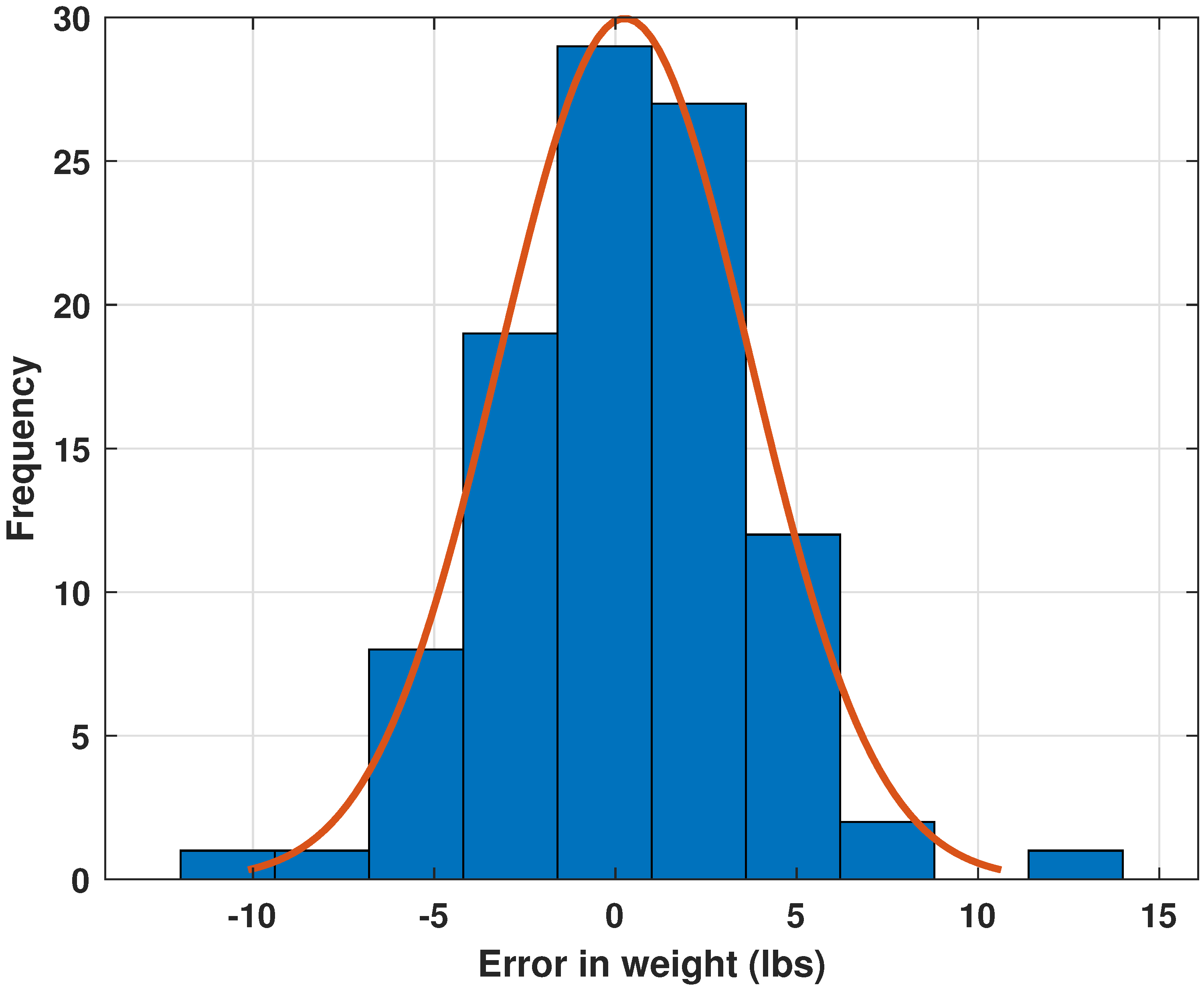
3.1.2. Distribution of Variables
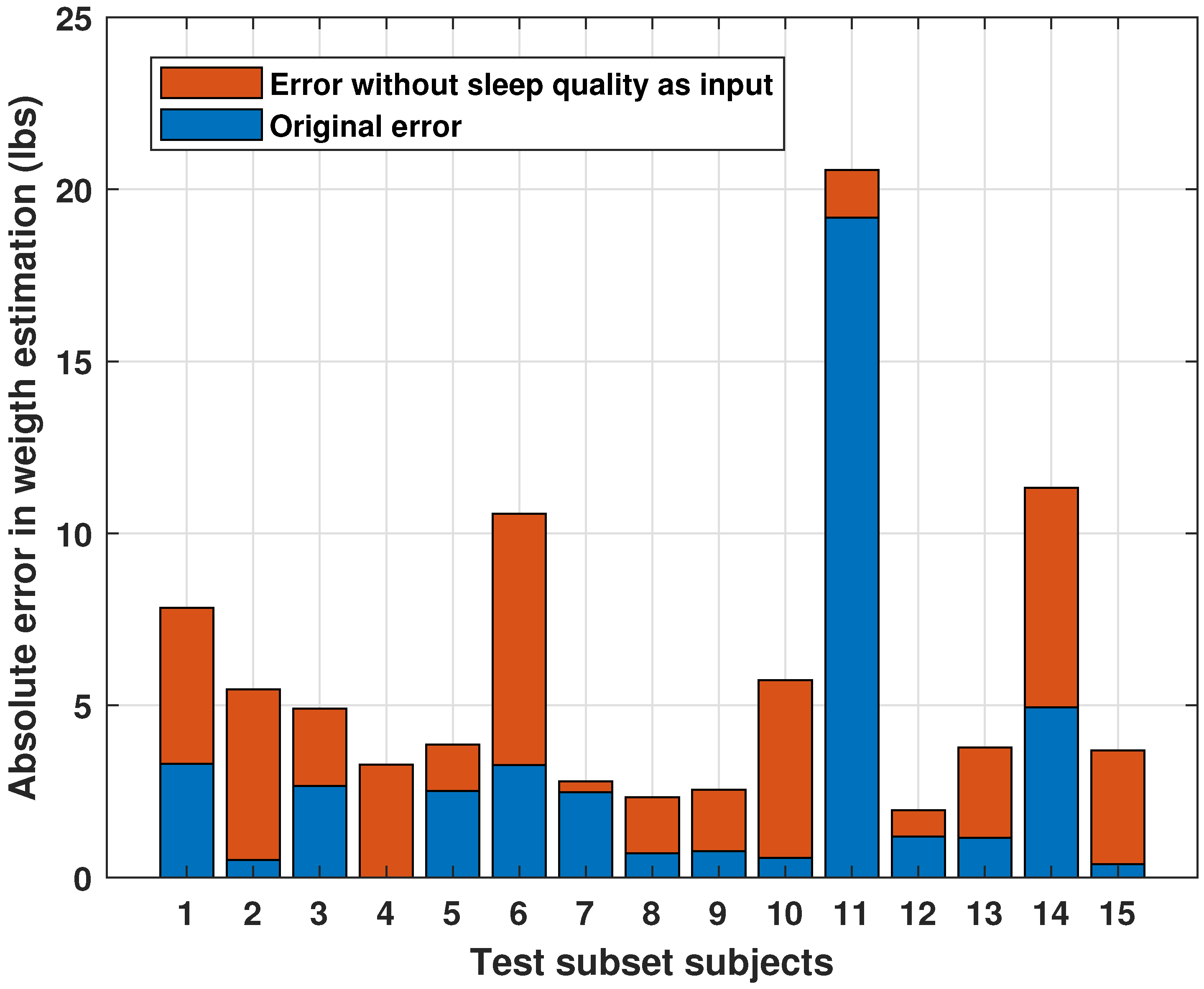
3.1.3. Inferential Analysis: Effect of Sleep Quality on Final Weight
3.1.4. Inferential Analysis: Effect of Stress Level on Final Body Weight
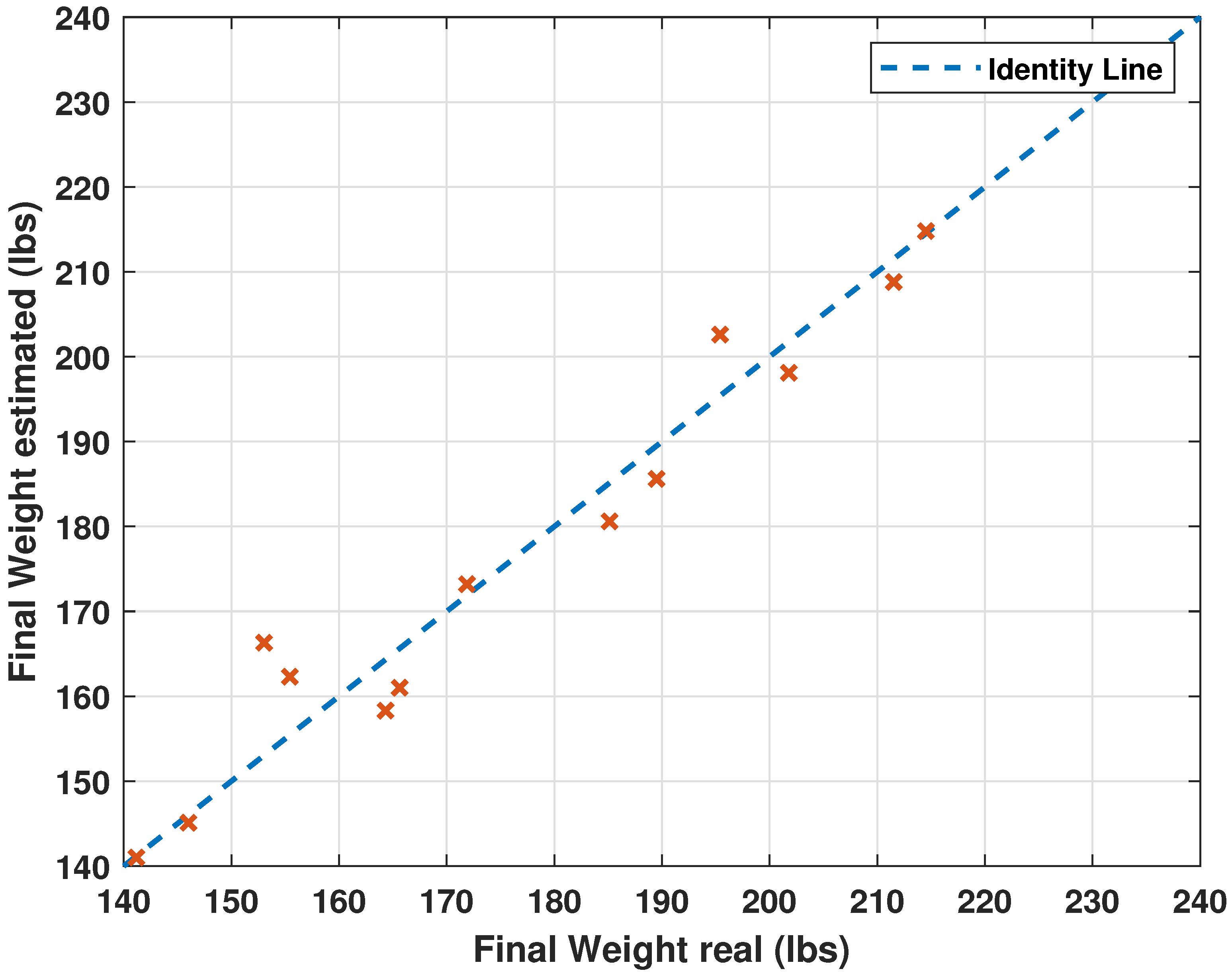
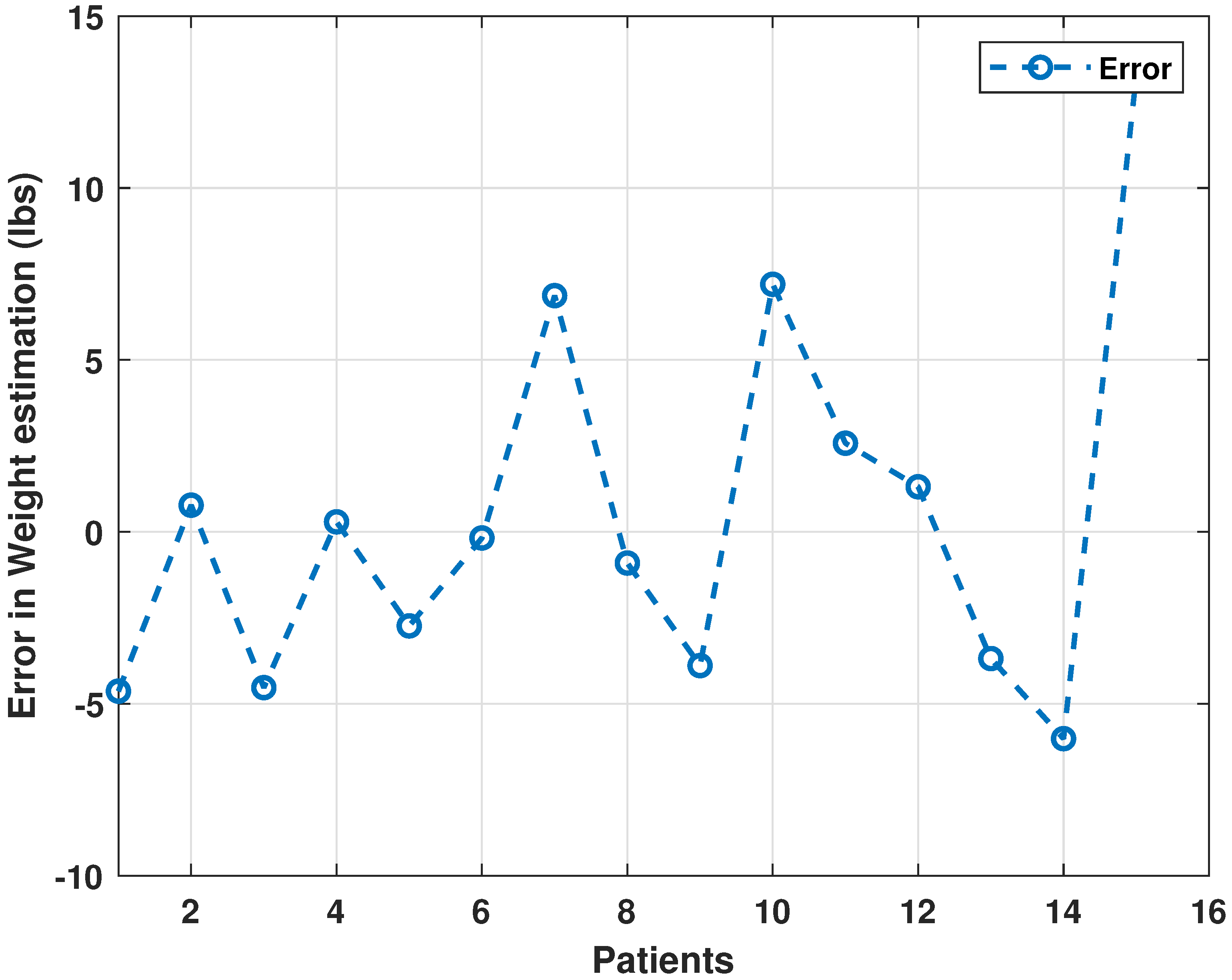
3.2. Performance Evaluation of Neural Network Architectures and Comparison with the Literature
4. Conclusions
- It introduces a lightweight and replicable ANN architecture, trained on open data, that achieves high accuracy without requiring clinical or laboratory measurements.
- It demonstrates the predictive strength of underutilized behavioral indicators, such as sleep and stress, which are rarely modeled quantitatively in AI frameworks despite their proven physiological effects.
- It offers an explainable machine learning strategy that bridges human-centered variables with model precision—contributing to the emerging field of behavioral-informed artificial intelligence.
- Support personalized interventions by generating real-time feedback based on user-reported behavior;
- Serve as a decision-support system for healthcare providers in monitoring patient progress without reliance on costly or invasive measurements;
- Inform public health strategies targeting obesity by highlighting modifiable, non-clinical determinants of weight regulation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kong, L.C.; Wuillemin, P.H.; Bastard, J.P.; Sokolovska, N.; Gougis, S.; Fellahi, S.; Darakhshan, F.; Bonnefont-Rousselot, D.; Bittar, R.; Doré, J.; et al. Insulin resistance and inflammation predict kinetic body weight changes in response to dietary weight loss and maintenance in overweight and obese subjects by using a Bayesian network approach. Am. J. Clin. Nutr. 2013, 98, 1385–1394. [Google Scholar] [CrossRef] [PubMed]
- Koliaki, C.; Dalamaga, M.; Liatis, S. Update on the Obesity Epidemic: After the Sudden Rise, Is the Upward Trajectory Beginning to Flatten? Curr. Obes. Rep. 2023, 12, 514–527. [Google Scholar] [CrossRef]
- Mohajan, D.; Mohajan, H.K. Obesity and Its Related Diseases: A New Escalating Alarming in Global Health. J. Innov. Med. Res. 2023, 2, 12–23. [Google Scholar] [CrossRef]
- Willoughby, D.; Hewlings, S.; Kalman, D. Body Composition Changes in Weight Loss: Strategies and Supplementation for Maintaining Lean Body Mass, a Brief Review. Nutrients 2018, 10, 1876. [Google Scholar] [CrossRef]
- Elfhag, K.; Rössner, S. Who succeeds in maintaining weight loss? A conceptual review of factors associated with weight loss maintenance and weight regain. Obes. Rev. 2005, 6, 67–85. [Google Scholar] [CrossRef]
- Grams, J.; Garvey, W.T. Weight Loss and the Prevention and Treatment of Type 2 Diabetes Using Lifestyle Therapy, Pharmacotherapy, and Bariatric Surgery: Mechanisms of Action. Curr. Obes. Rep. 2015, 4, 287–302. [Google Scholar] [CrossRef]
- Ma, C.; Avenell, A.; Bolland, M.; Hudson, J.; Stewart, F.; Robertson, C.; Sharma, P.; Fraser, C.; MacLennan, G. Effects of weight loss interventions for adults who are obese on mortality, cardiovascular disease, and cancer: Systematic review and meta-analysis. BMJ 2017, 359, j4849. [Google Scholar] [CrossRef]
- Sarma, S.; Sockalingam, S.; Dash, S. Obesity as a multisystem disease: Trends in obesity rates and obesity-related complications. Diabetes Obes. Metab. 2021, 23, 3–16. [Google Scholar] [CrossRef]
- Bellicha, A.; van Baak, M.A.; Battista, F.; Beaulieu, K.; Blundell, J.E.; Busetto, L.; Carraça, E.V.; Dicker, D.; Encantado, J.; Ermolao, A.; et al. Effect of exercise training on weight loss, body composition changes, and weight maintenance in adults with overweight or obesity: An overview of 12 systematic reviews and 149 studies. Obes. Rev. 2021, 22, e13256. [Google Scholar] [CrossRef] [PubMed]
- Varady, K.A.; Cienfuegos, S.; Ezpeleta, M.; Gabel, K. Clinical application of intermittent fasting for weight loss: Progress and future directions. Nat. Rev. Endocrinol. 2022, 18, 309–321. [Google Scholar] [CrossRef]
- Jéquier, E.; Tappy, L. Regulation of Body Weight in Humans. Physiol. Rev. 1999, 79, 451–480. [Google Scholar] [CrossRef] [PubMed]
- Hall, K.D. Computational model of in vivo human energy metabolism during semistarvation and refeeding. Am. J. Physiol.-Endocrinol. Metab. 2006, 291, E23–E37. [Google Scholar] [CrossRef] [PubMed]
- Hall, K.D. Predicting metabolic adaptation, body weight change, and energy intake in humans. Am. J. Physiol.-Endocrinol. Metab. 2010, 298, E449–E466. [Google Scholar] [CrossRef] [PubMed]
- Babajide, O.; Hissam, T.; Anna, P.; Anatoliy, G.; Astrup, A.; Alfredo Martinez, J.; Oppert, J.M.; Sørensen, T.I.A. A Machine Learning Approach to Short-Term Body Weight Prediction in a Dietary Intervention Program. In Proceedings of the Computational Science–ICCS 2020, Amsterdam, The Netherlands, 3–5 June 2020; Krzhizhanovskaya, V.V., Závodszky, G., Lees, M.H., Dongarra, J.J., Sloot, P.M.A., Brissos, S., Teixeira, J., Eds.; Springer: Cham, Switzerland, 2020; pp. 441–455. [Google Scholar]
- Goldstein, S.P.; Zhang, F.; Thomas, J.G.; Butryn, M.L.; Herbert, J.D.; Forman, E.M. Application of Machine Learning to Predict Dietary Lapses During Weight Loss. J. Diabetes Sci. Technol. 2018, 12, 1045–1052. [Google Scholar] [CrossRef] [PubMed]
- Ramyaa, R.; Hosseini, O.; Krishnan, G.P.; Krishnan, S. Phenotyping Women Based on Dietary Macronutrients, Physical Activity, and Body Weight Using Machine Learning Tools. Nutrients 2019, 11, 1681. [Google Scholar] [CrossRef]
- Rani, K. Linear Algebra as the Mathematical Foundation of Artificial Intelligence: Concepts, Applications, and Future Prospects. Int. J. Eng. Sci. Humanit. 2024, 14, 123–137. [Google Scholar] [CrossRef]
- Fujihara, K.; Yamada Harada, M.; Horikawa, C.; Iwanaga, M.; Tanaka, H.; Nomura, H.; Sui, Y.; Tanabe, K.; Yamada, T.; Kodama, S.; et al. Machine learning approach to predict body weight in adults. Front. Public Health 2023, 11, 1090146. [Google Scholar] [CrossRef]
- Dakanalis, A.; Voulgaridou, G.; Alexatou, O.; Papadopoulou, S.; Jacovides, C.; Pritsa, A.A.; Chrysafi, M.; Papacosta, E.; Kapetanou, M.G.; Tsourouflis, G.; et al. Overweight and Obesity Is Associated with Higher Risk of Perceived Stress and Poor Sleep Quality in Young Adults. Medicina 2024, 60, 983. [Google Scholar] [CrossRef] [PubMed]
- Papatriantafyllou, E.I.; Efthymiou, D.; Zoumbaneas, E.; Popescu, C.; Vassilopoulou, E. Sleep Deprivation: Effects on Weight Loss and Weight Loss Maintenance. Nutrients 2022, 14, 1549. [Google Scholar] [CrossRef] [PubMed]
- Tomiyama, J. Stress and Obesity. Annu. Rev. Psychol. 2019, 70, 703–718. [Google Scholar] [CrossRef]
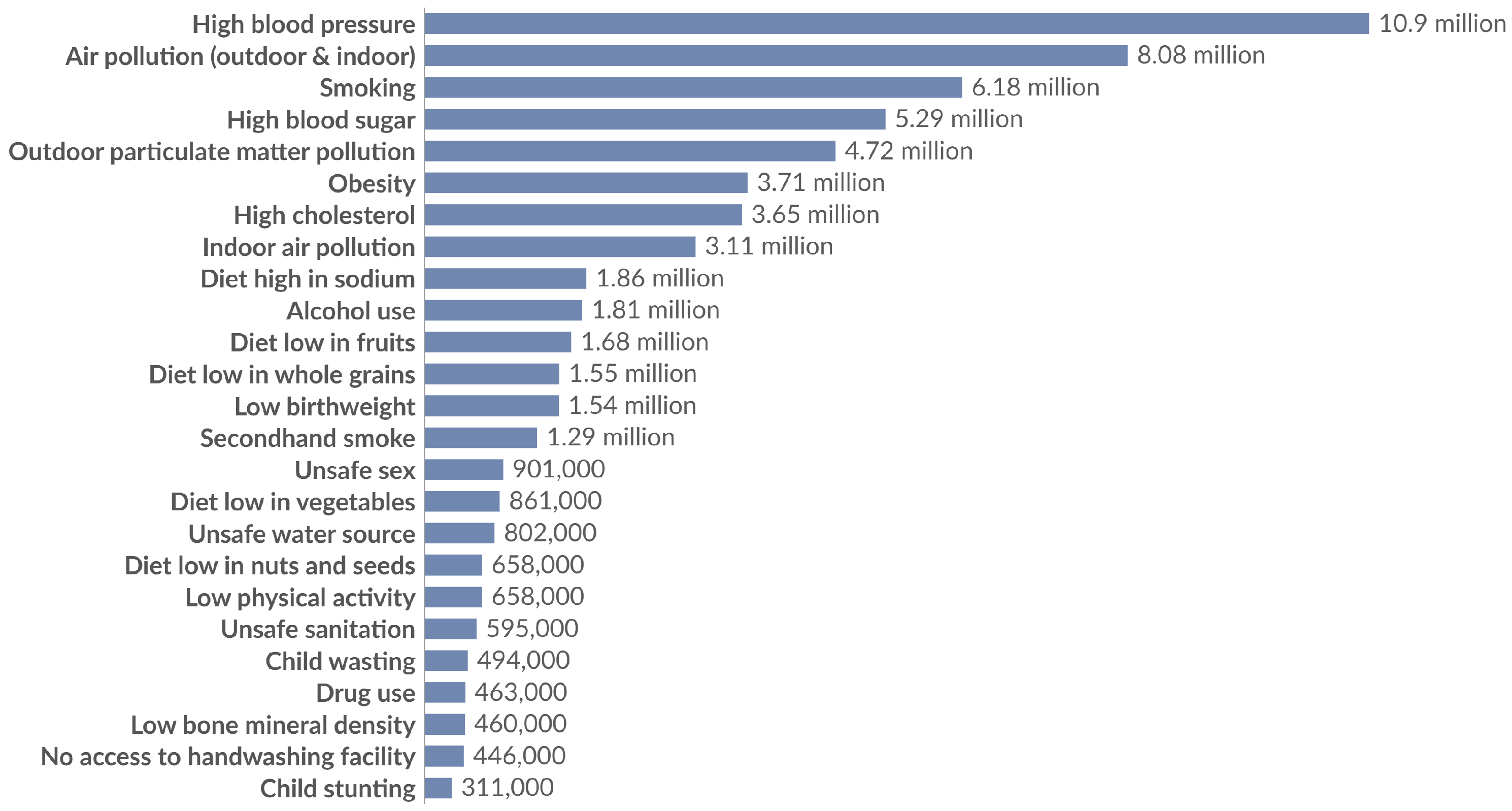
- Our World in Data. Deaths by Risk Factor, World, 2021. 2024. Available online: https://ourworldindata.org/ (accessed on 5 July 2025).
- Abdullah, M. Comprehensive Weight Change Prediction Dataset. 2023. Available online: https://www.kaggle.com/datasets/abdullah0a/comprehensive-weight-change-prediction/data (accessed on 5 July 2025).
- Chen, Y.; Liu, X.; Rao, M.; Qin, Y.; Wang, Z.; Ji, Y. Explicit speed-integrated LSTM network for non-stationary gearbox vibration representation and fault detection under varying speed conditions. Reliab. Eng. Syst. Saf. 2025, 254, 110596. [Google Scholar] [CrossRef]
- Mustafidah, H.; Suwarsito. Correlation Analysis Between Error Rate of Output and Learning Rate in Backpropagation Network. Adv. Sci. Lett. 2018, 24, 9182–9185. [Google Scholar] [CrossRef]
- Vakili, M.; Sabbagh-Yazdi, S.R.; Khosrojerdi, S.; Kalhor, K. Evaluating the effect of particulate matter pollution on estimation of daily global solar radiation using artificial neural network modeling based on meteorological data. J. Clean. Prod. 2017, 141, 1275–1285. [Google Scholar] [CrossRef]


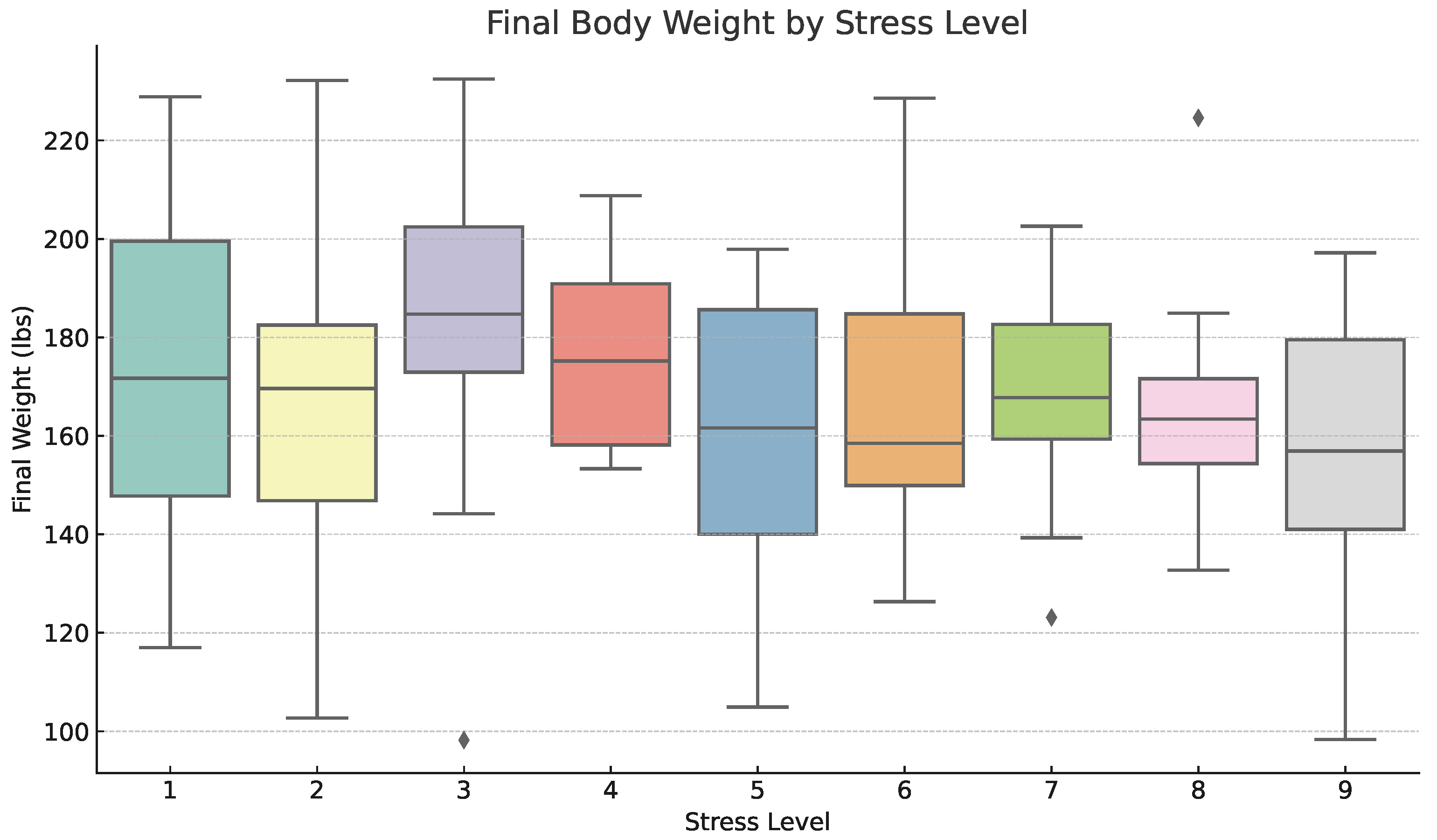
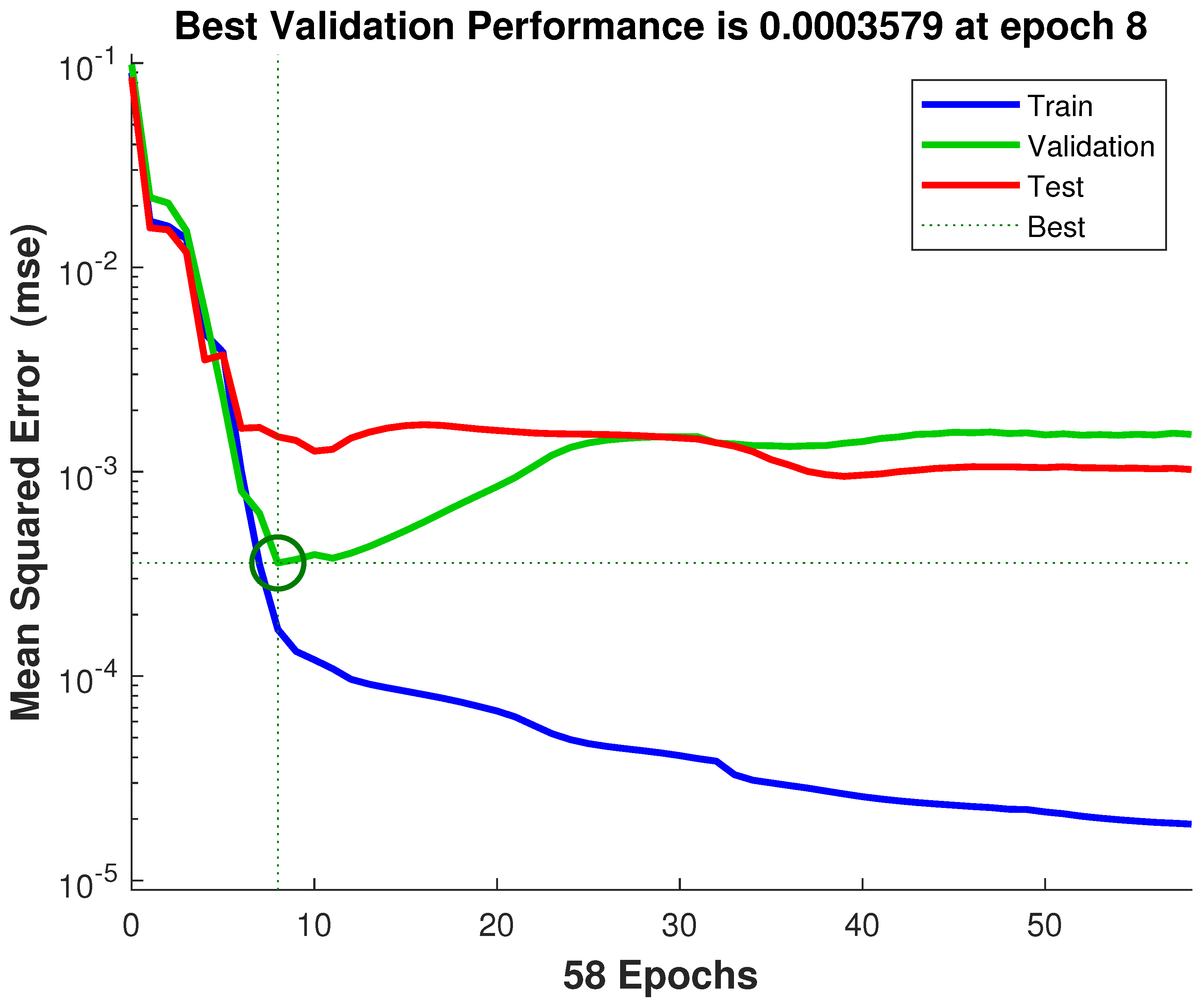

| Net | Neurons in Hidden Layers | Activation Functions | Mean RMSE (%) |
|---|---|---|---|
| Arch1 | 5 | Tanh | 2.7242% |
| Arch2 | 5 | Sigmoid | 2.2447% |
| Arch3 | 5-2 | Tanh-Tanh | 2.3652% |
| Arch4 | 5-2 | Tanh-Sigmoid | 2.7341% |
| Arch5 | 5-2 | Sigmoid-Tanh | 2.1015% |
| Arch6 | 5-2 | Sigmoid-Sigmoid | 1.9880% |
| Arch7 | 10 | Tanh | 2.8681% |
| Arch8 | 10 | Sigmoid | 2.1675% |
| Arch9 | 8-3 | Tanh-Tanh | 3.2043% |
| Arch10 | 8-3 | Tanh-Sigmoid | 2.9455% |
| Arch11 | 8-3 | Sigmoid-Tanh | 2.5803% |
| Arch12 | 8-3 | Sigmoid-Sigmoid | 2.3040% |
| Aspect | Description in This Study | Critical Appraisal |
|---|---|---|
| Sample size | 100 adult participants (aged 18–60 years) | Moderate sample size; appropriate for neural networks, though limited for statistical tests like ANOVA. |
| Predictive model | Artificial neural network with backpropagation (2 hidden layers) | Optimized architecture with low RMSE; validated and replicable configuration. |
| Included variables | Age, sex, current weight, BMR, caloric intake, physical activity, sleep, and stress | Innovative inclusion of behavioral variables; useful for low-cost personalized models. |
| Performance evaluation | Average RMSE of 2.40% with sleep and stress included | High predictive accuracy; improved when behavioral variables are integrated. |
| Statistical validation | ANOVA on sleep quality vs. final weight | Non-significant result (p > 0.05), but well interpreted in the context of a nonlinear model. |
| Model accessibility | Public and self-reported data (Kaggle) | Easy-to-replicate model; scalable for digital or clinical applications. |
| Identified limitations | Cross-sectional design and self-reported variables | Well-documented, longitudinal validation and objective measurements are recommended. |
| Author | AI Method | Key Variables | RMSE/Accuracy |
|---|---|---|---|
| [1] | Bayesian networks | Insulin, inflammation, diet | ∼4.5 lbs |
| [14] | Hybrid ML (ANN + rules) | Physical activity, diet | RMSE 3.9% |
| [18] | Classical ML (XGBoost) | 15 clinical variables | MAE 3.5 lbs |
| [16] | K-Means + ANN | Macronutrients and physical activity | RMSE 3.2% |
| This study | ANN (2 hidden layers, backpropagation) | Age, sex, BMR, physical activity, sleep, stress | RMSE 2.40% (with SQ and SL) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cruz Fernandez, M.; Castillo-Velásquez, F.A.; Rodriguez-Abreo, O.; Ortiz-Moctezuma, E.; Iturralde Carrera, L.A.; Estévez-Bén, A.A.; Álvarez-Alvarado, J.M.; Rodríguez-Reséndiz, J. Neural Network-Based Weight Loss Prediction: Behavioral Integration of Stress and Sleep in AI Decision Support. AI 2025, 6, 210. https://doi.org/10.3390/ai6090210
Cruz Fernandez M, Castillo-Velásquez FA, Rodriguez-Abreo O, Ortiz-Moctezuma E, Iturralde Carrera LA, Estévez-Bén AA, Álvarez-Alvarado JM, Rodríguez-Reséndiz J. Neural Network-Based Weight Loss Prediction: Behavioral Integration of Stress and Sleep in AI Decision Support. AI. 2025; 6(9):210. https://doi.org/10.3390/ai6090210
Chicago/Turabian StyleCruz Fernandez, Mayra, Francisco Antonio Castillo-Velásquez, Omar Rodriguez-Abreo, Enriqueta Ortiz-Moctezuma, Luis Angel Iturralde Carrera, Adyr A. Estévez-Bén, José M. Álvarez-Alvarado, and Juvenal Rodríguez-Reséndiz. 2025. "Neural Network-Based Weight Loss Prediction: Behavioral Integration of Stress and Sleep in AI Decision Support" AI 6, no. 9: 210. https://doi.org/10.3390/ai6090210
APA StyleCruz Fernandez, M., Castillo-Velásquez, F. A., Rodriguez-Abreo, O., Ortiz-Moctezuma, E., Iturralde Carrera, L. A., Estévez-Bén, A. A., Álvarez-Alvarado, J. M., & Rodríguez-Reséndiz, J. (2025). Neural Network-Based Weight Loss Prediction: Behavioral Integration of Stress and Sleep in AI Decision Support. AI, 6(9), 210. https://doi.org/10.3390/ai6090210











