Urban Traffic Congestion Prediction: A Multi-Step Approach Utilizing Sensor Data and Weather Information
Abstract
1. Introduction
2. Background
2.1. Smart City Context
2.2. ML-Based Time Series Forecasting
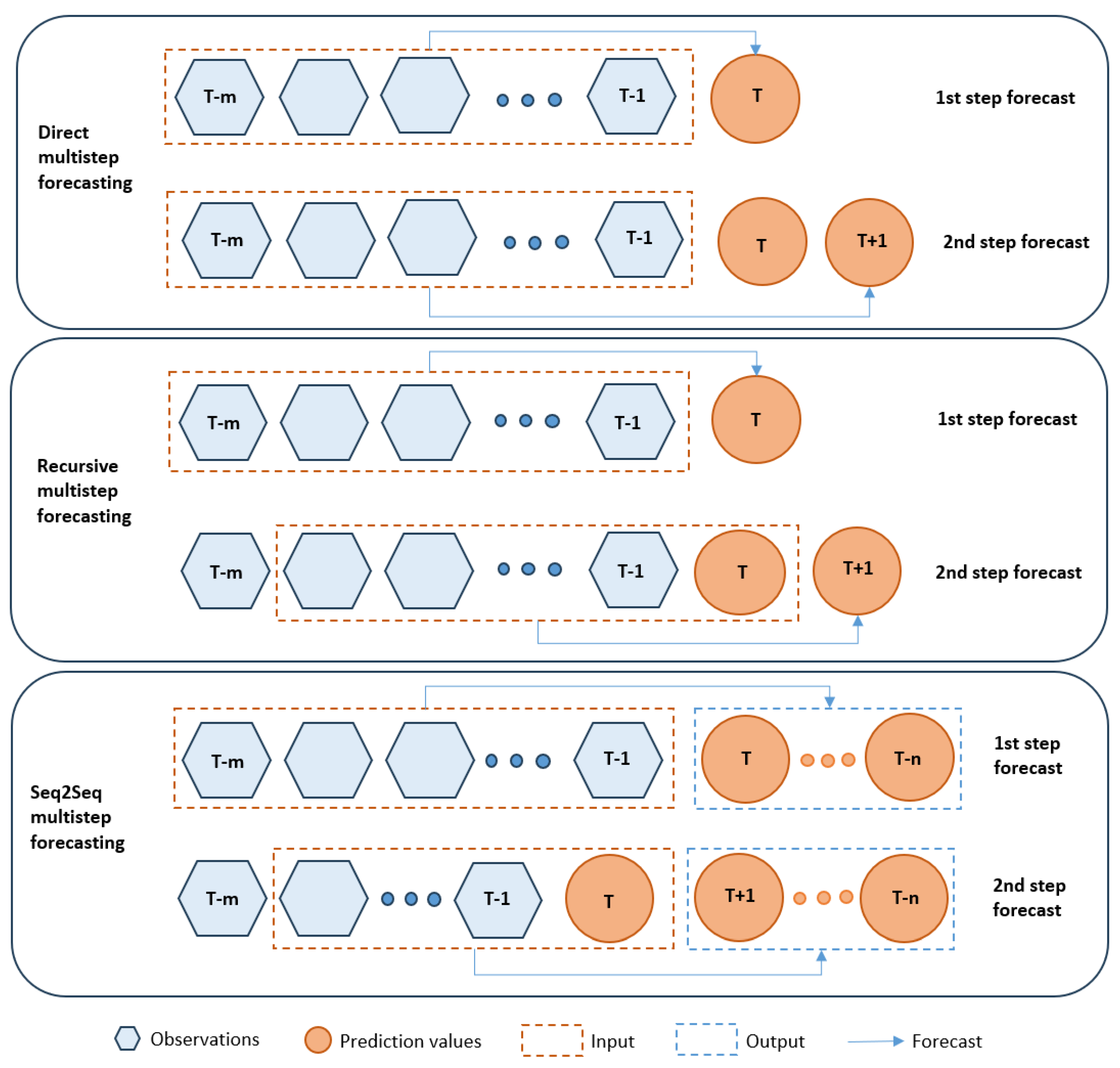
- Direct Forecasting: In this method, target values are anticipated for each subsequent step without reference to previously projected values. It is a simple strategy; however, it may suffer from the accumulation of errors [20].
- Recursive Forecasting: In this technique, the predicted values from previous steps are used as inputs to predict the values for the next step. Each predicted value serves as an input for the succeeding prediction in an iterative process. This method has the potential to better identify intertemporal dependencies [21].
- Sequence-to-Sequence Forecasting: In sequence-to-sequence (seq2seq) forecasting, a model consists of two main components: an encoder and a decoder. The decoder is trained to transform an input sequence of historical values into it into a fixed-size vector. This vector is fed into the decoder as an initial state, which focuses on different portions of the input sequence to generate the output sequence by predicting one value at a time. Transformers or RNNs are used for processing sequential data. Long-term forecasting can benefit from the use of sequence-to-sequence models since they can effectively capture complicated temporal trends [22].
ML Algorithms
- The Random Forest (RF) algorithm is a prime example of bagging. It creates bootstrap samples that are randomly selected from the dataset and then utilizes them to grow a Decision Tree. A random subsample of the features is used in each node-splitting process. Each tree’s prediction is examined, and the choice made is recorded by the RF model. The total number of vote predictions is used to make the ultimate choice (i.e., bagging) [28]. Other examples of the bagging technique are Extra Trees (ETs) [29] and the Bagging Regressor (BR).
- The Light Gradient Boosting Machine (LGBM) is a popular Gradient Boosting method. It employs a unique approach where, before constructing a new tree, all attributes are sorted, and a fraction of the splits are examined in each iteration. These splits are conducted leaf-wise, instead of using level-wise or tree-wise splitting. The LGBM is considered a lightweight histogram-based algorithm, resulting in faster training times [30], and it is highly effective when dealing with time series data [31]. Other notable examples of boosting include the XGB [32] and Histogram-Based Gradient-Boosted Reggresor (HGBR) [33] algorithms.
- In contrast to conventional feed-forward neural networks, the LSTM network core components include gate and memory cells in each hidden layer and feedback connections. This structure resembles a pipeline, linking all inputs together, and highlighting those of the previous inputs that relate the most to the current inputs while diminishing the importance of those connections that are less pertinent. It is capable of handling complete data sequences (like time series, voice, or video) in addition to individual data points (i.e., image). The LSTM architecture was developed to address the issue of the vanishing gradient problem encountered by conventional RNNs when attempting to model long-term dependencies in temporal sequences. A notable variant of the LSTM is the bidirectional LSTM (biLSTM). Unlike traditional LSTMs that process sequences from past to future, biLSTMs incorporate the ability to process information in both directions [36].
- First introduced in 2014, GRUs are used as a gating technique in a RNN. Lacking an output gate, each GRU operates like an LSTM with a forget gate [37,38] but with fewer parameters. For example, in polyphonic music modeling, voice signal modeling, and natural language processing, GRUs performed better than the LSTM. Also, on smaller datasets, GRUs have been shown, on some occasions, to outperform LSTMs [39].
2.3. Related Work on Traffic Flow Predictions
3. Methodology
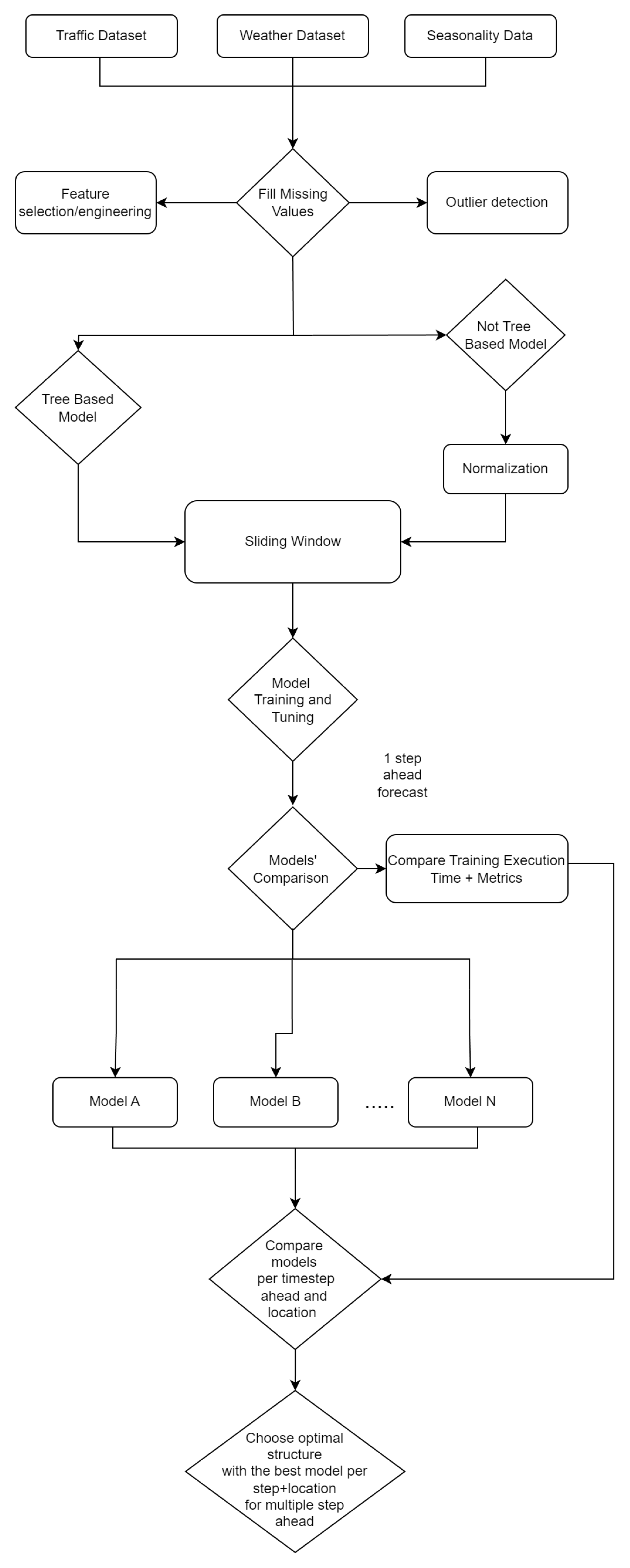
3.1. Dataset Description
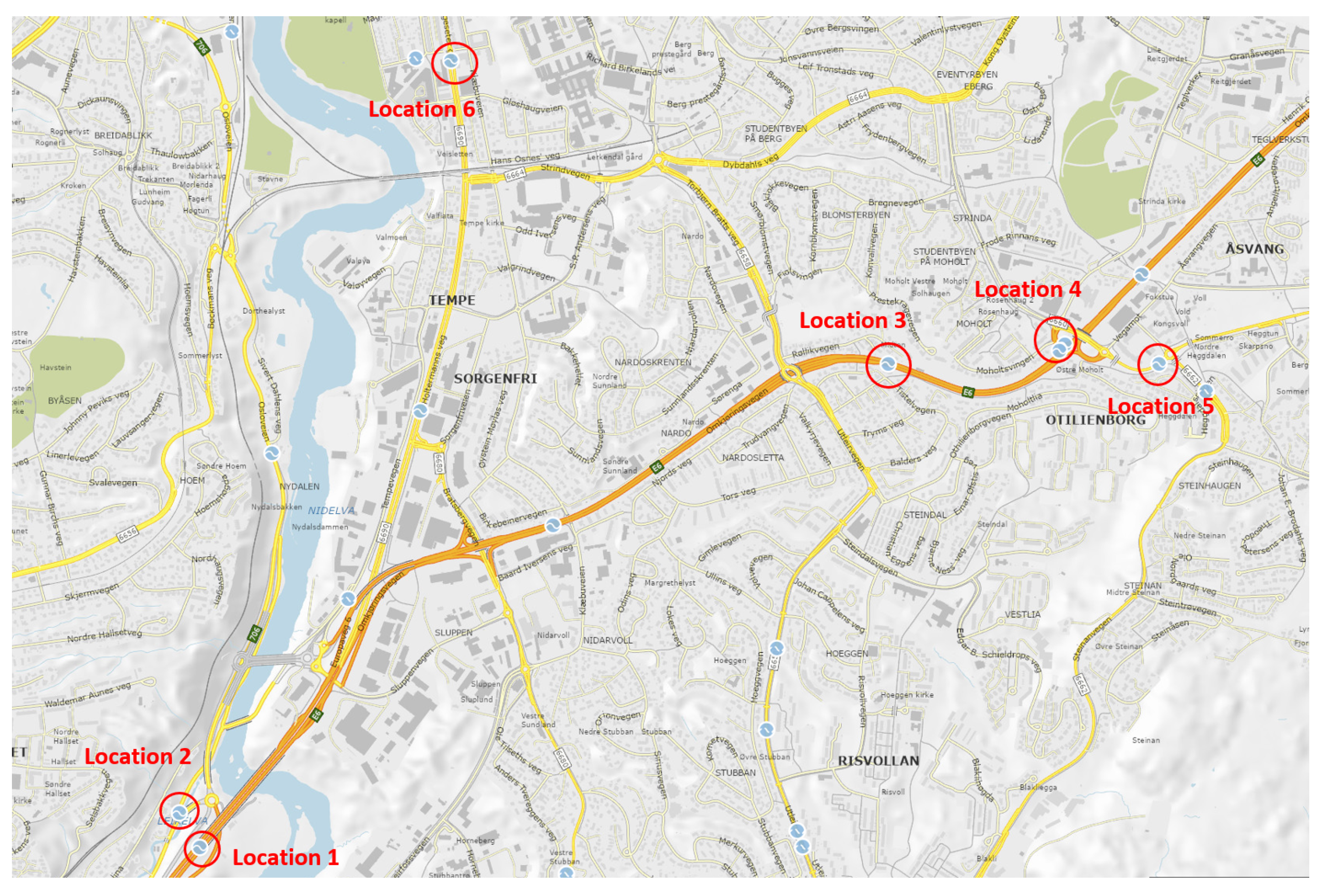
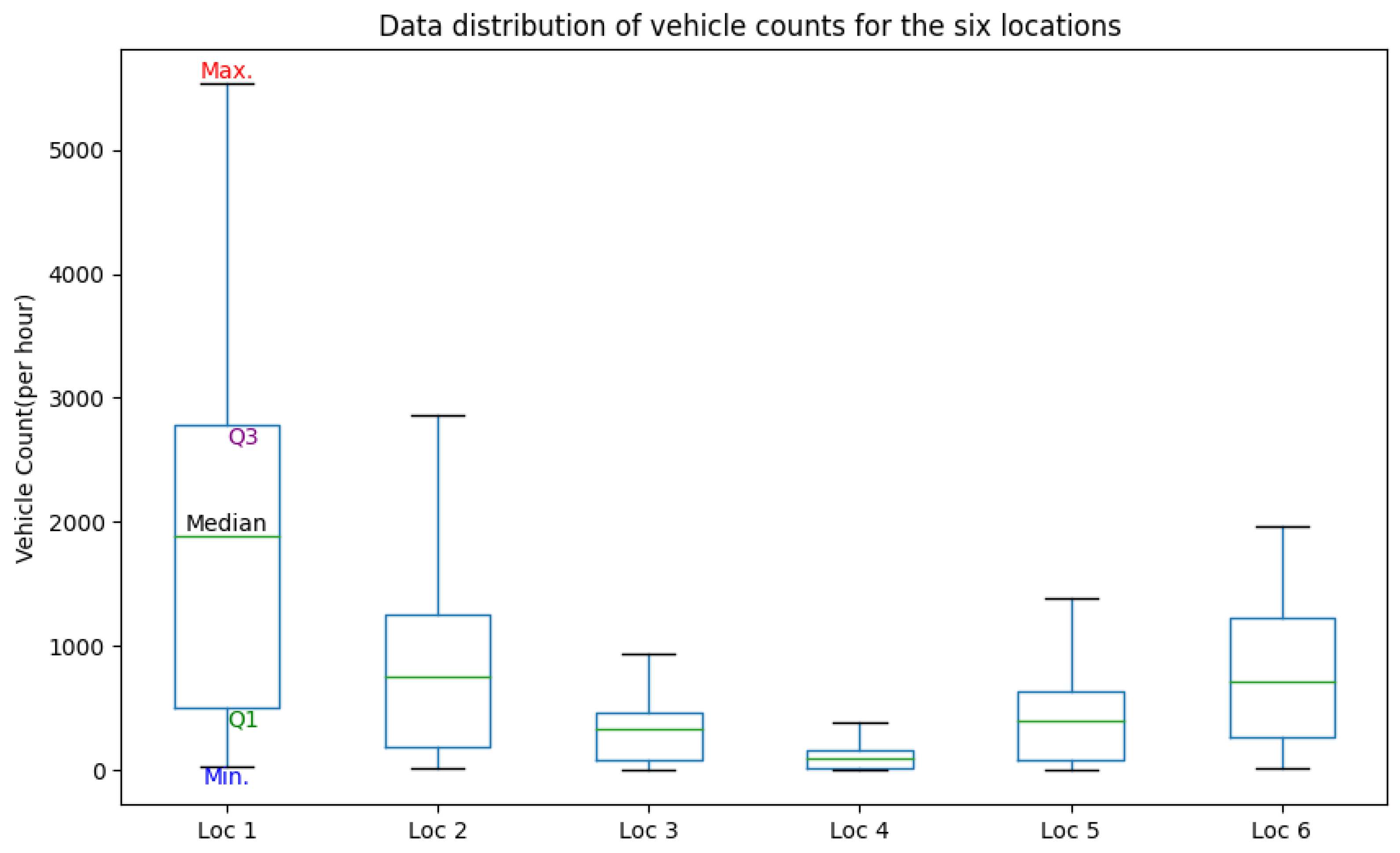
- Traffic flow data: Traffic data were collected from [62]. This web portal provides local hourly traffic flow sensor data for six traffic locations in the city of Trondheim (Figure 2). The time series data include an hourly count of vehicles shorter than 5.6 m (i.e., passenger cars) collected from December 2018 to January 2020.
- Weather condition data: Weather condition data were extracted from [63]. The data were gathered during the same period as for traffic flow data for the Trondheim area and included variables such as the relative humidity, temperature, wind speed, cloud coverage, snow depth, precipitation, and timestamp for each one hour gap.
3.2. Data Preprocessing
3.3. Feature Selection and Engineering
3.4. Forecasting Approach
- To investigate the utilization of ensemble techniques such as bootstrap aggregating (bagging) and boosting, which have been extensively employed in the existing literature for road traffic flow forecasting;
- To explore the deployment of more potent Deep Learning algorithms, allowing us to conduct a comprehensive comparative analysis of their predictive performances in contrast to traditional ensemble methods.
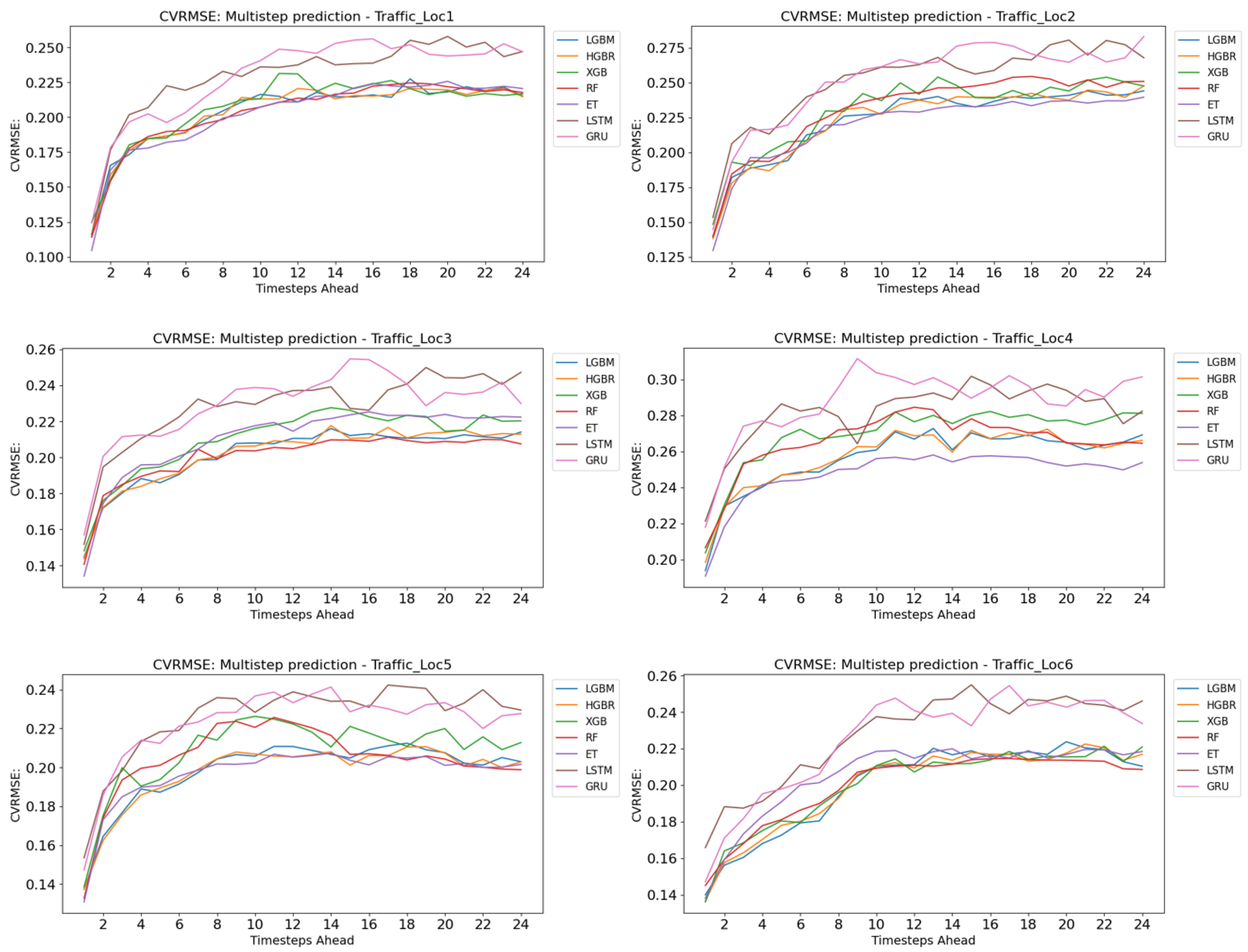
4. Results and Evaluation
5. Conclusions
5.1. Limitations
5.2. Future Work
- Introducing closely related spatial features to the developed models, for example, public bus arrivals and departures or ride-hailing orders in the area.
- The performance of experimental modeling utilizing larger and more diverse training datasets with added complexities. With the added data, the behavior of the implemented RNNs should be closely examined.
- Additional DL techniques could be explored, such as CNNs combined with a RNN implementation, possibly under a CNN-LSTM configuration. The public availability of comprehensive and extensive traffic flow datasets is typically limited. However, there are approaches within the field of Transfer Learning (TL) that have been developed to solve new but comparable problems by utilizing prior knowledge. Integrating existing knowledge when training such DL models allows a reduction in the amount of required training data and leads to better learning rates [76]. Examples of such methods can be found in [77,78], where the outputs of physics-based models were utilized as soft constraints to penalize or regulate data-driven implementations, and in [79], where a fusion of prior knowledge network was developed using self-similarity properties of network traffic data.
- Integration of this traffic forecasting approach as a component in another expanded forecasting framework. For example, a localized EV charging demand forecasting framework could be utilized to predict the short-term EV charging load demand.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ARIMA | Autoregressive Integrated Moving Average |
| biLSTM | biderectional LSTM |
| BR | Bagging Regressor |
| BRR | Bayesian Ridge Regression |
| CDT | Cell Dwell Time |
| CNN | Convolutional Neural Network |
| CV | Cross validation |
| CVRMSE | Coefficient of the Variation of the RMSE |
| DL | Deep Learning |
| DT | Decision Tree |
| ENR | Elastic Net Regression |
| ELM | Extreme Learning Machine |
| ET | Extra Tree |
| ETB | Ensemble Tree-Based |
| GA | Genetic Algorithm |
| GBDT | Gradient-Boosted Decision Trees |
| GPS | Global Positioning System |
| GRU | Gated Recurrent Units |
| GSCV | Grid Search Cross Validation |
| HGBR | Histogram-Based Gradient-Boosted Regressor |
| HR | Huber Regressor |
| ICT | Information and Communication Technologies |
| IoT | Internet of Things |
| ITS | Intelligent Transportation Systems |
| KELM | Kernel Extreme Learning Machine |
| KNN | K-Nearest Neighbors |
| LarsCV | Least Angle Regression CV |
| LGBM | Light Gradient Boosting Machine |
| LR | Linear Regressor |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| ML | Machine Learning |
| MLP | Multilayer Perceptron |
| MLR-LSTM | Multiple Linear Regression and LSTM |
| RFE | Recursive Feature Elimination |
| RF | Random Forest |
| RNN | Recurrent Neural Network |
| RR | Ridge Regression |
| R-squared | |
| RFECV | Recursive Feature Elimination with Cross Validation |
| RMSE | Root Mean Square Error |
| SC | Smart City |
| SFS | Sequential Forward Selection |
| SW | Sliding Window |
| SVM | Support Vector Machines |
| TL | Transfer Learning |
| XGB | eXtreme Gradient Boosting |
References
- United Nations. World Urbanization Prospects: The 2018 Revision; Technical Report; UN: New York, NY, USA, 2019. [Google Scholar]
- Zhang, K.; Batterman, S. Air pollution and health risks due to vehicle traffic. Sci. Total Environ. 2013, 450–451, 307–316. [Google Scholar] [CrossRef]
- Gakis, E.; Kehagias, D.; Tzovaras, D. Mining Traffic Data for Road Incidents Detection. In Proceedings of the 2014 IEEE 17th International Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014. [Google Scholar]
- Shokri, D.; Larouche, C.; Homayouni, S. A Comparative Analysis of Multi-Label Deep Learning Classifiers for Real-Time Vehicle Detection to Support Intelligent Transportation Systems. Smart Cities 2023, 6, 2982–3004. [Google Scholar] [CrossRef]
- Kontses, A.; Triantafyllopoulos, G.; Ntziachristos, L.; Samaras, Z. Particle number (PN) emissions from gasoline, diesel, LPG, CNG and hybrid-electric light-duty vehicles under real-world driving conditions. Atmos. Environ. 2020, 222, 117126. [Google Scholar] [CrossRef]
- European Commission. Impact of Driving Conditions and Driving Behaviour—ULEV. 2023. Available online: https://wikis.ec.europa.eu/display/ULEV/Impact+of+driving+conditions+and+driving+behaviour (accessed on 31 October 2023).
- Regragui, Y.; Moussa, N. A real-time path planning for reducing vehicles traveling time in cooperative-intelligent transportation systems. Simul. Model. Pract. Theory 2023, 123, 102710. [Google Scholar] [CrossRef]
- MACIOSZEK, E. Analysis of the volume of passengers and cargo in rail and road transport in Poland in 2009–2019. Sci. J. Silesian Univ. Technol. Ser. Transp. 2021, 113, 133–143. [Google Scholar] [CrossRef]
- Oladimeji, D.; Gupta, K.; Kose, N.A.; Gundogan, K.; Ge, L.; Liang, F. Smart Transportation: An Overview of Technologies and Applications. Sensors 2023, 23, 3880. [Google Scholar] [CrossRef]
- Razali, N.A.M.; Shamsaimon, N.; Ishak, K.K.; Ramli, S.; Amran, M.F.M.; Sukardi, S. Gap, techniques and evaluation: Traffic flow prediction using machine learning and deep learning. J. Big Data 2021, 8, 152. [Google Scholar] [CrossRef]
- Mystakidis, A.; Stasinos, N.; Kousis, A.; Sarlis, V.; Koukaras, P.; Rousidis, D.; Kotsiopoulos, I.; Tjortjis, C. Predicting Covid-19 ICU Needs Using Deep Learning, XGBoost and Random Forest Regression with the Sliding Window Technique. In Proceedings of the IEEE Smart Cities, Virtual, 17–23 March 2021; pp. 1–6. [Google Scholar]
- Mystakidis, A.; Ntozi, E.; Afentoulis, K.; Koukaras, P.; Gkaidatzis, P.; Ioannidis, D.; Tjortjis, C.; Tzovaras, D. Energy generation forecasting: Elevating performance with machine and deep learning. Computing 2023, 105, 1623–1645. [Google Scholar] [CrossRef]
- Tsalikidis, N.; Mystakidis, A.; Tjortjis, C.; Koukaras, P.; Ioannidis, D. Energy load forecasting: One-step ahead hybrid model utilizing ensembling. Computing 2023, 106, 241–273. [Google Scholar] [CrossRef]
- Koukaras, P.; Tjortjis, C.; Gkaidatzis, P.; Bezas, N.; Ioannidis, D.; Tzovaras, D. An interdisciplinary approach on efficient virtual microgrid to virtual microgrid energy balancing incorporating data preprocessing techniques. Computing 2022, 104, 209–250. [Google Scholar] [CrossRef]
- Olshausen, B.A.; Field, D.J. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature 1996, 381, 607–609. [Google Scholar] [CrossRef] [PubMed]
- Thianniwet, T.; Phosaard, S.; Pattara-atikom, W. Classification of Road Traffic Congestion Levels from GPS Data using a Decision Tree Algorithm and Sliding Windows. Lecture Notes in Engineering and Computer Science. In Proceedings of the World Congress on Engineering 2009 Vol I WCE 2009, London, UK, 1–3 July 2009. [Google Scholar]
- Heidari, A.; Navimipour, N.J.; Unal, M. Applications of ML/DL in the management of smart cities and societies based on new trends in information technologies: A systematic literature review. Sustain. Cities Soc. 2022, 85, 104089. [Google Scholar] [CrossRef]
- Adel, A. Unlocking the Future: Fostering Human–Machine Collaboration and Driving Intelligent Automation through Industry 5.0 in Smart Cities. Smart Cities 2023, 6, 2742–2782. [Google Scholar] [CrossRef]
- Lee, C.H.; Lin, C.R.; Chen, M.S. Sliding-Window Filtering: An Efficient Algorithm for Incremental Mining. In Proceedings of the International Conference on Information and Knowledge Management, Atlanta, GA, USA, 5–10 October 2001; pp. 263–270. [Google Scholar] [CrossRef]
- Feng, B.; Xu, J.; Zhang, Y.; Lin, Y. Multi-step traffic speed prediction based on ensemble learning on an urban road network. Appl. Sci. 2021, 11, 4423. [Google Scholar] [CrossRef]
- Xue, P.; Jiang, Y.; Zhou, Z.; Chen, X.; Fang, X.; Liu, J. Multi-step ahead forecasting of heat load in district heating systems using machine learning algorithms. Energy 2019, 188, 116085. [Google Scholar] [CrossRef]
- Mariet, Z.; Kuznetsov, V. Foundations of Sequence-to-Sequence Modeling for Time Series. In Proceedings of the Twenty-Second International Conference on Artificial Intelligence and Statistics, PMLR, Okinawa, Japan, 16–18 April 2019; Volume 89, pp. 408–417. [Google Scholar]
- Song, Y.Y.; Lu, Y. Decision tree methods: Applications for classification and prediction. Shanghai Arch. Psychiatry 2015, 27, 130–135. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Chapman & Hall: Boca Raton, FL, USA, 1984. [Google Scholar]
- Ruiz-Abellón, M.D.C.; Gabaldón, A.; Guillamón, A. Load forecasting for a campus university using ensemble methods based on regression trees. Energies 2018, 11, 2038. [Google Scholar] [CrossRef]
- Natras, R.; Soja, B.; Schmidt, M. Ensemble Machine Learning of Random Forest, AdaBoost and XGBoost for Vertical Total Electron Content Forecasting. Remote Sens. 2022, 14, 3547. [Google Scholar] [CrossRef]
- Omer, Z.M.; Shareef, H. Comparison of decision tree based ensemble methods for prediction of photovoltaic maximum current. Energy Convers. Manag. 2022, 16, 100333. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Ju, Y.; Sun, G.; Chen, Q.; Zhang, M.; Zhu, H.; Rehman, M.U. A model combining Convolutional Neural Network and LightGBM algorithm for ultra-short-term wind power forecasting. IEEE Access 2019, 7, 28309–28318. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. M5 accuracy competition: Results, findings, and conclusions. Int. J. Forecast. 2022, 38, 1346–1364. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The Performance of LSTM and BiLSTM in Forecasting Time Series. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019. [Google Scholar]
- Omlin, C.; Thornber, K.; Giles, C. Fuzzy finite-state automata can be deterministically encoded into recurrent neural networks. IEEE Trans. Fuzzy Syst. 1998, 6, 76–89. [Google Scholar] [CrossRef]
- Hochreiter, S.J.; Schmidhuber, J. Long short-term memory. Neural Computation 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Gers, F.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 1999, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; van Merrienboer, B.; Bahdanau, D.; Bengio, Y. On the Properties of Neural Machine Translation: Encoder-Decoder Approaches. arxiv 1409. [Google Scholar]
- Gruber, N.; Jockisch, A. Are GRU Cells More Specific and LSTM Cells More Sensitive in Motive Classification of Text? Front. Artif. Intell. 2020, 3, 00040. [Google Scholar] [CrossRef]
- Zhuang, W.; Cao, Y. Short-Term Traffic Flow Prediction Based on CNN-BILSTM with Multicomponent Information. Appl. Sci. 2022, 12, 8714. [Google Scholar] [CrossRef]
- Shi, R.; Du, L. Multi-Section Traffic Flow Prediction Based on MLR-LSTM Neural Network. Sensors 2022, 22, 7517. [Google Scholar] [CrossRef] [PubMed]
- Dong, X.; Lei, T.; Jin, S.; Hou, Z. Short-Term Traffic Flow Prediction Based on XGBoost. In Proceedings of the 2018 IEEE 7th Data Driven Control and Learning Systems Conference (DDCLS), Enshi, China, 25–27 May 2018; pp. 854–859. [Google Scholar] [CrossRef]
- Rizal, A.A.; Soraya, S.; Tajuddin, M. Sequence to sequence analysis with long short term memory for tourist arrivals prediction. J. Phys. Conf. Ser. 2019, 1211, 012024. [Google Scholar] [CrossRef]
- Khan, N.U.; Shah, M.A.; Maple, C.; Ahmed, E.; Asghar, N. Traffic Flow Prediction: An Intelligent Scheme for Forecasting Traffic Flow Using Air Pollution Data in Smart Cities with Bagging Ensemble. Sustainability 2022, 14, 4164. [Google Scholar] [CrossRef]
- Chai, W.; Zheng, Y.; Tian, L.; Qin, J.; Zhou, T. GA-KELM: Genetic-Algorithm-Improved Kernel Extreme Learning Machine for Traffic Flow Forecasting. Mathematics 2023, 11, 3574. [Google Scholar] [CrossRef]
- Billings, D.; Yang, J.S. Application of the ARIMA Models to Urban Roadway Travel Time Prediction—A Case Study. In Proceedings of the 2006 IEEE International Conference on Systems, Man and Cybernetics, Taipei, Taiwan, 8–11 October 2006; Volume 3, pp. 2529–2534. [Google Scholar] [CrossRef]
- Williams, B.M.; Hoel, L.A. Modeling and Forecasting Vehicular Traffic Flow as a Seasonal ARIMA Process: Theoretical Basis and Empirical Results. J. Transp. Eng. 2003, 129, 664–672. [Google Scholar] [CrossRef]
- Van Der Voort, M.; Dougherty, M.; Watson, S. Combining kohonen maps with arima time series models to forecast traffic flow. Transp. Res. Part C Emerg. Technol. 1996, 4, 307–318. [Google Scholar] [CrossRef]
- Lu, J.; Cao, L. Congestion evaluation from traffic flow information based on fuzzy logic. In Proceedings of the 2003 IEEE International Conference on Intelligent Transportation Systems, Shanghai, China, 12–15 October 2003; pp. 50–53. [Google Scholar] [CrossRef]
- Krause, B.; von Altrock, C.; Pozybill, M. Intelligent highway by fuzzy logic: Congestion detection and traffic control on multi-lane roads with variable road signs. In Proceedings of the IEEE 5th International Fuzzy Systems, New Orleans, LA, USA, 11 September 1996; Volume 3, pp. 1832–1837. [Google Scholar]
- Guo, J.; Huang, W.; Williams, B.M. Adaptive Kalman filter approach for stochastic short-term traffic flow rate prediction and uncertainty quantification. Transp. Res. Part C Emerg. Technol. 2014, 43, 50–64. [Google Scholar] [CrossRef]
- Lu, C.C.; Zhou, X.S. Short-Term Highway Traffic State Prediction Using Structural State Space Models. J. Intell. Transp. Syst. 2014, 18, 309–322. [Google Scholar] [CrossRef]
- Ghosh, B.; Basu, B.; O’Mahony, M. Bayesian Time-Series Model for Short-Term Traffic Flow Forecasting. J. Transp. Eng.—ASCE 2007, 133, 180–189. [Google Scholar] [CrossRef]
- Yang, X.; Zou, Y.; Tang, J.; Liang, J.; Ijaz, M. Evaluation of Short-Term Freeway Speed Prediction Based on Periodic Analysis Using Statistical Models and Machine Learning Models. J. Adv. Transp. 2020, 2020, 9628957. [Google Scholar] [CrossRef]
- Kohzadi, N.; Boyd, M.S.; Kermanshahi, B.; Kaastra, I. A comparison of artificial neural network and time series models for forecasting commodity prices. Neurocomputing 1996, 10, 169–181. [Google Scholar] [CrossRef]
- Kontopoulou, V.I.; Panagopoulos, A.D.; Kakkos, I.; Matsopoulos, G.K. A Review of ARIMA vs. Machine Learning Approaches for Time Series Forecasting in Data Driven Networks. Future Internet 2023, 15, 255. [Google Scholar] [CrossRef]
- Menculini, L.; Marini, A.; Proietti, M.; Garinei, A.; Bozza, A.; Moretti, C.; Marconi, M. Comparing Prophet and Deep Learning to ARIMA in Forecasting Wholesale Food Prices. Forecasting 2021, 3, 644–662. [Google Scholar] [CrossRef]
- Shaygan, M.; Meese, C.; Li, W.; Zhao, X.G.; Nejad, M. Traffic prediction using artificial intelligence: Review of recent advances and emerging opportunities. Transp. Res. Part C Emerg. Technol. 2022, 145, 103921. [Google Scholar] [CrossRef]
- Medina-Salgado, B.; Sánchez-DelaCruz, E.; Pozos-Parra, P.; Sierra, J.E. Urban traffic flow prediction techniques: A review. Sustain. Comput. Inform. Syst. 2022, 35, 100739. [Google Scholar] [CrossRef]
- Zheng, W.; Lee, D.H.; Shi, Q. Short-Term Freeway Traffic Flow Prediction: Bayesian Combined Neural Network Approach. J. Transp. Eng. 2006, 132, 114–121. [Google Scholar] [CrossRef]
- Tang, J.; Wang, H.; Wang, Y.; Liu, X.C.; Liu, F. Hybrid Prediction Approach Based on Weekly Similarities of Traffic Flow for Different Temporal Scales. Transp. Res. Rec. J. Transp. Res. Board 2014, 2443, 21–31. [Google Scholar] [CrossRef]
- Norwegian Public Roads Administration, Trafikkdata. Available online: https://trafikkdata.atlas.vegvesen.no (accessed on 1 September 2023).
- Weather Data & Weather API-Visual Crossing. Available online: https://www.visualcrossing.com/ (accessed on 1 September 2023).
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene Selection for Cancer Classification Using Support Vector Machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Ferri, F.; Pudil, P.; Hatef, M.; Kittler, J. Comparative study of techniques for large-scale feature selection. In Machine Intelligence and Pattern Recognition; North-Holland: Amsterdam, The Netherlands, 1994; Volume 16, pp. 403–413. [Google Scholar]
- Shafiee, S.; Lied, L.M.; Burud, I.; Dieseth, J.A.; Alsheikh, M.; Lillemo, M. Sequential forward selection and support vector regression in comparison to LASSO regression for spring wheat yield prediction based on UAV imagery. Comput. Electron. Agric. 2021, 183, 106036. [Google Scholar] [CrossRef]
- Murtagh, F. Multilayer perceptrons for classification and regression. Neurocomputing 1991, 2, 183–197. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2005, 67, 301–320. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Bayesian interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Seber, G.A.F.; Lee, A.J. Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Huber, P.J. Robust estimation of a location parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Cheng, H.; Tan, P.N.; Gao, J.; Scripps, J. Multistep-Ahead Time Series Prediction. In Advances in Knowledge Discovery and Data Mining; Ng, W.K., Kitsuregawa, M., Li, J., Chang, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 765–774. [Google Scholar] [CrossRef]
- Manibardo, E.L.; Laña, I.; Del Ser, J. Transfer Learning and Online Learning for Traffic Forecasting under Different Data Availability Conditions: Alternatives and Pitfalls. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, Y.; Shone, F.; Li, Z.; Frangi, A.F.; Xie, S.Q.; Zhang, Z.Q. Physics-Informed Deep Learning for Musculoskeletal Modeling: Predicting Muscle Forces and Joint Kinematics From Surface EMG. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 484–493. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, Y.; Bao, T.; Li, Z.; Qian, K.; Frangi, A.F.; Xie, S.; Zhang, Z.L. Boosting Personalized Musculoskeletal Modeling with Physics-Informed Knowledge Transfer. IEEE Trans. Instrum. Meas. 2022, 72, 1–11. [Google Scholar]
- Pan, C.; Wang, Y.; Shi, H.; Shi, J.; Cai, R. Network Traffic Prediction Incorporating Prior Knowledge for an Intelligent Network. Sensors 2022, 22, 2674. [Google Scholar] [CrossRef]


| Feature | Description | Unit | Selected |
|---|---|---|---|
| temp | Ambient temperature | °C | ✓ |
| feelslike | Human perceived temperature | °C | ✓ |
| dew | Dew point | °C | |
| humidity | Relative humidity | % | ✓ |
| precip | Precipitation | mm | ✓ |
| precipprob | Precipitation chance | % | |
| snowdepth | Depth of snow | % | ✓ |
| winddir | Direction of winds | degrees | |
| windspeed | Speed of wind | kph | ✓ |
| sealevelpressure | Sea level pressure | mb | ✓ |
| cloudcover | Cloud coverage | % | |
| visibility | Visibility | km | ✓ |
| solarradiation | Solar radiation | W/m2 | ✓ |
| solarenergy | Solar energy | MJ/m2 | |
| UVindex | Intensity of ultraviolet radiation | - |
| Feature | Description |
|---|---|
| quarter | Corresponding to the 3 month quarter |
| month | Corresponding to the month of the year |
| hour24 | Corresponding to the hour of the day |
| Week_day | Corresponding to the day of the week |
| is_weekend | Corresponding to Saturday, Sunday |
| off_hours | Distinguishing off-peak hours (i.e., after 17:00) |
| working_hours | Distinguishing peak hours (i.e., 8:00–17:00) |
| 00 to 03, 03 to 06, …21 to 00 | Distinguishing 3 h time intervals within the day |
| Parameter | LSTM | biLSTM | GRU |
|---|---|---|---|
| Hidden layers | 1 | 1 | 1 |
| Units (in each hidden layer) | 24 | 24 | 24 |
| Activ. function | ReLU | ReLU | ReLU |
| Batch size | 16 | 16 | 16 |
| Epochs | 35 | 35 | 35 |
| Optimizer | adam | adam | adam |
| Dropout | 0.2 | 0.2 | 0.2 |
| SW length | 24 | 24 | 24 |
| Loss function | MAE | MAE | MAE |
| Early stopping (consecutive epochs) | 10 | 10 | 10 |
| Location 1 | Location 2 | Location 3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | MAE | RMSE | (%) | CV-RMSE | MAE | RMSE | (%) | CV-RMSE | MAE | RMSE | (%) | CV-RMSE |
| ET | 107.89 | 190.68 | 98.16 | 0.105 | 64.74 | 115.00 | 97.64 | 0.130 | 24.69 | 39.45 | 94.76 | 0.134 |
| LBGM | 115.54 | 208.42 | 97.80 | 0.114 | 71.24 | 124.20 | 97.25 | 0.140 | 26.27 | 42.56 | 94.95 | 0.145 |
| HGBR | 117.76 | 211.43 | 97.74 | 0.116 | 70.18 | 122.59 | 97.32 | 0.138 | 26.26 | 42.29 | 94.79 | 0.144 |
| GBDT | 139.99 | 232.83 | 97.26 | 0.128 | 82.03 | 133.99 | 96.80 | 0.151 | 29.43 | 44.66 | 93.90 | 0.152 |
| XGB | 125.65 | 227.31 | 97.39 | 0.125 | 75.95 | 131.66 | 96.91 | 0.148 | 27.06 | 43.56 | 94.54 | 0.148 |
| RF | 112.54 | 208.25 | 97.81 | 0.114 | 68.47 | 123.64 | 97.27 | 0.139 | 25.28 | 41.38 | 94.69 | 0.141 |
| BR | 119.92 | 218.60 | 97.58 | 0.120 | 73.56 | 129.42 | 97.01 | 0.146 | 26.79 | 43.53 | 94.41 | 0.148 |
| LSTM | 210.01 | 354.80 | 93.66 | 0.194 | 184.56 | 315.08 | 92.58 | 0.212 | 38.11 | 62.75 | 93.20 | 0.203 |
| biLSTM | 227.91 | 356.84 | 93.59 | 0.195 | 196.22 | 314.99 | 92.59 | 0.212 | 38.99 | 60.25 | 93.73 | 0.195 |
| GRU | 234.79 | 381.81 | 92.66 | 0.208 | 172.40 | 296.89 | 93.41 | 0.200 | 39.68 | 64.99 | 92.71 | 0.210 |
| Location 4 | Location 5 | Location 6 | ||||||||||
| ET | 11.89 | 19.92 | 95.12 | 0.191 | 34.44 | 56.59 | 97.31 | 0.131 | 68.71 | 101.57 | 96.22 | 0.138 |
| LBGM | 12.39 | 20.24 | 94.96 | 0.194 | 37.51 | 59.43 | 97.04 | 0.137 | 66.75 | 102.95 | 96.12 | 0.140 |
| HGBR | 12.45 | 20.72 | 94.72 | 0.198 | 37.34 | 37.34 | 97.04 | 0.137 | 66.11 | 100.59 | 96.3 | 0.137 |
| GBDT | 13.22 | 21.63 | 94.25 | 0.207 | 40.77 | 63.26 | 96.64 | 0.146 | 79.94 | 114.45 | 95.2 | 0.156 |
| XGB | 13.13 | 21.25 | 94.45 | 0.204 | 38.03 | 59.97 | 96.98 | 0.139 | 66.91 | 100.09 | 96.33 | 0.136 |
| RF | 12.57 | 21.55 | 94.29 | 0.206 | 34.52 | 57.40 | 97.24 | 0.133 | 69.12 | 106.73 | 95.83 | 0.145 |
| BR | 13.60 | 23.09 | 93.44 | 0.221 | 37.50 | 61.33 | 96.84 | 0.142 | 75.03 | 115.20 | 95.14 | 0.157 |
| LSTM | 17.19 | 29.09 | 93.97 | 0.193 | 57.91 | 89.57 | 93.62 | 0.197 | 81.98 | 134.86 | 92.68 | 0.205 |
| biLSTM | 18.87 | 31.81 | 92.80 | 0.211 | 49.98 | 81.29 | 94.74 | 0.179 | 69.75 | 108.54 | 95.26 | 0.165 |
| GRU | 16.50 | 28.61 | 94.17 | 0.190 | 54.59 | 85.85 | 94.14 | 0.189 | 71.87 | 119.71 | 94.23 | 0.182 |
| RF | ET | HGBR | LGBM | XGB | GBDT | BR | |
|---|---|---|---|---|---|---|---|
| First 4 Steps | |||||||
| Location 1 | 4 | 4 | 4 | 3 | 3 | 2 | 0 |
| Location 2 | 4 | 4 | 4 | 4 | 3 | 1 | 0 |
| Location 3 | 4 | 4 | 4 | 4 | 3 | 1 | 0 |
| Location 4 | 3 | 4 | 4 | 4 | 3 | 0 | 2 |
| Location 5 | 4 | 4 | 4 | 4 | 2 | 0 | 2 |
| Location 6 | 4 | 4 | 4 | 4 | 4 | 0 | 0 |
| All 24 Steps | |||||||
| Location 1 | 24 | 23 | 22 | 21 | 17 | 8 | 5 |
| Location 2 | 22 | 24 | 24 | 24 | 20 | 5 | 1 |
| Location 3 | 24 | 12 | 24 | 24 | 15 | 8 | 13 |
| Location 4 | 19 | 24 | 24 | 24 | 16 | 12 | 1 |
| Location 5 | 19 | 24 | 24 | 24 | 13 | 10 | 6 |
| Location 6 | 24 | 19 | 23 | 23 | 22 | 0 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsalikidis, N.; Mystakidis, A.; Koukaras, P.; Ivaškevičius, M.; Morkūnaitė, L.; Ioannidis, D.; Fokaides, P.A.; Tjortjis, C.; Tzovaras, D. Urban Traffic Congestion Prediction: A Multi-Step Approach Utilizing Sensor Data and Weather Information. Smart Cities 2024, 7, 233-253. https://doi.org/10.3390/smartcities7010010
Tsalikidis N, Mystakidis A, Koukaras P, Ivaškevičius M, Morkūnaitė L, Ioannidis D, Fokaides PA, Tjortjis C, Tzovaras D. Urban Traffic Congestion Prediction: A Multi-Step Approach Utilizing Sensor Data and Weather Information. Smart Cities. 2024; 7(1):233-253. https://doi.org/10.3390/smartcities7010010
Chicago/Turabian StyleTsalikidis, Nikolaos, Aristeidis Mystakidis, Paraskevas Koukaras, Marius Ivaškevičius, Lina Morkūnaitė, Dimosthenis Ioannidis, Paris A. Fokaides, Christos Tjortjis, and Dimitrios Tzovaras. 2024. "Urban Traffic Congestion Prediction: A Multi-Step Approach Utilizing Sensor Data and Weather Information" Smart Cities 7, no. 1: 233-253. https://doi.org/10.3390/smartcities7010010
APA StyleTsalikidis, N., Mystakidis, A., Koukaras, P., Ivaškevičius, M., Morkūnaitė, L., Ioannidis, D., Fokaides, P. A., Tjortjis, C., & Tzovaras, D. (2024). Urban Traffic Congestion Prediction: A Multi-Step Approach Utilizing Sensor Data and Weather Information. Smart Cities, 7(1), 233-253. https://doi.org/10.3390/smartcities7010010









